Analysis of the scalar doubly charmed hexaquark state with QCD sum rules

Abstract

In this article, we study the scalar-diquark–scalar-diquark–scalar-diquark type hexaquark state with the QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension 16. We obtain a lowest hexaquark mass of $6.60^{+0.12}_{-0.09}\,\mathrm {GeV}$, which can be confronted with the experimental data in the future.

1 Introduction

In the past years, a number of new charmonium-like states have been observed; some are excellent candidates for the exotic states, such as tetraquark states and molecular states, and the spectroscopy of the charmonium-like states has attracted much attention [1]. The QCD sum rules play an important role in assigning those new charmonium-like states [2,3,4,5,6,7,8,9,10,11,12].

The scattering amplitude for one-gluon exchange is proportional to

$$\begin{aligned} t^a_{ij}t^a_{kl} = -\frac{1}{3}\left( \delta _{ij}\delta _{kl}-\delta _{il}\delta _{kj}\right) +\frac{1}{6}\left( \delta _{ij}\delta _{kl}+\delta _{il}\delta _{kj}\right) , \end{aligned}$$

(1)

where the $t^a$ are the generators of the $SU_c(3)$ gauge group. The negative sign in front of the antisymmetric antitriplet indicates the interaction is attractive, while the positive sign in front of the symmetric sextet indicates the interaction is repulsive. The attractive interaction of one-gluon exchange favors formation of the diquarks in color antitriplet $\overline{3}_{ c}$, flavor antitriplet $\overline{3}_{ f}$ and spin singlet $1_s$ or flavor sextet $6_{ f}$ and spin triplet $3_s$ [13, 14]. The color antitriplet diquarks $\varepsilon ^{ijk} q^{T}_j C\Gamma q^{\prime }_k$ have five structures in Dirac spinor space, where $C\Gamma =C\gamma _5$, C, $C\gamma _\mu \gamma _5$, $C\gamma _\mu$ and $C\sigma _{\mu \nu }$ for the scalar, pseudoscalar, vector, axialvector and tensor diquarks, respectively. The calculations based on the QCD sum rules indicate that the favored configurations are the $C\gamma _5$ and $C\gamma _\mu$ diquark states [15,16,17], while the heavy–light $C\gamma _5$ and $C\gamma _\mu$ diquark states have almost degenerate masses [15, 16]. We can construct the lowest tetraquark states by the $C\gamma _5$ and $C\gamma _\mu$ diquark states and antidiquark states, for example, the $Z_c(3900)$ can be tentatively assigned to the ground state $C\gamma _5\otimes \gamma _\mu C-C\gamma _\mu \otimes \gamma _5 C$ type tetraquark state [11]. The diquark–antidiquark type tetraquark states have been studied extensively with the QCD sum rules.

In the QCD sum rules for the four-quark states, the largest power of the QCD spectral densities $\rho (s)\propto s^4$, the integral $\int _{4m_c^2}^\infty \mathrm{d}s \rho (s) \exp \big ( -\frac{s}{T^2}\big )$ converges slowly, the pole dominance condition is difficult to satisfy, where the $T^2$ is the Borel parameter. In previous work, we study the energy-scale dependence of the QCD sum rules for the hidden-charm and hidden-bottom tetraquark states and molecular states for the first time, and we suggest a formula,

$$\begin{aligned} \mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}, \end{aligned}$$

(2)

with the effective mass ${\mathbb {M}}_Q$ to determine the energy scales of the QCD spectral densities [11, 12, 18,19,20], where the X, Y, Z denote the tetraquark states and molecular states. The formula enhances the pole contributions considerably.

In this article, we extend our previous work to the study of the scalar hexaquark state uuddcc with the QCD sum rules in detail. We construct the scalar-diquark–scalar-diquark–scalar-diquark type current, which is supposed to couple potentially to the lowest hexaquark state. In the QCD sum rules for the six-quark states, the largest power of the QCD spectral densities $\rho (s)\propto s^7$, the pole dominance condition is more difficult to satisfy compared to the QCD sum rules for the four-quark states. We use the energy-scale formula to enhance the pole contributions.

The article is arranged as follows: we derive the QCD sum rules for the mass and pole residue of the scalar doubly charmed hexaquark state. in Sect. 2; in Sect. 3, we present the numerical results and discussions; and Sect. 4 is reserved for our conclusion.

2 The QCD sum rules for the scalar doubly charmed hexaquark state

In the following, we write down the two-point correlation function $\Pi (p)$ in the QCD sum rules,

$$\begin{aligned} \Pi (p)=i\int d^4x e^{ip \cdot x} \langle 0|T\left\{ J(x) J^{\dagger }(0)\right\} |0\rangle , \end{aligned}$$

(3)

where

$$\begin{aligned} J(x)= & {} \varepsilon ^{abc}\varepsilon ^{aij}\varepsilon ^{bkl}\varepsilon ^{cmn}\, u^{T}_i(x)C\gamma _5d_j(x) \,u^{T}_k(x)C\gamma _5 c_l(x) \nonumber \\&\times \,d^{T}_m(x)C\gamma _5 c_n(x), \end{aligned}$$

(4)

the a, b, c, i, j, k, l, m, n are color indices, the C is the charge conjugation matrix. We construct the scalar-diquark–scalar-diquark–scalar-diquark type current J(x) to interpolate the lowest hexaquark state $Z_{cc}^{++}$.

At the phenomenological side, we insert a complete set of intermediate hadronic states with the same quantum numbers as the current operator J(x) into the correlation function $\Pi (p)$ to obtain the hadronic representation [21,22,23], and isolate the ground state contribution,

$$\begin{aligned} \Pi (p)=\frac{\lambda _{Z}^2}{M^2_{Z}-p^2} +\cdots , \end{aligned}$$

(5)

where the pole residue $\lambda _{Z}$ is defined by $\langle 0|J(0)|Z_{cc}^{++}(p)\rangle =\lambda _{Z}$.

In the following, we briefly outline the operator product expansion for the correlation function $\Pi (p)$ in perturbative QCD. We contract the u, d and c quark fields in the correlation function $\Pi (p)$ with the Wick theorem, and we obtain the result

$$\begin{aligned} \Pi (p)= & {} -i\varepsilon ^{abc}\varepsilon ^{aij}\varepsilon ^{bkl}\varepsilon ^{cmn}\varepsilon ^{a^\prime b^\prime c^\prime }\varepsilon ^{a^\prime i^\prime j^\prime }\varepsilon ^{b^\prime k^\prime l^\prime }\varepsilon ^{c^\prime m^\prime n^\prime } \nonumber \\&\times \,\int d^4x e^{ip \cdot x} \bigg \{\mathrm{Tr}\bigg [ \gamma _{5}D_{jj^{\prime }}(x)\gamma _{5} CU^T_{ii^{\prime }}(x)C\bigg ] \mathrm{Tr} \nonumber \\&\times \;\bigg [\gamma _{5}C_{ll^{\prime }}(x)\gamma _{5} CU^T_{kk^{\prime }}(x)C\bigg ]\nonumber \\&\times \;\mathrm{Tr}\bigg [ \gamma _{5}C_{nn^{\prime }}(x)\gamma _{5} CD^T_{mm^{\prime }}(x)C\bigg ] \nonumber \\&-\mathrm{Tr}\bigg [ \gamma _{5}C_{ll^{\prime }}(x)\gamma _{5} CU^T_{ik^{\prime }}(x)C \gamma _5 D_{jj^\prime }(x)\gamma _5C U^T_{ki^\prime }(x)C\bigg ] \nonumber \\&\times \;\mathrm{Tr}\bigg [ \gamma _{5}C_{nn^{\prime }}(x)\gamma _{5} CD^T_{mm^{\prime }}(x)C\bigg ] \nonumber \\&-\mathrm{Tr}\bigg [ \gamma _{5}C_{ll^{\prime }}(x)\gamma _{5} CU^T_{kk^{\prime }}(x)C\bigg ]\nonumber \\&\times \;\mathrm{Tr}\bigg [ \gamma _{5}C D^T_{mj^{\prime }}(x)C \gamma _{5} C_{nn^{\prime }}(x) \gamma _5 C D^T_{jm^\prime }(x)C\gamma _5U_{ii^\prime }(x)\bigg ] \nonumber \\&-\mathrm{Tr}\bigg [ \gamma _{5}D_{jj^{\prime }}(x)\gamma _{5} CU^T_{ii^{\prime }}(x)C\bigg ]\nonumber \\&\times \;\mathrm{Tr}\bigg [ \gamma _{5} C_{ln^{\prime }}(x) \gamma _{5} C D^T_{mm^{\prime }}(x)C \gamma _5 C_{nl^\prime }(x) \gamma _5CU^T_{kk^\prime }(x)C \bigg ] \nonumber \\&+\mathrm{Tr}\bigg [ \gamma _{5}C C^T_{ll^{\prime }}(x)C\gamma _{5} U_{ki^{\prime }}(x) \gamma _{5}C D^T_{mj^{\prime }}(x)C \gamma _{5} C_{nn^{\prime }} \nonumber \\&\times \;(x) \gamma _5 C D^T_{jm^\prime }(x)C\gamma _5U_{ik^\prime }(x)\bigg ] \nonumber \\&+\;\mathrm{Tr}\bigg [ \gamma _{5} C_{ln^{\prime }}(x)\gamma _{5} CD^T_{mm^{\prime }}(x)C \gamma _{5} C_{nl^{\prime }}(x) \gamma _{5} C U^T_{ik^{\prime }} \nonumber \\&\times \;(x)C \gamma _5 D_{jj^\prime }(x)\gamma _5CU^T_{ki^\prime }(x)C\bigg ] \nonumber \\&+\;\mathrm{Tr}\bigg [ \gamma _{5} C_{ln^{\prime }}(x)\gamma _{5} CD^T_{jm^{\prime }}(x)C \gamma _{5} U_{ii^{\prime }}(x) \gamma _{5} C D^T_{mj^{\prime }}\nonumber \\&\times \;(x)C \gamma _5 C_{nl^\prime }(x)\gamma _5CU^T_{kk^\prime }(x)C\bigg ] \nonumber \\&+\;\mathrm{Tr}\bigg [ \gamma _{5} C_{ln^{\prime }}(x)\gamma _{5} CD^T_{jm^{\prime }}(x)C \gamma _{5} U_{ik^{\prime }}(x) \gamma _{5} C C^T_{nl^{\prime }}\nonumber \\&\times \;(x)C \gamma _5 D_{mj^\prime }(x)\gamma _5CU^T_{ki^\prime }(x)C\bigg ] \bigg \}\, , \end{aligned}$$

(6)

Fig. 1

The diagrams contribute to the mixed condensate $\langle \bar{q}g_s\sigma Gq\rangle$ from the terms $\langle \bar{q}_j\sigma _{\mu \nu }q_i \rangle$. Other diagrams, obtained by interchanging of the heavy quark lines (dashed lines) or light quark lines (solid lines), are implied

Fig. 2

The diagrams contribute to the squared mixed condensate $\langle \bar{q}g_s\sigma Gq\rangle ^2$ from the terms $\langle \bar{q}_j\sigma _{\mu \nu }q_i \rangle$. Other diagrams, obtained by interchanging of the heavy quark lines (dashed lines) or light quark lines (solid lines), are implied

where the $U_{ij}(x)$, $D_{ij}(x)$ and $C_{ij}(x)$ are the full u, d and c quark propagators, respectively [23, 24], the $U_{ij}(x)$ and $D_{ij}(x)$ can be written as $S_{ij}(x)$,

$$\begin{aligned} S_{ij}(x)= & {} \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4} -\frac{\delta _{ij}\langle \bar{q}q\rangle }{12} -\frac{\delta _{ij}x^2\langle \bar{q}g_s\sigma Gq\rangle }{192} \nonumber \\&-\;\frac{ig_s G^{a}_{\alpha \beta }t^a_{ij}(\!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x})}{32\pi ^2x^2} \nonumber \\&-\;\frac{1}{8}\langle \bar{q}_j\sigma ^{\mu \nu }q_i \rangle \sigma _{\mu \nu } +\cdots , \end{aligned}$$

(7)

$$\begin{aligned} C_{ij}(x)= & {} \frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x} \nonumber \\&\times \;\left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_c} -\frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_c)+(\!\not \!{k}+m_c) \sigma ^{\alpha \beta }}{(k^2-m_c^2)^2}\right. \nonumber \\&\left. -\frac{g_s^2 (t^at^b)_{ij} G^a_{\alpha \beta }G^b_{\mu \nu }(f^{\alpha \beta \mu \nu }+f^{\alpha \mu \beta \nu }+f^{\alpha \mu \nu \beta }) }{4(k^2-m_c^2)^5}+\cdots \right\} , \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} f^{\lambda \alpha \beta }= & {} (\!\not \!{k}+m_c)\gamma ^\lambda (\!\not \!{k}+m_c)\gamma ^\alpha (\!\not \!{k}+m_c)\gamma ^\beta (\!\not \!{k}+m_c), \nonumber \\ f^{\alpha \beta \mu \nu }= & {} (\!\not \!{k}+m_c)\gamma ^\alpha (\!\not \!{k}+m_c)\gamma ^\beta (\!\not \!{k}+m_c)\gamma ^\mu (\!\not \!{k}+m_c)\gamma ^\nu (\!\not \!{k}+m_c), \nonumber \\ \end{aligned}$$

(9)

and $t^n=\frac{\lambda ^n}{2}$; the $\lambda ^n$ are the Gell-Mann matrix [23]. Then we compute the integrals both in coordinate space and in momentum space, and we obtain the correlation function $\Pi (p)$ at the quark level, therefore the QCD spectral density through dispersion relation. In Eq. (7), we retain the term $\langle \bar{q}_j\sigma _{\mu \nu }q_i \rangle$ originates from the Fierz rearrangement of the $\langle q_i \bar{q}_j\rangle$ to absorb the gluons emitted from other quark lines to form $\langle \bar{q}_j g_s G^a_{\alpha \beta } t^a_{mn}\sigma _{\mu \nu } q_i \rangle$ so as to extract the mixed condensate $\langle \bar{q}g_s\sigma G q\rangle$ and squared mixed condensate $\langle \bar{q}g_s\sigma G q\rangle ^2$, which play an important role in determining the Borel window; see the typical Feynman diagrams shown in Figs. 1 and 2. It is straightforward but very difficult to calculate those diagrams.

In this article, we carry out the operator product expansion to the vacuum condensates up to dimension-16, and we take into account the vacuum condensates which are vacuum expectations of the operators of the orders $\mathcal {O}( \alpha _s^{k})$ with $k\le 1$ consistently. The condensates $\langle g_s^3 GGG\rangle$, $\langle \frac{\alpha _s GG}{\pi }\rangle ^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle \langle \bar{q} g_s \sigma Gq\rangle$ have the dimensions 6, 8, 9, respectively, but they are the vacuum expectations of the operators of the order $\mathcal {O}( \alpha _s^{3/2})$, $\mathcal {O}(\alpha _s^2)$, $\mathcal {O}( \alpha _s^{3/2})$, respectively, and are discarded. Furthermore, the condensates $\langle \bar{q}q\rangle \langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle \bar{q}q\rangle ^2\langle \frac{\alpha _s}{\pi }GG\rangle$, $\langle \bar{q}q\rangle ^3\langle \frac{\alpha _s}{\pi }GG\rangle$ have dimensions 7, 10, 13, respectively, and they are the vacuum expectations of the operators of the order $\mathcal {O}( \alpha _s)$; however, they play a minor role and are neglected [11, 12, 18,19,20].

Once the QCD spectral density is obtained, we can take the quark–hadron duality and perform a Borel transform with respect to the variable $P^2=-p^2$ to obtain the following QCD sum rule:

$$\begin{aligned} \lambda ^2_{Z}\, \exp \left( -\frac{M^2_{Z}}{T^2}\right) = \int _{4m_c^2}^{s_0} \mathrm{d}s\, \rho (s) \, \exp \left( -\frac{s}{T^2}\right) , \end{aligned}$$

(10)

where

$$\begin{aligned} \rho (s)= & {} \rho _{0}(s)+\rho _{3}(s)+\rho _{4}(s)+\rho _{5}(s)+\rho _{6}(s)+\rho _{8}(s) \nonumber \\&+\;\rho _{9}(s)+\rho _{10}(s)+\rho _{11}(s)+\rho _{12}(s)\nonumber \\&+\;\rho _{13}(s)+\rho _{14}(s)+\rho _{16}(s), \end{aligned}$$

(11)

$$\begin{aligned} \rho _0(s)&=\frac{1}{183500800\pi ^{10}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\,yz(1-y-z)^5 \nonumber \\&\times \;\left( s-\overline{m}_c^2\right) ^6\left( 9s-2\overline{m}_c^2\right) +\frac{m_c^2}{235929600\pi ^{10}} \nonumber \\&\times \;\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\,(1-y-z)^5\left( s-\overline{m}_c^2\right) ^6, \end{aligned}$$

(12)

$$\begin{aligned} \rho _3(s)= & {} \frac{m_c\langle \bar{q}q\rangle }{491520\pi ^{8}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\,(y+z)(1-y-z)^4 \nonumber \\&\times \;\left( s-\overline{m}_c^2\right) ^4\left( 7s-2\overline{m}_c^2\right) , \end{aligned}$$

(13)

$$\begin{aligned} \rho _4(s)= & {} -\frac{m_c^2}{7864320\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\left( \frac{z}{y^2}+\frac{y}{z^2} \right) (1-y-z)^5\left( s-\overline{m}_c^2\right) ^3\left( 3s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{m_c^4}{35389440\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\left( \frac{1}{y^3}+\frac{1}{z^3} \right) (1-y-z)^5\left( s-\overline{m}_c^2\right) ^3 \nonumber \\&+\;\frac{m_c^2}{47185920\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\left( \frac{1}{y^2}+\frac{1}{z^2} \right) (1-y-z)^5\left( s-\overline{m}_c^2\right) ^4 \nonumber \\&-\;\frac{1}{251658240\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(1-y-z)^5\left( s-\overline{m}_c^2\right) ^4\left( 7s-2\overline{m}_c^2\right) \nonumber \\&+\;\frac{29}{251658240\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(y+z)(1-y-z)^4\left( s-\overline{m}_c^2\right) ^4\left( 7s-2\overline{m}_c^2\right) \nonumber \\&+\;\frac{19}{62914560\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z yz\nonumber \\&\times \;(1-y-z)^3\left( s-\overline{m}_c^2\right) ^4\left( 7s-2\overline{m}_c^2\right) \nonumber \\&-\;\frac{m_c^2}{188743680\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\frac{(1-y-z)^5}{yz}\left( s-\overline{m}_c^2\right) ^4 \nonumber \\&+\;\frac{11}{150994944\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\overline{m}_c^2 \, (1-y-z)^4\left( s-\overline{m}_c^2\right) ^4 \nonumber \\&+\;\frac{17m_c^2}{37748736\pi ^{8}}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(1-y-z)^3\left( s-\overline{m}_c^2\right) ^4, \end{aligned}$$

(14)

$$\begin{aligned} \rho _5(s)= & {} - \frac{91m_c\langle \bar{q}g_s\sigma Gq\rangle }{4718592\pi ^{8}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(y+z)(1-y-z)^3\left( s-\overline{m}_c^2\right) ^3\left( 3s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{11m_c\langle \bar{q}g_s\sigma Gq\rangle }{18874368\pi ^{8}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(1-y-z)^4\left( s-\overline{m}_c^2\right) ^3\left( 3s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{13m_c\langle \bar{q}g_s\sigma Gq\rangle }{3145728\pi ^{8}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\left( \frac{z}{y}+\frac{y}{z} \right) (1-y-z)^4\left( s-\overline{m}_c^2\right) ^3\left( 3s-\overline{m}_c^2\right) ,\nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned} \rho _6(s)= & {} \frac{7\langle \bar{q}q\rangle ^2}{18432\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\,yz \nonumber \\&\times \;(1-y-z)^2\left( s-\overline{m}_c^2\right) ^3\left( 3s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{7m_c^2\langle \bar{q}q\rangle ^2}{9216\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(1-y-z)^2\left( s-\overline{m}_c^2\right) ^3, \end{aligned}$$

(16)

$$\begin{aligned} \rho _8(s)= & {} -\frac{119\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{147456\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\,yz \nonumber \\&\times \;(1-y-z)\left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) \nonumber \\&-\;\frac{119m_c^2\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{49152\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(1-y-z)\left( s-\overline{m}_c^2\right) ^2 \nonumber \\&+\;\frac{19\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{393216\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(y+z)(1-y-z)^2\left( s-\overline{m}_c^2\right) ^2\left( 5s-2\overline{m}_c^2\right) \nonumber \\&+\;\frac{107\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{196608\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\overline{m}_c^2\,(1-y-z)^2\left( s-\overline{m}_c^2\right) ^2, \end{aligned}$$

(17)

$$\begin{aligned} \rho _{9}(s)= & {} \frac{m_c\langle \bar{q}q\rangle ^3 }{96\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;(y+z)(1-y-z)\left( s-\overline{m}_c^2\right) \left( 2s-\overline{m}_c^2\right) , \end{aligned}$$

(18)

$$\begin{aligned} \rho _{10}(s)= & {} \frac{ 253\langle \bar{q}g_s\sigma Gq\rangle ^2 }{393216\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\, yz \nonumber \\&\times \; \left( s-\overline{m}_c^2\right) \left( 2s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{ 253m_c^2\langle \bar{q}g_s\sigma Gq\rangle ^2 }{393216\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\left( s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{161 \langle \bar{q}g_s\sigma Gq\rangle ^2 }{1048576\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\,(y+z) \nonumber \\&\times \; (1-y-z)\left( s-\overline{m}_c^2\right) \left( 2s-\overline{m}_c^2\right) \nonumber \\&-\;\frac{2713 \langle \bar{q}g_s\sigma Gq\rangle ^2 }{4718592\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \;\overline{m}_c^2\,(1-y-z) \left( s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{7 m_c^2\langle \bar{q}g_s\sigma Gq\rangle ^2}{32768\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \; \frac{(1-y-z)^2}{yz} \left( s-\overline{m}_c^2\right) \nonumber \\&+\;\frac{329 \left\langle \bar{q}g_s\sigma Gq\right\rangle ^2 }{18874368\pi ^{6}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z \nonumber \\&\times \; (1-y-z)^2 \left( s-\overline{m}_c^2\right) \left( 2s-\overline{m}_c^2\right) , \end{aligned}$$

(19)

$$\begin{aligned} \rho _{11}(s)= & {} -\frac{ 283m_c \langle \bar{q}g_s\sigma Gq\rangle \langle \bar{q} q\rangle ^2 }{36864\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y \nonumber \\&\times \;\int _{z_i}^{1-y}\mathrm{d}z\,(y+z) \left( 3s-2\overline{m}_c^2\right) \nonumber \\&+\;\frac{ 29m_c \langle \bar{q}g_s\sigma Gq\rangle \langle \bar{q} q\rangle ^2 }{9216\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y \nonumber \\&\times \; \int _{z_i}^{1-y}\mathrm{d}z\left( \frac{z}{y}+\frac{y}{z} \right) (1-y-z) \left( 3s-2\overline{m}_c^2\right) \nonumber \\&+\;\frac{ 19m_c \langle \bar{q}g_s\sigma Gq\rangle \langle \bar{q} q\rangle ^2 }{12288\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y\nonumber \\&\times \;\int _{z_i}^{1-y}\mathrm{d}z\,(1-y-z) \left( 3s-2\overline{m}_c^2\right) , \end{aligned}$$

(20)

$$\begin{aligned} \rho _{12}(s)= & {} \frac{ \langle \bar{q} q\rangle ^4 }{864\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \,y(1-y) \nonumber \\&\times \;\left( 3s-2\widetilde{m}_c^2\right) +\frac{ m_c^2 \langle \bar{q} q\rangle ^4 }{96\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y, \end{aligned}$$

(21)

$$\begin{aligned} \rho _{13}(s)= & {} -\frac{ 355m_c \langle \bar{q}q\rangle \langle \bar{q}g_s\sigma G q\rangle ^2 }{110592\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y \nonumber \\&\times \;\int _{z_i}^{1-y}\mathrm{d}z\left( \frac{z}{y}+\frac{y}{z}\right) \left[ 1+\frac{s}{2} \,\delta \left( s-\overline{m}_c^2\right) \right] \nonumber \\&-\;\frac{ 313m_c \langle \bar{q}q\rangle \langle \bar{q}g_s\sigma G q\rangle ^2 }{196608\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y \int _{z_i}^{1-y}\mathrm{d}z\nonumber \\&\times \; \left[ 1+\frac{s}{2} \,\delta \left( s-\overline{m}_c^2\right) \right] \nonumber \\&+\;\frac{ 467m_c \langle \bar{q}q\rangle \langle \bar{q}g_s\sigma G q\rangle ^2 }{884736\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y\nonumber \\&\times \;\int _{z_i}^{1-y}\mathrm{d}z\left( \frac{1}{y}+\frac{1}{z}\right) (1-y-z) \left[ 1+\frac{s}{2} \,\delta \left( s-\overline{m}_c^2\right) \right] \nonumber \\&+\;\frac{139m_c \langle \bar{q}q\rangle \langle \bar{q}g_s\sigma G q\rangle ^2 }{36864\pi ^{4}}\int _{y_i}^{y_f}\mathrm{d}y \nonumber \\&\times \;\left[ 1+\frac{s}{2} \,\delta \left( s-\widetilde{m}_c^2\right) \right] , \end{aligned}$$

(22)

$$\begin{aligned} \rho _{14}(s)= & {} -\frac{ \langle \bar{q}q\rangle ^3 \langle \bar{q}g_s\sigma G q\rangle }{432\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \,y(1-y) \nonumber \\&\times \;\left[ 3+\left( \frac{13}{2}+\frac{5s}{T^2}\right) \,s\, \,\delta \left( s-\widetilde{m}_c^2\right) \right] \nonumber \\&+\;\frac{11 \langle \bar{q}q\rangle ^3 \langle \bar{q}g_s\sigma G q\rangle }{27648\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \nonumber \\&+\frac{185 \langle \bar{q}q\rangle ^3 \langle \bar{q}g_s\sigma G q\rangle }{55296\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \,s\,\delta \left( s-\widetilde{m}_c^2\right) ,\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned} \rho _{16}(s)= & {} \frac{ \langle \bar{q}q\rangle ^2 \langle \bar{q}g_s\sigma G q\rangle ^2 }{384\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \,y(1-y) \nonumber \\&\times \;\left( 1+\frac{s}{T^2}+\frac{s^2}{2T^4}+\frac{5s^3}{3T^6}\right) \,\delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{1255 \langle \bar{q}q\rangle ^2 \langle \bar{q}g_s\sigma G q\rangle ^2 }{5308416\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \,\delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&+\;\frac{151 \langle \bar{q}q\rangle ^2 \langle \bar{q}g_s\sigma G q\rangle ^2 }{196608\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \frac{s}{T^2} \,\delta \left( s-\widetilde{m}_c^2\right) \nonumber \\&-\;\frac{185 \langle \bar{q}q\rangle ^2 \langle \bar{q}g_s\sigma G q\rangle ^2 }{73728\pi ^{2}}\int _{y_i}^{y_f}\mathrm{d}y \frac{s^2}{T^4}\, \delta \left( s-\widetilde{m}_c^2\right) , \nonumber \\ \end{aligned}$$

(24)

$y_{f}=\frac{1+\sqrt{1-4m_c^2/s}}{2}$, $y_{i}=\frac{1-\sqrt{1-4m_c^2/s}}{2}$, $z_{i}=\frac{y m_c^2}{y s -m_c^2}$, $\overline{m}_c^2=\frac{(y+z)m_c^2}{yz}$, $\widetilde{m}_c^2=\frac{m_c^2}{y(1-y)}$, $\int _{y_i}^{y_f}\mathrm{d}y \rightarrow \int _{0}^{1}\mathrm{d}y$, $\int _{z_i}^{1-y}\mathrm{d}z \rightarrow \int _{0}^{1-y}\mathrm{d}z$ when the $\delta$ functions $\delta \left( s-\overline{m}_c^2\right)$ and $\delta \left( s-\widetilde{m}_c^2\right)$ appear, $s_0$ is the continuum threshold parameter.

We derive Eq. (10) with respect to $\tau =\frac{1}{T^2}$, then eliminate the pole residue $\lambda _{Z}$ to obtain the QCD sum rule for the mass,

$$\begin{aligned} M^2_{Z}= \frac{-\frac{d}{d \tau } \int _{4m_c^2}^{s_0} \mathrm{d}s\,\rho (s)\,e^{-\tau s}}{\int _{4m_c^2}^{s_0} \mathrm{d}s \,\rho (s)\,e^{-\tau s}}. \end{aligned}$$

(25)

3 Numerical results and discussions

We take the standard values of the vacuum condensates $\langle \bar{q}q \rangle =-(0.24\pm 0.01\, \mathrm {GeV})^3$, $\langle \bar{q}g_s\sigma G q \rangle =m_0^2\langle \bar{q}q \rangle$, $m_0^2=(0.8 \pm 0.1)\,\mathrm {GeV}^2$, $\langle \frac{\alpha _s GG}{\pi }\rangle =(0.33\,\mathrm {GeV})^4$ at the energy scale $\mu =1\, \mathrm {GeV}$ [21,22,23, 25], and we choose the $\overline{MS}$ mass $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$ from the Particle Data Group [1]. Moreover, we take into account the energy-scale dependence of the input parameters,

$$\begin{aligned} \langle \bar{q}q \rangle (\mu )= & {} \langle \bar{q}q \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{4}{9}}, \nonumber \\ \langle \bar{q}g_s \sigma Gq \rangle (\mu )= & {} \langle \bar{q}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{27}}, \nonumber \\ m_c(\mu )= & {} m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}}, \nonumber \\ \alpha _s(\mu )= & {} \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] ,\nonumber \\ \end{aligned}$$

(26)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213$, 296 and $339\,\mathrm {MeV}$ for the flavors $n_f=5$, 4 and 3, respectively [1], and we evolve all the input parameters to the optimal energy scale $\mu$ to extract the mass of the $Z^{++}_{cc}$.

Fig. 3

The pole contribution of the $Z_{cc}^{++}$ with variation of the Borel parameter $T^2$

Fig. 4

The contributions of different terms in the operator product expansion with variations of the Borel parameter $T^2$, where the 0, 3, 4, 5, 6, $\ldots$ denote the dimensions of the vacuum condensates

In Refs. [11, 12, 18,19,20], we study the acceptable energy scales of the QCD spectral densities for the hidden-charm (hidden-bottom) tetraquark states and molecular states in the QCD sum rules for the first time, and we suggest an empirical formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ to determine the optimal energy scales. The energy-scale formula enhances the pole contributions remarkably and works well. The energy-scale formula also works well in studying the hidden-charm pentaquark states [26]. In this article, we study the diquark–diquark–diquark type hexaquark state, the basic constituent are also diquarks, just like in the case of the diquark–antidiquark type tetraquark states [11, 12, 18]. So we extend our previous work to the study of the hexaquark state by taking the energy-scale formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_c)^2}$ with the updated value ${\mathbb {M}}_c=1.82\,\mathrm {GeV}$ as a constraint [27].

Experimentally, there is no candidate for the doubly charged hexaquark state $Z_{cc}^{++}$ with the symbolic quark structure uuddcc. In the scenario of tetraquark states, the QCD sum rules indicate that the $Z_c(3900)$ and Z(4430) can be tentatively assigned to the ground state and the first radial excited state of the axialvector tetraquark states, respectively [28], the Y(3915) and X(4500) can be tentatively assigned to the ground state and the first radial excited state of the scalar tetraquark states, respectively [29, 30]. The energy gap between the ground state and the first radial excited state of the hidden-charm tetraquark states is about $0.6\,\mathrm {GeV}$. Now we assume the energy gap between the ground state and the first radial excited state of the doubly charmed hexaquark states is about $0.6\,\mathrm {GeV}$, and tentatively we take the continuum threshold parameter to be $\sqrt{s_0}=M_{Z}+(0.4\sim 0.6)\,\mathrm {GeV}$, which also serves as a constraint.

We search for the optimal Borel parameter and continuum threshold parameter to satisfy the two criteria (pole dominance and convergence of the operator product expansion) of the QCD sum rules, and we obtain the values $T^2=(5.3-5.7)\,\mathrm {GeV}^2$ and $\sqrt{s_0}=(7.1\pm 0.1)\,\mathrm {GeV}$ for the energy scale $\mu =5.5\,\mathrm {GeV}$, the predicted mass satisfies the energy-scale formula and the continuum threshold parameter satisfies our naive expectation. The pole contribution is about (26–41)%, the pole dominance condition is not satisfied; see Fig. 3. In fact, if we do not use the energy-scale formula, the pole contribution is much smaller. In Fig. 4, we plot the contributions of the vacuum condensates in the operator product expansion with variations of the Borel parameter $T^2$ for the value $\sqrt{s_0}=7.1\,\mathrm {GeV}$. From the figure, we can see that the vacuum condensates of dimensions 10, 12, 13, 14, 16 play a minor role in the Borel window, the operator product expansion is well convergent. In calculations, we observe that the integral $\int _{4m_c^2}^{s_0} \mathrm{d}s\, \rho (s) \, \exp \left( -\frac{s}{T^2}\right)$ is negative at the region $T^2<4\,\mathrm {GeV}^2$ for $\sqrt{s_0}=7.1\,\mathrm {GeV}$. Although the vacuum condensates of dimensions 10, 12, 13, 14, 16 play a minor role in the Borel window, they play an important role in determining the Borel window. In Fig. 5, we plot the mass with variation of the Borel parameter $T^2$ by taking into account the vacuum condensates up to dimensions 16 and 10, respectively. From the figure, we can see that the predicted mass decreases monotonously with increase of the Borel parameter $T^2$ for the truncation $n\le 10$, there appears no platform.

Fig. 5

The mass of the $Z_{cc}^{++}$ with variation of the Borel parameter $T^2$, where the $D=16$ and $D=10$ denote the truncations in the operator product expansion

Fig. 6

The mass of the $Z_{cc}^{++}$ with variation of the Borel parameter $T^2$

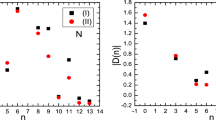
We take into account all uncertainties of the input parameters, and we obtain the values of the mass and pole residue of the $Z_{cc}^{++}$, which are shown explicitly in Figs. 6 and 7,

$$\begin{aligned} M_{Z}= & {} 6.60^{+0.12}_{-0.09}\,\mathrm {GeV}, \nonumber \\ \lambda _{Z}= & {} 7.64^{+1.17}_{-1.05}\times 10^{-3}\,\mathrm {GeV}^8. \end{aligned}$$

(27)

From Figs. 6 and 7, we see that there appear platforms at the Borel window $T^2=(5.3-5.7)\,\mathrm {GeV}^2$; no platform can be obtained at the value $T^2<5.2\,\mathrm {GeV}^2$. The predicted mass $M_{Z}=6.60^{+0.12}_{-0.09}\,\mathrm {GeV}$ lies above the thresholds $\Sigma _c(2455)\Sigma _c(2455)$ and $\Sigma _c(2520)\Sigma _c(2520)$, the decays to the charmed-baryon pairs $\Sigma _c(2455)\Sigma _c(2455)$ and $\Sigma _c(2520)\Sigma _c(2520)$ are Okubo–Zweig–Iizuka super-allowed, we can search for the $Z_{cc}^{++}$ in those decay channels. The diquark–diquark–diquark type hexaquark state is not a baryon–baryon type dibaryon [31] or a baryon–antibaryon type baryonium [32, 33], whose masses lie near the corresponding thresholds. In the QCD sum rules for the dibaryon or baryonium, the pole dominance is also failed to satisfy. In Ref. [34], it is observed that no stable hexaquark states exist below the corresponding two-baryon thresholds based on a simple potential quark model. In the present work, we observe that the scalar hexaquark state lies far above the $\Sigma _c(2455)\Sigma _c(2455)$ and $\Sigma _c(2520)\Sigma _c(2520)$ thresholds.

Fig. 7

The pole residue of the $Z_{cc}^{++}$ with variation of the Borel parameter $T^2$

4 Conclusion

In this article, we construct the scalar-diquark–scalar-diquark–scalar-diquark type current to interpolate the scalar hexaquark state, and we study it with QCD sum rules by carrying out the operator product expansion up to the vacuum condensates of dimension 16. In calculation, we take the energy-scale formula as a constraint to determine the energy scale of the QCD spectral density to extract the mass and pole residue. In the Borel window, the operator product expansion is well convergent, while the pole contribution is about (26–41)%. We obtain the lowest hexaquark mass $M_{Z}=6.60^{+0.12}_{-0.09}\,\mathrm {GeV}$, which can be confronted with the experimental data in the future, while the predicted pole residue can be used to study the strong decays of the hexaquark state with the three-point QCD sum rules.