1 Introduction

One of the most interesting and challenging problems in modern astrophysics is related to compact astrophysical objects like black hole which is widely accepted. The black holes are the end-point of a complete gravitational collapse of the massive star, which can be described by the Einstein theory of gravity, containing singularities and being surrounded by a boundary from which nothing, not even light, can escape. The event horizon of a black hole which acts like a one-way membrane, is a boundary between its exterior and its interior spacetime. Astronomers have found convincing evidence for the existence of supermassive black holes, especially the one corresponding to SgrA* in the Milky Way [1] thus establishing the concept of a black hole. However, extending the concept of Bose–Einstein condensate [2] to gravitational systems, the gravitational vacuum star (gravastar) was proposed as an alternative to black holes by Mazur and Mottola (MM) [3, 4], which does not involve horizons and could be stabilized through the exotic states of matter. For this purpose, they use the famous cut-and-paste technique with Israel junction conditions [5]. There are many applications of this cut-and-paste technique; for example thin-shell wormholes [6,7,8,9,10,11,12,13].

In this model a multi layered structure has been introduced: a de Sitter geometry in the interior filled with constant positive (dark) energy density accompanied by isotropic negative pressure \(p = -\rho \), while the exterior is defined by a Schwarzschild geometry, separated by a thin shell of stiff matter implying the configuration of a gravastar. Moreover, the gravastar model has no singularity at the origin and no event horizon [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

These alternative models are quite fascinating; they could solve two fundamental problems. One is the singularity problem and the other is the information loss paradox, two problems which are associated with black hole solutions. After this new emerging picture several researchers have analyzed the gravastar solutions using different approaches. A different development of the thick-shell anisotropic gravastar model idea is due to Cattoen et al. [29], with continuous profiles for the energy density and the anisotropic pressures. One development of the gravastar idea went in the direction of an analysis of stability against radial perturbations by Visser and Wiltshire [30], with the phase transition layer replaced by a single spherical \(\delta \)-shell. These facts, frequently motivating other possibilities for the interior solution, have been considered. Among them Bilić et al. [31] have replaced the de Sitter interior by a Born–Infeld phantom. Recently, the gravastar solution extended by introducing an electrically charged component in [32] and charged gravastar admitting conformal motion has proposed in [33]. Further expanding the work of Banerjee et al. have propose the braneworld gravastar configuration which is alternative to braneworld black hole [34]. This theoretical prediction is strongly supported by the different authors and for more comprehensive review is provided in [35,36,37,38].

The main topic that we would like to address in this paper is exact charged thin-shell gravastar solutions in the context of noncommutative geometry where coordinates of the target spacetime become noncommutating operators on a D-brane [39, 40] as \([\hat{x}^{\mu }, \hat{x}^{\nu }]\) = \(i\vartheta ^{\mu \nu }\), where \(\hat{x}\) and \(i\vartheta ^{\mu \nu }\) are the coordinate operators and an antisymmetric tensor of dimension (length)\(^2\), which determines the fundamental cell discretization of spacetime. In addition to noncommutativity elimination is characterized by a Gaussian function distribution with a minimal width \(\sqrt{\theta }\), i.e. a smeared particle, instead of the Dirac-delta function distribution. In spite of the progress a lot of work has been done on black holes with such Gaussian sources so far like higher dimensional black hole [41], charged black hole [42,43,44] and charged rotating black hole solutions [45, 46]. A way of implementing the energy density of a static and spherically symmetric, smeared and particle-like gravitational source has been considered in the following form [47]:

$$\begin{aligned} \rho _{\theta }=\frac{M}{(4\pi \theta )^{\frac{3}{2}}}e^{-\frac{r^{2}}{4\theta }}, \end{aligned}$$
(1)

where the mass M is diffused throughout a region of linear dimension \(\sqrt{\theta }\) due to the uncertainty.

Recently, one considers the LIGO detectors to have measured the first direct signal of the gravitational wave from rotating gravastars comparing the real and imaginary parts of the ringdown signal of GW150914 and one concluded that the modeling of the ringdown of GW150914 from the rotating gravastar is not possible [48].

In further research on noncommutative geometry the most significant development has been performed for obtaining exact solutions of self-sustained traversable wormholes [49, 50], thin-shell wormholes [51] and gravastar solutions in higher and lower dimensional spacetime [52, 53] etc. The main topics that we would like to address in this paper is finding exact gravastar solutions in the context of noncommutative geometry and exploring their physically accepted properties. The plan of our paper as follows. In Sect. 2 we construct the generic structure equations of charged gravastars, in the context of noncommutative geometry, and we specify the mass function. In Sect. 3 we discuss the matching conditions at the junction interface and determine the surface stresses. In Sect. 4 we investigate the stability of the charged thin-shell gravastar. In Sect. 5 we shall consider the thermodynamical stability. Finally, in Sect. 6, we comment on our results.

2 Exterior of gravastars: noncommutative geometry inspired charged BHs

The metric of a noncommutative charged black hole is described by the metric given by [42,43,44]

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+f(r)^{-1}\mathrm{d}r^{2}+r^{2}\mathrm{d}\Omega ^{2}, \end{aligned}$$
(2)

with \( f(r)=\left( 1-\frac{2M_{\theta }}{r}+\frac{Q_{\theta }^{2}}{r^{2}}\right) \), where the mass and charge functions are defined by

$$\begin{aligned} M_{\theta }(r)=\frac{2M}{\sqrt{\pi }}\gamma \left( \frac{3}{2},\frac{r^{2}}{4\theta }\right) , \end{aligned}$$
(3)
$$\begin{aligned} Q_{\theta }(r)=\frac{Q}{\sqrt{\pi }}\sqrt{\gamma ^{2}\left( \frac{1}{2}, \frac{r^{2}}{4\theta }\right) -\frac{r}{\sqrt{2\theta }}\gamma \left( \frac{1}{2},\frac{r^{2}}{2\theta }\right) ,} \end{aligned}$$
(4)

and

$$\begin{aligned} \gamma \left( \frac{a}{b},x\right) =\int _{0}^{x}u^{\frac{a}{b}-1}e^{-u}\mathrm{d}u. \end{aligned}$$
(5)

Here, the metric (2) leads to the result

$$\begin{aligned} f(r)= & {} 1-\frac{4M}{r\sqrt{\pi }}\gamma \left( \frac{3}{2},\frac{r^{2}}{4\theta }\right) \nonumber \\&+\frac{Q^{2}}{r^{2}\pi }\left[ \gamma ^{2}\left( \frac{1}{2},\frac{r^{2}}{4\theta }\right) -\frac{r}{\sqrt{2\theta }}\gamma \left( \frac{1}{2},\frac{r^{2}}{2\theta }\right) \right] \end{aligned}$$
(6)

where M is the total (constant) mass of the system and for the commutative case when r/\(\sqrt{\theta } \rightarrow \infty \), the smeared-like mass descends to the point-like mass, i.e. \(M_{\theta } \rightarrow M\). Q is the total charge of the black hole. It is noted that, for large r, Reissner–Nordstrm black hole will be obtained. The horizon radius (\(r_{\mathrm{h}}\)) can be found where \(f(r_{\mathrm{h}})=0\) in other words.

3 Structure equations of charged gravastars

To construct the charged gravastars, first we consider two noncommutative geometry inspired charged spacetime manifolds. The exterior is defined by \({M_{+}}\), and the interior is \({ M_{-}}\). Then we join them together by using the cut-and-paste method across a surface layer \(\Sigma \) [17]. The metric of interior is the nonsingular de Sitter spacetimes:

$$\begin{aligned} \mathrm{d}s^{2}=-\left( 1-\frac{r_{-}^{2}}{\alpha ^{2}}\right) \mathrm{d}t_{-}^{2}+\left( 1-\frac{r_{-}^{2}}{\alpha ^{2}}\right) ^{-1}\mathrm{d}r_{-}^{2}+r_{-}^{2}\mathrm{d}\Omega _{-}^{2} \end{aligned}$$
(7)

and the exterior of noncommutative geometry inspired charged spacetimes:

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)_{+}\mathrm{d}t_{+}^{2}+f(r)_{+}^{-1}\mathrm{d}r_{+}^{2}+r_{+}^{2}\mathrm{d}\Omega _{+}^{2} \end{aligned}$$
(8)

with

$$\begin{aligned} f(r)_{+}=\left( 1-\frac{2M_{\theta +}}{r}+\frac{Q_{\theta +}^{2}}{r^{2}}\right) . \end{aligned}$$
(9)

Note that ± stands for the exterior and interior geometry, respectively.

The induced metrics are \(g_{ij}^{+}\) and \(g_{ij}^{-}\), respectively. It is assumed that \(g_{ij}^{+}(\xi )=g_{ij}^{-}(\xi )=g_{ij}(\xi )\), where the hypersurface coordinates \(\xi ^{i}=(\tau ,\theta ,\phi )\). Our aim is to glue \({ M_{+}}\) and \({ M_{-}}\) at their boundaries to obtain a single manifold M so that \({ M}={M_{+}}\cup { M_{-}}\), at the boundaries \(\Sigma =\Sigma _{+}=\Sigma _{-}\).

To calculate the stress-energy tensor components, we use the intrinsic metric on \(\Sigma \) as follows:

$$\begin{aligned} \mathrm{d}s_{\Sigma }^{2}=-\mathrm{d}\tau ^{2}+a(\tau )^{2}\,(\mathrm{d}\theta ^{2}+\sin ^{2}{\theta }\,\mathrm{d}\phi ^{2}). \end{aligned}$$
(10)

Then we use the Einstein field equation, \(G_{{\mu }{\nu }}=8\pi \,T_{{\mu }{\nu }}\), where it is noted that \(c=G=1\). Note that the junction surface is located at \(x^{\mu }(\tau ,\theta ,\phi )=(t(\tau ),a(\tau ),\theta ,\phi )\). One finds that the unit normal vectors with respect to the junction surface are the following [17]:

$$\begin{aligned} n_{-}^{\mu }=\left( \frac{1}{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) }\dot{a},\sqrt{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) +\dot{a}^{2}},0,0\right) \,, \end{aligned}$$
(11)
$$\begin{aligned} n_{+}^{\mu }=\left( \frac{1}{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}}\dot{a},\sqrt{1-\frac{2M_{\theta _{+}}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}+\dot{a}^{2}},0,0\right) ,\nonumber \\ \end{aligned}$$
(12)

where the overdot stands for a derivative with respect to \(\tau \). For the spherical symmetric spacetimes, the condition of the normal vectors is \(n^{\mu }n_{\mu }=+1\). The extrinsic curvatures are calculated by the following equation [21]:

$$\begin{aligned} K_{ij}^{\pm }=-n_{\mu }\left( \frac{\partial ^{2}x^{\mu }}{\partial \xi ^{i}\,\partial \xi ^{j}}+\Gamma _{\;\;\alpha \beta }^{\mu \pm }\;\frac{\partial x^{\alpha }}{\partial \xi ^{i}}\,\frac{\partial x^{\beta }}{\partial \xi ^{j}}\right) \end{aligned}$$
(13)

so we find

$$\begin{aligned} K_{\;\theta }^{\theta \;-}= & {} \frac{1}{a}\,\sqrt{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) +\dot{a}^{2}}\;,\end{aligned}$$
(14)
$$\begin{aligned} K_{\;\tau }^{\tau \;-}= & {} \left\{ \frac{\left( \ddot{a}-\frac{a}{\alpha ^{2}}\right) }{\sqrt{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) +\dot{a}^{2}}}\right\} , \end{aligned}$$
(15)
$$\begin{aligned} K_{\;\theta }^{\theta \;+}= & {} \frac{1}{a}\,\sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}+\dot{a}^{2}}\;,\end{aligned}$$
(16)
$$\begin{aligned} K_{\;\tau }^{\tau \;+}= & {} \left\{ \frac{\ddot{a}+\frac{(M_{\theta +}a)-Q_{\theta +}^{2}}{a^{3}}}{\sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}+\dot{a}^{2}}}\right\} . \end{aligned}$$
(17)

It is noted that the prime is for a derivative with respect to the a. Then we calculate the discontinuity as follows: \(\kappa _{ij}=K_{ij}^{+}-K_{ij}^{-}\).

The stress-energy tensors \(S_{\;j}^{i}\) on \(\Sigma \) are calculated as follows:

$$\begin{aligned} S_{\;j}^{i}=-\frac{1}{8\pi }\,\left( \kappa _{\;j}^{i}-\delta _{\;j}^{i}\;\kappa _{\;k}^{k}\right) \,. \end{aligned}$$
(18)

Then using the relation of \(S_{\;j}^{i}=\mathrm{diag}(-\sigma ,{\mathscr {P}},{\mathscr {P}})\), one can find the surface energy density, \(\sigma \), and the surface pressure, \({\mathscr {P}}\), as follows [17]:

$$\begin{aligned} \sigma= & {} -\frac{\kappa _{\;\theta }^{\theta }}{4\pi }= -\frac{1}{4\pi a}\left[ \sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}+\dot{a}^{2}}\;\right. \nonumber \\&\left. -\sqrt{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) +\dot{a}^{2}}\;\right] ,\end{aligned}$$
(19)
$$\begin{aligned} {\mathscr {P}}= & {} \frac{\kappa _{\;\tau }^{\tau }+\kappa _{\;\theta }^{\theta }}{8\pi }= \frac{1}{8\pi a}\left[ \frac{1+\dot{a}^{2}+a\ddot{a}-\frac{M_{\theta +}}{a}}{\sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}+\dot{a}^{2}}}\right. \nonumber \\&\left. -\frac{\left( 1+a\ddot{a}+\dot{a}^2-\frac{2a^2}{\alpha ^{2}}\right) }{\sqrt{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) +\dot{a}^{2}}}\right] . \end{aligned}$$
(20)

Then we find

$$\begin{aligned} \sigma +2{\mathscr {P}}= & {} \frac{\kappa _{\;\tau }^{\tau }}{4\pi } =\frac{1}{4\pi }\left[ \left\{ \frac{\ddot{a}+\frac{(M_{\theta +}a)-Q_{\theta +}^{2}}{a^{3}}}{\sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}+\dot{a}^{2}}}\right\} \right. \nonumber \\&\left. -\left\{ \frac{\left( \ddot{a}-\frac{a}{\alpha ^{2}}\right) }{\sqrt{\left( 1-\frac{a^{2}}{\alpha ^{2}}\right) +\dot{a}^{2}}}\right\} \right] . \end{aligned}$$
(21)

To calculate the surface mass of the thin shell, one can use the equation \(M_{s}(a)=4\pi a^{2}\sigma \). To find a stable solution, we consider a static case [\(a_{0}\in (r_{-},r_{+})\)].

Then the surface charge and pressure in the static case reduce to

$$\begin{aligned} \sigma (a_{0})= & {} -\frac{1}{4\pi a_{0}}\left[ \sqrt{1-\frac{2M_{\theta +}}{a_{0}}+\frac{Q_{\theta +}^{2}}{a_{0}^{2}}}-\sqrt{\left( 1-\frac{a_{0}^{2}}{\alpha ^{2}}\right) }\right] ,\end{aligned}$$
(22)
$$\begin{aligned} {\mathscr {P}}(a_{0})= & {} \frac{1}{8\pi a_{0}}\left[ \frac{1-\frac{M_{\theta +}}{a_{0}}}{\sqrt{1-\frac{M_{\theta +}}{a_{0}}+\frac{Q_{\theta +}^{2}}{a_{0}^{2}}}}-\frac{\left( 1-\frac{2a_{0}^2}{\alpha ^{2}}\right) }{\sqrt{\left( 1-\frac{a_{0}^{2}}{\alpha ^{2}}\right) }}\right] . \end{aligned}$$
(23)

Then one can write

$$\begin{aligned} \sigma (a_{0})+2{\mathscr {P}}(a_{0})= & {} \frac{1}{4\pi }\left[ \left\{ \frac{\frac{(M_{\theta +}a_{0})-Q_{\theta +}^{2}}{a_{0}^{3}}}{\sqrt{1-\frac{2M_{\theta +}}{a_{0}}+\frac{Q_{\theta +}^{2}}{a_{0}^{2}}}}\right\} \right. \nonumber \\&+\left. \left\{ \frac{\left( \frac{a_{0}}{\alpha ^{2}}\right) }{\sqrt{\left( 1-\frac{a_{0}^{2}}{\alpha ^{2}}\right) }}\right\} \right] . \end{aligned}$$
(24)

Then we derive the conservation equation as follows:

$$\begin{aligned} \frac{\mathrm{d}(\sigma A)}{\mathrm{d}\tau }+{\mathscr {P}}\,\frac{\mathrm{d}A}{\mathrm{d}\tau }=0, \end{aligned}$$
(25)

using \(S_{\;j|i}^{i}=\left[ T_{\mu \nu }\;e_{\;(j)}^{\mu }n^{\nu }\right] _{-}^{+}\), where the surface area is \(A=4\pi a^{2}\). One can write them also as follows: \(\sigma '=-2\,(\sigma +{\mathscr {P}})/a\), where \(\sigma '=\mathrm{d}\sigma /\mathrm{d}a\).

4 Stability of the charged thin-shell gravastars in noncommutative geometry

In this section, we check the stability of the charged thin-shell gravastars in noncommutative geometry. To this purpose, we use the surface energy density \(\sigma (a)\) on the thin shell of the gravastars as follows:

$$\begin{aligned} \frac{1}{2}\dot{a}^{2}+V(a)=0, \end{aligned}$$
(26)

with the potential

$$\begin{aligned} V(a)=\frac{1}{2}\left\{ 1-\frac{B(a)}{a}-\left[ \frac{M_{s}(a)}{2a}\right] ^{2}-\left[ \frac{D(a)}{M_{s}(a)}\right] ^{2}\right\} \,. \end{aligned}$$
(27)

It is noted that B(a) and D(a) are

$$\begin{aligned} B(a)= & {} \frac{\left[ \left( 2M_{\theta +}-\frac{Q_{\theta +}^{2}}{a}\right) +\left( \frac{a^{3}}{\alpha ^{2}}\right) \right] }{2},\nonumber \\ D(a)= & {} \left[ \frac{\left[ \left( 2M_{\theta +}-\frac{Q_{\theta +}^{2}}{a}\right) -\left( \frac{a^{3}}{\alpha ^{2}}\right) \right] }{2}\right] . \end{aligned}$$
(28)

One can also easily obtain the surface mass as a function of the potential:

$$\begin{aligned} M_{s}(a)= & {} -a\left[ \sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}-2V(a)}\right. \nonumber \\&-\left. \sqrt{(1-\frac{a^{2}}{\alpha ^{2}})-2V(a)}\right] . \end{aligned}$$
(29)

Then the surface charge and the pressure are rewritten in terms of potential as follows:

$$\begin{aligned} \sigma =- & {} \frac{1}{4\pi a}\left[ \sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}-2V}\right. \nonumber \\&\left. -\sqrt{(1-\frac{a^{2}}{\alpha ^{2}})-2V}\right] , \end{aligned}$$
(30)
$$\begin{aligned} {\mathscr {P}}= & {} \frac{1}{8\pi a}\left[ \frac{1-2V-aV'-\frac{M_{\theta +}}{a}}{\sqrt{1-\frac{2M_{\theta +}}{a}+\frac{Q_{\theta +}^{2}}{a^{2}}-2V}}\right. \nonumber \\&\left. -\frac{1-2V-aV'-\left( \frac{2a}{\alpha ^{2}}\right) }{\sqrt{(1-\frac{a^{2}}{\alpha ^{2}})-2V}}\right] . \end{aligned}$$
(31)

To find the stable solution, we linearize it using the Taylor expansion around the \(a_{0}\) to second order as follows:

$$\begin{aligned} V(a)=\frac{1}{2}V''(a_{0})(a-a_{0})^{2}+O[(a-a_{0})^{3}]\,. \end{aligned}$$
(32)

Note that for stability, the conditions are \(V(a_{0})=V'(a_{0})=0\), \(\dot{a}_{0}=\ddot{a}_{0}=0\) and \(V''(a_{0})>0\). Using the relation \(M_{s}(a)=4\pi \sigma (a)a^{2}\), we use \(M_{s}''(a_{0})\) instead of \(V''(a_{0})\ge 0\) as follows [17]:

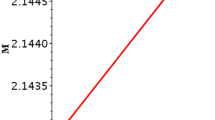
$$\begin{aligned} M_{s}''(a_{0})\ge & {} \frac{1}{4 a_{0}^{3}}\left\{ \frac{\left[ \frac{2\left( M_{\theta +}+Q_{\theta +}^{2}\right) }{a_{0}}\right] ^{2}}{\left[ 1-\frac{2M_{\theta +}}{a_{0}}+\frac{Q_{\theta +}^{2}}{a_{0}^{2}}\right] ^{3/2}}-\frac{[\frac{-a_{0}^{3}}{\alpha ^{2}}]^{2}}{\left[ \left( 1-\frac{a_{0}^{2}}{\alpha ^{2}}\right) \right] ^{3/2}}\right\} \nonumber \\&+\frac{1}{2}\left\{ \frac{\frac{2Q_{\theta +}^{2}}{a_{0}^{3}}}{\sqrt{1-\frac{2M_{\theta +}}{a_{0}}+\frac{Q_{\theta +}^{2}}{a_{0}^{2}}}}-\frac{\frac{4a_{0}}{\alpha ^{2}}}{\sqrt{\left( 1-\frac{a_{0}^{2}}{\alpha ^{2}}\right) }}\right\} , \end{aligned}$$
(33)

so for the stable solution, the above relation must be satisfied as shown in Fig. 1. Note that we have used the following equation:

$$\begin{aligned} V''(a_{0})= & {} -\frac{3 M_s^2(a_0)}{4 a_0^4}+\Big [\frac{M'_s(a_0)}{a_0^3}-\frac{M''_s(a_0)}{4 a_0^2}\Big ]M_s(a_0)\nonumber \\&-\frac{B''(a_0)}{2 a_0}+\frac{B'(a_0)}{a_0^2}-\frac{B(a_0)}{a_0^3}-\frac{M'_s(a_0)^2}{4 a_0^2}\nonumber \\&-\frac{D'^2(a_{0})+D(a_{0}) D''(a_{0})}{M_s^2(a_{0})}\nonumber \\&+\frac{4 D(a_{0}) D'(a_{0}) M'_s(a_{0})+D^2(a_{0}) M''_s(a_{0})}{M_s^3(a_{0})}\nonumber \\&-\frac{3 D^2(a_{0}) (M'_s)^2(a_{0})}{M_s^4(a_{0})}, \end{aligned}$$
(34)

where

$$\begin{aligned} M'_s(a_{0})=8 \pi a_0 \sigma _0-8 \pi a_0 (\sigma _0+p_0) \end{aligned}$$
(35)

and

$$\begin{aligned} M''_s(a_{0})= & {} 8 \pi \sigma _0-32 \pi (\sigma _0+p_0)\nonumber \\&+\, 4\pi \left[ 2(\sigma _0+p_0)+4 (\sigma _0+p_0)(1+\eta )\right] . \end{aligned}$$
(36)
Fig. 1
figure 1

We plot \(\sigma _0+p_0\) as a function of \(M_{\theta }\) and \(a_{0}\). We choose \(Q_{\theta }=1\) and \(\alpha =0.4\). Note that in this region the NEC is satisfied

Full size image

Moreover, we have also introduced \(\eta (a)={\mathscr {P}}'(a)/\sigma '(a)|_{a_0}\) as a parameter which will play a fundamental role in determining the stability regions of the respective solutions. Generally, \(\eta \) is interpreted as the speed of sound, so that one would expect the range of \(0 < \eta \le 1\); the speed of sound should not exceed the speed of light. But the range of \({\eta }\) may be lying outside the range of \(0 < \eta \le 1\), on the surface layer and for extensive discussion, see Refs. [54, 55]. Therefore, in this work the range of \(\eta \) will be relaxed and we use a graphical representation to determine the stability regions given by Eq. (34), due to the complexity of the expression (Figs. 2, 3, and 4).

Fig. 2
figure 2

Stability regions of the charged gravastar in terms of \(\eta =P'/\sigma '\) as a function of \(a_{0}\). We choose \(M_{\theta }=2\), \(Q_{\theta }=1.5\), \(\alpha =0.4\)

Full size image
Fig. 3
figure 3

Stability regions of the charged gravastar in terms of \(\eta =P'/\sigma '\) as a function of \(a_{0}\). We choose \(M_{\theta }=1.5\), \(Q_{\theta }=1\), \(\alpha =0.2\)

Full size image
Fig. 4
figure 4

Stability regions of the charged gravastar in terms of \(\eta =P'/\sigma '\) as a function of \(a_{0}\). We choose \(M_{\theta }=3\), \(Q_{\theta }=2.5\), \(\alpha =0.5\)

Full size image

5 Thermodynamics and stability conditions for the thin shell

Now, we turn to the thermodynamical stability of the thin shell. Following [56], we assume that the shell is in thermal equilibrium, with a locally measured temperature T and an entropy S. Here the entropy S can be expressed as a function of the state independent variables of the surface mass of the thin shell M, area A, and charge Q. Thus the first law of thermodynamics provides the following relationship:

$$\begin{aligned} T \mathrm{d}S = \mathrm{d}M +p\mathrm{d}A- \Phi \mathrm{d}Q, \end{aligned}$$
(37)

where \(\left( M, A, Q\right) \) can be considered as three generic parameters. It is important to note that we consider the particles N to be constant. Now it is a simple matter to obtain the entropy S we shall adopt three equations of state, namely, \(p\left( M, A, Q\right) \), \(\beta \left( M, A, Q\right) \), and \(\Phi \left( M, A, Q\right) \): the pressure, temperature, and charge equations of state, respectively and we define the inverse temperature \(\beta \equiv 1/T\).

It is of particular interest to obtain an expression for the entropy. The integrability conditions must be specified, which follow directly from the first law of thermodynamics and are given by

$$\begin{aligned}&\left( \frac{\partial \beta }{\partial A} \right) = \left( \frac{\partial \beta p}{\partial M} \right) _{A,Q},\end{aligned}$$
(38)
$$\begin{aligned}&\left( \frac{\partial \beta }{\partial Q} \right) = \left( \frac{\partial \beta \Phi }{\partial M} \right) _{A,Q},\end{aligned}$$
(39)
$$\begin{aligned}&\left( \frac{\partial \beta p}{\partial Q} \right) = \left( \frac{\partial \beta \Phi }{\partial A} \right) _{M,Q}. \end{aligned}$$
(40)

Thus, one may easily determine the relations between the three EOS of the system. This result also is at the basis of the study of the local intrinsic stability of the shell, by the first law in Eq. (2). It is more convenient to work out the thermodynamic stability as dictated by the following inequalities:

$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial M^2} \right) _{A,Q} \le 0, \end{aligned}$$
(41)
$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial A^2} \right) _{M,Q} \le 0, \end{aligned}$$
(42)
$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial Q^2} \right) _{M,A} \le 0, \end{aligned}$$
(43)
$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial M^2} \right) \left( \frac{\partial ^2 S}{\partial A^2} \right) - \left( \frac{\partial ^2 S}{\partial M \partial A} \right) ^{2} \ge 0, \end{aligned}$$
(44)
$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial A^2} \right) \left( \frac{\partial ^2 S}{\partial Q^2} \right) - \left( \frac{\partial ^2 S}{\partial A \partial Q} \right) ^{2} \ge 0, \end{aligned}$$
(45)
$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial M^2} \right) \left( \frac{\partial ^2 S}{\partial Q^2} \right) - \left( \frac{\partial ^2 S}{\partial M \partial Q} \right) ^{2} \ge 0, \end{aligned}$$
(46)
$$\begin{aligned} \left( \frac{\partial ^2 S}{\partial M^2} \right) \left( \frac{\partial ^2 S}{\partial Q \partial A} \right) - \left( \frac{\partial ^2 S}{\partial M \partial A} \right) \left( \frac{\partial ^2 S}{\partial M \partial Q} \right) \ge 0, \end{aligned}$$
(47)

For more discussion and derivation of these expression, see Refs. [57, 58].

6 Conclusions

In this paper, we have studied the stability of a particular class of thin-shell gravastar solutions, in the context of charged noncommutative geometry. For this purpose we consider the de Sitter geometry in the interior of the gravastar by matching an exterior charged noncommutative solution at a junction interface situated outside the event horizon. We showed that the gravastar’s shell satisfies the null energy conditions in Fig. 1.

We further explored the gravastar solution by the dynamical stability of the transition layer, which is sufficient close to the event horizon. It is found that for specific choices of the mass \(M_{\theta }\), charge \(Q_{\theta }\) and the values of \(\alpha \), stable configurations of the surface layer exist, sufficiently close to where the event horizon is expected to form. In future work we shall explore the thermodynamical stability of the thin-shell gravastar, using the shell in the thermal equilibrium.