Abstract
In curved space-time, the Hamilton–Jacobi equation is a semi-classical particle equation of motion, which plays an important role in the research of black hole physics. In this paper, starting from the Dirac equation of spin 1/2 fermions and the Rarita–Schwinger equation of spin 3/2 fermions, respectively, we derive a Hamilton–Jacobi equation for the non-stationary spherically symmetric gravitational field background. Furthermore, the quantum tunneling of a charged spherically symmetric Kinnersly black hole is investigated by using the Hamilton–Jacobi equation. The result shows that the Hamilton–Jacobi equation is helpful to understand the thermodynamic properties and the radiation characteristics of a black hole.
Similar content being viewed by others
1 Introduction
In 1974, considering quantum effects, Hawking proved that a black hole has thermal radiation [1]. After that, one has carried out a series of research for various types of black hole radiation [2,3,4,5,6,7,8]. About the source of Hawking radiation, a common viewpoint is to believe that, due to a vacuum fluctuation near the event horizon where a virtual particle pair could be created or annihilated, a negative energy particle falls in since there exists a negative energy orbit inside the black hole, however, the positive energy particle left outside is radiated to infinity, which causes Hawking radiation. In 2000, Parikh and Wilczek et al. put forward a quantum tunneling theory to study the thermal radiation of a black hole. By taking into account the background change before and after tunneling radiation, they have carried out modification to the previous tunneling probability [9]. In recent years, a series of significant studies have been made on the tunneling radiation of black holes [3, 10,11,12,13,14,15,16,17]. Zhang and Zhao et al. have developed this tunneling theory, and they studied the relationship between the tunneling radiation and the black hole entropy, which provided a reasonable explanation for the information loss paradox of a black hole [18, 19]. Further research of Lin and Yang et al. showed that the tunneling rate of the event horizon from a dynamic black hole is not only related to the black hole entropy, but also related to an integral function [20]. Therefore, the information loss paradox of a black hole still needs further research. According to the literature [21,22,23], the Hamilton–Jacobi equation in curved space-time is a basic equation describing the dynamic characteristics of all kinds of particles. Applying it to the Hamilton–Jacobi equation, the Dirac equation and the tunneling radiation of a stationary black hole have been studied. However, a black hole in the universe should show dynamic change due to radiation, accretion, merging and other reasons. Therefore, it is of practical significance to study the tunneling radiation characteristics of a dynamic black hole.
For a dynamic black hole, the Dirac equation describing the motion of spin 1/2 and the 3/2 particles is more complex than that of a stationary black hole. In this paper, according to the space-time line element of a Kinnersley black hole, using the advanced Eddington coordinate to represent its dynamic characteristics, we study the tunneling radiation of spin 1/2 and 3/2 particles in this space-time background.
The rest of the paper is organized as follows. Using the Dirac equation for a spin 1/2 particle and the Rarita–Schwinger equation for a spin 3/2 particle, we derived the Hamilton–Jacobi equation in Sect. 2. In Sect. 3, according to the Hamilton–Jacobi equation, the fermion tunneling behavior in a non-stationary Kinnersley black hole is addressed. Section 4 is devoted to our discussion and conclusion.
2 Dirac equation of spin particles and the Hamilton–Jacobi equation
The Dirac equation for a spin 1/2 particle can be described by
where
here the relationship between gamma matrices and the space-time metric is
Before resolving Eq. (1), one must know the space-time background. Let us consider a dynamic Kinnersley black hole of arbitrarily variably accelerated rectilinear motion. In the advanced Eddington coordinate, the line element of the black hole can be written as [24]
where \(f = - a( \upsilon )\sin \theta \), \(M = M( \upsilon )\). \(a( \upsilon )\) stands for the magnitude of acceleration. \(M( \upsilon )\) is the mass of the black hole. From Eq. (5), one gets the determinant of the metric and the non-zero components of the inverse metric tensor,
and
According to Eqs. (5)–(7), the gamma matrices of Eq. (4) can be constructed as follows:
where \(\chi = - ( {1 - 2ar\cos \theta - 2Mr^{ - 1} } )\), and in the gamma matrices of Eqs. (8)–(11), the Pauli matrices are
The wave function is expressed as
where S is the principal function. The coefficient term can be decomposed into
Substituting Eqs. (8)–(14) into Eq. (1) and neglecting the terms with \(\hbar \), one can get a matrix equation, i.e.
In Eq. (15), C, D and G are closely related to Eqs. (5)–(12). The expressions are, respectively,
Because of \(C D = D C\), in order to obtain non-trivial solutions, it is necessary to have
Taking into account the anti-commuting relationship of the Pauli matrices,
according to Eqs. (16)–(18), we can concretely express Eq. (19) as
This is the kinetic equation only holding for a spin 1/2 particle. That is to say, we derive Eq. (21) from Eq. (1). Equation (21) is just the Hamilton–Jacobi equation of the dynamic Kinnersley black hole of the variably accelerated rectilinear motion, which is described by Eq. (7). One can simplify it as \(g^{\mu \nu } ( {{{\partial S} / {\partial \mu }}} )( {{{\partial S} / {\partial \nu }}} ) + m^2 = 0\).
At the same time, one needs to explain that the Hamilton–Jacobi equation can also be used to describe the dynamical behavior of spin 3/2 particles. Now, let us simply illustrate it. Generally speaking, the motion equation for a spin 3/2 is described by the Rarita–Schwinger equation of the curved space-time. Its concrete expression is
where every \(\varPsi _\nu \) is a matrix. Equations (22) and (23) together can determine every wave function. In the semi-classical theory, the wave function in Eq. (22) can be expressed as
where \(A = \left( {\begin{array}{ll} {a_\nu } &{} {b_\nu } \\ \end{array}} \right) ^{TM}\) and \(B = \left( {\begin{array}{ll} {c_\nu } &{} {d_\nu } \\ \end{array}}\right) ^{TM}\) and \(a_\upsilon \), \(b_\upsilon \), \(c_\upsilon \), \(d_\upsilon \) express the corresponding matrix. Thus, for spin 3/2 particles, the gamma matrix can be chosen to be consistent with Eqs. (8)–(11). In the same way, we can still discuss the tunneling radiation of spin 3/2 particles in Eq. (7), which describes a dynamic Kinnersley black hole of the variably accelerated rectilinear motion. In the semi-classical approximation, we can still get
In the above expression, for C, D and G refer to Eqs. (16)–(18). Taking into account non-trivial solution conditions in Eq. (25), we can obtain
By calculation, the Hamilton–Jacobi equation which is consistent with Eq. (21) can still be obtained. So, for the Rarita–Schwinger equation of spin 3/2 fermion particles, we can also obtain the dynamic equation (21). This further shows that the Hamilton–Jacobi equation of curved space-time is a basic dynamic equation of the radiation particles.
3 Hamilton–Jacobi equation and the tunneling from a non-stationary Kinnersly black hole
The event horizon of a non-stationary Kinnersley black hole described by Eq. (5) satisfies the null hypersurface condition,
Because of the acceleration direction of a non-uniformly rectilinearly accelerating black hole is always pointing to the north pole, namely \(\theta = 0\), the space-time described by Eq. (5) is of axial symmetry. From Eq. (5) and Eq. (27), the event horizon of black hole satisfies the null hypersurface equation,
where \(\dot{r}_H = {{\partial r} / {\partial \upsilon }} \), \(r'_H = {{\partial r} / {\partial \theta }}\). From Eq. (28) we can see that the event horizon \(r_H\) is a function which depends not only on time \(\upsilon \), but also on the angle \(\theta \). In order to calculate the temperature of a black hole, here we introduce a new generalized tortoise coordinate transformation [25],
in which \(\alpha \) is an adjustable coefficient, \(\upsilon _0\) and \(\theta _0\) are arbitrary constants. The differential forms for the above expression become
Substituting Eq. (30) into Eq. (21), we have
In the above expression, we define \(P_\theta = {{\partial S} / {\partial \theta _* }}\) and \(P_\varphi = {{\partial S} / {\partial \varphi }} = j\). \(P_\varphi \) stands for the generalized momentum, j is a constant that is related to the Killing vector \(( {{\partial / {\partial \varphi }}} )\). After processing the above expression, we can get
where \(\mathscr {R} = r - r_H + \alpha r_H( {\upsilon _0 ,\theta _0 } )\). According to the conformally flatness condition, here we require that the limit of the coefficient of \(\big (\frac{\partial S}{\partial \upsilon _{*}}\big )^{2}\) in Eq. (32) is 1 when the radius of the black hole approaches the event horizon \(r_H\), namely
But we can find that, when \(r \rightarrow r_H\), an infinite limit of 0/0-type arises from the above expression. In order to study the tunneling radiation on the event horizon, we use the L’Hospital rule; thus we have
Therefore, on the event horizon, Eq. (32) can be expressed as
where the limit of the coefficient A is
By simplifying Eq. (35), we can get
In Eq. (37), we need \(\omega _0 = {{AP_\theta } / 2}\). At the same time, in previous work, we proved the relationship \({{\partial S} / {\partial \upsilon _* }} = \omega \), where \(\omega \) is the energy of radiation particles. So, by solving the above equation, we can get
In Eq. (38), it can be found that there is only one singularity, that is, \(r_H\). After integration, the result can be expressed as
where \( + ( - )\) is an outgoing (ingoing) solution. In order to obtain the tunneling rate, we have to consider both the outgoing and the ingoing solutions. As a result, the tunneling rate of the particle becomes
By using the Boltzmann factor expression, the Hawking temperature of the black hole is given by
where
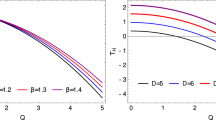
In the above expression, when ignoring the angular momentum a and the coefficients \(r'_H\), \(\dot{r}_H\), meanwhile setting \(r_H=2M\), we can find that the surface gravity of a dynamic Kinnersley black hole reduces to the case of the Schwarzschild hole. Therefore, Eq. (41) also reduces to the Hawking temperature of a Schwarzschild black hole. Furthermore, it is well known that the relationship between the temperature and the surface gravity is \(T=\kappa /(2 \pi )\), where the \(\kappa \) is the surface gravity of the black hole. Combined with this fact, from Eq. (41) we find the value of \(\alpha \) is equal to \( 1 / ( 2 \kappa )\).
In the calculation of the above process, by using the Hamilton–Jacobi equation, we study the tunneling behavior of spin 1/2 and 3/2 particles in a dynamic Kinnersley black hole, and get the Hawking temperature of the black hole. In fact, we can also prove that the Hamilton–Jacobi equation can describe the motion behavior in curved space-time for scalar particles. For instance, the Klein–Gordon equation for scalar particles can be described by
In a similar way, after substituting the wave function
into Eq. (43), and by neglecting the terms with \(\hbar \), it is easy for us to obtain the Hamilton–Jacobi equation,
This means, by using the Hamilton–Jacobi equation, the tunneling rate and the Hawking temperature for scalar particles can also be addressed in the non-stationary black hole. In a word, we confirm from Eqs. (21), (26), (43) and (45) that the Hamilton–Jacobi equation is a basic equation, and it can be used to study the tunneling behavior of any particle in curved space-time.
4 Conclusion
In this paper, starting from both the Dirac equation of spin 1/2 fermions and the Rarita–Schwinger equation of spin 3/2 fermions, we can obtain a Hamilton–Jacobi equation. Moreover, making use of this equation, we investigate the fermion tunneling rate and the Hawking temperature of a non-stationary Kinnersly black hole. According to our conclusion, the Hamilton–Jacobi equation can be derived from the kinetic equations of arbitrary spin particles. This shows that the Hamilton–Jacobi equation is a basic semi-classical equation, which can be used to study the quantum tunneling behavior of arbitrary spin particles. Furthermore, through the comparison of the previous work, we can obviously see that it is very convenient to study tunneling radiation by using the Hamilton–Jacobi equation. Especially for the fermion tunneling, since there is no need to construct the complex gamma matrix by a tedious calculation, which greatly reduces the workload, it is better to carry out creative research in depth.
References
S.W. Hawking, Commun. Math. Phys. 43, 199 (1975)
Q.Q. Jiang, S.Q. Wu, X. Cai, Phys. Rev. D 75, 064029 (2007)
D.Y. Chen, Eur. Phys. J. C 74, 2687 (2014)
G.M. Deng, Gen. Relativ. Gravit. 46, 1757 (2014)
Z.W. Feng, J. Deng, G.P. Li, S.Z. Yang, Int. J. Theor. Phys. 51, 3214 (2012)
Z.W. Feng, H.L. Li, X.T. Zu, S.Z. Yan, Eur. Phys. J. C 76, 212 (2016)
R. Li, J.R. Ren, S.W. Wei, Class. Quantum Gravity 25, 125016 (2008)
P. Kraus, F. Wilczek, Nucl. Phys. B 433, 403 (1995)
M.K. Parikh, F. Wilczek, Phys. Rev. Lett. 85, 5042 (2000)
S. Shankaranarayanan, T. Padmanabhan, K. Srinivasan, Class. Quantum Gravity 19, 2671 (2002)
Z.W. Feng, Y. Chen, X.T. Zu, Astrophys. Space Sci. 359, 48 (2015)
R. Kerner, R.B. Mann, Class. Quantum Gravity 25, 095014 (2008)
W.B. Liu, Phys. Lett. B 634, 541 (2006)
H.L. Li, R. Lin, L.Y. Cheng, EPL 98, 30002 (2012)
G.P. Li, Y.G. Zhou, X.T. Zu, Int. J. Theor. Phys. 52, 4025 (2013)
Y.W. Han, G. Chen, M.J. Lan, Chin. Phys. C 714, 127 (2012)
H.L. Li, Z.W. Feng, X.T. Zu, Gen. Relativ. Gravit. 48, 18 (2016)
J.Y. Zhang, Z. Zhao, Phys. Lett. B 638, 110 (2006)
J.Y. Zhang, Phys. Lett. B 668, 353 (2008)
K. Lin, S.Z. Yang, Chin. Phys. B 18, 2154 (2009)
K. Lin, S.Z. Yang, Phys. Rev. D 79, 064035 (2009)
K. Lin, S.Z. Yang, Phys. Lett. B 674, 127 (2009)
K. Lin, S.Z. Yang, Chin. Phys. B 20, 110403 (2011)
W. Kinners, Phys. Rev. 186, 1335 (1969)
Z. Zhao, W.H. Huang, Chin. Phys. Lett. 9, 333 (1992)
Acknowledgements
This work is supported by the Natural Science Foundation of China (Grant No. 11573022)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Li, GP., Feng, ZW., Li, HL. et al. Dirac equation of spin particles and tunneling radiation from a Kinnersly black hole. Eur. Phys. J. C 77, 250 (2017). https://doi.org/10.1140/epjc/s10052-017-4806-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-4806-9