1 Introduction

In general relativity (GR), polytropes play a very vital role in the modeling of relativistic compact objects (COs). Over the past few decades, many researchers have been engaged in the study of polytropes due to the simple form of the polytropic equation of state (EoS) and the corresponding Lane–Emden equation (LEE), which can be used for the description of various astrophysical phenomenons. Chandrasekhar [1] was the pioneer, who established the theory of polytropes originating with the laws of thermodynamics in the Newtonian regime. Tooper [2, 3] formulated the initial framework of the polytropes for a compressible and adiabatic fluid under quasi-static equilibrium condition to develop the LEE. After a few years, Kovetz [4] provided some corrections in the Chandrasekhar formalism for polytropes. The general form of the LEE in higher-dimensional space was developed by Abramowicz [5] in spherical, cylindrical, and planar geometry.

The study of anisotropy in the modeling of an astrophysical CO plays a very significant role and many physical problems cannot be modeled without taking anisotropic stress into account. In 1981, a very sophisticated process of modeling an anisotropic CO was provided by Cosenza [6]. In this scenario, Herrera and Santos [7] presented a detailed study of the existence of anisotropy in a self-gravitating CO. Herrera and Barreto [8] developed a general model for Newtonian and relativistic anisotropic polytropes. Herrera et al. [9] gave a complete set of equations with anisotropic stress for a self-gravitating spherical CO. A new way to check the stability of anisotropic polytropic models by the Tolman mass was provided by Herrera and Barreto [10, 11]. Herrera et al. [12] used a conformally flat condition in the analysis of anisotropic polytropes to reduce the parameters involved in the LEE. He et al. [13] also discussed the implementation of cracking criteria for the stability of anisotropic polytropes.

In GR, the existence of charge considerably affects the modeling of a relativistic CO. Bekenstein [14] investigated gravitational collapse by means of a hydrostatic equilibrium equation in a charged CO. Bonnor [15, 16] showed that gravitational collapse can be delayed by electric repulsions in a CO. A complete study of the contraction of a charged CO in isotropic coordinates was presented by Bondi [17]. Koppar et al. [18] developed a novel way to calculate a charge generalization of the static charged fluid solution of a CO. Ray et al. [19] investigated charged CO with high density and found that they can have large amount of charge approximately \(10^{20}\) coulomb. Herrera et al. [20] used structure scalars to study dissipative fluids in a charged spherical CO. Takisa [21] provided models of polytropic COs in the presence of charge. Sharif [22] developed a modified LEE for a charged polytropic CO with the conformally flat condition. Azam et al. [23–27] discussed the cracking of different charged CO models with linear and quadratic EoS.

It is always a crucial issue to choose the proper EoS for the modeling of astronomical objects. Chavanis [28, 29] proposed a modification in the conventional polytropic EoS \(P_r=K \rho ^{1+\frac{1}{n}}\), where \(P_r\) is radial pressure, n is the polytropic index, and K is a polytropic constant. He combined a linear EoS \(P_r=\alpha _1 \rho _o\) with a polytropic EoS as \(P_r=\alpha _1 \rho _o+K \rho ^{1+\frac{1}{n}}\) and used it to describe different cosmological situations. He developed the models of the early and the late universe for \(n>0\) and \(n<0\) through a generalized polytropic equation of state (GPEoS). Freitas [30] applied the modified polytropic EoS for the development of a model of the universe with constant energy density and discussed quantum fluctuations of the universe. Azam et al. [31] provided a comprehensive study for the development of a modified form of LEE with GPEoS for spherical symmetry.

Cylindrically symmetric spacetimes have been used widely in GR to describe various physically interesting aspects. For the first time, Kompaneets [32] provided the general form of a four-dimensional cylindrically symmetric metric. Some specific examples of a cylindrically symmetric metric which provide exact solutions to the system of Einstein’s field equations and cylindrical gravitational waves were studied in [33, 34]. Thorne [34] defined the C-energy of cylindrical systems as the “gravitational energy per unit specific length”. The most interesting fact about these spacetimes is the so-called C-energy and as a result gravitational waves are thought to be carriers of energy in a gravitational field. Whittaker [35] introduced the concept of a “mass potential” in GR. Herrera et al. [36] used a conformally flat condition with cylindrical symmetry to give a solution of the field equations which is completely matched to the Levi-Civita vacuum spacetime. Herrera and Santos [37] studied the matching condition for perfect fluid cylindrical gravitational collapse. Debbasch et al. [38] discussed regularity and the matching condition for a stationary cylindrical anisotropic fluid. Di Prisco et al. [39] studied cylindrical gravitational collapse with a shear-free condition. Sharif and Fatima [40] presented cylindrical collapse with a charged anisotropic fluid. Sharif and Azam [41] studied dynamical instability of cylindrical collapse in the Newtonian and the post Newtonian regime. Ghua and Banerji [42] described dissipative cylindrical collapse with a charged anisotropic fluid. Sharif and Sadiq [43] presented conformally flat polytropes with an anisotropic fluid for the cylindrical geometry. Mahmood et al. [44] considered a charged anisotropic fluid for the discussion of cylindrical collapse and found that the presence of charge enhances the anisotropy of the collapsing system.

In this paper, we will explore charged anisotropic polytropes by using GPEoS for a cylindrical symmetric configuration with a conformally flat condition. In Sect. 2, we present the Einstein–Maxwell field equations and a modified hydrostatic equilibrium equation. In Sect. 3, the LEE is developed for relativistic polytropes. The energy conditions, the conformally flat condition, and the stability of the model is given in Sect. 4. In the last section we conclude our results.

2 Matter distribution and Einstein–Maxwell field equations

In this section, we will describe the inner matter distribution and Einstein–Maxwell’s field equations. We assume a static cylindrically symmetric spacetime,

$$\begin{aligned} \mathrm{d}s^2=-A^{2}\mathrm{d}t^{2}+B^{2}\mathrm{d}r^{2}+C^2 \mathrm{d}\theta ^{2}+{\mathrm{d} z^2}, \end{aligned}$$
(1)

where \(t\in (-\infty ,\infty )\), \(r\in [0,\infty )\), \(\theta \in [0,2\pi ]\) and \(z\in (-\infty ,\infty )\) are the conditions on the cylindrical coordinates. The energy-momentum tensor for a charged anisotropic fluid distribution is

$$\begin{aligned} T_{i j}= & {} (P_r+\rho ) V_{i} V_{j} -(P_r-P_z)S_{i}S_{j} -(P_r-P_\theta )K_{i}K_{j}\nonumber \\&+P_r g_{ij}+\,\frac{1}{4\pi }(F_i^\gamma F_{j \gamma }- \frac{1}{4}F^{\gamma \beta } F_{\gamma \beta }g_{ij} ), \end{aligned}$$
(2)

where \(P_r,~P_\theta ,~P_z\), and \(\rho \) represent pressures in \(r,~\theta ,~z \) directions and energy density of fluid inside cylindrical symmetric distribution. The four-velocity \(V_{i}\) and four vectors \(S_{i},~K_{i}\) satisfying the following relations:

$$\begin{aligned} V^{i}V_{i} \!=\! -1,~S^{i}S_{i}\!=\!K^{i}K_{i}=1,~S^{i}k_{i}=V^{i}k_{i}=V^{i}S_{i}=0.\nonumber \\ \end{aligned}$$
(3)

These quantities in co-moving coordinates can be written as

$$\begin{aligned} V_{i}=A\delta _i^0,~K_{i}=C\delta _i^2,~S_{i}=A\delta _i^3. \end{aligned}$$
(4)

The Maxwell field equations are

$$\begin{aligned} F_{[ij;k]}=0,\quad F^{ij}_{;j}=4\pi J^i, \end{aligned}$$
(5)

where \(F_{ij}=\psi _{j,i}-\psi _{i,j}\) is field tensor and \(\psi _i\) is the four-potential and \(J^i\) is four-current. The four-potential and four-velocity are related to each other in co-moving coordinates by

$$\begin{aligned} \psi _{i}=\psi (r) \delta ^0_i,\quad J^i=\sigma V^i,\quad i=0,1,2,3, \end{aligned}$$
(6)

with \(\psi \) and \(\sigma \) represents scalar potential and charge density, respectively.

The Einstein–Maxwell field equations for the line element of Eq. (1) are given by

$$\begin{aligned}&\frac{B^\prime C^\prime }{B^3 C}-\frac{C^{\prime \prime }}{B^2C}= 8\pi \rho -4\pi ^2 E^2, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{A^\prime C^\prime }{A B^2 C}=8\pi P_r +4\pi ^2 E^2, \end{aligned}$$
(8)
$$\begin{aligned}&\frac{A^{\prime \prime }}{A B^2}-\frac{A^\prime B^\prime }{A B^3}= 8\pi P_\theta -4\pi ^2 E^2, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{A^{\prime \prime }}{A B^2}-\frac{A^\prime B^\prime }{A B^3} -\frac{B^\prime C^\prime }{B^3 C}-\frac{A^\prime C^\prime }{A B^2 C}\nonumber \\&\quad +\frac{C^{\prime \prime }}{ B^2 C}=8\pi P_z -4\pi ^2 E^2, \end{aligned}$$
(10)

where \(\prime \) denotes the differentiation with respect to r and \(E=\frac{q}{2\pi C}\) with \(q(r)=4 \pi \int _0^r \sigma B C \mathrm{d}r\) represents total amount of charge per unit length of cylinder. We consider the exterior metric for the cylindrical symmetric geometry with retarded time coordinate \(\nu \) defined as

$$\begin{aligned} \mathrm{d}s^2= & {} -\left( -\frac{2M}{R}+\frac{Q^2}{R^2}\right) \mathrm{d}\nu ^2-2\mathrm{d}\nu \mathrm{d}R\nonumber \\&+R^2(\mathrm{d}\theta ^2+\beta ^2\mathrm{d}z^2), \end{aligned}$$
(11)

where M is the total mass and \(\beta \) is an arbitrary constant.

The junction condition has a very important role to play in the theory of relativistic objects. This condition shows the feasibility of physically acceptable solutions. For the continuity and matching of two spacetimes, junction conditions on the boundary \(\Sigma \) yield [45–47]

$$\begin{aligned} m(r)-M\overset{\Sigma }{=}\frac{l}{8},~~\Leftrightarrow ~~Q^2\overset{\Sigma }{=}\frac{q l^2}{8},~~l\overset{\Sigma }{=}4C,~~P_r\overset{\Sigma }{=}0. \end{aligned}$$
(12)

The Schwarzschild coordinate is selected as \(C=r\) [43] and Einstein–Maxwell field equations reduced to the form [44]

$$\begin{aligned}&\frac{B^\prime }{r B^3}=8\pi \rho -4\pi ^2 E^2, \end{aligned}$$
(13)
$$\begin{aligned}&\frac{A^\prime }{A B^2 r}=8\pi P_r +4\pi ^2 E^2, \end{aligned}$$
(14)
$$\begin{aligned}&\frac{A^{\prime \prime }}{A B^2}-\frac{A^\prime B^\prime }{A B^3} =8\pi P_\theta -4\pi ^2 E^2, \end{aligned}$$
(15)
$$\begin{aligned}&\frac{A^{\prime \prime }}{A B^2}-\frac{A^\prime B^\prime }{A B^3} -\frac{B^\prime }{B^3 r}-\frac{A^\prime }{A B^2 r} =8\pi P_z -4\pi ^2 E^2. \end{aligned}$$
(16)

Solving Eqs. (13)–(15) simultaneously leads to the hydrostatic equilibrium equation

$$\begin{aligned} \frac{\mathrm{d} P_r}{\mathrm{d}r}+\frac{A^\prime }{A}\big (\rho +P_r\big )+\frac{\Delta }{r} +\pi E E^\prime +\frac{8\pi E^2}{r}=0, \end{aligned}$$
(17)

where we have used \(\Delta =P_r-P_\theta \).

Thorne [34] defined the C-energy (gravitational energy per unit specific length of cylindrical geometry), in the form of a mass function,

$$\begin{aligned} \widetilde{E} =\frac{1}{8}[1-l^{-2}\nabla ^a\widetilde{r}\nabla _a\widetilde{r}], \end{aligned}$$

with

$$\begin{aligned} \mu ^2=\xi _{(1)a}\xi ^a_{(1)},~~~l^2=\xi _{(2)a}\xi ^a_{(2)},~~~\widetilde{r}=\mu l, \end{aligned}$$

here \(\widetilde{r},\mu ,l\) represents the areal radius, the circumference radius, and the specific length, respectively, and for the static case the expression of the C-energy can be written as

$$\begin{aligned} m(r)=\widetilde{E}^\prime =\frac{1}{8}\Bigg [1-\frac{1}{B^2}\Bigg ]+2\pi r^2 E, \end{aligned}$$
(18)

Differentiating Eq. (18) and using Eq. (14), we get

$$\begin{aligned} \frac{A^\prime }{A}=\frac{8\pi r P_r+4\pi ^2r E^2}{1-8m+16\pi ^2rE^2}. \end{aligned}$$
(19)

Using Eq. (19), the hydrostatic equilibrium equation (17) becomes

$$\begin{aligned}&\frac{\mathrm{d} P_r}{\mathrm{d}r}+\frac{8\pi r P_r+4\pi ^2r E^2}{1-8m+16\pi ^2rE^2} \big (\rho +P_r\big )\nonumber \\&\quad +\frac{\Delta }{r} +\pi E E^\prime +\frac{8\pi E^2}{r}=0. \end{aligned}$$
(20)

The basic theory of polytropes is established with the hypotheses of a polytropic EoS and a hydrostatic equilibrium state of the relativistic object under consideration. In the next section, we will discuss relativistic polytropes with a generalized polytropic EoS in the presence of charge for cylindrical symmetry.

3 The relativistic polytropes

In this section, we provide a comprehensive way for the development of the LEE which is the main consequence of the theory of polytropes with GPEoS in the cylindrical regime. The EoS is the union of the linear EoS \(P_r=\alpha _1\rho _o\) and the polytropic EoS \(P_r=K\rho _o^{1+\frac{1}{n}}\). The linear EoS describes pressureless \((\alpha _1=0)\) or radiation \((\alpha _1=\frac{1}{3})\) matter. The polytropic part is related to the cosmological aspects of the early universe for \(n>0\) whereas it describes the late universe with \(n<0\) [18, 19]. The cosmic behavior of the universe is demonstrated with \(\rho _o\) as the Planck density but in the relativistic regime we take it as a mass density for case 1 and the total energy density in case 2. Here, we shall develop the general formalism for relativistic polytropes with GPEoS in the presence of charge.

3.1 Case 1

Here, the GPEoS is

$$\begin{aligned} P_r=\alpha _1\rho _o+K\rho _o^{\gamma }=\alpha _1\rho _o+K\rho _o^{1+\frac{1}{n}}. \end{aligned}$$
(21)

The original polytropic part remains conserved and the relationship of the mass density \(\rho _0\) with the total energy density \(\rho \) is given by [7]

$$\begin{aligned} \rho =\rho _{o}+n P_r. \end{aligned}$$
(22)

Now making the following assumptions:

$$\begin{aligned}&\alpha =\frac{P_{rc}}{\rho _{gc}},~~~r=\frac{\xi }{X},~~~\rho _{o}=\rho _{gc}\theta ^n,~~~ m(r)\nonumber \\&\quad =\frac{2\pi \rho _{gc} v({\xi })}{X^2},~~~X^2=\frac{16\pi P_{rc}}{\alpha }, \end{aligned}$$
(23)

where \(P_{rc}\) and \(\rho _{gc}\) represent the central pressure and mass density. Also \(\xi \), \(\theta \), and v are defined to be dimensionless variables. Using the assumptions (23) with the EoS (21), the hydrostatic equilibrium equation (20) transforms as

$$\begin{aligned}&\Bigg (\frac{1-v({\xi })+4\pi ^{3/2}\sqrt{\frac{\alpha }{ P_{rc}}}E^2 \xi }{1+(n+1)(\alpha _1+\alpha \theta )}\Bigg )\frac{\mathrm{d} \theta }{\mathrm{d} \xi } + \Bigg (\frac{2P_{rc}\alpha (\alpha _1+\alpha \theta )\theta ^n+\pi E^2}{n\alpha _1 \theta ^{-n}+(n+1)\alpha \theta }\Bigg )\frac{\alpha \xi }{4P_{rc}}\nonumber \\&\quad + \frac{(\Delta +\pi \xi E \frac{\mathrm{d} E}{\mathrm{d} \xi }+8 \pi E^2)(1-v({\xi })+4\pi ^{3/2} \sqrt{\frac{\alpha }{ P_{rc}}}E^2 \xi )}{(1+(n+1)(\alpha _1+\alpha \theta )) (n\alpha _1 \theta ^{-n}+(n+1)\alpha )}\frac{\theta ^n}{\alpha \xi P_{rc}}=0.\nonumber \\ \end{aligned}$$
(24)

Now taking the derivative of Eq. (18) with respect to r and applying the relations of Eq. (23), we obtain

$$\begin{aligned} \frac{\mathrm{d}v(\xi )}{\mathrm{d}\xi }=\xi \theta ^n(1+n\alpha _1+n\alpha \theta ) +\frac{(4-\pi )\alpha \xi E}{2 P_{rc}}+\frac{\alpha \xi ^2}{ P_{rc}}\frac{\mathrm{d} E}{\mathrm{d}\xi }.\nonumber \\ \end{aligned}$$
(25)

The combination of Eqs. (24) and (25) results in the modified LEE (Eq. (39) in the appendix), which describe the relativistic charged polytropes with GPEoS.

3.2 Case 2

In this case the GPEoS as \(P_r=\alpha _1\rho +K\rho ^{1+\frac{1}{n}}\), here mass density \(\rho _o\) is replaced by total energy density \(\rho \) in Eq. (21) and we have the following relation [7]:

$$\begin{aligned} \rho =\frac{\rho _o}{\big (1-K \rho _o^{\frac{1}{n}}\big )^n}. \end{aligned}$$
(26)

We make the following assumptions:

$$\begin{aligned} \alpha= & {} \frac{P_{rc}}{\rho _{c}},~~~ r=\frac{\xi }{X},~~~\rho =\rho _{c}\theta ^n,~~~\nonumber \\&m(r)=\frac{2\pi \rho _{c}v({\xi })}{X^2},~~~X^2=\frac{16\pi P_{rc}}{\alpha }, \end{aligned}$$
(27)

where c means that each quantity is calculated at the center of a CO. Using GPEoS and the assumptions of Eq. (27), the hydrostatic equilibrium Eq. (20) turns out to be

$$\begin{aligned}&\Bigg (\frac{1-v({\xi })+4\pi ^{3/2}\sqrt{\frac{\alpha }{ P_{rc}}}E^2 \xi }{1+\alpha _1+\alpha \theta }\Bigg )\frac{\mathrm{d} \theta }{\mathrm{d} \xi }\nonumber \\&\quad + \Bigg (\frac{2P_{rc}\alpha (\alpha _1+\alpha \theta )\theta ^n+\pi E^2}{n\alpha _1 \theta ^{-n}+(n+1)\alpha \theta }\Bigg )\frac{\alpha \xi }{4P_{rc}}\nonumber \\&\quad +\, \frac{(\Delta +\pi \xi E \frac{\mathrm{d} E}{\mathrm{d} \xi }+8 \pi E^2)(1-v({\xi })+4\pi ^{3/2} \sqrt{\frac{\alpha }{ P_{rc}}}E^2 \xi )}{(1+\alpha _1+\alpha \theta ) (n\alpha _1 \theta ^{-n}+(n+1)\alpha \theta )}\nonumber \\&\quad \times \frac{\theta ^n}{\alpha \xi P_{rc}}=0. \end{aligned}$$
(28)

Taking the derivative of Eq. (18) with respect to r and applying Eq. (27), we get

$$\begin{aligned} \frac{\mathrm{d}v(\xi )}{\mathrm{d}\xi }=\xi \theta ^n+\frac{(4-\pi )\alpha \xi E}{2 P_{rc}}+\frac{\alpha \xi ^2}{P_{rc}}\frac{\mathrm{d} E}{\mathrm{d}\xi }. \end{aligned}$$
(29)

We get a modified LEE by using Eqs. (29) and (28) given in the appendix, see (40)), representing the relativistic charged polytropes with GPEoS.

4 Energy conditions, conformally flat condition, and stability analysis

In the mathematical modeling of a CO, the energy conditions play a very peculiar role in the analysis of the developed model. The energy condition provides us with the maximum information without depending upon the EoS used in the modeling. These conditions have been developed with the understanding that the energy density is always positive; otherwise the empty space created due to positive and negative regions definitely become unstable. The energy conditions that should be satisfied by all the models are [48]

$$\begin{aligned} \rho +\frac{\pi }{2}E^2>0,~~~P_{r} \le \rho -\pi E^2,~~~\frac{P_{\theta }}{\rho }\le ,~~~\frac{P_{z}}{\rho }\le 1. \end{aligned}$$
(30)

If we take case 1 of the developed model, the energy conditions (30) transform as

$$\begin{aligned}&1+\frac{\pi E^2 }{1+n(\alpha _1 + \alpha \theta )\theta ^{n}}>0,~~~ 1\le \frac{\pi E^2}{(n-1)(\alpha _1+\alpha \theta )}, \nonumber \\&\frac{\alpha P_\theta }{P_{rc}(1+n(\alpha _1+\alpha \theta ))\theta ^n}\le 1,~~~\nonumber \\&\quad \times \frac{\alpha P_z}{P_{rc}(1+n(\alpha _1+\alpha \theta ))\theta ^n}\le 1, \end{aligned}$$
(31)

and for case 2 the energy conditions (30) emerge as

$$\begin{aligned}&1+\frac{\pi \alpha \theta ^{-n} E^2}{2 P_{rc}}>0, ~1 \le \frac{\pi \alpha E^2 \theta ^n+\alpha P_{rc} \theta }{P_{rc}(1-\alpha _1)},\nonumber \\&\quad \frac{P_\theta \alpha \theta ^{-n}}{P_{rc}}\le 1, ~\frac{P_z \alpha \theta ^{-n}}{P_{rc}}\le 1. \end{aligned}$$
(32)

We observe that the coupled Eqs. (24) and (25) and Eqs. (28) and (29) result in a system of differential equations with three variables. Thus, we need more information to study the charged polytropic CO with GPEoS in cylindrical symmetry. So, we use a conformally flat condition to reduce the systems of differential equations to two variables.

For this purpose, the Weyl scalar defined in terms of the Kretchman scalar, the Ricci tensor, and the Ricci scalar is given by [43]

$$\begin{aligned} C^2=\mathcal {R}+\frac{R^2}{3}-2R^{\mu \nu }R_{\mu \nu }. \end{aligned}$$
(33)

For our line element, the above equation becomes

$$\begin{aligned} C^2= & {} \frac{4}{3 r^2 A^2 B^6} [(A^2-r A A' +r^2 A'^2) B'^2\nonumber \\&+ B^2 (A'^2-r A' A''+r^2 A''^2)\nonumber \\&+ B B' (r A' (A'-2 r A'')+A (A'+r A''))]. \end{aligned}$$
(34)

Now applying conformal flatness i.e., \(C^2=0\), and using the field equations (13)–(16) and (19) in Eq. (34), we obtain the anisotropy as

$$\begin{aligned} \Delta= & {} -\pi E^2+\frac{1}{8 \pi }(8 \pi P_r+4 \pi ^2 E^2+ (8 \pi P_r+4 \pi ^2 E^2)^2\nonumber \\&+(8 \pi P_r+4 \pi ^2 E^2) (-4 \pi ^2 E^2+8 \pi \rho )\nonumber \\&+(-4 \pi ^2 E^2+8 \pi \rho )^2\nonumber \\&+(-1-8 \pi P_r-8 \pi ^2 E^2+8 \pi \rho ) \nonumber \\&\times \Biggl [\frac{(8 \pi P_r+4 \pi ^2 r E^2)^2}{(1-8 m+16 \pi ^2 r E^2)^2}\nonumber \\&-\frac{r (8 \pi P_r+4 \pi ^2 r E^2) (-4 \pi ^2 E^2+8 \pi \rho )}{1-8 m+16 \pi ^2 r E^2}\nonumber \\&+ \frac{4 \pi ^2 E^2+8 \pi P_r'+8 \pi ^2 r E E'}{1-8 m+16 \pi ^2 r E^2}\nonumber \\&- \frac{(8 \pi P_r+4 \pi ^2 r E^2) (16 \pi ^2 E^2-8 m'+ 32 \pi ^2 r E E')}{(1-8 m+16 \pi ^2 r E^2)^2}\biggr ]\nonumber \\&+\biggl [\frac{(8 \pi P_r+4 \pi ^2 r E^2)^2}{(1-8 m+16 \pi ^2 r E^2)^2}\nonumber \\&-\frac{r (8 \pi P_r+4 \pi ^2 r E^2) (-4 \pi ^2 E^2+8 \pi \rho )}{1-8 m+16 \pi ^2 r E^2} \nonumber \\&+ \frac{4 \pi ^2 E^2+8 \pi P_r'+8 \pi ^2 r E E'}{1-8 m+16 \pi ^2 r E^2}\nonumber \\&- \frac{(8 \pi P_r+4 \pi ^2 r E^2) (16 \pi ^2 E^2-8 m'+32 \pi ^2 r E E')}{(1-8 m+16 \pi ^2 r E^2)^2})^2\biggr ].\nonumber \\ \end{aligned}$$
(35)

Now using Eq. (23) in the above equation, we obtain anisotropy factor for case 1 given in the appendix; see Eq. (41). One can derive a modified LEE for conformally flat polytropes by using Eq. (41) in (24) and coupling with Eq. (25) for case 1. Similarly, the anisotropy parameter for case 2 turns out to be Eq. (42) (see the appendix) and the modified LEE by using Eq. (42) in (28) and coupling it with Eq. (29) for case 2, which can help in the study of conformally flat polytropes.

We will use a modified Whittaker [35] formula for the stability analysis of the model, which is the measure of the “active gravitational mass per unit length” of a cylinder defined by

$$\begin{aligned} m_L = 8 \pi \int _0^{r_\Sigma } (\rho + P_r + P_\theta + P_z-\pi E^2)\mathrm{d}r. \end{aligned}$$
(36)

For case 1, using the field equations (13)–(16), (19) and (23) in (36), we get

$$\begin{aligned}&m_L =\int _0^{1}-\frac{\pi \sqrt{\left( -\frac{2M}{R}+\frac{Q^2}{R^2}\right) \frac{P_{\text {rc}}}{\alpha }}}{\alpha \bigg (4 \pi ^{3/2} \alpha \xi E^2 \sqrt{\frac{P_{\text {rc}}}{\alpha }}- P_{\text {rc}} (-1+v)\Bigg ) \theta }\nonumber \\&\qquad \times \, \bigg (-16 \pi ^{5/2} \alpha ^2 \xi E^3 \sqrt{\frac{P_{\text {rc}}}{\alpha }} \theta +\pi ^2 \alpha ^2 \xi E^4\nonumber \\&\quad \times \,\bigg (3 \xi +32 \sqrt{\pi } \sqrt{\frac{P_{\text {rc}}}{\alpha }}\bigg ) \theta +4 \pi E P_{\text {rc}} \nonumber \\&\quad \times \, \theta (-\alpha +2 \xi (-\alpha +32 \pi P_{\text {rc}} \theta ^n (\alpha _1+\alpha \theta )) \frac{\mathrm{d} E}{\mathrm{d} \xi } \nonumber \\&\quad +v \bigg (\alpha +2 \alpha \xi \frac{\mathrm{d} E}{\mathrm{d} \xi }\bigg )\bigg )\nonumber \\&\quad + 8 P_{\text {rc}} \bigg (-\alpha \Delta (-1+v) \theta +2 \sqrt{\pi } \alpha \xi \nonumber \\&\quad \times \,\bigg (\frac{P_{\text {rc}}}{\alpha }\bigg ){}^{3/2} \alpha _1 (1+n \alpha _1) \theta ^{1+2 n} \nonumber \\&\quad + 2 \sqrt{\pi } \alpha ^2 \xi \bigg (\frac{P_{\text {rc}}}{\alpha }\bigg ){}^{3/2} (1+2 n \alpha _1) \theta ^{2+2 n}\nonumber \\&\quad +2 n \sqrt{\pi } \alpha ^3 \xi \bigg (\frac{P_{\text {rc}}}{\alpha } \bigg ){}^{3/2} \theta ^{3+2 n}\nonumber \\&\quad -\alpha P_{\text {rc}} \theta ^{2+n} \frac{\mathrm{d} v}{\mathrm{d} \xi }+n P_{\text {rc}} \alpha _1 (-1+v) \theta ^n \frac{\mathrm{d} \theta }{\mathrm{d} \xi }\nonumber \\&\quad - P_{\text {rc}} \theta ^{1+n} \Bigg (\alpha _1 \frac{\mathrm{d} v}{\mathrm{d} \xi }-(1+n) \alpha (-1+v)\frac{\mathrm{d} \theta }{\mathrm{d} \xi }\Bigg )\Bigg )\nonumber \\&\quad + \sqrt{\pi } E^2 \Bigg (128 \pi ^{3/2} P_{\text {rc}}^2 \theta ^{1+n} (\alpha _1+\alpha \theta )+\alpha ^2 \xi \nonumber \\&\quad \times \,\sqrt{\frac{P_{\text {rc}}}{\alpha }} \theta (1+32 \pi \Delta -v-\frac{\mathrm{d} v}{\mathrm{d} \xi }) \nonumber \\&\quad -2 \sqrt{\pi } \alpha P_{\text {rc}} (2 (-1+v) \theta +\alpha \xi (-n \xi +4 \sqrt{\pi } \sqrt{\frac{P_{\text {rc}}}{\alpha }}) \theta ^{2+n} \nonumber \\&\quad +16 n \sqrt{\pi } \xi \sqrt{\frac{P_{\text {rc}}}{\alpha }} \alpha _1 \theta ^n \frac{\mathrm{d} \theta }{\mathrm{d} \xi }\nonumber \\&\quad -\xi \theta ^{1+n} \Bigg (\xi +\Big (n \xi -4 \sqrt{\pi } \sqrt{\frac{P_{\text {rc}}}{\alpha }}\Bigg ) \alpha _1\nonumber \\&\quad -16 (1+n) \sqrt{\pi } \alpha \sqrt{\frac{P_{\text {rc}}}{\alpha }} \frac{\mathrm{d} \theta }{\mathrm{d} \xi }\Bigg )\Bigg )\Bigg )\Bigg )\mathrm{d}\xi . \end{aligned}$$
(37)

Similarly for case 2, the Whittaker formula yields

$$\begin{aligned}&m_L =\int _0^{1}-\frac{\pi \sqrt{\bigg (-\frac{2M}{R}+\frac{Q^2}{R^2}\bigg ) \frac{P_{\text {rc}}}{\alpha }}}{\alpha \Bigg (1+\frac{4 \pi ^{3/2} \xi E^2}{\sqrt{\frac{P_{\text {rc}}}{\alpha }}}-v\Bigg )}\nonumber \\&\quad \times \biggl (-\frac{16 \pi ^{5/2} \alpha \xi E^3}{\sqrt{\frac{P_{\text {rc}}}{\alpha }}}+\frac{\pi ^2 \alpha ^2 \xi E^4 \Bigg (3 \xi +32 \sqrt{\pi } \sqrt{\frac{P_{\text {rc}}}{\alpha }}\Bigg )}{P_{\text {rc}}} \nonumber \\&\quad +\,4 \pi \alpha E (-1+v) + 1\Big /\Bigg (\sqrt{\frac{P_{\text {rc}}}{\alpha }}\Bigg ) \sqrt{\pi } E^2\nonumber \\&\quad \times \Bigg (\alpha \Bigg (\xi +32 \pi \Delta \xi +4 \sqrt{\pi } \sqrt{\frac{P_{\text {rc}}}{\alpha }}\Bigg )-\alpha \Bigg (\xi +4 \sqrt{\pi } \sqrt{\frac{P_{\text {rc}}}{\alpha }}\Bigg ) v \nonumber \\&\quad +\,2 \sqrt{\pi } \Bigg (P_{\text {rc}} \Bigg (-4 \sqrt{\pi } \xi +64 \pi \sqrt{\frac{P_{\text {rc}}}{\alpha }}\Bigg ) \alpha _1\nonumber \\&\quad +\, \alpha \xi ^2 \sqrt{\frac{P_{\text {rc}}}{\alpha }} (1+n \alpha _1)\biggr ) \theta ^n\nonumber \\&\quad +\, 2 \sqrt{\pi } \alpha \Bigg (-4 \sqrt{\pi } \xi P_{\text {rc}}+n \alpha \xi ^2 \sqrt{\frac{P_{\text {rc}}}{\alpha }}\nonumber \\&\quad +\,64 \pi \alpha \Bigg (\frac{P_{\text {rc}}}{\alpha }\Bigg ){}^{3/2}\Bigg ) \theta ^{1+n}\Bigg )\nonumber \\&\quad +\, 8 \alpha \Bigg (\Delta -\Delta v+2 \sqrt{\pi } \xi \Bigg (\frac{P_{\text {rc}}}{\alpha }\Bigg ){}^{3/2} \theta ^{2 n}\nonumber \\&\quad \times (\alpha _1+\alpha \theta ) (1+n \alpha _1+n \alpha \theta )\Bigg )\biggr )\mathrm{d}\xi . \end{aligned}$$
(38)
Fig. 1
figure 1

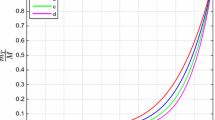
Case 1: \(m_L\) as a function of \(\xi \) for \(n=1\), curve a: \(\alpha =8\times 10^{-11}\),  \(Q=0.2\) \(M_\odot \), curve b: \(\alpha =10^{-10}\),  \(Q=0.4\) \(M_\odot \), curve c: \(\alpha =2 \times 10^{-10}\), \(Q=0.6\) \(M_\odot \), curve d: \(\alpha =4 \times 10^{-10}\), \(Q=0.64\) \(M_\odot \)

Full size image

In order to test the physical viability of polytropes, we formulate the energy condition and found that these conditions are satisfied only for case 1 and fail in case 2 for charged anisotropic polytropes with GPEoS. We also plot the Whittaker formula \((m_L)\) given in Eq. (37) with respect to the dimensionless radius \(\xi \) in the radial direction for a cylinder of unit radius. The bounded behavior of \((m_L)\) in the radial direction for various values of the charge shows that our model is stable. So, only case 1 for polytropes is physically viable.

5 Conclusion and discussion

In this article, we have formulated the general framework to study charged relativistic polytropes with GPEoS in the cylindrical regime. The GPEoS, \(P_r=\alpha _1 \rho +K \rho ^{1+\frac{1}{n}}\), is the combination of a linear EoS with a polytropic EoS, and it is used in cosmology for the description of eras of the universe. For the discussion of relativistic polytropes, we have developed the generalized framework to get the expressions of the modified LEE whose solutions are called polytropes. The polytropes mainly depend on the density function and the polytropic index decides the order of the solution. These polytropes are very useful in the description of various astrophysical aspects of a CO due to its simplicity. However, this simplicity is obtained at the cost of an empirical power-law relation between density and pressure, which should hold throughout in a CO. The LEE have been obtained with the anisotropic factor \(\Delta \) in the expressions (see the appendix, Eqs. (39) and (40)) depending upon three variables. In order to reduce one variable (\(\Delta \)), we have used a conformally flat condition and calculated the value of anisotropic factor in the form of other two variables (see the appendix, Eqs. (41) and (42)). One can easily obtain a modified LEE in two variables by substituting these values of anisotropy factor.

The stability analysis is very important in the development of mathematical models to check the physical viability. The energy conditions are very helpful in this regard, as they can entail maximum information without considering the EoS involved in the development of the model. The energy conditions have been obtained for both cases of GPEoS in the presence of an electromagnetic field. We have used a modified form of the Whittaker formula [35] for the stability analysis of charged anisotropic relativistic polytropes. We have calculated \(m_L\), which is a measure of the “active gravitational mass per unit length” in the z-direction, for both the case of GPEoS for different values of parameters involved in the model (see Fig. 1) for a cylinder of unit radius. We have taken these values from our previous work on the polytropes [31]. We have plotted \(m_L\) against the dimensionless radii \(\xi \) and found that its graph remains bounded in the radial direction even for very high values of the charge \(Q=0.2\) \(M_\odot \), 0.4 \(M_\odot \), 0.6 \(M_\odot \), and 0.64 \(M_\odot \). Also it is clear that more mass is concentrated near the center of cylinder and its magnitude decreases as we move away from the center in a radial direction. The highest magnitude is observed in the middle of cylindrical symmetry in the radial direction. As the gravitational mass cannot be negative, Fig. 1 shows the stable positive and bounded behavior of \(m_L\), which shows that our model is stable. The energy conditions are valid only for case 1 and fail to hold for case 2. Hence the model developed in case 2 is not physically viable due to the negation of the energy conditions.