Diphoton excess at 750 GeV: gluon–gluon fusion or quark–antiquark annihilation?

Abstract

Recently, ATLAS and CMS collaborations reported an excess in the measurement of diphoton events, which can be explained by a new resonance with a mass around 750 GeV. In this work, we explored the possibility of identifying if the hypothetical new resonance is produced through gluon–gluon fusion or quark–antiquark annihilation, or tagging the beam. Three different observables for beam tagging, namely the rapidity and transverse-momentum distribution of the diphoton, and one tagged bottom-jet cross section, are proposed. Combining the information gained from these observables, a clear distinction of the production mechanism for the diphoton resonance is promising.

1 Introduction

Very recently, both ATLAS and CMS collaborations presented new results from LHC Run 2. Although most of the measurements can still be fit in the Standard Model (SM) framework nicely, some intriguing excesses are reported. Of particular interest is the diphoton excess around 750 GeV seen by both collaborations. The ATLAS collaboration reported an excess above the standard model (SM) diphoton background with a local (global) significance of 3.9 (2.3) $\sigma$ [3]. The CMS collaboration, with a little less integrated luminosity, also reported an excess at 760 GeV with a local (global) significance of 2.6 (a little less than 1.2) $\sigma$ [2].

Though further data is required to establish the existence of a new resonance or other beyond the SM (BSM) mechanism responsible for the diphoton excess, significant theoretical efforts have been made to explain the possible diphoton excess in various BSM scenarios [4–9, 11–13, 15–19, 26–30, 32–34, 38, 41–45, 48–57, 59, 63, 65–69, 71, 72, 75–80, 83–87, 89, 90, 93–109, 115–128, 130–133, 136, 139–141]. While the models proposed vary significantly, there are some common features shared by most of them. Due to the quantum number of photon pair, most of the proposals suggest that the excess is either due to gluon–gluon fusion or quark–antiquark annihilation. Different production mechanisms can lead to very different UV models. Knowing the actual production mechanism responsible for the potential excess is of great importance for understanding the underlying theory. Unfortunately, very little can be said from the current data, except some considerations based on the consistency of experimental data from the LHC Run 1 and Run 2.

In this work, we shall study the following problem: if the diphoton excess persists in future data, and the existence of a new resonance is established, is it possible to distinguish different production mechanisms with enough amount of data? One can compare this question with the more frequently asked question, namely, how to tell whether an energetic hadronic jet in the final state is due to a quark or a gluon produced from hard scattering. This is also known as the quark and gluon jet tagging problem; see e.g. Refs. [31, 91, 92, 114].¹ One can view the question of differentiating the gg fusion and $q\bar{q}$ annihilation mechanism as a final-state-to-initial-state crossing of the quark and gluon jet tagging problem. For this reason we will call it the quark and gluon beam tagging problem in this work, or beam tagging for short. While our current work in the beam tagging problem was motivated by the diphoton excess, we believe that our results will be useful even if the excess disappear after more data is accumulated, because a bump might eventually show up at a different place and/or in a different channel.

An important feature of the beam tagging problem is that most of the QCD radiations from the initial-state partons are in the forward direction, and therefore are hard to make use of. This is contrasted with final-state jet tagging, in which the information of QCD radiations in the jet play crucial role in identifying the partonic origin of the jet. This feature makes the beam tagging problem difficult. Based on the consideration of general properties of initial-state QCD radiations, we explore different observables which are useful for the beam tagging problem. First of all, we consider the rapidity distribution of the diphoton system. It is well known from Drell–Yan production that for the $q\bar{q}$ initial state, contribution from valence quark and sea quark can have different shape in rapidity distribution. Using this information, we find that it is possible to distinguish the valence-quark scattering from sea-quark or gluon scattering. Second, we consider the transverse momentum ($Q_\mathrm{T}$) distribution of the diphoton system. It is well known that the $Q_\mathrm{T}$ distribution of a color neutral system exhibits a Sudakov peak at low $Q_\mathrm{T}$ due to initial-state QCD radiation. Interestingly, the strength of initial-state radiation differs for quark or gluon induced hard scattering and leads to substantial difference in the position of the Sudakov peak. Using this information, it is possible to distinguish light-quark scattering from bottom-quark or gluon scattering. Lastly, to further differentiate bottom-quark induced or gluon induced scattering, we consider tagging a b-quark jet in the final state.

The paper is organized as follows: In Sect. 2.1 we study the rapidity distribution of the diphoton system, and propose using centrality ratio, defined as ratio of cross section in central rapidity region and the total cross section, to discriminate production mechanism due to valence-quark scattering from sea-quark or gluon scattering. In Sect. 2.2 we study the transverse-momentum distribution of the diphoton system, and propose the ratio of cumulative cross section in two different transverse-momentum bins to discriminate light-quark scattering from bottom-quark or gluon scattering. In Sect. 2.3, we study b-tagged cross section to further discriminate bottom-quark scattering from gluon scattering. We conclude in Sect. 3.

2 Three methods for the beam tagging problem

We consider the following effective operators with an additional singlet scalar S:

$$\begin{aligned} {\mathscr {L}}_\mathrm{eff}&=- \frac{1}{4} \frac{\alpha _s}{3 \pi \Lambda _g} S G^a_{\mu \nu }G^{a,\mu \nu }\nonumber \\&\quad +\sum _{f=u,s,d,c,b} \left( \frac{v}{\Lambda _f} S \bar{q}_f q_f + \mathrm {h.c.}\right) . \end{aligned}$$

(1)

There could also be effective operators with a pseudo scalar. But their long distance behavior is in-distinguishable from the scalar case. Also the scalar has to couple to photon in order to be able to decay to diphoton. But that is irrelevant to most of our discussion.

Thanks to QCD factorization, the hadronic production cross section for S can be written as

$$\begin{aligned} \sigma ^{(i)}_0 =\tau \int ^1_\tau \frac{\mathrm{d}x}{x}\, \left( f_{i/N_1}(\tau /x) f_{\bar{i}/N_2}(x) + (i \leftrightarrow \bar{i}) \right) \hat{\sigma }^{(i)}_0,\nonumber \\ \end{aligned}$$

(2)

where $\tau = M^2_\mathrm{S}/E^2_\mathrm{CM}$. The operator in Eq. (1) leads to the following partonic cross section to the scalar production:

$$\begin{aligned}&{\hat{\sigma }}^{(g)}_0 = \frac{\pi }{16(N_\mathrm{c}^2 -1)} \left( \frac{\alpha _s}{3\pi \Lambda _g} \right) ^2, \nonumber \\&{\hat{\sigma }}^{(q)}_0 = \frac{\pi }{2 N_\mathrm{c}} \left( \frac{v}{\Lambda _q M_\mathrm{S}} \right) ^2. \end{aligned}$$

(3)

2.1 Rapidity distribution

It is well known that for W and Z boson production in the SM, contributions from different partonic channels have different shapes in rapidity distribution of the boson. Valence-quark contributions have a double shoulder structure while the sea-quark contributions peak in the central region due to different slopes of the parton distribution functions (PDFs) with respect to Bjorken x. The results are similar for a resonance of 750 GeV produced at 13 TeV LHC. One way to quantify the shape of rapidity distribution is to use the centrality ratio, which is defined as ratio of cross sections in central rapidity region $|y|<y_\mathrm{cut}$ and the total cross sections. In Fig. 1 we show the centrality ratio as a function of $y_\mathrm{cut}$ for a 750 GeV resonance produced through different parton combinations at leading order (LO). The hatched bands show the corresponding 68 % confidence level (C.L.) PDF uncertainties as calculated according to the PDF4LHC recommendation [39], which are small especially for the valence-quark contributions. The ratios approach one when $y_\mathrm{cut}$ approaches the endpoint of the rapidity distribution $\sim$2.8. As expected the valence-quark contributions have smaller values for the ratio than the ones from gluon or bottom quarks. The ratios are very close for gluon and bottom-quark or other sea-quark contributions, since the sea-quark PDFs are mostly driven by the gluon through DGLAP evolution. Taken $y_\mathrm{cut}$ to be 1, the centrality ratios are 0.74, 0.77, 0.63 and 0.50, for gg, $b\bar{b}$, $d \bar{d}$, and $u\bar{u}$ channels, respectively. Assuming most of the experimental systematics will cancel in the ratio and with high statistics, it will be possible to discriminate underlying theory with production initiated by valence quarks and by gluon or sea quarks. Higher-order perturbative corrections may change above numbers which depend on the full theory.

Fig. 1

Centrality ratio, defined as ratio of cross section in central rapidity region $|y|<y_\mathrm{cut}$ and the total cross section, as a function of $y_\mathrm{cut}$

2.2 Diphoton at small transverse momentum

We next consider the transverse momentum $Q_\mathrm{T}$ of the diphoton system. In the SM, transverse-momentum resummation for diphoton has been considered at Next-to-Next-to-Leading Logarithm (NNLL) level [58]. Fully differential distribution is also known at fixed next-to-next-to-leading order (NNLO) [46]. Here we consider the case where the diphoton originates from the decay of a new resonance at 750 GeV. At LO in QCD, $Q_\mathrm{T}$ is exactly zero due to momentum conservation in the transverse plane. However, as is well known from the study of Drell–Yan lepton pair transverse-momentum distribution, $Q_\mathrm{T}$ is not peaked at zero but rather at finite transverse momentum. The shift from $Q_\mathrm{T}=0$ to non-zero value is mostly due to initial-state QCD radiation. For example, if the diphoton is produced from gg fusion, the initial-state gluon in one proton can split into two gluons before colliding with the gluon from the other proton. The diphoton system is pushed to non-zero $Q_\mathrm{T}$ as a result of the splitting process. For large $Q_\mathrm{T}$, the strong coupling is small and perturbative expansion works well. However, when $Q_\mathrm{T}$ is much smaller than $M_\mathrm{S}$, large logarithms of the ratio between $M_\mathrm{S}$ and $Q_\mathrm{T}$ could arise, which spoils the convergence of the perturbative series. As an example, at NLO, the partonic cross section for the $Q_\mathrm{T}$ distribution of the diphoton system at leading power in $Q_\mathrm{T}^2/M^2_\mathrm{S}$ can be written as

$$\begin{aligned} \left. \frac{\mathrm{d}\sigma ^{(g)}}{\mathrm{d}Q^2_\mathrm{T}}\right| _{Q^2_\mathrm{T}>0}= & {} \,\left( \frac{\alpha _s}{4\pi } \right) 2 \tau \hat{\sigma }^{(g)}_0 \sum _{a,b} \int ^1_0 \mathrm{d}x_1 \int ^1_0 \mathrm{d}x_2 \, \delta ( x_1 x_2 - \tau ) \nonumber \\&\times \int ^1_{x_1} \frac{\mathrm{d}\xi _1}{\xi _1} f_{a/N_1}(x_1/\xi _1) \int ^1_{x_2} \frac{\mathrm{d}\xi _2}{\xi _2} f_{b/N_2}(x_2/\xi _2) \nonumber \\&\cdot \left\{ \phantom {\frac{ 2 P_{gb}(\xi _2) }{Q^2_\mathrm{T}}} \delta _{ag}\delta _{bg} \delta ( 1 - \xi _1) \delta ( 1 - \xi _2) \right. \nonumber \\&\times \left[ 4C_\mathrm{A} \frac{\ln (M^2_\mathrm{S}/Q^2_\mathrm{T})}{Q^2_\mathrm{T}} - \left( \frac{22}{3} C_\mathrm{A} - \frac{4}{3} N_f \right) \frac{1}{Q^2_\mathrm{T}} \right] \nonumber \\&+ \frac{2 P_{ga}(\xi _1) }{Q^2_\mathrm{T}} \delta _{bg} \delta (1 - \xi _2) \nonumber \\&+ \left. \frac{ 2 P_{gb}(\xi _2) }{Q^2_\mathrm{T}} \delta _{ag} \delta (1 - \xi _1) \right\} + {\mathscr {O}}(\alpha _s^2) \end{aligned}$$

(4)

for gg-fusion production. Similarly, for $q\bar{q}$ induced diphoton production, we have

$$\begin{aligned} \left. \frac{\mathrm{d}\sigma ^{(q)}}{\mathrm{d}Q^2_\mathrm{T}}\right| _{Q^2_\mathrm{T}>0}= & {} \, \left( \frac{\alpha _s}{4\pi } \right) \tau \hat{\sigma }^{(q)}_0 \sum _{a,b} \int ^1_0 \mathrm{d}x_1 \int ^1_0 \mathrm{d}x_2 \, \delta ( x_1 x_2 - \tau )\nonumber \\&\times \int ^1_{x_1} \frac{\mathrm{d}\xi _1}{\xi _1} f_{a/N_1}(x_1/\xi _1) \int ^1_{x_2} \frac{\mathrm{d}\xi _2}{\xi _2} f_{b/N_2}(x_2/\xi _2)\nonumber \\&\times \left\{ \phantom {\frac{ 2P_{gb}(\xi _2) }{Q^2_\mathrm{T}}} \delta _{aq}\delta _{b\bar{q}} \delta ( 1 - \xi _1) \delta ( 1 - \xi _2)\right. \nonumber \\&\times \left[ 4C_\mathrm{F} \frac{\ln (M^2_\mathrm{S}/Q^2_\mathrm{T})}{Q^2_\mathrm{T}} - 6 C_\mathrm{F}\frac{1}{Q^2_\mathrm{T}} \right] \nonumber \\&+ \frac{ 2P_{qa}(\xi _1) }{Q^2_\mathrm{T}} \delta _{\bar{q}g} \delta (1 - \xi _2) \nonumber \\&\left. + \frac{ 2P_{gb}(\xi _2) }{Q^2_\mathrm{T}} \delta _{ag} \delta (1 - \xi _1) \right\} + \left( q \leftrightarrow \bar{q} \right) + {\mathscr {O}}(\alpha _s^2),\nonumber \\ \end{aligned}$$

(5)

where $P_{ij}(z)$ are the LO QCD splitting functions:

$$\begin{aligned} P_{qq}(z)&= C_\mathrm{F} \left[ \frac{1+z^2}{1 - z} \right] _+, \nonumber \\ P_{qg}(z)&= \frac{1}{2} \left[ (1-z)^2 + z^2 \right] , \nonumber \\ P_{gg}(z)&= 2 C_\mathrm{A} \frac{(1 -z + z^2)^2}{z} \left[ \frac{1}{1-z} \right] _+ \nonumber \\&\quad + \left( \frac{11}{6} C_\mathrm{A} - \frac{1}{3} N_f \right) \delta ( 1 -z) ,\nonumber \\ P_{gq}(z)&= C_\mathrm{F} \frac{ 1 + (1-z)^2}{z}. \end{aligned}$$

(6)

It is clear from Eq. (4) that when $Q_\mathrm{T}$ is very small, the logarithm $\ln ^{(0,1)}(M^2_\mathrm{S}/Q^2_\mathrm{T})/Q^2_\mathrm{T}$ can become very large and perturbative expansion in $\alpha _s$ is no longer valid. The origin of these large logarithms is due to long distance QCD effects: soft and/or collinear radiation from initial-state partons. Thanks to QCD factorization, the dynamics of soft and/or collinear radiation can be well separated from the dynamics of UV physics. This is particular useful for us, because we would like to perform a beam tagging study in a way that does not rely too much on the underlying BSM models, e.g., tree-level induced or loop-induced S production. From Eq. (4), one can also see that the leading logarithmic term differs between gg-fusion cross section and $q\bar{q}$ annihilation cross section, which is mainly due to the difference in the associated color factor, $C_\mathrm{A}=3$ versus $C_\mathrm{F}= 4/3$. It is then expected that the difference can lead to different shape in the $Q_\mathrm{T}$ spectrum. Since the perturbative expansion of the $Q_\mathrm{T}$ spectrum does not converge at low $Q_\mathrm{T}$, resummation of the large $Q_\mathrm{T}$ logarithms is required before one can assess the significance of the change in shape for the $Q_\mathrm{T}$ spectrum when switch between gg fusion and $q\bar{q}$ annihilation. Fortunately, resumming the large logarithms due to small transverse momentum has been studied since the early days of QCD [47, 60–62, 81, 129]. The formalism developed in this pioneer work can be used in our 750 GeV diphoton study with little change, thanks to the universality of QCD at long distance. According to the celebrated Collins–Soper–Sterman (CSS) formula [62], the $Q_\mathrm{T}$ distribution of the diphoton system can be written as an inverse Fourier transformation:

$$\begin{aligned} \frac{\mathrm{d}\sigma ^{(i)}}{\mathrm{d}Q^2_\mathrm{T}}= & {} \, \tau \hat{\sigma }^{(i)}_0 \int ^\infty _0 \frac{\mathrm{d}b}{2 }\, bJ_0(b Q_\mathrm{T}) \sum _{a,b} \int ^1_0 \mathrm{d}x_1 \int ^1_0 \mathrm{d}x_2\, \nonumber \\&\times \, \delta ( x_1 x_2 -\tau ) \int ^1_{x_1} \frac{\mathrm{d}\xi _1}{\xi _1} C^{(i)}_{ia} \left( \xi _1; \mu =\frac{b_0}{b} \right) \nonumber \\&\times f_{a/N_1} \left( \frac{x_1}{\xi _1}; \mu = \frac{b_0}{b} \right) \int ^1_{x_2} \frac{\mathrm{d}\xi _2}{\xi _2}\, C^{(\bar{i})}_{\bar{i}b} \left( \xi _2; \mu =\frac{b_0}{b} \right) \nonumber \\&\times f_{b/N_2} \left( \frac{x_2}{\xi _2}; \mu = \frac{b_0}{b} \right) \exp \left\{ - \int ^{M^2_\mathrm{S}}_{b^2_0/b^2} \frac{\mathrm{d} \bar{\mu }^2}{\bar{\mu }^2}\right. \nonumber \\&\times \left. \left[ \ln \frac{M^2_\mathrm{S}}{\bar{\mu }^2} A^{(i)}[ \alpha _s(\bar{\mu })] + B^{(i)}[ \alpha _s(\bar{\mu })] \right] \right\} \nonumber \\&+ \left( i \leftrightarrow \bar{i} \right) + Y(Q^2_\mathrm{T},M^2_\mathrm{S},E_\mathrm{CM}^2), \end{aligned}$$

(7)

where $J_0(x)$ is the zeroth order Bessel function of the first kind, $b_0 = 2\mathrm{e}^{-\gamma _{\scriptscriptstyle \mathrm{E}}}$, $\gamma _{\scriptscriptstyle \mathrm{E}}=0.577216\ldots$ is Euler’s constant. The summation of a and b are over different parton species, $u,\bar{u}, d,\ldots ,g$. $A[ \alpha _s(\bar{\mu })]$ and $B[ \alpha _s(\bar{\mu })]$ are universal anomalous dimensions whose perturbative expansions can be written as

$$\begin{aligned} A^{(i)}[ \alpha _s(\mu )]&= \sum _{n=1}^\infty \left( \frac{\alpha _s(\mu )}{4\pi } \right) ^{n} A^{(i)}_n, \nonumber \\ B^{(i)}[ \alpha _s(\mu )]&= \sum _{n=1}^\infty \left( \frac{\alpha _s(\mu )}{4\pi } \right) ^{n} B^{(i)}_n. \end{aligned}$$

(8)

In this work, we restrict ourselves to resummation of $Q_\mathrm{T}$ logarithms at Next-to-Leading Logarithmic (NLL) accuracy only, for which only $A^{(i)}_1$, $A^{(i)}_2$, and $B^{(i)}_1$ are needed. They are given by [70, 110, 111]

$$\begin{aligned}&A^{(i)}_1 = 4 C^{(i)}, \nonumber \\&A^{(i)}_2 = 4 C^{(i)} \left( \left( \frac{67}{9}-\frac{\pi ^2}{3}\right) C_\mathrm{A}-\frac{10 N_f}{9}\right) , \nonumber \\&B^{(g)}_1 = - \frac{22}{3} C_\mathrm{A} + \frac{4}{3} N_f, \nonumber \\&B^{(q)}_1 = -6 C_\mathrm{F}, \end{aligned}$$

(9)

where $C^{(g)} = C_\mathrm{A}$, $C^{(q)}= C_\mathrm{F}$. The function $C^{(i)}_{ij}(x;\mu )$ is the hard collinear factor. For NLL resummation, we only need their LO expression:

$$\begin{aligned} C^{(i)}_{ij} (x;\mu ) = \delta _{ij} \delta (1-x). \end{aligned}$$

(10)

$Y(Q^2_\mathrm{T},\tau )$ denotes those terms which are not enhanced by $\ln (M^2_\mathrm{S}/Q^2_\mathrm{T})$. They can be computed using a naive expansion in $\alpha _s$. Sometimes they could have large impact at large $Q_\mathrm{T}$. But in the region we are interested in, they can be safely neglected. Note that in Eq. (7), when b is very large, the integral for $\bar{\mu }$ in the exponent would hit a Landau pole, where $\alpha _s(\bar{\mu })$ diverges. The existence of the Landau pole at small $\bar{\mu }$ indicates the onset of non-perturbative physics in that region, and an appropriate prescription to deal with the Landau pole is needed; see, e.g., Refs. [36, 62, 113, 134]. We emphasize that the CSS formula is quite general and does not depend too much on the UV dynamics of the underlying process. Remarkably, at NLL level, all the process dependent information have been encoded in the tree partonic cross section $\hat{\sigma }^{(i)}_0$, and in the label (i) for various dimension and collinear factor. Thus, we expect that the statement we make from the $Q_\mathrm{T}$ spectrum is rather model independent.

Fig. 2

$Q_\mathrm{T}$ distribution at small transverse momentum at NLL accuracy for the resonance production initiated by different parton flavors. The two plots show results obtained from two public codes, HqT and CuTe

To quantify the discussion above, we calculate the $Q_\mathrm{T}$ spectrum of the 750 GeV diphoton system numerically for 13 TeV LHC. Thanks to the previous QCD studies, several public computer codes are available which implement the resummation of transverse-momentum logarithms for Drell–Yan and Higgs production, both in the QCD framework and in the Soft-Collinear Effective theory framework [20–23]. Resummation of $Q_\mathrm{T}$ for 750 GeV diphoton resonance can be easily accomplished by modifying those existing codes. Specifically, we modify HqT, which is based on the work of Refs. [35–37, 74], and CuTe, which is based on the work of Refs. [24, 25], to calculate the transverse-momentum spectrum of the hypothetical 750 GeV resonance. In HqT, a Landau pole is avoided by deforming the b-space integral off the real axis slightly, while in CuTe, the Landau pole is avoided by imposing a cutoff for the $\bar{\mu }$ integral at very small value. In both calculations, we use the five-flavor scheme, namely the bottom quark is treated as a massless parton in the PDFs.

We calculate the $Q_\mathrm{T}$ spectrum by turning on the coupling of the diphoton resonance with each individual parton flavor at one time. The differential distribution is plotted in Fig. 2 for results from the two codes mentioned above at NLL resummed accuracy. Comparing the distributions for production initiated by different parton combinations, the shapes are mostly driven by two factors: (a) the color factor in Sudakov exponent, $C_\mathrm{A}$ for gluon versus $C_\mathrm{F}$ for quarks; (b) the evolution of PDFs. For light-quark contributions, which includes up, down, strange, and charm quark, the peak position stay at low values, less than 10 GeV in general. For bottom-quark case, the distributions are broader and shift to higher $Q_\mathrm{T}$. The reason for the rightward shift of the bottom contribution comparing to the light-quark contribution is as follows. For the formal treatment of the quark contribution in the CSS formula, Eq. (7), there are no essential difference between light quark and bottom quark. The only difference comes from their PDFs, which are evaluated at the scale $b_0/b$, the Fourier conjugate of $Q_\mathrm{T}$. While the DGLAP evolution for light quark and bottom quark are the same in the five-flavor scheme, the boundary conditions for these PDFs differ. For bottom quark, the threshold of the corresponding PDF lies around $m_b \sim 4.2$ GeV, below which the PDF vanishes. On the other hand, the threshold of the light-quark PDFs lies around much lower values than the bottom-quark one. It thus indicates that the Sudakov peak for bottom-quark contribution has to show up at larger value of $Q_\mathrm{T}$ in order to accommodate the fact that its threshold is higher. For the gluon contribution, the shape of the $Q_\mathrm{T}$ spectrum is further broadened, and has the largest value for the peak position. This is mainly due to the difference in color factor. In the gluon case, the Sudakov exponent has a stronger suppression effects because $C_\mathrm{A} \sim 2.25\, C_\mathrm{F}$. We have checked that if we naively change the color factor from $C_\mathrm{A}$ to $C_\mathrm{F}$ for the gluon contribution, its peak position move to a much lower value. From Fig. 2, we can see that the results from the two codes used for the calculation are similar, although they have a different framework for resummation and a different treatment of the Landau pole. The major difference comes from the bottom-quark contribution, where the peak position differ by about 5 GeV. This is mainly due to different ways in the two codes to avoid Landau pole. Because of the large mass of the resonance, non-perturbative effects are less pronounced as comparing with the W, Z boson production in the SM, as we checked by varying the non-perturbative parameter available in HqT and CuTe. Also, for the same reason, the subleading terms in $Q_\mathrm{T}$ are small in the region we plot.

Table 1 Ratio R for a 750 GeV resonance produced at 13 TeV LHC, initiated by different parton flavors as predicted by two resummation codes, HqT and CuTe

Ideally, a detailed comparison of the normalized $Q_\mathrm{T}$ distribution predicted by QCD factorization and the LHC data for the hypothetical resonance would provide most information as regards the beam tagging problem from $Q_\mathrm{T}$ spectrum. In reality, this is very difficult due to the limited statistics and experimental uncertainties in measuring the photon transverse momentum. To simplify the analysis, we introduce a ratio R, which is defined as the cross section in $Q_\mathrm{T}$ bin of $[\Delta _\mathrm{T},2 \Delta _\mathrm{T}]$ to the one in $Q_\mathrm{T}$ bin of $[0,\Delta _\mathrm{T}]$. The optimal choice for $\Delta _\mathrm{T}$ differs for different center of mass energy and different resonance mass. In our current case, we choose $\Delta _\mathrm{T}=20$ GeV. The results for the ratio are listed in Table 1 based on curves shown in Fig. 2 for the two codes and various parton flavors. We can see a clear distinction for production initiated by light quarks, which favor a value of R lower than 1, and production initiated by gluon, which favors a value of R larger than 1. As noted above, prediction for bottom-quark initiated production are quite different, indicating a larger theoretical uncertainty in the resummation treatment of heavy-quark induced diphoton production. This uncertainty prevents us from distinguishing it from gluon initiated case. The uncertainty might be reduced if the calculation is extended to NNLL level consistently, or using four-flavor scheme for the PDFs, which are beyond the scope of this work. We have also checked the theoretical uncertainties from other sources, e.g., PDFs and power corrections which are at a few percent level and can be neglected safely.

2.3 Diphoton with additional b-jet

In the previous two sections, we have shown that by measuring the rapidity and transverse-momentum distribution of the diphoton system, it is possible to distinguish the valence-quark induced diphoton production from sea-quark/gluon induced diphoton production, and light-quark induced diphoton production from gluon induced diphoton production. In this section, we focus on the remaining two production scenarios. In the first scenario (gg), the new scalar resonance is produced via the gluon fusion process. In the second scenario (bb), the scalar resonance is produced via $b\bar{b}$ initial state. We will show that a 99.7 % C.L. distinguish can be reached with less than 10 fb$^{-1}$ integrated luminosity at 13 TeV LHC. This means if the 750 GeV excess is indeed a new resonance, we do not need to wait for long to know its production mechanism.

In the gg scenario, the dominant production mode of the new resonance is gluon fusion process. With the initial-state radiation (ISR) effect, there are additional jets in the final state. The Feynman diagrams for jet production at LO in QCD are shown in Fig. 3. Since in the small-x region the gluon PDF is much larger than other partons, it is easy to see that most of the ISR jets are gluon and light (especially u and d) quarks. The b-jet fraction in the ISR jets is highly suppressed by the smallness of bottom-quark PDF. Thus we expect that the number of hard b-jet in the ISR jets is small.

Fig. 3

The Feynman diagrams of the resonance with one jet production process in gg scenario

In the bb scenario, we show the Feynman diagrams for jet production at LO in QCD in Fig. 4. The large gluon PDF induces a lot of b-jets from the $gb(\bar{b})$ initial-state processes. The b-jet fraction in the ISR jets then should be significant and can be tagged at the LHC Run 2.

Fig. 4

The Feynman diagrams of the resonance with one jet production process. In this scenario, the new resonance is produced via the $b\bar{b}$ initial state at the LHC

For a simple estimation, we generate parton level signal events with MadGraph5 [10] and CT14llo PDF (five-flavor scheme) [82]. The signal events are showered using Pythia6.4 [137] with Tune Z2 parameter [88]. The detector effect is simulated using DELPHES 3 [40, 73]. The b-tagging efficiency is tuned to be consistent with the distribution shown in Ref. [1]. For the signal strength, we scale the inclusive signal events (with MLM matching scheme) to fit the current data [2, 3] (in this work, we only fit the data from the ATLAS collaboration). We require the photon to satisfy

$$\begin{aligned} |\eta |<1.37,\quad {\text {or}}\quad 1.52<|\eta |<2.37. \end{aligned}$$

(11)

The transverse energy of the leading (subleading) photon should be larger than 40 (30) GeV. The leading and subleading photon candidates are then required to satisfy the conditions

$$\begin{aligned} \frac{E_{\text {T}}^{\gamma _1}}{m_{\gamma \gamma }}>0.4,\quad \frac{E_{\text {T}}^{\gamma _2}}{m_{\gamma \gamma }}>0.3. \end{aligned}$$

(12)

The inclusive diphoton spectrum is estimated with

$$\begin{aligned} 0.026\left[ 1-\left( \frac{m_{\gamma \gamma }}{13\,{\text {TeV}}}\right) ^{1/45}\right] ^{3.38}\left( \frac{m_{\gamma \gamma }}{13\,{\text {TeV}}}\right) ^{-3.49}\, {\text {fb/GeV}}. \end{aligned}$$

(13)

We solve the best-fit signal strength $\mu$ by maximizing [64, 135]

$$\begin{aligned} \sqrt{-2\ln \left[ \frac{L\left( \{b\}|\{n\}\right) }{L\left( \mu \{s\}+\{b\}|\{n\}\right) }\right] }, \end{aligned}$$

(14)

where the likelihood function is defined by

$$\begin{aligned} L\left( \{x\}|\{n\}\right) \equiv \prod _{i}\frac{x_i^{n_i}\exp \left( -x_i\right) }{\Gamma \left( n_i+1\right) }. \end{aligned}$$

(15)

Both the gg and the bb scenario give $3\sigma$ discovery significance.

After normalizing the inclusive cross section to the best-fit value, we select events with at least one hard jet in the final state. Jets in the final state are reconstructed using anti-$k_{\text {T}}$ jet algorithm with $R=0.4$. We demand the leading jet to have

$$\begin{aligned} |\eta |<2.5,\quad \hbox {and}\quad p_{\text {T}}>40\,{\text {GeV}}. \end{aligned}$$

(16)

To suppress the SM background, we further require the diphoton invariant mass to satisfy $|m_{\gamma \gamma }-750\,{\text {GeV}}|<150\,{\text {GeV}}$. Transverse momentum distributions of the leading jet are shown in Fig. 5 for different production mechanisms with and without requiring the leading jet is b-tagged.

Fig. 5

Transverse-momentum distribution of the leading-(b-)jet

At 13 TeV LHC, in gg scenario the inclusive one-jet events contain a fraction of 0.08 fb b-jet events out of a total cross section of 3.12 fb. Alternatively, the fraction is 1.21 fb out of 2.72 fb in bb scenario.

To give an estimation of the possibility of distinguishing the two production scenarios, we also need to simulate the SM backgrounds. There are lots of theoretical uncertainties. Only a data driven estimation of the backgrounds is reliable at present. In this work, we make a simple estimation by rescaling the current background with luminosity. Thus we only need to calculate the fraction of the background events with additional hard b-jet. The most important SM backgrounds are the irreducible $\gamma \gamma$ process and the reducible $\gamma j$ and jj processes with one or more jets faked to be photon in the detector. With the mass window cut, we count the fraction of events with at least one additional hard jet ($N_{+j}/N_\mathrm{incl}$), and the fraction of these events whose leading jet is tagged as a b-jet ($N_{+b}/N_{+j}$). Since the cut on the first and the second photon transverse energy are asymmetric, there are a lot of events which pass the cuts with additional jets from the ISR. The results are shown in Table 2. With the data driven background formula Eq. (13), the total background cross section in $600\,{\text {GeV}}<m_{\gamma \gamma }<900 \,{\text {GeV}}$ is 15.32 fb.

Table 2 The fraction of the background events with at least one additional hard jet. The fraction of the events with the leading jet is tagged as a b-jet in these events. In the last line, we show the $N_{+b}$ event number with the assumption that all background events are from the corresponding process

Since the background cross section is small, we estimate the ability of distinguishing the gg scenario from the bb scenario with [64, 135]

$$\begin{aligned} {\text {CL}}_{g}\equiv \sqrt{-2\log \left[ \frac{L\left( s_b+n_b|s_g+n_b\right) }{L\left( s_g+n_b|s_g+n_b\right) }\right] }, \end{aligned}$$

(17)

and the bb scenario from the gg scenario with

$$\begin{aligned} {\text {CL}}_{b}\equiv \sqrt{-2\log \left[ \frac{L\left( s_g+n_b|s_b+n_b\right) }{L\left( s_b+n_b|s_b+n_b\right) }\right] }, \end{aligned}$$

(18)

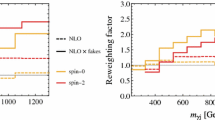
respectively, where $s_b,s_g$, and $n_b$ are the event numbers with the leading additional jet tagged as a b-jet in the scenario bb, scenario gg and the SM background. In Fig. 6, we show the discriminating abilities versus the integrated luminosity of the LHC in the 13 TeV run. It is shown clearly in this figure that, even with the most conservative assumption (all background events are from the jj process), one can distinguish the gg scenario from the bb scenario with 8.8 fb$^{-1}$ integrated luminosity, and distinguish the bb scenario from the gg scenario with 6.2 fb$^{-1}$ integrated luminosity at 13 TeV LHC. If the SM background are (a MC simulation will support this assumption) $\gamma \gamma$ process dominant, one can distinguish the gg scenario from the bb scenario with 6.0 fb$^{-1}$ integrated luminosity, and distinguish the bb scenario from the gg scenario with 3.3 fb$^{-1}$ integrated luminosity at 13 TeV LHC.

Fig. 6

The ability of distinguishing the gg (bb) scenario from the bb (gg) scenario. The solid lines are with the assumption that all of the background events are from the irreducible $\gamma \gamma$ background. The dashed lines are with the assumption that all of the background events are from the reducible jj background with two jets are faked as photon

3 Summary and conclusion

Recently, an intriguing excess in the diphoton events has been reported both by the ATLAS and CMS collaboration. The local significance is 3.9$\sigma$ from ATLAS and 2.6$\sigma$ from CMS. After taking into account the look-elsewhere effect, the significance reduces to 2.3$\sigma$ from ATLAS and 1.2$\sigma$ from CMS. Although the current experimental status is far from conclusive, a large number of BSM scenarios have been explored to explain the diphoton excess. A significant number of these BSM models contain a scalar resonance produced from hadron-hadron collision and subsequently decay to diphoton system, whose mass is around 750 GeV. In this work, we investigated whether the hadronic production mechanism for the hypothetical new scalar resonance can be identified. That is, is it mainly produced from gg fusion or $q\bar{q}$ annihilation. We dubbed this question the quark and gluon beam tagging problem. We expect that a successful solution to this problem will play a key role in unraveling the mystery of the 750 GeV diphoton excess. We have performed a model independent studied of this problem by considering a set of effective operators between the hypothetical resonance and gluon or quark. We discuss several differential distributions relevant for the determination of initial constituent for the 750 GeV excess. We concentrate on those distributions which are more sensitive to QCD dynamics at long distance, and thus less model dependent. To that end, we explored three different but complementary observables for beam tagging. First, we calculated the rapidity distribution of the diphoton system, and we found that it is helpful for distinguishing valence quark induced production from gluon or sea-quark induced production. The main reason is that the PDFs for u and d quarks are much larger at large x, comparing to $\bar{u}$ and $\bar{d}$ quarks. Second, we calculated the transverse-momentum spectrum of the diphoton system and focus on the small $Q_\mathrm{T}$ region, where a Sudakov peak is formed due to multiple soft and/or collinear radiation from initial state. We found that a clear distinction for the light-quark induced production from the gluon or b-quark induced production can be achieved. This is mainly due to the difference in the effective strength of initial-state bremsstrahlung: for light quark it is $C_\mathrm{F} \alpha _s = \frac{4}{3} \alpha _s$, while for gluon it is $C_\mathrm{A} \alpha _s = 3 \alpha _s$. Such difference leads to a notable shift of the peak toward larger $Q_\mathrm{T}$, as well as a much broader peak. For b quark induced production, the difference in the peak structure from gluon induced production is less pronounced, due to the large b quark mass and uncertainty associated with $Q_\mathrm{T}$ resummation in five-flavor scheme versus four-flavor scheme. Third, in order to distinguish the gluon induced production from b quark induced production, we calculated the diphoton plus jet production with a b tagging on the leading jet in five-flavor scheme. We find that an additional b jet is more favored in b quark induced production than in gluon induced production. Combining the knowledge gained from all there observables, we find that the perspective for identifying the exact production mechanism for the hypothetical diphoton resonance is promising, though detailed work is needed in order to further understand the theory and experimental uncertainties of our methods, which we leave for future work. Lastly, we emphasize that although the current work is mainly motivated by the diphoton excess recently reported by the ATLAS and CMS collaboration, the problem we proposed and the methods we suggested are useful and interesting in itself even the excess disappears after more data is collected.