The $\rho (\omega ) B^* (B)$ interaction and states of $J=0,1,2$

Abstract

In this work, we study systems composed of a $\rho /\omega$ and $B^*$ meson pair. We find three bound states in isospin, spin-parity channels $(1/2, 0^+)$, $(1/2, 1^+)$, and $(1/2, 2^+)$. The state with $J=2$ can be a good candidate for the $B_2^*(5747)$. We also study the $\rho B$ system, and a bound state with mass 5728 MeV and width around 20 MeV is obtained, which can be identified with the $B_1(5721)$ resonance. In the case of $I=3/2$, one obtains repulsion and, thus, no exotic (molecular) mesons in this sector are generated in the approach.

1 Introduction

Chiral symmetry, reflecting the QCD dynamics at low energies, has played a crucial role in the description of the hadron interactions. Originally developed for the interaction of pseudoscalar mesons [1] and of the meson nucleon system [2, 3], the need to incorporate vector mesons into the framework gave rise to the local hidden gauge approach [4–6], which incorporates the information of the chiral Lagrangians of [1] and extends it to accommodate the vector interaction with pseudoscalars and with themselves. Another important step to understand the dynamics of hadrons at low and intermediate energies was given by incorporating elements of non-perturbative physics, restoring two body unitarity in coupled channels, which gave rise to the chiral unitary approach, which has been instrumental in explaining many properties of hadronic resonances, mesonic [7–12], and baryonic [13–24]. Concerning the interaction of vector mesons in this unitary approach, the first work was done in [25], where surprisingly the $f_2(1270)$ and $f_0(1370)$ resonances appeared as a consequence of the interaction of $\rho$ mesons from the solution of the Bethe–Salpeter equation with the potential generated from the local hidden gauge Lagrangians [4–6]. The generalization to SU(3) of that work was done in [26] and further resonances came from this approach, the $f'_2(1525), f_0(1710)$ among others. Most of these findings were confirmed in the SU(6) spin-flavor symmetry scheme followed by [27]. The step to incorporate charm in the local hidden gauge approach of Refs. [25, 26] was given in [28], and the interaction of $\rho$, $\omega$, and $D^*$ was studied extrapolating to the charm sector the local hidden gauge approach. Three D states with spin $J=0,1,2$ were obtained, the second one identified with the $D^*(2640)$ and the last one with the $D^*_2(2460)$. The first state, with $J=0$, was predicted at 2600 MeV with a width of about 100 MeV. This state is also in agreement with the D(2600), with a similar width, reported after the theoretical work in [29]. The properties of these resonances are well described by the theoretical approach.

The success in the predictions of this theoretical framework in the light and the charm sectors suggests to give the step to the bottom sector and make predictions in this work. The extension is straightforward, because the interaction in the local hidden gauge approach is provided by the exchange of vector mesons. The exchange of light vectors is identical to the case of the $\rho D^*$ interaction, since the c or b quarks act as spectators. In the exchange of heavy vectors, the form and the coefficients are also the same, since the $\bar{B}$ meson can be obtained from the D simply replacing the c quark by the b quark. However, instead of exchanging a $D^*$ in the sub-dominant terms, one exchanges now a $B^*$ meson. These terms are anyway sub-dominant. Hence, it is not surprising that the predictions that we obtain in this work in the B sector are very similar to those obtained in [28] in the D sector.

We shall also discuss the heavy quark spin symmetry (HQSS), which we show is satisfied by the dominant terms of the interaction, and then discuss the relevance of the sub-dominant HQSS breaking terms. We make predictions for three states from the $\rho /\omega \, B^*$ interaction and compare with available experimental states. As we shall see, the role played by the $\omega$ meson is minor and it is not as important as that of the $\rho$ meson.

In a similar way, we also deal with the interaction of $\rho B$ in s-wave, which gives rise to a state of $J=1$ which we can identify with a state already existing. This interaction follows also from the local hidden gauge approach, although equivalent chiral Lagrangians have been used in the light sector [27, 30, 31] and in the D sector [32, 33].

2 Formalism

We are going to use the local hidden gauge approach where the interaction is given mainly by the exchange of vector mesons. We follow closely the approach of [28] and with minimal changes we can obtain most of the equations.

2.1 Vector–vector interaction

We take the vector–vector interaction from [4] as

$$\begin{aligned} \mathcal {L}_{III}=-\frac{1}{4}\left\langle V_{\mu \nu }V^{\mu \nu }\right\rangle . \end{aligned}$$

(1)

where the symbol $\langle \rangle$ represents the trace in SU(4) flavor space (we consider u, d, s, and b quarks), with

$$\begin{aligned} V_{\mu \nu }=\partial _\mu V_\nu -\partial _\nu V_\mu -ig[V_\mu ,V_\nu ] \end{aligned}$$

(2)

and

$$\begin{aligned} V_{\mu }=\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}} &{} \rho ^+ &{} K^{*+} &{} B^{*+} \\ \rho ^- &{} -\frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}} &{} K^{*0} &{} B^{*0} \\ K^{*-} &{} \bar{K}^{*0} &{} \phi &{} B_s^{*0} \\ B^{*-} &{} \bar{B}^{*0} &{} \bar{B}_s^{*0} &{} \Upsilon \\ \end{array} \right) _{\mu } \end{aligned}$$

(3)

standing for the vector representation of the different $q\bar{q}$ pairs, and the coupling g is given by

$$\begin{aligned} g=\frac{m_V}{2f} \end{aligned}$$

(4)

with the pion decay constant $f\simeq 93$ MeV, and $m_V\simeq 770$ MeV. One may wonder why still the value of g in SU(3) is used in the heavy sector. We give a justification at the end of Sect. 3 when we discuss the implications of HQSS for the $B^*B\pi$ vertex.

The local hidden gauge Lagrangians also contains a four vector contact term,

$$\begin{aligned} \mathcal {L}_{III}^{(c)}=\frac{g^2}{2}\langle V_\mu V_\nu V^{\mu }V^{\nu }-V_\nu V_\mu V^{\mu }V^{\nu }\rangle , \end{aligned}$$

(5)

which in the $\rho /\omega B^*$ channel gives rise to the term depicted in Fig. 1a.

Fig. 1

The model for the $\rho /\omega \, B^*$ interaction

From Eq. (1) we also get a three vector interaction term

$$\begin{aligned} \mathcal {L}_{III}^{3V}=ig\left\langle \left( V^\mu \partial _\nu V_\mu -\partial _\nu V_\mu V^\mu \right) V^\nu \right\rangle . \end{aligned}$$

(6)

The latter Lagrangian gives rise to a VV interaction term through the exchange of a virtual vector meson, as depicted in Fig. 1b, c. As in [28] we also assume that the three momenta of the particles are small compared to the vector masses. This helps to simplify the formalism.

We consider the $\rho /\omega \,B^*$ states

$$\begin{aligned}&\left| \rho B^*; I{=}1/2, I_3{=}1/2\right\rangle {=}-\sqrt{\frac{2}{3}}\left| \rho ^+B^{*0}\right\rangle {-}\sqrt{\frac{1}{3}}\left| \rho ^0B^{*+}\right\rangle , \nonumber \\&\left| \rho B^*; I=3/2, I_3=3/2\right\rangle =-\left| \rho ^+ B^{*+}\right\rangle ,\nonumber \\&\left| \omega B^*; I=1/2, I_3=1/2\right\rangle =\left| \omega B^{*+}\right\rangle . \end{aligned}$$

(7)

Here the isospin doublets are $(K^{*+},K^{*0})$, $(\bar{K}^{*0},-K^{*-})$, $(B^{*+},B^{*0})$, $(\bar{B}^{*0},-B^{*-})$, and the rho triplet is $(-\rho ^+, \rho ^0, \rho ^-)$.

The contact terms are all of the type

$$\begin{aligned} -it^{(c)}_{\rho B^*\rightarrow \rho B^*}&=-ig^2(\alpha \epsilon _\mu ^{(1)}\epsilon _\nu ^{(2)}\epsilon ^{(3)\nu }\epsilon ^{(4)\mu }\nonumber \\&\quad + \, \beta \epsilon _\mu ^{(1)}\epsilon _\mu ^{(2)}\epsilon ^{(3)\nu }\epsilon ^{(4)\nu }\nonumber \\&\quad + \,\gamma \epsilon _\nu ^{(1)}\epsilon _\mu ^{(2)}\epsilon ^{(3)\nu }\epsilon ^{(4)\mu }), \end{aligned}$$

(8)

with $\epsilon ^\mu$ the polarization vectors of the vector mesons in the order 1, 2, 3, 4, where these indices are used in the reaction $1+2\rightarrow 3+4$ ($\rho B^*\rightarrow \rho B^*$). Note that we are using real polarization vectors.

Analogously, the terms associated to vector exchange of the type of Fig. 1b are particularly easy, since, neglecting the external three momenta, these terms are of the type

$$\begin{aligned} t^{(ex)}&=\frac{g^2}{m_V^2}\alpha ^\prime (k_1+k_3)\cdot (k_2+k_4)\epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\mu }\epsilon ^{(4)\nu }. \end{aligned}$$

(9)

The form of Eq. (9) stems from Eq. (6) assuming the $\epsilon ^0$ component of the external vector mesons to be zero, and neglecting the linear terms in three momentum coming from Eq. (6), which is quite reasonable for an s-wave. An explicit evaluation of the latter extra terms was done in [34], in the study of the $\gamma p\rightarrow K^0\Sigma ^+$ reaction, which showed the relevance of the VB intermediate states, where one finds the same three vector vertex of Fig. 1 (see Section 2 of [34]). The center of mass photon momentum in the reaction of [34] is about 780 MeV/c in spite of which, the linear terms in three momentum neglected in Eq. (9) were found to be of the order of $15~\%$. This could also explain why in the decay of resonances like the $f_2(1270)$ into two mesons, which rely upon the same vertices and approximations [35], the widths are obtained to be in good agreement with experiment, in spite of having two photons with momentum of 635 MeV/c. Note that in this case, the $f_2(1270)$, which comes as a two $\rho$ bound state, is bound by about 270 MeV. Since the $\epsilon ^0$ component goes as $| \vec {k}|/M_V$, the ratio for the $\rho B^*$ and $\rho \rho$ bound states would be about $M_\rho \sqrt{\mu (\rho B^*)B(\rho B^*)}/M_{B^*}\sqrt{\mu (\rho \rho )B(\rho \rho )}$, with $\mu (\rho B^*)$, $\mu (\rho \rho )$ the reduced mass and $B(\rho B^*)$, $B(\rho \rho )$ the binding energy of the bound state in the $\rho B^*$ and $\rho \rho$ systems, respectively. Taking into account that we get about 350 MeV binding for the $\rho B^*$ system, this ratio is of the order of about 0.22, which reinforces neglecting the $\epsilon ^0$ component of the external vectors assumed in Eq. (9). One should also keep in mind that small changes in the kernel of Eq. (9) can be reabsorbed by suitable changes in the cut off, since the combination $[V]^{-1}-G$ (V would sum contributions from $t^{(c)}$ and $t^{(ex)}$ from Eqs. (8) and (9)) is what appears in the evaluation of the final T-matrix, and one finally always tunes the cut off to some experimental data. We shall come back to this point in Sect. .

One can also be concerned about the momentum transfer, which may be larger than the external momenta, inducing some q dependence on the exchanged $\rho$ propagator, which in Eq. (9) is also approximated by $1/m_\rho ^2$. Explicit calculations keeping the $q^2$ dependence of the propagator have been done in [36]. However, it was also found in a later work [37] that the problem can be equally solved using a sharp cut off in three momenta in the loops, G, neglecting the $q^2$ dependence of the propagator, since ultimately this cut off is fitted to some experimental data.

It is interesting to point out that the dominant vector exchange terms (with light vector exchange, Fig. 1b) contribute neither to the $\omega B^*\rightarrow \omega B^*$ nor to the $\omega B^*\rightarrow \rho B^*$ transitions. Indeed, the $\omega \omega \omega$ vertex is forbidden by C-parity. Similarly, $\omega \omega \rho ^0$ is also forbidden for the same reason, and isospin. Finally, the $\rho \rho \omega$ (even with charged $\rho$) is not allowed by G parity conservation. The only way to have a contribution to the $\omega B^*\rightarrow \omega B^*$ transitions is through intermediate steps that involve the exchange of heavy vector mesons (Fig. 1c).

With the polarization structure of the amplitudes we can separate these terms into different spin contributions (we work only with angular momentum $L=0$) which are given by [25]

$$\begin{aligned} \mathcal {P}(0)&=\frac{1}{3}\epsilon ^{(1)}_\mu \epsilon ^{(2)\mu } \epsilon ^{(3)}_\nu \epsilon ^{(4)\nu },\end{aligned}$$

(10)

$$\begin{aligned} \mathcal {P}(1)&=\frac{1}{2}\left( \epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\mu } \epsilon ^{(4)\nu }-\epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\nu } \epsilon ^{(4)\mu }\right) ,\end{aligned}$$

(11)

$$\begin{aligned} \mathcal {P}(2)&=\frac{1}{2}\left( \epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\mu } \epsilon ^{(4)\nu }+\epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\nu } \epsilon ^{(4)\mu }\right) \nonumber \\&\quad - \,\frac{1}{3}\epsilon ^{(1)}_\mu \epsilon ^{(2)\mu } \epsilon ^{(3)}_\nu \epsilon ^{(4)\nu }. \end{aligned}$$

(12)

We can see that, while the contact terms give rise to different combinations of spin, the vector exchange term of type of Fig. 1b, contains the sum $\mathcal {P}(0)+\mathcal {P}(1)+\mathcal {P}(2)$, with equal weights for the different spins. This combination, corresponding to the exchange of a light vector meson ($\rho$, $\omega$, $\phi$, $K^*$) if allowed, satisfies HQSS to which we shall come back later on. On the other hand, the exchange of a heavy vector meson contains the combination

$$\begin{aligned} \epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\nu } \epsilon ^{(4)\mu }=\mathcal {P}(0)-\mathcal {P}(1)+\mathcal {P}(2) \end{aligned}$$

(13)

and does not satisfy leading order HQSS constraints, as we shall see in Sect. 4. This goes in line with HQSS, since the exchange of heavy vectors is penalized versus the exchange of light ones by a factor $m_V^2/m_{B^*}^2$ from the propagators and become sub-dominant. The contact term is also sub-dominant since it goes like $m_V/m_{B^*}$ of the dominant term from the exchange of a light vector. HQSS is satisfied only for the dominant term in the $\mathcal {O}(\frac{1}{m_{B^*}})$ counting, as it should.

Fig. 2

Interaction of $\rho B$ with vector exchange

2.2 Vector–pseudoscalar interaction

We shall also consider the $\rho B$ interaction. This proceeds via the exchange of a vector meson as in Fig. 2 and in this case there is no contact term. One can see that in the limit (which we also take) that $q^2/m_V^2\rightarrow 0$, where q is the momentum transfer, one obtains the chiral Lagrangian of [30]. The lower vertex VBB is given by the Lagrangian provided by the extended local hidden gauge approach

$$\begin{aligned} \mathcal {L}=-ig \left\langle \left[ \phi , \partial _\mu \phi \right] V^\mu \right\rangle , \end{aligned}$$

(14)

where now $\phi$ is the corresponding matrix of Eq. (3) for $q\bar{q}$ in the pseudoscalar representation. We obtain the same expression as for $\rho B^*\rightarrow \rho B^*$ (direct term in Fig. 1b) replacing

$$\begin{aligned} \epsilon ^{(1)}_\mu \epsilon ^{(2)}_\nu \epsilon ^{(3)\mu } \epsilon ^{(4)\nu }\rightarrow -\epsilon ^{(1)}_\mu \epsilon ^{(3)\mu }. \end{aligned}$$

(15)

Then up to the factor $-\epsilon _\mu \epsilon ^\mu \rightarrow \vec {\epsilon }\cdot \vec {\epsilon }^{\,\prime }$, a scalar factor that becomes unit in the only possible spin state here, which is $J=1$ with $L=0$, we find the same potential for $\rho B\rightarrow \rho B$ as for $\rho B^*\rightarrow \rho B^*$ with the dominant light vector exchange in any spin channel.

3 Decay modes of the $\rho B^*$ and $\rho B$ channels

As in [28] we take into account the box diagrams of the type of Fig. 3. The details are identical as those in [28] (Sect. VI) by simply changing the masses of the particles $D^*$, D by those of the $B^*$, B mesons. Concerning to the $\rho B\rightarrow \rho B$ interaction, the decay modes that we will consider are those with a pion and a vector meson $B^*$ as intermediate state,¹ which will lead to the kind of box diagrams depicted in Fig. 4. The evaluation of these diagrams is very similar to the case of Fig. 3 but with some subtle differences that we will deal with in Sect. 5.3.

From the time of Ref. [28] some clarification [37] has come concerning the $B^*B\pi$ vertex, the formalism that we use and Heavy Meson $\chi$PT. In this latter formalism this coupling is given by $g_H$, which is flavor independent in the heavy quark limit. The width for the $B^*\rightarrow B\pi$ decay (formally, since there is no phase space here, unlike the case of $D^*\rightarrow D\pi$) is given by

$$\begin{aligned} \Gamma =\frac{g_H^2}{6\pi \tilde{f}^{\,2}_\pi }|\vec {p}_\pi |^3,~\tilde{f}_\pi =\sqrt{2}f_\pi , \end{aligned}$$

(16)

and according to [38] $g_H$ is heavy flavor independent at leading order. On the other hand, in our normalization [39] we have

$$\begin{aligned} \Gamma =\frac{g^2_{B^*B\pi }}{6\pi m_{B^*}^2}|\vec {p}_\pi |^3. \end{aligned}$$

(17)

Hence we must identify

$$\begin{aligned} g_{B^*B\pi }=\frac{g_H}{\tilde{f}_\pi }m_{B^*}. \end{aligned}$$

(18)

Fig. 3

Box diagram to account for the decay of $\rho B^*$ into $\pi B$ state

Fig. 4

Box diagram for $\rho B\rightarrow \rho B$ with $B^*\pi$ intermediate state

Fig. 5

Diagram of the $K^{*+}\rightarrow K^0\pi$ and $B^{*+}\rightarrow B^0\pi$ decay at the quark level

It is interesting to obtain this result from our formalism. If we take the diagrams of Fig. 5 one may accept that the $d\bar{d}$ hadronization acts in the same way in the case of $K^*\rightarrow K\pi$ or $B^*\rightarrow B\pi$, such that the matrix elements are the same at the quark level. Yet, in the normalization of the fields that we use [39] we would have at the microscopic level,

$$\begin{aligned} S^\mathrm{mic}=1-\mathrm{i}t\sqrt{\frac{2m_l}{2\omega _l}}\sqrt{\frac{2m_l^\prime }{2\omega _l^{\prime }}}\sqrt{\frac{1}{2\omega _\pi }}\frac{1}{\mathcal {V}^{3/2}}(2\pi )^4\delta ^{(4)}(P_{i}-P_{f}), \end{aligned}$$

(19)

where $m_l$ and $m_l^\prime$ are the masses of the incoming and outgoing light quarks respectively, $\omega _l$ and $\omega ^\prime _l$ their energies, $\omega _\pi$ the pion energy and $\mathcal {V}$ the volume of the box where the states are normalized to 1. However, in our normalization, we have, at the macroscopic level,

$$\begin{aligned} S^\mathrm{mac}_{K^*}= & {} 1-\mathrm{i}t_{K^*}\frac{1}{\sqrt{2\omega _{K^*}}}\frac{1}{\sqrt{2\omega _{K}}}\frac{1}{\sqrt{2\omega _{\pi }}}\nonumber \\&\times \frac{1}{\mathcal {V}^{3/2}}(2\pi )^4\delta ^{(4)}(P_{i}-P_{f}), \end{aligned}$$

(20)

$$\begin{aligned} S^\mathrm{mac}_{B^*}= & {} 1-\mathrm{i}t_{B^*}\frac{1}{\sqrt{2\omega _{B^*}}}\frac{1}{\sqrt{2\omega _{B}}}\frac{1}{\sqrt{2\omega _{\pi }}}\nonumber \\&\times \frac{1}{\mathcal {V}^{3/2}}(2\pi )^4\delta ^{(4)}(P_{i}-P_{f}). \end{aligned}$$

(21)

This means that in our normalization we would have

$$\begin{aligned} \frac{t_{B^*}}{t_{K^*}}\simeq \frac{\sqrt{m_{B^*}m_B}}{\sqrt{m_{K^*}m_K}}\simeq \frac{m_{B^*}}{m_{K^*}}, \end{aligned}$$

(22)

which gives us

$$\begin{aligned} g_{B^*B\pi }=g\frac{m_{B^*}}{m_{K^*}}. \end{aligned}$$

(23)

If we go now to Eq. (18) we find

$$\begin{aligned} g_H=\frac{g_{B^*B\pi }\tilde{f}_\pi }{m_{B^*}}=\frac{g\tilde{f}_\pi }{m_{K^*}}=\frac{m_V}{2f_\pi }\frac{1}{m_{K^*}}\tilde{f}_\pi =\frac{1}{\sqrt{2}}. \end{aligned}$$

(24)

As one can see, our argumentation naturally leads to a flavor independent $g_H$, as required by heavy quark symmetry at leading order. The value of Eq. (24) is relatively close to the one obtained in a lattice simulation [40] of $g_H\simeq 0.57\pm 0.1$, and using it, one also gets a good result for the $D^*\rightarrow D^0 \pi ^+$ decay width. Then we use this vertex in the box diagram instead of the empirical one $g^\prime _{D^*D\pi }$ used in [28]. In the former argumentation we are implicitly assuming that both the strange quark in the $K^*$ and the b quark in the $B^*$ meson act as spectators. Recoil corrections when going from the strange sector to the D or B sector seem to be small in this case, since the results obtained within the spectator assumption agree quite well with both the empirical and the lattice QCD values of the $g_H$ coupling.

The same argument can be applied for the $B^* B^{*\prime }\rho$ vertices, but the Weinberg–Tomozawa coupling is proportional to the sum of the $B^*$, $B^{*\prime }$ energies and then the normalization factor of Eq. (23) is automatically implemented.

4 Heavy quark spin symmetry considerations

Let us consider the $\rho B^{(*)}$ meson pair. In the particle basis we have four states for each isospin combination, namely $\left| \rho B,\,J=1\right\rangle$, $\left| \rho B^*,\,J=0\right\rangle$, $\left| \rho B^*,\,J=1\right\rangle$, and $\left| \rho B^*,\,J=2\right\rangle$. In the HQSS basis [41], the states are classified in terms of the quantum numbers: J, total spin of the meson pair system and $\mathcal L$, total spin of the light quark degrees of freedom. In addition, for this particular simple case in the HQSS basis, the total spin of the heavy quark subsystem, $S_Q$, is fixed to 1 / 2. The spin of the light quarks in each of the two mesons is also trivially fixed. Thus, the four orthogonal states in the HQSS basis are given by $\left| \mathcal {L}=1/2,\,J=0\right\rangle$, $\left| \mathcal {L}=1/2,\,J=1\right\rangle$, $\left| \mathcal {L}=3/2,\,J=1\right\rangle$, and $\left| \mathcal {L}=3/2,\,J=2\right\rangle$. In all the cases the spin of the $\bar{b}$-antiquark, $S_Q$, is coupled to $\mathcal L$ to give J. The approximate HQSS of QCD leads at leading order (LO), i.e., neglecting $\mathcal {O}\left( \Lambda _{\text {QCD}}/m_Q\right)$ to important simplifications when the HQSS basis is used,

$$\begin{aligned} \left\langle \mathcal {L}',J';\alpha '\right| H^{\text {QCD}}\left| \mathcal {L},J;\alpha \right\rangle =\delta _{\alpha \alpha '}\delta _\mathcal{{L}\mathcal {L}'}\delta _{J J'}\mu ^{\alpha }_{2\mathcal {L}} \end{aligned}$$

(25)

where $\alpha$ stands for other quantum numbers (isospin and hypercharge), which are conserved by QCD. The reduced matrix elements, $\mu ^{\alpha }_{2\mathcal {L}}$, depend only on the spin (parity) of the light quark subsystem, $\mathcal {L}$, and on the additional quantum numbers, $\alpha$, which for the sake of simplicity we will omit in the following.

The particle and HQSS bases are easily related through the 9-j symbols (see [41]), and one finds

$$\begin{aligned} \left| \rho \,B,\,J=1 \right\rangle =&\, -\sqrt{\frac{1}{3}}\left| \mathcal {L}=1/2,\,J=1 \right\rangle \nonumber \\&+\sqrt{\frac{2}{3}}\left| \mathcal {L}=3/2,\,J=1\right\rangle ,\nonumber \\ \left| \rho \,B^*,\, J=0 \right\rangle =&\, \left| \mathcal {L}=1/2,\,J=0 \right\rangle , \nonumber \\ \left| \rho \,B^*,\,J=1 \right\rangle =&\,\sqrt{\frac{2}{3}}\left| \mathcal {L}=1/2,\,J=1 \right\rangle \nonumber \\&+\sqrt{\frac{1}{3}}\left| \mathcal {L}=3/2,\,J=1\right\rangle , \nonumber \\ \left| \rho \,B^*,\, J=2 \right\rangle =&\, \left| \mathcal {L}=3/2,\,J=2 \right\rangle . \end{aligned}$$

(26)

In the infinite heavy quark mass limit we obtain

$$\begin{aligned}&\left\langle \rho B\right| H^{\text {QCD}} \left| \rho B\right\rangle = \frac{1}{3}\mu _1+\frac{2}{3}\mu _3,\end{aligned}$$

(27)

$$\begin{aligned}&\left\langle \rho B^*,J=0\right| H^{\text {QCD}} \left| \rho B^*,J=0\right\rangle = \mu _1,\end{aligned}$$

(28)

$$\begin{aligned}&\left\langle \rho B^*,J=1\right| H^{\text {QCD}} \left| \rho B^*,J=1\right\rangle = \frac{2}{3}\mu _1+\frac{1}{3}\mu _3,\end{aligned}$$

(29)

$$\begin{aligned}&\left\langle \rho B^*,J=2\right| H^{\text {QCD}} \left| \rho B^*,J=2\right\rangle = \mu _3,\end{aligned}$$

(30)

$$\begin{aligned}&\langle \rho B\vert H^{\text {QCD}} \vert \rho B^*,J=1\rangle = -\frac{\sqrt{2}}{3}\mu _1+\frac{\sqrt{2}}{3}\mu _3 . \end{aligned}$$

(31)

Since we have not coupled the $\rho B$ with $\rho B^*$ in our model because it involves anomalous terms which are very small in this case, then $\mu _1 =\mu _3$ and we conclude that all the matrix elements are equal for $\rho B^*$ in $J =0,1,2$ and also for $\rho B$. An explicit evaluation of the box diagrams involving those transitions, and particularly considering $\rho$, $\omega$ transitions was done in [25] and their contribution was found very small. We can see that the dominant term for the light vector exchange (Eq. (9)) fulfills the rules of HQSS relations, but the contact term and $B^*$ exchange, which are sub-dominant in the $\left( \frac{1}{m_{B^*}}\right)$ counting, do not satisfy those relations, since they do not have to. Note that when rewriting this potential in the usual normalization of HQSS, we would have an extra $\left( \frac{1}{2\omega _{B^*}}\right)$ factor that makes the $\rho$ exchange to go like $\left( \frac{1}{m_{B^*}}\right) ^0$, the contact term like $\frac{1}{m_{B^*}}$ and the $B^*$ exchange like $\frac{1}{m_{B^*}}$.

In the present approach the $\rho B^*\rightarrow \rho B$ transition would be sub-dominant. There are other models where this might not be the case. For instance, in Ref. [27] a model is used imposing SU(6) spin-flavor symmetry that, extended to the present problem, could have this transition non-suppressed.

We should note that the approach followed here is consistent with HQSS, as discussed above, despite the $\rho B^*\rightarrow \rho B$ transition being suppressed. Treating B and $B^*$ on an equal footing, as HQSS requires, does not imply that a model where the $\rho B^*\rightarrow \rho B$ transition is suppressed necessarily breaks HQSS. Examples of this can also be seen in the work of [42] for the $B^*\bar{B}^*$ interaction and in [41] for the meson baryon system.

5 Results

5.1 Bethe–Salpeter re-summation

As in [28], we resum the diagrams of the Bethe–Salpeter series to obtain the scattering matrix T in coupled channels by using

$$\begin{aligned} T=[1-VG]^{-1}V, \end{aligned}$$

(32)

where V is the potential $\rho B^*\rightarrow \rho B^*$, $\rho B^*\rightarrow \omega B^*$, $\omega B^*\rightarrow \omega B^*$, and $\rho B\rightarrow \rho B$ that one obtains using the former sections (from Eqs. (8) and (9) after spin projection), and G is the vector–vector loop function used in this type of studies and also given explicitly in [28]. All the relevant matrix elements can be obtained from Tables I, II, and III of [28]. The finite width of the $\rho$ meson is also explicitly taken into account by considering the $\rho$ mass distribution in the construction of the G function.

In the next section we shall discuss our results for both the $\rho /\omega B^*$ and the $\rho B$ systems by using the coupled channel unitary approach, where we only consider the contribution of s-wave. The interaction in the $I=3/2$ case is repulsive, and thus in the following we will focus in the $I=1/2$ sector.

5.2 $\rho /\omega \, B^*$ system

In the first step, we introduce the kernel or potential V, corresponding to the contact and vector exchange contributions. We can get an intuitive idea of the results by using the results of Table I of [28], adapted to the present case in Table 1.

Table 1 $V(\rho B^*\rightarrow \rho B^*)$ in isospin 1/2 sector and for the different spin channels. Here $\kappa =m_\rho ^2/m_{B^*}^2$

Fig. 6

Squared amplitudes for $J=0$ and $J=2$, which depend on the energy in the center of mass including the convolution of $\rho$ mass distribution and the box diagram. The very sharp peaks correspond to the squared amplitude without the box diagram contribution

By calculating the potential at the threshold of $\rho B^*$, summing the contact, $\rho$ exchange and $B^*$ exchange contributions we get potentials with weights ($\kappa$ of [28] is now $m_\rho ^2/m_{B^*}^2$) $-51g^2$, $-50g^2$, $-58g^2$ for $J=0, 1, 2$, respectively. These results correspond to $-16g^2$, $-14.5g^2$, $-23.5g^2$ of [28]. The strength is bigger than for the $\rho D^*$ system because of the bigger masses of the heavy quarks and we still find that the strength is bigger for $J=2$. However, we also see that the weights for different spins are now more similar in accordance with HQSS as discussed in Sect. 4.

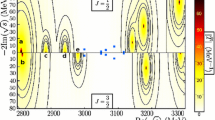
With the potentials evaluated as a function of the energy as given in Tables I, II, III of [28] we solve the Bethe–Salpeter equation (32) in the $\rho B^*$, $\omega B^*$ coupled channels though the contribution of the $\omega$ channel is fairly small. We need to regularize the G function and use the cut off prescription using $q_\mathrm{max}=1.3$ GeV. The G function is also convoluted with the $\rho$ mass distribution as in [28]. With this prescription we obtain three bound states for $J=0, 1, 2$, which we plot in Figs. 6 and 7. The value of $q_\mathrm{max}$ has been chosen to obtain a mass of 5745 MeV within the range of $5743\pm 5$ MeV of the nominal mass of the $B_2^*(5747)$ state [43].

The masses for the other two states are then predictions: we obtain a state with $J=0$ at 5812 MeV and another one for $J=1$ at 5817 MeV. Here, we can see that the mass of the spin 1 state is larger than that of spin 2, while in the PDG, the resonance $B_1(5721)$ with spin 1 has a mass smaller than the mass of $B_2^*(5747)$. Henceforth, the state with spin 1 that we obtain presents some difficulties to be identified with the $B_1(5721)$. One possibility is that it could be the resonance generated by the $\rho B$ interaction, which we shall discuss later. Note that the LO HQSS relation $\mu _1=\mu _3$ deduced in Sect. 4 has some $1/m_Q$ corrections.

It is interesting to mention here that the heavy quark symmetry imposes relations to the potential of Eq. (32). However, there are also constrains on the T matrix and masses of partner states in different heavy flavor sectors (charm and bottom) if one assumes that the binding energies are the same. To implement this, some arguments have to be imposed on the loop function (G) as well. This was discussed in [42] for the $B\bar{B}$ systems and found that the G function should go as $1/m_Q^2$, with $m_Q$ the mass of the heavy quarks. The same arguments as used in [42] for the present case with one light meson and a heavy one would demand the G function to go as $1/m_Q$. It is interesting to see that the same conclusion was obtained from an elaborate treatment of the meson–meson interaction using the covariant heavy meson chiral perturbation theory approach in the KD scattering [44, 45], based on chiral power counting and demanding that G goes as 1 / M in the $M\rightarrow \infty$ limit, where M is the mass of the heavy meson. Furthermore, in [42] it was found that this behavior in G for heavy meson masses was obtained using a flavor independent cut off $q_\mathrm{max}$, in the evaluation of G. In [44] a new G function is proposed that implements the right heavy quark flavor behavior. Interestingly, in [46] it was found that the use of a flavor independent cut off for the G function was remarkably similar to the prescription of [44] as the mass of the heavy baryon changed.

Fig. 7

Squared amplitude for the $\rho B^*$ and the $\rho B$ sector with spin 1

Table 2 The mass of the states obtained with different values of $q_\mathrm{max}$

The former argumentation can be used to choose a cut off to make predictions on the B sector starting from the D sector. In [28] the authors studied the $\rho D^*$ interaction and reproduced states using a cut off of the order of $q_\mathrm{max}\approx 1-1.2$ GeV. So one should use a value of this order of magnitude to make predictions in the B sector. In practice, more accurate predictions can be obtained by fitting $q_\mathrm{max}$ to some data. This is what is done in [46] and what we also do here, taking $q_\mathrm{max}=1.3$ GeV. However, it is rewarding to see that this value is very close to the one used in [28].

We have given the rational of choosing the value of the cut off to fit one datum. Nevertheless, we test the sensitivity of the mass of the $J=2$ state in the cutoff. The results are shown in Table 2, where we observe variations of about 40 MeV by varying the cut off in 100 MeV. Changes in other spin channels are similar, as can also be seen in Table 2.

We have also taken the advantage to make a test of the stability of the results when we change the strength of the potential and readjust the cut off to get the mass of the $J=2$ resonance at the experimental value. For this purpose we take the diagonal (largest) $\rho B^*$ potential and multiply it by 1.5 or 0.75. The results are shown in Table 3. We observe that the variation of the masses for the predicted $J=0$ and $J=1$ states are small, quite smaller than the differences found with the changes in $q_\mathrm{max}$ for fixed potential shown in Table 2.

Table 3 The mass of the states obtained for different strengths of the potential

The T matrix element close to a pole behaves like

$$\begin{aligned} T_{ij}\approx \frac{g_ig_j}{z-z_R} \end{aligned}$$

(33)

where $g_i$ is the coupling to channel i ($i=\rho B^*, \omega B^*$) and z, $z_R$ are the complex values for s and the resonance position $s_R$. We can get the coupling of one channel:

$$\begin{aligned} g_i^2=\lim _{z\rightarrow z_R}T_{ii}(z-z_R). \end{aligned}$$

(34)

We choose the $\rho B^*$ coupling with positive sign, and for the other channels we use

$$\begin{aligned} \frac{g_i}{g_j}&=\displaystyle {\lim _{z\rightarrow z_R} \frac{T_{ii}}{T_{ij}}}, \end{aligned}$$

(35)

which gives us the relative sign for the $\omega B^*$ channel. Note here that the right hand side of Eq. (34) is the residue of the amplitude $T_{ii}$. The couplings to the different channels are listed in Table 4.

As commented on above, the $\rho$ mass distribution is also involved via the convoluted G function and should give a width different from zero to the states. Nonetheless, we see that the widths for $J=0$, $J=1$, and $J=2$ are much smaller than one MeV (see Figs. 6, 7). However, in the PDG the width of the $B_2^*(5747)$ state is $23^{+5}_{-11}$ MeV, which is much larger than the one obtained here. To reconcile the difference, the $\pi B$ decay channel must be included.

Table 4 Couplings of the bound states to the $\rho B^*$ and $\omega B^*$ channels with $I=1/2$ and $J=0,1,2$ in units of GeV

The energies of the resonances are closer to the threshold of $\rho$ and $B^*$ than to that of $\pi$ and B. We do not need to treat the $\pi B$ as a coupled channel, since it does not have much weight compared to the $\rho B^*$ and $\omega B^*$ channels. Henceforth, as in [28], one can compute the box diagrams that are mediated by $\pi B$ and put them in the potential V in order to get the width. The $\rho B^*$ contribution corresponding to the box diagram was shown in Fig. 3. We use directly the result of Eq. (41) of [28], which is the sum of all the terms after the $q^0$ integration using the Cauchy residue theorem,

$$\begin{aligned} V^{\pi B}&=g^4(\epsilon _i^{(1)}\epsilon _i^{(2)}\epsilon _j^{(3)}\epsilon _j^{(4)} {+}\epsilon _i^{(1)}\epsilon _j^{(2)}\epsilon _i^{(3)}\epsilon _j^{(4)} {+}\epsilon _i^{(1)}\epsilon _j^{(2)}\epsilon _j^{(3)}\epsilon _i^{(4)})\nonumber \\&\quad \times \frac{8}{15\pi ^2}\int _0^{q_\mathrm{max}}dq\vec {q}^{\,\,6}\left( \frac{1}{2\omega _\pi }\right) ^3\left( \frac{1}{k_1^0+2\omega _\pi }\right) ^2\nonumber \\&\quad \times \frac{1}{k_2^0-\omega _\pi -\omega _B+i\epsilon }\frac{1}{k_4^0-\omega _\pi -\omega _B+i\epsilon }\frac{1}{k_1^0-2\omega +i\epsilon }\nonumber \\&\quad \times \frac{1}{k^0_3-2\omega _\pi +i\epsilon }\frac{1}{P^0-\omega _\pi -\omega _B+i\epsilon }\frac{1}{P^0+\omega _\pi +\omega _B}\nonumber \\&\quad \times \left( \frac{1}{k_2^0+\omega _\pi +\omega _B}\right) ^2\frac{1}{2\omega _B}f(P^0,\vec {q}^{\,2}) \end{aligned}$$

(36)

Fig. 8

The real part of box potential for $(I,J)=(1/2,0)$ and $(I,J)=(1/2,2)$ compared with those from contact and vector exchange terms

Fig. 9

The imaginary part of box potential for $(I,J)=(1/2,0)$ and $(I,J)=(1/2,2)$

where

$$\begin{aligned} f(P^0,\vec {q}^{\,2})&=4\left\{ -32k^0_3P^0\omega _\pi ^2\omega _B((P^0)^2-2\omega _\pi ^2-3\omega _\pi \omega _B-\omega _B^2)\right. \nonumber \\&\quad +2(k_3^0)^3P^0\omega _B((P^0)^2-5\omega _\pi ^2-2\omega _\pi \omega _B-\omega _B^2)\nonumber \\&\quad +(k_3^0)^4(2\omega _\pi ^3-(P^0)^2\omega _B+3\omega _\pi ^2\omega _B+2\omega _\pi \omega _B^2+\omega _B^3)\nonumber \\&\quad +4\omega _\pi ^2(8\omega _\pi ^5+33\omega _\pi ^4\omega _B+54\omega ^3\omega _B^2+3\omega _B((P^0)^2\nonumber \\&\quad -\omega _B^2)^2+18\omega _\pi \omega _B^2(-(P^0)^2+\omega _B^2)+\omega _\pi ^2(-12(P^0)^2\omega _B\nonumber \\&\quad +44\omega _B^3))-(k_3^0)^2(16\omega ^5+63\omega ^4\omega _B+74\omega _\pi ^3\omega _B^2\nonumber \\&\quad +\omega _B((P^0)^2-\omega _B^2)^2+32\omega _\pi ^2\omega _B(-(P^0)^2+\omega _B^2)\nonumber \\&\quad \left. + \, \omega _\pi (-6(P^0)^2\omega _B^2+6\omega _B^4))\right\} , \end{aligned}$$

(37)

$\omega _\pi = \displaystyle \sqrt{\vec {q}^{\,2}+m_\pi ^2}$, $\omega _B = \displaystyle \sqrt{\vec {q}^{\,2}+m_B^2}$, and $P^0=k_1^0+k^0_2$.

Here, in order to calculate the box diagram amplitude, one has first integrated analytically the $q^0$ variable. Note that the integral is logarithmically divergent, and as in [28] we use a form factor to regularize the loop in addition to the $q_\mathrm{max}$ value used before. The spin structure only allows for $J=0$ and 2. The reason why $J=1$ is forbidden is that the parity of the $\rho B^*$ system is positive with s-wave, and the angular momentum of the $\pi B$ system has to be $L=0, 2$. Therefore, the spin of the $\pi B$ pair would be 0 or 2, but not 1. Using again the results of [28] we find the spin projections

$$\begin{aligned} \delta V^{\pi B,I=1/2,J=0}=20\tilde{V}^{(\pi B)}, \quad \delta V^{\pi B,I=1/2,J=2}=8\tilde{V}^{(\pi B)}, \end{aligned}$$

(38)

where $\tilde{V}^{(\pi B)}$ is given in Eq. (36) after removing the polarization vectors. As already mentioned, the box diagram is logarithmically divergent and needs regularization. In this work, we also use a form factor in each vertex of the box diagram, and then finally, $g^4$ is replaced with

$$\begin{aligned} g^2_{\rho \pi \pi }g_{B^*B\pi }^2\left( e^{-\vec {q}^{\,2}/\Lambda ^2}\right) ^4 \end{aligned}$$

(39)

where $g_{\rho \pi \pi }\equiv g=m_{\rho }/(2f_\pi )$ and $g_{B^*B\pi }=gm_{B^*}/m_{V}$ (see Eq. (23)), and $\Lambda$ is of the order of 1 GeV.

We take the form factor in exponential form from QCD sum rules calculations carried out in [47]. In that work values of $\Lambda \approx 1.2$ GeV were determined for the $D^*D\pi$ vertex for the case when the pion is virtual (Eq. (17) of Ref. [47]). We allow the value of $\Lambda$ to change when moving to the beauty sector in the present case, and tune it to obtain the phenomenological width. It is thus a free parameter of the theory. The sensitivity of the result to changes in this parameter is discussed below.

The real part of the box diagram contribution is neglected, since it is very small compared with those of the contact and vector exchange terms as we can see in Fig. 8. The imaginary part that we focus on is shown in Fig. 9. If $\Lambda$ is taken as 0.67 GeV and $q_\mathrm{max}$ as 1.3 GeV, the width for $J=2$ is 25.5 MeV which is in agreement with the experimental value in the PDG. For $J=0$ the width is then 24.7 MeV, while the state with $J=1$ has no width in our approach. If $\Lambda$ is increased to 0.73 GeV, we obtain a width for $J=2$ of 37.5 MeV, and 47.8 MeV for $J=0$. We see that we can obtain a width comparable to experiment using cut offs or form factors of natural size.

In Fig. 6 we show the line shape of $\vert T\vert ^2$ including the box diagram contribution, which generates a final width for the $J=0,2$ states. On the other hand, for $J=1$ we still have the results of Fig. 7, since as discussed above, in this case there is no box diagram.

5.3 $\rho B$ system

As we have mentioned in the previous subsection, in the PDG the mass of the $B_1(5721)$ is smaller than that of the $B^*_2(5747)$. However, for the $\rho B^*$ systems the mass of the $J=1$ state is larger than that of the $J=2$ state. Henceforth, we turn to the $\rho B$ system and investigate its interaction.

For this system there are no contact terms, but we have the vector exchange terms only. In addition, the $\omega$ channel is now inoperative since the $\rho \rho \omega$ vertex is zero by G-parity and $\omega \omega \rho$ is zero by C-parity and isospin. Note that in the case of the vector–vector interaction it is the exchange term of Fig. 1c that makes $\omega B^*$ mix with $\rho B^*$. The equivalent diagrams would involve anomalous terms which are small. In any case the factor $m_V^2/m_{B^*}^2$ of these terms renders them negligible, of the order of $1~\%$ also in the case of the vector–vector interaction.

Since the strength of the interaction is the same as in the $\rho B^*\rightarrow \rho B^*$ case we expect to find a bound state as before. If the cut off $q_\mathrm{max}$ in the G function is taken as 1.3 GeV, we find the pole position at 5728 MeV (see Fig. 7), which is consistent with the PDG value of the $B_1(5721)$. The coupling to $\rho B$ channel is also computed and found to be $g_{\rho B}=41.6$ GeV. It is very interesting to also calculate the width of this state. The PDG does not quote any value, but it states that the dominant decay mode is $B^*\pi$. This comes out naturally in our approach by means of the box diagram of Fig. 4.

It is easy to find the contribution for this new box diagram following the steps of [28]. There we had the combination

$$\begin{aligned}&\int d^3q \epsilon _i^{(1)}\epsilon _j^{(2)}\epsilon _l^{(3)}\epsilon _m^{(4)}q_iq_jq_lq_m \mathcal {F}(\vec {q}^{\,2})\nonumber \\&\quad =\frac{1}{15}\int d^3q \epsilon _i^{(1)}\epsilon _j^{(2)}\epsilon _l^{(3)}\epsilon _m^{(4)}\vec {q}^{\,4}\left( \delta _{ij}\delta _{lm}\right. \nonumber \\&\quad \quad \left. + \, \delta _{il}\delta _{jm}+\delta _{im}\delta _{jl}\right) \mathcal {F}(\vec {q}^{\,2})\nonumber \\&\quad =\frac{1}{15}\left( 5\mathcal {P}(0)+2\mathcal {P}(2)\right) \int d^3q \vec {q}^{\,4}\mathcal {F}(\vec {q}^{\,2}) , \end{aligned}$$

(40)

here $\mathcal {F}(\vec {q}^{\,2})$ is a function depending on the square of the three momentum $\vec {q}^{\,2}$, the center of mass energy and the masses of the mesons appearing in Fig. 4.

Now we have the same original form as in the beginning of the equation but we must sum over the $B^*$ polarization of the intermediate $B^*$ state. Since we are only concerned about the imaginary part, the on shell approximation for the intermediate $B^*$ is sufficient and the contraction of $\epsilon _j^{(2)}\epsilon _m^{(4)}$ gives $\delta _{jm}$. Then the remaining structure is

$$\begin{aligned}&\int d^3q \epsilon _i^{(1)}\epsilon _l^{(3)}q_iq_l\vec {q}^{\,2}\displaystyle {\tilde{\mathcal {F}}}(\vec {q}^{\,2}) =\epsilon _i^{(1)}\epsilon _i^{(3)}\int d^3q \frac{1}{3}\vec {q}^{\,4}\displaystyle {\tilde{\mathcal {F}}}(\vec {q}^{\,2}) , \end{aligned}$$

(41)

where $\displaystyle \tilde{\mathcal {F}}(\vec {q}^{\,2})$ has the same form as $\mathcal {F}(\vec {q}^{\,2})$ after making the change $m_{B^*}\rightarrow m_{B}$ and $m_{B}\rightarrow m_{B^*}$, up to a constant factor that we shall discuss right now. The interaction Lagrangian of Eq. (14) involves derivatives of the pseudoscalar fields. In comparison with the previous situation which is depicted in the box diagram of Fig. 3, now the $B^*B\pi$ vertex does not have a B meson carrying the q momenta of the integral, since this meson is external (see Fig. 4). Before we had in the incoming $B^*B\pi$ vertex a factor

$$\begin{aligned} \propto \left( (P-q)+(k_1-q)\right) _\mu \xrightarrow {\vec {k}_i\rightarrow 0} -2q_i, \end{aligned}$$

(42)

corresponding to the momentum of the B and $\pi$ internal mesons in Fig. 3. Now in Fig. 4 the incoming $B^*B\pi$ vertex is

$$\begin{aligned} \propto \left( -k_2+(k_1-q)\right) _\mu \xrightarrow {\vec {k}_i\rightarrow 0} -q_i, \end{aligned}$$

(43)

because the derivatives involve the external pseudoscalar B and the internal $\pi$. As a consequence, the amplitudes will lack a factor two in each of the $B^*B\pi$ vertex, so $\tilde{\mathcal {F}}=\mathcal {F}/4$. When we remove the polarization vectors the structure is

$$\begin{aligned} \int d^3q \frac{1}{3}\vec {q}^{\,4}\displaystyle {\tilde{\mathcal {F}}}(\vec {q}^{\,2})=\int d^3q \frac{1}{3}\vec {q}^{\,4}{\mathcal {F}}(\vec {q}^{\,2})\frac{1}{4}. \end{aligned}$$

(44)

Hence, comparing with Eq. (40) we see that the strength of the $\rho B$ box potential is identical to the former one with $J=0$ of the $\rho B^*$, divided by four (changing the intermediate mass of the B to the present one of $B^*$ and vice versa). In Fig. 10 we plot $\vert T\vert ^2$ for this case with the same parameters used before to obtain the width of the $B_2^*(5747)$. We see that we obtain a width around 20 MeV, which is a prediction of the present work.

Fig. 10

Squared amplitude of $\rho B$ system as a function of the c.m. energy including the convolution of the $\rho$ mass distribution and the box diagram contribution

6 Summary

In this work we have studied the $\rho B^*$, $\omega B^*$, and $\rho B$ interactions by using the local hidden gauge unitary approach. First we have solved the Bethe–Salpeter equation in coupled channels for the $\rho B^*$ and the $\omega B^*$ sectors, using the tree level amplitudes and regularizing the loop function with a cut off of 1.3 GeV. In this way we have found three bound states, with masses 5812, 5817, and 5745 MeV for $I=1/2$ and $J=0, 1, 2$, respectively, identifying the $J=2$ state with the $B_2^*(5747)$ [43] of mass $5743\pm 5$ MeV. Despite having considered the $\rho$ mass distribution, all the states that we have found show small widths. In order to generate the correct width of the state with $J=2$ as that of the experimental $B_2^*(5747)$, which is quoted as $23^{+5}_{-11}$ MeV, we have taken into account the box diagram mediated by the $\pi B$, which accounts for this decay channel. We have also considered a form factor for the off-shell pions and a rescaled coupling in the $B^* B\pi$ vertex. In this way, we have obtained the widths 25.5–37.5 MeV for $J=2$ and 24.7–47.8 MeV for $J=0$, taking $\Lambda =0.67$–0.73 GeV and $q_\mathrm{max}=1.3$ GeV. Since the pole position of $J=1$ is larger than that of $J=2$, while in the PDG there is a spin one state $B_1(5721)$, which mass is smaller than the $B_2^*(5747)$ mass, we have considered the $\rho B$ system.

For the $\rho B$ interaction in the local hidden gauge approach we have found a bound state of mass 5728 MeV, which is consistent with the experimental value of the $B_1(5721)$. We have also predicted a width for this state considering the box diagram contribution in a similar manner as for the $\rho B^*$ system. The width that we have obtained is around 20 MeV. We summarize our results in Table 5.

The free parameters in the present approach have been fixed in the $J=2$ sector. The same parameters have been used in the $J=0,1$ sectors to make predictions. We should acknowledge some uncertainties in the predictions obtained for these two latter channels. Quantifying these systematic errors is difficult but we can get some confidence in the predictions recalling that in the charm related sector we predicted the $D_0(2600)$ in [28] and some time later it was found in [29]. To estimate uncertainties we can make an educated guess by accepting as uncertainties the differences found in Table 2 when the cut off was changed by $\pm 100$ MeV. This tells us that about 30 MeV, and smaller, uncertainties in the masses of the $J=0,1$ states seem reasonable.

Finally we have investigated if there is some aspect in the interaction which can be related to the heaviness of the system under consideration. The fact that the B mesons have a large mass can justify the study of the $\rho B$ and $\rho B^*$ systems under the frame of heavy quark spin symmetry. We have splitted these states in terms of eigenstates of total angular momentum of the light quarks as in [41].

We find that the dominant terms in our approach, due to light vector exchange, which go like $\mathcal {O}\left( \frac{1}{m_{B^*}}\right) ^0$ fulfill the LO constrains of HQSS, while the contact terms and those coming from the exchange of $B^*$ are sub-dominant $\left( \mathcal {O}\left( \frac{1}{m_{B^*}}\right) \right)$ and do not fulfill the LO HQSS rules. While in the $D\rho$ sector these terms were not too small, in the present case they are much smaller and we have a near degeneracy in the $\rho B^*$ states with $J=0,1,2$.

Table 5 Summary of the states found in the $\rho (\omega ) B^*$ and $\rho B$ sectors