KK-parity non-conservation in UED confronts LHC data

Abstract

Kaluza–Klein (KK) parity can be violated in a five-dimensional universal extra-dimensional model with boundary-localised (kinetic or mass) terms (BLTs) at the fixed points of $S^1/Z_2$ orbifold. In this framework we study the resonant production of Kaluza–Klein excitations of the neutral electroweak gauge bosons at the LHC and their decay into an electron–positron pair or a muon–antimuon pair. We use the results (for the first time, to our knowledge) given by the LHC experiment to constrain the mass range of the first KK-excitation of the electroweak gauge bosons ($B^1\ \mathrm{and } \ W_3^1$). It is interesting to note that the LHC result puts an upper limit on the masses of the $n=1$ KK-leptons for positive values of the BLT parameters depending upon the mass of the $\ell ^{+}\ell ^{-}$ resonance.

1 Introduction

The discovery of the Higgs boson at the Large Hadron Collider (LHC) at CERN is a milestone in the success of Standard Model (SM). However, there are still many unanswered questions and unsolved puzzles, ranging from dark matter to the hierarchy problem to the strong-CP problem. But there is no experimental result that can explain such unsolved problems with standard particle physics. Out of various interesting alternatives, supersymmetry (SUSY) and extra-dimensional models are the most popular frameworks for going beyond the SM of particle physics. In this work we consider a typical extra-dimensional model where all SM particles can access an extra space-like dimension $y$. We use the results [1] presented by the ATLAS Collaborations of the search for a high-mass resonances decaying into the $\ell ^{+}\ell ^{-}$ ($\ell \equiv e \ \mathrm{or } \ \mu$) pair to constrain the parameter space of such a model where the lowest ($n = 1$) KK-excitations are unstable due to lack of any specified symmetry.

We are interested in a specific framework, called the universal extra dimension (UED) [2] scenario, characterised by a single flat extra space-like dimension $y$ which is compactified on a circle $S^1$ of radius $R$ and has an imposed $Z_2$ symmetry ($y \rightarrow -y$) to accommodate chiral fermions; hence the compactified space is called a $S^1/Z_2$ orbifold. From a four-dimensional viewpoint, every field will then have an infinite tower of KK-modes, the zero modes being identified as the SM states. In this orbifold a translation by $\pi R$ in the $y$-direction leads to a conserved KK-parity given by $(-1)^n$. The conservation of KK-parity ensures that the lightest $n = 1$ KK-particle, called the lightest Kaluza–Klein (LKP), is absolutely stable and hence is a potential dark matter candidate. As the masses of the SM particles are small compared to $1/R$, this scenario leads to an almost degenerate particle spectrum at each KK-level. This mass degeneracy could be lifted by radiative corrections. Being an extra-dimensional theory and hence being non-renormalizable, this can only be an effective theory characterised by a cutoff scale $\Lambda$. So at the two fixed points ($y = 0$ and $y = \pi R$) of $S^1/Z_2$ orbifold, one can include four-dimensional kinetic and/or mass terms for the KK-states. These terms are also required as counterterms for cutoff dependent loop-induced contributions [3] of the five-dimensional theory. In the minimal universal extra-dimensional models (mUED) these terms are fixed by requiring that the five-dimensional loop contributions [4, 5] are exactly cancelled at the cutoff scale $\Lambda$ and the boundary values of the corrections, e.g., logarithmic mass corrections of KK-particles, can be taken to be zero at the scale $\Lambda$. There are several publications [2, 6–43] in which we can find how the experimental results constrain the values of the two basic parameters ($R$ and $\Lambda$) of mUED theory.

In this work we generate non-conservation of KK-parity¹ by adding unequal boundary terms at the two fixed boundary points. Consequently $n = 1$ KK-states are no longer stable. Hence the single production of $n = 1$ KK-states and its subsequent decay into $n = 0$ states would be possible via this non-conservation of KK-parity. We will utilise this KK-parity-non-conserving coupling of the $B^1 (W_3^1)$ to a pair of SM fermions ($n =0$ states) [44] to calculate the (resonance) production cross section of $B^1 (W_3^1)$ in $pp$ collisions at the LHC (8 TeV) and its subsequent decays to $e^+ e^-$/$\mu ^+ \mu ^-$, assuming $B^1\ \mathrm{and } \ W_3^1$ to be the lightest KK-particles. Once $B^1\ \mathrm{and } \ W_3^1$ are produced via KK-parity-non-conserving coupling, the KK-parity-conserving decaying mode being kinematically disallowed, the $B^1\ \mathrm{and } \ W_3^1$ decay to a pair of zero-mode fermions via the same KK-parity-non-conserving coupling. A search for high-mass resonances based on 8 TeV LHC $pp$ collision data collected by the ATLAS and CMS have been reported in [1] and [45], respectively. References [1] and [45] present the expected and observed exclusion upper limits on cross section times branching ratio at 95 % C.L. for the combined dielectron and dimuon channels for resonance search. In this article we have used the above results to constrain the masses of the $n = 1$ level KK-fermions and $B^1\ (\ W_3^1)$ of the model. In Ref. [46] we have reported the production of the $n=1$ KK-excitation of gluon and its subsequent decay to $t\bar{t}$ pair at the LHC. Both the production and the decay are governed by the KK-parity-non-conserving interaction. Constraints have also been derived by comparing the $t\bar{t}$ cross section with LHC data from the CMS [47] and ATLAS [48] Collaborations.

The plan of this article is as follows. At first we present the relevant couplings and masses in the framework of UED with asymmetric boundary-localised kinetic terms. We then review the expected $\ell ^{+}\ell ^{-}$ signal from the combined production of the $B^1\ \mathrm{and } \ W_3^1$ at the LHC and their subsequent decay. This is compared with the ATLAS [1] 8 TeV results and the restrictions on the couplings and KK-excitation masses are exhibited. Finally we will summarise the results in Sect. 5.

2 KK-parity-non-conserving UED in a nutshell

In a non-minimal version of five-dimensional UED theory, we put boundary-localised kinetic terms (BLKTs) [44, 49–54] at the orbifold fixed points ($y=0$ and $y=\pi R$). $\Psi _{L,R}$ are the free fermion fields, the zero-modes of which are the chiral projections of the SM fermions. In the presence of BLKTs, the five-dimensional action can be written as [44, 55]

(1)

Here, $\sigma ^\mu \equiv (I, \vec {\sigma })$ and $\bar{\sigma }^\mu \equiv (I, -\vec {\sigma })$, $\vec {\sigma }$ being the $(2 \times 2)$ Pauli matrices. $r^a_f, r^b_f$ are the free BLKT parameters which are equal for $\Psi _L$ and $\Psi _R$ for the purpose of illustration.

The KK-decomposition of five-dimensional fermion fields using two component chiral spinors are introduced as² [44, 55]

$$\begin{aligned} \Psi _L(x,y)&= \begin{pmatrix}\phi _L(x,y) \\ \chi _L(x,y)\end{pmatrix} = \sum ^{\infty }_{n=0} \begin{pmatrix}\phi _n(x) f_L^{n}(y) \\ \chi _n(x) g_L^{n}(y)\end{pmatrix},\end{aligned}$$

(2)

$$\begin{aligned} \Psi _R(x,y)&= \begin{pmatrix}\phi _R(x,y) \\ \chi _R(x,y)\end{pmatrix} = \sum ^{\infty }_{n=0} \begin{pmatrix}\phi _n(x) f_R^{n}(y) \\ \chi _n(x) g_R^{n}(y)\end{pmatrix}. \end{aligned}$$

(3)

Using appropriate boundary conditions [44], we can have the solutions for $f_L^n$ and $g_R^n$ which are simply denoted by $f$ and $g$ for illustrative purposes:

$$\begin{aligned} f^n(y)&= N_n \left[ \cos (m_n y) - \frac{r_f^a m_n}{2} \sin (m_n y) \!\right] ,\;\; 0 \!\le \! y \!<\! \pi R, \nonumber \\ f^n(y)&= \! N_n \left[ \cos (m_n y) \!+\! \frac{r_f^a m_n}{2} \sin (m_n y) \!\right] \!, -\pi R \!\le \! y < 0.\nonumber \\ \end{aligned}$$

(4)

Here the KK-masses $m_n$ for $n = 0,1, \ldots$ are solutions of the transcendental equation [50]

$$\begin{aligned} (r^a_f r^b_f ~m_n^2 - 4) \tan (m_n \pi R)= 2(r^a_f + r^b_f) m_n. \end{aligned}$$

(5)

The non-trivial wave functions are combinations of a sine and a cosine function, different from the case of mUED where they are either only sine or cosine function. The departure of the wave functions from mUED theory and the fact that the KK-masses are solutions of Eq. (5) rather than just $n/R$ are the key features of this non-minimal universal extra-dimensional (nmUED) model.

In our analysis we study the KK-parity-non-conserving UED in two ways. In the first case, we take equal strengths of the BLKTs (at two fixed point $y = 0$ and $y = \pi R$) for fermion, i.e., $r^a_f = r^b_f \equiv r_f$, while the other case has the BLKT at one of the fixed points only: $r^a_f \ne 0, ~r^b_f = 0$. In the latter situation Eq. (5) becomes

$$\begin{aligned} \tan (m_n \pi R)=-\frac{r^a_f m_n}{2}. \end{aligned}$$

(6)

In both cases the mass eigenvalues can be solved by the transcendental equations (Eqs. (5) and (6)) using numerical techniques.

For small values of $\frac{r^a_f}{R}$ $(<<1)$ the approximate KK-mass formula becomes (using Eq. (6))

$$\begin{aligned} m_n\approx \frac{n}{R}\left( \frac{1}{1+\frac{r^a_f}{2\pi R}}\right) \approx \frac{n}{R}\left( 1-\frac{r^a_f}{2\pi R}\right) \!. \end{aligned}$$

(7)

It is clear from the above expression that for $r^a_f>0$, the KK-mass diminishes with $r^a_f$. This result also holds good when the BLKTs are present at both boundary points.

$N_n$ is the normalisation constant, determined from the orthonormality condition [44]:

$$\begin{aligned} \int dy \left[ 1 + r^a_f \delta (y) + r^b_f \delta (y - \pi R) \right] ~f^n(y) ~f^m(y) = \delta ^{n m}, \end{aligned}$$

(8)

and it is given by

$$\begin{aligned} N_n = \sqrt{\frac{2}{\pi R}}\left[ \frac{1}{\sqrt{1 + \frac{r_f^2 m_n^2}{4} + \frac{r_f}{\pi R}}}\right] \!, \end{aligned}$$

(9)

for equal strengths of the boundary terms ($r^b_f = r^a_f\equiv r_f$).

For the other situation when $r^b_f = 0$ and where we use $r^a_f \equiv r_f$, one has

$$\begin{aligned} N_n = \sqrt{\frac{2}{\pi R}}\left[ \frac{1}{\sqrt{1 + \frac{r_f^2 m_n^2}{4} + \frac{r_f}{2 \pi R}}}\right] \!. \end{aligned}$$

(10)

Now it is evident from Eqs. (9) and (10) that, for $\frac{r_f}{R}<-\pi$ (for a double brane setup) and $\frac{r_f}{R}<-2\pi$ (for a single brane setup), the squared norm of the zero-mode solutions become negative. Moreover, for $\frac{r_f}{R}=-\pi$ (for a double brane setup) and $\frac{r_f}{R}=-2\pi$ (for a single brane setup) the solutions become divergent. Beyond these region the fields become ghost-like; consequently the values of $\frac{r_f}{R}$ beyond these should be avoided. However, for simplicity we stick to positive values of BLKTs only in the rest of our analysis.

Our concern here is only with the zero-modes and the $n=1$ KK-wave functions of the five-dimensional fermion fields.

Masses and $y$-dependent wave functions for the electroweak gauge bosons are very similar to the fermions and can be obtained³ in a similar manner. We do not repeat them in this article. This is readily available in [44].

As the KK-masses obtained from transcendental equations are similar for fermions and gauge bosons, we use $r_\alpha ^a, r_\alpha ^b$ to pameterise the strengths of the BLKT with $\alpha = f$ (fermions) or $V$ (gauge bosons) for the purposes of our discussion. It has been assumed in the following that the KK-quarks are either mass degenerate with or heavier than the KK-leptons. However, they do not enter in our analysis. For simplicity we have assumed that the BLKTs for U(1) and SU(2) gauge bosons are the same, so that $B^1$ and $W_3^1$ are degenerate in mass. We are only interested in the $n = 1$ state.

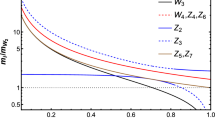
In Fig. 1 we have shown in the plots the dimensionless quantity $M_{(1)} \equiv m_{\alpha ^{(1)}} R$, in the two different cases. The left panel reflects the mass profile for the $n = 1$ KK-excitation when the BLKTs are present at the two fixed points ($y=0$ and $y=\pi R$), while the right panel shows the case when the BLKTs are present only at $y = 0$. In both cases the KK-mass decreases with the increasing values of BLKT parameter. The detailed illustrations of this non-trivial KK-mass dependence has been discussed and can be found in Ref. [46].

Fig. 1

Left panel The dependence of $M_{(1)}\equiv m_{\alpha ^{(1)}} R$ with respect to $R_\alpha \equiv r_\alpha ^a/R$ when $r_\alpha ^a = r_\alpha ^b$. In the inset is shown the variation of $M_{(1)}$ on ${\Delta R_\alpha } \equiv (r_\alpha ^b - r_\alpha ^a)/R$ for two different $R_\alpha$. Right panel $M_{(1)}$ with respect to $R_\alpha$ when the BLKT is present only at the $y = 0$ fixed point. The inset shows a magnified portion of the variation, which gives the actual range of $R_\alpha$ that is considered later. The insets of both panels show small variations of $M_{(1)}$ with respect to BLKTs. Here $\alpha = f$ (fermions) and $V$ (gauge bosons)

3 Interacting coupling of ${\varvec{V^1 (B^1 \mathrm{or} W_3^1)}}$ with zero-mode fermions

The coupling of the states $B^1$ or $W_3^1$ to two zero-mode fermions $f^0$ is given by

$$\begin{aligned} g_{V^{1}f^{0}f^{0}}&= g_5(G) \!\int ^{\pi R}_{0}\! (1\!+\!r_{f}\{\delta (y)\!+\!\delta (y\!-\!\pi R)\}) f_{L}^{0}f_{L}^{0}a^{1} \mathrm{d}y, \nonumber \\&= g_5(G) \!\int ^{\pi R}_{0} \!(1\!+\!r_{f}\{\delta (y)\!+\!\delta (y\!-\!\pi R)\}) g_{R}^{0}g_{R}^{0}a^{1} \mathrm{d}y.\nonumber \\ \end{aligned}$$

(11)

Further, the five-dimensional gauge coupling $g_{5}(G)$ which appears above is related to the usual coupling $g$ through

$$\begin{aligned} g_{5}(G) = g ~\sqrt{\pi R \left( 1+\frac{R^a_V+ R^b_V}{2\pi }\right) }. \end{aligned}$$

(12)

We denote the zero-mode fermion wave functions by $f_L^0$ and $g_R^0$ while the KK ($n = 1$)-gauge boson wave functions are denoted by $a^1$ depending on the values of chosen BLKTs.

Let us first discuss the case in which BLKTs are presented at both fixed points. Here we assume for the fermions: $r_f^a = r_f^b = r_f$, but for the gauge bosons: $r_V^a \ne r_V^b$. Using $y$-dependent wave functions and a proper normalisation [44] we get

$$\begin{aligned} g_{V^{1}f^{0}f^{0}}&= \frac{g_{5}(G)}{\left( 1+\frac{R_{f}}{\pi }\right) } \;N^1_G\left[ \frac{\sin (\pi M_{(1)})}{\pi M_{(1)}}\left\{ 1\!-\!\frac{M_{(1)}^{2}R^{a}_VR_{f}}{4}\!\right\} \right. \nonumber \\&\left. +\frac{R^{a}_V}{2\pi }\left\{ \cos (\pi M_{(1)})\!-\!1\right\} \!+\! \frac{R_{f}}{2\pi }\left\{ \cos ( \pi M_{(1)})\!+\!1\right\} \!\right] \!,\nonumber \\ \end{aligned}$$

(13)

which vanishes⁴ when $\Delta R_V = 0$.

Here $M_{(1)} \equiv m_{V^{(1)}} R$ is the scaled KK-mass, and $R_f \equiv r_f/R, \;\; R^a_V \equiv r^a_V/R, \;\; \mathrm{and} \;\; R^b_V \equiv r^b_V/R$ are the scaled dimensionless variables defined earlier.

Now we turn to the case which could be considered the most asymmetric one, namely, the BLKT for the fermion and the gauge boson are present only at the $y=0$ fixed point. We obtain for this case [44]

$$\begin{aligned} g_{V^{1}f^{0}f^{0}}&= \frac{\sqrt{2} ~g\sqrt{\left( 1+\frac{R_{V}}{2\pi }\right) } }{\left( 1+\frac{R_{f}}{2\pi }\right) \sqrt{1+\left( \frac{R_V M_{(1)}}{2}\right) ^2+\frac{R_V}{2\pi }}} \left( \!\frac{R_{f}\!-\!R_V}{2\pi }\!\right) \!,\nonumber \\ \end{aligned}$$

(14)

and this becomes zero if we put $R_V = R_f$. Here⁵ $R_V \equiv r_V/R$ and $R_f \equiv r_f/R$.

Figure 2 depicts the KK-parity-non-conserving coupling strength in the two different cases. In the left panel (BLKTs are present at two fixed points $y=0$ and $y=\pi R$) we plot the square of the coupling for a fixed value⁶ of $R^a_V$ = 10 as a function of $R_f$ for several choices of $\Delta R_V$. The right panel shows the same thing with respect to $R_f$ (BLKTs are present only at $y = 0$) for different values of $R_V$. In both cases the KK-parity-non-conserving coupling decreases with the increasing values of the fermion BLKT parameters. The detailed analysis of this coupling strength with respect to the BLKT parameters can be found in Ref. [46].

Fig. 2

Left panel The dependence of the squared value of scaled KK-parity-non-conserving coupling between $B^1 (W_3^1)$ and a pair of zero-mode fermions with $R_f \equiv R_f^a = R_f^b$ for different $\Delta R_V$, for $R^a_V=10$. Right panel The dependence of the same coupling with $R_f$ for different choices of $R_V$ when the fermion and gauge boson BLKTs are present only at the $y = 0$ fixed point

4 Production and decay of ${\varvec{B^1 (W_3^1)}}$ via KK-parity-non-conservation

We are now in a position to discuss the main result of this paper. From now for the SM particles we will not explicitly write the KK-number $(n = 0)$ as a superscript. At the LHC we study the resonant production of $B^1 (W_3^1)$, via the process $p p ~(q \bar{q}) \rightarrow B^1 (W_3^1)$ followed by $B^1 (W_3^1) \rightarrow \ell ^{+}\ell ^{-}$. This results in an $\ell ^{+}\ell ^{-}$ resonance at the $B^1 (W_3^1)$ mass.

The final state leads to two leptons $(e ~\mathrm{or} ~\mu )$, with the invariant mass peaking at $m_{V^{(1)}}$, which is the KK-mass ($n=1$) of the gauge bosons. It should be noted that both the production and the decay of $n=1$ KK-excitations of the electroweak gauge bosons are driven by KK-parity-non-conserving couplings which depend on $R_f$, $R^a_V$ and $\Delta R_V$ ($R_f$, $R_V$ when BLKTs are present at only one fixed point). If in the future such a signature is observed at the LHC, then it would be a good channel to measure such KK-parity-non-conserving couplings.

Both the ATLAS [1] and the CMS [45] Collaborations have looked for a resonance decaying to $e^{+}e^{-}$/$\mu ^{+}\mu ^{-}$ pair in $pp$ collisions at 8 TeV in the LHC experiment. From the lack of observation of such a signal at 95 % C.L., upper bounds have been put on the cross section times branching ratio of such a final state as a function of the mass of the resonance. The calculated values of the event rate in the KK-parity-non-conserving framework when compared to the experimental data set limits on the parameter space of the model. To get the most up-to-date bounds we use the latest 8 TeV results⁷ from ATLAS [1].

The production of $B^1$ ($W_3^1$) (which we generically denote by $V^1$) in $pp$ collisions is driven $q \bar{q}$ fusion. A compact form of the production cross section in proton–proton collisions can be written as [44]

$$\begin{aligned}&\sigma (p p \rightarrow V^{1} + X) = \frac{4 \pi ^2}{3 m_{V^{(1)}}^3}\;\sum _i \Gamma (V^{1} \rightarrow q_i \bar{q}_i)\nonumber \\&\times \!\int _\tau ^1 \frac{\mathrm{d}x}{x} \!\left[ \!f_{\frac{q_{i}}{p}}(x,m_{V^{(1)}}^2) f_{\frac{{\bar{q}_{i}}}{p}}(\tau /x,m_{V^{(1)}}^2) \!+\! q_i \leftrightarrow \bar{q}_i \!\right] \!.\quad \end{aligned}$$

(15)

Here, $q_i$ and $\bar{q_i}$ denote a generic quark and the corresponding antiquark of the $i$th flavour, respectively. $f_{\frac{q_{i}}{p}}$ ($f_{\frac{{\bar{q}_{i}}}{p}}$) is the parton distribution function for a quark (antiquark) within a proton. We define $\tau \equiv {m_{V^{(1)}}^2 / S_{PP}}$, where $\sqrt{S_{PP}}$ is the proton–proton centre of momentum energy. $\Gamma (V^{1} \rightarrow q_i \bar{q}_i)$ represents the decay width of $V^1$ into the quark–antiquark pair and is given by $\Gamma = \left[ \frac{{g^{2}_{V^{1}q q}}}{32\pi }\right] \left[ (Y^{q}_L)^2 + (Y^{q}_R)^2 \right] m_{B^{(1)}}$ (with $Y^q _L$ and $Y^q _R$ being the weak-hypercharges for the left- and right-chiral quarks) for $B^1$ and $\Gamma = \left[ \frac{{g^{2}_{V^{1}q q}}}{32\pi }\right] m_{W_3^{(1)}}$ for the $W_3^1$. Here $g^{}_{V^1 q q}$ is the KK-parity-non-conserving coupling of the $V^1$ with the SM quarks—see Eqs. (13) and (14).

We use a parton-level Monte Carlo code with parton distribution functions as parametrised in CTEQ6L [56] for the determination of the numerical values of the cross sections. In our analysis we set the $pp$ centre of momentum energy at 8 TeV and the factorisation scales (in the parton distributions) at $m_{V^{(1)}}$. To obtain the event rate one must multiply the cross sections with the appropriate branching ratio⁸ of $B^1$ or $W_3^1$ into $e^{+}e^{-}$/$\mu ^{+}\mu ^{-}$. Here we have assumed without any loss of generality that $B^1$ and $W_3^1$ are lighter than the $n=1$ KK-excitation of the fermions. This implies that they are the lightest KK-particle and they can decay only to a pair of SM particles via KK-parity-non-conserving coupling—see Eqs. (13) and (14).

Let us comment on the values of the BLKT parameters used in our analysis. The BLKTs imposed in Eq. (1) are not five-dimensional operators in four-dimensional effective theory but some sort of boundary conditions on the respective fields at the orbifold fixed points. The masses (solutions of transcendental equations) and profiles in the $y$-directions for the fields are consequences of these boundary conditions. In fact, four-dimensional effective theory only contains the canonical kinetic terms for the fields and their KK-excitations along with their mutual interactions. The effect of BLKTs only shows up in modifications of some of these couplings via an overlap integral (see Eq. (11)) and also in deviations of the masses from UED values of $n/R$ (in the $n$th KK-level). So as long as these overlap integrals are not very large $(\lesssim 1)$ we do not have any problem with the convergence of perturbation series. In Fig. 2, we have shown that the values of the overlap integrals (involved in the couplings determined by the five-dimensional wave functions) are $\lesssim 1$ for the entire range of the strengths of the BLKTs which we have used in this article and never grow with these strengths. Furthermore it has been shown in [57] that theories with large strengths of the BLKTs (relative to their natural cutoff scale, $\Lambda$) were found to be perturbatively consistent and are thus favoured. Such results in Ref. [57] are in agreement with our observation that the numerical values of the overlap integral diminish with increasing magnitude of the BLKT coefficients ($r_{i}$’s).

We now present the main numerical results for two distinct cases, either BLKTs are present at both fixed points or only at one of the two, in the following subsections.

4.1 BLKTs are present at ${{y = 0}}$ and ${{y = \pi R}}$

In Fig. 3 we present the results for the case when the fermion BLKTs are symmetric at the two fixed points but unequal values of the gauge BLKTs break the KK-parity. Here we show the region of parameter space excluded by the ATLAS 8 TeV data [1] for two different choices of $R_V^a$. Each panel depicts that the region to the left of a curve in the $m_{V^{(1)}}$–$R_f$ plane is excluded by the ATLAS data.

Fig. 3

95 % C.L. exclusion plots in the $m_{V^{(1)}}$–$R_f$ plane for several choices of $\Delta R_V$. Each panel corresponds to a specific value of $R^a_V$. The region to the left of a given curve is excluded from the non-observation of a resonant $\ell ^{+}\ell ^{-}$ signal running at 8 TeV by ATLAS data [1]. $1/R$ and $M_{f^{(1)}} = m_{f^{(1)}} R$ are displayed in the upper and right-side axes, respectively (see text)

For a chosen $R^a_V$ there is an one-to-one correspondence of $m_{V^{(1)}}$ with $1/R$ which is shown on the upper axis of the panels, as the KK-mass is rather insensitive to $\Delta R_V$. Also, for any displayed value of $1/R$ we can estimate the first excitation of the fermion KK-mass $M_{f^{(1)}} = m_{f^{(1)}} R$ ( plotted on right-side axis) which is determined by $R_f$.

The exclusion plots can be understood easily in conjunction with Figs. 1 and 2. For a given $\Delta R_V$ and $R^a_V$ the KK-parity-non-conserving couplings are almost insensitive to $R_f$. Thus $R_f$ has no steering on the production of $e^{+}e^{-}$/$\mu ^{+}\mu ^{-}$. The signal rate thus solely depends on $R^a_V$ and $\Delta R_V$. The coupling (and in turn the signal strength) increases with $\Delta R_V$. Thus with higher and higher strength of KK-parity non-conservation one can exclude higher and higher masses (and higher values of $1/R$) as revealed in Fig. 3.

4.2 BLKTs are present only at ${{y = 0}}$

Now let us concentrate on the case of the fermion and gauge BLKTs at only one fixed point. In this case we display the exclusion curves in the $m_{V^{(1)}}$–$R_f$ plane for several choices of $R_V$ in Fig. 4. The region below a curve has been disfavoured by the ATLAS data.

Fig. 4

95 % C.L. exclusion plots in the $m_{V^{(1)}}$–$R_f$ plane for several choices of $R_V$. The region below a specific curve is ruled out from the non-observation of a resonant $\ell ^{+}\ell ^{-}$ signal in the 8 TeV run of LHC by ATLAS [1]. $1/R$ and $M_{f^{(1)}} = m_{f^{(1)}} R$ are displayed in the upper and right-side axes, respectively (see text)

One can explain Fig. 4 on the basis of Figs. 1 and 2. It is revealed in the left panel of Fig. 1, $M_{(1)} \equiv m_{V^{(1)}} R$ has mild variation with $R_V$. So we can take the mass of $V^1$ to be approximately proportional to $1/R$ (the relevant values of $1/R$ are displayed in the upper axis of the panel in Fig. 4). In our model we estimate the cross section times branching ratio corresponding to any $m_{V^{(1)}}$, and comparing this with the ATLAS data we can have a specific value of $(R_V, R_f)$ pair on each curve via KK-parity-non-conserving coupling. Alternatively, it is evident from Fig. 4, as $m_{V^{(1)}}$ increases, the production of the $B^1 (W_3^1)$ decreases. As a compensation, the KK-parity-non-conserving coupling must increase as we increase the $m_{V^{(1)}}$. So it is clear from the right panel of Fig. 2, increasing value of KK-parity-non-conserving coupling is achieved by the higher values of $R_V$ for a fixed value of $R_f$. In this case also, the KK-fermion mass of first excitation can be obtained in a correlated way from the right-side axis of this plot.

Let us pay some attention to Fig. 4. For a given curve (specified by a $R_V$), the allowed area in $m_{V^{(1)}}$–$R_f$ plane is bounded by the curve itself and a line parallel to $m_{V^{(1)}}$ axis corresponding to the value of $R_f$ determined by the specific value of $R_V$ of that curve. The choice of the $R_f<R_V$ ensures mass hierarchy among KK-electroweak gauge boson and KK-leptons. So the bounded region implies that for a given value of $m_{V^{(1)}}$, $R_f$ is bounded from below which in turn imposes an upper limit on the mass of the $n = 1$ KK-lepton.

5 Conclusions

In summary, we have investigated the phenomenology of KK-parity non-conservation in the UED model where all the SM fields propagate in 4+1 dimensional space time. We have achieved this non-conservation due to inclusion of asymmetric⁹ BLTs at the two fixed points of this orbifold. These boundary (kinetic in our case) terms can be thought of as a cutoff ($\Lambda$) dependent log divergent radiative corrections [4] which remove the degeneracy in the KK-mass spectrum of the effective 3+1 dimensional theory.

With positive values of BLKTs, we have studied the electroweak interaction, in two alternative ways. In the first case we put equal strengths of the fermion BLKTs at the two fixed points and parametrised by $r_f$, while for the electroweak gauge boson we have considered unequal strengths of BLKTs $(r_V^a \ne r_V^b)$. Equal strengths of electroweak gauge boson BLKTs would preserve the $Z_2$-parity. In the other situation we have considered the fermion and electroweak gauge boson BLKTs are present only at the $y = 0$ fixed point. These BLKTs modify the field equations and the boundary conditions of the solutions lead to the non-trivial KK-mass excitations and wave functions of the fermions and the electroweak gauge bosons in the $y$-direction in both cases. In this platform we have calculated the KK-parity-non-conserving coupling between the $n = 1$ KK-excitation of the electroweak gauge bosons and a pair of SM fermions ($n = 0$) in terms of $r_f, r^a_V, r^b_V ~\mathrm{and} ~1/R$ when BLKTs are present at both fixed points and $r_f, r_V, ~\mathrm{and} ~1/R$ for the other case. This driving coupling vanishes in the $\Delta R_V = 0$ limit in the first case and for $R_f = R_V$ in the second.

Finally we estimate the single production of $V^1$ at the LHC and its subsequent decay to $\ell ^{+}\ell ^{-}$; both the production and the decay are controlled by the KK-parity-non-conserving coupling. We compare our results with the $\ell ^{+}\ell ^{-}$ resonance production signature at the LHC running at 8 TeV $pp$ centre of momentum energy [1, 45]. The lack of observation of this signal with 20 $fb^{-1}$ accumulated luminosity by the ATLAS Collaboration [1] at the LHC already excludes a large part of the parameter space (spanned by $r_f, r^a_V, r^b_V$ and $1/R$ in one case and $r_f, r_V$ and $1/R$ in the other). Here we consider that the $B^1 (W_3^1)$ is lighter than the corresponding fermion and the bounds on the mass of the former are the same as that on the $\ell ^{+}\ell ^{-}$ resonance from the data.

At the end, we also like to point out another important observation regarding the excluded parameter space of this model that the $\ell ^{+}\ell ^{-}$ resonance search disfavoured more parameter space in comparison to the $t\bar{t}$ resonance search which we performed in Ref. [46].