Visualizations of exclusive central diffraction

Abstract

The case of low invariant mass exclusive central diffractive production is considered in the general theoretical framework. It is shown that diffractive patterns (differential cross sections in variables like transfer momenta squared, the azimuthal angle between final hadrons and their combinations) can serve as a unique tool to explore the picture of the $pp$ interaction and falsify theoretical models. Basic kinematical and dynamical properties of the process are considered in detail. As an example, visualizations of diffractive patterns in the model with three pomerons for processes $p+p\rightarrow p+R+p$ (R is a resonance) and $p+p\rightarrow p+\pi ^{+}\pi ^{-}+p$ are presented.

1 Introduction

The central exclusive production process with quasi-diffractively scattered initial particles is an important source of information as regards high-energy dynamics of strong interactions both in theory and experiment. If we consider only one particle production, this is the first “genuinely” inelastic process which not only retains a lot of features of elastic scattering but also shows clearly how the initial energy is being transformed into the secondary particles.

Theoretical consideration of these processes on the basis of Regge theory goes back to papers [1–9]. Experimental works were presented in [10–15]. Some new interest was related to signals of centrally produced particles like Higgs bosons, heavy quarkonia, di-gamma, exotics, dihadrons [16–19, 48]. Recent data from different experiments are also available [49–57].

In the previous paper [17] the exclusive central diffractive production of heavy states was considered in detail. In this paper we present properties of low-mass (central invariant masses are less than 3 GeV) exclusive production.

In addition to the general advantages like clear signature with two large rapidity gaps (LRG) [58, 59] and the possibility to use the “missing mass method” [60], there are several specific advantages of the low-mass case. The first one is rather large cross sections. It is important, since the schedule for LHC forward physics experiments is very limited, and we need also special low luminosity runs to suppress pile-up events. The second one is the possibility to use different diffractive patterns (differential cross sections on variables like transfer momenta squared, the azimuthal angle between final hadrons and their combinations) as a unique tool to explore the picture of the $pp$ interaction and falsify theoretical models.

The article is organized as follows. In the first chapter we consider general kinematical properties and variables of the process. In the second one we present some model approaches for low-mass exclusive central diffraction. In the third part we present visualizations of diffractive patterns for different processes and kinematical variables and discuss their general features. In the conclusions we touch on briefly the future experimental possibilities. Appendices are basically devoted to calculations of amplitudes.

2 General kinematics and cross sections

Let us consider the kinematics of two processes

$$\begin{aligned}&h_1(p_1)+h_2(p_2)\rightarrow h_1(p_1^{\prime })+R(p_R)+h_2(p_2^{\prime }),\end{aligned}$$

(1)

$$\begin{aligned}&h_1(p_1)+h_2(p_2)\rightarrow h_1(p_1^{\prime })+\{a(k_a)+b(k_b)\}+h_2(p_2^{\prime }),\nonumber \\ \end{aligned}$$

(2)

with four-momenta indicated in parentheses. Initial hadrons remain intact, $\{a\; b\}$ can be a diboson or dihadron system and R denotes a resonance; “+” signs denote large rapidity gaps. Let us call them exclusive double diffractive events (EDDE) as in our previous papers (see [61] and references therein). These processes are also known in the literature as exclusive double pomeron exchange (EDPE) or central exclusive diffractive production (CEDP).

We use the following set of variables:

$$\begin{aligned}&s=(p_1+p_2)^2,\; s^{\prime }=(p_1^{\prime }+p_2^{\prime })^2,\; t_{1,2}=(p_{1,2}-p_{1,2}^{\prime })^2,\nonumber \\&s_{1,2}=(p_{1,2}^{\prime }+p_R)^2\; \text{ or }\; (p_{1,2}^{\prime }+k_a+k_b)^2, \end{aligned}$$

(3)

In the light-cone representation $p=\{p_+,p_-; \varvec{p}_{\perp }\}$

$$\begin{aligned}&p_1\!=\!\left\{ \sqrt{\frac{\bar{s}}{2}},\frac{m^2}{\sqrt{2\bar{s}}};\; \varvec{0}\right\} ,\;\!\! \Delta _1\!=\!\left\{ \xi _1\sqrt{\frac{\bar{s}}{2}},\frac{-\varvec{\Delta }_1^2-\xi _1 m^2}{(1-\xi _1)\sqrt{2\bar{s}}};\; \varvec{\Delta }_1 \right\} ,\;\nonumber \\&p_2\!=\!\left\{ \frac{m^2}{\sqrt{2\bar{s}}},\sqrt{\frac{\bar{s}}{2}};\; \varvec{0}\right\} ,\;\!\! \Delta _2\!=\!\left\{ \frac{-\varvec{\Delta }_2^2-\xi _2 m^2}{(1-\xi _2)\sqrt{2\bar{s}}},\xi _2\sqrt{\frac{\bar{s}}{2}};\; \varvec{\Delta }_2 \right\} \nonumber \\&p_{1,2}^{\prime }=p_{1,2}-\Delta _{1,2},\; p_{1,2}^2=p_{1,2}^{\prime \; 2}=m^2,\nonumber \\&\bar{s}=\frac{s-2m^2}{2}+\frac{s}{2}\sqrt{1-\frac{4m^2}{s}}\simeq s. \end{aligned}$$

(4)

Here $\xi _{1,2}$ are the fractions of the hadrons’ longitudinal momenta lost.

The physical region of diffractive events with two large rapidity gaps is defined by the following kinematical cuts:

$$\begin{aligned}&0.01\; \mathrm{GeV}^2\le |t_{1,2}|\le \; \sim 1\; \mathrm{GeV}^2\;{,} \end{aligned}$$

(5)

$$\begin{aligned}&\xi _\mathrm{min}\simeq \frac{M^2}{s \xi _\mathrm{max}}\le \xi _{1,2}\le \xi _\mathrm{max}\sim 0.1,\end{aligned}$$

(6)

$$\begin{aligned}&\left( \sqrt{-t_1}-\sqrt{-t_2}\right) ^2\le \kappa \le \left( \sqrt{-t_1}+\sqrt{-t_2}\right) ^2\\&\kappa =\xi _1\xi _2s-M^2\ll M^2.\nonumber \end{aligned}$$

(7)

$M$ is the invariant mass of the central system. We can write the above relations in terms of $y_{1,2}$ (rapidities of hadrons), $y$ (rapidity of the central system) and $\eta =(\eta _b-\eta _a)/2$, where $\eta _{a,b}$ are the rapidities of particles $a,b$. For instance:

$$\begin{aligned}&|y|\le y_0=\ln \left( \frac{\sqrt{s}\xi _\mathrm{max}}{M}\right) ,\quad |y_{1,2}|=\frac{1}{2}\ln \frac{(1-\xi _{1,2})^2s}{m^2-t_{1,2}},\nonumber \\&|y|\le 6.5,\quad |y_{1,2}|\ge 8.75 \quad \text{ for } \sqrt{s}=7\;\mathrm {TeV},\nonumber \\&|\tanh \eta |\le \sqrt{1-\frac{4m_0^2}{M^2}}. \end{aligned}$$

(8)

Differential cross sections for the above processes can be represented as

$$\begin{aligned}&\frac{d\sigma _{R}}{d\varvec{\Delta }_1^2d\varvec{\Delta }_2^2d\phi dy}\simeq \frac{\left| \mathcal{M}^\mathrm{EDDE}_R\right| ^2}{2^9\pi ^4ss^{\prime }},\end{aligned}$$

(9)

$$\begin{aligned}&\frac{d\sigma ^\mathrm{EDDE}_{ab}}{d\varvec{\Delta }_1^2 d\varvec{\Delta }_2^2 d\phi dy dM^2 d\Phi _{ab}}\simeq \frac{\left| \mathcal{M}^\mathrm{EDDE}_{ab}\right| ^2}{2^{10}\pi ^5 ss^{\prime }}, \end{aligned}$$

(10)

where $\phi$ is the azimuthal angle between outgoing protons, $\Phi _{ab}$ is the phase space of the dihadron system and $\mathcal{M}^\mathrm{EDDE}_{R,\; ab}$ denote unitarized amplitudes of the corresponding processes (see $\mathcal{M}_i^U$ in Appendix C).

3 Double reggeon exchange amplitudes: approaches

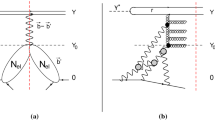
If the central mass produced in EDDE is low ($M\sim 1$ GeV, Fig. 1), it is not possible to use perturbative representation like in [17] for the amplitude of the process, and we have to use more general “nonperturbative” form. In this case we have to obtain somehow the pomeron–pomeron fusion vertex (see Refs. [17, 61, 62] for details). The scheme of the calculations is depicted in Fig. 1. The first step is the calculation of the “bare” reggeon–reggeon amplitude $\mathcal{M}$, which consists of diffractive form-factors $T$ and the fusion vertex $F$. If the “shoulder energies” $\sqrt{s_{1,2}}$ are high enough (say, greater than $100$ GeV), we also have to take into account rescattering corrections in these channels (denoted by $V_{1,2}$). For example, at $\sqrt{s}=7$ TeV in the kinematical region defined in (6) we obtain $~1\;\mathrm {GeV}<\sqrt{s_{1,2}}<2\;\mathrm {TeV}$. Then we should calculate rescattering corrections in the $pp$ channel, which are denoted by $V$. In some works [21] they are called “soft survival probability”. Recently it was shown in [21] that enhanced diagrams (additional soft interactions) can play a significant role.

Fig. 1

Scheme of calculation of the full EDDE amplitude in the case of low invariant masses ($M<3$ GeV), i.e. nonperturbative pomeron–pomeron fusion

All the phenomenological models need to obtain values of their parameters to make further predictions. For this purpose we can use so called “standard candle” processes, i.e. events which have the same theoretical ingredients for the calculations. For low central masses we can use the processes:

• $\gamma ^*+p\rightarrow V+p$ (EVMP), $m_V<3$ GeV [63–65];

• $p+p\rightarrow p+M+p$, $M=\{q\bar{q}\}$ (light meson) or “glueball” [10–14], $M=hh$ (dihadron system) [15].

From the first principles (covariant reggeization approach [61]) we can write the general structure of the vertex for different cases. For example, for the production of the low invariant mass system with $J^P$ (spin–parity), when $s_i\sqrt{-t_i}\gg \sim 1\;\mathrm{GeV}^3$ and contributions of secondary reggeons are small, we have for the “bare” amplitudes squared

$$\begin{aligned}&F^{0^{\pm }}_{{\mathbb P}{\mathbb P}}= \left| \prod _{i=1,2} \tilde{T}_0(t_i) \left( \frac{s_i}{M^2}\right) ^{\alpha _i} \sum _{k=0}^{\infty } \tilde{\tilde{f}}^k_{0^{\pm }} \left( \frac{2\sqrt{t_1t_2}\cos \phi }{M^2} \right) ^k \right| ^2,\nonumber \\&\tilde{T}_0(t_i)= \frac{\alpha ^{\prime }_{\mathbb P}}{2} T_0(t_i) \left( \frac{\sqrt{-t_i}}{m}\right) ^{\alpha _i}, \end{aligned}$$

(11)

$$\begin{aligned} \tilde{\tilde{f}}^k&= \tilde{f}^k \left[ \eta _1\eta _{21} \Gamma (k-\alpha _1)\Gamma (\alpha _1- \alpha _2-k)\right. \nonumber \\&\left. +\eta _2\eta _{12} \Gamma (k-\alpha _2)\Gamma (\alpha _2- \alpha _1-k) \right] , \end{aligned}$$

(12)

$$\begin{aligned}&\left| \mathcal{M}^{0^+}\right| ^2 \simeq F^{0^+}_{{\mathbb P}{\mathbb P}}, \end{aligned}$$

(13)

$$\begin{aligned}&\left| \mathcal{M}^{0^-}\right| ^2 \simeq F^{0^-}_{{\mathbb P}{\mathbb P}} \sin ^2\phi , \end{aligned}$$

(14)

$$\begin{aligned} \eta _i=(-1)^{\sigma _i}+\mathrm {e}^{-\mathrm {i}\pi \alpha _i}, \end{aligned}$$

$$\begin{aligned}&\eta _{ij}=(-1)^{\sigma _i}(-1)^{\sigma _j}+\mathrm {e}^{-\mathrm {i}\pi (\alpha _i-\alpha _j)},\end{aligned}$$

(15)

$$\begin{aligned}&\alpha _i=\alpha _{{\mathbb P}}(t_i),\; \sigma _i=0, \end{aligned}$$

(16)

with functions defined in Appendix A ($\tilde{f}^k$ are nonsingular at $t_i\rightarrow 0$, $\tilde{T}_0(t)$ is usually represented by the exponential $\mathrm {e}^{Bt_i}$ or $1/(1-t_i/B)$). The transformation from integer spins to trajectories was made like in Ref. [66].

As one can see from Appendix A, in the classical Regge scheme $(-t_i)^{\alpha _i/2}$ is absorbed into the unknown residue of the Regge pole. But for a fixed integer $J$ this factor always appears in the t-channel cosine. In Refs. [67, 68] results were obtained from the assumption that the pomeron acts as a $1^+$ conserved or nonconserved current. In particular, it was shown that the cross section is proportional to $t_1t_2$, when we replace the pomeron by the conserved vector current. To remove such zero authors of [67] proposed to use singular functions (nonconserved pomeron current).

Strictly speaking, in the real cross sections rescattering corrections at rather high energies can naturally remove zeroes of a cross section (see the typical situation in the Fig. 2) without introducing singular functions.

Fig. 2

The unitarization of the cross section $|t|{\mathrm e}^{-2B|t|}$ ($B\simeq 2.85\;\mathrm {GeV}^{-2}$, $\sqrt{s}=7$ TeV) corresponding to the amplitude (89) in Appendix C. The dashed curve represents the “bare” term and the solid one represents the unitarized result. $\sigma _B$ is the integrated “bare” cross section. The zero at $t=0$ disappears in the unitarized cross section

The general structure of EDDE amplitudes from the simple Regge behaviour was also considered in [62, 69] by the method of helicity amplitudes developed in [5]. As was shown in [61], experimental data are in good agreement with the above predictions.

There were some attempts to obtain the vertex in special models. Let us mention first the old paper [66], where reggeon–reggeon–particle vertex was exactly calculated in the covariant formalism, and the double reggeon amplitude has the form

$$\begin{aligned} \mathcal{M}&\simeq \sum _{i\ne j=1}^2 \frac{\alpha ^{\prime }_i\alpha ^{\prime }_j}{4} \left( \frac{s_i}{M^2}\right) ^{\alpha _i} \left( \frac{s_j}{s_0}\right) ^{\alpha _j} \eta _i\eta _{ji}\mathcal{F}_{ij},\nonumber \\ \mathcal{F}_{ij}&= \sum \limits _{k=0}^{\infty } \frac{1}{k!}\left( \frac{M_{\perp }^2}{s_0}\right) ^k \Gamma (k-\alpha _i)\Gamma (\alpha _i-\alpha _j-k)\nonumber \\&= \Gamma (-\alpha _i)\Gamma (\alpha _i-\alpha _j)\!\! _1 F_1\left( -\alpha _i,1-\alpha _i+\alpha _j; -\frac{M_{\perp }^2}{s_0}\right) , \nonumber \\ \alpha _i&= \alpha ^{\prime }_i(0) t_i+\alpha _i(0), \end{aligned}$$

(17)

where $s_0=1\;\mathrm {GeV}^2$ and $\sigma _i$ is the parity of a reggeon. For the double pomeron exchange $\alpha _{1,2}=\alpha ^{\prime }_{\mathbb P}(0) t_{1,2}+\alpha _{\mathbb P}(0)$. It is close to the representation (11) with exactly calculated couplings.

The pomeron–pomeron fusion based on the “instanton” or “glueball” dynamics was considered in [70–72]. One can see also recent papers [37, 73] devoted to calculations of the pomeron–pomeron fusion vertex in the nonperturbative regime.

4 Diffractive patterns

Since EDDE is the diffractive process, it retains almost all the features of the classical optical diffraction, namely the diffractive pattern or distribution in the scattering angle. It contains the diffractive peak at low angles and different structures (dips and kinks) at higher angles. Some speculations on the meaning of these features can be found in [23] and further publications. Here we would like to point out the following:

• From the diffractive pattern we extract model independent parameters of the interaction region such as the $t$-slope which is $R^2/2$, with $R$ the transverse radius of the interaction region.

• We can also estimate the longitudinal size of the interaction region [74]:

  $$\begin{aligned} \Delta x_L>\frac{\sqrt{s}}{2\sqrt{\langle t^2\rangle -\langle t\rangle ^2}}. \end{aligned}$$

  (18)

  The longitudinal interaction range is somehow “hidden” in the amplitude but it is this range that is responsible for the “absorption strength”. A rough analogue is the known expression for the radiation absorption in media which critically depends on the thickness of the absorber.

• The very presence of dips is the signal of the quantum interference of hadronic waves.

• The depth of the dips is determined by the real part of the scattering amplitude.

What else could we extract from it? What is the physical meaning of the dip position, number of dips or kinks and so on? These questions stimulate us for future investigations.

4.1 t-Like variables

In this subsection we present diffractive patterns in t-like variables for different physical situations. From the experimental point of view it would be more useful to have distinct structures in distributions, since their position can show the dynamics of the interaction and can help to extract parameters with better accuracy.

In Fig. 3 one can see distributions in t of one of the final protons integrated in other variables. Pictures correspond to “bare” amplitudes for $0^-$ (88), “glueball” (89) states and for the pion–pion production (72). For the simple ${\mathrm e}^{B(t_1+t_2)}$ (87) amplitude picture Fig.3d shows the significance of the rescattering corrections.

Fig. 3

Diffractive t-distributions for different final states (corresponding amplitudes are indicated): a “glueball-like” (89); b $\eta ^{\prime }$ (88); c $\pi ^+\pi ^-$ (72). Solid curves in a, b are given for $\sqrt{s}=30$ GeV, dashed and dotted curves in a, b, c represent $\sqrt{s}=7$ TeV and $\sqrt{s}=14$ TeV, respectively. Picture d shows the simple ${\mathrm e}^{2Bt}$ cross section (dashed curve) and the unitarized result (solid curve) at $\sqrt{s}=7$ TeV

Let us illustrate how the situation changes, when we use other variables that seem more natural for the study of diffractive structures. In Fig. 4 we present distributions in $\tau =(t_1+t_2)/2$ and $\varvec{\delta }^2=(\varvec{\Delta }_1-\varvec{\Delta }_2)^2/4$ for the case, when the “bare” amplitude is the simple exponent (87) without additional structures. For these variables the situation changes more drastically after taking into account the unitarization.

Fig. 4

Diffractive patterns in different t-like variables: a $\tau =(t_1+t_2)/2$; b $\varvec{\delta }^2=(\varvec{\Delta }_1-\varvec{\Delta }_2)^2/4$. Born amplitude (dashed curve) and the unitarized result (solid curve) are shown for $\sqrt{s}=7$ TeV

On the other hand, as one can see from Fig. 5, the effect can be the opposite. The “bare” amplitude contains the dip at some position, which disappears in the unitarized distribution, and other complicated structures arise. Here we use the toy model based on the parameters of the third pomeron from [84]:

$$\begin{aligned}&\mathcal{M}\sim \mathrm {e}^{\tilde{B}(t_1+t_2)/2} \left( \mathrm {e}^{\tilde{B}t_1/2}-\tilde{A}\right) \left( \mathrm {e}^{\tilde{B}t_2/2}-\tilde{A}\right) ,\end{aligned}$$

(19)

$$\begin{aligned}&\tilde{B}=1.2046+0.5912\left( \ln \left[ s (M_{\perp }^2))\right] -\imath \pi \right) /2, \end{aligned}$$

(20)

$$\begin{aligned}&\tilde{A}=49.138 \left( -\imath \sqrt{s}M_{\perp }\right) ^{0.0703}/(32\pi \tilde{B}),\end{aligned}$$

(21)

$$\begin{aligned}&M_{\perp }^2=M^2-t_1-t_2+2\sqrt{t_1t_2}\cos \phi ,\end{aligned}$$

(22)

$$\begin{aligned}&M=1.5\;\mathrm {GeV},\;\sqrt{s}=7\;\mathrm {TeV}. \end{aligned}$$

(23)

Fig. 5

The situation after the unitarization (solid curve), when the “bare” amplitude contains a dip structure (dashed curve)

4.2 Azimuthal correlations

As was shown earlier in Refs. [62, 69], as well as later on in Refs. [45, 47, 61], the distribution in the azimuthal angle between final protons can serve as a powerful tool to obtain quantum numbers of centrally produced particles.

In Fig. 6a–c we present diffractive azimuthal patterns for $0^-$, $0^+$ (“glueball”), $0^+$ (pion–pion) states. Shapes are very different and can be used as a peculiar “filter”. Furthermore, the $\phi$-distribution also has a strong dependence on the model that we use for diffractive processes. The unitarization effect for the “flat” distribution is shown in Fig. 6d.

Fig. 6

Azimuthal distributions for different final states: a “glueball-like” (89); b $\eta ^{\prime }$ (88); c $\pi ^+\pi ^-$ (72). Solid (red) curves in a, b are given for $\sqrt{s}=30$ GeV, dotted curves in a, b, c, d represent unitarized results at $\sqrt{s}=7$ TeV. Dashed curves show the behaviour of Born cross sections at $\sqrt{s}=7$ TeV: a $\cos ^2\phi$, b $\sin ^2\phi$, c $\pi ^+\pi ^-$, d “flat”

5 Conclusions

The phenomenon of diffraction is always accompanied by specific patterns, partially considered in this paper. We have to take it into account when we try to define the diffractive process experimentally. Many features of such distributions can be very helpful. To continue the paper [17], here we presented only general aspects of the exclusive central production of low invariant mass states, but it is possible to find the same properties in other processes (elastic scattering, single and double diffractive dissociation). For example, we could apply to them the procedure of the amplitude construction, which is similar to the one stated in Appendix A. This hopefully will be done in further work.

As one can see from the above figures, rescattering corrections can play significant role and drastically change the shape of diffractive patterns. We can use this property to falsify diffractive models, which are very numerous “on the market” [75], with an unprecedented accuracy.

Finally, let us mention some possible experimental facilities for this task. Since cross sections of the low-mass EDDE are rather large ($10\rightarrow 1000\;\mu b$), it is possible to use low luminocity runs of the LHC, as was proposed in the starting projects [76–78, 81]. The recent success of the TOTEM collaboration in t-measurements [82] shows that it is realistic.

Appendices

Appendix A

In this appendix we construct exact reggeon–reggeon fusion amplitudes for the exclusive production of $0^+$ and $0^-$ states by the covariant reggeization method proposed in [61]. For other states calculations are similarly based on formulae for vertices from [61].

The amplitude $\mathcal {M}^{J^P}$ (the left picture in Fig. 1) is composed of vertices $T^{\mu _1\cdots \mu _{J_1}}$, $T^{\nu _1\cdots \nu _{J_2}}$, $F^{\mu _1\dots \mu _{J_1},\;\nu _1\dots \nu _{J_2}}_{\alpha _1\dots \alpha _J}$ and propagators $d(J_i,t)/(m^2(J_i)-t)$ which have the poles at

$$\begin{aligned} m^2(J_i)-t=0,\; \text{ i.e. }\; J_i=\alpha _{{\mathbb R}_i}(t), \end{aligned}$$

(24)

after an appropriate analytic continuation of the signatured amplitudes in $J_i$. We assume that these poles, where $\alpha _{{\mathbb R}_i}$ are reggeon trajectories, give the dominant contribution at high energies after having taken the corresponding residues. Regge cuts are generated by unitarization.

For vertex functions $T_{1,2}$ we can obtain the following tensor decomposition:

$$\begin{aligned} T^{(J_i)}&\equiv T^{\mu _1\dots \mu _{J_i}}(p_i,\Delta _i)\nonumber \\&= T_0(\Delta _i^2) \sum _{n=0}^{\left[ \frac{J_i}{2}\right] } {\mathbb C}_{J_i}^n \left( P_i^{(J_i-2n)}G_i^{(n)}\right) , \end{aligned}$$

(25)

$$\begin{aligned} {\mathbb C}_{J_i}^n= \frac{(-1)^n (2(J_i-n))\text{! }}{(J_i-n)\text{! }n\text{! }(J_i-2n)\text{! }}, \end{aligned}$$

(26)

that satisfies Rarita–Schwinger conditions (transverse-symmetric-traceless):

$$\begin{aligned}&\Delta _{\mu _i}T^{\mu _1\dots \mu _i\dots \mu _J}=0\end{aligned}$$

(27)

$$\begin{aligned}&T^{\mu _1\dots \mu _i\dots \mu _j\dots \mu _J}=T^{\mu _1\dots \mu _j\dots \mu _i\dots \mu _J}\end{aligned}$$

(28)

$$\begin{aligned}&g_{\mu _i\mu _j}T^{\mu _1\dots \mu _i\dots \mu _j\dots \mu _J}=0 \end{aligned}$$

(29)

The tensor structures $\left( P_i^{(J_i-2n)}G_i^{(n)}\right) ^{\mu _1\dots \mu _{J_i}}$ satisfy only the two conditions (27) and (28) (transverse-symmetric) and consist of the elements $P_i^{\mu }$ and $G_i^{\mu _1\mu _2}$:

$$\begin{aligned}&P_i^{\;\mu }= \left( p_i^{\mu }-\Delta _i^{\mu }/2 \right) /\sqrt{m^2-\Delta _i^2/4},\end{aligned}$$

(30)

$$\begin{aligned}&G_i^{\mu _1\mu _2}=g^{\mu _1\mu _2}- \frac{\Delta _i^{\mu _1}\Delta _i^{\mu _2}}{\Delta _i^2}, \end{aligned}$$

(31)

$$\begin{aligned}&\left( P_i^{(J_i-2n)}G_i^{(n)}\right) \nonumber \\&\quad =\frac{P_i^{\; (\mu _1}\!\!\cdot _{\dots }\!\!\cdot P_i^{\; \mu _{J_i-2n}} G_i^{\mu _{J_i-2n+1}\mu _{J_i-2n+2}}\!\!\cdot _{\dots }\!\!\cdot G_i^{\mu _{J_i-1}\mu _{J_i})}}{N_{J_i}^n}, \end{aligned}$$

(32)

$$\begin{aligned} N_{J_i}^n=\frac{J_i\text{! }}{2^n n\text{! }(J_i-2n)\text{! }}. \end{aligned}$$

(33)

The coefficients ${\mathbb C}_{J_i}^n$ in (25) can be obtained from the condition (29), which leads to a recurrent set of equations. For each transverse-symmetric structure we have

$$\begin{aligned}&g_{\mu _1\mu _2}\left( P_i^{(J_i-2n)}G_i^{(n)}\right) ^{\mu _1\dots \mu _{J_i}} \nonumber \\&\quad = \frac{(J_i-2n)(J_i-2n-1)}{J_i(J_i-1)}\times \left( P_i^{(J_i-2n-2)}G_i^{(n)}\right) \nonumber \\&\quad +\frac{2n(2(J_i-2)N_{J_i-3}^{n-1}\!+\!(J_i-2)(J_i-3)N_{J_i-4}^{n-2}\!+\!3N_{J_i-2}^{n-1})}{J_i(J_i-1)N_{J_i-2}^{n-1}}\nonumber \\&\quad \times \left( P_i^{(J_i-2n)}G_i^{(n-1)}\right) =0, \end{aligned}$$

(34)

where the first term corresponds to the tensor contraction

$$\begin{aligned} P_i^{\mu _1}P_i^{\mu _2}g_{\mu _1\mu _2}=1, \end{aligned}$$

(35)

and three items in the second term correspond to

$$\begin{aligned}&P_i^{\mu _1} G_i^{\mu _2\mu _k}g_{\mu _1\mu _2}=P_i^{\mu _k},\end{aligned}$$

(36)

$$\begin{aligned}&G_i^{\mu _1\mu _k} G_i^{\mu _2\mu _l}g_{\mu _1\mu _2}=G_i^{\mu _k\mu _l},\end{aligned}$$

(37)

$$\begin{aligned}&G_i^{\mu _1\mu _2}g_{\mu _1\mu _2}=3. \end{aligned}$$

(38)

Finally, we have

$$\begin{aligned}&\sum _{n=0}^{\left[ \frac{J_i}{2}\right] } {\mathbb C}_{J_i}^n\times \left[ (J_i-2n)(J_i-2n-1)\times \left( P_i^{(J_i-2n-2)}G_i^{(n)}\right) \right. \nonumber \\&\qquad +\left. 2n (2J_i-2n+1)\times \left( P_i^{(J_i-2n)}G_i^{(n-1)}\right) \right] \nonumber \\&\quad =\sum _{n=1}^{\left[ \frac{J_i}{2}\right] } \left[ {\mathbb C}_{J_i}^{n-1}(J_i-2n+2)(J_i-2n+1) \right. \nonumber \\&\qquad +\left. {\mathbb C}_{J_i}^{n}2n(2J_i-2n+1) \right] \times \left( P_i^{(J_i-2n)}G_i^{(n-1)}\right) =0\nonumber \\ \end{aligned}$$

(39)

and

$$\begin{aligned} {\mathbb C}_{J_i}^n&= {\mathbb C}_{J_i}^{n-1} \frac{(-1)(J_i-2n+2)(J_i-2n+1)}{2n(2J_i-2n+1)}\nonumber \\&= \frac{(-1)^n (2(J_i-n))\text{! }}{(J_i-n)\text{! }n\text{! }(J_i-2n)\text{! }}\left[ {\mathbb C}_{J_i}^0\frac{(J_i\text{! })^2}{(2J_i)\text{! }}\right] , \end{aligned}$$

(40)

which is equal to (26), if we set the expression in square brackets to unity.

Now let us obtain the general expression for the vertex $F^{(J_1),(J_2)}_{(J)}\equiv F^{\mu _1\dots \mu _{J_1},\;\nu _1\dots \nu _{J_2}}_{\alpha _1\dots \alpha _J}$, when $J=0$. Since this tensor has to satisfy (27)–(29) in each group of indices, it should be represented as

$$\begin{aligned}&F^{(J_1),(J_2)}_{0^+}=\sum _{k=0}^{\min [J_1,J_2]} \sum _{n_i=0}^{\left[ \frac{J_i-k}{2}\right] } {\mathbb C}_{J_1,J_2}^{k,n_1,n_2}\nonumber \\&\quad \times \left( D_1^{(J_1-k-2n_1)}G_1^{(n_1)}G_{12}^{(k)}G_2^{(n_2)}D_2^{(J_2-k-2n_2)} \right) . \end{aligned}$$

(41)

Here the transverse-symmetric structure in parentheses contains two groups of indices: $\{\mu \}\equiv \mu _1\dots \mu _{J_1}$ and $\{\nu \}\equiv \nu _1\dots \nu _{J_2}$ and consists of the following elements:

$$\begin{aligned}&D_{1,2}^{\rho }=\left( \Delta _{1,2}^{\rho }+ \frac{d_{1,2}^2}{(\Delta _1\Delta _2)}\Delta _{2,1}^{\rho }\right) /\left( d_{1,2} K_{12}\right) ,\end{aligned}$$

(42)

$$\begin{aligned}&d_{1,2}=\sqrt{-t_{1,2}},\; K_{12}=\sqrt{1-\frac{d_1^2d_2^2}{(\Delta _1\Delta _2)^2}},\end{aligned}$$

(43)

$$\begin{aligned}&G_{12}^{\mu \nu }=g^{\mu \nu }- \frac{\Delta _2^{\mu }\Delta _1^{\nu }}{(\Delta _1\Delta _2)}, \end{aligned}$$

(44)

and $G_i$ is defined in (31). The number of different terms in each structure is

$$\begin{aligned} N_{J_1J_2}^{k,n_1,n_2}=\frac{N_{J_1}^{n_1}N_{J_2}^{n_2}}{k\text{! }}. \end{aligned}$$

(45)

For $0^-$ state we have to add the anti-symmetric element

$$\begin{aligned} F_A^{\mu \nu }=\epsilon ^{\mu \nu \rho \sigma }\Delta _{1,\rho }\Delta _{2,\sigma }/(d_1d_2), \end{aligned}$$

(46)

and the vertex looks as follows:

$$\begin{aligned}&F^{(J_1),(J_2)}_{0^-}=\sum _{k=0}^{\min [J_1,J_2]-1} \sum _{n_i=0}^{\left[ \frac{J_i-1-k}{2}\right] } {\mathbb C}_{J_1,J_2}^{k,n_1,n_2}\nonumber \\&\quad \times \left( F_A D_1^{(J_1-1-k-2n_1)}G_1^{(n_1)}G_{12}^{(k)}G_2^{(n_2)}D_2^{(J_2-1-k-2n_2)} \right) .\nonumber \\ \end{aligned}$$

(47)

For further calculations let us define additional quantities and functions (approximate values are given for $d_{1,2}\ll m\le M\ll \sqrt{s_{1,2}}$):

$$\begin{aligned}&X_{1,2}= \frac{(P_{1,2}\Delta _{2,1})\; d_{1,2}}{(\Delta _1\Delta _2)\; Q_{1,2}} \simeq \frac{s_{1,2}\;d_{1,2}}{M^2\; m},\end{aligned}$$

(48)

$$\begin{aligned}&Q_{1,2}=\sqrt{1+d_{1,2}^2/(\Delta _1\Delta _2)}, \end{aligned}$$

(49)

$$\begin{aligned}&Z_{12}= \frac{(P_1P_2)\; (\Delta _1\Delta _2)}{(P_1\Delta _2)\; (P_2\Delta _1)}\simeq 1-\frac{2\varvec{\Delta }_1\varvec{\Delta }_2}{M^2}, \end{aligned}$$

(50)

$$\begin{aligned}&{\mathbb C}_{J_1J_2}^{k,0,0}= \left( \frac{d_1d_2}{(\Delta _1\Delta _2)}\right) ^k f_{J_1J_2}^k, \end{aligned}$$

(51)

where $f_{J_1J_2}^k$ are nonsingular at $t_i\rightarrow 0$ functions of $t_1$, $t_2$ and $M^2$.

We can construct $F^{(J_1)(J_2)}_{0^{\pm }}$ vertices as we did for $T^{(J_i)}$ in (34)–(40), taking the trace in each group of indices and obtaining recurrent equations for ${\mathbb C}_{J_1J_2}^{k,n_1,n_2}$. It will be done in further work. Here we note that in the contraction

$$\begin{aligned} V_{J_1J_2,\; 0^{\pm }}=\frac{T^{(J_1)}_{\{\mu \}}}{T_0(t_1)}\otimes F^{(J_1),\;\{\mu \}\;(J_2),\;\{\nu \}}_{0^{\pm }}\otimes \frac{T^{(J_2)}_{\{\nu \}}}{T_0(t_2)} \end{aligned}$$

(52)

$F$-vertices can be replaced by

$$\begin{aligned}&F^{(J_1),(J_2)}_{0^+}\rightarrow \left( \frac{d_1}{(\Delta _1\Delta _2)K_{12}}\right) ^{J_1} \left( \frac{d_2}{(\Delta _1\Delta _2)K_{12}}\right) ^{J_2}\nonumber \\&\quad \times \sum _{k=0}^{\min [J_1,J_2]} f_{J_1,J_2}^{k} \left( (\Delta _1\Delta _2)K_{12}^2\right) ^k \nonumber \\&\quad \times \Delta _2^{\mu _{k+1}}\!\cdot _{\dots }\!\!\cdot \Delta _2^{\mu _{J_1}} G_{12}^{\mu _1\nu _1}\!\cdot _{\dots }\!\!\cdot G_{12}^{\mu _k\nu _k} \Delta _1^{\nu _{k+1}}\!\cdot _{\dots }\!\!\cdot \Delta _1^{\nu _{J_2}}, \end{aligned}$$

(53)

$$\begin{aligned}&F^{(J_1),(J_2)}_{0^-}\rightarrow \left( \frac{d_1}{(\Delta _1\Delta _2)K_{12}}\right) ^{J_1} \left( \frac{d_2}{(\Delta _1\Delta _2)K_{12}}\right) ^{J_2} \nonumber \\&\quad \times \sum _{k=0}^{\min [J_1-1,J_2-1]} f_{J_1,J_2}^{k} \left( (\Delta _1\Delta _2)K_{12}^2\right) ^k \nonumber \\&\quad \times F_A^{\mu _1\nu _1}\Delta _2^{\mu _{k+2}}\!\cdot _{\dots }\!\!\cdot \Delta _2^{\mu _{J_1}} G_{12}^{\mu _2\nu _2}\!\cdot _{\dots }\!\!\cdot G_{12}^{\mu _{k+1}\nu _{k+1}} \Delta _1^{\nu _{k+2}}\!\cdot _{\dots }\!\!\cdot \Delta _1^{\nu _{J_2}},\nonumber \\ \end{aligned}$$

(54)

due to transverse-symmetric-traceless properties of $T$ structures. It is possible to show that in the exact $F$-vertices coefficients ${\mathbb C}_{J_1J_2}^{k,n_1,n_2}$, $n_i> 0$ can be expressed in terms of $f_{J_1J_2}^k$ only, i.e. we can obtain the exact formulae for (52) by the use of the simplified expansions (53) and (54), which is done below.

Let us calculate leading terms in the expansions of contracted vertices,

$$\begin{aligned}&V_{J_1J_2,\; 0^+}=\sum _{k=0}^{\min [J_1,J_2]} V^k_{J_1J_2,\; 0^+},\end{aligned}$$

(55)

$$\begin{aligned}&V_{J_1J_2,\; 0^-}=\sum _{k=0}^{\min [J_1-1,J_2-1]} V^k_{J_1J_2,\; 0^-}. \end{aligned}$$

(56)

It is rather easy to show that

$$\begin{aligned}&V^0_{J_1J_2,\; 0^+}=f_{J_1J_2}^0 \prod _{i=1}^2 \left( \frac{2Q_i}{K_{12}}\right) ^{J_i}\mathcal{P}_{J_i}(X_i)\nonumber \\&\quad \simeq \tilde{f}^0_{J_1J_2} X_1^{J_1}X_2^{J_2}\quad \text{ for } X_i\gg 1,\; t_i\ll m^2, \end{aligned}$$

(57)

where $\mathcal{P}_J(X)$ are Legendre polynomials and numerical factors are absorbed into $\tilde{f}^0_{J_1J_2}$. For the next term we can apply the following trick:

$$\begin{aligned}&\left( P_1^{(J_1-2n_1)}G_1^{(n_1)}\right) _{\{\mu \}}\nonumber \\&\quad = P_1^{\mu _1}\frac{J_1-2n_1}{J_1} \left( P_1^{(J_1-2n_1-1)}G_1^{(n_1)}\right) ^{\{\mu \}\ne \mu _1}\nonumber \\&\quad \quad + \sum _{i=2}^{J_1}G_1^{\mu _1\mu _i}\frac{2n_1}{J_1} \left( P_1^{(J_1-2n_1)}G_1^{(n_1-1)}\right) ^{\{\mu \}\ne \mu _1,\mu _i} \end{aligned}$$

(58)

and the same for the second structure. Effectively in the contraction the following dimensionless factor has to be added:

$$\begin{aligned}&\left[ \frac{(J_1-2n_1)\sqrt{(\Delta _1\Delta _2)}}{J_1(P_1\Delta _2)}P_1^{\mu _1}+ \frac{(2n_1)d_1 K_{12}}{J_1\sqrt{(\Delta _1\Delta _2)}Q_1^2}D_1^{\mu _1} \right] \nonumber \\&\quad \times \left[ 1\rightarrow 2,\; \mu \rightarrow \nu \right] . \end{aligned}$$

(59)

Then we have to contract these structures with $G_{12}^{\mu _1\nu _1}$ and $F_A^{\mu _1\nu _1}$ to calculate $V^1_{J_1J_2,\; 0^+}$ and $V^0_{J_1J_2,\; 0^-}$, respectively. The final result can be represented as

$$\begin{aligned}&V^1_{J_1J_2,\; 0^+}= f_{J_1J_2}^1 \left( \frac{2Q_1}{K_{12}}\right) ^{J_1} \left( \frac{2Q_2}{K_{12}}\right) ^{J_2} \frac{K_{12}^2}{J_1J_2}\nonumber \\&\qquad \times \left\{ \left[ Z_{12}-1 \right] \mathcal{P}^{\prime }_{J_1}\mathcal{P}^{\prime }_{J_2}+ \frac{d_1^2d_2^2}{(\Delta _1\Delta _2)^2} \left[ \frac{K_{12}^2}{Q_1^2Q_2^2} \mathcal{P}^{\prime \prime }_{J_1}\mathcal{P}^{\prime \prime }_{J_2} \right. \right. \nonumber \\&\qquad + \left. \left. \frac{1}{Q_2^2}\mathcal{P}^{\prime }_{J_1}\mathcal{P}^{\prime \prime }_{J_2}+ \frac{1}{Q_1^2}\mathcal{P}^{\prime \prime }_{J_1}\mathcal{P}^{\prime }_{J_2} \right] \right\} \nonumber \\&\quad \simeq \tilde{f}^1_{J_1J_2}X_1^{J_1}X_2^{J_2} \frac{2\varvec{\Delta }_1\varvec{\Delta }_2}{M^2}, \end{aligned}$$

(60)

$$\begin{aligned}&V^0_{J_1J_2,\; 0^-}=f_{J_1J_2}^0 \left\{ \frac{\sqrt{1-\frac{4m^2}{s}}}{1- \frac{s_1+s_2}{2s}+\frac{M^2-4m^2-d_1^2-d_2^2}{4s}}\right\} \nonumber \\&\qquad \times \left( \frac{2Q_1}{K_{12}}\right) ^{J_1} \left( \frac{2Q_2}{K_{12}}\right) ^{J_2} \frac{Z_{12}}{J_1J_2} \mathcal{P}^{\prime }_{J_1}\mathcal{P}^{\prime }_{J_2} \frac{\left[ \varvec{\Delta }_1\times \varvec{\Delta }_2\right] }{d_1d_2}\nonumber \\&\quad \simeq \tilde{f}^0_{J_1J_2}X_1^{J_1}X_2^{J_2} \frac{\left[ \varvec{\Delta }_1\times \varvec{\Delta }_2\right] }{d_1d_2}, \end{aligned}$$

(61)

where the term in braces is close to unity and

$$\begin{aligned} \mathcal{P}^{\prime }_{J}&= X\frac{\partial }{\partial X}\mathcal{P}_{J}(X)\nonumber \\&= \frac{J\;X}{X^2-1}\left( X\;\mathcal{P}_{J}(X)- \mathcal{P}_{J-1}(X) \right) , \end{aligned}$$

(62)

$$\begin{aligned} \mathcal{P}^{\prime \prime }_{J}&= -\frac{\partial }{\partial X}\mathcal{P}_{J-1}(X)\nonumber \\&= -\frac{J}{X^2-1}\left( \mathcal{P}_{J}(X)-X\; \mathcal{P}_{J-1}(X) \right) . \end{aligned}$$

(63)

For $d_{1,2}\ll m\le M\ll \sqrt{s_{1,2}}\le \sqrt{s}$ and $X_i\gg 1$ we can write the expressions for leading terms of amplitudes

$$\begin{aligned} \mathcal{M}^{0^+}&\simeq \sum _{J_1,J_2} \prod _{i=1,2} \left[ T_0(t_i) X_i^{J_i} \right] \nonumber \\&\times \sum _{k=0}^{\min (J_1,J_2)} \tilde{f}^k_{J_1J_2}\left( \frac{2\sqrt{t_1t_2}\cos \phi }{M^2} \right) ^k, \end{aligned}$$

(64)

(65)

Then we have to continue analytically the above expressions to complex $J_{1,2}$ planes. It can be done like in Ref. [66], using the reggeization prescription

$$\begin{aligned} \sum _J\frac{F^J}{(t-m^2)}\rightarrow \frac{\alpha _{{\mathbb R}}^{\prime }}{2}\eta _{{\mathbb R}}(t)\Gamma (-\alpha _{{\mathbb R}}(t))F^{\alpha _{{\mathbb R}}(t)}. \end{aligned}$$

(66)

To check that the above approach coincides with the usual Regge one, let us calculate the amplitude of the elastic scattering of two particles with equal masses $m$. For the exchange of the meson with spin $J$ it is equal to the contraction

$$\begin{aligned}&\mathcal{M}^{el}(s,t)=T^{(J)}_{\{\mu \}}(p_1,\Delta )\otimes T^{(J)}_{\{\mu \}}(p_2,-\Delta )\nonumber \\&\quad =T_0(t)^2 2^J {\mathbb C}_J^0 \mathcal{P}_J\left( \frac{s-2m^2+t/2}{2m^2-t/2} \right) \sim \left( \frac{s}{m^2}\right) ^J, \end{aligned}$$

(67)

which leads to the basic reggeon exchange formula after appropriate analytical continuation to the complex $J$ plane.

More complicated situation occurs in the case of unequal masses. For example, let us consider the process $p+p\rightarrow p+X$, where $m_p=m$, $m_X=M\gg m$. For the exchange of the meson with spin $J$ we have

$$\begin{aligned}&\mathcal{M}(s,t)=T^{(J)}_{\{\mu \}}(p_1,\Delta )\otimes T^{(J)}_{\{\mu \}}(p_2,-\Delta )\nonumber \\&\quad = T_{01}(t)T_{02}(t) 2^J {\mathbb C}_J^0 \mathcal{P}_J\left( \frac{(2s-3m^2-M^2+t)\sqrt{-t}}{\sqrt{4m^2-t}\;\lambda ^{1/2}(t,m^2,M^2)} \right) \nonumber \\&\quad \sim \left( \frac{s\sqrt{-t}}{M^2m}\right) ^J. \end{aligned}$$

(68)

Here the argument of the Legendre function is the t-channel cosine $z_t=\cos \theta _t$, and

$$\begin{aligned} \lambda (x,y,z)=x^2+y^2+z^2-2xy-2xz-2yz. \end{aligned}$$

The factor $\sqrt{-t}$ is a consequence of the tensor meson current conservation (27). In the classical Regge scheme

$$\begin{aligned} \sum _J (2J+1)\mathcal{M}_J \mathcal{P}_J(-z_t)\rightarrow \eta _{\mathbb R}(t) \beta _{\mathbb R}(t) \left( \frac{s}{s_0}\right) ^{\alpha _{\mathbb R}(t)}, \end{aligned}$$

(69)

where this factor is absorbed into the unknown residue $\beta _{\mathbb R}(t)$. In our prescription the t dependence of the residue looks like

$$\begin{aligned} \beta _{\mathbb R}\sim T_{01}(t)T_{02}(t) (-t)^{\alpha _{\mathbb R}/2}. \end{aligned}$$

(70)

There is no zero in t, since the Regge approach is valid only for $|z_t|\gg 1$. But sometimes this behaviour at small t is extracted in an explicit form like in Ref. [83], devoted to the process of single diffraction dissociation.

Appendix B

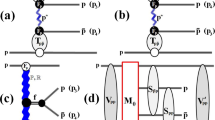
Here we present the general structure of the amplitude for the $2\rightarrow 4$ process $p+p\rightarrow p+h\bar{h}+p$. This amplitude is depicted in Fig. 7. The definitions for the kinematics are

$$\begin{aligned}&s_{1\{a,b\}}=(p_{1}^{\prime }+k_{a,b})^2,\; s_{2\{a,b\}}=(p_{2}^{\prime }+k_{a,b})^2,\nonumber \\&\hat{t}_{a,b}=(p_1-p_1^{\prime }-k_{a,b})^2=(p_2-p_2^{\prime }-k_{b,a})^2. \end{aligned}$$

(71)

Leading contribution to the reggeon–reggeon fusion vertex is given by the exchange amplitude (the right part of Fig. 7). In this case we can write

$$\begin{aligned}&\mathcal{M}_{h\bar{h}}= \mathcal{M}^{el}_{hp}(s_{1a},t_1) \frac{\left( F_h(\hat{t}_a)\right) ^2}{(\hat{t}_a-m_0^2)} \mathcal{M}^{el}_{\bar{h}p}(s_{2b},t_2)\nonumber \\&\quad +\mathcal{M}^{el}_{hp}(s_{1b},t_1) \frac{\left( F_h(\hat{t}_b)\right) ^2}{(\hat{t}_b-m_0^2)} \mathcal{M}^{el}_{\bar{h}p}(s_{2a},t_2). \end{aligned}$$

(72)

Here $\mathcal{M}^{el}_{hp}$ and $\mathcal{M}^{el}_{\bar{h}p}$ are amplitudes of the elastic hadron–proton scattering, which can be evaluated in any appropriate approach, $F_h$ is the formfactor taking into account the off-shellness of the exchanged hadron. For example, we can use simple reggeon exchanges for these amplitudes as was done in [47, 48]. Strictly speaking, we have to take into account rescattering (unitarity) corrections since $s_{i\{a,b\}}$ can be of the order $\sim \sqrt{s}$.

Fig. 7

Scheme of calculation of the “bare” EDDE amplitude in the case of the low invariant mass ($M<3$ GeV) dihadron production. Elastic amplitudes are shown here as reggeon exchanges enclosed in ellipses

Calculations for the $\pi ^+\pi ^-$ production in this paper are based on the simple Regge formula (as in [47, 48]) for pion–proton elastic amplitudes

$$\begin{aligned}&\mathcal{M}^{el}_{\pi ^{\pm }p}(s,t)=\sum _{i={\mathbb P},{\mathbb R}} C^{\pm }_i F_i(t)\left( \frac{s}{s_0}\right) ^{\alpha _i(t)},\end{aligned}$$

(73)

$$\begin{aligned}&F_i(t)={\mathrm e}^{B^0_i t},\quad \alpha _i(t)=\alpha _i^0+\alpha _i^{\prime }t, \end{aligned}$$

(74)

$$\begin{aligned}&C_{{\mathbb P}}=\mathrm {i} C_P,\; C^{\pm }_{{\mathbb R}}=C_f(a_f+\mathrm {i})\pm C_{\rho }(a_{\rho }-\mathrm {i}),\\&C_P=13.63\;{\mathrm mb},\; C_f=31.79\;{\mathrm mb},\; C_{\rho }=4.23\;{\mathrm mb}, \end{aligned}$$

$$\begin{aligned}&a_f=-0.860895,\; a_{\rho }=-1.16158,\end{aligned}$$

(75)

$$\begin{aligned}&B^0_{{\mathbb P}}=2.75\;\mathrm{GeV}^{-2},\; B^0_{{\mathbb R}}=2\;\mathrm{GeV}^{-2},\end{aligned}$$

(76)

$$\begin{aligned}&\alpha _{\mathbb P}(t)=1.088+0.25t,\; \alpha _{\mathbb R}=0.5475+0.93t, \end{aligned}$$

(77)

$$\begin{aligned}&F_{\pi }(\hat{t})\simeq {\mathrm e}^{\frac{\hat{t}-m_{\pi }^2}{\Lambda ^2_{eff}}},\; \Lambda ^2_{eff}=1\;\mathrm{GeV}^2. \end{aligned}$$

(78)

Appendix C

Here we calculate the hadron–hadron “soft” interaction in the initial and in the final states (unitary corrections or rescattering). It is denoted by $V$ in Fig. 1 and given by the following analytical expressions:

$$\begin{aligned}&\mathcal{M}^{U}(p_1, p_2, \Delta _1, \Delta _2) = \int \frac{d^2\varvec{q}_T}{(2\pi )^2} \, \frac{d^2\varvec{q}^{\;\prime }_T}{(2\pi )^2} \; V(s, \varvec{q}_T) \; \nonumber \\&\quad \times \mathcal{M}( p_1-q_T, p_2+q_T,\Delta _{1T}, \Delta _{2T}) \, V(s^{\prime }, \varvec{q}^{\;\prime }_T), \end{aligned}$$

(79)

$$\begin{aligned} V(s, \varvec{q}_T) = \int d^2\varvec{b} \, {\mathrm e}^{i\varvec{q}_T \varvec{b}} \sqrt{1+2\mathrm {i} T^{el}_{pp\rightarrow pp}(s, \varvec{b})}, \end{aligned}$$

(80)

where $\Delta _{1T} = \Delta _{1} -q_T - q^{\prime }_T$, $\Delta _{2T} = \Delta _{2} + q_T + q^{\prime }_T$, $\mathcal{M}$ is the “bare” amplitude of the process $p+p\rightarrow p+M+p$. In the case of the eikonal representation of the elastic amplitude $T^{el}_{pp\rightarrow pp}$ we have

$$\begin{aligned} V(s, \varvec{q}_T) = \int d^2\varvec{b} \, \mathrm {e}^{\mathrm {i}\varvec{q}_T \varvec{b}} \mathrm {e}^{\mathrm {i}\delta _{pp\rightarrow pp}(s,\varvec{b})}, \end{aligned}$$

(81)

where $\delta _{pp\rightarrow pp}$ is the eikonal function. In this case amplitude (79) can be rewritten as

$$\begin{aligned}&\mathcal{M}^{U}(\varvec{\Delta }_1, \varvec{\Delta }_2) = \int \frac{d^2\varvec{b}}{2\pi } \, {\mathrm e}^{ -{\mathrm i}\varvec{\delta }\varvec{b}-\Omega (s,b)-\Omega (s^{\prime },b) }\nonumber \\&\quad \times \int \frac{d^2\varvec{\kappa }}{2\pi } \, {\mathrm e}^{{\mathrm i}\varvec{\kappa }\varvec{b}} \mathcal{M}(\varvec{\Delta }-\varvec{\kappa }, \varvec{\Delta }+\varvec{\kappa }),\nonumber \\&\Omega (s,b)=-\mathrm {i}\delta _{pp\rightarrow pp}(s,b),\nonumber \\&\varvec{\Delta }=\frac{\varvec{\Delta }_2+\varvec{\Delta }_1}{2},\; \varvec{\delta }=\frac{\varvec{\Delta }_2-\varvec{\Delta }_1}{2},\;\nonumber \\&\varvec{\kappa }=\varvec{\delta }+\varvec{q}_T+\varvec{q}^{\;\prime }_T. \end{aligned}$$

(82)

Here we use the following representation for the elastic amplitude [84]:

$$\begin{aligned} T_{el}(s,b)=\imath \left( 1-\mathrm {e}^{-2\Omega (s,b)}\right) \Big /2. \end{aligned}$$

(83)

Some other groups [85, 86] use another conventions

$$\begin{aligned} T_{el}(s,b)=\imath \left( 1-\mathrm {e}^{-\Omega (s,b)/2}\right) , \end{aligned}$$

(84)

or [87]

$$\begin{aligned} T_{el}(s,b)=\imath \left( 1-\mathrm {e}^{-\Omega (s,b)}\right) , \end{aligned}$$

(85)

which are mathematically equivalent.

Let us consider calculations for concrete expressions of $\mathcal{M}$. To explore general features of diffractive patterns for the eikonal function we take the model [88] (which originates from [84] and uses simple eikonal approximation) as an example. Nevertheless, some authors [85, 89] point out that we have to use multichannel eikonals to take into account multiple diffractive eigenstates. Here we have to point out that the parametrization (83) satisfies exactly the unitarity condition and can be used without consideration of any inner structure of the eikonal (diffractive eigenstates) as it was done in the multichannel approach. We assume that the model [88] is rather good for our purposes, at least for $|t_i|<1.5\;\mathrm {GeV}^2$, since it describes well the latest data [82].

For the amplitude we perform calculations for several cases:

$$\begin{aligned} \mathcal{M}_i(\varvec{\Delta }_1, \varvec{\Delta }_2)&= \mathcal{H}(\varvec{\Delta }^2) {\mathrm e}^{-B_1\varvec{\Delta }_1^2-B_2\varvec{\Delta }_2^2} \mathcal{K}_i(\varvec{\Delta }_1, \varvec{\Delta }_2)\nonumber \\&\rightarrow \mathcal{H}(\varvec{\Delta }^2) {\mathrm e}^{ -B_+\left( \varvec{\Delta }^2+\varvec{\kappa }^2\right) +2B_-\left( \varvec{\Delta }\varvec{\kappa }\right) } \mathcal{K}_i\nonumber \\&\times (\varvec{\Delta }-\varvec{\kappa }, \varvec{\Delta }+\varvec{\kappa }), \end{aligned}$$

(86)

$$\begin{aligned} B_{\pm }&= B_1\pm B_2,\nonumber \\ \mathcal{K}_0&= 1,\;\end{aligned}$$

(87)

$$\begin{aligned} \mathcal{K}_V&= \left[ \varvec{\Delta }_1\times \varvec{\Delta }_2\right] \rightarrow 2\left[ \varvec{\Delta }\times \varvec{\kappa }\right] ,\end{aligned}$$

(88)

$$\begin{aligned} \mathcal{K}_S&= \left( \varvec{\Delta }_1\varvec{\Delta }_2\right) \rightarrow \varvec{\Delta }^2-\varvec{\kappa }^2,\end{aligned}$$

(89)

$$\begin{aligned} \mathcal{K}_T&= \varvec{\Delta }_1^2\varvec{\Delta }_2^2\rightarrow \left( \varvec{\Delta }^2+\varvec{\kappa }^2\right) ^2- 4\left( \varvec{\Delta }\varvec{\kappa }\right) ^2. \end{aligned}$$

(90)

We have to calculate the following auxiliary integrals:

$$\begin{aligned}&\mathcal{I}_{\varvec{\kappa }}^v =\int \frac{d^2\varvec{\kappa }}{2\pi }\; {\mathrm e}^{ {\mathrm i}\varvec{\kappa }\varvec{b}-B_+\varvec{\kappa }^2+2B_-\left( \varvec{\Delta }\varvec{\kappa }\right) }\; v,\end{aligned}$$

(91)

$$\begin{aligned}&\mathcal{I}_{\varvec{\kappa }}^1=\frac{1}{2B_+}{\mathrm e}^{a/B_+},\nonumber \\&a= B_-^2\varvec{\Delta }^2+{\mathrm i}B_-\left( \varvec{\Delta }\varvec{b}\right) -b^2/4,\end{aligned}$$

(92)

$$\begin{aligned}&\mathcal{I}_{\varvec{\kappa }}^{\varvec{\kappa }_{(i)}}= -{\mathrm i}\frac{\partial }{\partial \varvec{b}_{(i)}} \mathcal{I}_{\varvec{\kappa }}^1= \left( \frac{B_-}{B_+}\varvec{\Delta }_{(i)}+{\mathrm i}\frac{\varvec{b}_{(i)}}{2B_+} \right) \mathcal{I}_{\varvec{\kappa }}^1,\end{aligned}$$

(93)

$$\begin{aligned}&\mathcal{I}_{\varvec{\kappa }}^{\varvec{\kappa }^2}= -\frac{\partial }{\partial B_+}\mathcal{I}_{\varvec{\kappa }}^1= \frac{1}{B_+}\left( 1+\frac{a}{B_+}\right) \mathcal{I}_{\varvec{\kappa }}^1,\end{aligned}$$

(94)

$$\begin{aligned}&\mathcal{I}_{\varvec{\kappa }}^{\varvec{\kappa }^4}= -\frac{\partial }{\partial B_+}\mathcal{I}_{\varvec{\kappa }}^{\varvec{\kappa }^2}= \frac{1}{B_+^2}\left( 2+\frac{4a}{B_+}+\frac{a^2}{B_+^2}\right) \mathcal{I}_{\varvec{\kappa }}^1. \end{aligned}$$

(95)

Further calculations are expressed in terms of the function $h$ (see Fig. 8),

$$\begin{aligned}&h(\lambda ,B_+)=\int \frac{d^2\varvec{b}}{2\pi } {\mathrm e}^{-\mathrm {i}\varvec{\lambda }\varvec{b}-\Omega (s,b)-\Omega (s^{\prime },b)-b^2/(4B_+)}\nonumber \\&\qquad \qquad \quad =\int db\; b\; J_0(\lambda b) {\mathrm e}^{-\Omega (s,b)-\Omega (s^{\prime },b)-b^2/(4B_+)},\nonumber \\&\lambda =\left| \varvec{\lambda }\right| =\left| \varvec{\delta }-\frac{B_-}{B_+}\varvec{\Delta }\right| . \end{aligned}$$

(96)

We can write

$$\begin{aligned}&\mathcal{M}^U_i=\frac{1}{2B_+}\mathcal{H}(\varvec{\Delta }^2) {\mathrm e}^{-B_+\left( 1-\frac{B_-^2}{B_+^2}\right) \varvec{\Delta }^2}\hat{\mathcal{K}}_i h(\lambda ,B_+),\end{aligned}$$

(97)

$$\begin{aligned}&\hat{\mathcal{K}}_0=1,\end{aligned}$$

(98)

$$\begin{aligned}&\hat{\mathcal{K}}_V= -\frac{1}{B_+}\left[ \varvec{\Delta }\times \varvec{\lambda }\right] \frac{1}{\lambda }\frac{\partial }{\partial \lambda }, \end{aligned}$$

(99)

$$\begin{aligned} \hat{\mathcal{K}}_S&= -\frac{1}{B_+}+ \varvec{\Delta }^2\left( 1-\frac{B_-^2}{B_+^2}\right) \nonumber \\&+ \frac{B_-}{B_+^2}\left( \varvec{\Delta }\varvec{\lambda }\right) \frac{1}{\lambda }\frac{\partial }{\partial \lambda }+ \frac{\partial }{\partial B_+}, \end{aligned}$$

(100)

$$\begin{aligned} \hat{\mathcal{K}}_T&= \left[ \frac{2}{B_+^2}+\frac{2\varvec{\Delta }^2}{B_+}\left( 1+\frac{2B_-^2}{B_+^2}\right) + \varvec{\Delta }^4\left( 1-\frac{B_-^2}{B_+^2}\right) \right] \nonumber \\&+ \left[ \frac{2B_-}{B_+^2}\left( -\frac{2}{B_+}+\varvec{\Delta }^2\left( 1-\frac{B_-^2}{B_+^2}\right) \right) \left( \varvec{\Delta }\varvec{\lambda }\right) \right. \nonumber \\&-\left. \frac{\varvec{\Delta }^2}{B_+^2}\left( 1-\frac{B_-^2}{B_+^2}\right) \right] \frac{1}{\lambda }\frac{\partial }{\partial \lambda } \nonumber \\&- 2\left( \frac{1}{B_+}+\varvec{\Delta }^2\left( 1+\frac{B_-^2}{B_+^2}\right) \right) \frac{\partial }{\partial B_+} \nonumber \\&+ \frac{\partial ^2}{\partial ^2 B_+}+ 2\frac{B_-}{B_+^2}\left( \varvec{\Delta }\varvec{\lambda }\right) \frac{1}{\lambda }\frac{\partial }{\partial \lambda } \frac{\partial }{\partial B_+}\nonumber \\&- \frac{1}{B_+^2}\left( 1-\frac{B_-^2}{B_+^2}\right) \left( \varvec{\Delta }\varvec{\lambda }\right) ^2 \frac{1}{\lambda }\frac{\partial }{\partial \lambda } \frac{1}{\lambda }\frac{\partial }{\partial \lambda }. \end{aligned}$$

(101)

The ratio

$$\begin{aligned} \langle S^2\rangle =\frac{\int \int d^2\varvec{\Delta }_1 d^2\varvec{\Delta }_2 \left| \mathcal{M}^{U}\right| ^2}{\int \int d^2\varvec{\Delta }_1 d^2\varvec{\Delta }_2 \left| \mathcal{M}\right| ^2} \end{aligned}$$

(102)

is usually called the “soft survival probability”. For example, at $\sqrt{s}=14$ TeV the value of $\langle S^2\rangle$ is about $0.03$ for the slope of the t-distribution $\sim 4\;\mathrm{GeV}^{-2}$ (invariant masses about $100$ GeV) and $0.13$ for the slope $\sim 10\;\mathrm{GeV}^{-2}$ (invariant masses about $1$ GeV).

Fig. 8

Function $|h(\lambda ,B_+)|^2$ at a $\sqrt{s}=62$ GeV and b $\sqrt{s}=7$ TeV. $|h(0.,4.)|^2=20.5\;\mathrm{GeV}^{-2}$ at $\sqrt{s}=62$ GeV and $|h(0.,4.)|^2=5.27\;\mathrm{GeV}^{-2}$ at $\sqrt{s}=7$ TeV