Electrically charged one-and-a-half monopole solution

Abstract

Recently, we have discussed the coexistence of a finite energy one-half monopole and a ’t Hooft–Polyakov monopole of opposite magnetic charges. In this paper, we would like to introduce electric charge into this new monopoles configuration, thus creating a one-and-a-half dyon. This new dyon possesses finite energy, magnetic dipole moment, and angular momentum and is able to precess in the presence of an external magnetic field. Similar to the other dyon solutions, when the Higgs self-coupling constant, $\lambda$, is nonvanishing, this new dyon solution possesses critical electric charge, total energy, magnetic dipole moment, and dipole separation as the electric charge parameter, $\eta$, approaches 1. The electric charge and total energy increase with $\eta$ to maximum critical values as $\eta \rightarrow 1$ for all nonvanishing $\lambda$. However, the magnetic dipole moment decreases with $\eta$ when $\lambda \ge 0.1$ and the dipole separation decreases with $\eta$ when $\lambda \ge 1$ to minimum critical values as $\eta \rightarrow 1$.

1 Introduction

The SU(2) Yang–Mills–Higgs (YMH) field theory possesses a rich spectrum of monopole configurations which are invariant under a U(1) subgroup of the local SU(2) gauge group. The invariance of the U(1) subgroup is an important part of the theory as upon symmetry breaking it will give rise to Maxwell’s electromagnetic field theory [1]. Some of the well-known work on monopole solutions is listed in Refs. [1–14]. The ’t Hooft–Polyakov monopole solution is a numerical solution [1–6], whereas exact solutions can be obtained only in the Bogomol’nyi–Prasad–Sommerfield (BPS) limit when the Higgs potential vanishes [7–14]. Numerical BPS monopole solutions were discussed in Refs. [15, 16], whereas numerical solutions with axial symmetry and nonvanishing Higgs potential were given in Refs. [17–21]. Recently, numerical generalized Jacobi elliptic single monopole solutions and numerical generalized Jacobi elliptic MAP and single vortex ring solutions were also discussed in Refs. [22, 23]. The monopole solutions discussed in Refs. [1–23] possessed integer topological magnetic charge.

However, there are also papers with discussions on particles with one-half monopole magnetic charge. These include the work of Harikumar et al. [24] where they demonstrated the existence of generic smooth Yang–Mills (YM) potentials of one-half monopoles. Exact axially symmetric and mirror symmetric one-half monopole solutions with Dirac-like string were discussed in Ref. [25, 26]. However, these exact solutions possess infinite total energy.

Recently, axially symmetric, finite energy particles of one-half monopole magnetic charge [27, 28] and particles of positive one and negative half monopole magnetic charges [29] were shown to exist. The ’t Hooft magnetic fields of these solutions at spatial infinity correspond to the magnetic field of a positive one-half magnetic monopole located at the origin, $r=0$, and a semi-infinite Dirac string located on one-half of the $z$-axis which carries magnetic flux of $\frac{2\pi }{g}$ from infinity to the origin, thus making the net magnetic charge of the configuration 0. The non-Abelian solutions possess gauge potentials that are singular only along one-half of the $z$-axis; elsewhere they are regular [30]. The total energies of these new magnetic monopole solutions were found to increase with $\lambda$.

A dyon is a particle that possesses both magnetic and electric charges. A dyon with a fixed magnetic charge can possess varying electric charges [31] at the classical level. The dyons solutions of Julia and Zee [32–34] are time independent solutions that possess nonvanishing kinetic energy. The Julia–Zee solutions are non-self-dual even in the BPS limit when the electric charge is nonvanishing. The exact dyon solutions found by Prasad and Sommerfield [33] are actually Julia and Zee dyon solutions in the BPS limit. These solutions are stable as they are the absolute minima of the energy [35].

All the monopole solutions of the SU(2) YMH theory can acquire an electric charge to become a dyon as shown by the work of Refs. [32–34]. Axially symmetrical single pole dyons were constructed by Hartmann et al. [36]. These axial dyons are actually generalized ’t Hooft–Polyakov monopoles that possess magnetic charges, $n=1, 2, 3$ and nonvanishing electric charges. It was found in Refs. [36, 37] that when the strength of the Higgs potential $\lambda$ is nonvanishing, the total electric charge and total energy of the system approach finite critical (maximum) values when the electric charge parameter, $\eta$, approaches 1. However, when $\lambda =0$, the total electric charge and total energy approach infinity when the parameter $\eta$ approaches 1. Similarly when $\lambda$ is nonvanishing, the electric charge, total energy, and magnetic dipole moment of the 0 topological charge sector of the monopole–antimonopole pair (MAP) and vortex ring solutions [38] and the one-half dyon solution [39] approach finite critical (maximum) values when the electric charge parameter $\eta$ approaches 1. However, when $\lambda =0$, the electric charge, total energy, and magnetic dipole moment approach infinity when $\eta$ approaches 1. The MAP dyons were also investigated in Refs. [40–43] by varying $\lambda$ for fixed value of $\eta$.

Since the one-and-a-half monopoles solution of Ref. [29] is a new finite energy solution with properties that differ from the usual monopoles, we would like to further study its properties and behavior when electric charges are introduced into the configuration. This is done by using the standard procedure of Julia and Zee [32] for the magnetic ansatz [36–43]. We perform calculations numerically for the dimensionless electric charge $Q$, total energy $E$, angular momentum $J_z$ about the $z$-axis of symmetry, magnetic dipole moment $\mu _m$, and dipole separation, $d_z$, of the new dyon solution when the electric charge parameter $\eta$ is varied from 0 to 1 and when the Higgs self-coupling constant is varied from 0 to 12. Since this new dyon possesses finite magnetic dipole moment and angular momentum, it is able to precess in the presence of an external magnetic field.

Similar to the single pole dyon [36, 37] and the MAP dyons [38, 40–43], this new dyon possesses critical (maximum) electric charge and total energy when the Higgs self-coupling constant, $\lambda$, is nonvanishing and the electric charge parameter, $\eta$, approaches 1. When $\lambda$ vanishes, these quantities approach infinity when $\eta$ approaches 1. However, in contrast to the other previous dyon solutions, the magnetic dipole moment decreases with $\eta$ when $\lambda \ge 0.1$ and the dipole separation decreases with $\eta$ when $\lambda \ge 1$ to minimum critical values as $\eta \rightarrow 1$.

We also perform calculations for the total energy $E$, the total electric charge $Q$, the magnetic dipole moment $\mu _m$, and dipole separation, $d_z$, of this new dyon solution for fixed values of $\eta$ and for $\lambda$ from 0 to 12. In general, the total electric charge, magnetic dipole moment, and dipole separation decrease exponentially with increasing $\lambda ^{1/2}$. The total energy for small values of $\eta < 0.7$, however, increases logarithmically with increasing $\lambda ^{1/2}$. The total energy for larger values of $0.7 <\eta \le 1$ first decreases for small values of $\lambda ^{1/2}$, and then it increases with $\lambda ^{1/2}$.

We briefly review the SU(2) Yang–Mills–Higgs field theory in the next section. In Sect. 3, we discuss the construction of the new dyon solution. The magnetic ansatz used in obtaining the new dyon solution and some of its basic properties are given in this section. The numerical results of our calculations of the new dyon solution are presented and discussed in Sect. 4. We end with some comments in Sect. 5.

2 The SU(2) Yang–Mills–Higgs theory

The Lagrangian in this 3+1 dimensional theory is

$$\begin{aligned} {\fancyscript{L}} \!=\! -\frac{1}{4}F^a_{\mu \nu } F^{a\mu \nu } \!-\! \frac{1}{2}D^\mu \varPhi ^a D_\mu \varPhi ^a \!-\! \frac{1}{4}\lambda (\varPhi ^a\varPhi ^a - \xi ^2)^2,\nonumber \\ \end{aligned}$$

(1)

where the first two terms on the left-hand side Eq. (1) are the kinetic energy terms and the last term is the nonvanishing Higgs potential. Here the Higgs field mass is $\mu$ and the strength of the Higgs potential is $\lambda$, which are constants. The vacuum expectation value of the Higgs field is $\xi =\mu /\sqrt{\lambda }$. The covariant derivatives of the Higgs field and the gauge field strength tensor are given, respectively, by

$$\begin{aligned}&D_{\mu }\varPhi ^{a} = \partial _{\mu } \varPhi ^{a} + g\epsilon ^{abc} A^{b}_{\mu }\varPhi ^{c},\nonumber \\&F^a_{\mu \nu } = \partial _{\mu }A^a_\nu - \partial _{\nu }A^a_\mu + g\epsilon ^{abc}A^b_{\mu }A^c_\nu , \end{aligned}$$

(2)

where $g$ is the gauge field coupling constant. The metric used is $g_{\mu \nu } = (- + + +)$. The SU(2) internal group indices $a, b, c = 1, 2, 3$ and the space-time indices are $\mu , \nu , \alpha = 0, 1, 2$, and $3$ in Minkowski space. The equations of motion that follow from the Lagrangian (1) are

$$\begin{aligned}&D^{\mu }F^a_{\mu \nu } = \partial ^{\mu }F^a_{\mu \nu } + g\epsilon ^{abc}A^{b\mu }F^c_{\mu \nu } = g\epsilon ^{abc}\varPhi ^{b}D_{\nu }\varPhi ^c,\nonumber \\&D^{\mu }D_{\mu }\varPhi ^a = \lambda \varPhi ^a(\varPhi ^{b}\varPhi ^{b} - \xi ^2). \end{aligned}$$

(3)

In the limit of vanishing $\mu$ and $\lambda$, the Higgs potential vanishes and self-dual solutions can be obtained by solving the first order partial differential Bogomol’nyi equation,

$$\begin{aligned} B^a_i \pm D_i \varPhi ^a = 0,\quad \text{ where }\ B^a_i=-\frac{1}{2}\epsilon _{ijk}F^a_{jk}. \end{aligned}$$

(4)

The electromagnetic field tensor proposed by ’t Hooft [2–6] upon symmetry breaking is

$$\begin{aligned}&F_{\mu \nu } = \hat{\varPhi }^a F^a_{\mu \nu } - \frac{1}{g}\epsilon ^{abc}\hat{\varPhi }^{a}D_{\mu }\hat{\varPhi }^{b}D_{\nu }\hat{\varPhi }^c,\nonumber \\&\quad = \partial _{\mu }A_\nu - \partial _{\nu }A_\mu - \frac{1}{g}\epsilon ^{abc}\hat{\varPhi }^{a}\partial _{\mu }\hat{\varPhi }^{b}\partial _{\nu }\hat{\varPhi }^c\nonumber \\&\quad = G_{\mu \nu }+H_{\mu \nu },\quad \text{ where }\end{aligned}$$

(5)

$$\begin{aligned}&\quad G_{\mu \nu } = \partial _{\mu }A_\nu - \partial _{\nu }A_\mu \ \text{ and }\ H_{\mu \nu } = -\frac{1}{g} \epsilon ^{abc}\hat{\varPhi }^{a}\partial _{\mu }\hat{\varPhi }^{b}\partial _{\nu }\hat{\varPhi }^c\nonumber \\ \end{aligned}$$

(6)

are the non-topological Maxwell part and the topological Dirac part of the electromagnetic field, respectively. Here $A_\mu = \hat{\varPhi }^{a}A^a_\mu$, the Higgs unit vector, $\hat{\varPhi }^a = \varPhi ^a/|\varPhi |$, and the Higgs field magnitude $|\varPhi | = \sqrt{\varPhi ^{a}\varPhi ^{a}}$. The topological term $H_{\mu \nu }$ has been known as the ’t Hooft electromagnetic field, this is precisely the restricted field strength that we obtain from the gauge independent Abelian projection known as the Cho projection [44–46] Hence the decomposed magnetic field is

$$\begin{aligned} B_i = -\frac{1}{2}\epsilon _{ijk}F_{jk} = B^G_i + B^H_i, \end{aligned}$$

(7)

where $B_i^G$ and $B_i^H$ are the Maxwell part and Dirac part of the magnetic field, respectively. The net magnetic charge of the system is

$$\begin{aligned} M = \frac{1}{4\pi } \int \partial ^i B_i ~\mathrm{d}^{3}x = \frac{1}{4\pi } \oint \mathrm{d}^{2}\sigma _{i}~B_i. \end{aligned}$$

(8)

Since the topological magnetic current is [47] $k_\mu = \frac{1}{8\pi }~\epsilon _{\mu \nu \rho \sigma }~\epsilon _{abc}~\partial ^{\nu }\hat{\varPhi }^{a}~\partial ^{\rho }\hat{\varPhi }^{b}~\partial ^{\sigma }\hat{\varPhi }^c$ and

$$\begin{aligned} M_H&= \frac{1}{g}\int \mathrm{d}^{3}x~k_0 = \frac{1}{4\pi } \oint \mathrm{d}^{2}\sigma _{i}~B_i^H, \end{aligned}$$

(9)

$M_H$ is the corresponding conserved topological magnetic charge. The magnetic charge $M_H$ is the total magnetic charge of the system if and only if the gauge field is nonsingular [48]. If the gauge field is singular and carries Dirac string monopoles, then the magnetic charge carried by the gauge field is

$$\begin{aligned} M_G&= -\frac{1}{8\pi }\oint \mathrm{d}^{2}\sigma _{i}\epsilon _{ijk}\left( \partial _j A_k - \partial _k A_j\right) \nonumber \\&= \frac{1}{4\pi } \oint \mathrm{d}^{2}\sigma _{i}~B_i^G, \end{aligned}$$

(10)

and the total magnetic charge of the system is $M \!=\! M_G + M_H$.

3 The magnetic ansatz

The magnetic ansatz used are given by [39]

$$\begin{aligned} gA_i^a&= - \frac{1}{r}\psi _1(r, \theta ) \hat{n}^{a}_\phi \hat{\theta }_i + \frac{1}{r\sin \theta }P_1(r, \theta )\hat{n}^{a}_\theta \hat{\phi }_i\nonumber \\&+ \frac{1}{r}R_1(r, \theta )\hat{n}^{a}_\phi \hat{r}_i - \frac{1}{r\sin \theta }P_2(r, \theta )\hat{n}^{a}_r\hat{\phi }_i, \nonumber \\ gA^a_0&= \tau _1(r, \theta )~\hat{n}^a_r + \tau _2(r, \theta )\hat{n}^a_\theta ,, \nonumber \\ g\varPhi ^a&= \varPhi _1(r, \theta )~\hat{n}^a_r + \varPhi _2(r, \theta )\hat{n}^a_\theta , \end{aligned}$$

(11)

where $P_1(r, \theta )\!=\!\sin \theta ~\psi _2(r, \theta )$ and $P_2(r, \theta )\!=\!\sin \theta ~R_2(r, \theta )$. The spatial spherical coordinate orthonormal unit vectors are

$$\begin{aligned} \hat{r}_i&= \sin \theta ~\cos \phi ~\delta _{i1} + \sin \theta ~\sin \phi ~\delta _{i2} + \cos \theta ~\delta _{i3}, \nonumber \\ \hat{\theta }_i&= \cos \theta ~\cos \phi ~\delta _{i1} + \cos \theta ~\sin \phi ~\delta _{i2} - \sin \theta ~\delta _{i3}, \nonumber \\ \hat{\phi }_i&= -\sin \phi ~\delta _{i1} + \cos \phi ~\delta _{i2}, \end{aligned}$$

(12)

and the isospin coordinate orthonormal unit vectors are

$$\begin{aligned} \hat{n}_r^a&= \sin \theta ~\cos n\phi ~\delta _{1}^a + \sin \theta ~\sin n\phi ~\delta _{2}^a + \cos \theta ~\delta _{3}^a,\nonumber \\ \hat{n}_\theta ^a&= \cos \theta ~\cos n\phi ~\delta _{1}^a + \cos \theta ~\sin n\phi ~\delta _{2}^a - \sin \theta ~\delta _{3}^a,\nonumber \\ \hat{n}_\phi ^a&= -\sin n\phi ~\delta _{1}^a + \cos n\phi ~\delta _{2}^a;\quad \text{ where }\ n\ge 1. \end{aligned}$$

(13)

The $\phi$-winding number $n$ is in general a natural number. However, in our work here, we take $n=1$.

The general Higgs fields in the spherical and the rectangular coordinate systems are

$$\begin{aligned} g\varPhi ^a&= \varPhi _1(x)~\hat{n}^a_r + \varPhi _2(x)\hat{n}^a_\theta + \varPhi _3(x)\hat{n}^a_\phi \nonumber \\&= \tilde{\varPhi }_1(x) ~\delta ^{a1} + \tilde{\varPhi }_2(x) ~\delta ^{a2} + \tilde{\varPhi }_3(x) ~\delta ^{a3}, \end{aligned}$$

(14)

respectively, where

$$\begin{aligned} \tilde{\varPhi }_1&= \sin \theta \cos n\phi ~\varPhi _1 + \cos \theta \cos n\phi ~\varPhi _2 - \sin n\phi \varPhi _3 \nonumber \\&= |\varPhi |\sin \alpha \cos \beta \nonumber \\ \tilde{\varPhi }_2&= \sin \theta \sin n\phi ~\varPhi _1 + \cos \theta \sin n\phi ~\varPhi _2 + \cos n\phi \varPhi _3 \nonumber \\&= |\varPhi |\sin \alpha \sin \beta \nonumber \\ \tilde{\varPhi }_3&= \cos \theta ~\varPhi _1 - \sin \theta ~\varPhi _2 = |\varPhi |\cos \alpha . \end{aligned}$$

(15)

The axially symmetric Higgs unit vector in the rectangular coordinate system is

$$\begin{aligned}&\hat{\varPhi }^a = \sin \alpha \cos \beta ~\delta ^{a1} + \sin \alpha \sin \beta ~\delta ^{a2} + \cos \alpha ~\delta ^{a3},\end{aligned}$$

(16)

$$\begin{aligned}&\cos \alpha = h_1\cos \theta - h_2\sin \theta ,\quad \sin \alpha = h_1\sin \theta + h_2\cos \theta ,\nonumber \\&h_1 = \frac{\varPhi _1}{|\varPhi |},\quad h_2 = \frac{\varPhi _2}{|\varPhi |},\quad \beta =n\phi . \end{aligned}$$

(17)

By using the definition of $\cos \alpha$ (17), the Higgs part of the ’t Hooft magnetic field (7) can be reduced to

$$\begin{aligned} gB_i^H = -n\epsilon _{ijk} \partial ^j\cos \alpha \partial ^k\phi . \end{aligned}$$

(18)

The gauge part of the magnetic field (7) can be written in a similar form:

$$\begin{aligned} gB^G_i = -n\epsilon _{ijk}\partial _j\cos \kappa ~\partial _k \phi , \quad \cos \kappa = \frac{1}{n}\left( h_2P_1 - h_1P_2\right) .\nonumber \\ \end{aligned}$$

(19)

Hence the ’t Hooft magnetic field, which is the sum of the Higgs part (18) and the gauge part, (19), is given by

$$\begin{aligned} gB_i = -n\epsilon _{ijk}\partial _j(\cos \alpha + \cos \kappa )~\partial _k \phi = -\epsilon _{ijk}\partial _j{\fancyscript{A}}_k, \end{aligned}$$

(20)

where ${\fancyscript{A}}_i$ is the ’t Hooft gauge potential. The magnetic field lines of the configuration can be plotted by drawing the contour lines of $(\cos \alpha + \cos \kappa ) =$ constant on the vertical plane $\phi =0$ as shown in Fig. 1c. The orientation of the magnetic field can also be plotted by using the vector field plot of the magnetic field unit vector as shown in Fig. 1d,

$$\begin{aligned} {\hat{B}}_i \!=\! \frac{-\partial _\theta (\cos \alpha \!+\! \cos \kappa )\hat{r}_i \!+\! r \partial _r (\cos \alpha \!+\! \cos \kappa )\hat{\theta }_i}{\sqrt{[r \partial _r (\cos \alpha \!+\! \cos \kappa )]^2 \!+\! [\partial _\theta (\cos \alpha \!+\! \cos \kappa )]^2}}. \end{aligned}$$

(21)

Fig. 1

a Contour plot of the electric field equipotential lines. b Vector field plot of the electric field unit vector, ${\hat{E}}_i$. c Contour plot of the magnetic field lines. d Vector field plot of the magnetic field unit vector, ${\hat{B}}_i$. Here $\lambda =1$ and $\eta =0.9$

At spatial infinity in the Higgs vacuum, all the non-Abelian components of the gauge potential vanish and the non-Abelian electromagnetic field tends to

$$\begin{aligned} \left. F^a_{\mu \nu }\right| _{r\rightarrow \infty }&= \{\partial _\mu A_\nu - \partial _\nu A_\mu - \frac{1}{g}\epsilon ^{cde}\hat{\varPhi }^c\partial _\mu \hat{\varPhi }^d \partial _\nu \hat{\varPhi }^e\}\hat{\varPhi }^a \nonumber \\&= F_{\mu \nu }\hat{\varPhi }^a, \end{aligned}$$

(22)

where $F_{\mu \nu }$ is just the ’t Hooft electromagnetic field. However, there is no unique way of representing the Abelian electromagnetic field in the region of the monopole outside the Higgs vacuum at finite values of $r$ [49]. One proposal was given by ’t Hooft as in Eq. (5) and another was given by Bogomol’nyi [2–6] and Faddeev [50, 51]. In the latter definition, which is less singular, the magnetic and electric fields are given, respectively, by

$$\begin{aligned} {\fancyscript{B}}_i = B_i^a \left( \frac{\varPhi ^a}{\xi }\right) \quad \text{ and }\quad {\fancyscript{E}}_i = E_i^a \left( \frac{\varPhi ^a}{\xi }\right) , \end{aligned}$$

(23)

where $\xi$ is the vacuum expectation value of the Higgs field. With this definition of the electromagnetic field (23), there will be a magnetic charge density distribution contributed by the non-Abelian components of the gauge field in the finite $r$ region. Since the magnetic charge density of the one-half dyon solution is singular and yet integrable, we define the weighted magnetic charge density to be ${\fancyscript{M}} = \frac{1}{2}r^2\sin \theta \{\partial ^i {\fancyscript{B}}_i\}$, which can be plotted as in Fig. 2a. In the Higgs vacuum at spatial infinity, both definitions of the electromagnetic field, (5) and (23), become similar.

Fig. 2

The 3D surface and contour plots of a the weighted magnetic charge density, ${\fancyscript{M}}$, and b the weighted electric charge density, ${\fancyscript{Q}}$, of the one-and-a-half dyons solution in the $x$–$z$ plane at $y=0$ when $\lambda =1$ and $\eta =0.9$

We can also evaluate numerically the different magnetic charges at different distances $r$ from the origin by the following definitions:

$$\begin{aligned}&M_{\{UH\}} = -\frac{1}{2g}\left. \left\{ \cos \alpha + \cos \kappa \right\} \right| ^{\theta =\frac{1}{2}\pi }_{\theta =0, r},\nonumber \\&M_{\{LH\}} = -\frac{1}{2g}\left. \left\{ \cos \alpha + \cos \kappa \right\} \right| ^{\theta =\pi }_{\theta =\frac{1}{2}\pi , r}, \nonumber \\&M_G = -\frac{1}{2g}\left. \left\{ \cos \kappa \right\} \right| ^{\theta =\pi }_{\theta =0, r},\nonumber \\&M_H = -\frac{1}{2g}\left. \left\{ \cos \alpha \right\} \right| ^{\theta =\pi }_{\theta =0, r},\quad M=M_G + M_H, \end{aligned}$$

(24)

where $M_{\{UH\}}$ and $M_{\{LH\}}$ are the magnetic charges covered by the upper and lower hemispheres, respectively, at distances $r$ from the origin.

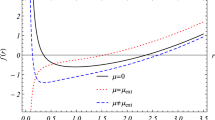
Using the definition (23), we similarly define the weighted electric charge density to be ${\fancyscript{Q}} =\frac{1}{2}r^2\sin \theta \{\partial ^i {\fancyscript{E}}_i\}$. The weighted electric charge density distribution ${\fancyscript{Q}}$ can be calculated and plotted numerically as in Fig. 2b, where ${\fancyscript{E}}_i = {\fancyscript{F}}_{i0}$ is the electric field. The weighted electric charge density, ${\fancyscript{Q}}$, of the dyon solutions is solely positive throughout space when $\eta$ is positive.

At spatial infinity in the Higgs vacuum,

$$\begin{aligned} {\fancyscript{E}}_i&= E_i = F_{i0}= \partial _i A_0 = \partial _i\left\{ \tau _1 \cos (\alpha -\theta )\right. \nonumber \\&\quad \left. +\, \tau _2 ~\sin (\alpha -\theta )\right\} = \partial _i |\tau |, \end{aligned}$$

(25)

where $|\tau |=\sqrt{\tau _1^2+\tau _2^2}$, since the time component of the gauge field, $A^a_0$, is assumed parallel to the Higgs field, $\varPhi ^a$, in isospin space [36–39]. Hence the two definitions for the electromagnetic field strength will give the same total electric charge, $Q(\lambda , \eta )$, with ${\fancyscript{E}}_i$ less singular than $E_i$ at finite values of $r$. Unlike the magnetic field, the electric field varies proportionally with the constant $0\le \eta < 1$. The electric field can therefore be switched off by setting $\eta =0$. The contour plot of the time component of the gauge potential, $A_0=$ constant, shown in Fig. 1a shows the line of equipotential of the electric field. The 2D vector field plot of the electric field unit vector, ${\hat{E}}_i = \partial _i A_0/\sqrt{\partial _i A_0 \partial _i A_0}$ is shown in Fig. 1b.

From Gauss’ law, the total electric charge of the dyon in units of $4\pi \xi$ is given by $Q(\lambda , \eta ) = \frac{1}{4\pi \xi }\int _{r\rightarrow \infty }{\fancyscript{E}}_i\hat{r}_i~r^2\sin \theta ~\mathrm{d}\theta \mathrm{d}\phi$. Since we assume that $A^a_0$ is parallel to the Higgs field at large $r$, $Q(\lambda , \eta ) =\frac{1}{\xi } \lim _{r\rightarrow \infty } r^2\partial _r |\tau |$ can be calculated numerically. An alternative way to find $Q$ is to assume that $|A_0^a|= |\tau |\rightarrow \eta \xi (1-\frac{a_1}{r})$, where $a_1$ is a constant, at large $r$. Then $Q=\eta \xi a_1$ can be obtained by plotting $r(|\tau |-\eta \xi )$ and reading off the value of $\eta \xi a_1$ at large $r$. In our case, we choose to evaluate $Q$ by numerically evaluating the volume integration

$$\begin{aligned} Q=\frac{1}{4\pi \xi }\int {\partial ^i{\fancyscript{E}}_i}~\mathrm{d}^3x. \end{aligned}$$

(26)

From Maxwell electromagnetic theory, the ’t Hooft gauge potential, ${\fancyscript{A}}_i$, of Eq. (20) at large $r$ tends to

$$\begin{aligned}&{\fancyscript{A}}_i \!=\! (\cos \alpha \!+\! \cos \kappa )\partial _i\phi |_{r\rightarrow \infty }\nonumber \\&\quad \quad \!=\! \frac{\hat{\phi }_i}{r\sin \theta }\left\{ \frac{1}{2}(\cos \theta \!+\!1) \!+\! \frac{F_G(\theta )}{r}\right\} , \end{aligned}$$

(27)

$$\begin{aligned}&F_G(\theta ) \!=\!-\mu _m\sin ^2\theta \!+\! \nu _m\left\{ \sin ^2\theta \ln \left| \frac{1\!+\!\cos \theta }{\sin \theta }\right| \!+\! \cos \theta \right\} ,\nonumber \\ \end{aligned}$$

(28)

where $\mu _m$ is the dimensionless magnetic dipole moment of the one-half monopole. From the numerical solution, $F_G(\theta )$ can be calculated numerically using the expression

$$\begin{aligned}&F_G(\theta ) = r\{h_2(P_1-\sin \theta ) - h_1(P_2-\cos \theta )\nonumber \\&\quad \quad \qquad -\frac{1}{2}(\cos \theta + 1)\}|_{r\rightarrow \infty }. \end{aligned}$$

(29)

Plotting the graphs of $F_G(\theta )$ versus angle $\theta$, we find that $F_G(\theta ) =-\mu _m\sin ^2\theta$, and $\mu _m$ is nonvanishing for all values of $\lambda$ and $0\le \eta < 1$. The constant, $\nu _m$, is, however, 0. The value of $\mu _m$ is read off from the graphs of $F_G(\theta )$ versus angle $\theta$ at $\theta =\frac{\pi }{2}$. The magnetic dipole moment, $\mu _m$, was obtained for various values of $0\le \eta < 1$ and $0<\lambda \le 12$ (Tables 1 and 2).

Table 1 Table of the electric charge $Q$, dimensionless magnetic dipole moment $\mu _m$, dimensionless total energy $E$, and monopole separation $d_z$ of the one-and-a-half dyon for different values of $\eta$ at $\lambda =0$, $\lambda =1.0$, and $\lambda =10.0$

Table 2 Table of the electric charge $Q$, dimensionless magnetic dipole moment $\mu _m$, dimensionless total energy $E$, and the monopole separation $d_z$ of the one-and-a-half dyon for different values of $\lambda$ at $\eta = 0.5, 0.9, 0.75$, and 1.0

From the energy momentum tensor of the YMH theory,

$$\begin{aligned} \theta _{\mu \nu }&= F_{\mu }^{a \beta } F^a_{\nu \beta } - \frac{1}{4}g_{\mu \nu }F^a_{\alpha \beta }F^{a\alpha \beta } + D_\mu \varPhi ^a D_\nu \varPhi ^a\nonumber \\&- \frac{1}{2}g_{\mu \nu }\left( D_\alpha \varPhi ^a D^\alpha \varPhi ^a + \frac{1}{4}\lambda (\varPhi ^a \varPhi ^a - \xi ^2)^2\right) , \end{aligned}$$

(30)

and some calculations as shown in Refs. [38–43], the total angular momentum in units of $4\pi \xi$ is found to be

$$\begin{aligned} J_z = \frac{1}{2\xi }\lim _{r\rightarrow \infty }r^2\partial _r\tau (r), \end{aligned}$$

(31)

if we assume that the time component of the gauge field, $A^a_0$, is parallel to the Higgs field, $\varPhi ^a$, at spatial infinity. Hence $J_z = \frac{1}{2}Q$ and the new dyon solutions possess kinetic energy of rotation.

In the electrically charged BPS limit when the Higgs potential vanishes, the energy which is a minimum is given by [36, 37]

$$\begin{aligned} E_\mathrm{min} = \frac{4\pi \xi }{g}\sqrt{M_H^2 + Q^2}, \end{aligned}$$

(32)

where $M_H$ is the “topological magnetic charge” and $Q$ as given by Eq. (26) is the total electric charge of the system when the vacuum expectation value of the Higgs field, $\xi$, is non-zero. Obviously the new dyon solution is a non-BPS solution even in the limit of vanishing $\lambda$, hence its energy must be greater than that given by Eq. (32). Its dimensionless value is given by

$$\begin{aligned} E&= \frac{g}{4\xi }\int \left\{ B^a_iB^a_i + E^a_iE^a_i + D_i\varPhi ^aD_i\varPhi ^a + D_0\varPhi ^aD_0\varPhi ^a\right. \nonumber \\&\left. +\frac{\lambda }{2}(\varPhi ^a\varPhi ^a-\xi ^2)^2\right\} \mathrm{d}^3x. \end{aligned}$$

(33)

Since this dyon solution possesses an integrable singular energy density, we define the weighted energy density to be

$$\begin{aligned} {\fancyscript{E}}=\text{ dimensionless } \text{ energy } \text{ density } \times 2\pi r^2 \sin \theta , \end{aligned}$$

(34)

which can be plotted as shown in Fig. 3b.

Fig. 3

The 3D surface and contour plots of a the Higgs field modulus, $|\varPhi |$, and b the weighted energy density, ${\fancyscript{E}}$, of the one-and-a-half dyon solution in the $x$–$z$ plane at $y=0$ when $\lambda =1$ and $\eta =0.9$

4 The Dyon solution

4.1 The numerical construction

The numerical one-and-a-half dyon solution was solved by using the ansatz (11), which reduced the equations of motion into eight coupled nonlinear second order partial differential equations. This new dyon solution is constructed by modifying the exact one-and-a-half monopole solution of Ref. [29] to include the electric charge parameter, $0\le \eta \le 1$,

$$\begin{aligned} \psi _1&= \frac{3}{2},\quad P_1 = \sin \theta + \frac{1}{2}\sin \frac{1}{2}\theta (1+\cos \theta ), \nonumber \\ R_1&= 0,\quad P_2=\cos \theta - \frac{1}{2}\cos \frac{1}{2}\theta (1+\cos \theta ), \nonumber \\ \tau _1&= \eta \xi \cos \frac{1}{2}\theta ,\quad \tau _2=\eta \xi \sin \frac{1}{2}\theta , \nonumber \\ \varPhi _1&= \xi \cos \frac{1}{2}\theta ,\quad \varPhi _2=\xi \sin \frac{1}{2}\theta , \end{aligned}$$

(35)

and using it as asymptotic solution at large distances ($r\rightarrow \infty$). In this asymptotic region, the time component of the gauge field and the Higgs field are assumed to be parallel in the isospin space, that is, $\varPhi _1 \propto \tau _1$ and $\varPhi _2 \propto \tau _2$. However, this is not necessarily true at finite $r$.

Near the origin, $r=0$, we have the common trivial vacuum solution. The asymptotic solution and boundary conditions at small distances that will give rise to a finite energy solution are

$$\begin{aligned}&\psi _1=P_1=R_1=P_2=0,\quad \varPhi _1=\xi _0\cos \theta ,\nonumber \\&\quad \varPhi _2=-\xi _0\sin \theta ,\end{aligned}$$

(36)

$$\begin{aligned}&\sin \theta \tau _1(0,\theta )+\cos \theta \tau _2(0,\theta )=0,\nonumber \\&\sin \theta \varPhi _1(0,\theta )+\cos \theta \varPhi _2(0,\theta )=0,\nonumber \\&\partial _r(\cos \theta \tau _1(r,\theta )-\sin \theta \tau _2(r,\theta ))|_{r=0}=0,\nonumber \\&\partial _r(\cos \theta \varPhi _1(r,\theta )-\sin \theta \varPhi _2(r,\theta ))|_{r=0}=0. \end{aligned}$$

(37)

The boundary conditions imposed along the positive $z$-axis for the profile functions (11) of the dyon solution are

$$\begin{aligned}&\partial _\theta \varPhi _1(r,\theta )|_{\theta =0} = 0,\quad \varPhi _2(r,0)=0, \nonumber \\&\partial _\theta \tau _1(r,\theta )|_{\theta =0} = 0, \quad \tau _2(r,0)=0,\nonumber \\&\partial _\theta \psi _1(r,\theta )|_{\theta =0} = 0,\quad R_1(r,0)=0,\nonumber \\&P_1(r,0)=0,\quad \partial _\theta P_2(r,\theta )|_{\theta =0}=0, \end{aligned}$$

(38)

and along the negative $z$-axis, the boundary conditions imposed are

$$\begin{aligned}&\varPhi _1(r,\pi )=0,\quad \partial _\theta \varPhi _2(r,\theta )|_{\theta =\pi } = 0,\quad \tau _1(r,\pi )=0,\nonumber \\&\quad \partial _\theta \tau _2(r,\theta )|_{\theta =\pi } = 0,\nonumber \\&\partial _\theta \psi _1(r,\theta )|_{\theta =\pi } = 0,\quad R_1(r,\pi )=0, \quad P_1(r,\pi )=0,\nonumber \\&\quad \partial _\theta P_2(r,\theta )|_{\theta =\pi }=0. \end{aligned}$$

(39)

In our work we set the expectation value $\xi =1$, and the gauge coupling constant $g=1$. The new dyon solution was obtained numerically by connecting the exact asymptotic solution (35) at large distances to the trivial vacuum solution (36) at small distances and subjecting this to the boundary conditions (37)–(39) together with the gauge fixing condition [17–21],

$$\begin{aligned} r\partial _rR_1-\partial _\theta \psi _1=0. \end{aligned}$$

(40)

The Maple and MATLAB software [39] is used for this calculation. Using the finite difference approximation, the eight reduced second order partial differential equations of motion are transformed into a system of nonlinear equations. The system of nonlinear equations are then discretized on a non-equidistant grid of size $90\times 80$ covering the integration regions $0\le {\bar{x}} \le 1$ and $0\le \theta \le \pi$, where ${\bar{x}}=\frac{r}{r+1}$ is the finite interval compactified coordinate. The first and second order partial derivatives with respect to $r$ are then replaced accordingly by $\partial _r \rightarrow (1-{\bar{x}})^2 \partial _{{\bar{x}}}$ and $\frac{\partial ^2}{\partial r^2} \rightarrow (1-{\bar{x}})^4\frac{\partial ^2}{\partial {\bar{x}}^2} - 2(1-{\bar{x}})^3\frac{\partial }{\partial {\bar{x}}}$. Maple was used to find the Jacobian sparsity pattern for the system of nonlinear equations, after which this information was provided to MATLAB to run the numerical computation. With suitable initial conditions, the system of nonlinear equations can be solved numerically using the trust-region-reflective algorithm.

The second order equations of motion Eq. (3) are solved when the $\phi$-winding number $n=1$, the electric charge parameter, $0\le \eta <1$, and with Higgs potential when the Higgs self-coupling constant $0\le \lambda \le 12$. The errors in this numerical computation come from the finite difference approximation of the functions which is of the order of $10^{-4}$ and also from the linearization of the nonlinear equations for MATLAB to solve numerically, which is of the order of $10^{-6}$. Hence the overall error estimate is $10^{-4}$.

4.2 The numerical results

The numerical solutions obtained for the new dyon solution are all regular functions of $r$ and $\theta$ except for the profile function $R_2$, which is singular along the $z$-axis. We calculate and draw the 3D surface graphs together with their respective contour plots for the Higgs field modulus $|\varPhi |$ (Fig. 3a), the weighted energy density ${\fancyscript{E}}$ (Fig. 3b), the weighted magnetic charge density ${\fancyscript{M}}$ (Fig. 2a), and the weighted electric charge density ${\fancyscript{Q}}$ (Fig. 2b), on the $x$–$z$ plane at $y=0$ numerically. The 3D surface plot of these physical quantities and their respective contour plots are drawn for the case when $\lambda =1$ and $\eta =0.9$. The magnetic charge density is positive above the $x$–$y$ plane and negative below it. Hence the ’t Hooft–Polyakov monopole located along the positive $z$-axis possesses magnetic charge $+1$ and the one-half monopole located at $r=0$ possesses magnetic charge $-\frac{1}{2}$. The electric charge density is, however, positive throughout space and this is so when the electric charge parameter $\eta$ is positive. Hence from Fig. 2 we can conclude that the one-half dyon carries negative magnetic and positive electric charge densities that are concentrated along a finite stretch of the negative $z$-axis near the origin while the ’t Hooft–Polyakov monopole at $z=2.15$ carries both positive magnetic and electric charge densities that are spherically concentrated around the monopole. The sign of the electric and magnetic charges are once again confirmed by the contour plots of the electric field equipotential lines and the magnetic field lines as shown in Fig. 1a and c, respectively, and the vector field plots of the electric field unit vector, ${\hat{E}}_i$, and the magnetic field unit vector, ${\hat{B}}_i$ as shown in Fig. 1b and d, respectively.

In general, the shape of the dyon remains the same as that of the one-and-a-half monopole solution of Ref. [29], while its size increases as $\eta$ increases from 0 to 1. This is because as the electric charge parameter $\eta \rightarrow 1$, the zeros of the Higgs modulus along the negative $z$-axis increase and the inverted cone becomes more stretched along the negative $z$-axis. However, at $\lambda =1$, the pole separation, $d_z$, does not vary much with $\eta$ as shown in the graphs of Fig. 4d.

Fig. 4

a Plots of the total electric charge, $Q$, b the magnetic dipole moment, $\mu _m$, c the total energy, $E$, and d the pole separation, $d_z$, versus $\eta$. Here $0\le \lambda \le 10$ and $0\le \eta <1$

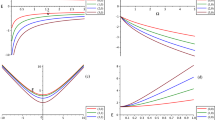
The quantities that vary with the electric charge parameter, $\eta$, are the total charge $Q$, the magnetic dipole moment, $\mu _m$, the total energy, $E$, and the dipole separation, $d_z$. The graphs for eight different values of $\lambda =0, 0.01, 0.1, 0.3, 1, 2, 5$, and 10 for each of the four quantities versus $\eta$ are shown in Fig. 4. The numerical values are given in Table 1 for $\lambda = 0, 1, 10$. From Fig. 4a, the graphs of $Q$ versus $\eta$ are all nondecreasing graphs with the critical value of $Q_\mathrm{critical}$ increasing with decreasing $\lambda$. When $\lambda \rightarrow 0$, $Q_\mathrm{critical}\rightarrow \infty$ and this behavior is similar to the other dyon solutions of Refs. [36–43].

The graphs of total energy, $E$, versus $\eta$, Fig. 4c, are similar to the graphs of Fig. 4a, that is, $Q$ versus $\eta$, as they are all nondecreasing graphs. However, the critical value of $E$ for large values of $\lambda$ decreases with decreasing $\lambda$ from $\lambda =12$ ($E_\mathrm{critical}=2.4646$) to $\lambda =0.4$ ($E_\mathrm{critical}=2.3183$), after which it increases to infinity as $\lambda$ approaches 0. Similar to the dyon solutions of Refs. [36–43] for small $\lambda <0.4$, $E_\mathrm{critical}\rightarrow \infty$ as $\lambda \rightarrow 0$.

The graphs of the magnetic dipole moment, $\mu _m$, versus $\eta$, Fig. 4b, and the dipole separation, $d_z$, versus $\eta$, Fig. 4d, possess critical values that increase with decreasing $\lambda$ such that, as $\lambda \rightarrow 0$, $\{\mu _m^\mathrm{critical}, ~d_z^\mathrm{critical}\}\rightarrow \infty$. This behavior is common to the other dyon solutions. However, the graphs of Fig. 4b and d are nondecreasing graphs only for small $\lambda \le 0.01$. For larger values of $\lambda$, the graphs become nonincreasing, and $\mu _m$ and $d_z$ decrease with $\eta$, different from the norm.

In Fig. 5, the graphs of the four quantities, the total charge $Q$, the magnetic dipole moment, $\mu _m$, the total energy, $E$, and the dipole separation, $d_z$, are plotted versus each other for constant values of $\lambda = 0, 0.01, 0.1, 0.3, 1, 2, 5, 10$, and for $\eta =0, 1$. The graphs of the magnetic dipole moment $\mu _m$ versus $d_z$ is in Fig. 5b; the dipole separation $d_z$ versus $Q$ in Fig. 5e; and the magnetic dipole moment $\mu _m$ versus $Q$ in Fig. 5f; at $\eta =1$ they are almost linear. The strange behavior of $\mu _m$ and $d_z$ decreasing with increasing $\eta$ at large values of $\lambda$ is once again reflected in the graphs of Fig. 5a, b, c, e, and f. The graphs of the total energy $E$ versus $Q$, Fig. 5d, for constant values of $\lambda$, however, behave normally as they are all nondecreasing graphs.

Fig. 5

Plots of a the total energy, $E$, and b magnetic dipole moment, $\mu _m$, versus the pole separation, $d_z$. c Plots of $E$ versus $\mu _m$. Plots of d $E$, e $d_z$, and f $\mu _m$, versus the electric charge, $Q$. Here $0\le \lambda \le 10$, and graphs of constant $\eta =0$ and 1 are shown

The total energy, $E$, the total charge $Q$, the magnetic dipole moment, $\mu _m$, and the dipole separation, $d_z$ are plotted versus $\lambda ^{1/2}$ in Fig. 6a–d, respectively. The behaviors of the graphs in Fig. 6a–c are similar to that of the one-half dyon solution [39] as $E$ increases with $\lambda ^{1/2}$ for values of $\lambda \ge 1$ and the graphs of $Q$ and $\mu _m$ versus $\lambda ^{1/2}$ are all nonincreasing graphs. The graphs of $d_z$ versus $\lambda ^{1/2}$ in Fig. 6d are also nonincreasing graphs. At small values of $0<\lambda ^{1/2}<0.548$, the dipole separation, $d_z$, increases with increasing $\eta$, which is an expected behavior due to the increase of the electrical repulsion. However, when $\lambda ^{1/2}> 2.746$, the dipole separation, $d_z$ decreases with increasing $\eta$.

Fig. 6

a Plot of the total energy, $E$, b the total electric charge, $Q$, c the magnetic dipole moment, $\mu _m$, and d the pole separation, $d_z$, versus $\sqrt{\lambda }$ for $\eta =0, 0.50, 0.75, 0.90$, and 1. Plots of e magnetic charges, $M$, $M_{UH}$, and $M_{LH}$ and f $M$, $M_H$, and $M_G$, versus the compactified coordinate, ${\bar{x}}$ when $\lambda =1$ and $\eta = 1$

The graphs of the magnetic charges, $M_{\{UH\}}$, $M_{\{LH\}}$, $M_H$, $M_G$, and $M$ when $\lambda =\eta =1$ are shown in Fig. 6e and f. The fact that $M_{\{UH\}}=M_{\{LH\}}$ at ${\bar{x}}=1$ or $r=\infty$ shows that the magnetic field is radially symmetrical at large distances. The value of $M_H$ is 0 at $r=0$ and $M_H=0.50$ at $r=\infty$. This indicates that the net topological charge of the system is 0. The topological charge of $-0.5$ carried by the Dirac string at $r$ infinity cannot be captured by the numerical calculation. The region between the over-shoot and under-shoot of the graph for $M_H$ is the region where the ’t Hooft–Polyakov monopole is located. The graphs also show that the ’t Hooft–Polyakov monopole is a real particle of magnetic charge $M=1$ whereas the one-half monopole of magnetic charge $M=-\frac{1}{2}$ is a virtual particle.

4.3 The Cho decomposition of the Dyon solution

In the Cho decomposition of the SU(2) YMH theory, the ansatz that follows is gauge independent once the Higgs field direction, $\hat{\varPhi }^a$, is chosen [44–46]. The magnetic ansatz (11) used to construct the solution is not gauge independent and the gauge independent ansatz can be given by the Cho decomposition. The Higgs field direction can be defined by writing the axially symmetric Higgs unit vector, $\hat{\varPhi }^a=h_1\hat{n}^a_r+h_2\hat{n}^a_\theta$, in the rectangular coordinate system as in Eq. (16) and (17). Hence the first and second perpendiculars of the Higgs field unit vector in isospin space are

$$\begin{aligned} \hat{\varPhi }_1^a&= -h_2\hat{n}^a_r+h_1\hat{n}^a_\theta =\cos \alpha \cos n\phi ~\delta _{1}^a\nonumber \\&\quad +\, \cos \alpha \sin n\phi ~\delta _{2}^a - \sin \alpha \delta _{3}^a,\nonumber \\ \hat{\varPhi }_2^a&= \hat{n}^a_\phi =-\sin n\phi ~\delta _{1}^a + \cos n\phi ~\delta _{2}^a. \end{aligned}$$

(41)

The Cho decomposition of the YM gauge potential is given by Refs. [44–46] as

$$\begin{aligned}&A_\mu ^a = \hat{A}^a_\mu + X^a_\mu ,\quad X^a_\mu \hat{\varPhi }^a=0, \end{aligned}$$

(42)

$$\begin{aligned}&\text{ where }\ \hat{A}^a_\mu = A_\mu \hat{\varPhi }^a - \frac{1}{g}\epsilon ^{abc}\hat{\varPhi }^b\partial _\mu \hat{\varPhi }^c \end{aligned}$$

(43)

is the restricted gauge potential and $X^a_\mu$ is the valence gauge potential. Both the Higgs part of the gauge potential, $- \frac{1}{g}\epsilon ^{abc}\hat{\varPhi }^b\partial _\mu \hat{\varPhi }^c$ and the non-Abelian gauge potential, $X^a_\mu$ are perpendicular to the Higgs field direction in isospin space, $\hat{\varPhi }^a$. The gauge independent Cho decomposition axially symmetric ansatz then takes the form [30]

$$\begin{aligned} gA_i^a&= A ~\hat{\phi }_i\hat{\varPhi }^a + (X_1+Y_1)\hat{\phi }_i\hat{\varPhi }_1^a + (X_3+Y_3)\hat{r}_i\hat{\varPhi }_2^a\nonumber \\&+(X_4+Y_4)\hat{\theta }_i\hat{\varPhi }_2^a, \nonumber \\ gA^a_0&= A_0\hat{\varPhi }^a + X_0\hat{\varPhi }_1^a,\quad g\varPhi ^a = |\varPhi |~\hat{\varPhi }^a, \end{aligned}$$

(44)

where $X_0$, $X_1$, $X_3$, $X_4$ are the components of the gauge covariant valence potential $X^a_\mu$ and $Y_1$, $Y_3$, $Y_4$, $A_0$, $A$ are the components of the restricted gauge potential $\hat{A}^a_\mu$. Comparing the ansatz (44) with the magnetic ansatz (11), we note that

$$\begin{aligned}&X_0 = \tau _2 h_1-\tau _1 h_2,\quad X_1+Y_1 = \frac{1}{r}(h_1\psi _2+h_2 R_2),\nonumber \\&X_3+Y_3 = \frac{1}{r}R_1,\quad X_4+Y_4 = - \frac{1}{r}\psi _1, \nonumber \\&A_0 = \tau _1 h_1+\tau _2 h_2,\quad A = \frac{1}{r}(h_2\psi _2-h_1 R_2), \nonumber \\&|\varPhi | = \sqrt{\varPhi _1^2+\varPhi _2^2}, \end{aligned}$$

(45)

where

$$\begin{aligned} Y_1&= \frac{n}{r\sin \theta }\left( h_1\sin \theta + h_2\cos \theta \right) = \frac{n\sin \alpha }{r\sin \theta }, \nonumber \\ Y_3&= \frac{\partial _r h_1}{h_2} = - \partial _r \alpha , ~~Y_4 = -\frac{1}{r}\left( 1-\frac{\partial _\theta h_1}{h_2}\right) = - \frac{1}{r}\partial _\theta \alpha .\nonumber \\ \end{aligned}$$

(46)

The electromagnetic field strength tensor of the Cho decomposed gauge potential (42) is given by

$$\begin{aligned} F^a_{\mu \nu } = \hat{F}_{\mu \nu }^a + \hat{D}_\mu X^a_\nu - \hat{D}_\nu X^a_\mu + g\epsilon ^{abc}X_\mu ^b X_\nu ^c, \end{aligned}$$

(47)

where $\hat{F}_{\mu \nu }^a = \hat{F}_{\mu \nu }\hat{\varPhi }^a$ is the field strength of the self-dual potential (43) and $\hat{F}_{\mu \nu }$ is the ’t Hooft electromagnetic field. The Higgs unit vector is invariant under the covariant derivative $\hat{D}_\mu$ of the self-dual gauge potential $\hat{A}^a_\mu$,

$$\begin{aligned} \hat{D}_\mu \hat{\varPhi }^a = \partial _\mu \hat{\varPhi }^a + g\epsilon ^{abc}\hat{A}^b_{\mu }\hat{\varPhi }^c = 0. \end{aligned}$$

(48)

The numerically Cho decomposed gauge field profile functions (45) are shown in Fig. 7 as 3D surface plots in the $x$–$z$ plane at $y$=0. The presence of the electrically charged ’t Hooft–Polyakov monopole and the one-half monopole are reflected in all the six profile functions as shown in Fig. 7 by the curvature of the surface plots. All the profile functions are regular bounded surfaces, except for $r(X_1+Y_1)$, which is singular along the negative $z$-axis, Fig. 7b. The nonvanishing of the function, $X_0$, at finite values of $r$ indicates that the time component of the gauge function, $A_0^a$, is only parallel to the Higgs field in isospin space at large distances.

Fig. 7

3D graphs of the profile functions a $rA$, b $rX_1 + rY_1$, c $rX_3 + rY_3$, d $rX_4 + rY_4$, e $A_0$, and f $X_0$ of the one-and-a-half dyons solution in the $x$–$z$ plane at $y=0$ for $g=\xi =\lambda =\eta =1$

5 Comments

Similar to the one-half dyon solution of Ref. [39], the new dyon solution possesses a net magnetic charge of $M=\frac{1}{2}$ when the magnetic charge carried by the Dirac string is excluded. It also possesses a nonvanishing magnetic dipole moment and angular momentum, $J_z=\frac{1}{2}Q$ when the electric charge $Q\not =0$. Hence both these dyon solutions are able to rotate in the presence of an external magnetic field. This is possible because the gauge potentials of both dyon solutions possess a semi-infinite Dirac string.

Upon performing the Cho decomposition of the dyon solution here, the infinite string singularity along the $z$-axis can be transformed into a semi-infinite Dirac string. A more comprehensive discussion of the Cho decomposition of the electrically neutral solution is given in Ref. [30].

Similar to the dyon solutions of Ref. [36, 37] and [40–43], the total electric charge, magnetic dipole moment, total energy, and dipole separation of the new dyon solution increases indefinitely as the electric charge parameter, $\eta \rightarrow 1$ when $\lambda$ vanishes. However, when $\lambda$ is nonvanishing, $Q$, $\mu _m$, $E$, and $d_z$ approach critical values as given in Tables 1 and 2. The difference between this new dyon solution and the other dipole dyon solutions of Ref. [38] is that, at large values of $\lambda$, the dipole separation, $d_z$, and the magnetic dipole moment, $\mu _m$, decrease instead of increase with increasing $\eta$. This behavior is not normal because as $\eta$ increases the electric charge $Q$ also increases and this will lead to repulsion between the two poles instead of attraction. This means that $\mu _m$ and $d_z$ should increase with increasing $\eta$. However, this new dyon solution behaves in the reverse way when $\lambda >1$.