Possible assignments of the $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ as axial-vector molecular states

Abstract

In this article, we construct both the color singlet–singlet type and the octet–octet type currents to interpolate $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$, and we calculate the vacuum condensates up to dimension-10 in the operator product expansion. Then we study the axial-vector hidden charm and hidden bottom molecular states with the QCD sum rules, explore the energy-scale dependence of the QCD sum rules for the heavy molecular states in details, and we use the formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ with the effective masses ${\mathbb {M}}_Q$ to determine the energy scales. The numerical results support assigning $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ as the color singlet–singlet type molecular states with $J^{PC}=1^{++}$, $1^{+-}$, $1^{+-}$, respectively, more theoretical and experimental work is still needed to distinguish the molecule and tetraquark assignments; while there are no candidates for the color octet–octet type molecular states.

1 Introduction

In 2003, the Belle collaboration reported the first observation of the charmonium-like state $X(3872)$ in the $\pi ^+ \pi ^- J/\psi$ mass spectrum in the exclusive processes $B^\pm \rightarrow K^\pm \pi ^+ \pi ^- J/\psi$ [1]. The evidence for the decay modes $X(3872) \rightarrow \gamma J/\psi , \, \gamma \psi ^{\prime }$ implies the positive charge conjugation $C=+$ [2, 3], while angular correlations between the final state particles in the $\pi ^+ \pi ^- J/\psi$ support the $J^{PC}=1^{++}$ assignment, and they strongly disfavor (or exclude) the $0^{++}$, $0^{-+}$, $1^{-+}$, $2^{-+}$ assignments [4–6]. The $X(3872)$ has been extensively studied since its first observation; for more articles on this subject, one can consult the reviews [7–11].

In 2011, the Belle collaboration reported the first observation of $Z_b(10610)$ and $Z_b(10650)$ in the $\pi ^{\pm }\Upsilon (\mathrm{1,2,3S})$ and $\pi ^{\pm } h_b(\mathrm{1,2P})$ mass spectra in the exclusive processes $\Upsilon (\mathrm{5S}) \rightarrow \Upsilon (\mathrm{1,2,3S})\, \pi ^+ \pi ^-$, $h_b(\mathrm{1,2P})\,\pi ^+\pi ^-$ [12]. The quantum numbers (isospin, G-parity, spin and parity) $I^G(J^P)=1^+(1^+)$ are favored [12]. Later, the Belle collaboration updated the parameters $M_{Z_b(10610)}=(10607.2\pm 2.0)\,\mathrm{MeV}$, $M_{Z_b(10650)}=(10652.2\pm 1.5)\,\mathrm{MeV}$, $\Gamma _{Z_b(10610)}=(18.4\pm 2.4) \,\mathrm{MeV}$, and $\Gamma _{Z_b(10650)}=(11.5\pm 2.2)\,\mathrm{MeV}$ [13]. In 2013, the Belle collaboration reported the first observation of the decay processes $\Upsilon (5\mathrm{S}) \rightarrow \Upsilon (\mathrm{1,2,3S}) \,\pi ^0 \pi ^0$, and they obtained the neutral particle $Z_b^0(10610)$ in a Dalitz analysis of the decays to $\Upsilon (2,3\mathrm{S})\, \pi ^0$ [14]. There have been several assignments of the $Z_b(10610)$ and $Z_b(10650)$, such as the molecular states [15–25], tetraquark states [26, 27], threshold cusps [28], rescattering effects [29, 30], etc.

In 2013, the BESIII collaboration reported the first observation of the structure $Z_c(3900)$ in the $\pi ^\pm J/\psi$ mass spectrum in the process $e^+e^- \rightarrow \pi ^+\pi ^-J/\psi$ [31]. The mass and decay width are $(3899.0\pm 3.6\pm 4.9)\,\mathrm{MeV}$ and $(46\pm 10\pm 20) \,\mathrm{MeV}$, respectively [31]. Then the $Z_c(3900)$ was confirmed by the Belle and CLEO collaborations [32, 33]. There have been several assignments, such as the molecular state [34–38], tetraquark state [39–43], hadro-charmonium [44], rescattering effect [45–48], etc.

In this article, we will focus on the scenario of molecular states. In Ref. [49, 50], Lee et al. take $X(3872)$ as the $D^{*0}\bar{D}^{0}$–$D^0\bar{D}^{*0}$ molecular state with $J^{PC}=1^{++}$, study its mass with the QCD sum rules by calculating the vacuum condensates up to dimension-6 in the operator product expansion, and they obtain the value $M_{X(3872)}=(3.88 \pm 0.06)\,\mathrm { GeV}$. In Ref. [51], Zhang and Huang study the masses of the $Q\bar{q}\bar{Q}q$ type molecular states with QCD sum rules in a systematic way by calculating the vacuum condensates up to dimension-6. In Ref. [52], Matheus et al. take the $X(3872)$ as a mixture between charmonium and exotic molecular state with $J^{PC}=1^{++}$, study the mass $M_{X(3872)}$ and decay width $\Gamma _{X(3872)\rightarrow J/\psi \pi ^+\pi ^-}$ with the QCD sum rules, and they conclude that $X(3872)$ is approximately 97 % a charmonium state $\bar{c}c$ and 3 % a molecular state $D^*\bar{D}$. In Ref. [53], Zhang et al. take the $Z_b(10610)$ as a bottomonium-like molecular state $B^*\bar{B}$, study its mass with the QCD sum rules by calculating the vacuum condensates up to dimension-6, and they obtain the value $M_{Z_b}=( 10.54\pm 0.22)\,\mathrm { GeV}$. In Ref. [54], Chen et al. take $X(3872)$ as the $J^{PC}=1^{++}$ mixed state of the charmonium hybrid and $D^*{\bar{D}}$ molecular state, study its mass with the QCD sum rules, and they observe that the mixing is robust. In Ref. [55], Zhang takes $Z_c(3900)$ as the $D^*{\bar{D}}$ molecular state without distinguishing its charge conjugation, studies the mass with the QCD sum rules by calculating the vacuum condensates up to dimension-9, and obtains the value $M_{Z_c}=(3.86 \pm 0.27)\,\mathrm { GeV}$.

In all those works [49–55], the $\overline{MS}$ masses are taken; however, the energy scales at which the QCD spectral densities are calculated are either not shown explicitly or not specified, and the energy-scale dependence of the QCD sum rules is not studied. In the QCD sum rules for the hidden charmed (or bottom) tetraquark states and molecular states, the integrals

$$\begin{aligned} \int \limits _{4m_Q^2}^{s_0} ds \rho _{QCD}(s)\exp \left( -\frac{s}{T^2} \right) \, , \end{aligned}$$

(1)

are sensitive to the heavy quark masses $m_Q$, where the $\rho _{QCD}(s)$ denotes the QCD spectral densities and the $T^2$ denotes the Borel parameters. Variations of the heavy quark masses lead to changes of integral ranges $4m_Q^2-s_0$ of the variable $\mathbf {ds}$ besides the QCD spectral densities, therefore changes of the Borel windows and predicted masses and pole residues. Furthermore, in Refs. [49–55], the higher-dimensional vacuum condensates are neglected in one way or another. The higher-dimensional vacuum condensates play an important role in determining the Borel windows, although they play a less important role in the Borel windows.

In Refs. [56–59], we focus on the scenario of tetraquark states, distinguish the charge conjugations of the interpolating currents, calculate the vacuum condensates up to dimension-10 in the operator product expansion, study the diquark–antidiquark type scalar, vector, axial-vector, tensor hidden charm tetraquark states and axial-vector hidden bottom tetraquark states systematically with the QCD sum rules, make reasonable assignments of $X(3872)$, $Z_c(3900)$, $Z_c(3885)$, $Z_c(4020)$, $Z_c(4025)$, $Z(4050)$, $Z(4250)$, $Y(4360)$, $Y(4630)$, $Y(4660)$, $Z_b(10610)$, and $Z_b(10650)$. Furthermore, we explore the energy-scale dependence of the QCD sum rules for the hidden charm and hidden bottom tetraquark states in details for the first time, and we suggest a formula,

$$\begin{aligned} \mu&= \sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2} \, , \end{aligned}$$

(2)

with the effective masses ${\mathbb {M}}_c=1.80\,\mathrm {GeV}$ and ${\mathbb {M}}_b=5.13\,\mathrm {GeV}$ to determine the energy scales of the QCD spectral densities, which works well.

In this article, we take $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ as the axial-vector hadronic molecular states, distinguish the charge conjugations, construct both the color singlet–singlet type currents and the color octet–octet type currents to interpolate them. We calculate the contributions of the vacuum condensates up to dimension-10, study the masses and pole residues, and we explore the energy-scale dependence in detail so as to see whether or not the formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ survives in the case of the molecular states, and we make tentative assignments of the $X(3872)$, $Z_c(3900)$, $Z_b(10610)$ in the scenario of molecular states.

The article is arranged as follows: we derive the QCD sum rules for the masses and pole residues of the axial-vector molecular states in Sect. 2; in Sect. 3, we present the numerical results and discussions; Sect. 4 is reserved for our conclusion.

2 QCD sum rules for the $J^{P}=1^{+}$ molecular states

In the following, we write down the two-point correlation functions $\Pi _{\mu \nu }(p)$ in the QCD sum rules,

$$\begin{aligned}&\!\!\!\Pi _{\mu \nu }(p)=i\int d^4x e^{ip \cdot x} \langle 0|T\{J_\mu (x)J_\nu ^{\dagger }(0)\}|0\rangle \, , \end{aligned}$$

(3)

$$\begin{aligned}&\!\!\!J^0_\mu (x)=\frac{\bar{u}(x)i\gamma _5 Q(x)\bar{Q}(x)\gamma _\mu d(x)+t\bar{u}(x)\gamma _\mu Q(x)\bar{Q}(x)i\gamma _5 d(x)}{\sqrt{2}} \, , \end{aligned}$$

(4)

$$\begin{aligned}&\!\!\!J^8_\mu (x)=\frac{\bar{u}(x)i\gamma _5 \lambda ^a Q(x)\bar{Q}(x)\gamma _\mu \lambda ^a d(x)+t\bar{u}(x)\gamma _\mu \lambda ^a Q(x)\bar{Q}(x)i\gamma _5 \lambda ^a d(x)}{\sqrt{2}} ,\nonumber \\ \end{aligned}$$

(5)

where $t=\pm 1$, $J_\mu (x)=J^0_{\mu }(x),\,J^8_{\mu }(x)$, the $\lambda ^a$ is the Gell-Mann matrix. We construct the color singlet–singlet type (0-0 type) currents $J^0_\mu (x)$ (see Refs. [49–55]) and color octet–octet type (8-8 type) currents $J^8_\mu (x)$ (see Refs. [60, 61]) to study the hadronic molecular states $X(3872)$ (to be more precise, the charged partner of the $X(3872)$), $Z_c(3900)$, $Z_b(10610)$, etc. We can rearrange the 8-8 type currents $J^8_\mu (x)$ in terms of the following 0-0 type currents:

$$\begin{aligned} J^8_\mu (x)&= \frac{\sqrt{2}}{4}\bar{u}(x)i\gamma _5d(x)\bar{Q}(x)\gamma _\mu Q(x)\nonumber \\&\,+t\frac{\sqrt{2}}{4}\bar{Q}(x)i\gamma _5Q(x)\bar{u}(x)\gamma _\mu d(x) \nonumber \\&+\frac{\sqrt{2}i}{4}\bar{u}(x)\gamma _5\gamma _\alpha d(x)\bar{Q}(x)\gamma _\mu \gamma ^\alpha Q(x)\nonumber \\&\,+t\frac{\sqrt{2}i}{4}\bar{Q}(x)\gamma _5\gamma _\alpha Q(x)\bar{u}(x)\gamma _\mu \gamma ^\alpha d(x) \nonumber \\&+\frac{\sqrt{2}i}{8}\bar{u}(x)\gamma _5\sigma _{\alpha \beta } d(x)\bar{Q}(x)\gamma _\mu \sigma ^{\alpha \beta } Q(x)\nonumber \\&\,+t\frac{\sqrt{2}i}{8}\bar{Q}(x)\gamma _5\sigma _{\alpha \beta } Q(x)\bar{u}(x)\gamma _\mu \sigma ^{\alpha \beta } d(x) \nonumber \\&+\frac{\sqrt{2}i}{4}\bar{u}(x) \gamma _\alpha d(x)\bar{Q}(x)\gamma _\mu \gamma ^\alpha \gamma _5 Q(x)\nonumber \\&\,+t\frac{\sqrt{2}i}{4}\bar{Q}(x) \gamma _\alpha Q(x)\bar{u}(x)\gamma _\mu \gamma ^\alpha \gamma _5 d(x) \nonumber \\&+\frac{\sqrt{2}i}{4}\bar{u}(x)d(x)\bar{Q}(x)\gamma _\mu \gamma _5 Q(x)\nonumber \\&\,+t\frac{\sqrt{2}i}{4}\bar{Q}(x)Q(x)\bar{u}(x)\gamma _\mu \gamma _5 d(x) \nonumber \\&-\frac{\sqrt{2}}{3}\bar{u}(x)i\gamma _5 Q(x)\bar{Q}(x)\gamma _\mu d(x)\nonumber \\&\,-t\frac{\sqrt{2}}{3}\bar{u}(x)\gamma _\mu Q(x)\bar{Q}(x)i\gamma _5 d(x) \, , \end{aligned}$$

(6)

with the identity

$$\begin{aligned} \lambda ^a_{ij}\lambda ^a_{mn}&= 2\delta _{in}\delta _{mj}-\frac{2}{3}\delta _{ij}\delta _{mn}\, \end{aligned}$$

(7)

in the color space. The 8-8 type current can be taken as a special superposition of the 0-0 type currents. Under a charge conjugation transformation $\widehat{C}$, the currents $J_\mu (x)$ have the properties

$$\begin{aligned} \widehat{C}J_{\mu }(x)\widehat{C}^{-1}&= \mp J_\mu (x)\mid _{u {\leftrightarrow }d} \,\,\,\, \mathrm{for}\,\,\,\, t=\pm 1\, . \end{aligned}$$

(8)

The values $t=\mp 1$ correspond to the positive and negative charge conjugations, respectively.

We can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_\mu (x)$ into the correlation functions $\Pi _{\mu \nu }(p)$ to obtain the hadronic representation [62, 63]. After isolating the ground state contributions from the pole terms, we get the following results:

$$\begin{aligned} \Pi _{\mu \nu }(p)&= \frac{\lambda _{X/Z}^2}{M^2_{X/Z}-p^2}\left( -g_{\mu \nu } +\frac{p_\mu p_\nu }{p^2}\right) +\cdots \nonumber \\&= \Pi (p)\left( -g_{\mu \nu } +\frac{p_\mu p_\nu }{p^2}\right) +\cdots \, \, , \end{aligned}$$

(9)

where the pole residues (or couplings) $\lambda _{X/Z}$ are defined by

$$\begin{aligned} \langle 0|J_\mu (0)|X/Z(p)\rangle =\lambda _{X/Z}\, \varepsilon _\mu \, , \end{aligned}$$

(10)

and the $\varepsilon _\mu$ are the polarization vectors of the axial-vector mesons $X(3872)$, $Z_c(3900)$, $Z_b(10610)$, etc.

Here we take a short digression to discuss the possible contaminations originate from the higher resonances and continuum states. In the following, we will discuss the hidden charm systems for simplicity, the conclusion survives in the hidden bottom systems. In the nonrelativistic and heavy quark limit, the $C=+$ currents are reduced to the forms

$$\begin{aligned} \bar{u}\gamma ^5 c \,\bar{c}\gamma ^j d-\bar{u}\gamma ^j c \,\bar{c}\gamma ^5 d&\propto \xi ^\dagger _u \xi _c \, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _d -\xi ^\dagger _u \frac{\sigma ^j}{2} \xi _c \, \xi _c^\dagger \xi _d \, , \nonumber \\ \bar{u}\gamma ^j c \,\bar{c}\gamma ^k d+\bar{u}\gamma ^k c \,\bar{c}\gamma ^j d&\propto \xi ^\dagger _u \frac{\sigma ^j}{2} \xi _c \, \xi _c^\dagger \frac{\sigma ^k}{2} \xi _d\nonumber \\&+\xi ^\dagger _u \frac{\sigma ^k}{2} \xi _c \, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _d\, , \end{aligned}$$

(11)

while the $C=-$ currents are reduced to the forms

$$\begin{aligned} \bar{u}\gamma ^5 c \,\bar{c}\gamma ^j d+\bar{u}\gamma ^j c \,\bar{c}\gamma ^5 d&\propto \xi ^\dagger _u \xi _c \, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _d +\xi ^\dagger _u \frac{\sigma ^j}{2} \xi _c \, \xi _c^\dagger \xi _d\, , \nonumber \\ \bar{u}\gamma ^j c \,\bar{c}\gamma ^k d-\bar{u}\gamma ^k c \,\bar{c}\gamma ^j d&\propto \xi ^\dagger _u \frac{\sigma ^j}{2} \xi _c \, \xi _c^\dagger \frac{\sigma ^k}{2} \xi _d\nonumber \\&-\xi ^\dagger _u \frac{\sigma ^k}{2} \xi _c \, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _d\, , \end{aligned}$$

(12)

where the $\xi _{c,u,d}$ are the two-component quark fields and the $\sigma ^i$ are the Pauli matrices. The bilinear fields $\xi ^\dagger _i \xi _j$ and $\xi ^\dagger _i \frac{\sigma ^k}{2} \xi _j$ have the spins 0 and 1, respectively, and they couple to (pseudo-) scalar and (axial-) vector meson fields, respectively. The currents $J^0_\mu$ with $C=\pm$ couple potentially to the $\frac{D\bar{D}^*{\mp } D^*\bar{D}}{\sqrt{2}}$ molecular or scattering states, while the currents $J^0_{\mu \nu }=\bar{u}\gamma _\mu c \,\bar{c}\gamma _\nu d\pm \bar{u}\gamma _\nu c \,\bar{c}\gamma _\mu d$ with $C=\pm$ couple potentially to the $D^* \bar{D}^*$ molecular or scattering states.

On the other hand, the octet currents are reduced to the following forms:

$$\begin{aligned}&\!\!\!\bar{u}i\gamma ^5 \lambda ^a c \, \bar{c}\lambda ^a\gamma ^j d\propto \xi ^\dagger _u \lambda ^a \xi _c \, \xi _c^\dagger \lambda ^a \frac{\sigma ^j}{2}\xi _d\nonumber \\&\quad = 4\xi ^\dagger _u \frac{\sigma ^k}{2}\frac{\sigma ^j}{2} \xi _d\, \xi ^\dagger _c \frac{\sigma ^k}{2}\xi _c\!+\!\xi ^\dagger _u \frac{\sigma ^j}{2}\xi _d \, \xi ^\dagger _c \xi _c \!-\!\frac{2}{3}\xi ^\dagger _u \xi _c\, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _d \nonumber \\&\quad =\xi ^\dagger _u \xi _d\, \xi ^\dagger _c \frac{\sigma ^j}{2}\xi _c -2\epsilon ^{ijk}\xi ^\dagger _u \frac{\sigma ^i}{2} \xi _d\, \xi ^\dagger _c \frac{\sigma ^k}{2}\xi _c\nonumber \\&\qquad +\xi ^\dagger _u \frac{\sigma ^j}{2}\xi _d\, \xi ^\dagger _c \xi _c -\frac{2}{3}\xi ^\dagger _u \xi _c \,\xi _c^\dagger \frac{\sigma ^j}{2} \xi _d \, , \nonumber \\&\bar{u}\lambda ^a\gamma ^j c \,\bar{c}\lambda ^a\gamma ^k d\propto \xi ^\dagger _u \lambda ^a\frac{\sigma ^j}{2} \xi _c \,\xi _c^\dagger \lambda ^a\frac{\sigma ^k}{2} \xi _d\nonumber \\&\quad = 4\xi ^\dagger _u\frac{\sigma ^i}{2}\frac{\sigma ^k}{2} \xi _d \, \xi _c^\dagger \frac{\sigma ^i}{2} \frac{\sigma ^j}{2} \xi _c +\xi ^\dagger _u\frac{\sigma ^k}{2} \xi _d \, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _c \nonumber \\&\qquad -\frac{2}{3}\xi ^\dagger _u \frac{\sigma ^j}{2} \xi _c \, \xi _c^\dagger \frac{\sigma ^k}{2} \xi _d \nonumber \\&\quad = \frac{\delta _{jk}}{4}\xi ^\dagger _u \xi _d \, \xi _c^\dagger \xi _c \,+\frac{1}{2}\epsilon ^{jkm} \xi ^\dagger _u\frac{\sigma ^m}{2} \xi _d \, \xi _c^\dagger \xi _c\nonumber \\&\qquad +\frac{1}{2}\epsilon ^{kjm} \xi ^\dagger _u\xi _d \, \xi _c^\dagger \frac{\sigma ^m}{2} \xi _c \nonumber \\&\qquad +\epsilon ^{ikm}\epsilon ^{ijn} \xi ^\dagger _u\frac{\sigma ^m}{2} \xi _d \, \xi _c^\dagger \frac{\sigma ^n}{2} \xi _c+\xi ^\dagger _u\frac{\sigma ^k}{2} \xi _d \, \xi _c^\dagger \frac{\sigma ^j}{2} \xi _c\nonumber \\&\qquad -\frac{2}{3}\xi ^\dagger _u \frac{\sigma ^j}{2} \xi _c \,\xi _c^\dagger \frac{\sigma ^k}{2} \xi _d \, . \end{aligned}$$

(13)

The octet current $J^8_\mu =\bar{u}i\gamma ^5 \lambda ^a c \, \bar{c}\lambda ^a\gamma _\mu d$ couples potentially to the $J/\psi \pi$, $\psi (3770)\pi$, $\eta _c \rho$, $J/\psi \rho$, $D\bar{D}^*$ molecular or scattering states. The octet current $J^8_{\mu \nu }=\bar{u}\lambda ^a\gamma _\mu c \,\bar{c}\lambda ^a\gamma _\nu d$ couples potentially to the $\eta _c \pi$, $\eta _c \rho$, $J/\psi \pi$, $\psi (3770)\pi$, $J/\psi \rho$, and $D^*\bar{D}^*$ molecular or scattering states. In this article, we take the currents $J^{0,8}_{\mu }$, not the currents $J^{0,8}_{\mu \nu }$; the $D^*\bar{D}^*$ molecular or scattering states have no contaminations.

In the scenario of meta-stable Feshbach resonances, $X(3872)$, $Z_c(3900)$, $Z_c(4025)$, $Z_b(10610)$, and $Z_b(10650)$ are taken as the $J/\psi \rho$ – $D\bar{D}^*$, $\psi (3770)\pi$ – $D\bar{D}^*$, $h_c(\mathrm{2P})\pi$ – $D^*\bar{D}^*$, $\chi _{b0}\rho$ – $B\bar{B}^*$, $\chi _{b1}\rho$ – $B^*\bar{B}^*$ hadro-charmonium-molecule mixed states, respectively, where $\chi _{b0}\rho$ and $\chi _{b1}\rho$ are P-wave systems [64]. The hadro-charmonium system admits bound states giving rise to a discrete spectrum of levels, a resonance occurs if one of such levels falls close to some open-charm threshold, as the coupling between channels leads to an attractive interaction and favors the formation of a meta-stable Feshbach resonance. The couplings of the currents $J_\mu$ to the near-threshold hadro-charmonium states $J/\psi \rho$, $\psi (3770)\pi$ and $\chi _{b0}\rho$ contribute to the molecular states $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$, respectively.

Now we study the contributions of the intermediate meson loops (or the scattering states $D D^*$, $J/\psi \pi$, $J/\psi \rho$, etc.) to the correlation functions $\Pi _{\mu \nu }(p)$,

$$\begin{aligned}&\!\!\!\Pi _{\mu \nu }(p)=-\frac{\widehat{\lambda }_{X/Z}^{2}}{ p^2-\widehat{M}_{X/Z}^2}\widetilde{g}_{\mu \nu }(p)\nonumber \\&\!\!\!\qquad -\frac{\widehat{\lambda }_{X/Z}}{p^2-\widehat{M}_{X/Z}^2}\widetilde{g}_{\mu \alpha }(p)\Sigma _{DD^*}(p) \widetilde{g}^{\alpha \beta }(p) \widetilde{g}_{\beta \nu }(p)\frac{\widehat{\lambda }_{X/Z}}{p^2-\widehat{M}_{X/Z}^2} \nonumber \\&\!\!\!\qquad -\frac{\widehat{\lambda }_{X/Z}}{p^2-\widehat{M}_{X/Z}^2}\widetilde{g}_{\mu \alpha }(p) \Sigma _{J/\psi \pi }(p) \widetilde{g}^{\alpha \beta }(p)\widetilde{g}_{\beta \nu }(p)\frac{\widehat{\lambda }_{X/Z}}{p^2-\widehat{M}_{X/Z}^2} \nonumber \\&\!\!\!\qquad -\frac{\widehat{\lambda }_{X/Z}}{p^2-\widehat{M}_{X/Z}^2}\widetilde{g}_{\mu \alpha }(p) \Sigma _{J/\psi \rho }^{\alpha \beta }(p) \widetilde{g}_{\beta \nu }(p)\frac{\widehat{\lambda }_{X/Z}}{p^2-\widehat{M}_{X/Z}^2} +\cdots \, ,\nonumber \\&\!\!\!\quad =-\frac{\widehat{\lambda }_{X/Z}^{2}}{ p^2-\widehat{M}_{X/Z}^2-\Sigma _{DD^*}(p)-\Sigma _{J/\psi \pi }(p)-\Sigma _{J/\psi \rho }(p)+\cdots }\nonumber \\&\qquad \times \,\widetilde{g}_{\mu \nu }(p)+\cdots , \end{aligned}$$

(14)

where

$$\begin{aligned} \Sigma _{DD^*}(p)&= i\int ~{d^4q\over (2\pi )^4}\frac{G^2_{X/ZDD^*}}{\left[ q^2-M_{D}^2\right] \left[ (p-q)^2-M_{D^*}^2\right] } \, ,\end{aligned}$$

(15)

$$\begin{aligned} \Sigma _{J/\psi \pi }(p)&= i\int ~{d^4q\over (2\pi )^4}\frac{G^2_{X/ZJ/\psi \pi }}{\left[ q^2-M_{J/\psi }^2\right] \left[ (p-q)^2-M_{\pi }^2\right] } \, ,\end{aligned}$$

(16)

$$\begin{aligned} \Sigma _{J/\psi \rho }^{\alpha \beta }(p)&= i\int ~{d^4q\over (2\pi )^4}\nonumber \\&\times \,\frac{G^2_{X/ZJ/\psi \rho }\epsilon ^{\alpha \theta \sigma \tau }\epsilon ^{\beta \theta ^{\prime }\sigma ^{\prime }\tau ^{\prime }}p_\tau p_{\tau ^\prime }\widetilde{g}_{\theta \theta ^{\prime }}(q)\widetilde{g}_{\sigma \sigma ^{\prime }}(p-q)}{\left[ q^2-M_{J/\psi }^2\right] \left[ (p-q)^2-M_{\rho }^2\right] }\, , \nonumber \\&= \Sigma _{J/\psi \rho }(p)\widetilde{g}^{\alpha \beta }(p)+\Sigma _{J/\psi \rho }^1(p) \frac{p^{\alpha }p^{\beta } }{p^2}\, , \end{aligned}$$

(17)

$\widetilde{g}_{\mu \nu }(p)=-g_{\mu \nu }+\frac{p_{\mu }p_{\nu }}{p^2}$, $G_{X/Z DD^*}$, $G_{X/Z J/\psi \pi }$, and $G_{X/Z J/\psi \rho }$ are hadronic coupling constants, the $\widehat{\lambda }_{X/Z}$ and $\widehat{M}_{X/Z}$ are bare quantities to absorb the divergences in the self-energies $\Sigma _{DD^*}(p)$, $\Sigma _{J/\psi \pi }(p)$, $\Sigma _{J/\psi \rho }(p)$, etc.

The renormalized self-energies contribute a finite imaginary part to modify the dispersion relation:

$$\begin{aligned} \Pi _{\mu \nu }(p)&= -\frac{\lambda _{X/Z}^{2}}{ p^2-M_{X/Z}^2+i\sqrt{p^2}\Gamma (p^2)}\widetilde{g}_{\mu \nu }(p)+\cdots ,\nonumber \\ \end{aligned}$$

(18)

the physical widths $\Gamma _{Z_c(3900)}(M_Z^2)=(46 \pm 10 \pm 20)\, \mathrm {MeV}$ and $\Gamma _{X(3872)}(M_X^2)<1.2\,\mathrm {MeV}$ are small enough, and the zero width approximation in the hadronic spectral densities works. The discussion survives in the hidden bottom systems according to the small physical widths, $\Gamma _{Z_b(10610)}=(18.4\pm 2.4) \,\mathrm {MeV}$ and $\Gamma _{Z_b(10650)}=(11.5\pm 2.2)\,\mathrm { MeV}$. The contaminations of the intermediate meson loops are expected to be small.

In the following, we briefly outline the operator product expansion for the correlation functions $\Pi _{\mu \nu }(p)$ in perturbative QCD. We contract the quark fields in the correlation functions $\Pi _{\mu \nu }(p)$ with the Wick theorem and obtain the results

$$\begin{aligned}&\!\!\!\Pi _{\mu \nu }^{0}(p)=-\frac{i}{2} \delta _{jk}\delta _{mn}\delta _{k^{\prime }j^{\prime }}\delta _{n^{\prime }m^{\prime }} \int d^4x e^{ip \cdot x} \nonumber \\&\!\!\!\quad \times \,\left\{ \mathrm{Tr}\left[ \gamma _5 S_Q^{kk^{\prime }}(x)\gamma _5 S^{j^{\prime }j}(-x)\right] \mathrm{Tr}\left[ \gamma _\mu S^{nn^{\prime }}(x)\gamma _\nu S_Q^{m^{\prime }m}(-x)\right] \right. \nonumber \\&\!\!\!\quad +\,\mathrm{Tr}\left[ \gamma _\mu S_Q^{kk^{\prime }}(x)\gamma _\nu S^{j^{\prime }j}(-x)\right] \mathrm{Tr}\left[ \gamma _5 S^{nn^{\prime }}(x)\gamma _5 S_Q^{m^{\prime }m}(-x)\right] \nonumber \\&\!\!\!\quad \pm \mathrm{Tr}\left[ \gamma _\mu S_Q^{kk^{\prime }}(x)\gamma _5 S^{j^{\prime }j}(-x)\right] \mathrm{Tr}\left[ \gamma _5 S^{nn^{\prime }}(x)\gamma _\nu S_Q^{m^{\prime }m}(-x)\right] \nonumber \\&\!\!\!\quad \left. \pm \mathrm{Tr}\left[ \gamma _5 S_Q^{kk^{\prime }}(x)\gamma _\nu S^{j^{\prime }j}(-x)\right] \mathrm{Tr}\left[ \gamma _\mu S^{nn^{\prime }}(x)\gamma _5 S_Q^{m^{\prime }m}(-x)\right] \right\} \, , \end{aligned}$$

(19)

$$\begin{aligned}&\!\!\!\Pi _{\mu \nu }^{8}(p)=\Pi _{\mu \nu }^{0}(p)\mid _{\delta _{jk}\delta _{mn}\delta _{k^{\prime }j^{\prime }}\delta _{n^{\prime }m^{\prime }} \rightarrow \lambda ^a_{jk}\lambda ^a_{mn}\lambda ^b_{k^{\prime }j^{\prime }}\lambda ^b_{n^{\prime }m^{\prime }}} \end{aligned}$$

(20)

where $\mp$ correspond to the positive and negative charge conjugations, respectively, $S^{ij}(x)$ and $S^{ij}_Q(x)$ are the full light and heavy quark propagators, respectively,

$$\begin{aligned} S^{ij}(x)&= \frac{i\delta _{ij}\!\not \!{x}}{ 2\pi ^2x^4}-\frac{\delta _{ij}\langle \bar{q}q\rangle }{12} -\frac{\delta _{ij}x^2\langle \bar{q}g_s\sigma Gq\rangle }{192}\nonumber \\&\, -\frac{ig_sG^{a}_{\alpha \beta }t^a_{ij}(\!\not \!{x} \sigma ^{\alpha \beta }+\sigma ^{\alpha \beta } \!\not \!{x})}{32\pi ^2x^2} -\frac{i\delta _{ij}x^2\!\not \!{x}g_s^2\langle \bar{q} q\rangle ^2}{7776}\nonumber \\&-\frac{\delta _{ij}x^4\langle \bar{q}q \rangle \langle g_s^2 GG\rangle }{27648} -\frac{1}{8}\langle \bar{q}_j\sigma ^{\mu \nu }q_i \rangle \sigma _{\mu \nu }\nonumber \\&\,-\frac{1}{4}\langle \bar{q}_j\gamma ^{\mu }q_i\rangle \gamma _{\mu }+\cdots \, , \end{aligned}$$

(21)

$$\begin{aligned} S^{ij}_Q(x)&= \frac{i}{(2\pi )^4}\int d^4k e^{-ik \cdot x} \left\{ \frac{\delta _{ij}}{\!\not \!{k}-m_Q} -\frac{g_sG^n_{\alpha \beta }t^n_{ij}}{4}\right. \nonumber \\&\times \,\left. \frac{\sigma ^{\alpha \beta }(\!\not \!{k}+m_Q)+(\!\not \!{k}+m_Q) \sigma ^{\alpha \beta }}{(k^2-m_Q^2)^2}\right. \nonumber \\&\left. +\frac{g_s D_\alpha G^n_{\beta \lambda }t^n_{ij}(f^{\lambda \beta \alpha }+f^{\lambda \alpha \beta }) }{3(k^2-m_Q^2)^4}\right. \nonumber \\&\left. -\frac{g_s^2 (t^at^b)_{ij} G^a_{\alpha \beta }G^b_{\mu \nu }(f^{\alpha \beta \mu \nu }+f^{\alpha \mu \beta \nu }+f^{\alpha \mu \nu \beta }) }{4(k^2-m_Q^2)^5}\right. \nonumber \\&\,\left. +\cdots \right\} \, ,\nonumber \\&f^{\lambda \alpha \beta }=(\!\not \!{k}+m_Q)\gamma ^\lambda (\!\not \!{k}+m_Q)\gamma ^\alpha (\!\not \!{k}+m_Q)\gamma ^\beta (\!\not \!{k}+m_Q)\, ,\nonumber \\&f^{\alpha \beta \mu \nu }=(\!\not \!{k}+m_Q)\gamma ^\alpha (\!\not \!{k}+m_Q)\gamma ^\beta (\!\not \!{k}+m_Q)\gamma ^\mu \nonumber \\&\times \,(\!\not \!{k}+m_Q)\gamma ^\nu (\!\not \!{k}+m_Q)\,, \end{aligned}$$

(22)

and $t^n=\frac{\lambda ^n}{2}$, $D_\alpha =\partial _\alpha -ig_sG^n_\alpha t^n$ [63]. We then compute the integrals both in the coordinate and momentum spaces, and we obtain the correlation functions $\Pi _{\mu \nu }(p)$ and therefore the spectral densities at the level of quark–gluon degrees of freedom. In Eq. (21), we retain the terms $\langle \bar{q}_j\sigma _{\mu \nu }q_i \rangle$ and $\langle \bar{q}_j\gamma _{\mu }q_i\rangle$ originate from the Fierz re-ordering of the $\langle q_i \bar{q}_j\rangle$ to absorb the gluons emitted from the heavy quark lines to form $\langle \bar{q}_j g_s G^a_{\alpha \beta } t^a_{mn}\sigma _{\mu \nu } q_i \rangle$ and $\langle \bar{q}_j\gamma _{\mu }q_ig_s D_\nu G^a_{\alpha \beta }t^a_{mn}\rangle$ so as to extract the mixed condensate and four-quark condensates $\langle \bar{q}g_s\sigma G q\rangle$ and $g_s^2\langle \bar{q}q\rangle ^2$, respectively.

Once analytical results are obtained, we can take the quark–hadron duality and perform the Borel transform with respect to the variable $P^2=-p^2$ to obtain the following QCD sum rules:

$$\begin{aligned} \lambda ^2_{X/Z}\, \exp \left( -\frac{M^2_{X/Z}}{T^2}\right) {=} \int \limits _{4m_Q^2}^{s_0} ds\, \rho ^{0/8}(s) \, \exp \left( -\frac{s}{T^2}\right) ,\nonumber \\ \end{aligned}$$

(23)

where

$$\begin{aligned} \rho ^{0/8}(s)&= \rho _{0}^{0/8}(s)+\rho _{3}^{0/8}(s) +\rho _{4}^{0/8}(s)+\rho _{5}^{0/8}(s)\nonumber \\&+\rho _{6}^{0/8}(s)+\rho _{7}^{0/8}(s) +\rho _{8}^{0/8}(s)+\rho _{10}^{0/8}(s)\, , \end{aligned}$$

(24)

$$\begin{aligned} \rho _{0}^{0}(s)&= \frac{1}{4096\pi ^6}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \, yz\,(1-y-z)^3\nonumber \\&\times \,\left( s-\overline{m}_Q^2\right) ^2 \left( 35s^2-26s\overline{m}_Q^2+3\overline{m}_Q^4 \right) \, , \end{aligned}$$

(25)

$$\begin{aligned} \rho _{0}^{8}(s)&= \frac{1}{1152\pi ^6}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \, yz\,(1-y-z)^3\nonumber \\&\times \,\left( s-\overline{m}_Q^2\right) ^2\left( 35s^2-26s\overline{m}_Q^2+3\overline{m}_Q^4 \right) \, , \end{aligned}$$

(26)

$$\begin{aligned} \rho _{3}^{0}(s)&= -\frac{3m_Q\langle \bar{q}q\rangle }{256\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \, (y+z)(1-y-z)\nonumber \\&\times \,\left( s-\overline{m}_Q^2\right) \left( 7s-3\overline{m}_Q^2 \right) \, , \end{aligned}$$

(27)

$$\begin{aligned} \rho _{3}^{8}(s)&= -\frac{m_Q\langle \bar{q}q\rangle }{24\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \, (y+z)(1-y-z)\nonumber \\&\times \,\left( s-\overline{m}_Q^2\right) \left( 7s-3\overline{m}_Q^2 \right) \, , \end{aligned}$$

(28)

$$\begin{aligned} \rho _{4}^{0}(s)&= -\frac{m_Q^2}{3072\pi ^4} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( \frac{z}{y^2}+\frac{y}{z^2}\right) \nonumber \\&\times \,(1-y-z)^3 \left\{ 8s-3\overline{m}_Q^2+\overline{m}_Q^4\, \delta \left( s-\overline{m}_Q^2\right) \right\} \nonumber \\&+\,\frac{1}{1024\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\,\nonumber \\&\times \, (y+z)(1-y-z)^2 \,s\,(5s-4\overline{m}_Q^2) \, , \end{aligned}$$

(29)

$$\begin{aligned} \rho _{4}^{8}(s)&= -\frac{m_Q^2}{864\pi ^4} \left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( \frac{z}{y^2}+\frac{y}{z^2}\right) \nonumber \\&\times \,(1-y-z)^3 \left\{ 8s-3\overline{m}_Q^2+\overline{m}_Q^4\, \delta \left( s-\overline{m}_Q^2\right) \right\} \nonumber \\&-\,\frac{1}{2304\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\, (y+z)\nonumber \\&\times \, (1-y-z)^2 \,s\,(5s-4\overline{m}_Q^2) \nonumber \\&+\,t\frac{m_Q^2}{1152\pi ^4}\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( s-\overline{m}_Q^2 \right) \nonumber \\&\times \,\left\{ 7-2\left( \frac{1}{y}+ \frac{1}{z}\right) (1-y-z) \right. \nonumber \\&\left. + \,\frac{7(1-y-z)^2}{2yz} -\frac{7(1-y-z)}{2}\right. \nonumber \\&\,\left. +\,\left( \frac{1}{y}+\frac{1}{z} \right) \frac{(1-y-z)^2}{2} -\frac{7(1-y-z)^3}{12yz} \right\} ,\nonumber \\ \end{aligned}$$

(30)

$$\begin{aligned} \rho _{5}^{0}(s)&= \frac{3m_Q\langle \bar{q}g_s\sigma Gq\rangle }{512\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \, (y+z) \left( 5s-3\overline{m}_Q^2 \right) \nonumber \\&-\frac{3m_Q\langle \bar{q}g_s\sigma Gq\rangle }{256\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( \frac{y}{z}+\frac{z}{y} \right) \nonumber \\&\times \, (1-y-z) \left( 2s-\overline{m}_Q^2 \right) , \end{aligned}$$

(31)

$$\begin{aligned} \rho _{5}^{8}(s)&= \frac{m_Q\langle \bar{q}g_s\sigma Gq\rangle }{48\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \, (y+z) \left( 5s-3\overline{m}_Q^2 \right) \nonumber \\&+\frac{m_Q\langle \bar{q}g_s\sigma Gq\rangle }{192\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( \frac{y}{z}+\frac{z}{y} \right) \nonumber \\&\times \,(1-y-z) \left( 2s-\overline{m}_Q^2 \right) \nonumber \\&+t\frac{m_Q\langle \bar{q}g_s\sigma Gq\rangle }{576\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( \frac{y}{z}+\frac{z}{y} \right) \nonumber \\&\times \,(1-y-z) \left( 5s-3\overline{m}_Q^2 \right) \, , \end{aligned}$$

(32)

$$\begin{aligned} \rho _{6}^{0}(s)&= \frac{m_Q^2\langle \bar{q}q\rangle ^2}{16\pi ^2}\int \limits _{y_i}^{y_f}dy +\frac{g_s^2\langle \bar{q}q\rangle ^2}{864\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\, yz \nonumber \\&\times \, \left\{ 8s-3\overline{m}_Q^2 +\overline{m}_Q^4\, \delta \left( s-\overline{m}_Q^2 \right) \right\} \nonumber \\&-\frac{g_s^2\langle \bar{q}q\rangle ^2}{576\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\, (1-y-z)\nonumber \\&\times \, \left\{ \left( \frac{z}{y}+\frac{y}{z} \right) \left( 7s-4\overline{m}_Q^2 \right) \right. \nonumber \\&\left. +\,\frac{1}{3}\left( \frac{z}{y^2}+\frac{y}{z^2} \right) m_Q^2\left[ 7+5\overline{m}_Q^2\,\delta \left( s-\overline{m}_Q^2 \right) \right] \right. \nonumber \\&\left. -\frac{1}{3}(y+z)\left( 4s-3\overline{m}_Q^2 \right) \right\} \, , \end{aligned}$$

(33)

$$\begin{aligned} \rho _{6}^{8}(s)&= \frac{2m_Q^2\langle \bar{q}q\rangle ^2}{9\pi ^2}\int \limits _{y_i}^{y_f}dy +\frac{g_s^2\langle \bar{q}q\rangle ^2}{243\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\, yz\nonumber \\&\!\!\!\times \, \left\{ 8s-3\overline{m}_Q^2 +\overline{m}_Q^4\, \delta \left( s-\overline{m}_Q^2 \right) \right\} \nonumber \\&\!\!\!+\frac{g_s^2\langle \bar{q}q\rangle ^2}{1296\pi ^4}\int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\, (1-y-z)\nonumber \\&\!\!\!\times \left\{ \left( \frac{z}{y}+\frac{y}{z} \right) \left( 7s-4\overline{m}_Q^2 \right) \right. \nonumber \\&\!\!\!\left. +\frac{1}{3}\left( \frac{z}{y^2}+\frac{y}{z^2} \right) m_Q^2\left[ 7+5\overline{m}_Q^2\,\delta \left( s-\overline{m}_Q^2 \right) \right] \right. \nonumber \\&\!\!\!\left. -\frac{1}{3}(y+z)\left( 4s-3\overline{m}_Q^2 \right) \right\} -\frac{g_s^2\langle \bar{q}q\rangle ^2}{1944\pi ^4}\int \limits _{y_i}^{y_f}dy\nonumber \\&\!\!\! \times \int \limits _{z_i}^{1-y}dz\,(1-y-z)\left\{ 3\left( \frac{z}{y}+\frac{y}{z} \right) \left( 2s-\overline{m}_Q^2 \right) \right. \nonumber \\&\left. +\left( \frac{z}{y^2}+\frac{y}{z^2} \right) m_Q^2\left[ 1+\overline{m}_Q^2\,\delta \left( s-\overline{m}_Q^2\right) \right] \right. \nonumber \\&\left. +2(y+z)\right. \left. \left[ 8s-3\overline{m}_Q^2 +\overline{m}_Q^4\, \delta \left( s-\overline{m}_Q^2\right) \right] \right\} ,\nonumber \\ \end{aligned}$$

(34)

$$\begin{aligned}&\rho _7^{0}(s)=\frac{m_Q^3\langle \bar{q}q\rangle }{1536\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\nonumber \\&\quad \times \, \left( \frac{y}{z^3}+\frac{z}{y^3}+\frac{1}{y^2}+\frac{1}{z^2}\right) (1-y-z) \nonumber \\&\quad \times \, \left( 1+\frac{2\overline{m}_Q^2}{T^2}\right) \delta \left( s-\overline{m}_Q^2\right) \nonumber \\&\quad -\frac{3m_Q\langle \bar{q}q\rangle }{256\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz \left( \frac{y}{z^2}+\frac{z}{y^2}\right) \nonumber \\&\quad \times \, (1-y-z)\left\{ 1+\frac{2\overline{m}_Q^2}{3}\delta \left( s-\overline{m}_Q^2\right) \right\} \nonumber \\&\quad -\frac{m_Q\langle \bar{q}q\rangle }{128\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy\int \limits _{z_i}^{1-y}dz \nonumber \\&\quad \times \left\{ 1+\frac{2\overline{m}_Q^2}{3}\delta \left( s-\overline{m}_Q^2\right) \right\} -\frac{m_Q\langle \bar{q}q\rangle }{512\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \nonumber \\&\quad \times \int \limits _{y_i}^{y_f}dy \left\{ 1+\frac{2\widetilde{m}_Q^2}{3}\delta \left( s-\widetilde{m}_Q^2\right) \right\} , \end{aligned}$$

(35)

$$\begin{aligned}&\!\!\!\rho _7^{8}(s)=\frac{m_Q^3\langle \bar{q}q\rangle }{432\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \int \limits _{z_i}^{1-y}dz\nonumber \\&\!\!\!\quad \times \, \left( \frac{y}{z^3}+\frac{z}{y^3}+\frac{1}{y^2}+\frac{1}{z^2}\right) (1-y-z) \nonumber \\&\!\!\!\quad \times \, \left( 1+\frac{2\overline{m}_Q^2}{T^2}\right) \delta \left( s-\overline{m}_Q^2\right) -\frac{m_Q\langle \bar{q}q\rangle }{24\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \nonumber \\&\!\!\!\quad \times \, \int \limits _{z_i}^{1-y}dz \left( \frac{y}{z^2}{+}\frac{z}{y^2}\right) (1-y-z) \left\{ 1{+}\frac{2\overline{m}_Q^2}{3}\delta \left( s-\overline{m}_Q^2\right) \right\} \nonumber \\&\!\!\!\quad +\frac{m_Q\langle \bar{q}q\rangle }{288\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy\int \limits _{z_i}^{1-y}dz\left\{ 1{+}\frac{2\overline{m}_Q^2}{3}\delta \left( s{-}\overline{m}_Q^2\right) \right\} \nonumber \\&\!\!\!\quad +t\frac{m_Q\langle \bar{q}q\rangle }{144\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy \nonumber \\&\!\!\!\quad \times \, \int \limits _{z_i}^{1-y}dz\left\{ 1-7\left( \frac{1}{y}+\frac{1}{z}\right) \frac{1-y-z}{4}\right\} \nonumber \\&\!\!\!\quad \times \, \left\{ 1+\frac{2\overline{m}_Q^2}{3}\delta \left( s-\overline{m}_Q^2\right) \right\} -\frac{m_Q\langle \bar{q}q\rangle }{144\pi ^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _{y_i}^{y_f}dy\nonumber \\&\!\!\!\quad \times \, \left\{ 1+\frac{2\widetilde{m}_Q^2}{3}\delta \left( s-\widetilde{m}_Q^2\right) \right\} \, , \end{aligned}$$

(36)

$$\begin{aligned} \rho _8^{0}(s)&= -\frac{m_Q^2\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{32\pi ^2}\int \limits _0^1 dy \left( 1+\frac{\widetilde{m}_Q^2}{T^2} \right) \nonumber \\&\times \,\delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&+\,\frac{m_Q^2\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{64\pi ^2}\int \limits _0^1 dy \left( \frac{1}{y}+\frac{1}{1-y} \right) \nonumber \\&\times \,\delta \left( s-\widetilde{m}_Q^2\right) , \end{aligned}$$

(37)

$$\begin{aligned} \rho _8^{8}(s)&= -\frac{m_Q^2\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{9\pi ^2}\int \limits _0^1 dy \left( 1+\frac{\widetilde{m}_Q^2}{T^2} \right) \nonumber \\&\times \, \delta \left( s-\widetilde{m}_Q^2\right) -\frac{m_Q^2\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{144\pi ^2}\nonumber \\&\times \, \int \limits _0^1 dy \left( \frac{1}{y}+\frac{1}{1-y} \right) \delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&-\,t\frac{\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma Gq\rangle }{144\pi ^2}\nonumber \\&\times \, \int \limits _{y_i}^{y_f} dy \left\{ 1+\frac{2\widetilde{m}_Q^2}{3}\delta \left( s-\widetilde{m}_Q^2\right) \right\} \, , \end{aligned}$$

(38)

$$\begin{aligned}&\!\!\!\rho _{10}^{0}(s)=\frac{m_Q^2\langle \bar{q}g_s\sigma Gq\rangle ^2}{256\pi ^2T^6} \int \limits _0^1 dy\, \widetilde{m}_Q^4\,\delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad -\frac{m_Q^4\langle \bar{q}q\rangle ^2}{288T^4}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \left\{ \frac{1}{y^3}+\frac{61}{(1-y)^3}\right\} \nonumber \\&\!\!\!\quad \times \delta \left( s{-}\widetilde{m}_Q^2\right) {+}\frac{m_Q^2\langle \bar{q}q\rangle ^2}{96T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \left\{ \! \frac{1}{y^2}\!+\!\frac{1}{(1-y)^2}\right\} \nonumber \\&\!\!\!\quad \times \delta \left( s-\widetilde{m}_Q^2\right) -\frac{m_Q^2\langle \bar{q}g_s\sigma Gq\rangle ^2}{256\pi ^2T^4}\int \limits _0^1 dy \left( \frac{1}{y}+\frac{1}{1-y}\right) \widetilde{m}_Q^2 \, \nonumber \\&\!\!\!\quad \times \delta \left( s-\widetilde{m}_Q^2\right) +t\frac{\langle \bar{q}g_s\sigma Gq\rangle ^2}{20736\pi ^2}\int \limits _0^1 dy \left( 1+\frac{2\widetilde{m}_Q^2}{T^2} \right) \nonumber \\&\!\!\!\quad \times \delta \left( s-\widetilde{m}_Q^2\right) +\frac{m_Q^2\langle \bar{q}q\rangle ^2}{288T^6}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \, \widetilde{m}_Q^4 \,\nonumber \\&\!\!\!\quad \times \delta \left( s-\widetilde{m}_Q^2\right) \, , \end{aligned}$$

(39)

$$\begin{aligned}&\!\!\!\rho _{10}^{8}(s)=\frac{m_Q^2\langle \bar{q}g_s\sigma Gq\rangle ^2}{72\pi ^2T^6}\int \limits _0^1 dy \,\widetilde{m}_Q^4\,\delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad -\,\frac{m_Q^4\langle \bar{q}q\rangle ^2}{81T^4}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \left\{ \frac{1}{y^3}{+}\frac{1}{(1{-}y)^3}\right\} \delta \left( s{-}\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad +\,\frac{m_Q^2\langle \bar{q}q\rangle ^2}{27T^2}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \left\{ \frac{1}{y^2}{+}\frac{1}{(1{-}y)^2}\right\} \delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad +\,7t\frac{\langle \bar{q}q\rangle ^2}{1296}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \left( 1+\frac{2\widetilde{m}_Q^2}{T^2}\right) \delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad +\,\frac{m_Q^2\langle \bar{q}g_s\sigma Gq\rangle ^2}{576\pi ^2T^4}\int \limits _0^1 dy \left( \frac{1}{y}+\frac{1}{1-y}\right) \widetilde{m}_Q^2 \, \delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad +\,t\frac{\langle \bar{q}g_s\sigma Gq\rangle ^2}{864\pi ^2}\int \limits _0^1 dy \left( 1+\frac{3\widetilde{m}_Q^2}{2T^2}+\frac{\widetilde{m}_Q^4}{T^4} \right) \delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad +\,t\frac{\langle \bar{q}g_s\sigma Gq\rangle ^2}{5832\pi ^2}\int \limits _0^1 dy \left( 1+\frac{2\widetilde{m}_Q^2}{T^2} \right) \delta \left( s-\widetilde{m}_Q^2\right) \nonumber \\&\!\!\!\quad +\,\frac{m_Q^2\langle \bar{q}q\rangle ^2}{81T^6}\left\langle \frac{\alpha _sGG}{\pi }\right\rangle \int \limits _0^1 dy \, \widetilde{m}_Q^4 \, \delta \left( s-\widetilde{m}_Q^2\right) \, , \end{aligned}$$

(40)

the subscripts $0$, $3$, $4$, $5$, $6$, $7$, $8$, $10$ denote the dimensions of the vacuum condensates, the superscripts $0$, $8$ denote the 0-0 type and 8-8 type interpolating currents, respectively; $y_{f}=\frac{1+\sqrt{1-4m_Q^2/s}}{2}$, $y_{i}=\frac{1-\sqrt{1-4m_Q^2/s}}{2}$, $z_{i}=\frac{ym_Q^2}{y s -m_Q^2}$, $\overline{m}_Q^2=\frac{(y+z)m_Q^2}{yz}$, $\widetilde{m}_Q^2=\frac{m_Q^2}{y(1-y)}$, $\int _{y_i}^{y_f}dy \rightarrow \int _{0}^{1}dy$, $\int _{z_i}^{1-y}dz \rightarrow \int _{0}^{1-y}dz$ when the $\delta$ functions $\delta \left( s-\overline{m}_Q^2\right)$ and $\delta \left( s-\widetilde{m}_Q^2\right)$ appear.

In this article, we carry out the operator product expansion to the vacuum condensates up to dimension-10, and we assume vacuum saturation for the higher-dimensional vacuum condensates. The condensates $\left\langle \frac{\alpha _s}{\pi }GG\right\rangle$, $\langle \bar{q}q\rangle \left\langle \frac{\alpha _s}{\pi }GG\right\rangle$, $\langle \bar{q}q\rangle ^2\left\langle \frac{\alpha _s}{\pi }GG\right\rangle$, $\langle \bar{q} g_s \sigma Gq\rangle ^2$ and $g_s^2\langle \bar{q}q\rangle ^2$ are the vacuum expectations of the operators of the order $\mathcal {O}(\alpha _s)$. The four-quark condensate $g_s^2\langle \bar{q}q\rangle ^2$ comes from the terms $\big \langle \bar{q}\gamma _\mu t^a q g_s D_\eta G^a_{\lambda \tau }\big \rangle$, $\left\langle \bar{q}_jD^{\dagger }_{\mu }D^{\dagger }_{\nu }D^{\dagger }_{\alpha }q_i\right\rangle$ and $\langle \bar{q}_jD_{\mu }D_{\nu }D_{\alpha }q_i\rangle$, rather than from the perturbative corrections of $\langle \bar{q}q\rangle ^2$. The condensates $\langle g_s^3 GGG\rangle$, $\left\langle \frac{\alpha _s GG}{\pi }\right\rangle ^2$, $\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \langle \bar{q} g_s \sigma Gq\rangle$ have the dimensions 6, 8, 9, respectively, but they are the vacuum expectations of the operators of the order $\mathcal {O}\left( \alpha _s^{3/2}\right)$, $\mathcal {O}\left( \alpha _s^2\right)$, $\mathcal {O}\left( \alpha _s^{3/2}\right)$, respectively, and they are discarded. We take the truncations $n\le 10$ and $k\le 1$ in a consistent way; the operators of the orders $\mathcal {O}( \alpha _s^{k})$ with $k> 1$ are discarded. Furthermore, the values of the condensates $\left\langle g_s^3 GGG\right\rangle$, $\left\langle \frac{\alpha _s GG}{\pi }\right\rangle ^2$, $\left\langle \frac{\alpha _s GG}{\pi }\right\rangle \langle \bar{q} g_s \sigma Gq\rangle$ are very small, and they can be neglected safely.

We differentiate Eq. (23) with respect to $\frac{1}{T^2}$, eliminate the pole residues $\lambda _{X/Z}$, and we obtain the QCD sum rules for the masses,

$$\begin{aligned} M^2_{X/Z}= \frac{\int _{4m_Q^2}^{s_0} ds\frac{d}{d \left( -1/T^2\right) }\rho ^{0/8}(s)e^{-\frac{s}{T^2}}}{\int _{4m_Q^2}^{s_0} ds \rho ^{0/8}(s)e^{-\frac{s}{T^2}}}\, . \end{aligned}$$

(41)

3 Numerical results and discussions

The input parameters are taken to be the standard values $\langle \bar{q}q \rangle =-(0.24\pm 0.01\, \mathrm {GeV})^3$, $\langle \bar{q}g_s\sigma G q \rangle =m_0^2\langle \bar{q}q \rangle$, $m_0^2=(0.8 \pm 0.1)\,\mathrm {GeV}^2$, $\left\langle \frac{\alpha _s GG}{\pi }\right\rangle =(0.33\,\mathrm {GeV})^4$ at the energy scale $\mu =1\, \mathrm {GeV}$ [62, 63, 65, 66]. The quark condensate and mixed quark condensate evolve with the renormalization group equation, $\langle \bar{q}q \rangle (\mu )=\langle \bar{q}q \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{4}{9}}$ and $\langle \bar{q}g_s \sigma Gq \rangle (\mu )=\langle \bar{q}g_s \sigma Gq \rangle (Q)\left[ \frac{\alpha _{s}(Q)}{\alpha _{s}(\mu )}\right] ^{\frac{2}{27}}$.

In the article, we take the $\overline{MS}$ masses $m_{c}(m_c)=(1.275\pm 0.025)\,\mathrm {GeV}$ and $m_{b}(m_b)=(4.18\pm 0.03)\,\mathrm {GeV}$ from the Particle Data Group [67], and we take into account the energy-scale dependence of the $\overline{MS}$ masses from the renormalization group equation,

$$\begin{aligned} m_c(\mu )&= m_c(m_c)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_c)}\right] ^{\frac{12}{25}},\nonumber \\ m_b(\mu )&= m_b(m_b)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_b)}\right] ^{\frac{12}{23}},\nonumber \\ \alpha _s(\mu )&= \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} \right. \nonumber \\&\,\left. +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] , \end{aligned}$$

(42)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213$, $296$ and $339\,\mathrm {MeV}$ for the flavors $n_f=5$, $4$, and $3$, respectively [67].

We tentatively take the threshold parameters of the axial-vector molecular states $X(3872)$ (or $Z_c(3900)$) and $Z_b(10610)$ as $s_0$= (18.5–20.5) and (122–126) GeV$^2$, respectively, to avoid the contaminations of the higher resonances and continuum states, and we search for the optimal values to satisfy the two criteria (pole dominance and convergence of the operator product expansion) of the QCD sum rules. In this article, we assume that the energy gap between the ground states and the first radial excited states is about (0.4–0.6) GeV, just like that of the conventional mesons.

The correlation functions $\Pi (p)$ can be written as

$$\begin{aligned} \Pi (p)&= \sum _n C_n(p^2,\mu )\langle {\mathcal {O}}_n(\mu )\rangle =\int \limits _{4m^2_Q(\mu )}^\infty ds \frac{\rho _{QCD}(s,\mu )}{s-p^2} \nonumber \\&= \int \limits _{4m^2_Q(\mu )}^{s_0} ds \frac{\rho _{QCD}(s,\mu )}{s-p^2}\,+\int \limits _{s_0}^\infty ds \frac{\rho _{QCD}(s,\mu )}{s-p^2} \, , \end{aligned}$$

(43)

at the QCD side, where the $C_n(p^2,\mu )$ are the Wilson coefficients and the $\langle {\mathcal {O}}_n(\mu )\rangle$ are the vacuum condensates of dimension-$n$. The short-distance contributions at $p^2>\mu ^2$ are included in the coefficients $C_n(p^2,\mu )$, the long-distance contributions at $p^2<\mu ^2$ are absorbed into the vacuum condensates $\langle {\mathcal {O}}_n(\mu )\rangle$. If $\mu \gg \Lambda _\mathrm{QCD}$, the Wilson coefficients $C_n(p^2,\mu )$ depend only on the short-distance dynamics, while the long-distance effects are taken into account by the vacuum condensates $\langle {\mathcal {O}}_n(\mu )\rangle$.

The correlation functions $\Pi (p)$ are scale independent,

$$\begin{aligned} \frac{d}{d\mu }\Pi (p)&= 0, \end{aligned}$$

(44)

which does not mean

$$\begin{aligned} \frac{d}{d\mu }\int \limits _{4m^2_Q(\mu )}^{s_0} ds \frac{\rho _{QCD}(s,\mu )}{s-p^2}\rightarrow 0 \, , \end{aligned}$$

(45)

in the present case due to the following two reasons:

• Perturbative corrections are neglected, the higher-dimensional vacuum condensates are factorized into lower-dimensional ones therefore the energy-scale dependence of the higher-dimensional vacuum condensates is modified.

• Truncations $s_0$ set in, the correlation between the threshold $4m^2_Q(\mu )$ and continuum threshold $s_0$ is unknown, the quark–hadron duality is an assumption.

We perform the Borel transform with respect to the variable $P^2=-p^2$ at the QCD side and obtain the result

$$\begin{aligned} \int \limits _{4m^2_Q(\mu )}^{s_0} ds \frac{\rho _{QCD}(s,\mu )}{s-p^2}&\rightarrow \!\! \int \limits _{4m^2_Q(\mu )}^{s_0}\!\!\!\! ds \frac{\rho _{QCD}(s,\mu )}{T^2}\exp \left( -\frac{s}{T^2}\right) .\nonumber \\ \end{aligned}$$

(46)

The QCD sum rules are characterized by two energy scales $\mu ^2$ and $T^2$. The Borel parameters $T^2$ have to be small enough such that the contributions from the higher resonances and continuum states are damped sufficiently. On the other hand, the Borel parameters $T^2$ must be large enough so that the higher-dimensional vacuum condensates are suppressed sufficiently.

The heavy tetraquark system $Q\bar{Q}q^{\prime }\bar{q}$ could be described by a double-well potential with two light quarks $q^{\prime }\bar{q}$ lying in the two wells, respectively. In the heavy quark limit, the $c$ (and $b$) quark can be taken as a static well potential, which binds the light quark $q^{\prime }$ to form a diquark in the color antitriplet channel or binds the light antiquark $\bar{q}$ to form a meson in the color singlet channel (or a meson-like state in the color octet channel). Then the heavy tetraquark states are characterized by the effective heavy quark masses ${\mathbb {M}}_Q$ (or constituent quark masses) and the virtuality $V=\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ (or bound energy not as robust). The effective masses ${\mathbb {M}}_Q$ have uncertainties, the optimal values in the diquark–antidiquark systems are not necessary the ideal values in the meson-meson systems.

Now the QCD sum rules have three typical energy scales: $\mu ^2$, $T^2$, and $V^2$. It is natural to take the energy scale

$$\begin{aligned} \mu ^2&= V^2={\mathcal {O}}(T^2)\, . \end{aligned}$$

(47)

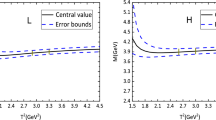
In Figs. 1, 2, and 3, we will plot only the lines for the 0-0 type molecular states for simplicity. In Fig. 1, the masses are plotted with variations of the Borel parameters $T^2$ and energy scales $\mu$ with the threshold parameters $s_0=19.5$ and $124\,\mathrm {GeV}^2$ for the 0-0 type hidden charm and hidden bottom molecular states, respectively. From the figure, we can see that the masses decrease monotonously with increase of the energy scales, just like that of the tetraquark states [56–59]. If the energy-scale formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ with the effective masses ${\mathbb {M}}_c=1.80\,\mathrm {GeV}$ and ${\mathbb {M}}_b=5.13\,\mathrm {GeV}$ is also an acceptable choice in the case of the hadronic molecular states, the energy scales $\mu =1.5$ and $2.7\,\mathrm {GeV}$ for the hidden charm and hidden bottom molecular states, respectively, should reproduce the experimental values of the masses of $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$.

Fig. 1

The masses with variations of the Borel parameters $T^2$ and energy scales $\mu$, where the (I) and (II) denote the 0-0 type hidden charm and hidden bottom molecular states, respectively; the horizontal lines denote the experimental values; the $C=\pm$ denote the charge conjugations

Fig. 2

The pole contributions with variations of the Borel parameters $T^2$ and threshold parameters $s_0$, where the (I) and (II) denote the 0-0 type hidden charm and hidden bottom molecular states, respectively; $A$, $B$, $C$, $D$, $E$, and $F$ denote the threshold parameters $s_0=16.5$, $17.5$, $18.5$, $19.5$, $20.5$, and $21.5\,\mathrm {GeV}^2$, respectively, for the hidden charm molecular states, $s_0=118$, $120$, $122$, $124$, $126$, and $128\,\mathrm {GeV}^2$, respectively, for the hidden bottom molecular states; the $C=\pm$ denote the charge conjugations

Fig. 3

The contributions of different terms in the operator product expansion with variations of the Borel parameters $T^2$, where the (I) and (II) denote the 0-0 type hidden charm and hidden bottom molecular states, respectively; the 0, 3, 4, 5, 6, 7, 8, 10 denote the dimensions of the vacuum condensates; the $C=\pm$ denote the charge conjugations

Table 1 The Borel parameters, continuum threshold parameters, pole contributions, masses, and pole residues of the 0-0 type and 8-8 type molecular states

In calculations, we observe that the effective masses ${\mathbb {M}}_c=1.80\,\mathrm {GeV}$ and ${\mathbb {M}}_b=5.13\,\mathrm {GeV}$ are acceptable values (if the uncertainties of the QCD sum rules are taken into account) but not the optimal values to reproduce the experimental values of the masses of $X(3872)$, $Z_c(3900)$, $Z_c(4020)$, $Z_c(4025)$, $Y(4140)$, $Z_b(10610)$, and $Z_b(10650)$ consistently in the scenario of molecular states [68]. The energy scales $\mu =1.3$ and $2.6\,\mathrm {GeV}$ are the optimal energy scales to reproduce the experimental data $M_{X(3872)}=3.87\,\mathrm {GeV}$, $M_{Z_c(3900)}=3.90\,\mathrm {GeV}$, $M_{Z_b(10610)}=10.61\,\mathrm {GeV}$ (also the experimental values of the masses of $Z_c(4020)$, $Z_c(4025)$, and $Y(4140)$, and $Z_b(10650)$ [68]) approximately. The modified values ${\mathbb {M}}_c=1.84\,\mathrm {GeV}$ and ${\mathbb {M}}_b=5.14\,\mathrm {GeV}$ work for the hadronic molecular states, and they can be used to update the QCD sum rules for the heavy molecular states [69–72].

In Fig. 2, the contributions of the pole terms are plotted with variations of the threshold parameters $s_0$ and Borel parameters $T^2$ at the energy scales $\mu =1.3$ and $2.6\,\mathrm{GeV}$ for the 0-0 type hidden charm and hidden bottom molecular states, respectively. In Fig. 3, the contributions of different terms in the operator product expansion are plotted with variations of the Borel parameters $T^2$ with the parameters $s_0=19.5\,\mathrm{GeV}^2$, $\mu =1.3\,\mathrm{GeV}$, and $s_0=124\,\mathrm{GeV}^2$, $\mu =2.6\,\mathrm{GeV}$ for the 0-0 type hidden charm and hidden bottom molecular states, respectively. From the figures, we can choose the optimal Borel parameters and threshold parameters to satisfy the two criteria of the QCD sum rules. The Borel parameters, continuum threshold parameters and the pole contributions are shown explicitly in Table 1.

We take into account all uncertainties of the input parameters, and we obtain the values of the masses and pole residues of the molecular states, which are shown in Table 1 and Figs. 4, 5.

Fig. 4

The masses of the 0-0 type molecular states with variations of the Borel parameters $T^2$, where the horizontal lines denote the experimental values; the (I) and (II) denote the hidden charm and hidden bottom molecular states, respectively; the $C=\pm$ denote the charge conjugations

Fig. 5

The masses of the 8-8 type molecular states with variations of the Borel parameters $T^2$, where the horizontal lines denote the experimental values; the (I) and (II) denote the hidden charm and hidden bottom molecular states, respectively; the $C=\pm$ denote the charge conjugations

The masses of the 0-0 type molecular states $\bar{u}c\bar{c}d (1^{++})$, $\bar{u}c\bar{c}d (1^{+-})$, and $\bar{u}b\bar{b}d (1^{+-})$ are consistent with that of $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$, respectively, within uncertainties,

$$\begin{aligned} M_{\bar{u}c\bar{c}d,1^{++},(0-0)}&= \left( 3.89^{+0.09}_{-0.09}\right) \,\mathrm{{GeV}} \approx M_{X(3872)}\nonumber \\&= (3871.68\pm 0.17 )\,\mathrm {MeV}\,(\mathrm {exp}) [34]\, , \end{aligned}$$

(48)

$$\begin{aligned} M_{\bar{u}c\bar{c}d,1^{+-},(0-0)}&= \left( 3.89^{+0.09}_{-0.09}\right) \,\mathrm{{GeV}} \approx M_{Z_c(3900)}\nonumber \\&= (3899.0\pm 3.6\pm 4.9)\,\mathrm { MeV}\,(\mathrm {exp})[12] \, , \end{aligned}$$

(49)

$$\begin{aligned} M_{\bar{u}b\bar{b}d,1^{+-},(0-0)}&= \left( 10.61^{+0.10}_{-0.09}\right) \,\mathrm{{GeV}} \approx M_{Z_b(10610)}\nonumber \\&= \left( 10607.2\pm 2.0\right) \,\mathrm { MeV}\,(\mathrm {exp})[6]\, . \end{aligned}$$

(50)

The present predictions favor assigning $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ as the $S$-wave $D^*\bar{D}$, $D^*\bar{D}$ and $B^*\bar{B}$ molecular states, respectively, while our previous work favors assigning $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ as the diquark–antidiquark type tetraquark states [56, 59].

Although the mass is a fundamental parameter in describing a hadron, a hadron cannot be identified unambiguously by the mass alone, more theoretical and experimental works on the productions and decays are still needed to identify $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$. At the present time, it is still an open problem. From Table 1, we can see that the charge conjugation partners have almost degenerate masses, and the 8-8 type molecular states have larger masses than that of the 0-0 type molecular states. The present predictions can be confronted with the experimental data in the future at BESIII, LHCb, and Belle-II.

4 Conclusion

In this article, we take $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ as the molecular states, construct both the color singlet–singlet type and the color octet–octet type currents to interpolate them, and we calculate the vacuum condensates up to dimension-10 in the operator product expansion. Then we study the axial-vector hidden charmed and hidden bottom molecular states with the QCD sum rules, explore the energy-scale dependence in detail for the first time, and use the energy-scale formula $\mu =\sqrt{M^2_{X/Y/Z}-(2{\mathbb {M}}_Q)^2}$ suggested in our previous works with the modified effective masses ${\mathbb {M}}_c=1.84\,\mathrm {GeV}$ and ${\mathbb {M}}_b=5.14\,\mathrm {GeV}$ to determine the energy scales of the QCD spectral densities. The energy-scale formula works well for both the hidden charm (or bottom) molecular states and tetraquark states. In the QCD sum rules for the hidden charm (or bottom) tetraquark states and molecular states, the hadronic masses and pole residues are sensitive to the heavy quark masses $m_Q$, the energy-scale formula has an outstanding advantage in determining the $m_Q$. The numerical results support assigning $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$) as the 0-0 type molecular states with $J^{PC}=1^{++}$, $1^{+-}$, $1^{+-}$, respectively; while there are no candidates for the 8-8 type molecular states. The present predictions can be confronted with the experimental data in the future at BESIII, LHCb, and Belle-II. More theoretical and experimental work on the productions and decays is still needed to distinguish the molecule and tetraquark assignments, as a hadron cannot be identified unambiguously by the mass alone. The pole residues can be taken as basic input parameters to study relevant processes of $X(3872)$, $Z_c(3900)$, and $Z_b(10610)$ with the three-point QCD sum rules.