Real-time correlation functions in the $O(N)$ model from the functional renormalization group

Abstract

In the framework of the functional renormalization group we present a simple truncation scheme for the computation of real-time mesonic $n$-point functions, consistent with the derivative expansion of the effective action. Via analytic continuation on the level of the flow equations we perform calculations of mesonic spectral functions in the scalar $O(N)$ model, which we use as an exploratory example. By investigating the renormalization-scale dependence of the 2-point functions we shed light on the nature of the sigma meson, whose spectral properties are predominantly of dynamical origin.

1 Introduction

Real-time observables in strongly interacting systems often pose major challenges for theoretical calculations. Spectral functions are key to many such observables. They provide information on quasi-particle spectra and collective excitations of the system. The spectral functions of the energy-momentum tensor, moreover, allow one to extract transport coefficients via the Kubo formulas [1–4] and thus to study macroscopic properties of strongly interacting matter.

In this letter we study spectral functions of the elementary sigma and pion correlations in the $O(N)$ model with the functional renormalization group (FRG). FRG methods [5–7] have been well developed over the last 30 years. Although various formulations exist, their underlying physical principles are always the same. The equations of motion are described as functional differential equations of a scale-dependent generating functional and functional derivatives of it.

Here we employ the approach pioneered by Wetterich [7] with the scale-dependent effective average action as the central object, which generalizes the usual effective action (see [8–12] for a general introduction). By integrating the Wetterich equation which describes the evolution of the effective average action with the RG scale $k$, one obtains the full quantum effective action in the limit $k\rightarrow 0$. The evolution equations for the $n$-point functions can be obtained from that of the effective action via functional derivatives.

A typical problem which one encounters in functional approaches is the fact that the flow equations for $n$-point functions involve information on up to $(n+2)$-point functions thereby leading to an infinite tower of coupled evolution equations. Practical applications thus require truncations in order to obtain a closed system of equations to solve. One frequently used truncation scheme is the derivative expansion based on expanding the effective action in terms of derivatives. The leading order in this expansion is the so-called local potential approximation (LPA). Despite their simplicity, derivative expansions in general and the LPA in particular, have been applied successfully to a broad range of physical systems and critical phenomena.

In this letter we present an extension of the derivative expansion to obtain real-time 2-point correlation functions consistent with the underlying truncation for the effective potential. Starting from the flow equation for 2-point functions we employ LPA vertices to obtained a closed system of flow equations involving as the only input the scale-dependent effective potential. A consistent truncation scheme for the calculation of the Euclidean 2-point correlators at finite external momentum is, however, only the first step toward a calculation of real-time quantities such as spectral functions or transport coefficients.

The crucial second step, a common challenge in Euclidean approaches to thermal quantum field theory, is the analytic continuation of the external momentum to Minkowski spacetime. At present, real-time correlation functions are usually either reconstructed from their Euclidean analogs using Padé approximants or by maximum entropy methods. Alternatively, they can be calculated directly in Minkowski spacetime by an analytical continuation at the level of the flow equations [13, 14]. In this respect, our approach is similar to that of Ref. [15] in which more refined truncations in real time were proposed to include effects of the back-coupling of a non-trivial propagator on the effective potential and the wavefunction renormalization. Actual solutions, however, require an Ansatz for the form of the propagator and its singularity structure. Our approach, on the other hand, does not rely on assuming a certain spectral shape, but it ignores back-coupling effects at present.

In the following, we concentrate on the calculation of spectral functions within the $O(N)$ model. The analysis of the $O(N)$ scalar model, which is frequently used as a chiral effective model for QCD $(N=4)$, has a long history. Spectral functions in $O(N)$ models have been calculated, for example, in optimized perturbation theory [16–19] by taking into account the $\sigma \rightarrow \pi + \pi$ process. The critical exponents have been evaluated in [17]. Although quantum fluctuations are included via a resummed loop expansion, the critical exponents remain at their mean-field values. To overcome this limitation a more suitable resummation scheme is required. Such a framework is provided by the FRG, where the application of the derivative expansion leads to very accurate results, e.g., for critical exponents in $O(N)$ models in higher orders of the derivative expansion [8, 20, 21] but to a surprising degree already also in the LPA [22, 23].

Spectral functions have been calculated with the FRG in non-relativistic models using different truncation schemes including the “BMW” approximation [24, 25], vertex expansions or derivative expansions [26–28]. In all these cases, however, the spectral functions were reconstructed from Euclidean 2-point correlators via analytic continuation using Padé approximants. Here we employ a simple LPA for the effective action which we then use to solve analytically continued flow equations for the 2-point functions at real frequency. For simplicity, we restrict ourselves to the zero-temperature case in this work. In principle, it is possible to extend the proposed approximation scheme to finite temperature and finite chemical potential or to include fermions [13, 14].

2 Formulation

2.1 Functional RG

The functional renormalization group provides a powerful non-perturbative tool, especially for the study of critical phenomena. It describes the evolution of a scale-dependent effective average action $\varGamma _k$ from the microscopic bare action, specified at an ultraviolet (UV) scale $k=\varLambda$, to the corresponding full quantum effective action for $k\rightarrow 0$ in terms of a functional differential equation [7],

$$\begin{aligned} \partial _k \varGamma _k = \frac{1}{2}\mathrm{Tr}\left[ \partial _k R_{k}(\varGamma ^{(2)}_k+R_{k})^{-1}\right] , \end{aligned}$$

(1)

where $\varGamma _k^{(n)}$ denotes the $n$th functional derivative of $\varGamma _k$ with respect to the fields, and $R_k$ is a suitable regulator function. The trace is taken over the internal degrees of freedom and momentum space. Figure 1 shows a diagrammatic representation of the flow equation (1). Note that although the flow equation has a one-loop structure, it is an exact equation, involving full (scale- and field-dependent) propagators.

Fig. 1

Diagrammatic representation of the flow equation for the effective action of the $O(N)$ model. Dashed lines represent scale-dependent boson propagators and gray filled circles correspond to regulator insertions $\partial _k R_k$

The precise form of the regulator function $R_{k}$ is not fixed but limited only by certain general requirements [8]. A convenient choice for our purposes is the sharp regulator

$$\begin{aligned} R_{k} = (k^2 - {\mathbf {q}}^2) \theta (k^2 - {\mathbf {q}}^2), \end{aligned}$$

(2)

which is the three-momentum analog of the LPA-optimized regulator [29]. The introduction of the regulator suppresses the propagation of field modes with momenta smaller than the renormalization scale $k$. Integrating the flow equation (1) from the bare classical action at $k=\varLambda$ down to $k=0$ yields the full quantum effective action which includes quantum fluctuations from all momentum modes. Taking $n$ functional derivatives of the flow equation (1) one obtains the flow equations for the $n$-point correlation functions which, in turn, contain up to $(n+2)$-point correlation functions.

Fig. 2

Diagrammatic representation of the flow equation for a mesonic 2-point function in the $O(N)$ model. Dashed lines represent scale-dependent boson propagators and gray filled circles correspond to regulator insertions $\partial _k R_k$. Black filled circles and gray filled squares denote the scale-dependent 3- and 4-point vertex functions

2.2 Flow equation for the effective action

The derivative expansion corresponds to an expansion of the effective action in terms of gradients

$$\begin{aligned} \varGamma _{k}[\phi ]&= \int dx \left\{ U_k(\phi ^2)-c \sigma \right. \nonumber \\&+ \left. \frac{1}{2}Z_{1,k}(\phi ^2) (\partial \phi )^2 + Z_{2,k}(\phi ^2) \; (\partial \phi )^4 + \cdots \right\} ,\nonumber \\ \end{aligned}$$

(3)

where the effective potential $U_k$ and the wavefunction renormalization factors $Z_{i,k}$ are parametrized in terms of the $O(N)$ invariant $\phi ^2 = \phi _i \phi ^i$ and an explicit symmetry breaking is induced by the $c\sigma$ term giving rise to a finite pion mass. To study the $O(N)$ symmetry breaking one decomposes $\varGamma ^{(2)}_k$ for constant background $\phi _i$ into its transverse ($\varGamma _{\pi }$) and longitudinal ($\varGamma _{\sigma }$) components in field space

$$\begin{aligned} \varGamma _{k,ij}^{(2)}(\phi ^2,p)&= \varGamma ^{(2)}_{k,\pi }(\phi ^2,p)\left( \delta _{ij} - \frac{\phi _i \phi _j}{ \phi ^2}\right) \nonumber \\&+ \varGamma ^{(2)}_{k,\sigma }(\phi ^2,p) \frac{\phi _i \phi _j}{ \phi ^2}. \end{aligned}$$

(4)

Inserting the Ansatz (3) into the flow equation (1) and evaluating it for a constant field configuration yields the corresponding flow equation for the effective potential. In the simplest case of the LPA which corresponds to setting $Z_{1,k} = 1$ and $Z_{i,k} = 0$ for $i>1$ one is left with solving the flow equation for the effective potential, which reads

$$\begin{aligned} \frac{\partial U_k}{\partial k} = \frac{1}{2} I^{(1)}_\sigma + (N-1) \frac{1}{2}I^{(1)}_\pi . \end{aligned}$$

(5)

Here we have defined the loop functions $I^{(n)}_{i}$ as

$$\begin{aligned} I^{(n)}_{i}\equiv \mathrm{Tr}_q\left[ \partial _k R_k(q) \left( \frac{1}{\varGamma _{k,i}^{(2)}+R_k}\right) ^n_{q} \right] , \end{aligned}$$

(6)

where the trace runs over the loop momentum $q$. For the regulator choice in (2), $I_i^{(1)}$ and $I_i^{(2)}$ are given by

$$\begin{aligned} I^{(1)}_{{i}} = \frac{k^4}{3 \pi ^2} \frac{1}{2 E_i}\quad \text {and}\quad I^{(2)}_{k,i} =\frac{k^4}{3 \pi ^2} \frac{1}{4E_i^3}, \end{aligned}$$

(7)

where $E_\pi =\sqrt{k^2+2 U'}$, $E_\sigma =\sqrt{k^2+2 U'+4 U''\phi ^2}$ and $U'= \frac{\partial U}{\partial (\phi ^2)}$. The curvatures $2U'$ and $2U' + 4U''$ at the minimum of the effective potential yield the screening masses squared of pion ($m^\mathrm {scr}_{\sigma }{}^2$) and sigma meson ($m^\mathrm {scr}_{\pi }{}^2$), respectively. They are defined as the spacelike limits $p\rightarrow 0$ of the pion and sigma 2-point functions, i.e., the inverse of the corresponding susceptibilities.

2.3 Flow equation for the 2-point functions

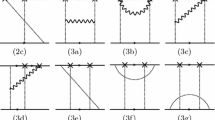
Applying two functional derivatives to the flow equation in (1), we obtain the exact flow equations for 2-point correlation functions. Their diagrammatic forms for the pion and the sigma in the $O(N)$ model are shown in Fig. 2. These flow equations contain scale-dependent 3- and 4-point functions. In order to close the infinite tower of functional equations for the $n$-point functions, truncations are required. A possible scheme has been proposed in Refs. [24, 25] (BMW). The idea is that, because of the insertion of the cutoff function, the external momentum dependence of the scale-dependent 3- and 4-point functions has a weaker effect than their dependence on the momenta of internal lines containing the loop momentum. One thus expands the 3- and 4-point functions in their external momenta in this scheme.

Here we choose a simpler truncation which is a natural extension of the derivative expansion. For this we replace the 3- and 4-point functions by their corresponding scale-dependent but, at the leading order derivative expansion, momentum-independent forms as obtained from the flow equation for the effective potential, i.e.,

$$\begin{aligned} \varGamma ^{(3)}_{ijm}&\rightarrow \frac{\partial ^3 \varGamma _{k}}{\partial \phi ^m \partial \phi ^j \partial \phi ^i} \nonumber \\ \varGamma ^{(4)}_{ijmn}&\rightarrow \frac{\partial ^4 \varGamma _{k}}{\partial \phi ^n \partial \phi ^m \partial \phi ^j \partial \phi ^i}. \end{aligned}$$

(8)

We then obtain the flow equations for the pion/sigma 2-point functions as follows:

$$\begin{aligned} \partial _k \varGamma _{k,\pi }^{(2)}&= (J_{\sigma \pi }+J_{\pi \sigma })(4U'' \phi )^2\nonumber \\&-\frac{1}{2} I^{(2)}_{\pi }4U'' (N+1) -\frac{1}{2} I^{(2)}_{\sigma }(4U'' + 8U'''\phi ^2) \nonumber \\ \partial _k \varGamma _{k,\sigma }^{(2)}&= J_{\sigma \sigma } (12 U''\phi +8U'''\phi ^3)^2 + J_{\pi \pi }(4U''\phi )^2(N-1) \nonumber \\&-\frac{1}{2} I^{(2)}_{\sigma } (12U''+48U'''\phi ^2 +16U''''\phi ^4) \nonumber \\&-\frac{1}{2} I^{(2)}_{\pi }(N-1) (4U''+8U'''\phi ^2), \end{aligned}$$

(9)

with loop functions $J_{ij}$ defined as

$$\begin{aligned} J(p)_{ij}\!\equiv \! \mathrm{Tr}_q \left[ \!\!\partial _k R_k(q) \left( \frac{1}{\varGamma _{k,i}^{(2)}\!+\!R_k}\right) _{p+q}\left( \frac{1}{\varGamma _{k,j}^{(2)}\!+\!R_k} \right) ^2_{q}\right] ,\nonumber \\ \end{aligned}$$

(10)

where the trace runs over the momentum $q$. Note that only the symmetric components of $J$ are needed in (9). In LPA, for vanishing spatial external momentum ${\mathbf {p}}$, and with the regulator in (2), these are obtained as

$$\begin{aligned}&J(p_0)_{ij} + J(p_0)_{ji} \nonumber \\&\quad =\frac{k^4}{3\pi ^2} \frac{(E_i+E_j)^3(E_i^2+E_iE_j+E_j^2) +(E_i^3+E_j^3) p_0^2}{4 E_i^3E_j^3\left( p_0^2+(E_i+E_j)^2\right) ^2}.\nonumber \\ \end{aligned}$$

(11)

In Fig. 3, we show diagrammatically the contributions to the pion/sigma 2-point functions. Although they look like 1-loop contributions, the internal lines represent full scale-dependent propagators which we evaluate for the constant field value at the minimum of the effective potential. These propagators correspond to resummations of perturbative diagrams. For the pion 2-point function the process $\pi \rightarrow \pi + \sigma$ is included and for the sigma 2-point function the processes $\sigma \rightarrow \sigma + \sigma$ and $\sigma \rightarrow \pi + \pi$. Other contributions, such as $\sigma \rightarrow \sigma + \pi$, would break the residual $O(N-1)$ symmetry of the broken phase and are excluded.

Fig. 3

Diagrammatic representation of the contributions to the flow of the 2-point functions. Full gray circles correspond to insertions of $\partial _k R_k$. Black circles and gray squares indicate the scale-dependent 3- and 4- point vertex functions, here obtained from (8)

In the following we discuss the solutions to (9) at zero temperature. Note that then, no term proportional to $1/[p_0^2+(E_{\sigma }-E_{\pi })^2]$ arises because Landau damping, i.e., the absorption of an on-shell particle from the heat bath, does not occur.

We reemphasize that the correlation functions at vanishing external momentum in our truncation are consistent with the effective action since the flow equations satisfy

$$\begin{aligned} \partial _k\varGamma ^{(2)}_{k,\pi }(p=0)&= 2\partial _k U_k',\end{aligned}$$

(12)

$$\begin{aligned} \partial _k\varGamma ^{(2)}_{k,\sigma }(p=0)&= 2 \partial _k U_k'+4 \partial _k U_k'' \phi ^2. \end{aligned}$$

(13)

This means that the equivalence between the static screening masses from the spacelike $p\rightarrow 0$ limit of the 2-point functions and from the curvatures of the effective potential at its minimum is manifest in our truncation. Moreover, note that (12) automatically ensures the existence of a dynamical Nambu–Goldstone boson in the chiral limit. Thus our truncation scheme is also “symmetry conserving.”

We solve the flow equation for the real and imaginary parts of the retarded 2-point correlators. These are obtained from (9) via the analytic continuation

$$\begin{aligned} \varGamma ^{(2) R}_{k,j} (\omega ) \!\equiv \! \varGamma ^{(2) R}_{k,j}(p_0\!=\!-i(\omega +i \varepsilon ),{\mathbf {p}}\!=\!0), \quad \text {for }j\!=\!\pi ,\sigma \nonumber \\ \end{aligned}$$

(14)

which is taken before the evaluation of the flow equations.

The spectral functions are proportional to the imaginary parts of the retarded propagators or more explicitly, for $\omega >0$,

$$\begin{aligned} \rho _i(\omega ) = - \tfrac{1}{\pi } \tfrac{\mathrm{Im } \, \varGamma ^{(2) R}_{i}(\omega )}{\left( \mathrm{Re}\, \varGamma ^{(2) R}_{i}(\omega )\right) ^2 +\left( \mathrm{Im}\, \varGamma ^{(2) R}_{i}(\omega )\right) ^2 }, \quad i=\pi ,\sigma , \end{aligned}$$

(15)

which are understood to be evaluated in the limit $\varepsilon \rightarrow 0^+$. In the numerical evaluations we have to keep a small but finite positive imaginary part in the external energy, however.

3 Numerical results

3.1 Numerical method

In order to solve the flow equations numerically, we employ the Taylor-expansion method. We expand the flow equations (5) and (9) by expanding $U_k$ and the real or imaginary part of $\varGamma ^{R}_{k,i}$ ($i=\sigma ,\pi$) around the scale-dependent minimum:

$$\begin{aligned} U_k&= \sum _{n=0}^{K} a_{n,k} (\phi ^2 - \phi _{k}^2)^n,\nonumber \\ \mathrm{Re}\,\varGamma ^{(2) R}_{k,i}(\omega )&= \sum _{n=0}^{L} b^i_{n,k}(\omega ) (\phi ^2 - \phi _{k}^2)^n, \nonumber \\ \mathrm{Im}\,\varGamma ^{(2) R}_{k,i}(\omega )&= \sum _{n=0}^{L} c^i_{n,k}(\omega ) (\phi ^2 - \phi _{k}^2)^n. \end{aligned}$$

(16)

The flow equations for the effective potential and the 2-point functions then translate into flow equations for the expansion coefficients $a_{n,k}$, $\phi _{k}^2$, $b^i_{n,k}(\omega )$ and $c^i_{n,k}(\omega )$ in the usual way. Choosing $L=K-1$ ensures that the consistency condition (12) between the pion 2-point function and the effective potential is maintained exactly also in a finite Taylor expansion for the numerical implementation. The flow equation for the sigma correlator involves up to four derivatives and thus requires $K\ge 4$. We will employ $K=5$ and $L=4$ in the following.

The numerical results presented in this article were obtained using the Taylor-expansion method as described above, which by construction does not take into account the full field-dependence of the effective potential. Hence we checked our results against the so-called grid method [22], which involves discretizing the effective potential on a set of grid points in field space and solving the corresponding flow equations at fixed values in field space, from which the full field-dependent effective potential can be reconstructed. The scale-dependent derivatives of the effective potential, evaluated at its minimum, can then be used as input for the corresponding flow equations (9) for the 2-point functions. The disadvantage of the grid method is that one incurs considerably larger numerical costs for reaching low IR cutoff values than with the Taylor expansions. Fortunately, we were able to verify that the results from the grid method generally reproduce the Taylor results for $k \ge 0.05\varLambda$ very well.

The parameter sets used here for the $O(4)$ model with UV potential of the form $U_{k=\varLambda }=a\phi ^2+b\phi ^4$ are listed in Table 1.

3.2 Pion and sigma meson spectral functions

In Figs. 4 and 5 we show the real and imaginary parts of the retarded 2-point functions $\varGamma ^{R}_\pi$ and $\varGamma ^{R}_\sigma$, respectively. These were obtained by solving the flow equations (9), separated into real and imaginary parts for a small but finite imaginary part $\epsilon \sim 0.1$ MeV in the external frequency $\omega +i\epsilon$ as a function its real part $\omega$. For the pion the imaginary part in Fig. 4 remains negligible, whereas the real part behaves as demonstrated in earlier investigations [13, 14]. The zero of the real part, which corresponds to the pion pole mass, is found at 135.1 MeV as compared to a screening mass of 137.2 MeV. This once more reflects the difference between screening and pole masses which is a small effect of only a few percent, however, in the purely bosonic model [13, 14]. At finite density, these values should be compared to the pion mass defined via the onset of pion condensation when coupling the model to an isospin chemical potential [14, 30]. The pole mass from our present truncation for the 2-point function is considerably closer to the exact mass from the Bose–Einstein condensation transition at zero temperature, in particular, when fermions are included as first observed in the Quark–Meson–Diquark model for two-color QCD [13].

Fig. 4

Real and imaginary parts of the retarded pion propagator as a function of the timelike external momentum $\omega$

Fig. 5

Real and imaginary parts of the retarded sigma propagator as a function of the timelike external momentum $\omega$ at the IR scale and at an intermediate scale

For the sigma meson, shown in Fig. 5, the imaginary part remains negligible but only up to the 2-pion threshold at $\omega \approx 2 m_\pi \approx 275$ MeV and tends to finite negative values thereafter. The two-pion emission threshold also shows up as a kink in the real part. The zero of the real part is found at 350.6 MeV and we will argue that this value might be a good estimate for the sigma mass even in cases where no clear maximum in the corresponding spectral function is visible. For comparison, the value of the sigma screening mass extracted from the curvature of the effective potential results to be 425.0 MeV for the parameter set with nearly physical pion mass in Table 1.

Table 1 Parameter sets for a UV cutoff $\varLambda =500$ MeV corresponding to two different pion masses. The physical parameters, $f_{\pi }$ and the meson masses, are given in MeV

Figure 6 displays the pion and sigma spectral functions as calculated from (15). The pion spectral function shows a sharp peak at 135 MeV to be identified with the pion mass. The sigma spectral function exhibits the 2-pion threshold as a characteristic increase in the spectral density followed by a broad maximum at about 312 MeV above this threshold. Considering a case in which the imaginary part ${\text {Im}}\,\varGamma ^{(2)}$ were independent of the (timelike) external momentum so that the only momentum-dependence was in the real part ${\text {Re}}\,\varGamma ^{(2)}$, it is obvious from (15) that the maximum of the spectral function would then occur at the zero of the real part with a width as determined by the constant imaginary part. This is the case for the pion 2-point function where the peak in the spectral function and zero of the 2-point function coincide as they must since the imaginary part practically vanishes. The same coincidence between the sigma mass defined via the maximum of the spectral function and the zero of the corresponding real part is of course no longer valid for a momentum-dependent imaginary part as obtained here, although the zero of the real part may still provide an estimate for the sigma mass. For the current parameter set the zero of the real part, however, overestimates the sigma mass defined via the maximum of the spectral function by 14 %. This illustrates the difficulties of a mass assignment for a broad resonance with a strongly momentum-dependent width. In this case the imaginary part does not vanish at the zero of the real part. Hence no zero is found in the complex plane of the physical sheet, consistent with the Källen–Lehmann representation, which allows only poles on the real axis. One expects a zero on the unphysical sheet, however, as illustrated in [16, 31].

Fig. 6

Spectral functions for the pion $(\rho _\pi \!)$ and the sigma meson $(\rho _\sigma \!)$

Except for a significantly lower sigma mass in our calculations, the zero-temperature spectral functions are in qualitative agreement with perturbation theory results [16–19]. All these calculations show a sharp peak in the pion spectral function which determines the pion mass, and a resonance peak beyond the two-pion threshold in the sigma spectral function. This agreement is reassuring since perturbation theory around the mean-field vacuum was found to work well outside the critical region. For comparison, we have also performed corresponding perturbative calculations by integrating the flow equations for the 2-point functions with constant values for renormalized interactions and masses. While the qualitative features discussed above are indeed all present already in this simple one-loop approximation, the quantitative differences are quite considerable, however. In particular, we generally observe that the difference between pole and screening mass in the pion propagator, which is on the few percent level in the fully non-perturbative FRG solution as described above, increases considerably. With deviations on the order of around 100 % between the two, with pion pole masses typically almost twice as large as the input screening masses, the one-loop calculations therefore yield quantitatively rather inconsistent results for all input parameters we have considered.

Fig. 7

Comparison of pion $(\rho _\pi \!)$ and sigma meson $(\rho _\sigma \!)$ spectral functions for parameter sets corresponding to two different pion masses

As a consistency check we have also calculated the pion and sigma spectral functions closer to the chiral limit using the second parameter set in Table 1 corresponding to a pion pole mass of 16.0 MeV. The comparison with the physical pion mass is shown Fig. 7. When approaching the chiral limit, one expects the spectral weight of the pion pole in its correlator to increase more and more as this pole moves closer to the $\omega =0$ axis where it eventually accumulates the full spectral weight in the chiral limit. Consequently, the spectral sum rule then implies that all other contributions to the spectral function should decrease with decreasing pion mass. Both these trends are seen in Fig. 7 where we extended the frequency range of Fig. 6 to include the $\sigma -\pi$ threshold in the pion spectral function. To explicitly verify the non-renormalization of the pion field in the chiral limit requires a more careful analysis, however, probably best done with polar coordinates in field space to correctly disentangle the Goldstone bosons from the radial mode [32].

Fig. 8

Zeros of the real part of the sigma 2-point function, the sigma screening mass ($\sqrt{2U' + 4 \phi ^2 U''}$) and the 2-pion threshold ($2\sqrt{k^2+2U'}$) as a function of the RG scale $k$

3.3 Spectral functions at intermediate scales

As described in the previous section, we find a resonance sigma at $k = 0$. It is illustrative to also consider the spectral functions at intermediate scales and thus their evolution with the RG scale $k$. In Fig. 8, we show the scale dependence of the zeros of the real part of the sigma’s 2-point function together with its screening mass, defined via $\sqrt{2U' + 4\phi ^2 U''}$, as well as the 2-pion threshold at $2\sqrt{k^2+2U'}$.

During the $k$-evolution two distinct zeros occur at intermediate scales. This is illustrated in Fig. 5 where we have also included the real and imaginary parts of $\varGamma ^{(2)}_{\sigma \sigma }$ at such a scale (dashed lines). The first zero in the real part (dashed-blue line) represents the pole corresponding to a renormalized sigma field. At the ultraviolet scale, the correlator $\varGamma ^{(2)}_\sigma$ agrees with the classical one and its unique zero thus coincides with the screening mass of the bare sigma field. This zero gets renormalized by quantum fluctuations and starts to deviate from the sigma’s screening mass at intermediate scales. It completely disappears at $\log (k/\varLambda ) \sim -2.2$ when it reaches the 2-pion threshold. It turns out, however, that before this happens, a second zero emerges at larger $\omega$ (solid red line in Fig. 8). This zero is dynamically generated via the $\sigma \rightarrow \pi + \pi$ process, and it is therefore not present at the ultraviolet cutoff scale yet. It arises above the scale-dependent $\sigma \rightarrow \pi + \pi$ threshold at $\omega \sim 2 E_{\pi }$. After decreasing alongside this threshold with the RG scale for a while, it approaches its constant infrared value before the 2-pion threshold eventually does as well. Thus we find that, while the original zero disappears at some scale, a second one is generated and survives corresponding to the zero of the real part at the IR scale as shown in Fig. 5 (solid-blue line).

Figure 9 displays the imaginary part of the sigma correlator, evaluated at the first zero (dashed green line), second zero (solid red line) and the curvature mass (dotted blue line), respectively. At large scales ($k \sim \varLambda$), both the first zero and the screening mass are below the scale-dependent 2-pion threshold and the corresponding imaginary parts vanish. The finite imaginary part in the numerical calculation is related to the finite imaginary external momentum employed to calculate the spectral function; see (14). Below $\log (k/\varLambda ) \sim -1$, the screening mass crosses the threshold and the corresponding imaginary part of the propagator becomes finite. This behavior should be compared to the scale-dependence of the imaginary part in [15], which corresponds in some sense to an expansion of the 2-point function around the screening mass, albeit in a more refined truncation scheme. The second zero, which corresponds to the zero in the real part that survives until $k=0$, arises above the threshold and hence the imaginary part assumes a finite value. It decreases with $k$ and becomes constant below $\log (k/\varLambda ) \sim -2$.

Fig. 9

Imaginary part of the retarded sigma propagator evaluated at the scale-dependent first zero (dashed green line), second zero (solid red line) and sigma screening mass (dotted blue line)

These observations at intermediate scales indicate that the final zero in the real part of the sigma 2-point function does not emerge from the original single-particle contribution of the sigma at the cutoff scale by renormalization effects, but that it is predominantly due to the $\sigma \rightarrow \pi + \pi$ process. This is in contrast to the pion 2-point function whose single-particle contribution does flow continuously from the ultraviolet to the infrared and thus corresponds to the renormalized original pion mass. Such considerations question the reliability of truncation schemes based on an expansion around a single scale-dependent pole [15]. It seems that the inclusion of the full external momentum dependence of the sigma 2-point function or at least an expansion around a more complicated singularity structure is required.

In order to contrast these conclusions for the sigma with the corresponding results for the pion correlator, we show in Fig. 10 the analog of Fig. 8, the zeros of the real part of the pion 2-point function. As before, we find two such zeros at intermediate scales, the first one (dashed green line) corresponding to the renormalized single-particle contribution from the pion screening mass at the UV scale, and the second (solid red line) corresponding to a dynamically generated pion via the $\pi \rightarrow \pi + \sigma$ process. In this case the zero at $k=0$ is connected to the first zero, however, whereas the second zero vanishes around $\log (k/\varLambda ) \sim -1.9$. This underlines the fact that the zero in the pion 2-point function originates from the ultraviolet pion mass by finite renormalization.

Fig. 10

Zeros of the real part of the pion 2-point function and the pion screening mass ($\sqrt{2U'}$) as a function of the RG scale $k$. The second zero was rescaled by a factor of $1/3$ to allow a comparison of all three quantities in a single figure

4 Summary and conclusions

In the present work we have extended the truncation scheme of Refs. [13, 14] for the functional renormalization group (FRG) equations of 2-point functions. This scheme is consistent with the truncation for the effective potential and therefore “symmetry conserving” by construction. In contrast to earlier approaches in the literature, we have employed an analytic continuation on the level of the flow equations which allows for a direct computation of retarded 2-point functions at real frequencies. The numerical solutions of the corresponding flow equations yield realistic spectral functions of collective excitations, as we have demonstrated for the pion and the sigma meson in the $O(4)$ model. Their shape was found to be in good qualitative agreement with general expectations and previous studies.

To gain further insight into the origin of the pion and the sigma meson, we have evaluated the sigma and pion correlators at intermediate scales $k$. It turns out that the pole in the pion propagator flows continuously from the initial screening mass at the ultraviolet cutoff to the physical single-particle pole for $k\rightarrow 0$ by the renormalization effects. Since there is no renormalization of the pion in the chiral limit this ensures the existence of a zero-mode as required by Goldstone’s theorem. In stark contrast, the sigma pole at the infrared scale originates from a dynamical process. We have found two distinct trajectories in the singularity structure of the propagator at intermediate scales; one corresponding to the renormalized initial mass and the other to a dynamically generated complex pole on the unphysical sheet via the $\sigma \rightarrow \pi + \pi$ coupling process. In particular, the sigma pole at $k=0$ belongs to the branch which is dynamically generated. The other branch, connected to the bare sigma mass, disappears at some intermediate scale.

We stress that it is possible to extend our approximation scheme to a thermal medium, and to include fermions. We are particularly interested in extending the framework to finite temperature and to investigate the medium-modified spectral functions. One should be able to observe the asymptotic restoration of chiral symmetry also directly in the spectral functions. In the region around the phase boundary one might expect to observe qualitative differences between the FRG and results based on perturbation theory.

Appendix: Breaking of Lorentz invariance

In this appendix we discuss the impact of the violation of Euclidean O(4) resp. Lorentz invariance by the employed three-dimensional regulator function in (2). On the one hand such regulator functions are particularly convenient as they do not introduce additional poles in the complex $p_0$-plane at finite RG scales $k$, and hence allow for a straightforward analytic continuation. On the other hand they have the slight disadvantage of breaking the underlying spacetime symmetries. Perhaps more severely, however, they also allow arbitrarily large momentum transfers in the frequency direction which can potentially be problematic in combination with the derivative expansion. Therefore, our present work should certainly be supplemented by computations using 4d-regulator functions in the future. For now we can assess the systematic errors of our approach by including finite spatial external momentum components in our flow equations for the 2-point functions. As an additional technical complication, the spatial loop-momentum integrations can then no-longer be performed analytically but have to be evaluated also numerically.

For Euclidean external 4-momenta, the O(4)-breaking effects induced by the three-dimensional regulator in the Euclidean 2-point functions are truly negligible. We have compared the relative differences in their integrated flows for spatial external momenta between zero and $|{\mathbf {p}}|=500$ MeV and found that the Euclidean 2-point functions agree with each other within better than 1 % when plotted over the invariant $\sqrt{p_0^2+{\mathbf {p}}^2}$ up to 300 MeV.

For timelike external momenta the effect is somewhat more pronounced. In Fig. 11 we compare the spectral function of the pion as obtained for different fixed values of the spatial external momentum but now plotted as a function of the invariant $\sqrt{\omega ^2-{\mathbf {p}}^2}$. Deviations of similar size are observed for the sigma spectral function. Except in the very small momentum region where these deviations are enhanced by the finiteness of our small residual imaginary part $\epsilon$ in the frequency components (for the retarded boundary conditions) the results are nevertheless in reasonable agreement with the required Lorentz symmetry at vanishing temperature. The general shape and, most importantly, the peak position at the pion mass remain unchanged and are hence rather robust results of our approach.

Fig. 11

Pion spectral function for Minkowski external momenta $\omega$ and finite spatial momenta $p=0,50,\ldots ,250$ MeV as a function of $\sqrt{\omega ^2-{\mathbf {p}}^2}$ ($\varepsilon =1$ MeV)