1 Introduction

Cosmological inflation is clearly the most studied and popular scenario that can provide an answer to some of the shortcomings that plague the hot big bang model, while it predicts a spectrum of adiabatic fluctuations that can fit the cosmic microwave background (CMB) temperature anisotropies measurements [1]. Despite its success, one must, however, keep in mind that the inflationary scenario faces some problems, like the onset of inflation [2–4] and the fine tuning of the parameters in the inflationary potential so that the inflationary predictions satisfy the data [5–8]. Moreover, despite the more than three decades of work on the subject, inflation still remains a paradigm in search of a model [9]. If one accepts the validity of Grand Unified Theories (GUTs) and the standard thermal history of the universe, then one finds that the universe started at a symmetric phase with high temperature and then as the universe expanded and the temperature dropped, it underwent a series of Spontaneous Broken Symmetries (SSBs), followed by phase transitions (PTs), which could have left behind topological defects, as remnants of a previous more symmetric phase. Combining GUTs with Supersymmetry (SUSY), one can consider hybrid inflationary models, which may be of the type with the F-term (often plagued by the \(\eta \)-problem, where contributions to the slow-roll parameters of the order of 1, due to Planck mass suppressed corrections to the inflaton potential, may impede a sufficiently long slow-roll period) or with the D-term type (leading always to cosmic string formation, due to the breaking of an extra U(1) symmetry)Footnote 1. Given the plethora of precise data, arriving either from astrophysical (in particular, the CMB), or from particle physics (in particular, the large Hadron Collider (LHC)) experiments, one can examine the validity of the various inflationary models and constrain their free parameters. Moreover, one can also study whether such models can arise naturally within the framework in which they have been proposed. Following the latter approach we will study whether, within minimal supersymmetric SO(10), there is a singlet field that could play the rôle of the inflaton and thus realise an F-term hybrid supersymmetric inflationary model [9].

In the first part of our study, we show that none of the (existing) scalar fields can satisfy the conditions necessary in order to play the rôle of the inflaton. We thus introduce, in the second part of our analysis, an extra SO(10)-singlet superfield and write down the most general Higgs superpotential. We may thus propose a model of F-term inflation embedded in SO(10) that can be in agreement with all current particle physics constraints. Certainly F-term inflation can be realised within SO(10), but the necessity to introduce an extra singlet renders SO(10) less appealing as a gauge group describing the early evolution of our universe. We study the realisation of inflation within SO(10), because it is a well-studied gauge group in the context of hybrid inflation.

2 Spontaneous symmetry breaking schemes within SO(10)

The framework we will perform our analysis in is specified as follows:

  • F-term hybrid inflation with superpotential [10],

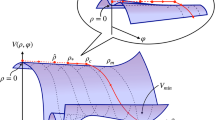
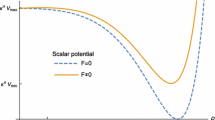
    $$\begin{aligned} W^\mathrm{F}=\kappa S (\Psi \bar{\Psi }-M^2), \end{aligned}$$
    (1)

    where \(S\) is a GUT singlet, \(\bar{\Psi }\) and \(\Psi \) are GUT Higgs fields in complex conjugate representations which lower the rank of the group by one unit when acquiring non-zero vacuum expectation values (VEVs), and \(\kappa \) and \(M\) are two constants (\(M\) has dimensions of mass) which can both be taken positive with field redefinitions. The superpotential in Eq. (1) is the most general superpotential consistent with an R-symmetry under which \(W^\mathrm{F}\rightarrow \hbox {e}^{i\beta }W^\mathrm{F}, \bar{\Psi }\rightarrow \hbox {e}^{-i\beta }\bar{\Psi }, \Psi \rightarrow \hbox {e}^{i\beta }\Psi \) and \(S\rightarrow \hbox {e}^{i\beta } S\). The scalar potential has a valley of local minima for \(S>S_\mathrm{crit}=M, \bar{\Psi }=\Psi \), and one global supersymmetric minimum at \(S=0, \bar{\Psi }=\Psi =M\). Imposing initial conditions such that \(S\gg S_\mathrm{crit}\), the fields quickly settle down the valley of local minima; the potential becomes \(V=\kappa ^2 M^4\ne 0\), supersymmetry is broken and inflation can take place. One-loop corrections to the effective scalar potential introduce a tilt and assist the scalar field \(S\) to slowly roll down the valley of minima. When \(S\) reaches a value below \(S_\mathrm{crit}\), inflation stops by a waterfall regime and the fields settle down to the global minimum of the potential and supersymmetry gets restored.

  • A series of SSBs from SO(10) down to the Standard Model (SM) times Z\(_2\) that does not generate harmful topological defects, like monopoles and domain walls, at the end of inflation. The discrete symmetry Z\(_2\) must remain unbroken down to low energies, to ensure proton stability. Following the detailed study presented in Ref. [11], the SSB cascade should take one of the following paths:

    $$\begin{aligned}&\mathrm{SO}(10)\rightarrow \dots \rightarrow \mathrm{G}_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\rightarrow \mathrm{G}_\mathrm{SM}\times Z_2\nonumber \\&\quad \rightarrow \mathrm{SU}(3)_\mathrm{C} \times \mathrm{U}(1)_\mathrm{Q} \times Z_2, \end{aligned}$$
    (2)
    $$\begin{aligned}&\mathrm{SO}(10)\rightarrow \dots \rightarrow \mathrm{G}_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\rightarrow \mathrm{G}_\mathrm{SM}\times Z_2\nonumber \\&\quad \rightarrow \mathrm{SU}(3)_\mathrm{C} \times \mathrm{U}(1)_\mathrm{Q} \times Z_2, \end{aligned}$$
    (3)

    where the (compact) notation \(\mathrm{G}_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\) stands for the \(\mathrm{SU(3)}_\mathrm{C}\times \mathrm{SU(2)}_\mathrm{L}\times \mathrm{SU(2)}_\mathrm{R}\times \mathrm{U(1)}_\mathrm{B}\hbox {-}\mathrm{L}\), similarly \(\mathrm{G}_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\) stands for \(\mathrm{SU(3)}_\mathrm{C}\times \mathrm{SU(2)}_\mathrm{L}\times \mathrm{U(1)}_\mathrm{R} \times \mathrm{U(1)}_\mathrm{B}\hbox {-}\mathrm{L}\), and \(Z_2\) is the R-parity.

  • Conservation of R-parity at low energies to accommodate proton lifetime stability. This requires the use of only ‘safe’ Higgs representations [12]; thus one can use \(\mathbf {10, 45, 54, 120, 126, 210}\) but not \(\mathbf {16, 144, 560}\).

  • Only renormalisable contributions to the superpotential.

  • Type I or II see-saw mechanism. This requires a \(\mathbf {\overline{126}}_\mathrm{H}\) to participate to the Yukawa couplings to fermions and appropriate Higgs couplings [13]. The type II may be more natural in the context of SO(10). The above assumptions are compatible with the framework of Ref. [11], where the formation of cosmic strings were found to be generic for a large number of SUSY GUTs. To accommodate the CMB measurements one will then have to either fine tune the parameters [5–8], or to complicate the models and render the strings unstable [14]. Note that the GUT singlet \(S\) in Eq. (1) needs not be a singlet of SO(10): in fact, inflation can be triggered at any stage in the SSB cascade that finally leads to the SM. In the spirit of a minimal GUT SO(10), we will not add any SO(10) singlet, but we will rather look for the possibility that F-term hybrid inflation is triggered during the symmetry breaking cascade initiated by a minimal GUT Higgs field content.

3 Inflation purely within minimal SO(10)

Let us consider the following two well-studied classes of SO(10) models: the first one is based on the Higgs content \(\mathbf {210, 126, \overline{126}, 10}\) [15]; the second one focuses on realising a doublet-triplet splitting and its Higgs content is \(\mathbf {54, 45, 45', 16, \overline{16}, 10, 10'}\) [16], sometimes extended by the introduction of singlets [17].

In the vein of the first class, it has been noticed that its minimal Higgs content is not fully able to account for the observed masses and mixings of the fermions when the neutrino see-saw mechanism is implemented [18]. To cure this problem, it has been proposed [19] to enlarge the model with a \(\mathbf {120}\). In what follows, we will adopt this context to perform our study, following the principle of minimal number of Higgs fields. An example of inflation embedded in the second class can be found in [20].

3.1 Higgs content and scalar superpotential

The Higgs sector of the Lagrangian is based on the minimal model (see, e.g., Refs. [15, 18, 21]) and contains the following superfields:

  • \(\Phi \) in the representation \(\mathbf {210}\). In tensor notation, it is written as a fourth rank symmetric tensor \(\Phi _{ijkl}\).

  • \(\Sigma \) and \(\bar{\Sigma }\) in the representations \(\mathbf {126}\) and \(\mathbf {\overline{126}}\), respectively. In tensor notation, they are written as an antisymmetric fifth rank tensor \(\Sigma _{ijklm}\).

  • \(H\) in the representation \(\mathbf {10}\). In tensor notation, it is written as a 10-dimensional vector \(H_i\).

  • \(\Omega \) in the representation \(\mathbf {120}\). In tensor notation, it is written as a third rank antisymmetric tensor \(\Omega _{ijk}\).

Note that all indices in the tensor notation are SO(10) indices and run from 1 to 10. We will first examine whether inflation can be fully embedded within this (minimal) field content, without introducing any additional superfields.

Imposing that the requirement that the superpotential is an SO(10) invariant with these superfields, the most general Higgs superpotential can be written as

$$\begin{aligned} \tilde{W}_\mathrm{H}&= m\, \Phi ^2+\lambda \,\Phi ^3 + m_H\, H^2 +m_\Sigma \, \Sigma \bar{\Sigma } +\eta \, \Phi \Sigma \bar{\Sigma }\nonumber \\&+\Phi H (\alpha \, \Sigma +\bar{\alpha }\, \bar{\Sigma }) + m_\Omega \, \Omega ^2 +\beta \, H \Phi \Omega \nonumber \\&+\gamma \, \Omega ^2 \Phi +\Omega \Phi (\zeta \, \Sigma +\bar{\zeta }\, \bar{\Sigma })~. \end{aligned}$$
(4)

In the above expression, it should be understood that \(\Phi ^2\) means \(\mathrm{Tr}\, \Phi ^2=\Phi _{ijkl}\Phi _{ijkl}\), where a summation is implicit on any repeated indices Footnote 2. The first line was obtained in Ref. [15]. The second one adds all the terms that the new 120 Higgs allows [18]; this contribution is relevant only for the precise fit of the SM fermion masses and will be omitted in the following. Note that we have omitted contributions from the vector field \(H\), since it corresponds to the MSSM sector.

One can easily notice that no term of the form of the second contribution to Eq. (1) can be constructed with the current field content since \(S\) would have to be a singlet of SO(10) for the term \(S M^2\) to be SO(10) invariant. However, as shown in Ref. [11], F-term inflation should not occur during the first stage of SO(10) breaking, but at a later stage during the SSB cascade, in order to solve the monopole problem. Thus, we shall look for the F-term superpotential not in SO(10) notation but in \(\mathrm{G}_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\). Moreover, F-term inflation should involve SM singlet components of the superfields of the theory since their value at the end of inflation will not necessarily vanish. Here we are not limiting ourselves to the SSB cascade via \(\mathrm{G}_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\): the other cascade via \(\mathrm{G}_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\) is also described in our formalism, as the fields that may play the rôle of the inflaton must have no charge under U(1)\(_\mathrm{R}\). Limiting ourselves to the fields satisfying the above requirements, the superpotential effectively reduces to [15]

$$\begin{aligned} W_\mathrm{singlet}&= m\, (p^2+3a^2+6b^2)+2\lambda \, (a^3 +3pb^2+6ab^2)\nonumber \\&+m_\Sigma \, \sigma \bar{\sigma } +\eta \, \sigma \bar{\sigma }(p+3a-6b), \end{aligned}$$
(5)

where

$$\begin{aligned} p=\Phi (1,1,1),\\ \quad a=\Phi (15,1,1), \quad b= \Phi (15,1,3),\\ \quad \sigma =\Sigma (\bar{10},1,3), \quad \bar{\sigma }= \bar{\Sigma }(10,1,3), \end{aligned}$$

and the integers in parentheses indicate the representation under the Pati–Salam group \(\mathrm{SU}(4)_\mathrm{C}\times \mathrm{SU(2)}_\mathrm{L} \times \mathrm{SU}(2)_\mathrm{R}\). In terms of the other SSB cascade containing U(1)\(_\mathrm{R}\), it is enough to replace the triplets with their ‘neutral’ component. Note that \(\Omega (10,1,1)\) cannot be safely given a VEV without breaking part of the Standard Model. Furthermore, we do not consider \(H\) as it has a small VEV because it contains the MSSM Higgs fields, and we do not expect it to play any significant rôle at the time of inflation. A phase redefinition of the superfields can be used to set \(m\), \(m_\Sigma \) and \(\eta \) to be real and positive, while \(\lambda \) can be a complex couplings.

It is clear that the only two fields that belong to conjugate representations are \(\sigma \) and \(\bar{\sigma }\); therefore, they must be the GUT Higgses that couple to the inflaton, like the superfields \(\Psi \) and \(\bar{\Psi }\) in Eq. (1). Let us address the question of whether we have an inflaton candidate. Clearly, \(a\), \(b\) and \(p\), though they all possess a coupling to \(\sigma \bar{\sigma }\), also all have a mass term, which implies that none of them can play the rôle of the inflaton field. We therefore want to find a combination of the fields \(a\), \(b\) and \(p\) that couples with \(\sigma \bar{\sigma }\) and is massless. Other conditions apply, but firstly we should ensure that there is a massless combination.

We will assume that the three superfields develop VEVs (\(a_0\), \(b_0\) and \(p_0\)), and they can be expanded around the new vacuum as

$$\begin{aligned} p= p_0 + P, \quad a= a_0 + A, \quad b= b_0 + B. \end{aligned}$$

We also assume that the would-be inflaton is a linear combination of the three superfields, and not of their complex conjugates. We can then calculate the mass matrix for the complex scalar components of \(\{A,B,P\}\) and, as a first step, check if there is a massless combination by imposing the vanishing of the determinant of the mass matrix. This will give some relations between the vacua, and allow one to define the scalar field that could play the rôle of the inflaton. In a second step, we will check whether other conditions necessary for inflation to start are satisfied. In the mass matrix, we set to zero the VEVs of \(\sigma \) and \(\bar{\sigma }\), as it should be at the onset of inflation, and consider the VEVs to be complex. The determinant, as a function of the VEVs of the fields, is

$$\begin{aligned} \text{ Det } \left( \mathcal {M}^2_{ij}\right)&= \text{ Det } \left( \sum _{k=A,B,P}\; \frac{\partial F_k}{\partial \phi _i} \frac{\partial F^*_k}{\partial \phi ^*_j} \right) \nonumber \\&= 20736 \left| m^3 + (4a_0+p_0) \lambda m^2 \right. \nonumber \\&\left. + 2 (2a_0^2+a_0 p_0 - 7 b_0^2) \lambda ^2 m - 12 a_0 b_0^2 \lambda ^3 \right| ^2,\nonumber \\ \end{aligned}$$
(6)

where \(F_k = \partial W_\mathrm{singlet}/\partial \phi _k\) is the \(F\)-term associated with the scalar component \(\phi _k\) of the superfield \(k=A,B,P\), and the indices \(i,j = A, B, P\) label the three relevant superfields. In general, \(\text{ Det } \left( \mathcal {M}^2\right) \) is non-zero, unless some special conditions apply on the VEVs; we list below all possible cases.

3.1.1 Case \(a_0\ne -\frac{m}{2 \lambda }\)

In this case, we can solve for \(p_0\) and get

$$\begin{aligned} p_0 = \frac{12 a_0 b_0^2 \lambda ^3 - 2 (2 a_0^2 - 7 b_0^2) \lambda ^2 m - 4 a_0 \lambda m^2 - m^3}{m \lambda (m+2 \lambda a_0)}~.\nonumber \\ \end{aligned}$$
(7)

The massless eigenstate, a candidate for the rôle of the inflaton, is given by

$$\begin{aligned} X =\frac{1}{N} \left[ -4 m \lambda b_0\; A + m (m+2 \lambda a_0) \; B \right. \nonumber \\ \left. -6 \lambda b_0 (m+2 \lambda a_0)\; P\right] \!, \end{aligned}$$
(8)

with \(N\) a normalisation. The other two combinations are massive, unless

$$\begin{aligned} |b_0|^2 = - \frac{ m^2 |m+2 \lambda a_0|^2}{4 |\lambda |^2 (13 m^2 + 36 m \mathfrak {R}( \lambda a_0) + 36 |\lambda a_0|^2)}\,, \end{aligned}$$
(9)

where we define the real part of \( \lambda a_0\) by \(\mathfrak {R}(\lambda a_0)\). However, it is easy to show that the above condition, Eq. (9), is never satisfied: in fact, the numerator is positive definite, so there exists a solution only if the denominator is negative, more precisely if \(\mathfrak {R}(\lambda a_0)<0\) and

$$\begin{aligned} |\lambda a_0| > |\mathfrak {R}( \lambda a_0)| > \frac{36 |\lambda a_0|^2 + 13 m^2}{36 m}\nonumber \\ \Rightarrow \left( \frac{|\lambda a_0|}{m} \right) ^2 - \frac{|\lambda a_0|}{m} + \frac{13}{36} < 0. \end{aligned}$$
(10)

The latter inequality is, however, never satisfied. Hence for \(a_0 \ne - \frac{m}{2 \lambda }\), there can be only a single massless scalar, denoted by \(X\) and given in Eq. (8).

Subcase \(b_0=0\) (and \(a_0\ne -\frac{m}{2 \lambda }\))

The previous case simplifies considerably for \(b_0=0\). Imposing Eq. (7), the mass matrix in the basis \(\{A,B,P\}\) reads

$$\begin{aligned} \mathcal {M}^2 = \left( \begin{array}{ccc} 36 |m+2\lambda a_0|^2\quad &{}\quad 0 &{}\quad 0 \\ 0\quad &{}\quad 0 &{}\quad 0 \\ 0\quad &{}\quad 0 &{}\quad 4 m^2 \end{array} \right) . \end{aligned}$$
(11)

The inflaton candidate is therefore \(B\) itself, while the other two fields \(A\) and \(P\) are always massive.

3.1.2 Case \(a_0 = -\frac{m}{2 \lambda }\)

In this case one cannot solve for \(p_0\), which disappears from Eq. (6), and the determinant reduces to

$$\begin{aligned} \text{ Det } (\mathcal {M}^2) = 1327104\, m^2 |\lambda b_0|^4, \end{aligned}$$
(12)

therefore the presence of a massless mode requires \(b_0=0\). In this case, the mass matrix simplifies to

$$\begin{aligned} \mathcal {M}^2 = \left( \begin{array}{lll} 0\quad &{}\quad 0 &{}\quad 0 \\ 0\quad &{}\quad 144 |\lambda p_0|^2 &{}\quad 0 \\ 0\quad &{}\quad 0 &{}\quad 4 m^2 \end{array} \right) \end{aligned}$$
(13)

and the massless field is \(A\). There is a second massless field \(B\) only if \(p_0=0\).

3.2 Conditions for inflation

We now study in detail the further conditions that ensure the existence of an inflationary potential, in order to pin down the successful VEV configurations.

3.2.1 Case \(a_0 = -\frac{m}{2 \lambda }\), \(b_0 = 0\), \(p_0 \ne 0\)

Let us start with the simple case \(a_0 = -\frac{m}{2 \lambda }\), \(b_0 = 0\) and \(p_0 \ne 0\). The massless field is \(A\) and one can expand the superfields around the vacua, namely

$$\begin{aligned} a = -\frac{m}{2 \lambda } + A, \qquad b = B, \qquad p = p_0 + P, \end{aligned}$$
(14)

to obtain the following superpotential for the superfields of the would-be inflaton \(A\):

$$\begin{aligned} W_\mathrm{singlet}&= 3 \left( \eta \sigma \bar{\sigma } -\frac{m^2}{2 \lambda } \right) A + 2 \lambda A^3 + 12 \lambda B^2 A\nonumber \\&+ \text{ other } \text{ terms }. \end{aligned}$$
(15)

The first term in the superpotential is exactly of the form of Eq. (1); however, \(A\) cannot play the rôle of the inflaton since its superpotential contains a trilinear coupling. Thus, this case is excluded.

3.2.2 Case \(a_0 = -\frac{m}{2 \lambda }\), \(b_0 = p_0 = 0\)

In this case there are two massless fields, \(A\) and \(B\), hence the field that could play the rôle of the inflaton must be a linear combination of these two fields. Expanding around the VEVs, the superpotential for the massless scalars reads

$$\begin{aligned} W_\mathrm{singlet}&= 3 \eta \sigma \bar{\sigma } (A-2 B) - 3 \frac{m^2}{2 \lambda } A+ 2 \lambda A (A^2 + 6 B^2) \nonumber \\&+ 6 \lambda P B^2 + \text{ other } \text{ terms }. \end{aligned}$$
(16)

This superpotential contains dangerous trilinear terms involving \(A\) and \(B\): in order to check the feasibility of this configuration of vacua, we can study the potential for the scalar components of the superfields, which contains

$$\begin{aligned} V_\mathrm{scalar}&= 4 m^2 \phi _P^*\phi _P - 9 m^2 (\phi _A^2 + (\phi _A^*)^2)\nonumber \\&- 18 m^2 (\phi _B^2 + (\phi _B^*)^2) + \text{ other } \text{ terms }. \end{aligned}$$
(17)

The potential, therefore, contains mass terms for the real and imaginary parts of \(A\) and \(B\), and the mass has the wrong sign for the real parts. This signals the fact that the vacuum configuration is not a local minimum of the scalar potential, therefore it cannot be used to trigger inflation.

3.2.3 Case \(a_0 \ne -\frac{m}{2 \lambda }\)

One can also in this case expand the superfields around the VEVs, as

$$\begin{aligned} a = a_0 + A, \qquad b = b_0 + B, \qquad p = p_0 + P \end{aligned}$$

where \(p_0\) is related to \(a_0\) and \(b_0\) by Eq. (7), in order for the fields \(A\), \(B\) and \(P\) to contain a massless eigenstate. The field \(X\) that could play the rôle of the inflaton is therefore given by Eq. (8), and we can express the fields \(A\), \(B\), and \(P\) in terms of \(X\), as

$$\begin{aligned} A&= \frac{1}{N} \left( - 4 \lambda ^* m b_0^*X + \cdots \right) , \nonumber \\ B&= \frac{1}{N} \left( m (m + 2 \lambda ^*a^*_0 ) X + \cdots \right) , \nonumber \\ P&= \frac{1}{N} \left( - 6 \lambda ^*(m + 2 \lambda ^*a^*_0) b^*_0 X + \cdots \right) . \end{aligned}$$
(18)

to obtain a superpotential for \(X\), which contains a trilinear term:

$$\begin{aligned} W_\mathrm{singlet}&\subset - \frac{4 m^2 (\lambda ^*)^2 b^*_0}{N^3} \left[ 21 m^3 + 102 m^2 \lambda ^*a^*_0 \right. \nonumber \\&\left. + 4 m (\lambda ^*)^2 (39 (a^*_0)^2 + 8 (b^*_0)^2) + 72 (\lambda ^*)^3 a_0^3\right] X^3 \nonumber \\&+ \text{ interactions } + \text{ other } \text{ terms }. \end{aligned}$$
(19)

For the trilinear term to vanish, one should impose a condition on the VEVs \(a_0\) and \(b_0\), namely

$$\begin{aligned} b_0 = 0 \qquad \text{ or } \quad b_0 = \pm i \frac{m+2 \lambda a_0}{4 \lambda } \sqrt{\frac{3 (7 m + 6 \lambda a_0)}{2 m}}\,. \end{aligned}$$
(20)

Let us now study these two subcases in detail.

Subcase \(a_0 \ne -\frac{m}{2 \lambda }\), \(b_0 = 0\)

In this case, the field that could play the rôle of the inflaton is \(X = B\), with superpotential given by

$$\begin{aligned} W_\mathrm{singlet} = - 6 \eta \sigma \bar{\sigma } B + 6 \lambda (2 A + P) B^2 + \text{ other } \text{ terms }\,. \end{aligned}$$
(21)

Since \(B\) does not have a linear term, this subcase is excluded.

Subcase \(a_0 \ne -\frac{m}{2 \lambda }\), \(b_0 \ne 0\)

Fixing the vacuum \(b_0\) to the second solution in Eq. (20), the superpotential for \(X\) contains both a linear term in \(X\) and a coupling \(\sigma \bar{\sigma } X\), as required, but also a dangerous quadratic term. The quadratic term only vanishes when \(a_0\) is real, i.e. \(a_0 = a_0^*\), so that we will impose this condition from now on.

The vanishing of the quadratic term is, however, still not enough to ensure that the would-be inflaton is massless: in fact, we assumed that the inflaton \(X\) is a superposition of the chiral superfields. The condition we imposed at the beginning, makes sure that a mass in the form \(\phi _X^*\phi _X\) is zero; however, it does not ensure the vanishing of mass terms in the form \((\phi _X^*)^2 + \phi _X^2\). We numerically checked that there is no massless state once the full mass matrix, written in terms of real scalar fields, is considered in this vacuum structure. We can therefore conclude that this last subcase is excluded.

Below we will therefore assume that the minimal SO(10) is extended with the introduction of a singlet \(S\) that will play the rôle of the inflaton field.

4 Extending the minimal SO(10)

Let us then introduce an extra scalar field \(S\), which could play the rôle of the inflaton and examine whether we can find flat directions with a stable inflationary valley. We will focus on the simple case where \(S\) is a singlet of SO(10), while non-singlets may also be used to play the rôle of the inflaton [22].

4.1 Higgs content and scalar superpotential

The Higgs sector is based on the minimal model described in Refs. [15, 18, 21], with the additional introduction of an SO(10) singlet superfield \(S\). By imposing that the superpotential is a scalar function of the superfields, the most general Higgs superpotential takes the form

$$\begin{aligned} \tilde{W}_\mathrm{H}&= m\, \Phi ^2+\lambda \, \Phi ^3 + m_H\, H^2 +m_\Sigma \, \Sigma \bar{\Sigma } \nonumber \\&+\eta \, \Phi \Sigma \bar{\Sigma }+\Phi H (\alpha \, \Sigma +\bar{\alpha }\, \bar{\Sigma })\nonumber \\&+ m_\Omega \, \Omega ^2+\beta \, H \Phi \Omega +\gamma \, \Omega ^2 \Phi +\Omega \Phi (\zeta \, \Sigma +\bar{\zeta }\, \bar{\Sigma })\nonumber \\&+ \kappa \, S(\Sigma \bar{\Sigma }-M^2) + m_S\, S^2 +\lambda _S\, S^3\nonumber \\&+ S(\delta _1\, H^2+\delta _2\, \Omega ^2+ \delta _3\, \Phi ^2). \end{aligned}$$
(22)

The first three lines contain the superpotential in Eq. (4); the terms in the last two lines of the above expression appear because of the presence of an extra singlet in the theory, included in order to realise inflation.

Of the above superpotential, we can safely neglect terms involving \(\Omega \), because it does not contain a singlet component under the SM gauge symmetries, and \(H\), since this superfield realises the electroweak SSB and has therefore a very small VEV. The third line in Eq. (22) contains the superpotential terms required for F-term inflation. The terms in the fourth line, containing the singlet field, are potentially dangerous as they can spoil hybrid inflation by generating mass or quartic terms for the inflaton field. In the following, therefore, we will set all the extra terms containing \(S\) to zeroFootnote 3: this shows that some tuning is necessary in order to obtain inflation.

The Higgs superpotential, relevant for our study, reads

$$\begin{aligned} {\tilde{W}}_\mathrm{H}&= m\, \Phi ^2+\lambda \, \Phi ^3 + m_\Sigma \, \Sigma \bar{\Sigma }\nonumber \\&+\eta \, \Phi \Sigma \bar{\Sigma } + \kappa \, S(\Sigma \bar{\Sigma }-M^2). \end{aligned}$$
(23)

Here, we can use the phases of the superfields to set \(m\), \(m_\Sigma \), \(\kappa \) and \(M\) to be real and positive, while \(\lambda \) and \(\eta \) may be complex couplings. Following our results from the previous section, the inflaton must be contained in the SO(10) singlet \(S\).

4.2 Vacuum expectation values and superfields

We will follow the procedure of Ref. [15] to describe how the cascade of SSB, given in Eq. (3), can be realised. We need first to identify the components of the Higgs fields that can take a non-vanishing VEV; they are necessarily singlets under the SM. Using Ref. [23], the only superfields that can be considered are

$$\begin{aligned} \begin{aligned}&p= \Phi (1,1,1), \quad a=\Phi (15,1,1\\&b=\Phi (15,1,3), \quad \sigma =\Sigma (\bar{10},1,3\\&\sigma = \bar{\Sigma }(10,1,3), \quad s=S(1,1,1). \end{aligned} \end{aligned}$$
(24)

This is the same set used in the previous section, with the addition of the SO(10) singlet. The superpotential that one has to study reads

$$\begin{aligned} W_\mathrm{H}&= m\,(p^2+3a^2+6b^2)+2\lambda \,(a^3 +3pb^2+6ab^2)\nonumber \\&+m_\Sigma \, \sigma \bar{\sigma }+\eta \, \sigma \bar{\sigma }(p+3a-6b) \nonumber \\&+\kappa \, s(\sigma \bar{\sigma }-M^2). \end{aligned}$$
(25)

4.3 Minimisation of the superpotential

In the absence of a Fayet–Iliopoulos term \(\xi \), as in our case, the condition for the D-term, \((\xi +1/2\sum _iq_i \langle \Phi _i \rangle ^2)^2\), to vanish is

$$\begin{aligned} \sum _iq_i \langle \Phi _i\rangle ^2=0, \end{aligned}$$

where \(q\) stands for the charge under U(1) and \(\langle \Phi _i\rangle \) denote the VEVs of the superfields in question. Since the only charged superfields are \(\sigma \) and \(\bar{\sigma }\), which have opposite charges, the condition for the D-term to vanish is \(\langle \sigma \rangle =\pm \langle \bar{\sigma } \rangle \). The F-terms, \(F_i \equiv \partial W_H/\partial \Phi _i\), read

$$\begin{aligned} \begin{aligned} F_p&= 2m p +6 \lambda b^2 +\eta \sigma \bar{\sigma },\\ F_a&= 3[2 m a +2 \lambda (2b^2+a^2) + \eta \sigma \bar{\sigma }],\\ F_b&= 6[2 m b + 2 \lambda b (2a+p) - \eta \sigma \bar{\sigma }],\\ F_\sigma&= \bar{\sigma } [m_\Sigma +\eta (p +3a -6b) + \kappa s],\\ F_{\bar{\sigma }}&= \sigma [m_\Sigma +\eta (p +3a -6b) + \kappa s],\\ F_s&= \kappa (\sigma \bar{\sigma } -M^2), \end{aligned} \end{aligned}$$
(26)

and the scalar potential is the sum \(V=\sum _i |F_i|^2\). The VEVs of the fields will take values in order to minimise the scalar potential \(V\).

4.3.1 Global minima

Let us study whether it is possible to choose the VEVs such that all F-terms vanish, thus the potential itself vanishes, corresponding to global (SUSY preserving) minima of the potential. Here we use a subscript \(0\) to label the VEVs in order to distinguish them from the superfields, so that \(s_0\) is the VEV of the superfield \(s\), and so on. The F-term associated to \(s\) vanishes only if \(\sigma _0 = \bar{\sigma }_0 = \pm M\). To construct a SUSY preserving global minimum, the other VEVs have to satisfy the following conditions:

$$\begin{aligned} \begin{aligned}&2m p_0 +6 \lambda b_0^2 +\eta M^2 =0,\\&2 m a_0 +4 \lambda b_0^2 + \eta M^2 =0,\\&2 m b_0 + 2 \lambda b_0 (2a_0+p_0) - \eta M^2=0,\\&m_\Sigma +\eta (p_0 +3a_0 -6b_0)+\kappa s_0 =0. \end{aligned} \end{aligned}$$
(27)

The latter equation sets the value of \(s_0\):

$$\begin{aligned} s_0 = - \frac{m_\Sigma }{\kappa } + \frac{\eta }{\kappa } (6b_0 - p_0 -3a_0). \end{aligned}$$
(28)

We first solve the system in the limit \(\eta M^2\ll m^2\), where we can approximate the equations by setting \(M=0\). This approximation is a realistic one, because in our setting \(M^2\) is likely to be lower than \(m^2\), in order for the B-L symmetry breaking to occur as a second stage in the SSB pattern, and for the validity of a perturbation analysis, \(\eta \) is required to be lower than 1. In this case, the six solutions for the VEVs \(a_0,b_0,p_0\) and \(s_0\) are given by

  • \(p_0=0, \ \ a_0=0, \ \ b_0=0, \ \ s_0=-\frac{m_\Sigma }{\kappa }\) ;

  • \(p_0=0, \ \ a_0=-\frac{m}{\lambda }, \ \ b_0=0\)  \(s_0=-\frac{m_\Sigma }{\kappa }+ 3 \frac{\eta m}{\kappa \lambda }\);

  • \(p_0=-\frac{m}{3\lambda }\ , \ a_0=-\frac{m}{3\lambda }\ , \ b_0=\pm \frac{m}{3\lambda }\ , \ s_0=-\frac{m_\Sigma }{\kappa }+ \frac{4 \pm 6}{3} \frac{\eta m}{\kappa \lambda }\) ;

  • \(p_0=\frac{3m}{\lambda }\ , \ a_0=-\frac{2m}{\lambda }\ , \ b_0=\pm \frac{im}{\lambda }\ , \ s_0=-\frac{m_\Sigma }{\kappa }+ 3(1 \pm 2 i) \frac{\eta m}{\kappa \lambda }\).

When \(M\) is not set equal to zero, there are six general solutions. Two of them are found by noticing that \(p_0=-b_0=a_0\) is a solution of the system above. It gives

$$\begin{aligned}&p_0=-b_0,\quad a_0=-b_0, \nonumber \\&b_0=\frac{m}{6 \lambda } \left( 1 \pm \sqrt{1-6\frac{\lambda \eta M^2}{m^2}}\right) . \end{aligned}$$
(29)

The other four solutions are obtained by solving the following equation in \(b_0\):

$$\begin{aligned}&6\left( \frac{\lambda }{m} b_0 \right) ^4 + 2 \left( \frac{\lambda }{m} b_0 \right) ^3 + \left( 6 + \frac{\lambda \eta M^2}{m^2} \right) \left( \frac{\lambda }{m} b_0 \right) ^2\nonumber \\&\quad + 2 \left( 1 + \frac{\lambda \eta M^2}{m^2} \right) \left( \frac{\lambda }{m} b_0 \right) + \frac{\lambda \eta M^2}{m^2} =0. \end{aligned}$$
(30)

For these solutions, the VEVs \(a_0\) and \(p_0\) then read

$$\begin{aligned} p_0&= - \frac{m}{\lambda } \left( \frac{1}{2} \frac{\lambda \eta M^2}{m^2} + 3 \frac{\lambda ^2 b_0^2}{m^2} \right) ,\nonumber \\ a_0&= \frac{m}{\lambda } \left( \frac{3 \lambda ^2 b_0^2}{2 m^2} - \frac{1}{2} + \frac{1}{4} \frac{\lambda \eta M^2}{m^2} \left( 1 + \frac{m}{\lambda b_0} \right) \right) . \end{aligned}$$
(31)

Let us now discuss the properties of these solutions. It is interesting to note that the SO(10) preserving minimum found in Ref. [15] (with \(\sigma _0 = \bar{\sigma }_0 =p_0=a_0=b_0=0\)) is not preserved by our superpotential; SO(10) must be broken with the choice of superpotential given in Eq. (23). Note also that if some SUSY preserving minima exist, they are never reached at a vanishing VEV for the inflaton \(s\), unless \(m_\Sigma \) is tuned to vanish on the given solution. The latter situation is, however, not generic, as the other terms in \(s_0\) may have non-trivial phases, while \(m_\Sigma \) is real and positive. The symmetries preserved by these minima are those of the SM, which is what is required at the end of the B-L symmetry breaking.

The exact equations determining the vacua depend on two combinations of parameters: \(m/\lambda \) and \(x = \lambda \eta M^2/m^2\). To better understand the vacua, we can expand the solutions for small \(x \ll 1\) (which corresponds, at zero order, to the solutions for \(M=0\)): we will focus on three particular solutions that will be relevant for the onset of inflation. At leading order in \(x\), we find

$$\begin{aligned} a_0&= \frac{m}{\lambda } \left( -1 + \frac{1}{4} x + \cdots \right) , \nonumber \\ b_0&= \frac{m}{\lambda } \left( - \frac{1}{2} x + \cdots \right) , \nonumber \\ p_0&= \frac{m}{\lambda } \left( - \frac{1}{2} x + \cdots \right) , \nonumber \\ s_0&= - \frac{m_\Sigma }{\kappa } + \frac{\eta m}{\kappa \lambda } \left( 3 - \frac{13}{4} x + \cdots \right) ; \end{aligned}$$
(32)

for the first solution, and

$$\begin{aligned} a_0&= \frac{m}{\lambda } \left( -2 + \frac{3\pm i}{10} x + \cdots \right) , \nonumber \\ b_0&= \frac{m}{\lambda } \left( \pm i + \frac{1\pm 2 i}{10} x + \cdots \right) , \nonumber \\ p_0&= \frac{m}{\lambda } \left( 3 - \frac{2 \pm 9 i}{10} x + \cdots \right) , \nonumber \\ s_0&= - \frac{m_\Sigma }{\kappa } + \frac{\eta m}{\kappa \lambda } \left( 3 (1\pm 2i) + \frac{4 \pm 3 i}{5} x + \cdots \right) , \end{aligned}$$
(33)

for the remaining two. From these approximate solutions we see that the vacua break SO(10) completely to the SM gauge symmetries.

4.3.2 Local minima at the onset of inflation

As a next step, one has to look for the local minimum of the potential assuming an initially large value of the VEV of the inflaton \(s\). Indeed, this is the state of the field usually assumed in chaotic inflation. To preserve the global picture of F-term inflation, we will assume that the intermediate stage of symmetry is obtained while being in the false vacuum corresponding to \(\sigma _0 =\bar{\sigma }_0 =0\), in order to minimise the contribution from \(F_\sigma \) and \(F_{\bar{\sigma }}\) to the potential.

It is worth noting that, contrary to the F-term inflation toy model, where only the large value of \(s\) induces a mass term for the \(\sigma \) and \(\bar{\sigma }\) fields, in our case here also the mass term \(m_\Sigma \) as well as the VEVs of \(p, a\) and \(b\) make a contribution. Once the VEVs \(\sigma _0\), and \(\bar{\sigma }_0\) vanish, the F-term VEVs read

$$\begin{aligned} \begin{aligned} F_p&= 2m p_0 +6 \lambda b_0^2,\\ F_a&= 3[2 m a_0 +2 \lambda (2b_0^2+a_0^2)],\\ F_b&= 6[2 m b_0 + 2 \lambda b (2a_0+p_0)],\\ F_\sigma&= 0 = F_{\bar{\sigma }},\\ F_s&= -M^2 \kappa . \end{aligned} \end{aligned}$$
(34)

As a consequence, even if the first three F-terms in the scalar potential \(V\) can be cancelled by an appropriate choice of \(p_0\), \(a_0\) and \(b_0\), the potential will be constant and given by \(V_0=\kappa ^2 M^4\); this is an \(s\)-flat direction. The minimum of the potential is obtained for the VEVs of \(a_0\), \(b_0\) and \(p_0\) that set to zero the associated \(F\)-terms. The six solutions are the same as the ones we found for the global minima for \(M=0\):

  • \(p_0=0\), \(a_0=0\), \(b_0=0\). This minimum is obviously invariant under SO(10).

  • \(p_0=0\), \(a_0=-\frac{m}{\lambda }\), \(b_0=0\). Since \(a_0\equiv \langle \Phi (15,1,1)\rangle \), it is clear that SU(2)\(_\mathrm{L}\times \) SU(2)\(_\mathrm{R}\) is preserved by this minimum. The component of the 15 of SU(4)\(_\mathrm{C} \supset \mathrm{SU(3)}_\mathrm{C}\times U(1)_\mathrm{B-L}\) that can take a VEV is the one that preserves SU(3)\(_\mathrm{C}\), which is also uncharged under \(U(1)_\mathrm{B-L}\) [23]. This minimum is thus invariant under G\(_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\).

  • \(p_0=\frac{3m}{\lambda }\), \(a_0=-\frac{2m}{\lambda }\), \(b_0=\pm \frac{im}{\lambda }\). For the symmetries left unbroken by these minima, this case is similar to the above one (since the VEV \(p_0\) has no effect on symmetries), except that the VEV \(b_0\equiv \langle \Phi (15,1,3)\rangle \) induces the additional breaking SU(2)\(_\mathrm{R} \rightarrow \mathrm{U(1)}_\mathrm{R}\). This minimum is thus invariant under G\(_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\).

  • \(p_0=-\frac{m}{3\lambda }\), \(a_0=-\frac{m}{3\lambda }\), \(b_0=\pm \frac{m}{3\lambda }\). A careful analysis of these minima shows that they are invariant under SU(5)\(\times \mathrm{U(1)}\) [15].

Note that we have not made any assumption on the values of the potential parameters and our solutions are exact. These solutions, already found in Ref. [15], are now of phenomenological interest even though they do not give rise to the SM, since inflation will drive the last part of the symmetry breaking.

4.3.3 Stability of the inflationary valley

The vacua that we are interested in are the ones that have an unbroken G\(_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\) and G\(_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\) symmetry. To compute the scalar potential for the former case (\(a_0 = - m/\lambda \) and \(b_0 = p_0 = 0\)), we expand the scalar components of the superfields around the local vacua

$$\begin{aligned} a=\varphi _a-\frac{m}{\lambda }, \ b=\varphi _b,\ p=\varphi _p\ , \nonumber \\ \sigma = \varphi _\sigma , \quad \bar{\sigma } = \varphi _{\bar{\sigma }}, \ s = s_0 + \varphi _s, \end{aligned}$$
(35)

where \(\varphi _x\) are the scalar perturbations around the vacuum expectation value of the field \(x\). The scalar potential then reads

$$\begin{aligned}&V =\Big |2m\varphi _p+6\lambda \varphi _b^2+ \eta \varphi _\sigma \varphi _{\bar{\sigma }}\Big |^2\nonumber \\&+\Big | 12m \varphi _b + 2 \lambda \big ( 6 \varphi _p \varphi _b+12\left( \varphi _a-\frac{m}{\lambda }\right) \varphi _b \big )-6 \eta \varphi _\sigma \varphi _{\bar{\sigma }} \Big |^2\nonumber \\&+\Big | 6m\left( \varphi _a - \frac{m}{\lambda }\right) + 2 \lambda \big ( 3 \left( \varphi _a - \frac{m}{\lambda }\right) ^2+6\varphi _b^2\big ) +3\eta \varphi _\sigma \varphi _{\bar{\sigma }}\Big |^2\nonumber \\&+\kappa ^2\Big |\varphi _\sigma \varphi _{\bar{\sigma }}-M^2\Big |^2\nonumber \\&+\Big (\Big |\varphi _\sigma |^2+|\varphi _{\bar{\sigma }}|^2\Big ) \Big | m_\Sigma + \eta \left( \varphi _p + 3\varphi _a - 3 \frac{m}{\lambda } - 6\varphi _b\right) \nonumber \\&+\kappa \big ( s_0 + \varphi _s \Big ) \Big |^2. \end{aligned}$$
(36)

Expanding the potential up to quadratic terms, we have

$$\begin{aligned} V&= \kappa ^2 M^4 + 36 m^2 \varphi _a^* \varphi _a + 144 m^2 \varphi _b^* \varphi _b + 4 m^2 \varphi _p^* \varphi _p \nonumber \\&+\Big | m_\Sigma - \frac{3 \eta m}{\lambda } + \kappa s_0 \Big |^2 (\varphi _\sigma ^* \varphi _\sigma + \varphi _{\bar{\sigma }}^* \varphi _{\bar{\sigma }})\nonumber \\&- \kappa ^2 M^2 (\varphi _\sigma \varphi _{\bar{\sigma }} + \varphi _\sigma ^* \varphi ^*_{\bar{\sigma }}) + \cdots . \end{aligned}$$
(37)

We note that the scalar perturbations in \(a\), \(b\) and \(p\) correspond to massive fields, while the scalar perturbations in \(\sigma \) and \(\bar{\sigma }\) have a mass matrix that depends on the VEV of the inflaton. For large values of \(s_0\), the mass squares are positive and the vacuum \(\sigma _0 = \bar{\sigma }_0 = 0\) is stable. During inflation, the value of \(s_0\) will slowly roll along the flat direction, until the condition

$$\begin{aligned} s_0^\mathrm{crit} = - \frac{m_\Sigma }{\kappa } + 3\frac{\eta m}{\kappa \lambda } \pm M \end{aligned}$$
(38)

is met: this is the critical value of the inflaton VEV below which the \(\varphi _\sigma \)–\(\varphi _{\bar{\sigma }}\) system will develop a tachyonic mass and the system will quickly settle on a stable vacuum. For small \(M\), the unstable point is close to the minimum in Eq. (32), so it is likely that the fields will settle on this minimum: at this point, supersymmetry is restored and SU(2)\(_\mathrm{R} \times \) U(1)\(_\mathrm{B}\hbox {-}\mathrm{L}\) is broken to the hypercharge by the non-vanishing vacua of \(\sigma \) and \(\bar{\sigma }\) at a scale \(M\).

We can now repeat the calculation in the latter case, which corresponds to the \(\mathrm{G}_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\) SSB cascade, by expanding the fields around the VEVs as follows:

$$\begin{aligned}&a=\varphi _a - 2 \frac{m}{\lambda } , \ b= \pm i \left( \varphi _b + \frac{m}{\lambda } \right) , \ p=\varphi _p + 3 \frac{m}{\lambda },\nonumber \\&\sigma = \varphi _\sigma , \ \bar{\sigma } = \varphi _{\bar{\sigma }}, \ \quad s = s_0 + \varphi _s . \end{aligned}$$
(39)

Following the same procedure as for the former case, the potential up to quadratic terms in the fields is given by

$$\begin{aligned} V&= \kappa ^2 M^4 + 900 m^2 \varphi _a^* \varphi _a + 720 m^2 \varphi _b^* \varphi _b + 148 m^2 \varphi _p^* \varphi _p \nonumber \\&+ 432 m^2 (\varphi _a^* \varphi _b + \varphi _b^* \varphi _a) + 288 m^2 (\varphi _a^* \varphi _p + \varphi _p^* \varphi _a)\nonumber \\&- 24 (\varphi _p^* \varphi _b + \varphi _b^* \varphi _p) \nonumber \\&+ \Big | m_\Sigma - \frac{3 (1\pm 2 i) \eta m}{\lambda } + \kappa s_0 \Big |^2 (\varphi _\sigma ^* \varphi _\sigma + \varphi _{\bar{\sigma }}^* \varphi _{\bar{\sigma }})\nonumber \\&- \kappa ^2 M^2 (\varphi _\sigma \varphi _{\bar{\sigma }} + \varphi _\sigma ^* \varphi ^*_{\bar{\sigma }}) + \cdots . \end{aligned}$$
(40)

Once more, the inflaton field is massless, and the first three lines define a mass matrix for the three complex fields \(\varphi _{a,b,p}\), whose eigenvalues are numerically given by \(m_i = \{ 1.841, 21.768, 35.927\} \cdot m\). The valley is stable, until the inflaton VEV reaches the critical value

$$\begin{aligned} s_0^\mathrm{crit} = - \frac{m_\Sigma }{\kappa } + \frac{3 (1\pm 2 i) \eta m}{\kappa \lambda } \pm M. \end{aligned}$$
(41)

For small \(M\), the nearest global vacuum is one of the two in Eq. (33), which also restore supersymmetry and break the remaining symmetries down to the SM ones.

We were thus able to propose a model and a superpotential such that F-term inflation is explicitly embedded in a detailed and minimal model of SO(10) that has successfully passed particle physics phenomenology tests. We have found three local minima (out of six) for the scalar potential for which the symmetries are such that no harmful topological defects are formed at the end of inflation and where there are no tachyonic modes that will destabilise the inflationary valley:

$$\begin{aligned} \sigma _0 = \bar{\sigma }_0=p_0=b_0=0,~~ a_0=-\frac{m}{\lambda },~~ s_0\ne 0,\nonumber \\ V_0=\kappa ^2 M^4, \end{aligned}$$
(42)

or

$$\begin{aligned}&\sigma _0 = \bar{\sigma }_0=0,~~ a_0=-2\frac{m}{\lambda },~~ p_0=3\frac{m}{\lambda },\nonumber \\&b_0=\pm i\frac{m}{\lambda },~~ s_0\ne 0,~~ \quad V_0=\kappa ^2 M^4. \end{aligned}$$
(43)

The first local minimum can give rise to a successful phase of F-term inflation that will dynamically break G\(_{3,2,2,\mathrm{B}\hbox {-}\mathrm{L}}\) into the G\(_\mathrm{SM}\times Z_2\) symmetry group, thus realising the SSB patterns of Eq. (2). The latter two minima will do the same with G\(_{3,2,1,\mathrm{B}\hbox {-}\mathrm{L}}\). Cosmic strings are formed at the end of inflation [11] at an energy scale related to inflationary physics and are expected to have some impact in cosmology [5, 6, 24]. By doing so, the system will evolve to one of the minima detailed in Sect. 4.3.1.

5 Conclusions

The inflationary paradigm has been extensively studied in the context of Supersymmetric Grand Unified Theories. Given that SO(10) is a well-studied gauge group, we have investigated whether it can accommodate an inflationary era without the introduction of an extra scalar field to play the rôle of the inflaton. In particular, we have studied whether F-term hybrid inflation can be incorporated in a rather natural way. We have shown that none of the scalar fields of SO(10) can play the rôle of the inflaton and one has to introduce an extra scalar field. This result may be considered as an element that spoils the naturalness of inflation within SO(10).

Adding an extra scalar field, singlet under SO(10), which could play the rôle of the inflaton, we have shown the existence of an appropriate superpotential that can have flat directions preserving the stability of the inflationary valley.