Coupling constants of bottom (charmed) mesons with the pion from three-point QCD sum rules

Abstract

In this article, the three-point QCD sum rules are used to compute the strong coupling constants of vertices containing the strange bottomed (charmed) mesons with the pion. The coupling constants are calculated when both the bottom (charm) and the pion states are off-shell. A comparison of the obtained results of the coupling constants with existing predictions is also made.

1 Introduction

During the last ten years, there have been published numerous research articles devoted to the precise determination of the strong form factors and coupling constants of meson vertices via QCD sum rules (QCDSR) [1–4]. The QCDSR formalism has also been successfully used to study some of the ‘exotic’ mesons made of quark–gluon hybrid ($q\bar{q}g$), tetraquark states ($q\bar{q}q\bar{q}$), molecular states of two ordinary mesons, glueballs, and many others [5]. Coupling constants can provide a real opportunity for studying the nature of the bottomed and charmed pseudoscalar and axial vector mesons. A more accurate determination of these coupling constants plays an important role in understanding of the final state interactions in the hadronic decays of the heavy mesons. Our knowledge of the form factors in hadronic vertices is of crucial importance to estimate hadronic amplitudes when hadronic degrees of freedom are used. When all of the particles in a hadronic vertex are on mass-shell, the effective fields of the hadrons describe point-like physics. However, when at least one of the particles in the vertex is off-shell, the finite size effects of the hadrons become important. The following coupling constants have been determined by various research groups: $D^* D \pi$ [6, 7], $D D \rho$ [8], $D^* D \rho$ [9], $D^* D^* \rho$ [10], $D D J/\psi$ [11], $D^* D J/\psi$ [12], $D^* D^* J/\psi$ [13], $D_s D^* K$, $D_s^* D K$ [14], $D D \omega$ [15] and $VD_{s0}^{*} D_{s0}^{*}$, $VD_{s} D_{s}$, $VD_{s}^{*} D_{s}^{*}$, and $VD_{s1} D_{s1}$ [16], in the framework of three-point QCD sum rules. It is very important to know the precise functional form of the form factors in these vertices and even to know how this form changes when one or the other (or both) mesons are off-shell [16].

In this review, we focus on the method of three-point QCDSR to calculate the strong form factors and coupling constants associated with the $B_1B^*\pi$, $B_1B_0\pi$, $B_1B_1\pi$, $D_1D^*\pi$, $D_1D_0\pi$, and $D_1D_1\pi$ vertices, for both the bottom (charm) and the pion states being off-shell. The three-point correlation function is investigated from the phenomenological and the theoretical sides. As regards the physical or phenomenological part, the representation is in terms of hadronic degrees of freedom, which is responsible for the introduction of the form factors, decay constants, and masses. In QCD or the theoretical part, which consists of two contributions, perturbative and non-perturbative (in the present work the calculations contributing the quark–quark and quark–gluon condensate diagrams are considered as non-perturbative effects), we evaluate the correlation function in quark–gluon language and in terms of QCD degrees of freedom, such as the quark condensate, the gluon condensate, etc., with the help of the Wilson operator product expansion (OPE). Equating the two sides and applying the double Borel transformations with respect to the momentum of the initial and final states, to suppress the contribution of the higher states and continuum, the strong form factors are estimated.

The outline of the paper is as follows. In Sect. 2, by introducing the sufficient correlation functions, we obtain QCD sum rules for the strong coupling constant of the considered $B_1B^*\pi$, $B_1B_0\pi$, and $B_1B_1\pi$ vertices. With the necessary changes in the quarks, we can easily apply the same calculations to the $D_1D^*\pi$, $D_1D_0\pi$, and $D_1D_1\pi$ vertices. In obtaining the sum rules for physical quantities, both light quark–quark and light quark–gluon condensate diagrams are considered as non-perturbative contributions. In Sect. 3, the obtained sum rules for the considered strong coupling constants are numerically analysed. We will obtain the numerical values for each coupling constant when both the bottom (charm) and the pion states are off-shell. Then taking the average of the two off-shell cases, we will obtain the final numerical values for each coupling constant. In this section, we also compare our results with the existing predictions of other work.

2 The three-point QCD sum rules method

In order to evaluate the strong coupling constants, it is necessary to know the effective Lagrangians of the interaction which, for the vertices $B_{1}B^*\pi$, $B_{1}B_{0}\pi$, and $B_{1}B_{1}\pi$, are [17, 18]

$$\begin{aligned} {{\mathcal {L}}}_{B_1B^*\pi }&= g_{B_1B^*\pi } B_{1}^{\alpha }(\pi ^{+} B^{*-}_{\alpha }- \pi ^{-} B^{*+}_{\alpha }), \nonumber \\ {{\mathcal {L}}}_{B_1B_0\pi }&= ig_{B_1B_0\pi } B_1^{\alpha }( B_0^{-} \partial _{\alpha } \pi ^{+} -\partial _{\alpha }B_0^{-} \pi ^{+} )+H.c. , \nonumber \\ {{\mathcal {L}}}_{B_1B_1\pi }&= -g_{B_1B_1\pi } \epsilon ^{ \alpha \beta \gamma \sigma }\partial _{\alpha } B_{1\beta }(\partial _{\gamma } B_{1\sigma }^{+} \pi ^{-} +\pi ^{+} \partial _{\gamma } B^{-}_{1\sigma }).\nonumber \\ \end{aligned}$$

(1)

From these Lagrangians, we can extract elements associated with the $B_{1}B^*\pi$, $B_{1}B_{0}\pi$, and $B_{1}B_{1}\pi$ momentum dependent vertices that can be written in terms of the form factors:

$$\begin{aligned} \langle B_{1}(p', \epsilon ') | B^*(p,\epsilon ) \pi (q) \rangle&= g_{ B_{1}B^*\pi }(q^2) (\epsilon '.\epsilon ) \frac{p.q}{m_{B1}},\nonumber \\ \langle B_{1}(p', \epsilon ') | B_{0}(p) \pi (q) \rangle&= g_{B_{1}B_{0}\pi }(q^2) \epsilon '.q,\nonumber \\ \langle B_1(p', \epsilon ') | B_1(p,\epsilon ) \pi (q) \rangle&= i g_{ B_1B_1\pi }(q^2) \epsilon ^{ \alpha \beta \gamma \sigma } \epsilon '_\gamma (p')\nonumber \\&\quad \times \,\epsilon _\sigma (p) p'_\beta q_\alpha , \end{aligned}$$

(2)

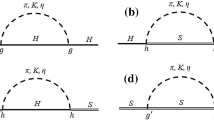
where $p$ and $p'$ are the four momenta of the initial and final mesons; we have $q=p'-p$, and $\epsilon$, and $\epsilon '$ are the polarization vectors of the $B^*$ and $B_{1}$ mesons. We study the strong coupling constants $B_{1}B^*\pi$, $B_{1}B_{0}\pi$, and $B_{1}B_{1}\pi$ vertices when both $\pi$ and $B^*[B_{0}(B_1)]$ can be off-shell. The interpolating currents $j^{\pi }=\bar{q} \gamma _5 q$, $j^{B_{0}}=\bar{q} Q$, $j_{\nu }^{B^*}=\bar{q} \gamma _{\nu } Q$, and $j_{\mu }^{B_{1}}=\bar{q} \gamma _{\mu } \gamma _5 Q$ are interpolating currents of the $\pi$, $B_{0}$, $B^*$, $B_{1}$ mesons, respectively with $q$ being the up or down quark and $Q$ being for the heavy quark fields. We write the three-point correlation function associated with the $B_{1}B^*\pi$, $B_{1}B_{0}\pi$, and $B_{1}B_{1}\pi$ vertices. For the off-shell $B^*[B_{0}(B_1)]$ meson, Fig. 1 (left), these correlation functions are given by

$$\begin{aligned} \Pi ^{B^*}_{\mu \nu }(p, p')&= i^2 \int \mathrm{d}^4x \mathrm{d}^4y e^{i(p'x-py)}\nonumber \\&\quad \times \left\langle 0 |\mathcal {T}\left\{ j_{\mu }^{B_{1}}(x) {j_{\nu }^{B^*}}^{\dagger }(0) {j^{\pi }}^{\dagger }(y)\right\} | 0 \right\rangle , \end{aligned}$$

(3)

$$\begin{aligned} \Pi ^{B_0}_{\mu }(p, p')&= i^2 \int \mathrm{d}^4x \mathrm{d}^4y e^{i(p'x-py)}\nonumber \\&\quad \times \left\langle 0 |\mathcal {T}\left\{ j_{\mu }^{B_{1}}(x) {j^{B_0}}^{\dagger }(0) {j^{\pi }}^{\dagger }(y)\right\} | 0 \right\rangle , \end{aligned}$$

(4)

$$\begin{aligned} \Pi ^{B_1}_{\mu \nu }(p, p')&= i^2 \int \mathrm{d}^4x \mathrm{d}^4y e^{i(p'x-py)}\nonumber \\&\quad \times \left\langle 0 |\mathcal {T}\left\{ j_{\mu }^{B_{1}}(x) {j_{\nu }^{B_1}}^{\dagger }(0) {j^{\pi }}^{\dagger }(y)\right\} | 0 \right\rangle , \end{aligned}$$

(5)

and for the off-shell $\pi$ meson, Fig. 1 (right), these quantities are

$$\begin{aligned} \Pi ^{\pi }_{\mu \nu }(p, p')&= i^2 \int \mathrm{d}^4x \mathrm{d}^4y e^{i(p'x-py)}\nonumber \\&\quad \times \left\langle 0 |\mathcal {T}\left\{ j_{\mu }^{B_{1}}(x) {j^{\pi }}^{\dagger }(0) {j_{\nu }^{B^*}}^{\dagger }(y)\right\} | 0 \right\rangle , \end{aligned}$$

(6)

$$\begin{aligned} \Pi ^{\pi }_{\mu }(p, p')&= i^2 \int \mathrm{d}^4x \mathrm{d}^4y e^{i(p'x-py)}\nonumber \\&\quad \times \left\langle 0 |\mathcal {T}\left\{ j_{\mu }^{B_{1}}(x) {j^{\pi }}^{\dagger }(0) {j^{B_0}}^{\dagger }(y)\right\} | 0 \right\rangle , \end{aligned}$$

(7)

$$\begin{aligned} \Pi ^{\pi }_{\mu \nu }(p, p')&= i^2 \int \mathrm{d}^4x \mathrm{d}^4y e^{i(p'x-py)}\nonumber \\&\quad \times \left\langle 0 |\mathcal {T}\left\{ j_{\mu }^{B_{1}}(x) {j^{\pi }}^{\dagger }(0) {j_{\nu }^{B_1}}^{\dagger }(y)\right\} | 0 \right\rangle . \end{aligned}$$

(8)

Fig. 1

Perturbative diagrams for off-shell bottom (left) and off-shell pion (right)

Correlation function in (Eqs. 3–8) in the OPE and in the phenomenological side can be written in terms of several tensor structures. We can write a sum rule to find the coefficients of each structure, leading to as many sum rules as structures. In principle all the structures should yield the same final results, but the truncation of the OPE changes different structures in different ways. Therefore some structures lead to sum rules which are more stable. In the simplest cases, such as in the $B_1B^*\pi$ vertex, we have five structures, $g_{\mu \nu }$, $p_{\mu }p_{\nu }$, $p_{\mu }p'_{\nu }$, $p'_{\mu }p_{\nu }$, and $p'_{\mu }p'_{\nu }$. We have selected the $g_{\mu \nu }$ structure. In this structure the quark condensate (the condensate of lower dimension) contributes in the case of bottom meson off-shell. We also did the calculations for the structure $p'_{\mu }p_{\nu }$, and the final results of both structures in predicting of $g_{\mu \nu }$ are the same for $g_{B_1B^*\pi }$, and in the $B_1B_0\pi$ vertex, we have the two structures $p'_{\mu }$ and $p_{\mu }$. The two structures give the same result for $g_{B_1B_0\pi }$. We have chosen the $p'_{\mu }$ structure. In the $B_1B_1\pi$ vertex we have only one structure $\epsilon ^{ \alpha \beta \mu \nu } p_\alpha p'_\beta$ is written as

$$\begin{aligned} \Pi ^{B^*(\pi )}_{\mu \nu }(p^2, p'^2,q^2)&= (\Pi ^{B^*(\pi )}_{per}+\Pi ^{B^*(\pi )}_{nonper}) g_{\mu \nu }+\cdots ,\nonumber \\ \Pi ^{B_0(\pi )}_{\mu }(p^2, p'^2,q^2)&= (\Pi ^{B_0(\pi )}_{per} +\Pi ^{B_0(\pi )}_{nonper})p'_{\mu }+\cdots ,\nonumber \\ \Pi ^{B_1(\pi )}_{\mu \nu }(p^2, p'^2,q^2)&= (\Pi ^{B_1(\pi )}_{per}+\Pi ^{B_1(\pi )}_{nonper}) \epsilon ^{ \alpha \beta \mu \nu } p_\alpha p'_\beta g\nonumber \\ \end{aligned}$$

(9)

where $\cdots$ denotes other structures and higher states.

The phenomenological side of the vertex function is obtained by considering the contribution of three complete sets of intermediate states with the same quantum number that should be inserted in Eqs. (3–8). We use the standard definitions for the decay constants $f_M$ ($f_{\pi }$, $f_{B_0}$, $f_{B^*}$ and $f_{B_{1}}$) and we have

$$\begin{aligned} \begin{aligned}&\langle 0 | j^{\pi } | \pi (p) \rangle = \frac{m_{\pi }^2 f_{\pi }}{m_u+m_d}, \\&\langle 0 | j^{B_{0}} | B_{0}(p) \rangle = m_{B_{0}} f_{B_{0}}, \\&\langle 0 | j_{\nu }^{B^*} | B^*(p, \epsilon ) \rangle = m_{B^*} f_{B^*} \epsilon _{\nu }(p), \\&\langle 0 | j_{\mu }^{B_{1}} | {B_{1}}(p', \epsilon ') \rangle = m_{B_{1}} f_{B_{1}} \epsilon '_{\mu }(p'). \end{aligned} \end{aligned}$$

(10)

The phenomenological part for the $g_{\mu \nu }$ structure associated with the $B_1B^*\pi$ vertex, when $B^*(\pi )$ is an off-shell meson, is as follows:

$$\begin{aligned}&\Pi ^{B^*(\pi )}_{\mu \nu }=-g_{B_{1}B^*\pi }^{B^*(\pi )}(q^2) \nonumber \\&\quad \times \frac{ m_{\pi }^2 m_{B^*}f_{\pi } f_{B^*} f_{B_1}(m_{B_{1}}^2- m_{\pi (B^*)}^2-q^2)}{2(q^2-m_{B^*(\pi )}^2)(p^2-m_{\pi (B^*)}^2) (p'^2-m_{B_{1}}^2)(m_u+m_d)}\nonumber \\&\quad \times g_{\mu \nu } +h.r. \end{aligned}$$

(11)

The phenomenological part for the $p'_{\mu }$ structure related to the $B_1B_0\pi$ vertex, when $B_0(\pi )$ is an off-shell meson, is

$$\begin{aligned}&\Pi ^{B_0(\pi )}_{\mu }=-g_{B_{1}B_0\pi }^{B_0(\pi )}(q^2) \nonumber \\&\quad \times \frac{ m_{\pi }^2m_{B_0}m_{B^*} f_{\pi } f_{B^*} f_{B_{1}}(m_{B_{1}}^2+ m_{\pi (B_0)}^2-q^2)}{2(q^2-m_{B_0(\pi )}^2)(p^2-m_{\pi (B_0)}^2) (p'^2-m_{B_{1}}^2)(m_u+m_d)}\nonumber \\&\quad \times p'_{\mu }+h.r. \end{aligned}$$

(12)

The phenomenological part for the $\epsilon ^{ \alpha \beta \mu \nu } p_\alpha p'_\beta$ structure related to the $B_1B_1\pi$ vertex, when $B_1(\pi )$ is an off-shell meson, is

$$\begin{aligned}&\Pi ^{B_1(\pi )}_{\mu \nu }=-i g_{B_1B_1\pi } ^{B_1(\pi )}(q^2)\nonumber \\&\quad \times \frac{m_{\pi }^2 m_{B_1} ^2 f_{\pi } f_{B_1}^2 }{(q^2-m_{B_1(\pi )}^2) (p^2-m_{\pi (B_1)}^2)(p'^2-m_{B_1}^2)(m_u+m_d)}\nonumber \\&\quad \times \epsilon ^{ \alpha \beta \mu \nu } p_\alpha p'_{\beta }+h.r. \end{aligned}$$

(13)

In Eqs. (11–13), h.r. represents the contributions of the higher states and continuum.

With the help of the operator product expansion (OPE) in the Euclidean region, where $p^2,p'^2\rightarrow -\infty$, we calculate the QCD side of the correlation function (Eqs. 3–8) containing perturbative and non-perturbative parts. In practice, only the first few condensates contribute significantly, the most important ones being the 3-dimension, $\langle \bar{d}d\rangle$, and the 5-dimension, $\langle \bar{d}\sigma _{\alpha \beta } T^{a}G^{a\alpha \beta }d\rangle$, condensates. For each invariant structure, i, we can write

$$\begin{aligned} \Pi ^{(\mathrm {theor})}_{i}(p^2, p'^2, q^2) \!&= \! -\frac{1}{4 \pi ^2} \int _{(m_d+m_b)^2}^{\infty } \mathrm{d}s'\int _{s_{1(2)}}^{\infty } \nonumber \\&\times \mathrm{d}s\frac{\rho _{i}(s, s', q^2)}{(s-p^2)(s'-p'^2)}+C^{3}_{i}\langle \bar{d}d\rangle \nonumber \\&+ C_{i}^5\langle \bar{d}\sigma _{\alpha \beta } T^{a}G^{a\alpha \beta }d\rangle + \cdots , \end{aligned}$$

(14)

where $\rho _i(s, s', q^2)$ is the spectral density, $C_i$ are the Wilson coefficients, and $G^{a\alpha \beta }$ is the gluon field strength tensor. We take for the strange quark condensate $\langle \overline{d}d\rangle =- (0.24\pm 0.01)^3 ~\mathrm{GeV}^3$ [19] and for the mixed quark–gluon condensate $\langle \bar{d}\sigma _{\alpha \beta } T^{a}G^{a\alpha \beta }d\rangle =m_0^2\langle \overline{d}d\rangle$ with $m_0^2=(0.8\pm 0.2)~\mathrm{GeV}^2$ [20, 21].

Furthermore, we make the usual assumption that the contributions of higher resonances are well approximated by the perturbative expression

$$\begin{aligned} -\frac{1}{4 \pi ^2} \int _{s'_0}^{\infty } \mathrm{d}s'\int _{s_0}^{\infty } \mathrm{d}s\frac{\rho _{i}(s, s', q^2)}{(s-p^2)(s'-p'^2)}, \end{aligned}$$

(15)

with appropriate continuum thresholds $s_0$ and $s'_0$.

The Cutkosky rule allows us to obtain the spectral densities of the correlation function for the Lorentz structures appearing in the correlation function. The leading contribution comes from the perturbative term, shown in Fig. 1. As a result, the spectral densities are obtained in the case of the double discontinuity in Eq. (15) for the vertices; see Appendix A.

We proceed to calculate the non-perturbative contributions on the QCD side that contain the quark–quark and quark–gluon condensate. The quark–quark and quark–gluon condensate is considered for the case when the light quark is a spectator [22, 23]. Therefore only three important diagrams of dimension 3 and 5 remain from the non-perturbative part contributions when the bottom mesons are off shell. These diagrams, named quark–quark and quark–gluon condensates, are depicted in Fig. 2. For the off-shell pion, there are no quark–quark and quark–gluon condensate contributions.

Fig. 2

Contribution of the quark–quark and quark–gluon condensate for the bottom off-shell

After some straightforward calculations and applying the double Borel transformations with respect to $p^2(p^2\rightarrow M^2)$ and $p'^2(p'^2\rightarrow M'^2)$,

$$\begin{aligned} \begin{aligned} {{B}}_{p^2}(M^2)\left( \frac{1}{p^2-m^2_u}\right) ^m=\frac{(-1)^m}{\Gamma (m)} \frac{e^{-\frac{m_u^2}{M^2}}}{(M^2)^m}, \\ {{B}}_{{p^{'}}^2}(M'^2)\left( \frac{1}{{p^{'}}^2-m^2_b}\right) ^n=\frac{(-1)^n}{\Gamma (n)} \frac{e^{-\frac{m_b^2}{M'^2}}}{(M'^2)^n}, \end{aligned} \end{aligned}$$

(16)

where $M^2$ and $M'^2$ are the Borel parameters, the contributions of the quark–quark and quark–gluon condensate, for the bottom meson off-shell case, are given by

$$\begin{aligned} \Pi _{(\mathrm{non-per})}^\mathrm{bottom}&= \langle \overline{d}d\rangle ~\frac{C^\mathrm{bottom}}{M^4M'^4}. \end{aligned}$$

(17)

The explicit expressions for $C_{B_1B^*\pi [B_1B_0\pi (B_1B_1\pi )]}^\mathrm{bottom}$ associated with the $B_1B^*\pi$, $B_1B_0\pi$, and $B_1B_1\pi$ vertices are given in Appendix B.

The gluon–gluon condensate is considered when the heavy quark is a spectator [24], the bottom mesons are off-shell, and there is no gluon–gluon condensate contribution. Our numerical analysis shows that the contribution of the non-perturbative part containing the quark–quark and quark–gluon diagrams is about 13 % and the gluon–gluon contribution is about 4 % of the total and the main contribution comes from the perturbative part of the strong form factors and we can ignore the gluon–gluon contribution in our calculation.

The QCDSR for the strong form factors are obtained after performing the Borel transformation with respect to the variables $p^2 (B_{p^2}(M^2))$ and $p'^2(B_{p'}^2(M'^2))$ on the physical (phenomenological) and QCD parts; equating these two representations of the correlations, we obtain the corresponding equations for the strong form factors as follows.

$\bullet$ For the $g_{B_1B^*\pi }(Q^2)$ form factors:

$$\begin{aligned} \quad ~ g^{B^*}_{B_1B^*\pi }(Q^2) \!&= \! \frac{2(Q^2+m^2_{B^*})(m_u+m_d)}{m_{\pi }^2 m_{B^*} f_{\pi }f_{B^*}f_{B_1}(m_{B_1}^2-m_{\pi }^2+Q^2)} ~e^{\frac{m_{\pi }^2}{M^2}}\nonumber \\&\times \,e^{\frac{m_{B_1}^2}{M'^2}} \left\{ -\frac{1}{4\pi ^2}\int ^{s'_0}_{(m_b +m_d)^2} \mathrm{d}s' \int ^{s_0}_{s_{1}} \mathrm{d}s \rho ^{B^*}(s,s',Q^2)\right. \nonumber \\&\left. \times \, e^{-\frac{s}{M^2}} e^{-\frac{s'}{M'^2}}+ \langle d\bar{d} \rangle \frac{C_{B_1B^*\pi }^{B^*}}{M^2M'^2} \right\} , \end{aligned}$$

(18)

$$\begin{aligned} g^{\pi }_{B_1B^*\pi }(Q^2) \!&= \! \frac{2(Q^2+m^2_{\pi })(m_u+m_d)}{m_{\pi }^2 m_{B^*} f_{\pi }f_{B^*}f_{B_1}(m_{B_1}^2-m_{B^*}^2+Q^2)}\nonumber \\&\times \,~e^{\frac{m_{B^*}^2}{M^2}} e^{\frac{m_{B_1}^2}{M'^2}} \left\{ -\frac{1}{4\pi ^2}\int ^{s'_0}_{(m_b +m_d)^2} \mathrm{d}s'\right. \nonumber \\&\left. \times \int ^{s_0}_{s_{2}} \mathrm{d}s \rho ^{\pi }(s,s',Q^2) e^{-\frac{s}{M^2}} e^{-\frac{s'}{M'^2}}\right\} . \end{aligned}$$

(19)

$\bullet$ For the $g_{B_1B_0\pi }(Q^2)$ form factors:

$$\begin{aligned} \quad ~ g^{B_0}_{B_1B_0\pi }(Q^2)&= \frac{2(Q^2+m^2_{B_0})(m_u+m_d)}{m_{\pi }^2 m_{B_0}m_{B_1} f_{\pi }f_{B_0}f_{B_1}(m_{B_1}^2+m_{\pi }^2+Q^2)}\nonumber \\&\times \,~e^{\frac{m_{\pi }^2}{M^2}} e^{\frac{m_{B_1}^2}{M'^2}} \left\{ -\frac{1}{4\pi ^2}\int ^{s'_0}_{(m_b +m_d)^2} \mathrm{d}s'\right. \nonumber \\&\left. \!\times \! \int ^{s_0}_{s_{1}} \mathrm{d}s \rho ^{B_0}(s,s',Q^2) e^{-\frac{s}{M^2}} e^{-\frac{s'}{M'^2}}\!+\!\langle d\bar{d} \rangle \frac{C_{B_1B_0\pi }^{B_0}}{M^2M'^2}\!\! \right\} ,\nonumber \\ \end{aligned}$$

(20)

$$\begin{aligned} \quad ~ g^{\pi }_{B_1B_0\pi }(Q^2)&= \frac{2(Q^2+m^2_{\pi })(m_u+m_d)}{m_{\pi }^2 m_{B_0}m_{B_1} f_{\pi }f_{B_0}f_{B_1}(m_{B_1}^2+m_{B_0}^2+Q^2)}\nonumber \\&\times \,~e^{\frac{m_{B_0}^2}{M^2}} e^{\frac{m_{B_1}^2}{M'^2}} \left\{ -\frac{1}{4\pi ^2}\int ^{s'_0}_{(m_b \!+\! m_d)^2} \mathrm{d}s'\right. \nonumber \\&\left. \times \int ^{s_0}_{s_{2}} \mathrm{d}s \rho ^{\pi }(s,s',Q^2) e^{-\frac{s}{M^2}} e^{-\frac{s'}{M'^2}}\right\} . \end{aligned}$$

(21)

$\bullet$ For the $g_{B_1B_1\pi }(Q^2)$ form factors:

$$\begin{aligned} \quad ~ g^{B_1}_{B_1B_1\pi }(Q^2)&= -i \frac{(Q^2+m^2_{B_1})(m_u+m_d)}{m_{\pi }^2 m_{B_1}^2 f_{\pi }f_{B_1}^2}\nonumber \\&\times \, ~e^{\frac{m_{\pi }^2}{M^2}}e^{\frac{m_{B_1}^2}{M'^2}} \left\{ -\frac{1}{4\pi ^2}\int ^{s'_0}_{(m_b +m_d)^2} \mathrm{d}s'\right. \nonumber \\&\left. \!\times \! \int ^{s_0}_{s_{1}} \mathrm{d}s \rho ^{B_1}(s,s',Q^2) e^{-\frac{s}{M^2}} e^{-\frac{s'}{M'^2}}\!+\!\langle d\bar{d} \rangle \frac{C_{B_1B_1\pi }^{B_1}}{M^2M'^2} \right\} ,\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned} \quad ~ g^{\pi }_{B_1B_1\pi }(Q^2)&= -i\frac{(Q^2+m^2_{\pi })(m_u+m_d)}{m_{\pi }^2 m_{B_1}^2 f_{\pi }f_{B_1}^2}\nonumber \\&\times \, ~e^{\frac{m_{B_1}^2}{M^2}}e^{\frac{m_{B_1}^2}{M'^2}} \left\{ -\frac{1}{4\pi ^2}\int ^{s'_0}_{(m_b +m_d)^2} \mathrm{d}s'\right. \nonumber \\&\left. \times \int ^{s_0}_{s_{2}} \mathrm{d}s \rho ^{\pi }(s,s',Q^2) e^{-\frac{s}{M^2}} e^{-\frac{s'}{M'^2}}\right\} , \end{aligned}$$

(23)

where $Q^2=-q^2$, $s_0$, and $s'_0$ are the continuum thresholds, and $s_1$ and $s_2$ are the lower limits of the integrals over $s$, thus

$$\begin{aligned} s_{1(2)}=\frac{(m_{d(b)}^{2}+q^2-m_{u}^{2}-s') (m_{u}^{2}s'-q^2m_{d(b)}^{2})}{(m_{u}^{2}-q^2)(m_{d(b)}^{2}-s')}. \end{aligned}$$

(24)

3 Numerical analysis

In this section, the expressions of QCDSR obtained for the considered strong coupling constants are investigated. We choose the values of the meson and quark masses as $m_u=(1.7\hbox {--}3.3)~\mathrm{MeV}$, $m_d = (3.5\hbox {--}6.0)~\mathrm{MeV}$, $m_{\pi }=14~\mathrm{MeV}$, $m_{B^*}=5.32~\mathrm{GeV}$, $m_{D^*}=2.01~\mathrm{GeV}$, $m_{B_1}=5.72~\mathrm{GeV}$, $m_{D_1}=2.42~\mathrm{GeV}$, $m_{B_0}=5.70~\mathrm{GeV}$, and $m_{D_0}=2.36~\mathrm{GeV}$. Also the leptonic decay constants used in this calculation are taken as $f_{\pi }=130.41~\mathrm{MeV}$ [25], $f_{B^*}=238\pm 10~\mathrm{MeV}$, $f_{D^*}=340\pm 12~\mathrm{MeV}$ [26], $f_{B_1}= 196.9 \pm 8.9~ \mathrm{MeV}$, $f_{D_1}= 218.9 \pm 11.3~\mathrm{MeV}$ [27], $f_{B_0}=280\pm 31~\mathrm{MeV}$, and $f_{D_0}=334 \pm 8.6~\mathrm{MeV}$ [28]. For a comprehensive analysis of the strong coupling constants, we use the following values of the quark masses $m_b$ and $m_c$ in two sets: set I, $m_b(\overline{MS})=4.67~\mathrm{GeV}$ [29], $m_c=1.26~\mathrm{GeV}$ [16, 30] and set II, $m_b(1S)=4.19~\mathrm{GeV}$ [29], $m_c=1.47~\mathrm{GeV}$ [16, 30].

The expressions for the strong form factors in Eqs. (18–23) should not depend on the Borel variables $M^2$ and $M'^2$. Therefore, one has to work in a region where the approximations made are supposedly acceptable and where the result depends only moderately on the Borel variables. In this work we use the following relations between the Borel masses $M ^2$ and $M'^2$ [8, 9]: $\frac{M^2}{M'^2}=\frac{m_{\pi }^2}{m_{B_1}^2-m_{b}^2}$ for the bottom meson off-shell and $M^2=M'^2$ for the pion meson off-shell. The values of the continuum thresholds $s_0=(m+\Delta )^2$ and $s'_0=(m_{B_1}+\Delta )^2$, where m is the $\pi$ mass, for $B^*[B_0(B_1)]$ off-shell and the $B^*[B_0(B_1)]$ meson mass, for $\pi$ off-shell and $\Delta$ varies between $0.4~\mathrm{GeV} \le \Delta \le 1~\mathrm{GeV}$ [16, 30].

Using $\Delta =0.7~\mathrm{GeV}$, $m_b=4.67~\mathrm{GeV}$, and fixing $Q^2 = 1~\mathrm{GeV}^2$, we found a good stability of the sum rule in the interval $10~\mathrm{GeV}^2\le M ^2\le 20~\mathrm{GeV}^2$ for the two cases of bottom and pion being off-shell. The dependence of the strong form factors $g_{B_1B^*\pi }$, $g_{B_1B_0\pi }$, and $g_{B_1B_1\pi }$ on the Borel mass parameters for off-shell bottom and pion mesons are shown in Fig. 3.

Fig. 3

The strong form factors $g_{B_1B^*\pi }$, $g_{B_1B_0\pi }$, and $g_{B_1B_1\pi }$ as functions of the Borel mass parameter $M^2$ for the two cases of bottom off-shell meson (left) and pion off-shell mesons (right)

We have chosen the Borel mass to be $M^2= 13~\mathrm{GeV}^2$. Having determined $M^2$, we calculated the $Q^2$ dependence of the form factors. We present the results in Fig. 4 for the $g_{B_1B^*\pi }$, $g_{B_1B_0\pi }$, and $g_{B_1B_1\pi }$ vertices. In these figures, the small circles and boxes correspond to the form factors in the interval where the sum rule is valid. As is seen, the form factors and their fit functions well coincide.

Fig. 4

The strong form factors $g_{B_1B^*\pi }$, $g_{B_1B_0\pi }$, and $g_{B_1B_1\pi }$ on $Q^2$ for the bottom off-shell and the pion off-shell mesons. The small circles and boxes correspond to the form factors via the 3PSR calculations

We discuss a difficulty inherent to the calculation of coupling constants with QCDSR. The solution of Eqs. (18–23) is numerical and restricted to a singularity-free region in the $Q^2$ axis, usually located in the space-like region. Therefore, in order to reach the pole position, $Q^2 = -m_m^2$, we must fit the solution, by finding a function $g(Q^2)$ which is then extrapolated to the pole, yielding the coupling constant.

The uncertainties associated with the extrapolation procedure, for each vertex, are minimized by performing the calculation twice, first putting one meson and then another meson off-shell, to obtain two form factors $g^\mathrm{bottom}$ and $g^\mathrm{pion}$, and equating these two functions at the respective poles. The superscripts in parentheses indicate which meson is off-shell. In order to reduce the freedom in the extrapolation and constrain the form factor, we calculate and fit simultaneously the values of $g(Q^2)$ with the pion off-shell. We tried to fit our results to a monopole form, since this is often used for form factors [31].

For the off-shell pion meson, our numerical calculations show that the sufficient parametrization of the form factors with respect to $Q^2$ is

$$\begin{aligned} g(Q^2)=\frac{A}{Q^2+B}, \end{aligned}$$

(25)

and for the off-shell bottom meson the strong form factors can be fitted by the exponential fit function as given by

$$\begin{aligned} g(Q^2)=A~e^{-Q^2/B}. \end{aligned}$$

(26)

The values of the parameters $A$ and $B$ are given in Table 1. We define the coupling constant as the value of the strong coupling form factor at $Q^2 = -m_m^2$ in Eqs. (25) and (26), where $m_m$ is the mass of the off-shell meson. Considering the uncertainties that result with the continuum threshold and the uncertainties in the values of the other input parameters, we obtain the average values of the strong coupling constants in the different sets as shown in Table 2.

Table 1 Parameters appearing in the fit functions for the $g_{B_1B^*\pi }$, $g_{B_1B_0\pi }$, and $g_{B_1B_1\pi }$ vertices for $\Delta _1=0.7 ~\mathrm{GeV}$ and $m_b(\overline{MS})=4.67~\mathrm{GeV}$ (set I) and $m_b(1S)=4.19~\mathrm{GeV}$ (set II)

Table 2 The strong coupling constants $g_{B_1B^*\pi }$, $g_{B_1B_0\pi }$, and $g_{B_1B_1\pi }$

We see that the two cases considered here, the off-shell bottom and pion meson, give compatible results for the coupling constant.

With the same method as described in Sect. 2 with little change in the containing perturbative and non-perturbative parts, where $\rho _{D_1D^*\pi [D_1D_0\pi (D_1D_1\pi )]}^{\mathrm{charm}(\mathrm{pion})}=\rho _{B_1B^*\pi [B_1B_0\pi (B_1B_1\pi )]}^{\mathrm{bottom}(\mathrm{pion})}{|}_{b\rightarrow c}$, $C^{\mathrm{charm}}_{D_1D^*\pi [D_1D_0\pi (D_1D_1\pi )]}=C_{B_1B^*\pi [B_1B_0\pi (B_1B_1\pi )]}^{\mathrm{bottom}}{|}_{b\rightarrow c}$, we can easily find similar results in Eqs. (18–23) for strong form factors $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$, and also we use the following relations between the Borel masses $M ^2$ and $M'^2$: $\frac{M^2}{M'^2}=\frac{m_{\pi }^2}{m_{D_1}^2-m_{c}^2}$ for the charm meson off-shell and $M^2=M'^2$ for the pion meson off-shell. The values of the continuum thresholds $s_0=(m+\Delta )^2$ and $s'_0=(m_{D_1}+\Delta )^2$, where m is the $\pi$ mass, for $D^*[D_0(D_1)]$ off-shell and the $D^*[D_0(D_1)]$ meson mass, for the $\pi$ off-shell and $\Delta$ with $0.4~\mathrm{GeV} \le \Delta \le 1~\mathrm{GeV}$.

Using $\Delta =0.7~\mathrm{GeV}$, $m_c=1.26~\mathrm{GeV}$ and fixing $Q^2 = 1~\mathrm{GeV}^2$, we found a good stability of the sum rule in the interval $7~\mathrm{GeV}^2\le M^2\le 17~\mathrm{GeV}^2$ for the two cases of charm and pion off-shell. The dependences of the strong form factors $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$ on the Borel mass parameters for the off-shell charm and pion mesons are shown in Fig. 5.

Fig. 5

The strong form factors $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$ as functions of the Borel mass parameter $M^2$ for the two cases of charm off-shell meson (left), and pion off-shell meson (right)

We have chosen the Borel mass to be $M^2= 10~\mathrm{GeV}^2$. Having determined $M^2$, we calculated the $Q^2$ dependence of the form factors. We present the results in Fig. 6 for the $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$ vertices.

Fig. 6

The strong form factors $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$ dependence on $Q^2$ for the charm off-shell and the pion off-shell mesons. The small circles and boxes correspond to the form factors via the 3PSR calculations

The dependence of the above strong form factors on $Q^2$ for the full physical region is estimated, using Eqs. (25) and (26), for the pion and charm off-shell mesons, respectively. The values of the parameters $A$ and $B$ are given in Table 3.

Table 3 Parameters appearing in the fit functions for the $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$ vertices for $\Delta _1=0.7 ~\mathrm{GeV}$ and $m_c=1.26$ (set I) and $m_c=1.47$ (set II)

Considering the uncertainties that result with the continuum threshold and the uncertainties in the values of the other input parameters, we obtain the average values of the strong coupling constants in different values of the different sets shown in Table 4.

Table 4 The strong coupling constants $g_{D_1D^*\pi }$, $g_{D_1D_0\pi }$, and $g_{D_1D_1\pi }$

In Table 5 we compare our obtained values, with the findings of others, previously calculated. From this Table we see that our result of the coupling constants is in a fair agreement with the calculations in Refs. [32, 33, 35].

Table 5 Comparison of our results with the other published results

4 Conclusion

In this article, we analyzed the vertices $B_1B^*\pi$, $B_1B_0\pi$, $B_1B_1\pi$, $D_1D^*\pi$, $D_1D_0\pi$, and $D_1D_1\pi$ within the framework of the three-point QCDSR approach in an unified way. The strong coupling constants could give useful information about strong interactions of the strange bottomed and strange charmed mesons and also are important ingredients for estimating the absorption cross section of the $J/\psi$ by the $\pi$ mesons.

Appendices

Appendix A: Perturbative contributions

In this appendix, The perturbative contributions for the sum rules defined in Eqs. (18–23) are

$$\begin{aligned} \rho ^{B^*(\pi )}_{B_1B^*\pi } \!&= \! 4 N_c I_0 k\left[ 2A\left( m_1-m_{3(2)}\right) -m_1m_2m_3+m_2m_3^2+m_3^3 \right. \nonumber \\&\left. -m_1m_3^2-\frac{\Delta }{2}\left( m_2+m_3\right) \!+\! \frac{\Delta '}{2}\left( m_1-m_3\right) \!+\! \frac{m_3u}{2}\right] ,\nonumber \\ \rho ^{B_0(\pi )}_{B_1B_0\pi } \!&= \! 4 N_c I_0\left[ B_2\left( m_2m_3-km_1m_2 \!+\! km_1m_3-m_3^2 \!+\! \Delta \!-\! \frac{u}{2}\right) \right. \nonumber \\&\left. +km_3^2-m_3m_1-k\frac{\Delta }{2}\right] , \nonumber \\ \rho ^{B_1(\pi )}_{B_1B_1\pi } \!&= \! 4i N_c I_0\left[ B_1\left( m_3-km_1\right) +B_2\left( m_2+m_3\right) +m_3\right] . \end{aligned}$$

The explicit expressions of the coefficients in the spectral densities entering the sum rules are given as

$$\begin{aligned} I_0(s,s',q^2)&= \frac{1}{4\lambda ^\frac{1}{2}(s,s',q^2)},\nonumber \\ \Delta&= (s+m_3^2-m_1^2),\nonumber \\ \Delta '&= (s'+m_3^2-m_2^2),\nonumber \\ u&= s+s'-q^2,\nonumber \\ \lambda (s,s',q^2)&= s^2+ s'^2+ q^4- 2sq^2- 2s'q^2- 2ss',\nonumber \\ A&= -\frac{1}{2\lambda (s,s',q^2)}[4ss'm_3^2-s\Delta '^2-s'\Delta ^2\nonumber \\&-u^2m_3^2+u\Delta \Delta '],\nonumber \\ B_1&= \frac{1}{\lambda (s,s',q^2)} \left[ 2 s' \Delta -\Delta ' u\right] ,\nonumber \\ B_2&= \frac{1}{\lambda (s,s',q^2)} \left[ 2 s \Delta ' -\Delta u\right] , \end{aligned}$$

where $k=1$, $m_1=m_u$, $m_2=m_b$, $m_3=m_d$ for the bottom meson off-shell and $k=-1$, $m_1=m_u$, $m_2=m_d$, $m_3=m_b$ for the pion meson off-shell, $N_c=3$ represents the color factor.

Appendix B: Non-perturbative contributions

In this appendix, the explicit expressions of the coefficients of the quark–quark and quark–gluon condensate of the strong form factors for the vertices $B_1B^*\pi$, $B_1B_0\pi$, and $B_1B_1\pi$ on applying the double Borel transformations are given:

$$\begin{aligned} C_{B_1B^*\pi }^{B^*}&= \left( \frac{7M^2m_b^2m_0^2}{24}-\frac{M^2M'^2m_0^2}{6}+\frac{M'^2m_b^2m_0^2}{8}\right. \\&-\frac{m_0^2m_b^4}{8}-\frac{M^2M'^2m_bm_d}{4}+\frac{M^2M'^2m_b^2}{2}\\&-\frac{M^2m_b^3m_d}{4}+\frac{M^2m_bm_dq^2}{4}-\frac{M^2m_b^2m_d^2}{2}\\&-\frac{M^2m_0^2m_bm_u}{4}-\frac{3M'^2m_0^2m_bm_u}{4}\\&-M^2M'^2m_bm_u+\frac{m_0^2m_b^3m_u}{4}+\frac{M'^2m_0^2m_b^3m_u}{2M^2}\\&-\frac{M^2M'^2m_dm_u}{4}+\frac{M^2m_b^2m_dm_u}{2}\\&+\frac{M'^2m_b^2m_dm_u}{4}+\frac{M^2m_bm_d^2m_u}{2}+\frac{M'^2m_bm_d^2m_u}{2}\\&-\frac{m_b^3m_d^2m_u}{2}+\frac{M^2m_0^2m_u^2}{24}\\&+\frac{M'^2m_0^2m_u^2}{4}+\frac{M^2M'^2m_u^2}{2}-\frac{m_0^2m_b^2m_u^2}{4}\\&-\frac{M'^2m_bm_dm_u^2}{2}-\frac{M'^2m_d^2m_u^2}{2}+\frac{m_b^2m_d^2m_u^2}{2}\\&+\frac{m_0^2m_bm_u^3}{4}-\frac{M'^2m_0^2m_bm_u^3}{2M^2}+\frac{M'^2m_dm_u^3}{4}\\&-\frac{m_bm_d^2m_u^3}{2}-\frac{M'^2m_dm_uq^2}{4}-\frac{7M^2m_0^2q^2}{24}\\&-\frac{3M'^2m_0^2q^2}{8}-\frac{M^2M'^2q^2}{2}+\frac{m_0^2m_b^2q^2}{4}\\&+\frac{M^2m_d^2q^2}{2}+\frac{M'^2m_d^2q^2}{2}-\frac{m_b^2m_d^2q^2}{2}\\&\left. -\frac{m_0^2m_bm_uq^2}{4}\right) \times e^{-\frac{m_u^2}{M^2}}~e^{-\frac{m_b^2}{M'^2}},\\ C_{B_1B_0\pi }^{B_0}&= \left( \frac{M^2m_0^2m_b}{4}-\frac{M^2m_b^2m_d}{2}-\frac{M^2m_bm_d^2}{2}\right. \\&-\frac{3m_0^2M'^2m_u}{4}-M^2M'^2m_u+\frac{m_0^2m_b^2m_u}{4}\\&-\frac{M^2m_bm_dm_u}{2}+\frac{M^2m_d^2m_u}{2}-\frac{m_b^2m_d^2m_u}{2}\\&-\frac{M^2m_dm_u^2}{2}-\frac{M'^2m_dm_u^2}{2}+\frac{M'^2m_d^2mu}{2}\\&+\frac{m_0^2m_u^3}{4}-\frac{m_d^2m_u^3}{2}+\frac{M^2m_dq^2}{2}\\&\left. -\frac{m_0^2m_uq^2}{4}+\frac{m_d^2m_uq^2}{2}\right) \times e^{-\frac{m_u^2}{M^2}}~e^{-\frac{m_b^2}{M'^2}},\nonumber \\ C_{B_1B_1\pi }^{B_1}&= i\left( \frac{7m_0^2M^2}{12}+\frac{3m_0^2M'^2}{4}+M^2M'^2\right. \\&-\frac{m_0^2m_b^2}{2}-\frac{M^2m_bm_d}{2}-M^2m_d^2-M'^2m_d^2\\&\left. +\frac{M'^2m_dm_u}{2}-\frac{m_0^2m_u^2}{2} \!+\! \frac{m_0^2q^2}{2}-m_d^2q^2 \!+\! m_b^2m_d^2\right) \\&\times e^{-\frac{m_u^2}{M^2}}~e^{-\frac{m_b^2}{M'^2}}. \end{aligned}$$