Skip to main content
SpringerLink
Log in

Regular and chaotic motion of two bodies swinging on a rod

  • Regular Article - Statistical and Nonlinear Physics
  • Published:
The European Physical Journal B Aims and scope Submit manuscript

Abstract

We investigate regular and chaotic dynamics of two bodies swinging on a rod, which differs from all the other mechanical analogies: depending on initial conditions, its oscillation could end very quickly and the reason is not a drag force or energy loss. We use various tools to analyze motion, such as Poincaré section for quasi-periodic and chaotic cases. We calculate Lyapunov characteristic exponent by different methods including Finite Time Lyapunov Exponent analysis. Our calculations show that the maximal Lyapunov exponent is always positive except in the marginal cases when one observes quasi-periodic oscillations.

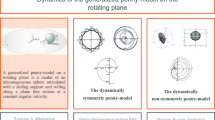
Graphic abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

References

  1. H. Poincaré, Mémoire sur les courbes définies par une équation différentielle (I). Journal de Mathatiques Pures et Appliquées 7, 375 (1881)

    MATH  Google Scholar 

  2. I. Bendixson, Sur les courbes définies par des équations différentielles, Acta Mathematica, vol. 24. (Springer, Heidelberg, 1901), p.1

    MATH  Google Scholar 

  3. P. Gaspard, Chaos and hydrodynamics. Phys. A 240, 54 (1997)

    Article  Google Scholar 

  4. J. Petrzela, Z. Hrubos, T. Gottans, Modeling deterministic chaos using electronic circuits. Radioengineering 20, 438 (2011)

    Google Scholar 

  5. T. Devolder et al., Chaos in magnetic nanocontact vortex oscillators. Phys. Rev. Lett. 123, 147701 (2019)

    Article  ADS  Google Scholar 

  6. E. Ott, Chaos in dynamical systems (University of Maryland, College Park, 1993)

    MATH  Google Scholar 

  7. D. Acheson, From calculus to chaos: an introduction to dynamics (Jesus College, Oxford, 1997)

    MATH  Google Scholar 

  8. G. Khomeriki, Parametric resonance induced chaos in magnetic damped driven pendulum. Phys. Lett. A 380, 2382 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  9. H.N. Huynh, L.Y. Chew, Two-coupled pendulum system: bifurcation, chaos and the potential landscape approach. Int. J. Bifurcat. Chaos 20, 2427 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. H. huynh, T. Nguyen, L. Chew, Numerical simulation and geometrical analysis on the onset of chaos in a system of two coupled pendulums. Commun. Nonlinear Sci. Numer. Simulat. 18, 291 (2013)

  11. K. Polczyn, A. Wijata, J. Awrejcewicz G. Wasilewski, Numerical and experimental study of dynamics of two pendulums under a magnetic field. Syst. Control Eng. 233, 441 (2019)

  12. J. Awrejcewicz. G. Kudra, G. Wasilewski, Experimental and numerical investigation of chaotic regions in the triple physical pendulum. Nonlinear Dyn. 50, 755 (2015)

  13. H. Suetani, K. Soejima, R. Matsuoka, U. Parlitz, H. Hata, Manifold learning approach for chaos in the dripping faucet. Phys. Rev. E 86, 036209 (2012)

    Article  ADS  Google Scholar 

  14. H.J. Hubbard, The forced damped pendulum: chaos, complication and control. Am. Math. Mon. 106, 741 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  15. N. Kudryashev, The generalized Duffing oscillator. Commun. Nonlinear Sci. Numer. Simul. 93, 105526 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  16. T. Stachowiak, T. Okada, A numerical analysis of chaos in the double pendulum. Elsevier 29, 4172437 (2006)

    MATH  Google Scholar 

  17. T. Stachowiak, T. Okada, A numerical analysis of chaos in the double pendulum. Chaos Solit. Fract. 29, 417 (2006)

    Article  ADS  MATH  Google Scholar 

  18. T. Shinbrot, C. Grebogi, J. Wisdom, J.A. Yorke, Chaos in a double pendulum. Am. J. Phys. 60, 491 (1992)

    Article  ADS  Google Scholar 

  19. Y. Lai, T. Tel, Transient chaos (2011)

  20. G. Haller, Distinguished material surfaces and coherent structures in 3d fluid flows. Phys. D 149, 248 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  21. C. Manchein, M.W. Beims, J.M. Rost, Characterizing the dynamics of higher dimensional nonintegrable conservative, systems. Chaos Interdiscip. J. Nonlinear Sci. 22, 033137 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  22. C. Manchein, M.W. Beims, J.M. Rost, Characterizing weak chaos in nonintegrable Hamiltonian systems: the fundamental role of stickiness and initial conditions. Phys. A 400 (2014)

  23. S. Sabarathinam, K. Thamilmanar, Transient chaos in a globally coupled system of nearly conservative Hamiltonian Duffing oscillators, Chaos, Solitons & Fractals, 73 (2015)

  24. D.R. Gonzalez, R.L. Speth, D.V. Gaitonde, M.J. Lewis, Finite-time Lyapunov exponent-based analysis for compressible flows. Chaos 26, 083112 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  25. F. Lekien, S.D. Ross, The computation of finite-time Lyapunov exponents on unstructured meshes and for non-Euclidean manifolds. Chaos 20, 017505 (2010)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. D. Garaboa-Paz, J. Eiras-Barca, F. Huhn, V. Perez-Munuzuri, Lagrangian coherent structures along atmospheric rivers. Chaos 25, 063105 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  27. S.C. Shadden, J.O. Dabiri, J.E. Marsden, Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18, 047105 (2006)

  28. M.A. Green, C.W. Rowley, A.J. Smits, Using hyperbolic Lagrangian coherent structures to investigate vortices in bioinspired fluid flows. Chaos 20, 017510 (2010)

    Article  ADS  MathSciNet  Google Scholar 

  29. T. Tel, M. Gruiz Chaotic dynamics: an introduction based on classical mechanics. Cambridge university (2006)

  30. E.M.A.M. Mendes , E.G. Nepomuceno, A very simple method to calculate the (positive) largest Lyapunov’s Exponent using interval extensions. Int. J. Bifurcat. Chaos 26 (2016)

  31. A. Wolf, J.B. Swift, H.L. Swinney, J.A. Vastano, Determining Lyapunov’s exponents from a time series. Phys. D 16, 285 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  32. M.T. Rosenstein, J.J. Collins, C.J. De Luca, A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D 65, 117 (1993)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank T. Gachechiladze, G. Bakhtadze, G. Khomeriki and M. Osmanov-Baisera for interesting discussions and valuable comments.

Author information

Authors and Affiliations

  1. School of Physics, Free University of Tbilisi, David Aghmashenebeli Alley, 0159, Tbilisi, Georgia

    Lazare Osmanov

  2. Department of Physics, Ivane Javakhishvili Tbilisi State University, 3 Chavchavadze, 0128, Tbilisi, Georgia

    Ramaz Khomeriki

Authors
  1. Lazare Osmanov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ramaz Khomeriki
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

LO contributed in setting general idea and implementation its numerical simulations as well as in writing manuscript draft. RK participated in choosing the methods for problem treatment and presentation of the simulation results as well as writing the paper draft.

Corresponding author

Correspondence to Lazare Osmanov.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Osmanov, L., Khomeriki, R. Regular and chaotic motion of two bodies swinging on a rod. Eur. Phys. J. B 95, 182 (2022). https://doi.org/10.1140/epjb/s10051-022-00435-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjb/s10051-022-00435-5

Search

Navigation