Skip to main content
Download PDF

Agent-based model for the h-index – exact solution

The European Physical Journal B volume 89, Article number: 21 (2016) Cite this article

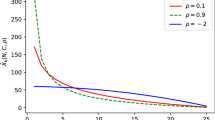
Abstract

Hirsch’s h-index is perhaps the most popular citation-based measure of scientific excellence. In 2013, Ionescu and Chopard proposed an agent-based model describing a process for generating publications and citations in an abstract scientific community [G. Ionescu, B. Chopard, Eur. Phys. J. B 86, 426 (2013)]. Within such a framework, one may simulate a scientist’s activity, and – by extension – investigate the whole community of researchers. Even though the Ionescu and Chopard model predicts the h-index quite well, the authors provided a solution based solely on simulations. In this paper, we complete their results with exact, analytic formulas. What is more, by considering a simplified version of the Ionescu-Chopard model, we obtained a compact, easy to compute formula for the h-index. The derived approximate and exact solutions are investigated on a simulated and real-world data sets.

References

  1. A.L. Barabási, R. Albert, Science 286, 509 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  2. D. Wang, C. Song, A.-L. Barabási, Science 342, 127 (2013)

    Article  ADS  Google Scholar 

  3. P. Deville, D. Wang, R. Sinatra, C. Song, V.D. Blondel, A.-L. Barabasi, Sci. Rep. 4, 4770 (2014)

    Article  ADS  Google Scholar 

  4. Q. Zhang, N. Perra, B. Goncalves, F. Ciulla, A. Vespignani, Sci. Rep. 3, 1640 (2013)

    ADS  Google Scholar 

  5. A. Mazloumian, D. Helbing, S. Lozano, R.P. Light, K. Borner, Sci. Rep. 3, 1167 (2013)

    Article  ADS  Google Scholar 

  6. S. Redner, Eur. Phys. J.B. 4, 131 (1998)

    Article  ADS  Google Scholar 

  7. M. Golosovsky, S. Solomon, J. Stat. Phys. 151, 340 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  8. H. Jeong, Z. Néda, A.L. Barabási, Europhys. Lett. 61, 567 (2003)

    Article  ADS  Google Scholar 

  9. Y.-H. Eom, S. Fortunato, PLoS One 6, e24926 (2011)

    Article  ADS  Google Scholar 

  10. P.L. Krapivsky, S. Redner, F. Leyvraz, Phys. Rev. Lett. 85, 4629 (2000)

    Article  ADS  Google Scholar 

  11. M.E.J. Newman, Phys. Rev. E 64, 025102 (2001)

    Article  ADS  Google Scholar 

  12. M. Golosovsky, S. Solomon, Phys. Rev. Lett. 109, 098701 (2012)

    Article  ADS  Google Scholar 

  13. D.J. de Solla Price, Science 149, 510 (1965)

    Article  ADS  Google Scholar 

  14. M. Wang, G. Yu, D. Yu, Physica A 387, 4692 (2008)

    Article  ADS  Google Scholar 

  15. M. Wang, G. Yu, D. Yu, Physica A 388, 4273 (2009)

    Article  ADS  Google Scholar 

  16. M. Perc, J. R. Soc. Interface 11, 20140378 (2014)

    Article  Google Scholar 

  17. G. Ionescu, B. Chopard, Eur. Phys. J. B 86, 426 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  18. J.E. Hirsch, Proc. Natl. Acad. Sci. 102, 16569 (2005)

    Article  ADS  Google Scholar 

  19. K. Fan, Math. Z. 49, 681 (1943)

    Article  Google Scholar 

  20. M. Gagolewski, R. Mesiar, Inf. Sci. 263, 166 (2014)

    Article  MathSciNet  Google Scholar 

  21. L. Egghe, R. Rousseau, Scientometrics 69, 121 (2006)

    Article  Google Scholar 

  22. A.F.J. van Raan, Scientometrics 67, 491 (2006)

    Article  Google Scholar 

  23. Q.L. Burrell, J. Informetrics 1, 16 (2007)

    Article  Google Scholar 

  24. M. Gagolewski, in Synergies of Soft Computing and Statistics for Intelligent Data Analysis, edited by R. Kruse et al. (Springer-Verlag, 2013), p. 359

  25. M. Gagolewski, J. Informetrics 4, 678 (2011)

    Article  Google Scholar 

  26. K. Barcza, A. Telcs, Scientometrics 81, 513 (2009)

    Article  Google Scholar 

  27. W. Glänzel, Scientometrics 77, 369 (2008)

    Article  Google Scholar 

  28. W. Glänzel, Scientometrics 77, 187 (2008)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Systems Research Institute, Polish Academy of Sciences, ul. Newelska 6, 01-447, Warsaw, Poland

    Barbara Żogała-Siudem, Anna Cena & Marek Gagolewski

  2. Institute of Computer Science, Polish Academy of Sciences,, International Ph.D. Studies Program, 01-248, Warsaw, Poland

    Barbara Żogała-Siudem & Anna Cena

  3. Faculty of Physics, Warsaw University of Technology, ul. Koszykowa 75, 00-662, Warsaw, Poland

    Grzegorz Siudem

  4. Faculty of Mathematics and Information Science, Warsaw University of Technology, ul. Koszykowa 75, 00-662, Warsaw, Poland

    Marek Gagolewski

Authors
  1. Barbara Żogała-Siudem
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Grzegorz Siudem
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Anna Cena
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Marek Gagolewski
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Grzegorz Siudem.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Żogała-Siudem, B., Siudem, G., Cena, A. et al. Agent-based model for the h-index – exact solution. Eur. Phys. J. B 89, 21 (2016). https://doi.org/10.1140/epjb/e2015-60757-1

Download citation

  • Received:

  • Revised:

  • Published:

  • DOI: https://doi.org/10.1140/epjb/e2015-60757-1

Keywords

  • Statistical and Nonlinear Physics