Magnetic moment of the $X_1(2900)$ state in the diquark–antidiquark picture

Abstract

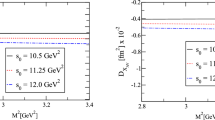
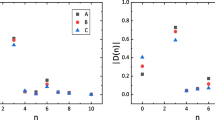
Motivated by the discovery of fully open-flavor tetraquark states $X_0(2900)$ and $X_1(2900)$ by the LHCb Collaboration, the magnetic dipole moment of the $X_1(2900)$ state with the quantum numbers $J^{P} = 1^{-}$ is determined in the diquark–antidiquark picture using the light-cone sum rules. The numerical result is obtained as $\mu _{X_1}=0.79^{+0.36}_{-0.39}\,\mu _N$. The magnetic moments of hadrons encompasses useful knowledge on the distributions of charge and magnetization their inside, which can be used to better understand their geometrical shapes and quark-gluon organizations. The observation of the $X_0(2900)$ and $X_1(2900)$ as the first two fully open-flavor multiquark states has opened a new window for investigation of the exotic states. The obtained results in the present study may shed light on the future experimental and theoretical searches on the properties of fully open-flavor multiquark states.

Appendix: explicit expression of \(\Delta (M^2,s_0)\)

In this appendix, we present the explicit expression of the function $\Delta (M^2,s_0)$ entering into the sum rule for the magnetic moment of the $X_1$ state. It is obtained as

$$\begin{aligned}&\Delta (M^2,s_0) = -\frac{e_c}{36864 m_c^2 \pi ^6} \Bigg [ 3 m_c^{12} \big (3 I[-6, 4] - 4 I[-5, 3]\big )\nonumber \\&\quad -48 m_c^{10} \big (I[-5, 4] + I[-4, 3]\big ) -48 m_c^9 m_s I[-4, 3] \nonumber \\&\quad + 3 m_c^8 \Big (30 I[-4, 4]+ P_ 1 (I[-4, 2] - 2 I[-3, 1]) \nonumber \\&\quad + 96 m_s P_ 3 \pi ^2 \big (I[-4, 2] - 2 I[-3, 1]\big ) - 24 I[-3, 3]\Big ) \nonumber \\&\quad +144 m_c^7 \big (4 P_ 3 \pi ^2 I[-3, 2] - m_s I[-3, 3]\big )\nonumber \\&\quad - 12 m_c^6 \Big (-32 m_ 0^2 m_s P_ 3 \pi ^2 I[-3, 1] \nonumber \\&\quad + 512 P_ 2^2 \pi ^4 I[-3, 1] + P_1 I[-3, 2] \nonumber \\&\quad + 96 m_s P_ 3 \pi ^2 I[-3, 2] + 6 I[-3, 4] + P_ 1 I[-2, 1]\nonumber \\&\quad + 96 m_s P_ 3 \pi ^2 I[-2, 1] + 4 I[-2, 3]\Big ) \nonumber \\&\quad - 12 m_c^5 \Big (48 P_ 3 \pi ^2 (m_ 0^2 I[-2, 1]+ 2 I[-2, 2]) \nonumber \\&\quad + m_s (P_ 1 I[-2, 1] + 12 I[-2, 3])\Big ) \nonumber \\&\quad + 3 m_c^4 \Big (64 m_ 0^2 m_s P_ 3 \pi ^2 I[-2, 1] \nonumber \\&\quad - 1024 P_ 2^2 \pi ^4 I[-2, 1] + 3 P_ 1 I[-2, 2] + 288 m_s P_ 3 \pi ^2 I[-2, 2] \nonumber \\&\quad + 7 I[-2, 4] - 2 P_ 1 I[-1, 1]- 192 m_s P_ 3 \pi ^2 I[-1, 1] \nonumber \\&\quad - 4 I[-1, 3]\Big ) + 8 \Big (-192 P_ 2^2 \pi ^4 (m_ 0^2 I[0, 0] + 2 I[0, 1]) \nonumber \\&\quad + m_s P_ 3 \pi ^2 \big (P_ 1 I[0, 0] + 24 m_ 0^2 I[0, 1]\big )\Big )- 192 m_c^2 I[0, 3] \nonumber \\&\quad - 16 m_c \Big (P_ 1 P_ 3 \pi ^2 I[0, 0] + 24 m_s \big (-8 P_ 2^2 \pi ^4 I[0, 0] + I[0, 3]\big )\Big ) \nonumber \\&\quad + 12 m_c^3 \big (48 P_ 3 \pi ^2 \big (I[-1, 2] \nonumber \\&\quad - m_ 0^2 I[1, 0]\big )- m_s \big (4 I[-1, 3] + P_ 1 I[1, 0]\big )\Big )\Bigg ]\nonumber \\&\quad +\frac{e_d}{442368 m_c^2 \pi ^6}\Bigg [ f_ {3\gamma } \pi ^2 \Bigg (-11 P_ 1 \big (m_c^6 I[-3, 1] \nonumber \\&\quad + 3 m_c^4 I[-2, 1] + 2 I[0, 1]\big ) I_ 1[\mathcal {A}] + 12 \Big (5 m_c^{10} I[-5, 3] \nonumber \\&\quad - 12 m_c^8 I[-4, 3] -36 m_c^7 m_s I[-3, 2] \end{aligned}$$

$$\begin{aligned}&\quad + m_c^6 \big (48 m_s P_ 3 \pi ^2 I[-3, 1] - 9 I[-3, 3]\big )\nonumber \\&\quad + 24 m_c^5 \big (8 P_ 3 \pi ^2 I[-2, 1] \nonumber \\&\quad + 3 m_s I[-2, 2]\big ) - 2 m_c^4 \big (24 m_s P_ 3 \pi ^2 I[-2, 1] \nonumber \\&\quad + 5 I[-2, 3]\big ) - 36 m_c^3 m_s I[-1, 2] + 48 m_ 0^2 m_c P_ 3 \pi ^2 I[0, 0] \nonumber \\&\quad + 8 m_s P_ 3 \pi ^2 \big (m_ 0^2 I[0, 0] - 12 I[0, 1]\big )\nonumber \\&\quad - 20 I[0, 3]\Big ) I_ 1[{\mathcal {V}}]\Bigg ) + 4 \Bigg (1152 m_c^4 P_ 2^2 \pi ^4 I_ 4[{\mathcal {S}}] I[-2, 1] \nonumber \\&\quad - 6 m_c^5 P_ 1 \big (m_c (2 m_c (m_c + m_s) I[-3, 1] \nonumber \\&\quad + I[-3, 2]) + (3 m_c + 2 m_s) I[-2, 1]\big ) \nonumber \\&\quad + 9 m_c^4 P_ 1 I[-2, 2] - 6 m_c^4 P_ 1 I[-1, 1] \nonumber \\&\quad - 6 m_c^3 m_s P_ 1 I[-1, 1] + 12 m_c^3 m_s P_ 1 I[0, 0] \nonumber \\&\quad + 16 m_c P_ 1 P_ 3 \pi ^2 I[0, 0] +8 m_s P_ 1 P_ 3 \pi I[0, 0] \nonumber \\&\quad - 1152 m_c m_s P_ 2^2 \pi ^4 I_ 4[\mathcal {S}] I[0, 0] - 48 m_c m_s P_ 1 I[0, 1] \nonumber \\&\quad + 1152 P_ 2^2 \pi ^4 I_ 4[{\mathcal {S}}] I[0, 1] - 144 P_ 2^2 \pi ^4 \big (6 m_c^6 I[-3, 1] \nonumber \\&\quad + 4 m_c^4 I[-2, 1] + m_ 0^2 I[0, 0] + 2 I[0, 1]\big ) I_ 1[\mathcal {S}] \nonumber \\&\quad + 9 P_ 1 I[0, 2] + 18 m_c^3 m_s P_ 1 I[1, 0] \nonumber \\&\quad + 2 f_ {3\gamma } P_ 1 \pi ^2 \big (3 m_c^6 I[-3, 1]\nonumber \\&\quad + 2 m_c^4 I[-2, 1] + 3 I[0, 1] + 2 m_c^3 m_s I[1, 0]\big ) I_ 6[\psi _a] \nonumber \\&\quad + 4 f_ {3\gamma } P_ 1 \pi ^2 \big (3 m_c^6 I[-3, 1] \nonumber \\&\quad + 2 m_c m_s I[0, 0] - I[0, 1]\big ) \psi ^a[u_ 0]\Bigg )\Bigg ] \nonumber \\&\quad +\frac{e_u}{442368 m_c^2 \pi ^6}\Bigg [ f_ {3\gamma } \pi ^2 \Bigg (12 \Big (5 m_c {10} I[-5, 3] \nonumber \\&\quad - 12 m_c^8 I[-4, 3] - 36 m_c^7 m_s I[-3, 2]\nonumber \\&\quad + m_c^6 \big (48 m_s P_ 3 \pi ^2 I[-3, 1] \nonumber \\&\quad - 9 I[-3, 3]\big ) + 24 m_c^5 \big (8 P_ 3 \pi ^2 I[-2, 1] + 3 m_s I[-2, 2]\big ) \nonumber \\&\quad - 2 m_c^4 \big (24 m_s P_ 3 \pi ^2 I[-2, 1] + 5 I[-2, 3]\big ) \nonumber \\&\quad - 36 m_c^3 m_s I[-1, 2] + 48 m_ 0^2 m_c P_ 3 \pi ^2 I[0, 0] \nonumber \\ \end{aligned}$$

$$\begin{aligned}&\quad + 8 m_s P_ 3 \pi ^2 \big (m_ 0^2 I[0, 0] - 12 I[0, 1]\big ) - 44 I[0, 3]\Big ) I_ 2[{\mathcal {V}}] \nonumber \\&\quad + P_ 1 \Big (11 \big (m_c^6 I[-3, 1] + 3 m_c^4 I[-2, 1] \nonumber \\&\quad + 2 I[0, 1]\big ) I_ 2[{\mathcal {A}}] + 8 \big (3 m_c^6 I[-3, 1] \nonumber \\&\quad + 2 m_c^4 I[-2, 1] + 3 I[0, 1] \nonumber \\&\quad + 2 m_c^3 m_s I[1, 0]\big ) I_ 6[\psi ^a] \nonumber \\&\quad + 16 \big (3 m_c^6 I[-3, 1] + 2 m_c m_s I[0, 0] \nonumber \\&\quad -I[0, 1]\big ) \psi ^a[u_ 0])\Bigg ) - 24 m_c^5 (3 m_c + 2 m_s) P_ 1 I[-2, 1] \nonumber \\&\quad - 4608 P_ 2^2 \pi ^4 \big (m_c^4 I[-2, 1] - m_c m_s I[0, 0] + I[0, 1]\big ) I_ 3[\mathcal {S}] \nonumber \\&\quad + 576 P_ 2^2 \pi ^4 \big (6 m_c^6 I[-3, 1] + 4 m_c^4 I[-2, 1] + m_ 0^2 I[0, 0] \nonumber \\&\quad + 2 I[0, 1]\big ) I_ 2[{\mathcal {S}}] + 4 P_ 1 \Big (m_c^4 (9 I[-2, 2] - 6 I[-1, 1])\nonumber \\&\quad + 8 m_s P_ 3 \pi ^2 I[0, 0] + 16 m_c \big (P_ 3 \pi ^2 I[0, 0] - 3 m_s I[0, 1]\big )\nonumber \\&\quad + 9 I[0, 2] - 6 m_c^3 m_s (I[-1, 1] - 2 I[0, 0] - 3 I[1, 0])\Big )\Bigg ]\nonumber \\&\quad -\frac{e_s}{221184 m_c^2 \pi ^4} \Bigg [ m_c^{12} (6 I[-6, 4] + 8 I[-5, 3]) \nonumber \\&\quad - 24 m_c {10} (I[-5, 4] - I[-4, 3]) \nonumber \\&\quad +m_c^8 \big (P1 I[-4, 2] + 30 I[-4, 4] \nonumber \\&\quad + 2 P_1 I[-3, 1] +24 I[-3, 3]\big ) \nonumber \\&\quad + 2 m_c^6 \big (512 P_ 2^2 \pi ^4 I[-3, 1] - P_ 1 I[-3, 2]\nonumber \\&\quad - 6 I[-3, 4] + P_ 1 I[-2, 1] + 4 I[-2, 3]\big ) \nonumber \\&\quad + 1024 P_ 2^2 \pi ^4 I[0, 1] - 3 P_ 1 I[0, 2] + 64 m_c^2 I[0, 3] \end{aligned}$$

$$\begin{aligned}&\quad + P_ 3 \Bigg (864 \big (m_c^6 I[-3, 2] - m_c^4 I[-2, 2]\big )\mathcal {A}[u_ 0] \nonumber \\&\quad - 432 m_c^2 \big (I_ 4[\mathcal {S}] + I_ 4[\mathcal {T}_1] +I_ 4[\mathcal {T}_2] - I_ 4[\mathcal {T}_3] \nonumber \\&\quad - I_ 4[\mathcal {T}_4] - I_ 4[\mathcal {\tilde{S}}]\big ) \big (m_c^4 I[-3, 2] \nonumber \\&\quad - 2 m_c^2 I[-2, 2] + I[-1, 2]\big ) \nonumber \\&\quad + P_ 1 \Big (23 I_ 4[\mathcal {S}] + 23 I_ 4[\mathcal {T}_1] +23 I_ 4[\mathcal {T}_2]\nonumber \\&\quad - 12 \big (I_ 4[\mathcal {T}_3] + I_ 4[\mathcal {T}_4] + I_ 4[\mathcal {\tilde{S}}]\big )\Big ) I[0, 0] \nonumber \\&\quad + 24 \Big (36 m_c^4 (m_c^4 I[-4, 2] - 2 m_c^2 I[-3, 2] \nonumber \\&\quad + I[-2, 2]) - P_ 1 I[0, 0]\Big ) I_ 6[h_ {\gamma }]\Bigg )\nonumber \\&\quad - f_{3\gamma } \Bigg (144 m_c^8 I_ 1[\mathcal {A}] I[-4, 3] \nonumber \\&\quad + 144 m_c^8 I_ 1[\mathcal {V}] I[-4, 3] + 288 m_c^6 I_ 1[\mathcal {A}] I[-3, 3] \nonumber \\&\quad + 288 m_c^6 I_ 1[\mathcal {V}] I[-3, 3] \nonumber \\&\quad + 23 m_c^4 P_ 1 I_ 1[\mathcal {A}] I[-2, 1]+ 23 m_c^4 P_ 1 I_ 1[\mathcal {V}] I[-2, 1] \nonumber \\&\quad + 144 m_c^4 I_ 1[\mathcal {A}] I[-2, 3] + 144 m_c^4 I_ 1[\mathcal {V}] I[-2, 3] \nonumber \\&\quad + 23 P_ 1 I_ 1[\mathcal {A}] I[0, 1] + 23 P_ 1 I_ 1[\mathcal {V}] I[0, 1]\nonumber \\&\quad + 576 I_ 1[\mathcal {A}] I[0, 3] + 576 I_ 1[\mathcal {V}] I[0, 3]\nonumber \\&\quad + 24 \Big (m_c^6 (12 m_c^4 I[-5, 3] + 24 m_c^2 I[-4, 3]\nonumber \\&\quad + P_ 1 I[-3, 1] + 12 I[-3, 3]) - P_ 1 I[0, 1] \nonumber \\&\quad + 48 I[0, 3]\Big ) I_ 6[\psi ^a] \nonumber \\&\quad + 96 \Big (m_c^6 (12 m_c^4 I[-5, 3] + 24 m_c^2 I[-4, 3] \nonumber \\&\quad + P_ 1 I[-3, 1] + 12 I[-3, 3]) + P_ 1 I[0, 1] \nonumber \\&\quad + 48 I[0, 3]\Big ) I_ 6[\varphi _{\gamma }] \nonumber \\&\quad + 576 m_c^{10} I[-5, 3] \psi ^a[u_ 0] + 48 m_c^6 P_ 1 I[-3, 1] \psi ^a[u_ 0] \nonumber \\&\quad - 576 m_c^6 I[-3, 3] \psi ^a[u_ 0] + 48 P_ 1 I[0, 1] \psi ^a[u_ 0] \nonumber \\&\quad + 48 \Big (m_c^6 \big (12 m_c^4 I[-5, 3]\nonumber \\&\quad + 24 m_c^2 I[-4, 3] + P_ 1 I[-3, 1] \nonumber \\&\quad + 12 I[-3, 3]\big ) + P_ 1 I[0, 1] \nonumber \\&\quad + 48 I[0, 3]\Big ) \varphi _{\gamma }[u_ 0]\Bigg )\Bigg ], \end{aligned}$$

(20)

where $P_1 =\langle g_s^2 G^2\rangle$ is gluon condensate, $P_2 =\langle \bar{q} q \rangle$ stands for u/d quark condensate, and $P_3 = \langle \bar{s} s \rangle$ represents the s-quark condensate. The functions I[n, m], $I_1[\mathcal {A}]$, $I_2[\mathcal {A}]$, $I_3[\mathcal {A}]$, $I_4[\mathcal {A}]$, $I_5[\mathcal {A}]$ and $I_6[\mathcal {A}]$ are defined as

$$\begin{aligned} I[n,m]&= \int _{m_c^2}^{s_0} ds \int _{m_c^2}^s dl~ e^{-s/M^2}~\frac{(s-l)^m}{l^n}\\ I_1[\mathcal {A}]&=\int D_{\alpha _i} \int _0^1 dv~ \mathcal {A}(\alpha _{\bar{q}},\alpha _q,\alpha _g) \delta '(\alpha _ q +\bar{v} \alpha _g-u_0),\\ I_2[\mathcal {A}]&=\int D_{\alpha _i} \int _0^1 dv~ \mathcal {A}(\alpha _{\bar{q}},\alpha _q,\alpha _g) \delta '(\alpha _{\bar{q}}+ v \alpha _g-u_0),\\ I_3[\mathcal {A}]&=\int _0^1 du~ A(u)\delta '(u-u_0),\\ I_4[\mathcal {A}]&=\int D_{\alpha _i} \int _0^1 dv~ \mathcal {A}(\alpha _{\bar{q}},\alpha _q,\alpha _g) \delta (\alpha _ q +\bar{v} \alpha _g-u_0),\\ I_5[\mathcal {A}]&=\int D_{\alpha _i} \int _0^1 dv~ \mathcal {A}(\alpha _{\bar{q}},\alpha _q,\alpha _g) \delta (\alpha _{\bar{q}}+ v \alpha _g-u_0),\\ I_6[\mathcal {A}]&=\int _0^1 du~ A(u), \end{aligned}$$

where $\mathcal {A}$ stands for the corresponding photon DAs and $D_{\alpha _i}$ is the measure defined as

$$\begin{aligned} \int \mathcal{D} \alpha _i = \int _0^1 d \alpha _{\bar{q}} \int _0^1 d \alpha _q \int _0^1 d \alpha _g \delta (1-\alpha _{\bar{q}}-\alpha _q-\alpha _g). \end{aligned}$$