1 Introduction

In recent years, a growing interest on nuclear deeply virtual Compton scattering (DVCS), i.e., hard photon electroproduction from nuclear targets, has arisen. This is mainly motivated by the possibility to shed light on the European Muon Collaboration (EMC) effect, i.e., the elusive nuclear modifications of the nucleon parton structure (see, e.g., Refs. [1, 2] for recent reports), as well as the possibility to distinguish the so-called coherent and incoherent channels of the DVCS process. This latter feature has been experimentally recently achieved by the CLAS collaboration at JLab using a \(^4\)He gaseous target [3,4,5], paving the way to a new class of precise measurements at high luminosity facilities. Coherent DVCS takes place when the nucleus recoils elastically, while in the incoherent process the struck proton is detected in the final state. Recently, the measurement of positron initiated DVCS has been experimentally proposed at Jefferson Lab (JLab) [6]. In the present paper, we analyze the impact that these measurements may have using \(^4\)He and \(^3\)He targets. This is done, separately for the coherent and incoherent channels, in the next two sections. Some additional remarks on higher twist effects are reported in the fourth section, followed by the conclusions of our investigation.

2 Coherent DVCS

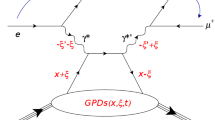
To explore the insights on how positron beams could help in this field, let us first discuss coherent DVCS off \(^4\)He, the only process which has been clearly accessed so far, and illustrated in the handbag approximation in Fig. 1. In DVCS, the relevant non-perturbative information is encoded in the so called generalized parton distribution functions (GPDs), giving access, in specific kinematic configurations, to the location of one parton of given longitudinal momentum, in the transverse plane of the target (the so-called hadron tomography). We recall that, at leading-twist, \(^4\)He has only one chiral-even GPD.

In the coherent DVCS data analysis from the EG6 experiment by the CLAS collaboration [3], the measured observable was the single beam-spin asymmetry, \(A_{LU}\), which can be extracted from the reaction yields for the two electron helicities (\(N^{\pm }\)):

$$\begin{aligned} A_{LU} = \frac{1}{P_{B}} \frac{N^{+} - N^{-}}{N^{+} + N^{-} }, \end{aligned}$$
(1)

where \(P_{B}\) is the degree of longitudinal polarization of the incident electron beam.

Fig. 1
figure 1

The leading-order, twist-2, handbag approximation to the coherent DVCS process off \(^4\)He, where the four-vectors of the initial/final electron, photon, and \(^4\)He nucleus are denoted by \(k/k^{\prime }\), \(q/q^{\prime }\), and \(p/p^{\prime }\), respectively. The quantity \(x+\xi \) is the hadron’s longitudinal momentum fraction carried by the struck quark, \(-2\xi \) is the longitudinal momentum fraction of the momentum transfer \(\Delta (= q - q^{\prime }=p^{\prime } -p\)), and t (\(=\Delta ^2\)) is the squared momentum transfer

Full size image

Within the accessed kinematical phase-space of the EG6 experiment, the cross section of real photon electroproduction is dominated by the so-called Bethe–Heitler(BH) process, where the real photon is emitted by the incoming or the outgoing lepton, while the pure DVCS contribution is very small. However, the DVCS contribution is enhanced in the observables sensitive to the interference term, i.e. the quantity \(A_{LU}\) given above, which depends on the azimuthal angle \(\phi \) between the \((e,e^{\prime })\) and \((\gamma ^*,^4\)He\(^{\prime })\) planes. The asymmetry \(A_{LU}\) for a spin-zero target can be approximated at leading-twist as

$$\begin{aligned} A_{LU}(\phi ) = \frac{\alpha _{0}(\phi ) \, \mathfrak {I}m {\mathcal {H}}_{A}}{den(\phi )} \, , \end{aligned}$$
(2)

with:

$$\begin{aligned} den(\phi )= & {} \alpha _{1}(\phi ) + \alpha _{2}(\phi ) \, \mathfrak {R}e {\mathcal {H}}_{A} \nonumber \\&\quad +&\alpha _{3}(\phi ) \, \big [ (\mathfrak {R}e {\mathcal {H}}_{A})^{2} + (\mathfrak {I}m {\mathcal {H}}_{A})^{2} \big ]. \end{aligned}$$
(3)

The kinematic factors \(\alpha _i\) are known (see, e.g., Ref. [7, 8]). In the experimental analysis, using the different contributions proportional to \(\sin (\phi )\) and \(\cos (\phi )\) in Eq. (3), both the real and imaginary parts of the so-called Compton Form Factor (CFF) \({\mathcal {H}}_{A}\), \(\mathfrak {R}e {\mathcal {H}}_{A}\) and \(\mathfrak {I}m {\mathcal {H}}_{A}\), respectively, have been extracted by fitting the \(A_{LU}(\phi )\) distribution. CFF will be formally defined later on in terms of the nuclear GPDs. Results of the impulse approximation (IA) calculation of Ref. [9], are shown together with the data of Ref. [3] in Figs. 2 and 3. In the theoretical evaluation, state-of-the-art ingredients are used for the description of the nuclear and nucleon structure (older calculations are found in [10, 11]). We remark here that, as a consequence of the IA, the nuclear GPD is obtained as a convolution formula between a one-body non-diagonal spectral function and the nucleon GPDs. In the actual calculation (see Ref. [9] for details) the spectral function is based on the Av18 nucleon nucleon interaction [12] and the Urbana IX three body forces [13], while the nucleon GPDs are implemented following the Goloskokov–Kroll model [14,15,16]. Big statistical errors are seen everywhere in the data but, in particular, \(\mathfrak {R}e {\mathcal {H}}_{A}\) is less precisely extracted than \(\mathfrak {I}m {\mathcal {H}}_{A}\), due to the small coefficient \(\alpha _2\) in Eq. (3). This fact is easily understood looking at Fig. 3 where it is evident that the predicted contribution of the real part of the CFF to the symmetry is really small.

Fig. 2
figure 2

The imaginary part of the CFF measured in coherent DVCS off \(^4\)He. Data from Ref. [3]; calculations (red crosses) from Ref. [9]

Full size image
Fig. 3
figure 3

The real part of the CFF measured in coherent DVCS off \(^4\)He. Data from Ref. [3]; calculations (red crosses) from Ref. [9]

Full size image
Fig. 4
figure 4

The beam spin asymmetry measured in coherent DVCS off \(^4\)He, for \(\phi =90^o\). Data from Ref. [3]; calculations (red dots) from Ref. [9]. The result obtained neglecting the real part of the CFF \({\mathcal {H}}_A\) is also shown (blue triangles)

Full size image

Forth-coming data from JLab with the 12 GeV electron beam at high luminosity, using also the detector system developed by the ALERT run-group [17], will be affected by much smaller statistical errors. Together with refined realistic theoretical calculations, in progress for light nuclei [18], the new data will help to unveil an exotic behavior of the real and imaginary part of \({\mathcal {H}}_{A}\), possibly due to  modifications of the nucleon size and shape in the medium [2] beyond that predicted in a conventional realistic scenario using the Impulse Approximation. Nonetheless, the extracted \(\mathfrak {R}e {\mathcal {H}}_{A}\) will be always less precise than \(\mathfrak {I}m({\mathcal {H}}_{A})\), intrinsically, due to the small coefficient \(\alpha _2\) in (3) previously introduced. A precise knowledge of \(\mathfrak {R}e {\mathcal {H}}_{A}\) for light nuclei would be, instead, crucial as explained briefly below for the \(^4\)He target. Formally one can write, for the quantities \(\mathfrak {R}e {\mathcal {H}}_{A}\) and \(\mathfrak {I}m {\mathcal {H}}_{A}\) shown in Figs. 2 and 3 respectively [19]:

$$\begin{aligned} \mathfrak {R}e {\mathcal {H}}_{A} (\xi ,t) \equiv {{{\mathcal {P}}}} \int _0^1 dx H_+(x,\xi ,t) C_+(x,\xi ) , \end{aligned}$$
(4)

and

$$\begin{aligned} \mathfrak {I}m {\mathcal {H}}_{A} = -\pi H_+(\xi ,\xi ,t) , \end{aligned}$$
(5)

with:

$$\begin{aligned} H_+ = H(x,\xi ,t)-H(-x,\xi ,t) , \end{aligned}$$
(6)

and

$$\begin{aligned} C_+(x,\xi ) = \frac{1}{x+\xi }+\frac{1}{x-\xi } , \end{aligned}$$
(7)

with \(H(x,\xi ,t)\) the chiral-even, leading twist generalized parton distribution (GPD).

Besides, it is also known that \(\mathfrak {R}e {\mathcal {H}}_{A}\) satisfies a once subtracted dispersion relation at fixed t can be, therefore, related to \(\mathfrak {I}m {\mathcal {H}}_{A}\), leading to [20,21,22,23]

$$\begin{aligned} \mathfrak {R}e {\mathcal {H}}_{A} (\xi ,t) \equiv {{{\mathcal {P}}}} \int _0^1 dx H_+(x,x,t) C_+(x,\xi ) - \delta (t) . \end{aligned}$$
(8)

It is worth noting that, while in the convolution integral defining the real part of the CFF in Eq. (4) the GPD enters for unequal values of its first and second argument, the integrated GPD in the dispersion relation has its first and second arguments equal.

The subtraction term \(\delta (t)\) can be related to the so-called \(d-\)term and accurate measurements, supplemented by precise calculations, would allow therefore to study this quantity for nuclei, for the first time. This \(d-\)term, introduced initially to recover the so-called polinomiality property in double distribution (DD) approaches to GPDs modelling [24], has been related to the form factor of the QCD energy momentum tensor (see e.g. Ref. [25, 26]). It encodes information on the distribution of forces and pressure between elementary QCD degrees of freedom in the target. For nuclei, it has been predicted to behave as \(A^{7/3}\) in a mean field scheme, both in the liquid drop model of nuclear structure [27] and in the Walecka model [28]. None of these approaches makes much sense for light nuclei, for which accurate realistic calculations are possible. Using light nuclei one would, therefore, explore at the parton level, the onset and evolution of the mean field behavior across the periodic table, from deuteron to \(^4\)He, whose density and binding are not far from those of medium-heavy nuclei.

In this context, coherent DVCS off \(^3\)He targets acquires an important role since an intermediate behavior is expected between the almost unbound deuteron system and the deeply bound alpha particle.

The formal description of coherent DVCS off \(^3\)He in terms of CFFs and related GPDs, is the same of the proton [7, 8], a spin one-half target, and they can be accessed by properly defining spin dependent asymmetries.

Realistic theoretical calculations are available for GPDs [29,30,31,32,33] and are in progress for the relevant CFFs, cross sections and asymmetries, representing an important support for the planning of measurements [18].

We notice that, as it has been shown in Refs. [31, 32], the \(^3\)He chiral-even GPDs are strongly dominated by the neutron GPDs, which can be safely extracted by properly taking into account the nuclear effects described in the Impulse Approximation. One could object that the use of \(^3\)He, either longitudinally or transversely polarized, in a coherent DVCS experiment where the slow recoiling nucleus has to be detected, represents at the moment a challenge, either with electron or positron beams. The same problem does not arise at the EIC.

With an unpolarized \(^3\)He target it is possible to access the \(\mathfrak {R}e {\mathcal {H}}_A\), and therefore, to explore the d-term of this relevant light nucleus, by measuring the beam-charge asymmetries, as described below. The sign of the lepton beam charge (\(C=\pm 1\)) and polarization (\(\lambda \)) dependence of the cross section, for an unpolarized target, is expressed by the following terms [6]:

$$\begin{aligned} \sigma ^C= & {} \sigma _{BH} + \sigma _{DVCS} + \lambda {\tilde{\sigma }}_{DVCS} \nonumber \\&+ C \sigma _{INT} + C \lambda {\tilde{\sigma }}_{INT} , \end{aligned}$$
(9)

where the index INT denotes the BH-DVCS quantum interference contribution to the cross section. The following relations hold between the terms in the Eq. (9) and those appearing in the Eqs. (2) and (3):

$$\begin{aligned} \sigma _{BH}\propto & {} \alpha _1(\phi ) , \nonumber \\ \sigma _{DVCS}\propto & {} \alpha _{3}(\phi ) \big [( \mathfrak {R}e{\mathcal {H}}_{A})^{2} + (\mathfrak {I}m {\mathcal {H}}_{A})^{2} \big ] , \nonumber \\ \sigma _{INT}\propto & {} \alpha _{2}(\phi ) \, \mathfrak {R}e {\mathcal {H}}_{A} , \nonumber \\ {\tilde{\sigma }}_{INT}\propto & {} \alpha _{0}(\phi ) \, \mathfrak {I}m {\mathcal {H}}_{A} , \end{aligned}$$
(10)

while \({\tilde{\sigma }}_{DVCS} \) is proportional to a term suppressed at JLab kinematics, depending on higher twist CFFs. As it will become clear later in this section, using asymmetries built by properly considering cross sections measured with a specific beam with a given spin, one could access all the five cross sections in Eq. (9). For example, using positron beams, the beam-charge asymmetry, proportional to \(\sigma ^+-\sigma ^-\) in Eq. (9), would be at hand and one could attempt to extract \(\sigma _{INT}\). Explicit examples are discussed in the following.

Using unpolarized electrons and positrons, the real part of the CFF, \(\mathfrak {R}e {\mathcal {H}}_{A}\), would be directly accessed by measuring charge beam asymmetries. By following the same formalism adopted in Ref. [7], the beam charge asymmetry (BCA\(_A\)) for a nucleus with A nucleons, is defined as follows:

$$\begin{aligned} \text{ BCA}_A= \dfrac{d \sigma ^{+} - d\sigma ^{-}}{d \sigma ^{+} + d\sigma ^{-}}, \end{aligned}$$
(11)

where here \(d\sigma ^\pm \) represents the five times differential unpolarized cross section for an electron (−) or a positron (\(+\)) beam, respectively. Let us recall that such a cross section for, e.g., the process \(e^\pm ~ ^3He \rightarrow e^\pm ~ ^3He \gamma \) [7, 8], reads:

$$\begin{aligned} d\sigma ^C\equiv \dfrac{d\sigma ^C}{dx_B~dy~dt~d\phi ~d \varphi } = \dfrac{\alpha ^3 x_B y}{16 \pi ^2 Q^2 \sqrt{1+\varepsilon ^2}} \left| \dfrac{T_C}{e^3} \right| ^2 \nonumber \\ \end{aligned}$$
(12)

where \(x_B=x_{Bj}\) is the Bjorken x, \(Q^2\) is the photon virtuality, \(\alpha \) is fine-structure constant, \(\varepsilon =2 x_B M_3/Q\), \(M_3\) is the \(^3\)He mass and y is the lepton energy loss fraction. Moreover \(\phi \) is the azimuthal angle between the lepton plane and the recoiled nucleus. \(\varphi \) is the difference between the azimutal angle of the transverse part of the nucleon polarization and the azimuthal angle of the recoiled hadron. Finally, \(T^2_C=|T_{BH}|^2+|T_{DVCS}|^2+I_C\) where only the interference term, \(I_C\), depends on the beam charge [7]. Therefore:

$$\begin{aligned} d\sigma ^+-d\sigma ^- = \dfrac{2 \alpha ^3 x_B y}{16 \pi ^2 Q^2 \sqrt{1+\varepsilon ^2}} \dfrac{I}{e^6} \end{aligned}$$
(13)

where \(I=I_C/C\). Within this formalism:

$$\begin{aligned} I&= \dfrac{e^6}{x_B y^3 t P_1(\phi ) P_2(\phi )} \nonumber \\&\quad \times \Big \{c_0^I+\sum _{n=1}^3 \big [c_n^I \cos (n \phi )+s_n^I \sin (n \phi ) \big ] \Big \}. \end{aligned}$$
(14)

These harmonic coefficients depend on the \(^3\)He CFFs. In particular, if unpolarized targets and beams are considered, \(s_n^I\) do not contribute to the BCA\(_3\). The functions \(P_1\) and \(P_2\) [7] cancel out in the evaluation of BCA\(_3\). On the other hand:

$$\begin{aligned} d\sigma ^++d\sigma ^- = \dfrac{2 \alpha ^3 x_B y}{16 \pi ^2 Q^2 \sqrt{1+\varepsilon ^2}} \dfrac{|T_{DVCS}|^2+|T_{BH}|^2}{e^6}. \end{aligned}$$
(15)

We remind that, when terms of the order \(t/Q^2\) can be neglected, BCA\(_3\) is directly related to the real part of CFFs. As a matter of fact, in this kinematic conditions, the \(|T_{DVCS}|^2\) can be neglected:

$$\begin{aligned} \text{ BCA}_3(\phi ) \sim \dfrac{e^6}{x_B y^3 t P_1(\phi ) P_2(\phi )} \dfrac{c_1^I \cos (\phi )}{|T_{BH}|^2}. \end{aligned}$$
(16)

Besides, since \(c_3^I\) is related to the gluon distribution, in this initial analysis such a contribution is also neglected, together with \(c_0^I\) and \(c_2^I\). Finally, we have \(c_1^I \propto Re~c_{unp}^I \) where \(c_{unp}^I=F_1 {\mathcal {H}}+x_B/(2-x_B)(F_1+F_2)\mathcal {{\tilde{H}}}-t/(4 M_{3}^{2})F_2 {\mathcal {E}}\) (for details see Ref. [7]). We recall that \(F_1\) and \(F_2\) are the Dirac and Pauli form factors respectively and \({\mathcal {F}}=\mathcal {H,E, {\tilde{H}}}\) is the CFF. Finally:

$$\begin{aligned} \text{ BCA}_3(\phi ) =\dfrac{x_B (1+\varepsilon ^2)^2}{y} \dfrac{c_1^I \cos (\phi )}{ c_0^{BH}+c_1^{BH} \cos (\phi )}. \end{aligned}$$
(17)

Let us point out that, here and in the following, we consider, for the moment being, the infinitely small bin approximation in our theoretical idealized predictions. Numerical results for the \(^3\)He BCA, evaluated in a kinematical range typical at JLab, are shown for the first time in the upper panel of Fig. 5. Here the \(^3\)He GPDs have been calculated using the off-forward spin dependent spectral function obtained with the AV18 nuclear potential [34,35,36], following the procedure described in Refs. [31, 32].

The nucleonic GPDs, needed as an input to the calculation, have been chosen among the phenomenological parametrizations of Refs. [14,15,16]. In addition, we take advantage of this discussion to present, for the first time, IA predictions for the \(^3\)He beam spin asymmetry (BSA). This result is fundamental since from the combined data for the BCA and BSA the \(^3\)He leading twist CFF could be extracted. In general, one can introduce the nuclear beam spin asymmetry (BSA):

$$\begin{aligned} \text{ BSA}_A= \dfrac{d \sigma ^{\uparrow }-d\sigma ^{\downarrow }}{d \sigma ^{\uparrow }+d\sigma ^{\downarrow }}. \end{aligned}$$
(18)

By using the previously discussed strategy and approximations, one can relate the above quantity to the imaginary part of CFF. For a 1/2 spin target like the \(^3\)He one gets:

$$\begin{aligned} \text{ BSA}_3 \sim \pm \dfrac{x_{Bj}}{y} \dfrac{s_{1}^I}{c_{0}^{BH}} \sin (\phi ), \end{aligned}$$
(19)

where now \(s^I_1 \propto ~ Im~c^I_{unp}\).

Fig. 5
figure 5

Upper panel: The \(^3\)He beam charge asymmetry Eq.  (17) for a specific kinematic configuration, typical at JLab. Lower panel: the same but for the \(^3\)He beam spin asymmetry Eq. (19)

Full size image

The formalism above discussed for the beam charge asymmetry of the \(^3\)He nucleus can be easily extended to the \(^4\)He nucleus. While the beam spin asymmetry for a longitudinally polarized electron beam off an unpolarized target has already demonstrated to be a key observable to access the imaginary part of the CFF, the BCA is mostly useful to extract information of the real part of the CFF. Looking at Eq. (17), the numerator encapsulates the real part of CFF linked to the chiral even GPD of the \(H^A\) up to radiative corrections leading to further \(\phi \) dependence, to be investigated. Unlike the \(^3\)He case, \(^4\)He as a spin-zero hadron, at leading-twist is parametrized by only one chiral even GPD. We show here our first estimates of the BCA for \(^4\)He, where we use, for the expression of the GPD \(H^A\), the Impulse Approximation model presented in Ref. [9].

Although the non diagonal momentum and the energy dependencies of the spectral function are just modeled, our approach is able to describe conventional nuclear effects, as can be seen in Figs. 2, 3. We note that the twist-two CFF of the \(^4\)He nucleus receives the contribution of the GPD H and E of the bound nucleons in the form \(H^{N/A}=\sqrt{(1-\xi ^2)}\bigg [ H^N - \frac{\xi ^2}{1-\xi ^2}E^N\bigg ]\). As observed in Ref. [18], the contribution of the GPD \(E^N\) is practically negligible at the kinematics probed at JLab due to the smallness of the skweness (an even greater kinematical suppression for such a factor will be observed in the typical kinematic ranges expected at the EIC [37]).

For the nucleon GPDs we used the same GK models used for \(^3\)He, and described in Refs. [15, 38].

In Fig. 6, a sizable asymmetry is observed for \(^4\)He shown at various kinematics accessible at JLab. Two of these are the same already probed in Ref. [3], while the other one is the same foreseen for the free proton using positron beams (see. Ref. [39]). As a reference, we show in Fig. 7 the same quantity for one of the kinematic points envisioned at the EIC for a positron beam at 18 GeV colliding with a \(^4\)He beam with an energy of 110 GeV. The values of the kinematical variables plotted, in the present paper, have been obtained as pseudo-data generated with the Monte-Carlo TOPEG.

While in Ref. [37] the possibility to reach the first tomographic view of the nucleus is shown, here the big asymmetry found in some of the kinematical ranges investigated, allowing one an easier extraction of information from the observable, confirms the prominent role that the EIC together with the upgraded JLab will play with the aim to reach a deeper comprehension of the innermost structure of hadronic targets and hadronic matter.

Fig. 6
figure 6

The \(^4\)He beam charge asymmetry shown at different kinematic points, typically probed at JLab

Full size image
Fig. 7
figure 7

The \(^4\)He beam charge asymmetry shown at different EIC kinematics. The energy configuration corresponding to these plots is \(E_{positron}\times E_{nucleus}=(18\times 110)\) GeV

Full size image
Fig. 8
figure 8

The leading-order, twist-2, handbag approximation to incoherent DVCS off \(^4\)He. See Fig. 1 for the definition of the variables

Full size image

3 Incoherent DVCS

A separate topic is incoherent DVCS off He nuclei, i.e., the process where, in the final state, the struck proton is detected. Therefore, in this case the bound nucleon CFFs could be accessed and the relative GPDs extracted and, ultimately, its tomography obtained. Figure 8 illustrates the leading-twist handbag diagram for the incoherent DVCS process off \(^4\)He. Such measurements would provide a pictorial representation of the realization of the EMC effect and a great progress towards the understanding of its dynamical origin. As already stressed, this channel has been successfully isolated by the EG6 experiment of the CLAS collaboration at JLab [4] and a first glimpse at the parton structure of the bound proton in the transverse coordinate space is therefore at hand. Recent impulse approximation calculations, using again a description based on the Av18 interaction for the nuclear effects and, for the nucleon part, the GK model and the one proposed in Ref. [40], evaluated using the PARTONS software [41], have been presented in Refs. [42, 43]. The theoretical description of the recent data with conventional realistic ingredients is rather encouraging. The program of the JLab at 12 GeV includes an improvement of the accuracy of these measurements, in particular, for the first time in DVCS, tagging the struck nucleon detecting slow recoiling nuclei, using the detector developed by the ALERT run group [44]. This would allow to keep possible final state interactions, relevant in principle in this channel, under control. Measurements performed with electron and positron beams would allow for example the measurement of the \(d-\)term for the bound nucleon, either proton in \(^3\)He (tagging \(^2\)H from DVCS on \(^3\)He) or in \(^4\)He (tagging \(^3\)H from DVCS on \(^4\)He) or neutron in \(^4\)He (tagging \(^3\)He from DVCS on \(^4\)He). Modifications of the \(d-\)term of the nucleon in the nuclear medium, studied e.g. in Ref. [28], would be at hand, as well as a glimpse at the structure of the neutron in the transverse plane, complementary to that obtained with deuteron targets.

4 Beyond a chiral even GPDs description of DVCS on \(^4\)He

As a last argument, we quickly note that, from the measurement of beam spin asymmetries built using cross sections measured with polarized electrons and positrons in coherent DVCS off \(^4\)He, the terms \(\tilde{\sigma }_{DVCS}\) and \(\tilde{\sigma }_{INT}\), appearing in Eq. 9, could be independently accessed. This would allow, for example for \(^4\)He, to study the other leading twist CFF of a spinless target, the so called gluon transversity GPD \(H_T\), giving a corresponding name to the CFF \({{{\mathcal {H}}}}_T\), appearing in \({\tilde{\sigma }}_{DVCS}\). In Ref. [8], it is shown how the contribution of \({{{\mathcal {H}}}}_T\) to the cross section occurs through an interference between twist-two and effective twist-three CFFs. A first glimpse at this complicated interrelation would be obtained for a spin-less target, in particular for a nuclear target, for the first time. As for any other gluon-sensitive observable, data for the cross section \({\tilde{\sigma }}_{DVCS}\) would be a perfect tool to study gluon dynamics in nuclei. For example, a comparison between the above observable and calculations performed in an Impulse Approximation scheme, where the relevant nuclear degrees of freedom are colorless nucleons and mesons, would have the potential to expose possible exotic gluon dynamics in nuclei. This would be a pretty new possibility, complementary to that planned at JLab with 12 GeV, using exclusive vector meson electroproduction off \(^4\)He [44]. Such an interersting behavior would be very hardly seen using electrons only, due to the strong kinematical suppression of \({\tilde{\sigma }}_{DVCS}\) with respect to the other contributions in Eq. (9).

5 Conclusions

The unique possibilities offered by the use of positron beams in DVCS off three- and four-body nuclear systems have been reviewed. Summarizing, we can conclude that the main advantages will be:

  • in coherent DVCS off \(^3\)He and \(^4\)He, using polarized electrons and unpolarized positrons, the real part of the chiral even unpolarized CFFs would be measured with a precision comparable to that of their imaginary part, providing a tool for the study of the so called d-term. In turn, the distribution of pressure and forces between the partons in nuclei, a new way to look at the nuclear medium modifications of nucleon structure, could be investigated;

  • in incoherent DVCS off \(^3\)He and \(^4\)He, possibly tagging slow recoiling nuclear systems, the same programme could be run for the bound proton and neutron;

  • using polarized \(^3\)He targets, a more complicated setup for the moment, spin dependent and parton helicity flip CFFs would be accessed for the first time for a nucleus, in both their real and imaginary parts. Moreover, in this case these quantities would be dominated by the neutron contributions and, in turn, an extraction of the neutron CFFs would be feasible;

  • coherent DVCS off \(^4\)He, initiated with polarized positrons, would allow a first analysis of nuclear chiral odd CFFs and GPDs, with higher twist contamination suitable to tentatively explore the gluon dynamics in nuclei.

A programme of nuclear measurements with positron beams would represent therefore an exciting complement to the experiments planned with nucleon targets, and to those planned with nuclear targets and electron beams. In this paper, we have shown for the first time realistic Impulse Approximation predictions for spin-independent charge asymmetries, at JLab kinematics for \(^3\)He and \(^4\)He and, in this last case, also in one of the typical kinematic setups foreseen at the EIC. In a comprehensive forthcoming investigation these calculations will be extended to the incoherent channels and to other spin dependent asymmetries.