Abstract
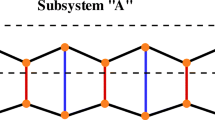
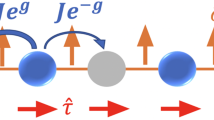
We consider a two-leg boson ladder in artificial gauge field with hard-core intraleg and negligible interleg interactions. Using numerical simulations based on the Density Matrix Renormalization Group (DMRG) algorithm, combined with a bosonization approach, we study its commensurate-incommensurate transition to a vortex phase at a critical flux. We discuss the finite-size scaling behavior of the longitudinal current near the transition. For weak interchain boson hopping, the finite size scaling is in agreement with the predictions from bosonization.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. Lewenstein, A. Sanpera, V. Ahufinger, B. Damski, A. Sen De, U. Sen, Ann. Phys. (N. Y.) 56, 243 (2007)
K. Osterloh, M. Baig, L. Santos, P. Zoller, M. Lewenstein, Phys. Rev. Lett. 95, 010403 (2005)
J. Ruseckas, G. Juzeliūnas, P. Öhberg, M. Fleischhauer, Phys. Rev. Lett. 95, 010404 (2005)
Y. Lin, K. Jimenez-Garcia, I.B. Spielman, Nature 471, 83 (2011)
V. Galitski, I.B. Spielman, Nature (London) 494, 49 (2013)
M. Kardar, Phys. Rev. B 33, 3125 (1986)
E. Granato, Phys. Rev. B 42, 4797 (1990)
Y. Nishiyama, Eur. Phys. J. B 17, 295 (2000)
E. Orignac, T. Giamarchi, Phys. Rev. B 64, 144515 (2001)
M.C. Cha, J.G. Shin, Phys. Rev. A 83, 055602 (2011)
G.I. Japaridze, A.A. Nersesyan, JETP Lett. 27, 334 (1978)
V.L. Pokrovsky, A.L. Talapov, Phys. Rev. Lett. 42, 65 (1979)
P.A. Bobbert, R. Fazio, G. Schön, G.T. Zimanyi, Phys. Rev. B 41, 4009 (1990)
S.E. Korshunov, Europhys. Lett. 9, 107 (1989)
M. Atala, M. Aidelsburger, M. Lohse, J. Barreiro, B. Paredes, I. Bloch, Nat. Phys. 10, 588 (2014)
A. Petrescu, K. Le Hur, Phys. Rev. Lett. 111, 150601 (2013)
A. Dhar, M. Maji, T. Mishra, R.V. Pai, S. Mukerjee, A. Paramekanti, Phys. Rev. A 85, 041602 (2012)
A. Dhar, T. Mishra, M. Maji, R.V. Pai, S. Mukerjee, A. Paramekanti, Phys. Rev. B 87, 174501 (2013)
D. Hügel, B. Paredes, Phys. Rev. A 89, 023619 (2014)
A. Tokuno, A. Georges, New J. Phys. 16, 073005 (2014)
M. Piraud, Z. Cai, I.P. McCulloch, U. Schollwöck, Phys. Rev. A 89, 063618 (2014)
L. Barbiero, M. Abad, A. Recati, Magnetic Phase Transition in Coherently Coupled Bose Gases in Optical Lattices [arXiv:1403.4185] (2014)
S. Peotta, L. Mazza, E. Vicari, M. Polini, R. Fazio, D. Rossini, J. Stat. Mech.: Theor. Exp. 2014, P09005 (2014)
Z. Xu, W. Cole, S. Zhang, Phys. Rev. A 89, 051604(R) (2014)
J. Zhao, S. Hu, J. Chang, F. Zheng, P. Zhang, X. Wang, Phys. Rev. B 90, 085117 (2014)
C. Hamner, Y. Zhang, M. Khamehchi, M.J. Davis, P. Engels, Spin-orbit Coupled Bose-Einstein Condensates in a One-dimensional Optical Lattice [arXiv:1405.4048] (2014)
M. Piraud, F. Heidrich-Meisner, I.P. McCulloch, S. Greschner, T. Vekua, U. Schollwöck [arXiv:1409.7016]
A. Petrescu, K. Le Hur [arXiv:1410.6105]
A. Keles, M.Ö. Oktel [arXiv:1411.0749]
F.D.M. Haldane, Phys. Rev. Lett. 47, 1840 (1981)
M. Cazalilla, R. Citro, T. Giamarchi, E. Orignac, M. Rigol, Rev. Mod. Phys. 83, 1406 (2011)
F. Crépin, N. Laflorencie, G. Roux, P. Simon, Phys. Rev. B 84, 054517 (2011)
A. Luther, Phys. Rev. B 15, 403 (1977)
S.R. White, Phys. Rev. B 48, 10345 (1993)
U. Schollwöck, Rev. Mod. Phys. 77, 259 (2005)
D. Senechal, An Introduction to Bosonization, in Theoretical Methods for Strongly Correlated Electrons, edited by D. Sénechal et al. (Springer, New York, 2003), CRM Series in Mathematical Physics
M.A. Cazalilla, J. Phys. B 37, S1 (2004)
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Di Dio, M., Citro, R., De Palo, S. et al. Meissner to vortex phase transition in a two-leg ladder in artificial gauge field. Eur. Phys. J. Spec. Top. 224, 525–531 (2015). https://doi.org/10.1140/epjst/e2015-02382-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjst/e2015-02382-2