Abstract.
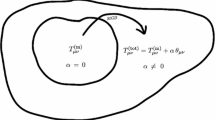
This work is focused on the study of analytic anisotropic solutions to Einstein’s field equations, describing spherically symmetric and static configurations by way of the gravitational decoupling through the method of minimal geometric deformation (MGD). For this we apply MGD to Heintzmann’s solution obtaining two new analytic and well behaved anisotropic solutions, in which all their parameters such as the effective density, the effective radial and tangential pressure, as well as radial and tangential sound speed, fulfill each of the requirements for the physical acceptability available in the literature.
Similar content being viewed by others
References
M.K. Mak, T. Harko, Chin. J. Astron. Astrophys. 2, 248 (2002)
M.K. Mak, T. Harko, Proc. R. Soc. London A 459, 393 (2003)
K.N. Singh, N. Pant, M. Govender, Indian J. Phys. 90, 1215 (2016)
S.K. Maurya, Y.K. Gupta, Saibal Ray, Debabrata Deb, Eur. Phys. J. C 76, 693 (2016)
S.K. Maurya, Eur. Phys. J. A 53, 89 (2017)
B.V. Ivanov, Eur. Phys. J. C 77, 738 (2017)
M.K. Jasim, S.K. Maurya, Y.K. Gupta, Astrophys. Space Sci. 361, 352 (2016)
S.K. Maurya, Y.K. Gupta, Baiju Dayanandan, Saibal Ray, Eur. Phys. J. C 76, 266 (2016)
Piyali Bhar, Ksh. Newton Singh, Tuhina Manna, Int. J. Mod. Phys. D 26, 1750090 (2017)
S. Thirukkanesh, F.C. Ragel, Ranjan Sharma, Shyam Das, Eur. Phys. J. C 78, 31 (2018)
L. Herrera, J. Ospino, A. Di Prisco, Phys. Rev. D 77, 027502 (2008)
M. Chaisi, S.D. Maharaj, Pramana 66, 313 (2006)
J. Ovalle, Phys. Rev. D 95, 104019 (2017)
J. Ovalle, Mod. Phys. Lett. A 23, 3247 (2008)
J. Ovalle, Braneworld Stars: Anisotropy Minimally Projected Onto the Brane, in Proceedings of the Ninth Asia-Pacific International Conference (Singapore, 2009) p. 173--182
Roberto Casadio, J. Ovalle, Roldao da Rocha, Class. Quantum Grav. 32, 215020 (2015)
J. Ovalle, Int. J. Mod. Phys. Conf. Ser. 41, 1660132 (2016)
J. Ovalle, F. Linares, Phys. Rev. D 88, 104026 (2013)
J. Ovalle, Laszl A. Gergely, Roberto Casadio, Class. Quantum Grav. 32, 045015 (2015)
Roberto Casadio, J. Ovalle, Roldao da Rocha, EPL 110, 40003 (2015)
L. Gabbanelli, A. Rincon, C. Rubio, Eur. Phys. J. C 78, 370 (2018)
J. Ovalle, R. Casadio, R. da Rocha, A. Sotomayor, Eur. Phys. J. C 78, 122 (2018)
Delgaty, Kayll Lake, Comput. Phys. Commun. 115, 395 (1998)
H. Heintzmann, Z. Phys. 228, 489 (1969)
N. Pant, R.N. Mehta, M. Pant, Astrophys. Space Sci. 332, 473 (2011)
K.N. Singh, N. Pant, Indian J. Phys. 90, 843 (2016)
Cristiano Germani, Roy Maartens, Phys. Rev. D 64, 124010 (2001)
Herrera, N.O. Santos, Phys. Rep. 286, 53 (1997)
George Ellis, Roy Maartens, Malcolm MacCallum, Gen. Relativ. Gravit. 39, 1651 (2007)
Private communication with Luis Herrera
Private communication with Tiberiu Harko
H. Abreu, H. Hernandez, L.A. Nunez, Class. Quantum Grav. 24, 4631 (2007)
L. Herrera, Phys. Lett. A 165, 206 (1992)
R. Chan, L. Herrera, N.O. Santos, Mon. Not. R. Astron. Soc. 265, 533 (1993)
R. Chan, L. Herrera, N.O. Santos, Mon. Not. R. Astron. Soc. 267, 637 (1994)
H. Heintzmann, W. Hillebrandt, Astron. Astrophys. 38, 51 (1975)
R. Chan, S. Kichenassamy, G. Le Denmat, N.O. Santos, Mon. Not. R. Astron. Soc. 239, 91 (1989)
S.K. Maurya, Y.K. Gupta, Saibal Ray, Baiju Dayanandan, Eur. Phys. J. C 75, 225 (2015)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Estrada, M., Tello-Ortiz, F. A new family of analytical anisotropic solutions by gravitational decoupling. Eur. Phys. J. Plus 133, 453 (2018). https://doi.org/10.1140/epjp/i2018-12249-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/i2018-12249-9