Abstract
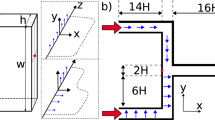
Motivated by the experimental ability to produce monodisperse particles in microfluidic devices, we study theoretically the hydrodynamic stability of driven and active crystals. We first recall the theoretical tools allowing to quantify the dynamics of elongated particles in a confined fluid. In this regime hydrodynamic interactions between particles arise from a superposition of potential dipolar singularities. We exploit this feature to derive the equations of motion for the particle positions and orientations. After showing that all five planar Bravais lattices are stationary solutions of the equations of motion, we consider separately the case where the particles are passively driven by an external force, and the situation where they are self-propelling. We first demonstrate that phonon modes propagate in driven crystals, which are always marginally stable. The spatial structures of the eigenmodes depend solely on the symmetries of the lattices, and on the orientation of the driving force. For active crystals, the stability of the particle positions and orientations depends not only on the symmetry of the crystals but also on the perturbation wavelengths and on the crystal density. Unlike unconfined fluids, the stability of active crystals is independent of the nature of the propulsion mechanism at the single-particle level. The square and rectangular lattices are found to be linearly unstable at short wavelengths provided the volume fraction of the crystals is high enough. Differently, hexagonal, oblique, and face-centered crystals are always unstable. Our work provides a theoretical basis for future experimental work on flowing microfluidic crystals.
Similar content being viewed by others
References
S. Ramaswamy, Adv. Phys. 50, 297 (2001).
E. Guazzelli, J. Hinch, Annu. Rev. Fluid Mech. 43, 97 (2011).
X.L. Wu, A. Libchaber, Phys. Rev. Lett. 84, 3017 (2000).
C. Dombrowski, L. Cisneros, S. Chatkaew, R.E. Goldstein, J.O. Kessler, Phys. Rev. Lett. 93, 098103 (2004).
L. Cisneros, R. Cortez, C. Dombrowski, R. Goldstein, J. Kessler, Exp. Fluids 43, 737 (2007).
A. Baskaran, M. Marchetti, Proc. Natl. Acad. Sci. U.S.A. 106, 15567 (2009).
S. Ramaswamy, Annu. Rev. Condens. Matter 1, 323 (2010).
G. Subramanian, D.L. Koch, Ann. Rev. Fluid Mech. 43, 637 (2011).
D. Saintillan, M.J. Shelley, Phys. Rev. Lett. 99, 058102 (2007).
D. Saintillan, M. Shelley, Phys. Fluids 20, 123304 (2008).
D. Dendukuri, P.S. Doyle, Adv. Mater 21, 4071 (2009).
M. Baron, J. Blawzdziewicz, E. Wajnryb, Phys. Rev. Lett. 100, 174502 (2008).
J. Blawzdziewicz, R.H. Goodman, N. Khurana, E. Wajnryb, Y.N. Young, Physica D 239, 1214 (2010).
T. Beatus, T. Tlusty, R. Bar-Ziv, Nat. Phys. 2, 743 (2006).
M. Hashimoto, B. Mayers, P. Garstecki, G. Whitesides, Small 2, 1292 (2006).
J. Howse, R. Jones, A. Ryan, T. Gough, R. Vafabakhsh, R. Golestanian, Phys. Rev. Lett. 99, 048102 (2007).
W.F. Paxton, K.C. Kistler, C.C. Olmeda, A. Sen, S.K.S. Angelo, Y. Cao, T.E. Mallouk, P.E. Lammert, V.H. Crespi, J. Am. Chem. Soc. 126, 13424 (2004).
S. Thutupalli, R. Seemann, S. Herminghaus, New J. Phys. 13, 073021 (2011).
D. Saintillan, M.J. Shelley, Phys. Rev. Lett. 100, 178103 (2008).
G.K. Batchelor, An Introduction to Fluid Dynamics (Cambridge University Press, Cambridge, UK, 1967). .
T. Beatus, R. Bar-Ziv, T. Tlusty, Phys. Rev. Lett. 99, 124502 (2007).
G.B. Jeffery, Proc. R. Soc. London, Ser. A 102, 161 (1922).
N. Liron, S. Mochon, J. Eng. Mech. 10, 287 (1976).
D. Long, A. Ajdari, Eur. Phys. J. E 4, 29 (2001).
E. Lauga, T. Powers, Rep. Prog. Phys. 72, 096601 (2009).
A. Baskaran, M. Marchetti, Proc. Natl. Acad. Sci. U.S.A. 106, 15567 (2009).
J. Crowley, Phys. Fluids 19, 1296 (1976).
A.A. Evans, T. Ishikawa, T. Yamaguchi, E. Lauga, Phys. Fluids 23, 111702 (2011).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Desreumaux, N., Florent, N., Lauga, E. et al. Active and driven hydrodynamic crystals. Eur. Phys. J. E 35, 68 (2012). https://doi.org/10.1140/epje/i2012-12068-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1140/epje/i2012-12068-y