1 Introduction

Einstein’s General Relativity (GR) has continued to withstand the test of time in its predictions of physical phenomena within the realms of astrophysics and cosmology. From the classical predictions of the precession of Mercury’s orbit and the deflection of starlight by a massive gravitating body to present day detection of gravitational waves and observations of black holes GR has triumphed. Early attempts seeking solutions of the Einstein field equations which describe stellar objects were crude and for most part unrealistic. The first exact solution of the Einstein field equations describing a self-gravitating sphere was obtained by Schwarzschild. The so-called interior Schwarzschild solution which described a constant density sphere suffered from various pathologies, the most notable being that the propagation speed for any signals within the fluid sphere was noncausal [1]. A survey of exact solutions appearing in the literature describing stellar objects by Delgaty and Lake [2] revealed that only a small subset of solutions meet the rigorous tests for physical viability, regularity and stability of fluid spheres.

The search for more realistic stellar models within GR required researchers to connect the macroscopic properties of stars determined through observations to the microphysics. A new era of stellar modeling was born, which went beyond the mathematical excursion of the Einstein field equations where ad hoc assumptions were made just to generate a toy model. Standard approaches which included assumptions on the metric function, density profiles, pressure profiles, anisotropy parameter and even the matter content which allowed for the system of equations to be integrated gave way to well-motivated techniques intrinsically connected to physics which include an equation of state (EoS), mass profiles linked to surface redshift and compactness of typical stellar structures. The linear EoS which links the radial pressure to the energy density has been generalized to include the microphysics (at least on a phenomenological level) via the so-called MIT bag model. The departure from pressure isotropy makes the modeling of stellar objects mathematically tractable. Imposing a barotropic EoS of the form \(p_{\mathrm{r}} = p_{\mathrm{r}}(\rho )\) reduces the problem of finding an exact model of the Einstein field equations using a single generating function. The imposition of an EoS has richly rewarded researchers with a handle on understanding complicated microphysics on a macroscale [3,4,5,6]. The color–flavor locked (CFL) EoS describing strange quark matter was shown to mimic the linear EoS. The CFL EoS has also been used to investigate the surface tension of stars which placed tighter restrictions on the bag constant as well as tangential pressure associated with the model. It has been recently demonstrated that the pressure isotropy condition is unstable. A self-gravitating sphere in quasi-static equilibrium will evolve into a regime in which the radial and transverse pressures are unequal. A shear-free fluid sphere will evolve into a shear-like epoch due to contributions from the Weyl tensor, density inhomogeneities and/or dissipative fluxes [7].

Though General Relativity (GR) has been used successfully to predict various phenomena that Newtonian gravitation fails to explain, there are still many unresolved issues. After the discovery of the accelerated expansion of the universe, several extended theories of gravity have been developed, like f(R) gravity, \(f(R,\,T)\) gravity, f(T) gravity, \(f(G,\,T)\) gravity, and EGB gravity. In our present paper, we will consider \(f(R,\,T)\) gravity, which has got immense interest in recent years. In fact, \(f(R,\,T)\) gravity was phenomenologically introduced by Harko et al. [8]. In this connection, we want to mention that recently the anisotropic charged and uncharged models in modified \(f(R,\,T )\) theory gravity have been studied in [9,10,11,12,13]. Pretel et al. [14] examined the static structure configurations and radial stability of compact stars within the context of \(f(R,\,T)\) gravity. Mahanta [15] constructed Locally Rotationally Symmetric Bianchi type I (LRSBI) cosmological models in the \(f(R,\,T)\) theory of gravity when the source of gravitation is a bulk viscous fluid. The models were constructed for \(f(R,\,T)=R+2f(T)\) and \(f(R,\,T)=f_1(R)+f_2(T)\). Singh et al. [16] have studied a flat Friedmann–Lemaitre–Robertson–Walker (FLRW) model with a modified Chaplygin gas (MCG) in \(f(R,\,T)\) gravity with particle creation. The cosmological reconstruction of the Little Rip model in \(f(R,\,T)\) gravity was investigated by Houndjo et al. [17], perfectly reproducing the present stage of the universe, characterized by the \(\Lambda \)CDM model, without singularity at future finite time (without the Big Rip). The problem of the violation of causality in \(f(R,\,T)\) modified gravity was proposed by Santos and Ferst [18]. Static spherically symmetric wormholes in \(f(R,\,T)\) gravity were proposed by Zubair et al. [19]. Azmat and Zubair [20] have adopted gravitational decoupling by a minimal geometric deformation (MGD) approach and have developed an anisotropic version of the well-known Tolman VII isotropic solution in the framework of f(R, T) gravity.

Charged compact objects have been studied for about a century within the context of classical GR. The Einstein–Maxwell field equations can be interpreted as an anisotropic system in which the electric field intensity mimics the anisotropy factor. These toy models have helped us in understanding the (in)stability of static fluid spheres in the presence of a charge. There have been various mechanisms put forward to account for a significant residual charge in stars. Several researchers have discovered the solution of the Einstein–Maxwell equations to describe the model of strange quark stars, charged black holes and other astrophysical compact objects [21,22,23,24,25,26]. Kiczek and Rogatko [27] studied the properties of ultra-compact spherically symmetric dark matter sector star objects, being the solution of Einstein equations with two U(1)-gauge fields—the first one is the ordinary Maxwell field, while the second one is auxiliary gauge field pertains to the hidden sector, mimicking the properties of dark matter. Arbañil and Malheiro [28] studied the hydrostatic equilibrium and the stability against a radial perturbation of charged strange quark stars composed of a charged perfect fluid. To construct the model one considered the perfect fluid to follow the MIT bag model equation of state and the radial charge distribution to follow a power law. Negreiros and collaborators [29, 30] modeled compact objects considering spheres composed of strange matter that follows the MIT bag model equation of state (EoS) and a Gaussian distribution of the electric charge on the surface of the star. In this paper the authors estimated that the electric charge that has a significant impact on the structure of the strange stars produces a surface electric field of the order of \(E \sim 10^{22}\) [V/m].

We have organized the paper as follows: In Sect. 2 we briefly summarize \(f(R,\,T)\) gravity and we present the corresponding relativistic equations within the framework of \(f(R,\,T )= R+2\gamma T\) model in the presence of an electric field. Section 3 deals with the solution of the field equations by choosing Tolman–Kuchowicz ansatz. In the next section we describe various physical properties of our present model analytically as well as graphically. The stability of the model is studied under various forces in Sect. 5. Finally in Sect. 6, our conclusions are summarized.

2 Basic field equations in \(f(R,\,T)\) gravity with charge

The general formulation of the Einstein–Hilbert (EH) action in General Relativity is expressed by

$$\begin{aligned} S_{\mathrm{EH}}= & {} \frac{1}{16 \pi }\int \mathrm{d}^4x \sqrt{-g}R. \end{aligned}$$
(1)

The above expression of the action in f(R, T) theory of gravity in the presence of charge is modified as [31]

$$\begin{aligned} S= & {} \frac{1}{16 \pi }\int f(R,T)\sqrt{-g} \mathrm{d}^4 x + \int {\mathcal {L}}_{\mathrm{m}}\sqrt{-g} \mathrm{d}^4 x \nonumber \\&+\int {\mathcal {L}}_{\mathrm{e}}\sqrt{-g} \mathrm{d}^4 x, \end{aligned}$$
(2)

where \(g = det(g_{\mu \nu }\)), \(f(R,\,T )\) represents the general function of Ricci scalar R and trace T of the energy–momentum tensor \(T_{\mu \nu }\), \({\mathcal {L}}_{\mathrm{m}}\) and \({\mathcal {L}}_{\mathrm{e}}\), respectively, denote the Lagrangian matter density and the Lagrangian for the electromagnetic field.

Let us assume a static spherically symmetric spacetime in curvature coordinates \((t,\,r,\,\theta ,\,\phi )\) as follows:

$$\begin{aligned} \mathrm{d}s^{2}= & {} -e^{\nu }\mathrm{d}t^{2}+e^{\lambda }\mathrm{d}r^{2}+r^{2}\left[ \sin ^{2}\theta \mathrm{d}\phi ^{2}+\mathrm{d}\theta ^{^2}\right] , \end{aligned}$$
(3)

the metric potentials \(\nu \) and \(\lambda \) are purely dependent on the radial co-ordinate r and it ranges from 0 to \(\infty \). The main aim of our present work is to obtain a physically reasonable and singularity-free model of a compact star and for this reason our present paper is developed by utilizing the following ansatz:

$$\begin{aligned} e^{\lambda }= 1 + ar^2 + br^4,\quad e^{\nu }= & {} C^2 e^{B r^2}, \end{aligned}$$
(4)

where a, b, B, C are constants. These metric potentials are known as the Tolman–Kuchowicz ansatz [32, 33]; it was successfully used earlier by several authors to model a compact star both in the context of General Relativity and of modified gravity. In the background of Tolman–Kuchowicz spacetime, Javed et al. [34] obtained anisotropic spheres in \(f(R,\,G)\) modified gravity, Majid and Sharif [35] obtained quark stars in massive Brans–Dicke gravity, Farasat Shamir and Fayyaz [36] obtained the model of charged compact star in f(R) gravity, Naz and Shamir [37] found the stellar model in f(G) gravity and its charged version [38], Biswas et al. [39] obtained an anisotropic strange star with \(f(R,\,T)\) gravity, Bhar et al. [40] modeled a compact star in EGB modified gravity.

It is worth to mention that, for an asymptotically flat spacetime, both the metric potential \(\nu (r)\) and \(\lambda (r)\) tend to 0 as \(r~\rightarrow ~\infty \), but in our present case this condition is not satisfied. Here, we have taken the signature of the spacetime as \((-,\, +,\, +,\,+)\). Now the Einstein–Maxwell field equations for obtaining the hydrostatic stellar structure of the charged sphere in modified \(f(R,\,T)\) gravity corresponding to action (2) is given by

$$\begin{aligned}&f_R R_{\mu \nu }-\frac{1}{2} g_{\mu \nu } f +(g_{\mu \nu }\Box -\nabla _{\mu }\nabla _{\nu })f_R \nonumber \\&\quad = 8\pi (T_{\mu \nu }+E_{\mu \nu })-f_T (T_{\mu \nu }+ \Theta _{\mu \nu }). \end{aligned}$$
(5)

Here \(f=f(R,T)\), \(f_R(R,T)=\frac{\partial f(R,T)}{\partial R},~f_T(R,T)=\frac{\partial f(R,T)}{\partial T}\). \(\nabla _{\nu }\) represents the covariant derivative associated with the Levi-Civita connection of \(g_{\mu \nu }\), \(\Theta _{\mu \nu }=g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}\) and \(\Box \equiv \frac{1}{\sqrt{-g}}\partial _{\mu }(\sqrt{-g}g^{\mu \nu }\partial _{\nu })\) represents the D’Alembert operator.

Landau and Lifshitz [41] defined the stress-energy tensor of matter as follows:

$$\begin{aligned} T_{\mu \nu }= & {} -\frac{2}{\sqrt{-g}}\frac{\delta \sqrt{-g}{\mathcal {L}}_{\mathrm{m}}}{\delta \sqrt{g_{\mu \nu }}}, \end{aligned}$$
(6)

and its trace T is defined by \(T=g^{\mu \nu }T_{\mu \nu }\). Now, if the Lagrangian density \({\mathcal {L}}_{\mathrm{m}}\) depends only on \(g_{\mu \nu }\), not on its derivatives, the above equation of \(T_{\mu \nu }\) takes the following form:

$$\begin{aligned} T_{\mu \nu }= & {} g_{\mu \nu }{\mathcal {L}}_{\mathrm{m}}-2\frac{\partial {\mathcal {L}}_{\mathrm{m}}}{\partial g_{\mu \nu }}. \end{aligned}$$
(7)

Now the matter Lagrangian density could be a function of both density and pressure, \({\mathcal {L}}_{\mathrm{m}} = {\mathcal {L}}_{\mathrm{m}} (\rho ,\, p)\), or it becomes an arbitrary function of the density of the matter \(\rho \) only, so that \({\mathcal {L}}_{\mathrm{m}} = {\mathcal {L}}_{\mathrm{m}}(\rho )\) [42]. For the present paper, we choose the matter Lagrangian as \({\mathcal {L}}_{\mathrm{m}}=\rho \) and the expression of \(\Theta _{\mu \nu }=-2T_{\mu \nu }-\rho g_{\mu \nu }.\)

Let us assume that the underlying fluid distribution of our proposed model is anisotropic in nature and therefore \(T_{\mu \nu }\) has an anisotropic fluid form having the components

$$\begin{aligned} T_{\mu \nu }= diag (-\rho ,\,p_{\mathrm{r}},\,p_{\mathrm{t}},\,p_{\mathrm{t}}), \end{aligned}$$
(8)

\(\rho \) being the matter density, \(p_{\mathrm{r}}\) and \(p_{\mathrm{t}}\) being, respectively, the radial and transverse pressure in modified gravity. The electromagnetic energy–momentum tensor \(E_{\mu \nu }\) has the following form:

$$\begin{aligned} E_{\mu \nu }= & {} \frac{1}{4 \pi }\left( F_{\mu }^{\alpha }F_{\nu \alpha }-\frac{1}{4}F^{\alpha \beta }F_{\alpha \beta } g_{\mu \nu }\right) , \end{aligned}$$
(9)

where \(F_{\mu \nu }\) is the antisymmetric electromagnetic field strength tensor defined by

$$\begin{aligned} F_{\mu \nu }= & {} \frac{\partial A_{\nu }}{\partial x^{\mu }}-\frac{\partial A_{\mu }}{\partial x^{\nu }}, \end{aligned}$$
(10)

and it satisfies the Maxwell equations,

$$\begin{aligned} F^{\mu \nu }_{;\nu }=\frac{1}{\sqrt{-g}}\frac{\partial }{\partial x^{\nu }}(\sqrt{-g}F^{\mu \nu })= & {} -4\pi j^{\mu }, \end{aligned}$$
(11)
$$\begin{aligned} F_{\mu \nu ;\lambda }+F_{\nu \lambda ;\mu }+F_{\lambda \mu ;\nu }= & {} 0, \end{aligned}$$
(12)

where \(A_{\nu }=(\phi (r),\,0,\,0,\,0)\) is the four-potential and \(j^{\mu }\) is the four-current vector, defined by

$$\begin{aligned} j^{\mu }= & {} \frac{\rho _{\mathrm{e}}}{\sqrt{g_{00}}}\frac{\mathrm{d}x^{\mu }}{\mathrm{d}x^0}, \end{aligned}$$
(13)

where \(\rho _{\mathrm{e}}\) denotes the proper charge density. The expression for the electric field can be obtained from Eq. (11) as follows:

$$\begin{aligned} F^{01}= & {} -e^{\frac{\lambda +\nu }{2}}\frac{q(r)}{r^2}, \end{aligned}$$
(14)

here q(r) represents the net charge inside a sphere of radius r and it can be obtained as follows:

$$\begin{aligned} q(r)= & {} 4\pi \int _0^r \rho _{\mathrm{e}} e^{\frac{\lambda }{2}} r^2 \mathrm{d}r. \end{aligned}$$
(15)

In order to discuss the coupling effects of matter and curvature components in \(f (R,\,T )\) gravity, let us consider a separable functional form,

$$\begin{aligned} f(R,\,T)= & {} R+2 \gamma T, \end{aligned}$$
(16)

where \(\gamma \) is some small positive constant. Harko et al. [31] proposed that for \(\gamma ~\rightarrow ~0\), Eq. (16) produces the field equations in General Relativity. The term \(2 \gamma T\) induces a time-dependent coupling between curvature and matter.

For the line element (3), the field equations in modified gravity can be written as follows:

$$\begin{aligned} 8\pi \rho ^{\text {eff}}+\frac{q^2}{r^4}= & {} \frac{\lambda '}{r}e^{-\lambda }+\frac{1}{r^{2}}(1-e^{-\lambda }), \end{aligned}$$
(17)
$$\begin{aligned} 8 \pi p_{\mathrm{r}}^{\text {eff}}-\frac{q^2}{r^4}= & {} \frac{1}{r^{2}}(e^{-\lambda }-1)+\frac{\nu '}{r}e^{-\lambda }, \end{aligned}$$
(18)
$$\begin{aligned} 8 \pi p_{\mathrm{t}}^{\text {eff}}+\frac{q^2}{r^4}= & {} \frac{1}{4}e^{-\lambda }\left[ 2\nu ''+\nu '^2-\lambda '\nu '+\frac{2}{r}(\nu '-\lambda ')\right] . \nonumber \\ \end{aligned}$$
(19)

The quantity q(r) actually determines the electric field as follows:

$$\begin{aligned} E(r)= & {} \frac{q(r)}{r^2}, \end{aligned}$$
(20)

where \(\rho ^{\text {eff}}\), \(p_{\mathrm{r}}^{\text {eff}}\) and \(p_{\mathrm{t}}^{\text {eff}}\) are, respectively, the density and pressures in Einstein Gravity where

$$\begin{aligned} \rho ^{\text {eff}}= & {} \rho +\frac{\gamma }{8\pi }( \rho -p_{\mathrm{r}}-2p_{\mathrm{t}}), \end{aligned}$$
(21)
$$\begin{aligned} p_{\mathrm{r}}^{\text {eff}}= & {} p_{\mathrm{r}}+\frac{\gamma }{8\pi }(\rho +3p_{\mathrm{r}}+2p_{\mathrm{t}}), \end{aligned}$$
(22)
$$\begin{aligned} p_{\mathrm{t}}^{\text {eff}}= & {} p_{\mathrm{t}}+\frac{\gamma }{8\pi }(\rho +p_{\mathrm{r}}+4p_{\mathrm{t}}). \end{aligned}$$
(23)

The prime denotes differentiation with respect to r. Our aim is to find the solution of the system (17)–(19) which will fully specify the behavior of the interior of the stellar object. \(\rho ,\,p_{\mathrm{r}}\) and \(p_{\mathrm{t}}\), respectively, denote the matter density and pressures in modified gravity.

Now by the taking the covariant divergence of (5), the divergence of the stress-energy tensor \(T_{\mu \nu }\) can be obtained [31, 43, 44],

$$\begin{aligned} \nabla ^{\mu }T_{\mu \nu }= & {} \frac{f_T(R,T)}{8\pi -f_T(R,T)}\Big [(T_{\mu \nu }+\Theta _{\mu \nu })\nabla ^{\mu }\ln f_T(R,T)\nonumber \\&+\nabla ^{\mu }\Theta _{\mu \nu }-\frac{1}{2}g_{\mu \nu }\nabla ^{\mu }T-\frac{8\pi }{f_T}\nabla ^{\mu }E_{\mu \nu }\Big ]. \end{aligned}$$
(24)

From Eq. (24), we can check that \(\nabla ^{\mu }T_{\mu \nu }\ne 0\) if \(f_T(R,T)\ne 0\). So the system will not be conserved like Einstein gravity. In the next section we are interested to find the solutions of the field equations in the charged case in the \(f(R,\,T)\) modified theory of gravitation.

3 Our proposed model in \(f(R,\,T)\) modified gravity

Employing the expressions of the metric coefficients given in (4), in Eqs. (17)–(19), the following set of equations are obtained:

$$\begin{aligned} 8\pi \rho ^{\text {eff}}+\frac{q^2}{r^4}= & {} \frac{3 a + (a^2 + 5 b) r^2 + 2 a b r^4 + b^2 r^6}{{\Psi }^2}, \end{aligned}$$
(25)
$$\begin{aligned} 8\pi p_{\mathrm{r}}^{\text {eff}}-\frac{q^2}{r^4}= & {} -\frac{a - 2 B + b r^2}{\Psi }, \end{aligned}$$
(26)
$$\begin{aligned} 8 \pi p_{\mathrm{t}}^{\text {eff}}+\frac{q^2}{r^4}= & {} \frac{1}{{\Psi }^2}\Big [-a + 2 B + \big ( B (a + B)-2b\big ) r^2 \nonumber \\&+ a B^2 r^4 + bB^2r^6\Big ], \end{aligned}$$
(27)

where \(\Psi \) is a function of r given by

$$\begin{aligned} \Psi= & {} (1 + a r^2 + b r^4). \end{aligned}$$

To describe strange quark matter, a very general approach is to use the MIT bag model equation of state. A stellar object whose matter content consists only of up, down and strange quarks, the MIT bag model is the simplest equation of state to study the equilibrium configuration of the model. This equation of state takes into account that these quarks are massless and non-interacting quarks confined by a bag constant \(B_{\mathrm{g}}\). For the anisotropic fluid studied, we consider the energy density and the radial pressure of the fluid to be connected through the relation

$$\begin{aligned} \rho= & {} 3p_{\mathrm{r}}+4 B_{\mathrm{g}} . \end{aligned}$$
(28)

Here \(B_{\mathrm{g}}\) is defined as the bag constant. Mak and Harko investigated the difference between the bag constant and the mass density of the perturbed and non-perturbed QCD vacuum, in units of the bag constant, \(\hbox {MeVfm}^{-3}\), as derived by Chodos et al. [45].

Equation (28) can be written as follows:

$$\begin{aligned} p_{\mathrm{r}}= & {} \frac{1}{3} (\rho - 4 B_{\mathrm{g}}). \end{aligned}$$
(29)

Witten [46] proposed that the formation of strange matter can be classified into two possibilities: the quark–hadron phase transition in the early universe and conversion of neutron stars into strange stars at ultra-high densities. Farhi and Jaffe [47] showed that, for massless and non-interacting quarks, the Witten conjecture is verified for a bag constant approximately between the values 57 MeV/\(\hbox {fm}^3\) and 94 MeV/\(\hbox {fm}^3\). For our present paper we consider \(B_{\mathrm{g}} = 60\) MeV/\(\hbox {fm}^3\).

With the help of (29), we solve Eqs. (25)–(27) and obtain the expressions for matter density and pressures in Einstein gravity as follows:

$$\begin{aligned} \rho ^{\text {eff}}= & {} {B_{\mathrm{g}}} +\frac{ 3 (a + B + (2 b + a B) r^2 + b B r^4)}{16 \pi {\Psi }^2}, \end{aligned}$$
(30)
$$\begin{aligned} p_{\mathrm{r}}^{\text {eff}}= & {} -{ B_{\mathrm{g}}} +\frac{a + B + (2 b + a B) r^2 + b B r^4}{16 \pi {\Psi }^2}, \end{aligned}$$
(31)
$$\begin{aligned} p_{\mathrm{t}}^{\text {eff}}= & {} {B_{\mathrm{g}}} + \frac{1}{16 \pi {\Psi }^2} \Big [-5 a + 7 B + (-2 a^2 - 8 b \nonumber \\&+ 5 a B + 2 B^2) r^2 + \big (3 b B + 2 a (-2 b + B^2)\big ) r^4 \nonumber \\&+ 2 b (-b + B^2) r^6 \Big ]. \end{aligned}$$
(32)

The expression for the anisotropic factor in General Relativity is given by (Fig. 1)

$$\begin{aligned} \Delta ^{\text {eff}}= & {} p_{\mathrm{t}}^{\text {eff}}-p_{\mathrm{r}}^{\text {eff}} \nonumber \\= & {} 2~{ B_{\mathrm{g}}} +\frac{-2 a + 2 B - 4 b r^2 + a B r^2}{8 \pi {\Psi }^2} \nonumber \\&+ \frac{-a + B + (-b + B^2) r^2}{8 \pi \Psi }. \end{aligned}$$
(33)
Fig. 1
figure 1

The matching condition of the metric potential \(e^{\lambda }\) and \(e^{\nu }\) are shown against the radius for the compact star SAX J \(1808.4-3658\)

Full size image

The electric field \(E^2\) in modified gravity is obtained as follows:

$$\begin{aligned} E^2= & {} \frac{1}{3\gamma + 4 \pi }\bigg [-4~{ B_{\mathrm{g}}} (\gamma + 2 \pi ) (\gamma + 4 \pi )\nonumber \\&+\frac{1}{\Psi }\Big \{2 a (\gamma + 2 \pi ) - 2 B (\gamma + 3 \pi )\nonumber \\&+\Big (B^2 \gamma + 2 b (\gamma + 2 \pi )\Big ) r^2\Big \}+\frac{1}{{\Psi }^2} \Big \{2 B \gamma \nonumber \\&+2 b (\gamma + 2 \pi ) r^2 + a (\gamma + 2 \pi + B \gamma r^2)\Big \}\bigg ]. \end{aligned}$$
(34)

To obtain the expressions for \(\rho ,\,p_{\mathrm{r}}\) and \(p_{\mathrm{t}}\) we solve Eqs. (21)–(23) by using the expressions given in (30)–(32). Solving those equations, we find the expressions for matter density and pressures in modified gravity as follows:

$$\begin{aligned} \rho= & {} \frac{3}{4}\Big [\frac{4B_{\mathrm{g}}}{3} + \frac{a + B + (2 b + a B) r^2 + b B r^4}{(\gamma + 4 \pi ) {\Psi }^2}\Big ], \end{aligned}$$
(35)
$$\begin{aligned} p_{\mathrm{r}}= & {} -{B_{\mathrm{g}}} + \frac{a + B + (2 b + a B) r^2 + b B r^4}{4 (\gamma + 4 \pi ) {\Psi }^2}, \end{aligned}$$
(36)
$$\begin{aligned} p_{\mathrm{t}}= & {} \frac{1}{4 (\gamma + 4 \pi ) (3 \gamma + 4 \pi )} \bigg [ 4 B_{\mathrm{g}} (\gamma + 4 \pi )^2 \nonumber \\&+ \frac{1}{\Psi }\Big [-B (\gamma - 12 \pi ) - 2 a (\gamma + 4 \pi ) \nonumber \\&+ 2 (-b + B^2) (\gamma + 4 \pi ) r^2\Big ] +\frac{1}{{\Psi }^2}\Big \{4 B (\gamma + 4 \pi ) \nonumber \\&- 2 b (7 \gamma + 12 \pi ) r^2 + a \Big ( 2 B (\gamma + 4 \pi ) r^2 \nonumber \\&-(7 \gamma + 12 \pi )\Big )\Big \} \bigg ]. \end{aligned}$$
(37)

The anisotropic factor \(\Delta =p_{\mathrm{t}}-p_{\mathrm{r}}\) in modified gravity is obtained as follows:

$$\begin{aligned} \Delta= & {} \frac{1}{2 (3 \gamma + 4 \pi )} \bigg [ 8{ B_{\mathrm{g}}} (\gamma + 2 \pi )+ \frac{1}{(\gamma + 4 \pi ) {\Psi }^2}\nonumber \\&\quad \times \Big \{(2 B-5a) \gamma +(B-a)8\pi + \Big (a B (\gamma + 4 \pi ) \nonumber \\&- 2 b (5 \gamma + 8 \pi )\Big ) r^2\Big \}+\frac{1}{(\gamma + 4 \pi )\Psi }\Big \{2 B (2 \pi -\gamma ) \nonumber \\&- a (\gamma + 4 \pi )- (b - B^2) (\gamma + 4 \pi ) r^2 \Big \}\bigg ]. \end{aligned}$$
(38)

So, the model parameters, like density, radial and transverse pressure, anisotropic factor, and electric field, in the background of General Relativity as well as in modified gravity have been successfully obtained.

Table 1 The numerical values of central density, surface density, central pressure, relativistic adiabatic index, mass and effective surface redshift for different values of \(\gamma \) for the compact star SAX J1808.4-3658 by assuming \(M = 0.88~M_{\odot },\, R = 8.9 \) km, Q = 0.0089
Full size table

To find the various constants in the TK metric potentials, we match our interior solution to the exterior spacetime smoothly outside the event horizon \(r>M+\sqrt{M^{2}-Q^2}\), where M and Q are, respectively, the total mass and charge enclosed within the boundary \(r=R\). Now one can note that the exterior spacetime is zero as there is no matter in the vacuum spacetime. Therefore, there will be no change of the GR solution for the exterior spacetime metric even in the \(f(R,\,T )\) theory of gravity. The exterior spacetime of the star will be described by the Reissner–Nordström metric [48, 49] given by

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( 1 - \frac{2M}{r} + \frac{Q^2}{r^2}\right) \mathrm{d}t^2 + \left( 1 - \frac{2M}{r} + \frac{Q^2}{r^2}\right) ^{-1}\mathrm{d}r^2 \nonumber \\&+ r^2(\mathrm{d}\theta ^2+\sin ^2\theta \mathrm{d}\phi ^2). \end{aligned}$$
(39)

Now the continuity of the metric coefficients \(g_{tt}\), \(g_{rr}\) and \(\frac{\partial g_{tt}}{\partial r}\) across the boundary surface \(r= R\) between the interior and the exterior regions gives the following set of relations:

$$\begin{aligned} 1 - 2{\tilde{x}}+ {\tilde{y}}= & {} C^2 e^{BR^2}, \end{aligned}$$
(40)
$$\begin{aligned} 1 - 2{\tilde{x}} + {\tilde{y}}= & {} (1 + a R^2 + b R^4)^{-1}, \end{aligned}$$
(41)
$$\begin{aligned} {\tilde{x}} - {\tilde{y}}= & {} B R^2 C^2 e^{BR^2}, \end{aligned}$$
(42)

where \({\tilde{x}}=\frac{M}{R}\) and \({\tilde{y}}=\frac{Q^2}{R^2} \) and both \({\tilde{x}},\,{\tilde{y}}\) are dimensionless quantities.

Solving Eqs. (40)–(42) and using the condition \(p_{\mathrm{r}}(R)=0\), one can determine the values of the constants B, C, a and b as follows:

$$\begin{aligned} B= & {} \frac{U}{R^2} \left[ {\tilde{x}} - {\tilde{y}}\right] , \end{aligned}$$
(43)
$$\begin{aligned} C= & {} e^{-\frac{BR^2}{2}} U^{-\frac{1}{2}}, \end{aligned}$$
(44)
$$\begin{aligned} a= & {} \frac{1}{(\gamma + 2 \pi ) R^2 (1 + 3U^2)}\Big [-2 (\gamma + 2 \pi ) + (\gamma + 2 \pi ) \nonumber \\&\times (2 + B R^2)U+6 B \pi U^2 R^2 \Big ], \end{aligned}$$
(45)
$$\begin{aligned} b= & {} \frac{-1 - aR^2 + U}{R^4}, \end{aligned}$$
(46)

where \( U = \Big (1 - 2{\tilde{x}} + {\tilde{y}}\Big )^{-1}\).

Now from the condition that the radial pressure vanishes at the boundary of the star \((p_{\mathrm{r}}(r=R)=0)\) one can get

$$\begin{aligned} \rho _{\mathrm{s}} = 4 B_{\mathrm{g}}, \end{aligned}$$
(47)

where \(\rho _{\mathrm{s}}\) is the surface density given by

$$\begin{aligned} \rho _{\mathrm{s}}= & {} B_{\mathrm{g}} + \frac{3 \big (a + B + (2 b + a B) R^2 + b B R^4\big )}{4 (\gamma + 4 \pi ) (1 + a R^2 + b R^4)^2}. \end{aligned}$$
(48)

For drawing the plots we have considered the compact star SAX J 1808.4-3658 by assuming \(M = 0.88~M_{\odot },\, R = 8.9 \) km. Along with this we have also assumed \(Q = 0.0089\). The central density, surface density and central pressure for different values of \(\gamma \) have been obtained in Table 1.

4 Physical aspects of \(f(R,\,T)\) gravity

In this section we perform both an analytic and a graphical analysis in order to check the physical and mathematical properties of our present model. Now we shall check the conditions one by one.

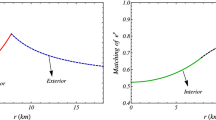
  • Metric potentials In this paper, we choose the metric potentials as follows: \(e^{\nu }=C^2 e^{Br^2},~~e^{\lambda }=(1 + a r^2 + b r^4)\), we note that \(e^{\nu }|_{r=0}=e^{C}>0\) and \(e^{\lambda }|_{r=0}=1\), moreover, \(\left( e^{\nu }\right) '=2 B e^{C + B r^2} r ,~~\left( e^{\lambda }\right) '=2 A e^{A r^2} r\). We will notice in a later section that this behavior allows one to match the inner geometry to the exterior spacetime in a smooth way at the boundary \(r=R\) to get the constant parameters that characterize the model. So the metric potentials are well behaved in the interval (0, R).

  • Pressure and density In this regard the main thermodynamic variables must respect some criteria. From Eqs. (35)–(37), at the center of the compact configuration we have

    $$\begin{aligned} \rho _{\mathrm{c}}= & {} \frac{3 a + 3 B + 4 { B_{\mathrm{g}}} (\gamma + 4 \pi )}{4 (\gamma + 4 \pi )}, \\ p_{\mathrm{c}}= & {} -{ B_{\mathrm{g}}}+\frac{a + B}{4 (\gamma + 4 \pi )}, \end{aligned}$$

    where \(\rho _{\mathrm{c}}\) and \(p_{\mathrm{c}}\) are, respectively, the central density and central pressure of the compact star in modified gravity. The corresponding quantities in GR can be obtained by simply putting \(\gamma =0\). We obtain the density and pressure gradients for our present model by differentiation of Eqs. (35)–(37) with respect to r as follows:

    $$\begin{aligned} \rho '= & {} -\frac{3r}{2 (\gamma + 4 \pi ){\Psi }^3}\Big [a^2 (2 + B r^2) + a (B \\&+ 6 b r^2 + 3 b B r^4) + 2 b \big \{-1 + 3 b r^4 \\&+ B (r^2 + b r^6)\big \}\Big ]<0, \\ p_{\mathrm{r}}'= & {} -\frac{r}{2 (\gamma + 4 \pi ){\Psi }^3}\Big [a^2 (2 + B r^2) + a (B \\&+ 6 b r^2 + 3 b B r^4) + 2 b \big \{-1 + 3 b r^4 \\&+ B (r^2 + b r^6)\big \} \Big ]<0, \\ p_{\mathrm{t}}'= & {} \frac{r}{2 (\gamma + 4 \pi ) (3 \gamma + 4 \pi ) {\Psi }^3} \Big [2\Psi \big \{a B (\gamma + 4 \pi ) \\&- b (7 \gamma + 12 \pi )\big \} -\Psi (a + 2 b r^2) \big \{B (12 \pi -\gamma ) \\&- 2 a (\gamma + 4 \pi ) +2 (-b + B^2) (\gamma + 4 \pi ) r^2\big \} \\&+2{\Psi }^2 (-b + B^2) (\gamma + 4 \pi )-2 (a + 2 b r^2)\\&\times \Big \{4 B (\gamma + 4 \pi ) - 2 b (7 \gamma + 12 \pi ) r^2 \\&- a \big \{7 \gamma + 12 \pi -2 B (\gamma + 4 \pi ) r^2\big \}\Big \} \Big ]<0. \end{aligned}$$

    We see that

    $$\begin{aligned} \rho '|_{r=0}=0,\,p_{\mathrm{r}}'|_{r=0}=0,\,p_{\mathrm{t}}'|_{r=0}=0, \end{aligned}$$

    and

    $$\begin{aligned} \rho ''|_{r=0}= & {} \frac{6 b - 3 a (2 a + B)}{2 (\gamma + 4 \pi )},\\ p_{\mathrm{r}}''|_{r=0}= & {} \frac{2 b - a (2 a + B)}{2 (\gamma + 4 \pi )},\\ p_{\mathrm{t}}''|_{r=0}= & {} \frac{-2 b + a (2 a + B)}{(\gamma + 4 \pi )}\\&+ \frac{4 a^2 - 4 b - 11 a B + 2 B^2}{ (6 \gamma + 8 \pi )}. \end{aligned}$$
Fig. 2
figure 2

(Top) Matter density \(\rho \), (middle) radial pressure \(p_{\mathrm{r}}\), (bottom) transverse pressure \(p_{\mathrm{t}}\) against r inside the stellar interior for different values of \(\gamma \) mentioned in the figure

Full size image

The profiles of the matter density and both the pressures are plotted against the radius in Fig. 2. The profiles show that \(\rho ,\,p_{\mathrm{r}}\) and \(p_{\mathrm{t}}\) all are positive for \(r \in (0,\,R)\). All are monotonically decreasing functions of r, i.e., all of them take maximum value at the center of the star and take minimum value at the boundary. Moreover, the radial pressure vanishes at the boundary of the star but both transverse pressure and matter density are positive at the boundary of the star.

For a physically acceptable model, the pressure should be non-negative inside the fluid sphere, and therefore, \(p_{\mathrm{c}}>0~ \Rightarrow ~ \frac{a+B}{4(\gamma +4\pi )}>B_{\mathrm{g}}\). Again by the Zeldivich condition [50] \(p_{\mathrm{c}}/\rho _{\mathrm{c}}~<1~\Rightarrow ~B_{\mathrm{g}}>-\frac{a+B}{4(\gamma +4\pi )}\). This lower limit for the bag constant \(B_{\mathrm{g}}\) is always satisfied since \(B_{\mathrm{g}}\) is positive. So we obtain a reasonable upper bound for the bag constant as follows:

$$\begin{aligned} B_{\mathrm{g}}<\frac{a+B}{4(\gamma +4\pi )}. \end{aligned}$$
(49)

  • Causality condition In order to fulfill the physical requirements for realistic models, it is necessary to examine the causality and hydrostatic equilibrium of the present self-gravitating system. First, we discuss the causality condition of the model, which says that the velocity of sound must be less than the velocity of light everywhere within the object. The square of radial and transverse velocity of sound \(V_{\mathrm{r}}^2\) and \(V_{\mathrm{t}}^2\), respectively, are given by

    $$\begin{aligned} V_{\mathrm{r}}^2= \frac{\mathrm{d}p_{\mathrm{r}}}{\mathrm{d}\rho }= & {} \frac{1}{3}, \end{aligned}$$
    (50)
    $$\begin{aligned} V_{\mathrm{t}}^2=\frac{\mathrm{d}p_{\mathrm{t}}}{\mathrm{d}\rho }= & {} \frac{1}{\chi }\Big [-16 a^2 \gamma + 16 b \gamma + 5 a B \gamma \nonumber \\&- 2 B^2 \gamma - 32 a^2 \pi + 32 b \pi \nonumber \\&+ 36 a B \pi - 8 B^2 \pi \nonumber \\&+ D_1r^2 -3 b D_2 r^4 +2 b D_3 r^6 \nonumber \\&- 2 b^2 (b - B^2) (\gamma + 4 \pi ) r^8\Big ], \end{aligned}$$
    (51)

    where \(\chi =\chi (r)\) and its expression is given by

    $$\begin{aligned} \chi= & {} 3 (3 \gamma + 4 \pi ) \Big [a^2 (2 + B r^2) + a (B + 6 b r^2 + 3 b B r^4) \\&+ 2 b \big (-1 + 3 b r^4 + B (r^2 + b r^6)\big )\Big ], \end{aligned}$$

    and \(D_1,\,D_2\) and \(D_3\) are constants dependent on \(\gamma \) and their expressions are as follows:

    $$\begin{aligned} D_1= & {} -2 a^3 (\gamma + 4 \pi ) + a^2 B (\gamma + 20 \pi ) +2 b B (7 \gamma + 44 \pi ) \\&- 2 a \big (B^2 (\gamma + 4 \pi ) + b (22 \gamma + 40 \pi )\big ), \\ D_2= & {} 2 a^2 (\gamma + 4 \pi ) + 2 b (7 \gamma + 12 \pi ) - a B (\gamma + 20 \pi ),\\ D_3= & {} -b B (\gamma - 12 \pi ) - a (3 b - B^2) (\gamma + 4 \pi ). \end{aligned}$$
Fig. 3
figure 3

(Top) Square of the radial sound velocity \(V_{\mathrm{r}}^2\), (middle) square of the transverse sound velocity \(V_{\mathrm{t}}^2\) and (bottom) the stability factor \(|V_{\mathrm{t}}^2-V_{\mathrm{r}}^2|\) against r for the strange star candidate SAX J1808.4-3658 by taking different values of \(\gamma \)

Full size image

Moreover, for a relativistic object, Herrera [52] proposed the method of “cracking” which is related to the stability of anisotropic stars under small radial perturbations. Using the concept of cracking, Abreu et al. [51] proved that the region of an anisotropic star where the radial speed of sound crosses the transverse speed of sound is potentially stable, otherwise, the region is potentially unstable. In mathematical terms, it can be written as follows:

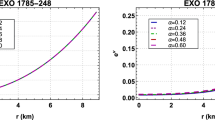
$$\begin{aligned} -1 \le V_{\mathrm{t}}^2-V_{\mathrm{r}}^2\le 0~\Rightarrow ~\text {Potentially stable region},\\ 0 < V_{\mathrm{t}}^2-V_{\mathrm{r}}^2 \le 1~\Rightarrow ~\text {Potentially unstable region}. \end{aligned}$$

Since both sound speeds maintain causality, we have \(V_{\mathrm{r}}^2,\,V_{\mathrm{t}}^2 <1\) [51, 52]. Again, Le Chatelier’s principle requires that \(V_{\mathrm{r}}^2,\,V_{\mathrm{t}}^2>0\). Combining the above two cases we get \(0<V_{\mathrm{r}}^2,\,V_{\mathrm{t}}^2<1\) and it gives, \(-1<V_{\mathrm{r}}^2-V_{\mathrm{t}}^2<1\), it further implies that \(|V_{\mathrm{r}}^2-V_{\mathrm{t}}^2|<1\). The profiles of \(V_{\mathrm{r}}^2,\,V_{\mathrm{t}}^2\) and \(|V_{\mathrm{r}}^2-V_{\mathrm{t}}^2|\) for different values of \(\gamma \) are plotted in Fig. 3.

  • Relativistic adiabatic index To study the stability of both relativistic and non-relativistic compact star models, the relativistic adiabatic index is used and it also characterizes the stiffness of the EoS for a given density. After the pioneering work by Chandrasekhar [53], many scientists studied the dynamical stability of the stellar system against an infinitesimal radial adiabatic perturbation. The collapsing condition of the anisotropic model is given by \(\Gamma _{\mathrm{r}}<4/3\) [54]. The radial adiabatic index \(\Gamma _{\mathrm{r}}\) reads [55]

    $$\begin{aligned} \Gamma _{\mathrm{r}}=\left( \frac{\rho }{p_{\mathrm{r}}}+1\right) \left( \frac{\mathrm{d}p_{\mathrm{r}}}{\mathrm{d}\rho }\right) _S. \end{aligned}$$
    (52)
Fig. 4
figure 4

The relativistic adiabatic index \(\Gamma _{\mathrm{r}}\) against r inside the stellar interior

Full size image

Here the derivation is performed at constant entropy S and \(\frac{\mathrm{d}p_{\mathrm{r}}}{\mathrm{d}\rho }\) is the speed of sound in units of the speed of light. From the expression of \(\Gamma _{\mathrm{r}}\) we see that the adiabatic index depends on the ratio \(\rho /p_{\mathrm{r}}\). The profile of \(\Gamma _{\mathrm{r}}\) is plotted in Fig. 4 for different values of \(\gamma \).

  • Behavior of electric field and anisotropic factor The expression of the electric field is given in Eq. (34). Now for a physically acceptable model it is required that \(E^2(r=0)=0\), which leads to the following equation:

    $$\begin{aligned} \frac{3 a \gamma - 4 \gamma ^2 B_{\mathrm{g}} + 6 a \pi - 6 B \pi - 24 \gamma B_{\mathrm{g}} \pi - 32 B_{\mathrm{g}} \pi ^2}{3 \gamma + 4 \pi }=0. \end{aligned}$$
    (53)

    The above equation gives the expression of the bag constant as follows:

    $$\begin{aligned} B_{\mathrm{g}}=\frac{3}{4}\left( -\frac{B}{\gamma +2\pi } + \frac{a+B}{\gamma +4\pi }\right) . \end{aligned}$$

    The expression of the anisotropic factor is given in Eq. (38), which is defined as the difference between the transverse and radial pressure. It may be positive or negative, according as \(p_{\mathrm{t}}>p_{\mathrm{r}}\) or \(p_{\mathrm{t}}<p_{\mathrm{r}}\), and it is denoted by \(\Delta \). The anisotropic force is defined by \(\frac{2\Delta }{r}\), and this force may be positive or negative, depending upon the sign of \(\Delta \), this force vanishes for the isotropic case. The profiles of electric field and anisotropic factor are plotted in Fig. 5.

Fig. 5
figure 5

(Top) \(E^2\) and (bottom) anisotropic factor \(\Delta \) are shown against the radius for different values of \(\gamma \) mentioned in the figure

Full size image

  • Energy conditions Our proposed model of a charged compact star will satisfy the null energy condition (NEC), the weak energy condition (WEC), the strong energy condition (SEC) and the dominant energy condition (DEC) if the following inequality holds simultaneously for each and every point inside the stellar model:

    • NEC: \(\rho +p_{\mathrm{r}} \ge 0,~\rho + p_{\mathrm{t}} +\frac{E^2}{4\pi } \ge 0,\) and this energy condition implies that an observer crossing a null diagram will quantify the usual matter density to be nonnegative.

    • WEC: \(\rho +p_{\mathrm{r}} \ge 0,~\rho + p_{\mathrm{t}} +\frac{E^2}{4\pi } \ge 0,~ \rho + \frac{E^2}{8\pi } \ge 0,\) and WEC suggests that the matter density measured by an observer traversing a time-like diagram is always positive.

    • SEC: \(\rho +p_{\mathrm{r}} \ge 0,~\rho + p_{\mathrm{t}} +\frac{E^2}{4\pi } \ge 0, \rho + p_{\mathrm{r}} +2 p_{\mathrm{t}}+ \frac{E^2}{4\pi } \ge 0,\) and SEC indicates that the trace of the tidal tensor tested by the relating observers is always positive.

    • DEC: \(\rho -p_{\mathrm{r}} +\frac{E^2}{4 \pi }\ge 0,~\rho - p_{\mathrm{t}} \ge 0,~ \rho + \frac{E^2}{8\pi } \ge 0\), and DEC represents the mass-energy never to be seen to be flowing faster than light.

    The expressions on the l.h.s. of the above inequalities are plotted in Fig. 8. From the figure we see that all the energy conditions are satisfied. In our study on the charged compact star, SEC is satisfied, implying the fact that gravity will be attractive and also the matter-energy density will be always positive.

  • Equation of state The equation of state parameters \(\omega _{\mathrm{r}}\) and \(\omega _{\mathrm{t}}\) can be obtained from the following relation:

    $$\begin{aligned} p_{\mathrm{r}}=\omega _{\mathrm{r}} \times \rho ,~~p_{\mathrm{t}}=\omega _{\mathrm{t}} \times \rho . \end{aligned}$$

    Moreover, we know that the radial pressure maintains a linear relationship from our assumptions but the variation of the transverse pressure with respect to the density is unknown to us. The equation of state parameter and variation of pressure with respect to the density is depicted in Fig. 7.

  • Mass, compactness and redshift The effective gravitational mass within the radius r of the charged strange star can be obtained from the following formula [56]:

    $$\begin{aligned} m(r)= & {} 4\pi \int _0^r \rho ({\tilde{r}})~{\tilde{r}}^2 \mathrm{d}{\tilde{r}} +\frac{q^2}{2r}+\frac{1}{2}\int _0^r\frac{q({\tilde{r}})^2}{{\tilde{r}}^2}\mathrm{d}{\tilde{r}}\nonumber \\= & {} m^{\text {eff}} -\frac{\gamma }{2}\int _0^r(\rho -p_{\mathrm{r}}-2p_{\mathrm{t}})({\tilde{r}})~{\tilde{r}}^2 \mathrm{d}{\tilde{r}}\nonumber \\&+\frac{q^2}{2r}+\frac{1}{2}\int _0^r\frac{q({\tilde{r}})^2}{{\tilde{r}}^2}\mathrm{d}{\tilde{r}}. \end{aligned}$$
    (54)

    In Eq. (54), \(m^{\text {eff}}=4\pi \int _0^r \rho ^{\text {eff}} ({\tilde{r}}){\tilde{r}}^2 \mathrm{d}{\tilde{r}}\). In Einstein–Maxwell gravity the mass function is obtained when \(\gamma ~\rightarrow ~0\). The mass function inside the radius r of the charged fluid sphere can be obtained as follows:

    $$\begin{aligned} m(r)= & {} \frac{r}{2} \Big (1 - \frac{1}{\Psi }\Big ) + \frac{r^3}{2 (3 \gamma + 4 \pi )} \bigg [-4 ~{ B_{\mathrm{g}}}\nonumber \\&\times (\gamma + 2 \pi ) (\gamma + 4 \pi ) + \frac{1}{\Psi }\Big [2 a (\gamma + 2 \pi ) \nonumber \\&- 2 B (\gamma + 3 \pi ) +\Big (B^2 \gamma + 2 b (\gamma + 2 \pi )\Big ) r^2\Big ] \nonumber \\&+ \frac{1}{{\Psi }^2}\Big [2 B \gamma +2 b (\gamma + 2 \pi ) r^2 \nonumber \\&+ a (\gamma + 2 \pi + B \gamma r^2)\Big ]\bigg ]. \end{aligned}$$
    (55)
Fig. 6
figure 6

The variation of mass function and compactness against the radius for different values of \(\gamma \) mentioned in the figure

Full size image

The mass function is regular at the center as \(m(r)\rightarrow 0\) as \(r\rightarrow 0\). The compactness factor inside the radius r for our present model is obtained as follows:

$$\begin{aligned} u(r)=\frac{m(r)}{r}. \end{aligned}$$
(56)

We denote \({\mathcal {U}}={\mathcal {M}}/R\), where \({\mathcal {M}}=m(R)\). The compactness factor is useful to classify the compact objects in different categories: for a normal star \({\mathcal {U}}~\sim ~10^{-5}\), in the case of white dwarfs \(\frac{M}{R}~\sim ~10^{-3}\), for a neutron star, \({\mathcal {U}} \in (10^{-1},\,\frac{1}{4})\), when \({\mathcal {U}}\) lies between \(\left( \frac{1}{4},\,\frac{1}{2}\right) \), it denotes an ultra-compact star and if \({\mathcal {U}}=\frac{1}{2}\), it represents a black hole.

For a charged compact star model, Böhmer and Harko [57] proposed a lower bound for the compactness factor, whereas Andréasson [58] proposed an upper bound for the compactness factor. Combining the two results a bound for the compactness factor for a model of a charged compact star is obtained as follows:

$$\begin{aligned} \frac{3Q^2}{4R^2}\frac{1+\frac{Q^2}{18R^2}}{1+\frac{Q^2}{12R^2}} \le {\mathcal {U}}\le \left( \frac{1}{3}+\sqrt{\frac{1}{9}+\frac{Q^2}{3R^2}}\right) ^2, \end{aligned}$$
(57)

where Q is the total charge inside the star, i.e., \(q(r=R)=Q\). In the case of an uncharged compact object \(Q=0\) and under this condition the upper limit of \({\mathcal {U}}\) in Eq. (57) obeys the Buchdahl limit [59], \({\mathcal {U}}<\frac{4}{9}\). We have shown the nature of the mass function and compactness in Fig. 6 for different values of \(\gamma \) mentioned in the figure.

Now we are in a position to check the bound for \({\mathcal {U}}\) given in Eq. (57) for different values of \(\gamma \). For this purpose we have to find the numerical values of \({\mathcal {U}}\) from our model which are presented in the following table and it confirms that the inequality is verified for our model of a charged compact star in \(f(R,\,T)\) gravity.

\(\gamma \)

Value of lower limit of Eq. (57)

\(u^{\text {eff}}(R)\)

Value of upper limit of Eq. (57)

0.0

0.0007499

0.145843

0.666667

0.08

0.0382305

0.147145

0.667967

0.16

0.0535169

0.148398

0.669213

0.24

0.0649036

0.149605

0.670408

0.32

0.0742308

0.150767

0.671556

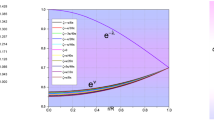
Now the surface redshift for a compact star model is obtained as follows: \(z_{\mathrm{s}}(R)=\frac{1}{\sqrt{\left( 1-2{\mathcal {U}}\right) }}-1\). The numerical values of the surface redshift for different values of \(\gamma \) are presented in Table 1. The gravitational redshift of our present model is calculated as follows:

$$\begin{aligned} z=e^{-\frac{\nu }{2}}-1,\Rightarrow z=\frac{1}{C}e^{-\frac{Br^2}{2}}-1, \end{aligned}$$

and its central value is obtained as \(z_{\mathrm{c}}=\frac{1}{C}-1\). Now \(z_{\mathrm{c}}>0\) gives \(1/C>1\), which consequently gives \(C<1\). Now \(\frac{\mathrm{d}z}{\mathrm{d}r}=-\frac{B}{C}e^{-\frac{Br^2}{2}}r\), at the origin \(\frac{\mathrm{d}z}{\mathrm{d}r}=0\) and \(\frac{\mathrm{d}^2z}{\mathrm{d}r^2}=-\frac{B}{C}<0\). It indicates that the gravitational redshift is a monotonically decreasing function of the radius of the star.

  • Generating function Based on the choice of a single monotone function subject to boundary conditions which generates all regular static spherically symmetric perfect-fluid solutions of Einstein equations, an algorithm was proposed by Lake [60]. Herrera et al. [61] extended this work to the case of locally anisotropic fluids and proved that two functions instead of one are required to generate all possible solutions for an anisotropic fluid. Thus they proved that any solution describing a static anisotropic fluid distribution is fully determined by means of the two generating functions \(\Pi \) and Z, where the expression for these two generating functions are given by

    $$\begin{aligned} \Pi (r)= & {} 8\pi (p_{\mathrm{r}}-p_{\mathrm{t}}),\\ e^{\nu (r)}= & {} e^{\int \left( 2Z(\tau )-\frac{2}{\tau }\right) \mathrm{d}\tau }. \end{aligned}$$

    For our present model, these two generating functions are obtained:

    $$\begin{aligned} \Pi (r)= & {} 8\pi (p_{\mathrm{r}}-p_{\mathrm{t}})=-8\pi \Delta , \end{aligned}$$
    (58)
    $$\begin{aligned} Z(r)= & {} Br+\frac{1}{r}. \end{aligned}$$
    (59)

Here the expression of \(\Delta \) present in Eq. (58) has been given in Eq. (38).

5 Equilibrium condition under different forces

In this section we shall check the equilibrium condition of our present model under different forces acting on our present system. The equilibrium equation can be decomposed into five different forces, namely: the hydrostatic force \(F_{\mathrm{h}}\), the gravitational force \(F_{\mathrm{g}}\), the anisotropic force \(F_{\mathrm{a}}\), the electric force \(F_{\mathrm{e}}\) and finally the force related to modified gravity, i.e., \(F_{\mathrm{m}}\). Moreover, the explicit form of these forces can be written as

$$\begin{aligned} F_{\mathrm{g}}= & {} -\frac{\nu '}{2}(\rho +p_{\mathrm{r}})\nonumber \\= & {} -\frac{B r \big (a + B + (2 b + a B) r^2 + b B r^4 \big )}{(\gamma + 4 \pi ){\Psi }^2}, \end{aligned}$$
(60)
$$\begin{aligned} F_{\mathrm{h}}= & {} -\frac{\mathrm{d}p_{\mathrm{r}}}{\mathrm{d}r} \nonumber \\= & {} \frac{2 (a^2 - 4 b) r + \Psi r \big (a B + 2 b (3 + B r^2)\big )}{2 (\gamma + 4 \pi ){\Psi }^3},\nonumber \\ F_{\mathrm{a}}= & {} \frac{2}{r}(p_{\mathrm{t}}-p_{\mathrm{r}})=\frac{2}{r}\Delta ,\end{aligned}$$
(61)
$$\begin{aligned} F_{\mathrm{e}}= & {} \frac{8\pi }{8\pi +2\gamma }\frac{q}{4\pi r^4}\frac{\mathrm{d}q}{\mathrm{d}r} \nonumber \\= & {} \frac{1}{4\pi +\gamma }\left( \frac{2}{r}E^2+\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}r}(E^2)\right) , \end{aligned}$$
(62)
$$\begin{aligned} F_{\mathrm{m}}= & {} -\frac{\gamma }{8\pi +2\gamma }(\rho '+p_{\mathrm{r}}'+2p_{\mathrm{t}}')\nonumber \\= & {} \frac{\gamma r}{2 (\gamma + 4 \pi ) (3 \gamma + 4 \pi ) {\Psi }^3} \Big [4(b-a^2)+ 11 a B \nonumber \\&- 2 B^2-\big (2 a^3-7 a^2 B-26 b B + 2 a (4 b + B^2)\big ) r^2 \nonumber \\&-3 b \big (2 (a^2 + b) - 7 a B\big ) r^4 +2 b^2 (-b + B^2) r^8 \nonumber \\&+ 2 b \big (5 b B + a (-3 b + B^2)\big ) r^6 \Big ] . \end{aligned}$$
(63)

The TOV equation in modified gravity can be written as follows:

$$\begin{aligned}&-\frac{\nu '}{2}(\rho +p_{\mathrm{r}})-\frac{\mathrm{d}p_{\mathrm{r}}}{\mathrm{d}r}+\frac{2}{r}(p_{\mathrm{t}}-p_{\mathrm{r}})\nonumber \\&\quad +\frac{\gamma }{8\pi +2\gamma }\left( \frac{\mathrm{d}\rho }{\mathrm{d}r}+\frac{p_{\mathrm{r}}}{\mathrm{d}r}+2\frac{\mathrm{d}p_{\mathrm{t}}}{\mathrm{d}r}\right) \nonumber \\&\quad +\frac{8\pi }{8\pi +2\gamma }\frac{q}{4\pi r^4}\frac{\mathrm{d}q}{\mathrm{d}r}=0. \end{aligned}$$
(64)

In Eq. (64), for \(\gamma =0\) we regain the conservation equation in Einstein–Maxwell gravity. Now the above equation can be denoted by

$$\begin{aligned} F_{\mathrm{g}}+F_{\mathrm{h}}+F_{\mathrm{a}}+F_{\mathrm{m}}+F_{\mathrm{e}}= & {} 0. \end{aligned}$$
(65)

The expression of the different forces acting on our system are depicted in Fig. 9 for different values of the coupling constant \(\gamma \).

6 Discussion

In this exposition we have successfully modeled the compact star SAX J 1808.4-3658 within the framework of \(f(R,\,T)\) modified gravity theory. We have employed the physically motivated Tolman–Kuchowicz ansatz [32, 33] for the metric potentials. We also argued that most researchers consider an ad hoc equation of state (EoS) \(\rho + p = 0\) in constructing the electromagnetic mass model, which results in a negative pressure. Instead of choosing this type of EoS, in order to solve the system of governing equations, we adopted the MIT bag model equation of state. Our model has been subjected to rigorous regularity, causality and stability tests which highlighted the role of charge and the \(f(R,\,T)\) coupling constant \(\gamma \). The free constants arising from integrating the field equations are fixed through the boundary conditions. In order to bring out the contributions from the modified theory we have plotted the thermodynamical and physical properties of the star for various values of the \(f(R,\,T)\) coupling constant. The main findings of this analysis can be summarized as follows:

Fig. 7
figure 7

The pressure density relation for different values of \(\gamma \) mentioned in the figure

Full size image
Fig. 8
figure 8

All the energy conditions inside the stellar interior for the strange star SAX J1808.4-3658 for different values of \(\gamma \) mentioned in the figure

Full size image

  • In Fig. 1 we have plotted the metric potential with respect to the radius. The exterior spacetime is also shown in the figure. One can also note that, at the boundary, the interior and exterior metrics coincide. The interior metric potentials are free from singularities and continuous inside the boundary. We can see that the metric potentials do not depend on the coupling constant \(\gamma \).

  • In Fig. 2 the profiles of density and both radial and transverse pressures are plotted with respect to the radius for different values of \(\gamma \). The black, red, blue, purple and cyan colored plots correspond to \(\gamma =0,\,0.08,\,0.16,\,0.24\) and 0.32, respectively. The pressure and density all are monotonic decreasing functions of r, i.e., they have a maximum value at the center and then it gradually decreases toward the boundary. It is also verified that the density and both the pressures are non-negative inside the stellar interior and at the boundary \(r=R\), \(\rho (r=R)>0\), \(p_{\mathrm{t}}(r=R)>0\) for different values of \(\gamma \). The radial pressure \(p_{\mathrm{r}}\) vanishes at the point \(r=R\), i.e., it determines the size of the compact object.

  • In Fig. 3 we have shown the behavior of the radial and transverse velocity of sound and the stability factor for different values of \(\gamma \). One can note that the radial velocity of sound is independent of \(\gamma \) but the transverse velocity of sound depends on the coupling constant. For higher values of \(\gamma \) the value of \(V_{\mathrm{t}}^2\) increases. The profiles of \(|V_{\mathrm{t}}^2-V_{\mathrm{r}}^2|\) have been plotted for different values of \(\gamma \) and it is clear that the Andréasson condition is satisfied.

  • In Fig. 4 the profiles of the radial relativistic adiabatic index are shown for \(\gamma =0,\,0.08,\,0.16,\,0.24\) and 0.32. For larger values of \(\gamma \), \(\Gamma _{\mathrm{r}}\) takes higher values. \(\Gamma _{\mathrm{r}}\) is monotonic increasing function of r and greater than 4/3 everywhere inside the fluid sphere for each values of \(\gamma \) mentioned in the figure; hence our model of charged compact star is stable.

  • In Fig. 5 the nature of the electric field and pressure anisotropy are plotted for different values of \(\gamma \) and one can note that \(E^2\) is positive everywhere inside the fluid sphere. Moreover, we note that \(E^2\) is monotonic increasing up to about 7 km for different values of \(\gamma \); then it becomes monotonically decreasing.

Fig. 9
figure 9

Different forces acting on the present model against r for the strange star candidate SAX J1808.4-3658 by taking different values of \(\gamma \)

Full size image

We found that an increase in the coupling constant lowers the density and the radial and transverse pressures at each interior point of the configuration, while there is a corresponding increase in the star’s mass. Further investigation by Astashenok et al. [62] gives a non-perturbative model of strange spherical objects in \(f(R)=R+2\alpha R^2\) gravity theory, where \(\alpha \) is a constant. They have shown that the masses of candidate strange spherical objects increase when the value of the parameter \(\alpha \) increases progressively. In our present work, we have obtained the same trend. We conclude that \(f(R,\,T)\) stars have larger masses compared to their 4D classical GR counterparts. The stability of the star is derived from the fact that the force due to anisotropy is attractive (\(p_{\mathrm{t}} < p_{\mathrm{r}}\)) up to some radius \(r = r_0\) within the boundary. The repulsive contributions from the electromagnetic field and the \(f(R,\,T)\) coupling constant help to stabilize the inner core. The anisotropic factor becomes positive closer to the surface layers of the star, leading to greater stability in this region. The surface redshift increases as \(\gamma \) increases. It is well known that the presence of anisotropy within the stellar core leads to higher surface redshifts compared to an isotropic, perfect-fluid matter distribution.

  • In Fig. 7 the equation of state parameters \(\omega _{\mathrm{r}}\) and \(\omega _{\mathrm{t}}\) are plotted for different values of the coupling constant and we note that both are monotonically decreasing functions of r and moreover \(0<\omega _{\mathrm{r}},\,\omega _{\mathrm{t}}<1\) and it corresponds to the radiating era [63]. The variation of the radial pressure with respect to the density follows a linear relationship, which is clear from our assumption. On the other hand the variation of the transverse pressure with respect to the density follows almost a parabolic curve.

  • The charged compact star model obeys all the energy conditions namely the null energy conditions, weak energy conditions, strong energy conditions and dominant energy conditions for different values of \(\gamma \), which is shown in Fig. 8.

  • In Fig. 9 all five different forces, namely gravitational force, anisotropic force, hydrostatic force, electric force and force due to modified gravity, are shown for \(\gamma =0,\,0.08,\,0.16,\,0.24\) and 0.32. We see that the gravitational force \(F_{\mathrm{g}}\) is always negative and the hydrostatic force \(F_{\mathrm{h}}\) is always positive; the another three forces show mixed behaviors. In this situation, the contribution of the force due to modified gravity \(F_{\mathrm{m}}\) is very negligible compared to the other four forces so that it seems likely to be overlapped with the X-axis. This means that the effect of coupling also becomes less effective.

  • In Fig. 10 we have shown the variation of the bag constant \(B_{\mathrm{g}}\) with respect to the coupling constant \(\gamma \) and it is observed that the value of the bag constant takes a lower value when \(\gamma \) increases.

To summarize, in the present paper we have obtained a singularity-free model of a charged anisotropic compact star in the presence of an electric field in \(f(R,\,T)\) modified theory of gravity and the results have been analyzed both analytically and graphically. We show that solutions of the field equations depend on the MIT bag model EoS, which is a familiar equation of state already having been used by several researchers for modeling a compact star. Finally, it is worth mentioning that taking \(\gamma \rightarrow 0\) GR results in a situation where models in four dimensions are recovered.

Fig. 10
figure 10

The variation of \(B_{\mathrm{g}}\) with respect to \(\gamma \)

Full size image