Motion of spinning particles in non asymptotically flat spacetimes

Abstract

The assumption of asymptotic flatness for isolated astrophysical bodies may be considered an approximation when one considers a cosmological context where a cosmological constant or vacuum energy is present. In this framework we study the motion of spinning particles in static, spherically symmetric and asymptotically non-flat spacetimes with repulsive cosmological vacuum energy and quintessential field. Due to the combined effects of gravitational attraction and cosmological repulsion, the region where stable circular orbits are allowed is restricted by an innermost and an outermost stable circular orbits. We show that taking into account the spin of test particles may enlarge or shrink the region of allowed stable circular orbits depending on whether the spin is co-rotating or counter-rotating with the angular momentum of the particles.

1 Introduction

Our current confidence in the existence of astrophysical black holes relies on the ability of mathematical model to describe observations. This is true for the gravitational wave signals observed from binary black hole mergers [1, 2] as well as for the observational evidence based on electromagnetic radiation coming from accretion disks surrounding the black holes [3] like for example in the case of the Event Horizon Telescope (EHT) collaboration’s image of the supermassive black hole at the center of the galaxy M87 [4].

All the theoretical models used to describe the observables obtained from accretion disks rely on the mathematical description of the motion of test particles and viscous plasma fluid in the surroundings of the black hole candidate. However, the motion of test particles may be influenced by a large number of factors, including, for example, the geometry [5,6,7,8], the presence of external fields [9, 10], the spin of the particles [11,12,13,14,15] and possible deviations from classical general relativity [16, 17].

In particular, when describing astrophysical isolated bodies one is usually led to consider asymptotically flat space-times. This is the result of the assumption that every other gravitational influence on the astrophysical object can be neglected. However, in a cosmological context this assumption may not hold as we may have to take into account the effects of the cosmological constant. It is well known that stable circular orbits in non asymptotically flat spacetimes have both an inner and an outer boundary and the outer boundary may have astrophysical relevance [18, 19]. Similarly, it is well known that circular orbits are altered once one includes the effects of the spin of the test particles. The motion of spinning particles in the different spacetimes with different physical conditions has been studied by several authors [20,21,22,23,24,25].

In spite of the fact that the Einstein field equations contain all the necessary information to derive the equations governing the motion of a spinning body, given the non linearity of the field equations, one must necessarily simplify the problem with additional assumptions. Typically one considers test particles for which mass and size are negligible as compared to those of the central object. Within the test particle approximation one can neglect the effects of gravitational radiation and model the particle’s motion as following geodesics. However, the study of particles’ motion can be improved by considering the spin of the test particles. In this context, the motion of spinning particles in general relativity has been widely studied in the pole-dipole approximation, where the gravitational field and the higher multipoles of the particle are neglected and the particle itself is completely characterized by its mass monopole and spin dipole [26]. If the particle is electromagnetically neutral, it interacts with the spacetime only gravitationally. However, due to the interaction between the spin of the particle and the curvature of the spacetime, its trajectory deviates from a geodesics. In such description the motion of spinning particles is governed by the Mathisson–Papapetrou–Dixon equations [27,28,29].

In the setup described above one is led to a set of equations which is not closed, as there are more unknowns than equations. This leads to the necessity of introducing some extra condition. Typically one can introduce the spin-supplementary condition that ensures that the spin tensor has only three independent components. There are several variations of the spin-supplementary condition such as the ones given by Tulczyjew [30], Pirani [31], etc. (for details, see [32].).

On the other hand, when considering real astrophysical phenomena at large scales, one should take into account cosmological effects. Measurements of the expansion rate of the universe show that the expansion is accelerating due to some unknown repulsive effect which has been given the name of “dark energy”. Such acceleration can be modeled via the introduction of a cosmological constant $\Lambda$ in Einstein’s equations. This cosmological constant can in turn be identified as the product of some other physical effect. For example, in the inflationary paradigm one can attempt to identify $\Lambda$ with the residual vacuum energy [33]. Similarly, one can interpret $\Lambda$ as resulting from a slowly evolving homogeneous repulsive fluid called “quintessence” [34]. Recent cosmological tests point out that about 70% of the energy content of the observable universe is due to dark energy and that the equation of state of dark energy is very close, if not identical, to that obtained from a repulsive cosmological constant. Also, numerical estimates based on the cosmic microwave background indicate the value of the cosmological constant to be of the order of $\mathrm{\Lambda \approx 10^{-52}}$ $\mathrm{m^{-2}}$ [35]. Therefore, when studying astrophysical phenomena at large scales it seems reasonable to take into account the repulsive effects arising from the presence of $\Lambda$.

The inclusion of a repulsive cosmological constant into a spacetime changes significantly its asymptotic structure, as a black hole, naked singularity, or any compact body becomes asymptotically de Sitter i.e., not flat [36,37,38,39,40,41].

On the other hand, one could consider a different model for dark energy, the so called quintessence, for which the accelerated expansion of the universe is due to a slowly evolving, spatially homogeneous matter fluid with negative pressure [34, 42]. According to the idea of quintessence, dark energy in the universe is dominated by the potential of a scalar field which is still rolling to its minimum [43]. This model can be parameterized by providing the equation of state for the quintessence fluid in the form $P=\omega \rho$ with $\omega <0$, where the parameter $\omega$ is in the range of $-1<\omega <-2/3$. One retrieves the cosmological constant model from the value $\omega =-1$.

In this paper we combine the above mentioned scenarios and study the motion of spinning particles in the pole-dipole approximation in non asymptotically flat spacetimes with a dark energy content described by either a cosmological constant or a quintessence fluid. The paper is organized as follows: in Sect. 2 the equations of motion governing the motion of spinning particle in generic, spherically symmetric spacetimes is presented. In Sects. 3 and 4 we apply the derived equations for spinning particles to the Schwarzschild–de Sitter spacetime and Schwarzschild spacetime immersed in quintessence, respectively. Finally, in Sect. 5 we summarize the obtained results and discuss the possible implications for astrophysics. Throughout the paper, we use natural units setting $G=c=1$.

2 Basic equations

In this section we present the general formalism for a spinning test particle in the Mathisson–Papapetrou–Dixon approximation (up to the pole-dipole order) [27,28,29] considering the spinning particle is moving in the field of a static, spherically symmetric compact object described by the following line element:

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{dr^2}{f(r)}+r^2d{\Omega _2}^2, \end{aligned}$$

(1)

where $d{\Omega _2}^2=d\theta ^2+\sin ^2\theta d\phi ^2$ is the line element on the unit 2-sphere and the metric function f depends only on the radial coordinate r.

The dynamics of spinning test particle is governed by the Mathisson-Papapetrou-Dixon equation that can be written as follows:

$$\begin{aligned}&\frac{Dp^\mu }{d\lambda }=-\frac{1}{2} {R^{\mu }} _{\nu \delta \sigma }u^\nu S^{\delta \sigma }\ , \end{aligned}$$

(2)

$$\begin{aligned}&\frac{DS^{\mu \nu }}{d\lambda } =2p^{[\mu }u^{\nu ]}= p^\mu u^\nu - p^\nu u^\mu , \end{aligned}$$

(3)

where $D/d\lambda$ is the covariant derivative along the particle’s trajectory with the affine parameter $\lambda$ given by $D/d\lambda \equiv u^\mu \nabla _\mu$ and ${R^{\mu }} _{\nu \delta \sigma }$ is the Riemann tensor. The dynamical 4-momentum and kinematical 4-velocity of the particle are denoted by $p^\mu$ and $u^\mu$, respectively and the anti-symmetric spin tensor is denoted by $S^{\mu \nu }$ (with $S^{\mu \nu }=-S^{\nu \mu }$). Therefore, the spin tensor can have only up to six independent components. The first equation of motion (2) shows that the spinning particle does not follow a geodesic trajectory due to the spin-curvature interaction term ${R^{\mu }} _{\nu \delta \sigma }u^\beta S^{\delta \sigma }$.

Equations (2) and (3) cannot be solved unless an extra condition, the so called spin-supplementary condition is introduced. The spin-supplementary condition fixes the center of the particle and ensures that the spin tensor has three independent components only. In the literature one can find several spin-supplementary conditions such as the one proposed by Tulczyjew [30], or the one introduced by Pirani [31] (see [32] for details). In our case, to restrict the spin tensor to generate rotations only, we employ the so called Tulczyjew spin-supplementary condition that is given by

$$\begin{aligned} S^{\mu \nu }p_{\mu }=0. \end{aligned}$$

(4)

The Tulczyjew spin-supplementary condition (4) implies that the components of the 4-velocity $u^\alpha$ are determined from the following relation [44]:

$$\begin{aligned} u^\mu = \frac{k}{m^2} \left( p^\mu + \frac{2S^{\mu \nu }R_{\nu \delta \sigma \rho }p^{\delta }S^{\sigma \rho }}{4m^2+R_{abcd}S^{ab} S^{cd}}\right) , \end{aligned}$$

(5)

where k is the kinematical mass (or rest mass) of the particle and it is given by $u^\mu p_\mu =-k$. Moreover, the above spin-supplementary condition ensures that both the mass, m, and the spin, S, of the particle are conserved and are given by

$$\begin{aligned}&p^{\mu }p_{\mu }=-m^2\ , \end{aligned}$$

(6)

$$\begin{aligned}&S^{\mu \nu }S_{\mu \nu }=2S^2. \end{aligned}$$

(7)

Although the momentum (or mass) of the spinning particle is conserved, the four-velocity of the spinning particle does not necessarily satisfy the normalization condition $u_\mu u^\mu =-1$, due to the fact that the four-vectors $p^\mu$ and $u^\mu$ are not always parallel.

In order to simplify the calculations, hereafter, we consider the motion of the spinning particles as confined in the equatorial plane, $\theta =\pi /2$. In general, fixing the value of $\theta$, reduces the number of independent components of the spin tensor to three as $S^{\theta \alpha }=0$. Taking this condition together with the spin-supplementary condition further reduces the number of independent components of the spin tensor to one. Let this component be the $S^{tr}$, then by using the Tulczyjew spin-supplementary condition (4), we find the following relations:

$$\begin{aligned}&S^{t\phi }=-\frac{p_r}{p_\phi }S^{tr}, \end{aligned}$$

(8)

$$\begin{aligned}&S^{r\phi }=\frac{p_t}{p_\phi }S^{tr}. \end{aligned}$$

(9)

Moreover, one has the usual geometry-dependent conserved quantities associated with the spacetime symmetries via the Killing vectors, $\xi ^\mu$, that can be expressed in the form

$$\begin{aligned} C_{\xi }=p^\mu \xi _\mu - \frac{1}{2}S^{\mu \nu }\nabla _\nu \xi _\mu . \end{aligned}$$

(10)

For the line element (1), which has both axial and timelike Killing vectors, there are two conserved quantities for test particles, i.e. energy E and total angular momentum L, and they are given by

$$\begin{aligned}&\mathrm{E}= -p_t - \frac{1}{2}f'S^{tr}, \end{aligned}$$

(11)

$$\begin{aligned}&\mathrm{L}=p_\phi +rS^{r\phi }, \end{aligned}$$

(12)

where prime denotes the partial derivative with respect to radial coordinate. From the above equations we can now derive the equations of motion for spinning test particles. From the normalization condition (6) one finds square of the radial momentum of the particle as

$$\begin{aligned} (p^r)^2 = p_t^2- f\left( \frac{p_\phi ^2}{r^2}+m^2\right) . \end{aligned}$$

(13)

Now by using the relations (8), (9), and momentum (13), from the spin conservation (7), one can find $S^{tr}$ as

$$\begin{aligned} S^{tr}=\frac{s p_\phi }{r}, \end{aligned}$$

(14)

where $s=S/m$ is specific spin parameter. It should be noted that s can have both negative and positive values depending on the direction of spin with respect to direction of $p_\phi$. Finally, from the conservation of energy (11) and angular momentum (12), we find the t and $\phi$ components of the four-momentum as

$$\begin{aligned}&p_t=\frac{-2\mathrm{E}r-\mathrm{L}s f'}{2 r-s^2f'}, \end{aligned}$$

(15)

$$\begin{aligned}&p_\phi =\frac{2 r (\mathrm{E}s+\mathrm{L})}{2r-s^2 f'}. \end{aligned}$$

(16)

One can easily notice that for a particle without spin, i.e. $s=0$, the momenta corresponding to the time and orbital angular coordinates are conserved and they are, $p_t=-\mathrm{E}$, and $p_\phi =\mathrm{L}$. By inserting covariant momenta (15) and (16) into the radial contravariant momentum (13), one finds the expression

$$\begin{aligned} \left( p^r\right) ^2=A(\mathrm{E}-V_+)(\mathrm{E}-V_-), \end{aligned}$$

(17)

where the coefficient A is given by

$$\begin{aligned} A=\frac{4(r^2-s^2f)}{(2r-s^2f')^2}, \end{aligned}$$

(18)

and $V_\pm$ are given by

$$\begin{aligned} \mathrm{V_{\pm }}= & {} \frac{s\left( 2f-rf'\right) \mathrm{L}}{2( r^2-s^2 f)}\pm \frac{\left( 2r-s^2 f'\right) }{2\left( r^2-s^2f\right) }\nonumber \\&\sqrt{f\left[ \mathrm{L}^2+m^2 (r^2-s^2f)\right] }. \end{aligned}$$

(19)

One can see from (17) that in order to have $(p^r)^2\ge 0$, the energy of the particle must satisfy one of the following conditions: (i) $\mathrm{E}< V_-$ or (ii) $\mathrm{E}>V_+$. Hereafter, we focus on the case of spinning test particle with positive energy which coincides with the effective potential to be $\mathrm{V_{eff}}=V_+$.

Now by using the effective potential one can study the characteristic circular orbits of the spinning test particle in the field described by the line element (1). The particle moves along a circular orbit in the central field (1) when the following two criteria are satisfied simultaneously:

• 1. The particle has zero radial velocity, i.e.

  $$\begin{aligned} \frac{dr}{d\lambda }=0, \quad \Rightarrow \quad \mathrm{V_{eff}}=\mathrm{E}, \end{aligned}$$

  (20)

• 2. The particle has zero radial acceleration, i.e.

  $$\begin{aligned} \frac{d^2r}{d\lambda ^2}=0, \quad \Rightarrow \quad \frac{d\mathrm{V_{eff}}}{dr}=0. \end{aligned}$$

  (21)

By solving Eqs. (20) and (21) with respect to the conserved quantities energy and angular momentum one finds four pairs of expressions for s and L. These four scenarios appear due to the relative orientation of the spin with respect to the angular momentum ($\mathrm{s\ versus\ L}$) and they are the following:

• (i) In the case for $\mathrm{s}>0$ and $\mathrm{L}>0$ spin and angular momentum are co-rotating.

• (ii) In the case for $\mathrm{s}>0$ and $\mathrm{L}<0$ spin and angular momentum are counter-rotating.

• (iii) In the case for $\mathrm{s}<0$ and $\mathrm{L}>0$ spin and angular momentum are counter-rotating.

• (iv) In the case for $\mathrm{s}<0$ and $\mathrm{L}<0$ spin and angular momentum are co-rotating.

Noting the symmetry of the spacetime and looking at the form of the effective potential (19), it is easy to see that each scenario depends only on the sign of the product $\mathrm{sL}$. Therefore one can conclude that the above four scenarios effectively describe only two possible situations, i.e, co-rotating and counter-rotating spin and angular momentum. Namely

• (i) Co-rotating: $\mathrm{sL}>0$;

• (ii) Counter-rotating: $\mathrm{sL}<0$.

The analytic expression for the energy and angular momentum of a spinning particle moving along circular orbit at a fixed radius r is rather complicated and therefore we shall not report it here. One must note that in order for the energy of the particle to be real, the following condition must be satisfied:

$$\begin{aligned} 8rf'+S^2\left( r^2 f''^2-3 f'^2-6rf'f''\right) +2S^4f'^2f''\ge 0.\nonumber \\ \end{aligned}$$

(22)

If the spin of the particle is neglected, the condition (22) reduces to $f'\ge 0$ and the solution of this inequality for asymptotically flat spacetimes is just $r\le \infty$. However, in the case of non asymptotic flatness the situation is quite different, as there are repulsive large scale cosmic effects by the field coupled to gravitation. In this case, circular orbits can exist only in a region of the spacetime restricted by a boundary radius, the so-called static radius, $r_{st}$, that is determined by the equality in Eq. (22). At the static radius the gravitational attraction is just balanced by the cosmic repulsion of the spacetime.

Another property of circular orbits that is of extreme importance in astrophysics is their stability. Stability of the orbit is guaranteed by positivity of the second derivative of the effective potential with respect to radial coordinate as

$$\begin{aligned} \frac{d^2\mathrm{V_{eff}}}{dr^2}\le 0, \end{aligned}$$

(23)

where equality corresponds to the smallest allowed value for the radius of stable circular orbits, namely the innermost stable circular orbit (ISCO).

One must note that as we have mentioned before, canonical momentum $p^\mu$ and kinematical velocity $u^\mu$ are not parallel. Conservation of mass of the spinning particle, $p_\mu p^\mu =-m^2$, guarantees that the canonical momentum remains timelike along the trajectory. However, the kinematical four-velocity of the spinning particle, $u^\mu$, may change from timelike to spacelike. Of course, a spacelike 4-velocity, i.e. superluminal, motion is physically meaningless, and therefore the relation $u_\mu u^\mu >0$ must not be allowed for real particles, thus imposing an extra condition. In fact, before $u_\mu u^\mu$ becomes positive the particle must cross the boundary between timelike and spacelike trajectories where the relation $u_\mu u^\mu =0$ holds. Therefore, in order to keep the motion of the spinning particle from becoming spacelike, one must impose that the condition $u_\mu u^\mu =0$ is not achieved on the whole trajectory. The kinematical four-velocity and dynamical momentum relation depends strongly on the spin-supplementary condition. In the Tulczyjew spin-supplementary condition (4) this relation is given by (5). Let us now consider the superluminal limit for a spinning particle moving on circular orbit. For simplicity, we introduce the notation vector $v^\mu$ given by

$$\begin{aligned} v^\mu =\frac{2S^{\mu \nu }R_{\nu \delta \sigma \rho }p^{\delta }S^{\sigma \rho }}{4m^2+\Delta }, \end{aligned}$$

(24)

where

$$\begin{aligned} \Delta \equiv R_{abcd}S^{ab}S^{cd}=\frac{2S^2 }{r^2} \left( f''p_\phi ^2-\frac{r f'}{f}p_t^2\right) , \end{aligned}$$

(25)

so that the kinematical four-velocity is written in the form of $u^\mu =p^\mu /m+v^\mu$. The components of vector $v^\mu$ for a spinning particle moving on a circular orbit are given by

$$\begin{aligned} v^\mu = \frac{2S^2 p_t p_\phi \left( f'-r f''\right) }{r^3f\left( \Delta +4 m^2\right) }\left\{ -p_\phi ,0,0,p_t\right\} ,\nonumber \\ \end{aligned}$$

(26)

Then in terms of the spacetime with line element (1) equation $u_\mu u^\mu =0$ takes the following form:

$$\begin{aligned} \left[ \frac{2S^2p_t p_\phi \left( f'-r f''\right) }{r^2 \left( \Delta +4 m^2\right) }\right] ^2=f, \end{aligned}$$

(27)

The above relation confirms the fact that in the case of absence of spin of the particle, i.e. $S=0$, the particle crosses the superluminal bound at the horizon of the spacetime that is determined by the equation $f=0$. One should note here that the superluminal limit of the spinning particle is spin-supplementary condition dependant, i.e., with switching to another spin-supplementary condition, one would have different equation for the superluminal limit than (27). For example, if the 4-velocity, $u^\mu$, is parallel to the 4-momentum, $p^\mu$, ($u^\mu \Vert p^\mu$) spin-supplementary condition is applied, the spinning particle would cross the superluminal limit at the horizon of the black hole as in the case of non-spinning particle [45].

Finally, there is one more important quantity that characterizes the particle and is worth discussing. This is the particle’s angular velocity on the circular orbit and it is defined by

$$\begin{aligned} \Omega =\frac{u^\phi }{u^t}. \end{aligned}$$

(28)

In the following sections we apply the above setup to two line elements, one describing the Schwarzschild–de Sitter spacetime and the other describing a black hole in an expanding universe with quintessence. Given the complicated nature of the equations most results will be obtained from numerical calculations.

3 Spinning particle in the Schwarzschild–de Sitter spacetime

The line element of the Schwarzschild–de Sitter spacetime is given by (1) with the metric function

$$\begin{aligned} f(r)=1-\frac{2M}{r}-\frac{\Lambda }{3}r^2, \end{aligned}$$

(29)

where M is the total mass of the black hole, while $\Lambda$ is a cosmological constant. For convenience, let us use dimensionless coordinates by redefining t and r as $t/M\rightarrow t$, $r/M\rightarrow r$ and introducing the dimensionless cosmological parameter in place of the cosmological constant as:

$$\begin{aligned} \lambda =\frac{\Lambda }{3}M^2. \end{aligned}$$

(30)

The main properties of the Schwarzschild–de Sitter spacetime have been widely studied in the literature (– see Refs. [46, 47]), however, for the sake of our further calculations, it is useful to present some crucial results here. For $0<\lambda <1/27$, the Schwarzschild–de Sitter black hole spacetime has two coordinate singularities given by $f=0$, which indicate the event and cosmological horizons. They are located at

$$\begin{aligned}&r_h=\frac{2}{\sqrt{3\lambda }}\cos \frac{\pi +\arccos (3\sqrt{3\lambda })}{3}, \end{aligned}$$

(31)

$$\begin{aligned}&r_c=\frac{2}{\sqrt{3\lambda }}\cos \frac{\pi -\arccos (3\sqrt{3\lambda })}{3}, \end{aligned}$$

(32)

The regions inside event horizon, $r<r_h$, and beyond cosmological horizon, $r>r_c$, are dynamic. Therefore, we consider the static region between these two horizons, $r_h<r<r_c$ where particle motion is timelike.

For $\lambda =1/27$, the event and cosmological horizons merge into one degenerate horizon which coincides with the unstable lightring and is located at $r_h=r_c=3$. For $\lambda >1/27$, the Schwarzschild-de Sitter spacetime represents a naked singularity.

Fig. 1

Qualitative picture of the radial profile of the effective potential for spinning particles with fixed angular momentum in the Schwarzschild–de Sitter spacetime for a given value of the cosmological parameter. Dot-dashed, solid, and dashed curves correspond to spinning particles with positive ($s>0$), zero ($s=0$), and negative ($s<0$) spin, respectively

Fig. 2

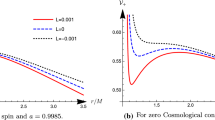
Radii of marginally stable circular orbits as a function of the cosmological parameter $\lambda$ for different values of the spin of the test particle. For a given value of $\lambda$ the intersection with the lower (upper) part of the curve determines the ISCO (OSCO). Dashed, solid, and dotdashed curves correspond to the cases of spinning particle with negative ($s<0$), zero ($s=0$), and positive ($s>0$) spins. The dotted curve represents the static radius. The shaded regions correspond to regions where stable circular orbits can exist, while in the white region between OSCO and the static radius circular orbits exist but are unstable. Beyond the static radius (in cyan region), circular orbits cannot exist

The motion of spinning particles in the Schwarzschild–de Sitter spacetime has been studied before in [48, 49]. Here we will present a more detailed analysis, to gain some general insight on different non asymptotically flat spacetimes. As we know, the motion of test particles in a central field is governed by the effective potential. Therefore, before studying the motion of the spinning particles, it is important to know the form of the effective potential and the effects of the spin parameter. To this aim, in Fig. 1 we present a qualitative picture of the effective potential for the spinning particle with positive, zero and negative spin in the field of Schwarzschild–de Sitter spacetime. It can be seen that an increase in the value of the spin raises the height of effective potential. Moreover, the existence of two local maxima in the effective potential indicates that the existence of bound orbits occurs only between these two maxima. In asymptotically flat spacetimes circular orbits can exist at every radius outside the ISCO. However, in asymptotically non-flat spacetimes such as the Schwarzschild-de Sitter one, circular orbits can exist only in a region bounded between the ISCO and another radius, where the cosmological repulsive vacuum effect is balanced by the gravitational attraction of central objects. This radius is determined by the equality holding in (22), which, for the Schwarzschild–de Sitter case takes the form

$$\begin{aligned}&4 r^6 \left( -1+\lambda r^3\right) +r^3 S^2\left( -13-4 \lambda r^3+8 \lambda ^2r^6\right) \nonumber \\&\quad +4 S^4 \left( 2-3 \lambda r^3+\lambda ^3r^9\right) =0. \end{aligned}$$

(33)

The solution of Eq. (33) is very sensitive to the cosmological parameter, while a change in the spin of the particle does not effect much the value of the static radius. However, this equation cannot be solved analytically. Therefore, in order for the solution of Eq. (33) to be more informative, we included it (dotted curve) into Fig. 2.

On the other hand, the stability of circular orbits is one of the most important characterizations of astrophysical spacetimes. As we have mentioned in the previous section, the stability is guaranteed by the condition (23). Unlike the case of asymptotically flat spacetimes, in the Schwarzschild–de Sitter metric the region where stable circular orbits can exist is bounded not only by an inner radius, called innermost stable circular orbit (ISCO), but also by outer radius that is called outermost stable circular orbit (OSCO). Non-spinning particles can have stable circular orbits around Schwarzschild–de Sitter black holes only if values of the cosmological parameter is in the following range: $\lambda \in [0,4/16875]$ (that corresponds to $\Lambda \in [0,4/5625M^2]$) (solid curve in Fig. 2). If the value of cosmological parameter is equal to the upper limit, $\lambda =4/16875$, particles can have only one stable orbit where the ISCO and OSCO coincide. For larger values of y there are no stable orbits anymore anywhere in the spacetime. As it was shown in Fig. 2, the inclusion of the particle’s spin can expand or shrink the range of y for which circular orbits exist, depending on the sign of product of spin and angular momentum of the particle.

All circular orbits in the region between OSCO and the static radius (in Fig. 2 white region) are unstable. Increasing the value of the spin causes the ISCO to tend towards the horizon of the black hole. However, before reaching the event horizon, it crosses superluminal motion limit. Therefore, for increasing values of the spin parameter, the stable circular orbits change from being bounded by the superluminal motion radius, ISCO, and OSCO to be bounded by superluminal motion radius and OSCO only. Regarding the effect of the spin on the OSCO, an increase in the value of the spin pushes the OSCO towards the static radius. Since the static radius is not very sensitive to changes in the value of the spin, increase in the value of the spin causes an increase in the region where stable circular orbits are allowed.

Table 1 Values of the characteristic parameters of spinning test particles with superluminal bound ($u_\mu u^\mu =0$) at the ISCO of the Schwarzschild–de Sitter black hole. Where $\mathrm{l_{ISCO}}$=$\mathrm{L_{ISCO}}+\mathrm{s(threshold)}$

As said, one must ensure that the particle’s motion is always time-like. Therefore it is important to consider the allowed limits for the parameters of spinning test particles moving along ISCO and OSCO around Schwarzschild–de Sitter black hole due to the existence of the superluminal bound. Such parameters are the particle’s energy, angular momentum and angular velocity at the ISCO, labelled as $\mathrm{E_{ISCO}}$, $\mathrm{L_{ISCO}}$ and $\mathrm{\Omega _{ISCO}}$. To find these values, one must solve the Eqs. (23) and (33), simultaneously. In Table 1 and Fig. 3 are shown the values of the parameters for a spinning test particle with superluminal limit ($u_\mu u^\mu =0$) at the ISCO of the Schwarzschild–de Sitter black hole. One can see from Table 1 that as the influence of cosmological repulsion increases, the superluminal limits of radius of ISCO and spin of the particle increase. However, the corresponding energy and angular velocity of the particle decrease.

In Table 2 we present some values for the characteristic parameters of a spinning particle at the ISCO and OSCO of the Schwarzschild–de Sitter spacetime for different values of spin and cosmological parameter $\lambda$. A particle moving along the ISCO always has smaller energy and angular momentum than one with the same spin moving along the OSCO of the Schwarzschild–de Sitter spacetime. Of course, the values corresponding to $\lambda =0$ represent the ones of the Schwarzschild spacetime, i.e. if the cosmological constant is absent, the radius of the OSCO shifts to infinity, the particle at the OSCO can be considered as rest and its angular velocity becomes negligible.

Fig. 3

Relation between the threshold value for the spin of test particles and the radius of the ISCO in the Schwarzschild–de Sitter spacetime depending on the cosmological parameter $\lambda \in [0,1/27]$. The solid line corresponds to the solution of the superluminal limit relation $u_\mu u^\mu =0$, with the black point at the bottom left corresponding to the superluminal limit of the spinning particle at the ISCO of the Schwarzschild black hole ($\lambda =0$)

4 Spinning particle in the Schwarzschild spacetime with quintessence

We now turn the attention to the case of a black hole immersed in quintessence and perform a similar analysis to the one presented in the previous section. The simplest solution of this kind was suggested by Kiselev [50] and it is given by the line element (1) with the following metric function:

$$\begin{aligned} f(r)=1-\frac{2M}{r}-cr^{-1-3\omega }, \end{aligned}$$

(34)

where M is the gravitational mass of the black hole and c is the quintessential parameter representing the strength of the quintessential field around the black hole. The parameter $\omega$ is related to the dark energy equation of state (EoS). The equation of state relating the pressure, P to the energy density, $\rho$, of the quintessential field is assumed to be linear, in agreement with standard cosmological model. Thus we set $P=\omega \rho$ and in order for the EoS to describe a dark energy fluid the values of $\omega$ must be chosen in the following range: $\omega \in (-1;-1/3)$.

In the following, for simplicity, we will focus on the commonly used value $\omega =-2/3$. In this case, the metric function (34) takes the simple form:

$$\begin{aligned} f(r)=1-\frac{2M}{r}-cr. \end{aligned}$$

(35)

As it was shown in [51], this spacetime represents either a black hole or a naked singularity depending on the values of the parameters c. If the value of quintessence parameter is in the range of $0<c\le 1/8M$, the spacetime represents the black hole with two horizons, the event horizon and a cosmological ‘quintessential’ horizon. The horizons are located at

$$\begin{aligned}&r_{h}=\frac{1-\sqrt{1-8cM}}{2c}, \end{aligned}$$

(36)

$$\begin{aligned}&r_q=\frac{1+\sqrt{1-8cM}}{2c}. \end{aligned}$$

(37)

In the region between these two horizons, the spacetime is static, outside this region, it is dynamic. Therefore, we hereafter consider the particle’s motion in the static region. If the value of the quintessence parameter is $c=1/8M$, similarly to the Schwarzschild-de Sitter case, both horizons merge into one degenerate horizon at $r_h=r_q=4M$. If the value of quintessence parameter is $c>1/8M$ no horizon is present and the spacetime represents a naked singularity.

Table 2 Values of the characteristic parameters of spinning particles at ISCO and OSCO of the Schwarzschild–de Sitter black hole

As this spacetime is also not asymptotically flat, similarly to the Schwarzschild-de Sitter case, we find that there exists a static radius here as well. The static radius is the obtained by solving the following equation:

$$\begin{aligned}&8\left( \frac{2M}{r}-cr\right) +S^2 \left( -3 c^2-\frac{12 c M}{r^2}+\frac{52 M^2}{r^4}\right) \nonumber \\&\quad -\frac{8 M S^4}{r^5}\left( \frac{2M}{r}-cr\right) ^2=0. \end{aligned}$$

(38)

Again, circular orbits are bounded by the static radius. However, not all circular orbits are stable. For a non spinning particle to have stable circular orbits in this spacetime, the value of the quintessence parameter must be in the following range: $c\in [0;(3-2\sqrt{2})/32M]$ and stable circular orbits are bounded by an inner radius at the ISCO and by an outer radius at the OSCO. The dependence of radii of stable circular orbits on the spin of the particle and the quintessence parameter is qualitatively similar to the Schwarzschild-de Sitter spacetimes, therefore we will not repeat the whole analysis here.

In Table 3 we list the values of the characteristic parameters $\mathrm{E_{ISCO}}$, $\mathrm{L_{ISCO}}$ and $\mathrm{\Omega _{ISCO}}$ for a spinning particle with superluminal limit, moving along stable circular orbits in the Schwarzschild spacetime with quintessence for several values of the quintessence parameter.

Table 3 The same as Table 1 for the case of a Schwarzschild black hole with quintessence

For small values of the spin parameter, stable circular orbits are bounded by the ISCO and OSCO, while the superluminal limit radius is located below the ISCO and just above the event horizon. Increasing the value of the spin of the particle, the radius of ISCO approaches the event horizon, while the superluminal limit radius tends to the ISCO. At some point, for an intermediate values of the spin parameter they meet and after that, as the value of the spin increases, the stable circular orbits are restricted by superliminal limit radius, ISCO and OSCO. Finally, for the large values of the spin parameter the stable circular orbits are bounded by the superluminal limit radius and OSCO only.

Table 4 The same as Table 2 for the case of a Schwarzschild black hole with quintessence

Moreover, similarly to Table 2 for the Schwarzschild-de Sitter spacetime, some values of the characteristic parameters of the spinning particle moving along the ISCO and OSCO of the Schwarzschild black hole immersed in quintessence are given in Table 4. Again, the qualitative behaviour of the characteristic parameters is similar to the Schwarzschild-de Sitter case.

5 Conclusion

In this paper we studied the motion of spinning particles in the equatorial plane of non asymptotically flat, static and spherically symmetric spacetimes. The condition of non asymptotic flatness has been imposed to account for an accelerating cosmological boundary to the black hole spacetime. It is well known that such a condition at spatial infinity bears important consequences for the orbits of test particles in the spacetime, since, as a result of the repulsive cosmological effects, particles have only a finite range of distances where stable circular orbits can exist. In [19] it was shown that for a non spinning particle around a supermassive black hole such a range is comparable with the diameter of a galaxy. Therefore one can not exclude that non asymptotic flatness may have some relevance in astrophysics. Here we showed that the presence of spin for the test particles may alter this structure and modify the extent of the region where stable circular orbits exist.

Fig. 4

The same as Fig. 3 for the case of a Schwarzschild black hole with quintessence. The solid line corresponds to the values of the quintessence parameter in the range $c\in [0, 0.043]$

Fig. 5

The same as Fig. 2 for the case of a Schwarzschild black hole with quintessence