Abstract
In this paper, higher order quantum gravity effects on the thermodynamics of Hořava–Lifshitz black hole investigated. Both Kehagius–Sfetsos and Lu–Mei–Pop solutions of Hořava–Lifshitz black hole considered and higher order corrected thermodynamics quantities obtained. The first order correction is logarithmic and second order correction considered proportional to the inverse of entropy. These corrections are due to the thermal fluctuation and interpreted as quantum loop corrections. Effect of such quantum corrections on the stability and critical points of Horava–Lifshitz black holes studied. We find that higher order correction affects critical point and stability of Lu–Mei–Pop solution and yield to the second order phase transition for the case of Kehagius–Sfetsos solution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Black holes are gravitational objects with maximum entropy [1, 2] which is related to the black hole event horizon area A. In that case, statistical mechanics help us to study the black hole thermodynamics and it is one of the important field of theoretical physics [3, 4]. Hence, the thermodynamics study of several kinds of black hole is important subject of the recent researches. Lower dimensional black holes are interesting and usually considered as a toy model to obtain gravitational solutions. For example, two-dimensional black holes may be considered to study thermodynamics [5,6,7,8,9,10]. Higher dimensional black holes are also interesting in several theories like near-extremal solutions of Einstein-Maxwell-scalar theory [11], or hyperscaling violation backgrounds [12,13,14].
Due to the thermal fluctuations, the black hole entropy modified and correction terms interpreted as quantum effect, because the quantum gravity modified the manifold structure of space-time at Planck scale [15, 16]. Almost all methods of quantum gravity indicated that the leading order correction is logarithmic [17, 18] and it has been argued that the general structure of the correction terms is a universal. In that case, leading order quantum corrections to the geometry of large AdS black holes and their effects on the thermodynamics given by the Ref. [19]. Hence, the thermal fluctuations in a hyperscaling violation background considered by the Ref. [20]. Thermodynamics of Kerr–Newman–AdS black holes already studied by the Ref. [21]. Similar black hole (uncharged but d-dimensional) considered under the effect of the thermal fluctuations [22] and found that logarithmic correction becomes important when the size of the black hole becomes small due to the Hawking radiation [23]. Also, statistical mechanics of charged black holes considered by the Ref. [24]. Black hole thermodynamics in modified theories of gravity like f(r) [25,26,27,28] also studied by the Ref. [29].
It is also possible to obtain higher order corrections [30, 31] and such corrected terms has the same universal shape as expected from the quantum gravitational effects [17, 18, 30]. Black holes in Gödel universes already introduced by the Ref. [32], in that case Kerr–Gödel black hole thermodynamics investigated by the Ref. [33]. Logarithmic correction to the Gödel black hole has been studied by Ref. [34]. Higher order correction to the Kerr–Newman–Gödel black hole recently given by the Ref. [35] and demonstrated that second order correction is proportional to the inverse of entropy. Thermodynamics of higher order entropy corrected Schwarzschild–Beltrami–de Sitter black hole investigated by the Ref. [36] and found that higher order corrections may affect the black hole stability.
STU black holes [37] are other interesting kinds of black hole which has been studied by the Ref. [38] from statistical point of view [39]. This kind of black hole is interesting in AdS/CFT correspondence [40], for example it is possible to compute hydrodynamics and thermodynamics properties of quark-gluon plasma [41,42,43,44] in presence of quantum correction. Other properties of quark-gluon plasma like drag force [45,46,47,48], jet-quenching [49,50,51,52] and shear viscosity to entropy ratio [53] may also affected by thermal fluctuations, and this can observed by experiments [54].
It is important to note that corrections to the black hole thermodynamics can study using the non-perturbative quantum general relativity. Moreover, it is possible to investigate black hole thermodynamics under effects of thermal fluctuations by using the effect of matter fields surrounding a black hole [55,56,57]. The corrected thermodynamics of a dilatonic black hole from Cardy formula have been already studied by the Ref. [58] and show the same universal form of correction term as previous studies. This universality can be understood in the Jacobson formalism [59, 60]. Corrected thermodynamics of a black hole can be obtained by using the partition function [61]. Such corrections have already considered for different black objects. For example, the first order correction of the AdS charged black hole has been studied, and modified thermodynamics obtained [62], which is extended to the case of AdS charged rotating black hole [63]. In the Ref. [62] it is argued that leading order correction is logarithmic its coefficient can be considered as free parameter of the theory. Thermal fluctuations effect of a black saturn have been studied [64]. It was observed by considering charged dilatonic black saturn that the thermal fluctuations can be obtained either using a conformal field theory or by analyzing the fluctuations in the energy of this system and both yields to the similar results for a charged dilatonic black saturn [65].
An interesting kind of regular black holes is Hayward black hole [66] which can be modified [67, 68]. In that case, the logarithmic corrections of a modified Hayward black hole considered to calculate some thermodynamics quantities, and found that this leading order correction affect the pressure and internal energy by decreasing value of them [69]. Thermal fluctuations of charged black holes in gravity’s rainbow investigated by the Ref. [70], and quantum corrections to thermodynamics of quasitopological black holes studied by the Ref. [71].
Investigation of thermal fluctuation in gravitational systems may help us to test the quantum gravity effects, for examples, on dumb holes [72] or graphene [73]. Logarithmic and higher order corrections may affect the critical behaviors of black objects, for example in the Ref. [74] a dyonic charged anti-de Sitter black hole thermodynamics considered and show that holographic picture (a van der Waals fluid) is still valid. In that case logarithmic corrected van der Waals black holes in higher dimensional AdS space investigated by the Ref. [75]. Also, thermodynamics of higher dimensional black holes with higher order thermal fluctuations studied in [76].
BTZ black holes [77] also considered to investigate effects of thermal fluctuations [78] including higher order corrections [79,80,81]. P-V criticality of black holes also may affected by thermal fluctuations [82,83,84].
Hořava–Lifshitz (HL) black holes are important kind of black holes in theoretical physics [85]. The HL gravity is also an interesting theory of quantum gravity [86,87,88,89] which considered in particle physics and cosmological literatures [90, 91]. We expect that the HL black hole solutions, asymptotically, become Einstein gravity solutions. In that case, Refs. [92,93,94,95] investigated thermodynamics quantities of HL black holes. It has been reported some instabilities in HL black holes. Hence, such thermodynamics using logarithmic corrected entropy investigated to find quantum gravity effects [96] and found that some instabilities removed due to thermal fluctuations.
In the Ref. [96], only LMP solutions of HL black hole considered and first order correction (logarithmic correction) investigated. Now, in this paper, we would like to consider both LMP and KS solutions and investigate effects of higher order quantum corrections.
This paper organized as follows. In the Sect. 2 we review higher order correction and propose a general form with free correction coefficients. In Sect. 3, Hořava–Lifshitz (HL) black holes properties called. General thermodynamics relations introduced in Sect. 4. In Sect. 5, effects of higher order corrections on the thermodynamics of Lu–Mei–Pop solution investigated for three different cases of flat, spherical and hyperbolic spaces. In Sect. 6 we consider Kehagius–Sfetsos solution of HL black hole and study corrected thermodynamics. Finally, in Sect. 7 we give conclusion.
2 Higher order corrections
In the canonical ensemble, one can calculate the density of state. Partition function of N particles given by the following expression [97, 98],
where E is the average energy in the canonical ensemble. Having partition function, one can write entropy as,
Now, it is possible to consider thermal fluctuations and use Taylor expansion around \(\beta \) and write,
where maximum of entropy at equilibrium point \(\beta =\beta _{0}\) established. It can written as,
where \(S_0\) is uncorrected entropy.
Indeed, correction terms are due to statistical fluctuations around equilibrium, hence one can assume the system in equilibrium and use usual thermodynamics relations. Equation (3) yields to a general form for different black geometries,
In this paper, we would like to study the second order correction hence neglect higher order terms. \(\alpha \) and \(\gamma \) consider as free parameter of the theory and they are depending on black hole physics. For example it is found that \(\alpha =-\frac{3}{2}\) and \(\gamma =-\frac{3}{16}\) for the BTZ black hole, \(\alpha =-1\) and \(\gamma =-\frac{5}{36}\) for the AdS Schwarzschild black hole [30]. Now, we can examine some values of free parameters to see their effects on the thermodynamics quantities of HL black hole. Indeed we would like to test only presence of corrections with positive or negative values. Calculation of exact values of \(\alpha \) and \(\gamma \) are also interesting which is not aim of this paper. In the next section, we give brief review of Hořava–Lifshitz black holes.
3 Hořava–Lifshitz black hole
First of all, we review some important properties of HL black holes. The action of HL theory in four-dimensional gravity is given by [99,100,101,102,103],
where \(\kappa ^2\), \(\lambda \), \(\omega \), \(\Lambda \) and \(\mu \) are constant parameters, and \(C_{ij}\) is cotton tensor given by [104, 105],
and \(K_{ij}\) is extrinsic curvature,
where \(N_i\) is shift function and N is lapse function, also the cosmological constant is given by \(\Lambda =\frac{3}{2}\Lambda _{W}\) [106], where \(\Lambda _{W}\) is a constant negative parameter (we consider \(\Lambda _{W}=-l\)).
The corresponding metric is given by [99],
where,
and f(r) is given by the following relation [100],
where B is an integration constant.
In the case of \(\Lambda _W=0\) and \(B=4\omega M\) we have Kehagius–Sfetsos (KS) solution [107],
while in the case of \(\omega =0\) and \(B=-\frac{\alpha ^2}{\Lambda _W}\) we have Lu–Mei–Pop (LMP) solution [99],
Black hole thermodynamics in KS solution of HL Gravity have been studied by the Ref. [106], and thermodynamical quantities of LMP solution of HL black hole for three different cases of spherical, flat and hyperbolic spaces given by the Ref. [92]. Also, first order correction on LMP solution of HL black hole studied by the Ref. [96]. In the next section we write some important thermodynamics relations of HL black holes.
4 Thermodynamics
The first law of thermodynamic may be given by [108]
The black hole entropy and Hawking temperature obtained by using the following equations [109],
where H denotes the enthalpy and interpreted as the black hoe mass (\(H=M\)) [110]. Also temperature of black hole is given by the following relation [110],
It is easy to check that \(T=T_{H}\) and black hole pressure obtained by \(P=\frac{1}{2}TS\) [111, 112]. The volume of black hole is given by,
The heat capacity can be found by using the following relation [110, 113],
where the internal energy is given by,
where
is Helmholtz free energy which related to the Gibbs free energy via,
Thermodynamical quantities of the HL black hole for LMP and KS solutions are different for spherical space \((k=1)\), flat space \((k=0)\), and hyperbolic space \((k=-1)\).
5 Lu–Mei–Pop solution
LMP solution given by the Eq. (13) and there are three different cases corresponding to space curvature.
5.1 Spherical space
In this case the black hole mass given by,
It has been found that the magnitude of the cosmological constant increases the black hole mass. However there is a minimum for the black hole mass at \(r_{h}=1/\sqrt{-3\Lambda _W}\).
By using the Eq. (15) one can obtain the entropy and Hawking temperature as follow,
and
It has been also finding that the magnitude of the cosmological constant increases the black hole temperature. The zero temperature limit obtained by \(r_{h}=1/\sqrt{-3\Lambda _W}\).
Now, we can use the Eq. (5) to obtain corrected thermodynamics due to higher order quantum corrections.
In this case the black hole Helmholtz free energy obtained using the relations (20), (23), (24), and (5), as
where we set \(\Lambda _{W}=-l\).
In the Fig. 1 we can see behavior of the Helmholtz free energy and obtain the effect of the quantum corrections. We examined both positive and negative values of correction coefficients. Generally, we find that Helmholtz free energy is decreasing function of correction parameters (see Fig. 1b). It means that quantum corrections reduced value of Helmholtz free energy. In the case of \(\gamma =0\) we recover result of the Ref. [96]. We can see that there is special radius where corrected and uncorrected curves crossed, which means thermal fluctuations have no any effect in special radius. In the Fig. 1 this special radius is about \(r_{h}=0.7\). There is a maximum value for the Helmholtz free energy at small radius, which we can see by solid cyan line of the Fig. 1a corresponding to the second order quantum correction with \(\alpha =\gamma =-1\). Such maximum may relate to the critical point of the black hole. One can obtain pressure as follow,
while the black hole volume by using the Eq. (17) obtained as follow,
Having P and V, we can study \(P-V\) critical points where
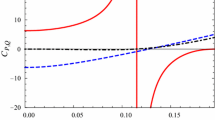
The points which satisfy condition (28) called critical points. In the Fig. 2 we analyze critical points for the ordinary case (\(\alpha =\gamma =0\)) and corrected cases (Fig. 2a, c). Dashed red lines represent \(\frac{dP}{dV}\), while solid blue lines represent \(\frac{d^{2}P}{dV^{2}}\), when both curves cross each other in zero axis, then the corresponding \(r_{h}\) is the black hole radius where critical points happen. We can see from the Fig. 2a that only in the case of \(\alpha =\gamma =-1\) (presence of higher order correction) we have critical points near \(r_{h}\approx 0.3\). It is corresponding to black solid line of the Fig. 1a at maximum point of Helmholtz free energy. It means that in order to have critical points, presence of the higher order corrections is necessary. For the cases of correction with positive coefficients and uncorrected entropy the critical points exist only at \(r_{h}=0\).
Heat capacity is important parameter to study stability of the black hole. By using the Eq. (18), we can calculate heat capacity as,
It is clear that logarithmic correction increases value of heat capacity while the second order correction reduces its value.
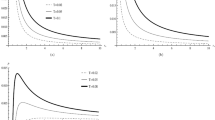
Without the logarithmic correction we saw some instabilities corresponding to the small horizon radius (see dotted blue line of Fig. 3). It has been found that the magnitude of the cosmological constant increases the black hole heat capacity. The zero heat capacity limit obtained by \(r_{h}=1/\sqrt{3l}\). It means that there are some instabilities for small \(r_{h}\) where C is negative. Although, quantum corrections have not any important effect on this point but may make other stable points at very small radius. In all cases there is no any asymptotic behavior corresponding to phase transition. Solid cyan line of the Fig. 3 is corresponding to the case of \(\alpha =\gamma =-1\) which shows a turning point near \(r_{h}\approx 0.3\) (critical point and maximum of Helmholtz free energy). Some cases of corrected heat capacity (dashed lines) show that there is some stable region for small radius, then the black hole is unstable in a finite rage of \(r_{h}\). It means that, when the black hole size reduced due to the Hawking radiation, and thermal fluctuations become important, then the black hole is stable at quantum scales. Hence, we can’t neglect thermal fluctuations of small black holes.
Finally the internal energy is obtained using the Eq. (19). We give graphical analysis of internal energy by Fig. 4. Neglecting correction, we can see internal energy has a maximum, while in presence of quantum corrections there is also a minimum. It may be corresponding to stable point at small radius which discussed already.
5.2 Hyperbolic space
In the case of hyperbolic space \((k=-1)\) the black hole mass in the horizon given by,
It has been find that the magnitude of the cosmological constant increases the black hole mass. Therefore, one can obtain black hole entropy and temperature as follow,
and,
It is clear that the magnitude of the cosmological constant increases the black hole temperature. In that case Helmholtz free energy obtained as,
As we can see from the Fig. 5, Helmholtz free energy of this case is completely negative with an extremum for the uncorrected entropy and two extrema for the higher order corrected entropy.
One can obtain pressure as follow,
while the black hole volume by using the Eq. (17) obtained as follow,
From the plots of Fig. 6 we can see the uncorrected case has critical point near \(r_{h}\approx 0.325\) (see Fig. 6b). Also, higher order corrected case with positive coefficients have critical point near \(r_{h}\approx 0.4\) (see Fig. 6c). However, opposite to the spherical case, LMP solution in hyperbolic space in presence of higher order corrections with negative coefficients (Fig. 6a) don’t have critical point. It means that higher order corrections affect critical points and remove them.
We can calculate heat capacity as,
It is clear that logarithmic correction increase value of heat capacity while the second order correction reduces its value which is similar to the previous case. In the Fig. 7 we can see behavior of specific heat of LMP solution of HL black hole in hyperbolic space and see that there is phase transition in all cases of corrected and uncorrected entropy. It means that higher order corrections have no any effects on the phase transition.
Finally, in the Fig. 8 we can see behavior of the internal energy of LMP solution in hyperbolic space. We can see that in presence of higher order corrections the internal energy is completely negative (see solid cyan line of Fig. 8). We can see that increasing or decreasing internal energy is depend on sign of correction coefficients.
5.3 Flat space
This case obtained by setting \(k=0\), hence the black hole mass given by,
By using the Eq. (15) one can obtain the entropy and Hawking temperature as follow,
and
It has been also finding that the magnitude of the cosmological constant increases the black hole temperature.
Now, we can use the Eq. (5) to obtain corrected thermodynamics due to higher order quantum corrections.
As before, the black hole Helmholtz free energy obtained as
where we set \(\Lambda _{W}=-l\) as previous subsections.
In the Fig. 9 we can see behavior of Helmholtz free energy of the LMP solution in flat space and find important effect of quantum corrections. Neglecting thermal fluctuations, the Helmholtz free energy is completely negative. In presence of higher order corrections (solid cyan line of the Fig. 9) the Helmholtz free energy has a maximum in positive regions.
One can obtain pressure as follow,
Then, the black hole volume obtained as follow,
The points which satisfy condition (28) illustrated by plots of the Fig. 10. Critical points analysis for the ordinary case (\(\alpha =\gamma =0\) which given by the Figs. 10b) and corrected cases (Fig. 10a, c) show that there is no critical point except at \(r_{h}=0\) of uncorrected case (see Fig. 10b).
Heat capacity of this case given by,
It is clear that logarithmic correction increases value of heat capacity while the second order correction reduces its value.
In absence of higher order corrections, the heat capacity is positive. Logarithmic correction reduces value of heat capacity to make it negative for the small black hole, when \(r_{h}\) is large, the effect of thermal fluctuation is negligible. Higher order correction with positive coefficient also decrease value of heat capacity hence affect black hole stability. In the case of \(\alpha =\gamma =-1\) the heat capacity has a minimum.
Finally, we give graphical analysis of internal energy by Fig. 11. Effect of quantum corrections are important which may reduce or increase value of internal energy as illustrated by the Fig. 11.
6 Kehagius–Sfetsos solution
In this case, by using the Eq. (12) one can obtain inner and outer horizons as,
Hence, the black hole mass given by,
Also, black hole temperature obtained as,
Inserting M from (45) into the temperature (46) one can obtain,
Then, we can obtain entropy as follow,
Therefore, we can obtain corrected entropy due to higher order corrections, and calculate thermodynamics quantities.
Corrected pressure calculated as,
Then, we can obtain black hole volume and find that logarithmic correction decreases it while the second order correction increases the black hole volume. Also, as illustrated by plots of the Fig. 12, higher order corrections do not affect the critical point. In absence of quantum correction there is a critical point as well as in presence of higher order corrections.
Finally, we can calculate heat capacity as,
In the Fig. 13 we can see that quantum correction has no any important effect of the first order phase transition and black hole stability. However, presence of the logarithmic correction (see dash dot green line of the Fig. 13a) make another asymptotic region at small radius which may be interpreted as the second order phase transition.
7 Conclusion
In this paper, we considered Hořava–Lifshitz black hole to study its thermodynamics in presence of quantum correction by consideration of thermal fluctuations. We considered two special case of Kehagius–Sfetsos and Lu–Mei–Pop solutions to study critical points and thermodynamics stability separately. In the case of KS solution, we consider general case and found that logarithmic correction may yield to the second order phase transition. Higher order correction with positive coefficient may yield to some instabilities at small event horizon radius (see Fig. 13b). We found that there are also critical points in presence of higher order correction as well as in absence of quantum corrections.
In the case of LMP solution, we considered three cases of flat, spherical and hyperbolic spaces and studied modified thermodynamics separately. Both analytical and numerical study on the thermodynamics quantities under effects of quantum corrections show that quantum corrections are important when the black hole size reduced due to the Hawking radiation. In all cases we found that Helmholtz free energy is decreasing function of correction parameters. Then, we obtained pressure and volume to study critical points. In the case of LMP solution with spherical space we found that higher order corrections are important to have critical point. Fig. 2a shows that only higher order corrections with negative coefficients yields to critical point which is opposite to hyperbolic space. It means that LMP solution in hyperbolic space have critical point for higher order corrections with positive coefficients. In flat space there is no critical point and quantum corrections have no any effects on critical points.
We study black hole stability by using heat capacity. We found that first order correction increases value of heat capacity while the second order correction reduces its value. In the case of spherical space, we found some stable points at very small radius due to higher order corrections and black hole is stable at quantum scales. In the case of hyperbolic space, we found that there is phase transition in all cases of corrected and uncorrected entropy. It means that higher order corrections have no any effects on the black hole phase transition. In the case of flat space heat capacity is completely positive without higher order corrections. Logarithmic correction reduces value of heat capacity to make it negative for the small black hole, when event horizon radius grows up, then the effect of thermal fluctuation is negligible. Higher order correction with positive coefficient also decrease value of the heat capacity, hence change the black hole stability.
In this paper, we considered only presence or absence of corrections by choosing \(\alpha \) and \(\gamma \) as 0 or \(\pm 1\). It is interesting to calculate exact values of these parameters which may be yields to experimental setup to test quantum gravity. It may be aim of our future study.
In summary, this paper is extension of previous work to include higher order correction to LMP solution, while logarithmic and higher order corrections of KS solution of HL black holes. It is interesting to consider higher order correction of a new regular black hole [114], Myerse–Perry black holes [115], rotating charged hairy black hole [116, 117], or five dimensional AdS black hole at \(N=2\) supergravity [118, 119].
Recently, Thermodynamic of a black hole surrounded by perfect fluid in Rastall theory have been studied [120]. Now, it is interesting to obtain thermal fluctuation effects on such kind of solutions.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This paper is theoretical work without any observational data or simulation, hence there is no data used in this paper.]
References
S.F. Ross, Black hole thermodynamics. arXiv: hep-th/0502195
J.D. Bekenstein, Black holes and entropy. Phys. Rev. D 7, 2333 (1973)
R.M. Wald, The thermodynamics of black holes. Living Rev. Relativ. 4, 6 (2001). arXiv:gr-qc/9912119
R.D. Sorkin, The statistical mechanics of black hole thermodynamics. arXiv:gr-qc/9705006
M. Cadoni, P. Carta, 2D black holes, conformal vacua and CFTs on the cylinder. Phys. Lett. B 522, 126 (2001)
M. Cadoni, M. Cavaglia, Two-dimensional black holes as open strings: a new realization of the ADS/CFT correspondence. Phys. Lett. B 499, 315 (2001)
J. Sadeghi, M.R. Setare, B. Pourhassan, Two dimensional black hole entropy. Eur. Phys. J. C 53, 95 (2008)
J. Sadeghi, B. Pourhassan, Entropy function in the Liouville theory. Int. J. Theor. Phys. 48, 3526 (2009)
J. Sadeghi, M.R. Setare, B. Pourhassan, Entropy of extremal black holes in two dimensions. Acta Phys. Pol. B 40, 251 (2009)
J. Sadeghi, B. Pourhassan, Higher order corrections of 2D gravity on \(S_{2}\). Int. J. Theor. Phys. 48, 3629 (2009)
J. Sadeghi, B. Pourhassan, Z.S. Rostami, Thermodynamics of near-extremal solutions of Einstein–Maxwell-scalar theory. Int. J. Theor. Phys. 52, 2564 (2013)
J. Sadeghi, B. Pourhassan, F. Pourasadollah, Thermodynamics of Schrodinger black holes with hyperscaling violation. Phys. Lett. B 720, 244 (2013)
J. Sadeghi, B. Pourhassan, A. Asadi, Thermodynamics of string black hole with hyperscaling violation. Eur. Phys. J. C 74, 2680 (2014)
J. Sadeghi, B. Pourhassan, A. Asadi, Application of hyperscaling violation in QCD. Can. J. Phys. 92, 280 (2014)
D. Bak, S.J. Rey, Holographic principle and string cosmology. Class. Quantum Gravity 17, L1 (2000)
S.K. Rama, Holographic principle in the closed universe: a resolution with negative pressure matter. Phys. Lett. B 457, 268 (1999)
S. Das, P. Majumdar, R.K. Bhaduri, General logarithmic corrections to black hole entropy. Class. Quantum Gravity 19, 2355 (2002)
J. Sadeghi, B. Pourhassan, F. Rahimi, Logarithmic corrections to charged hairy black hole in (2+1) dimensions. Can. J. Phys. 92, 1638 (2014)
S. Hemming, L. Thorlacius, Thermodynamics of large AdS black holes. J. High Energy Phys. 0711, 086 (2007)
B. Pourhassan, M. Faizal, S. Upadhyay, L. Al Asfar, Thermal fluctuations in a hyperscaling violation background. Eur. Phys. J. C 77, 555 (2017)
M.M. Caldarelli, G. Cognola, D. Klemm, Thermodynamics of Kerr–Newman–AdS black holes and conformal field theories. Class. Quantum Gravity 17, 399 (2000)
B. Pourhassan, M. Faizal, Thermodynamics of a sufficient small singly spinning Kerr–AdS black hole. Nucl. Phys. B 913, 834 (2016)
D.N. Page, Hawking radiation and black hole thermodynamics. New J. Phys. 7, 203 (2005)
B. Harms, Y. Leblanc, Statistical mechanics of black holes. Phys. Rev. D 46, 2334 (1992)
M. Khurshudyan, B. Pourhassan, A. Pasqua, Higher derivative corrections of \(f(R)\) gravity with varying equation of state in the case of variable \(G\) and \(\Lambda \). Can. J. Phys. 93, 449 (2015)
S. Upadhyay, S. Soroushfar, R. Saffari, First-order corrected thermodynamic geometry of a static black hole in \(f(R)\) gravity. arXiv:1801.09574
J. Sadeghi, B. Pourhassan, A.S. Kubeka, M. Rostami, Logarithmic corrected polynomial f(R) inflation mimicking a cosmological constant. Int. J. Mod. Phys. D 25, 1650077 (2016)
S. Upadhyay, B. Pourhassan, S. Capozziello, Thermodynamics and phase transitions of galactic clustering in higher-order modified gravity. Int. J. Mod. Phys. D 28, 1950027 (2019)
J.R. Mureika, J.W. Moffat, M. Faizal, Black hole thermodynamics in MOdified Gravity (MOG). Phys. Lett. B 757, 528 (2016)
S.S. More, Higher order corrections to black hole entropy. Class. Quantum Gravity 22, 4129 (2005)
B. Pourhassan, K. Kokabi, Effect of higher order corrected entropy on the black hole physics. Can. J. Phys. 96, 262 (2018)
E. Gimon, A. Hashimoto, Black holes in Godel universes and pp-waves. Phys. Rev. Lett. 91, 021601 (2003)
A. Pourdarvish, B. Pourhassan, M. Mirebrahimi, Thermodynamics and statistics of Kerr–Godel black hole. Int. J. Theor. Phys. 53, 3101 (2014)
A. Pourdarvish, J. Sadeghi, H. Farahani, B. Pourhassan, Int. J. Theor. Phys. 52, 3560 (2013)
B. Pourhassan, K. Kokabi, Z. Sabery, Higher order corrected thermodynamics and statistics of Kerr–Newman–Godel black hole. Ann. Phys. 399, 181 (2018)
B. Pourhassan, S. Upadhyay, H. Farahani, Thermodynamics of higher order entropy corrected Schwarzschild–Beltrami–de Sitter black hole. arXiv:1701.08650
B. Pourhassan, J. Sadeghi, STU/QCD correspondence. Can. J. Phys. 91, 995 (2013)
A. Pourdarvish, B. Pourhassan, M. Tabassomi, Statistical analysis of STU black holes. Int. J. Theor. Phys. 53, 1814 (2014)
S. Carlip, Black hole thermodynamics. Int. J. Mod. Phys. D 23, 1430023 (2014)
J. Sadeghi, B. Pourhassan, S. Heshmatian, Application of AdS/CFT in quark-gluon plasma. Adv. High Energy Phys. 2013, 759804 (2013)
G. Policastro, D.T. Son, A.O. Starinets, From AdS/CFT correspondence to hydrodynamics. J. High Energy Phys. 0209, 043 (2002). arXiv:hep-th/0205052
J. Sadeghi, B. Pourhassan, A.R. Amani, The effect of higher derivative correction on \(\eta /s\) and conductivities in STU model. Int. J. Theor. Phys. 52, 42 (2013)
A. Buchel, J.T. Liu, Universality of the shear viscosity in supergravity. Phys. Rev. Lett. 93, 090602 (2004)
P. Kovtun, D.T. Son, A.O. Starinets, Holography and hydrodynamics: diffusion on stretched horizons. J. High Energy Phys. 0310, 064 (2003)
J. Sadeghi, B. Pourhassan, Drag force of moving quark at N= 2 supergravity. J. High Energy Phys. 0812, 026 (2008)
J. Sadeghi, M.R. Setare, B. Pourhassan, S. Heshmatian, Drag force of moving quark in STU background. Eur. Phys. J. C 61, 527 (2009)
J. Sadeghi, M.R. Setare, B. Pourhassan, Drag force with different charges in STU background and AdS/CFT. J. Phys. G Nucl. Part. Phys. 36, 115005 (2009)
C.P. Herzog, A. Karch, P. Kovtun, C. Kozcaz, L.G. Yaffe, Energy loss of a heavy quark moving through \({\cal{N}} =4\) supersymmetric Yang–Mills plasma. J. High Energy Phys. 0607, 013 (2006)
J. Sadeghi, B. Pourhassan, Energy loss and jet quenching parameter in a thermal non-relativistic, non-commutative Yang–Mills plasma. Acta Phys. Pol. B 43, 1825 (2012)
J. Sadeghi, B. Pourhassan, Jet-quenching of the rotating heavy meson in a \(N=4\) SYM plasma in presence of a constant electric field. Int. J. Theor. Phys. 50, 2305 (2011)
K.B. Fadafan, B. Pourhassan, J. Sadeghi, Calculating the jet-quenching parameter in STU background. Eur. Phys. J. C 71, 1785 (2011)
N. Armesto, J.D. Edelstein, J. Mas, Jet quenching at finite t Hooft coupling and chemical potential from AdS/CFT. J. High Energy Phys. 0609, 039 (2006)
B. Pourhassan, M. Faizal, The lower bound violation of shear viscosity to entropy ratio due to logarithmic correction in STU model. Eur. Phys. J. C 77, 96 (2017)
J. Letessier, J. Rafelski, A. Tounsi, Formation and evolution of the quark-gluon plasma. Phys. Lett. B 333, 484 (1994)
R.B. Mann, S.N. Solodukhin, Universality of quantum entropy for extreme black holes. Nucl. Phys. B 523, 293 (1998)
A.J.M. Medved, G. Kunstatter, Quantum corrections to the thermodynamics of charged 2D black holes. Phys. Rev. D 60, 104029 (1999)
A.J.M. Medved, G. Kunstatter, One-loop corrected thermodynamics of the extremal and nonextremal spinning Banados–Teitelboim–Zanelli black hole. Phys. Rev. D 63, 104005 (2001)
J. Jing, M.L. Yan, Statistical entropy of a stationary dilaton black hole from Cardy formula. Phys. Rev. D 63, 024003 (2001)
T. Jacobson, Thermodynamics of spacetime: the Einstein equation of state. Phys. Rev. Lett. 75, 1260 (1995)
R.G. Cai, S.P. Kim, First law of thermodynamics and Friedmann equations of Friedmann–Robertson–Walker universe. J. High Energy Phys. 0502, 050 (2005)
D. Birmingham, S. Sen, Exact black hole entropy bound in conformal field theory. Phys. Rev. D 63, 047501 (2001)
B. Pourhassan, M. Faizal, Thermal fluctuations in a charged AdS black hole. Europhys. Lett. 111, 40006 (2015)
S. Upadhyay, Leading-order corrections to charged rotating AdS black holes thermodynamics. Gen. Relativ. Gravit. 50, 128 (2018)
M. Faizal, B. Pourhassan, Corrections terms for the thermodynamics of a black saturn. Phys. Lett. B 751, 487 (2015)
B. Pourhassan, M. Faizal, Effect of thermal fluctuations on a charged dilatonic black saturn. Phys. Lett. B 755, 444 (2016)
S.A. Hayward, Formation and evaporation of nonsingular black holes. Phys. Rev. Lett. 96, 031103 (2006)
T. De Lorenzo, C. Pacilioy, C. Rovelli, S. Speziale, On the effective metric of a Planck star. Gen. Relativ. Gravit. 47, 41 (2015)
B. Pourhassan, U. Debnath, Particle acceleration in rotating modified Hayward and Bardeen black holes. Gravit. Cosmol. 25, 196 (2019)
B. Pourhassan, M. Faizal, U. Debnath, Effects of thermal fluctuations on the thermodynamics of modified Hayward black hole. Eur. Phys. J. C 76, 145 (2016)
S. Upadhyay, S.H. Hendi, S. Panahiyan, B.E. Panah, Thermal fluctuations of charged black holes in gravity’s rainbow. Prog. Theor. Exp. Phys. 2018, 093E01 (2018)
S. Upadhyay, Quantum corrections to thermodynamics of quasitopological black holes. Phys. Lett. B 775, 130 (2017)
B. Pourhassan, M. Faizal, S. Capozziello, Testing quantum gravity through dumb holes. Ann. Phys. 377, 108 (2017)
B. Pourhassan, M. Faizal, S.A. Ketabi, Logarithmic correction of the BTZ black hole and adaptive model of graphene. Int. J. Mod. Phys. D 27, 1850118 (2018)
J. Sadeghi, B. Pourhassan, M. Rostami, P-V criticality of logarithm-corrected dyonic charged AdS black holes. Phys. Rev. D 94, 064006 (2016)
S. Upadhyay, B. Pourhassan, Logarithmic corrected Van der Waals black holes in higher dimensional AdS space. Prog. Theor. Exp. Phys. 2019, 013B03 (2019)
B. Pourhassan, K. Kokabi, S. Rangyan, Thermodynamics of higher dimensional black holes with higher order thermal fluctuations. Gen. Relativ. Gravit. 49, 144 (2017)
S.H. Hendi, S. Panahiyan, S. Upadhyay, B. Eslam Panah, Charged BTZ black holes in the context of massive gravity’s rainbow. Phys. Rev. D 95, 084036 (2017)
Nadeem-ul-islam, P.A. Ganai, S. Upadhyay, Thermal fluctuations to thermodynamics of non-rotating BTZ black hole. arXiv:1811.05313
B. Pourhassan, M. Faizal, Z. Zaz, A. Bhat, Quantum fluctuations of a BTZ black hole in massive gravity. Phys. Lett. B 773, 325 (2017)
B. Pourhassan, K. Kokabi, Higher order quantum corrections of rotating BTZ black hole. Int. J. Theor. Phys. 57, 780 (2018)
S. Chougule, S. Dey, B. Pourhassan, M. Faizal, BTZ black holes in massive gravity. Eur. Phys. J. C 78, 685 (2018)
D. Kubiznak, R.B. Mannitem, P-V criticality of charged AdS black holes. J. High Energy Phys. 1207, 033 (2012)
S. Upadhyay, B. Pourhassan, H. Farahani, P-V criticality of first-order entropy corrected AdS black holes in massive gravity. Phys. Rev. D 95, 106014 (2017)
R.-G. Cai, L.-M. Cao, L. Li, R.-Q. Yang, P-V criticality in the extended phase space of Gauss–Bonnet black holes in AdS space. J. High Energy Phys. 1309, 005 (2013)
P. Horava, Spectral Dimension of the Universe in Quantum Gravity at a Lifshitz Point. Phys. Rev. D 79, 084008 (2009). arXiv:0902.3657 [hep-th]
G. Calcagni, Cosmology of the Lifshitz universe. J. High Energy Phys. 0909, 112 (2009). arXiv:0904.0829 [hep-th]
R.G. Cai, L.M. Cao, N. Ohta, Topological black holes in Horava–Lifshitz gravity. Phys. Rev. D 80, 024003 (2009). arXiv:0904.3670 [hep-th]
R.G. Cai, Y. Liu, Y.W. Sun, On the \(z=4\) Horava–Lifshitz gravity. J. High Energy Phys. 0906, 010 (2009). arXiv:0904.4104 [hep-th]
B.R. Majhi, Hawking radiation and black hole spectroscopy in Horava–Lifshitz gravity. Phys. Lett. B 686, 49 (2010). arXiv:0911.3239 [hep-th]
B. Pourhassan, Extended Chaplygin gas in Horava–Lifshitz gravity. Phys. Dark Universe 13, 132 (2016)
J. Sadeghi, B. Pourhassan, K. Jafarzadeh, E. Reisi, M. Rostami, Massless fermion quasinormal modes in the Horava–Lifshitz background. Can. J. Phys. 91, 251 (2013)
J. Sadeghi, K. Jafarzade, B. Pourhassan, Thermodynamical quantities of Horava–Lifshitz black hole. Int. J. Theor. Phys. 51, 3891 (2012)
Y.S. Myung, Y.W. Kim, Thermodynamics of Horava–Lifshitz black holes. Eur. Phys. J. C 68, 265 (2010)
S.-W. Zhou, W.-B. Liu, Black hole thermodynamics of Horava–Lifshitz and IR modified Horava–Lifshitz gravity theory. Int. J. Theor. Phys. 50, 1776 (2011)
H. Quevedo, A. Sanchez, S. Taj, A. Vazquez, Geometrothermodynamics in Horava–Lifshitz gravity. J. Phys. A 45, 055211 (2012)
B. Pourhassan, S. Upadhyay, H. Saadat, H. Farahani, Quantum gravity effects on Horava–Lifshitz black hole. Nucl. Phys. B 928, 415 (2018)
G.W. Gibbons, S.W. Hawking, Action integrals and partition functions in quantum gravity. Phys. Rev. D. 15, 2752 (1977)
V. Iyer, R.M. Wald, Comparison of the Noether charge and Euclidean methods for computing the entropy of stationary black holes. Phys. Rev. D. 52, 4430 (1995)
H. Lu, J. Mei, C.N. Pope, Solutions to Horava gravity. Phys. Rev. Lett. 103, 091301 (2009)
M.-I. Park, The black hole and cosmological solutions in IR modified Horava gravity. J. High Energy Phys. 0909, 123 (2009)
H.W. Lee, Y.-W. Kim, Y.S. Myung, Slowly rotating black holes in the Horava–Lifshitz gravity. Eur. Phys. J. C 70, 367 (2010)
E. Kiritsis, G. Kofinas, Horava–Lifshitz cosmology. Nucl. Phys. B 821, 467 (2009)
J. Sadeghi, B. Pourhassan, Particle acceleration in Horava–Lifshitz black holes. Eur. Phys. J. C 72, 1984 (2011)
D.Y. Chen, H. Yang, X.T. Zu, Analytical expressions for greybody factor and dynamic evolution for scalar field in Horava–Lifshitz black hole. Phys. Lett. B 681, 463 (2009). arXiv:1004.4440 [hep-th]
H.W. Lee, Y.W. Kim, Y.S. Myung, Slowly rotating black holes in the Horava–Lifshitz gravity. Eur. Phys. J. C 70, 367 (2010)
R. Biswas, S. Chakraborty, Black hole thermodynamics in Horava Lifshitz gravity and the related geometry. Astrophys. Space Sci. 332, 193 (2011)
A. Kehagias, K. Sfetsos, The black hole and FRW geometries of non-relativistic gravity. Phys. Lett. B 678, 123 (2009)
B.P. Dolan, Pressure and volume in the first law of black hole thermodynamics. Class. Quantum Gravity 28, 235017 (2011)
E. Kiritsis, G. Kofinas, On Horava–Lifshitz black holes, CCTP-2009-16. arXiv:0910.5487 [hep-th]
B.P. Dolan, The cosmological constant and black hole thermodynamic potentials. Class. Quantum Gravity 28, 125020 (2011)
I. Amado, A. Faedo, Lifshitz black holes in string theory. J. High Energy Phys. 1107, 004 (2011)
K. Balasubramanian , J. Mc Greevy, An analytic Lifshitz black hole, MIT-CTP/4068, NSF-KITP-09-136. arXiv:0909.0263 [hep-th]
J. Tarro, S. Vandoren, Black holes and black branes in Lifshitz spacetimes. J. High Energy Phys. 1109, 017 (2011)
A. Pourdarvish, B. Pourhassan, Statistical mechanics of a new regular black hole. Int. J. Theor. Phys. 52, 3908 (2013)
A. Pourdarvish, B. Pourhassan, Statistics of Myerse–Perry black holes. Int. J. Theor. Phys. 53, 136 (2014)
J. Sadeghi, B. Pourhassan, H. Farahani, Rotating charged hairy black hole in (2+1) dimensions and particle acceleration. Commun. Theor. Phys. 62, 358 (2014)
B. Pourhassan, The Klein–Gordon equation of a rotating charged hairy black hole in (2+1) dimensions. Mod. Phys. Lett. A 31, 1650057 (2016)
J. Sadeghi, A. Chatrabhuti, B. Pourhassan, Quasi-normal modes of AdS5 black hole at \(N=2\) supergravity. Int. J. Theor. Phys. 50, 129 (2011)
B. Pourhassan, J. Sadeghi, A. Chatrabhuti, \(AdS_{5}\) black hole at N=2 supergravity. Indian J. Phys. 87, 691 (2013)
S. Soroushfar, R. Saffari, S. Upadhyay, Thermodynamic geometry of a black hole surrounded by perfect fluid in Rastall theory. arXiv:1908.02133
Acknowledgements
Author would like to thanks Iran Science Elites Federation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Pourhassan, B. PV criticality of the second order quantum corrected Hořava–Lifshitz black hole. Eur. Phys. J. C 79, 740 (2019). https://doi.org/10.1140/epjc/s10052-019-7257-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-7257-7