Abstract
Topological gluon configurations in quantum chromodynamics induce quark chirality imbalance in local domains, which can result in the chiral magnetic effect (CME) – an electric charge separation along a strong magnetic field. Experimental searches for the CME in relativistic heavy ion collisions via the charge-dependent azimuthal correlator (\(\Delta \gamma \)) suffer from large backgrounds arising from particle correlations (e.g. due to resonance decays) coupled with the elliptic anisotropy. We propose differential measurements of the \(\Delta \gamma \) as a function of the pair invariant mass (\(m_\mathrm{inv}\)), by restricting to high \(m_\mathrm{inv}\) thus relatively background free, and by studying the \(m_\mathrm{inv}\) dependence to separate the possible CME signal from backgrounds. We demonstrate by model studies the feasibility and effectiveness of such measurements for the CME search.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
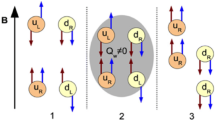
Vacuum fluctuations in quantum chromodynamics (QCD) can result in metastable local domains of gluon fields with non-vanishing topological charges [1,2,3]. Interactions with those gluon fields can, under the approximate chiral symmetry restoration, change the overall chirality of quarks in those domains [4, 5]. The chirality imbalance yields an electric charge separation under a strong magnetic field, a phenomenon called the chiral magnetic effect (CME) [6,7,8]. Strong magnetic fields are generated at early times by the spectator protons in relativistic heavy ion collisions, raising the possibility to detect the CME in those collisions [9, 10]. An observation of the CME would confirm a fundamental property of QCD and is therefore of great importance [11]. CME-like phenomena are not specific only to QCD and may have been observed in condense matter physics [12].
A commonly used variable to measure the CME-induced charge separation in heavy ion collisions is the three-point correlator [9],
where \(\alpha \) and \(\beta \) are the azimuthal angles of two particles and \(\psi \) is that of the reaction plane (span by the beam and impact parameter directions of the colliding nuclei). Charge separation along the magnetic field (\(\vec {B}\)), which is perpendicular to \(\psi \) on average, would yield different values of \(\gamma \) for particle pairs of same-sign (SS) and opposite-sign (OS) charges: \(\gamma _\mathrm{SS}=-1, \gamma _\mathrm{OS}=+1\). However, there exist background correlations unrelated to the CME [9, 13,14,15,16,17,18,19,20]. For example, transverse momentum conservation induces correlations among particles enhancing back-to-back pairs [14,15,16,17,18]. This background is independent of particle charges, affecting SS and OS pairs equally and cancels in the difference, \(\Delta \gamma \equiv \gamma _\mathrm{OS}-\gamma _\mathrm{SS}\). Recent experimental searches have thus focused on the \(\Delta \gamma \) observable [11, 21, 22]; the CME would yield \(\Delta \gamma >0\). There are, however, also mundane physics that differ between SS and OS pairs. One such physics is resonance/cluster decays [9, 13,14,15,16,17,18], more significantly affecting OS pairs than SS pairs. Backgrounds arise from the coupling of elliptical anisotropy (\(v_2\), a common phenomenon in heavy ion collisions [23]) of resonances/clusters and the angular correlations between their decay daughters (nonflow) [9, 13, 14, 17]. Take \(\rho \rightarrow \pi ^{+}\pi ^{-}\) as an example. The background is \((\Delta \gamma )_{\rho }=r_{\rho }\gamma _{\rho }\), where \(r_{\rho }=N_{\rho }/(N_{\pi ^{+}}N_{\pi ^{-}})\) is the relative abundance of \(\rho \)-decay pairs over all OS pairs, and \(\gamma _{\rho }\equiv \langle f_{\rho }v_{2,\rho }\rangle =\langle \cos (\alpha +\beta -2\phi _{\rho })\cos 2(\phi _{\rho }-\psi )\rangle \) quantifies the \(\rho \) decay angular correlations coupled with its \(v_2\) [9, 21, 22, 24].
Experimentally, significant positive \(\Delta \gamma \) values have been observed at the Relativistic Heavy Ion Collider (RHIC) and the Large Hadron Collider (LHC) [25,26,27,28,29]. The relative background and CME contributions are under extensive debate [30]. The recent observations of comparable \(\Delta \gamma \) in small system collisions [31,32,33,34,35,36], where any CME signals would average to zero [31, 37], challenge the CME interpretation of the measured \(\Delta \gamma \) in heavy ion collisions. The major difficulty in distinguishing CME from backgrounds with the \(\Delta \gamma \) observable is their similar behaviors with respect to the event multiplicity [34,35,36]. This is because the magnetic field strength, to which the CME is sensitive, has a similar dependence as the \(v_2\) (backgrounds) on the event multiplicity [10, 38,39,40,41]. There have been various proposals and attempts to reduce or eliminate the backgrounds [24, 32, 42,43,44,45,46]. The central idea is to “hold” the magnetic field fixed (in a narrow centrality) and vary the event-by-event \(v_2\) from statistical and dynamical fluctuations [41, 44, 47]. The first attempt was carried out by STAR [44] where a charge asymmetry observable was analyzed as a function of the observed event-by-event \(v_2\). A linear dependence was observed, expected from background, and the intercept was extracted representing a background-suppressed signal. ALICE [46] divided their data in each collision centrality according to \(v_2\) in one phase space, and found the \(\Delta \gamma \) to be approximately proportional to the \(v_2\) in the phase space of the \(\Delta \gamma \) measurement, consistent with background contributions. However, as recently pointed out by two of us [24], those methods suppressing background may not completely eliminate it. Another way to help search for the CME is to compare isobaric collisions [47], where the magnetic fields differ and the backgrounds are expected to be the same [48]. However, these simple expectations may not be correct because of the non-identical isobaric nuclear structures [49].
A new method to search for the CME, as we demonstrate in this article, is to eliminate the resonance background contributions using particle pair invariant mass (\(m_\mathrm{inv}\)) by (i) applying a lower cut on the \(m_\mathrm{inv}\), (ii) fitting the low \(m_\mathrm{inv}\) region by a two-component (TC) model, and (iii) fitting the low \(m_\mathrm{inv}\) region by a two-component model aided by event-shape engineering (TC+ESE). We illustrate our method using the AMPT (A Multi-Phase Transport) model [50] and a toy Monte Carlo (MC) simulation. In both, the resonance masses are sampled from Breit-Wigner distributions [51, 52]. We use pions within pseudorapidity \(|\eta |<1\) and \(0.2<p_{T}<2\) \(\hbox {GeV}/c\), except otherwise specified.
It is worthwhile to note here, since the CME is generally a low \(p_{T}\) phenomenon, that large \(m_\mathrm{inv}\) region may not be the best place to search for it. If no CME is found at large \(m_\mathrm{inv}\), it does not necessarily mean that CME does not exist at low \(m_\mathrm{inv}\). However, if a finite signal is observed at large \(m_\mathrm{inv}\), where background sources diminish, it could be a strong evidence for the possible existence of the CME that would call for further investigations. It is also worthwhile to note that our low \(m_\mathrm{inv}\) fitting procedure is not without assumptions. Although the background shape may be assessed by the ESE method, there is still the question of the CME shape as function of \(m_\mathrm{inv}\). In principle, if the CME and the background have the same \(m_\mathrm{inv}\) shape, then our invariant mass method would not be able to distinguish the two contributions. Theoretical inputs are much needed in this respect. Nevertheless, our method provides a potentially powerful way to extract the CME with reasonable assumptions of the \(m_\mathrm{inv}\) dependence of the CME, which can be gauged to some extent by the fitting quality.
The rest of the paper is organized as follows. Section 2 presents the AMPT and toy-model studies by applying a lower \(m_\mathrm{inv}\) cut to extract the \(\Delta \gamma \) in the high \(m_\mathrm{inv}\) region. Section 3 describes a two-component model fit to the \(\Delta \gamma (m_\mathrm{inv})\). Section 4 extends the fitting method further by using ESE to determine the background \(\Delta \gamma (m_\mathrm{inv})\) shape to help extract the CME signal. Section 5 puts our methods into experimental context and summarizes the paper.
2 High-\(m_\mathrm{inv}\) region
2.1 A transport model study with null CME
AMPT is a parton transport model [50]. It consists of a fluctuating initial condition, parton elastic scatterings, quark coalescence for hadronization, and hadronic interactions. The initial condition is taken from HIJING [53]. The string melting version [54] is used in this study. Two-body elastic parton scatterings are treated with Zhang’s Parton Cascade [55], where the parton scattering cross section is set to 3 mb. After partons stop interacting, a simple quark coalescence model is applied to describe the hadronization process that converts partons into hadrons [56]. Subsequent interactions of these formed hadrons are modeled by a hadron cascade [56]. However, it is known that this version of the hadron cascade does not conserve charge, which is critical to the charge correlation study here. The hadronic scatterings, while responsible for the majority of the \(v_2\) mass splitting, are unimportant for the main development of \(v_2\) [57, 58], and thus may not be critical for the CME backgrounds. We thus turn off hadronic cascade in AMPT for our study here, as was done in Ref. [59]. AMPT has been quite successful in describing variety of heavy ion data [52]. It reproduces approximately the measured particle yields and distributions, and therefore should approximately describe those of resonances as well, which is relevant to the CME background study here. We simulate Au+Au collisions at \(\sqrt{s_{_\mathrm{NN}}}=200\) GeV of various impact parameter (b) ranges. For simplicity we use the known reaction plane in our analysis, fixed at \(\psi =0\).
Figure 1a shows the \(m_\mathrm{inv}\) distribution of the excess OS over SS pion pairs (\(N\equiv N_\mathrm{OS}-N_\mathrm{SS}\)), with \(b=6.8\)–8.2 fm (corresponding to the 20–30% centrality of Au+Au collisions [60], and average pion multiplicities \(N_{\pi ^{+}}\approx N_{\pi ^{-}}\approx 210\) within \(|\eta |<1\)). The \(\rho \) peak is evident; the lower mass peaks are from Dalitz decays of \(\eta \) and \(\omega \) mesons (the \(K_S\) is kept stable in AMPT). Figure 1b shows the \(\Delta \gamma \) as a function of \(m_\mathrm{inv}\). The \(\rho \) contribution is clearly seen in the \(\rho \) mass region. Since no CME is present in AMPT, the finite \(\Delta \gamma \) at \(m_\mathrm{inv}\lesssim 2\) \(\hbox {GeV}/c^2\) must be due to correlations from resonance decays, or generally, correlated pion pairs. This has been observed before [34, 59]. For \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\) where resonance contribution to the OS over SS excess is small, the \(\Delta \gamma \) value is essentially zero, as expected.
Figure 2 shows the \(\Delta \gamma \) in AMPT from all pairs and \(\Delta \gamma \)(\(m_\mathrm{inv}>2~\hbox {GeV}/c^2\)) from pairs with \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\). The positive \(\Delta \gamma \) is due to backgrounds; in \(\Delta \gamma \)(\(m_\mathrm{inv}>2~\hbox {GeV}/c^2\)) this background is essentially eliminated, and as expected the result is consistent with zero. With the \(11\times 10^6\) AMPT events simulated for 200 GeV Au+Au collisions with \(b=6.6\)–8.2 fm, the inclusive \(\Delta \gamma \) value is \((8.1\pm 0.1)\times 10^{-5}\), and \(\Delta \gamma \)(\(m_\mathrm{inv}>2~\hbox {GeV}/c^2\))\(=\,(-\,0.6\pm 0.8)\times 10^{-5}\). This represents a null signal with an upper limit of 20% of the inclusive \(\Delta \gamma \) with 98% confidence level (CL).
2.2 A toy model study with finite CME
In light of the AMPT results, we propose to apply a lower \(m_\mathrm{inv}\) cut in real data analysis to search for the CME. We illustrate this point further by using a toy MC with input CME signal. Our toy model generates primordial \(\pi ^{\pm }\), \(K_S\), and resonances (\(\rho ,\eta ,\omega \)), and decays the \(K_S\) and resonances (via both two- and three-body decays [51]). Particle kinematics are sampled according to
where \(a_1\) is the CME signal parameter [9]. The particle dN / dy, \(p_{T}\) spectra, and \(v_2(p_{T})\) correspond to the 40-50% centrality of Au+Au collisions; they are as same as those used in Ref. [61] except that the primordial pion \(p_{T}\) spectra are parameterized here with a better agreement with data at high \(p_{T}\), and we have added \(K_S\). The pion multiplicities within \(|\eta |<1\) are \(N_{\pi ^{+}}\approx N_{\pi ^{-}}\approx 100\) and those of primordial pions are \(N^\mathrm{prim}_{\pi ^{+}}\approx N^\mathrm{prim}_{\pi ^{-}}\approx 60\). The \(K_S\) multiplicity is taken to be 1/5 of the measured \(\rho \)’s [62], because some \(K_S\)’s would have both their decay pions reconstructed as primary particles in experiments (such as STAR). We generate \(200\times 10^6\) events with an input CME signal of overall strength \(a_1=\pm \,0.008\) for primordial \(\pi ^{\pm }\); for \(K_S\) and resonances \(a_1=0\). Our input CME is independent of the particle \(p_{T}\). This is supported by a recent theoretical study [63], where the CME is insensitive to \(p_{T}\) once \(p_{T}\) is above 0.2 \(\hbox {GeV}/c\).
Figure 3a shows the relative OS pair excess, \(r(m_\mathrm{inv})\equiv (N_\mathrm{OS}-N_\mathrm{SS})/N_\mathrm{OS}\) as a function of \(m_\mathrm{inv}\) from the toy MC. The \(K_S\) and \(\rho \) peaks are evident. Figure 3b shows the \(\Delta \gamma (m_\mathrm{inv})\); the \(K_S\) and \(\rho \) contributions are clear. The inclusive \(\Delta \gamma \) from Fig. 3b is \((24.5\pm 0.1)\times 10^{-5}\); our input CME signal of \(2a_1^2\), diluted by \((N^\mathrm{prim}_{\pi }/N_{\pi })^2\), is \(4.6\times 10^{-5}\), about 20% of the inclusive \(\Delta \gamma \) value. The \(\Delta \gamma (m_\mathrm{inv})\) distribution in Fig. 3b has a pedestal corresponding to the input CME signal. The pedestal extends to high \(m_\mathrm{inv}\) (not shown) where resonance backgrounds vanish. A lower \(m_\mathrm{inv}\) cut removes backgrounds to \(r(m_\mathrm{inv})\) but not the CME signal. The value \(\Delta \gamma \)(\(m_\mathrm{inv}>2~\hbox {GeV}/c^2\)) \(=(4.5\pm 0.8)\times 10^{-5}\) is consistent with the input CME signal, and it would present a \(5\sigma \) measurement.
The CME is generally believed to be a low-\(p_{T}\) phenomenon [5], and would thus be more prominent in the low \(m_\mathrm{inv}\) region. With a \(m_\mathrm{inv}>2\) \(\hbox {GeV}/c^2\) cut we used here, the particle average \(p_{T}\) is typically 1.2 \(\hbox {GeV}/c\) [64]. This is not very high and the CME may still be present above such a mass cut. Moreover, a recent study [63] indicates that the CME signal is rather independent of \(p_{T}\) at \(p_{T}>0.2\) \(\hbox {GeV}/c\), suggesting that the signal can persist to high \(m_\mathrm{inv}\). Nevertheless, our proposal to apply a lower \(m_\mathrm{inv}\) cut will eliminate resonance contributions to \(\Delta \gamma \); any measured remaining positive \(\Delta \gamma \) would point to the interesting possibility of the existence of the CME. A null measurement at high \(m_\mathrm{inv}\), on the other hand, does not necessarily mean null CME also at low \(m_\mathrm{inv}\).
a \(r=(N_\mathrm{OS}-N_\mathrm{SS})/N_\mathrm{SS}\), b \(\Delta \gamma \), and c \(\Delta \gamma /r\) as a function of \(m_\mathrm{inv}\) from the toy MC simulation of total \(200\times 10^6\) events. Included are primordial \(\pi ^{\pm }\), and \(K_S, \rho , \eta , \omega \) resonances, using parameters corresponding to measurements in Au+Au collisions of the 40–50% centrality. A CME signal \(a_1=\pm \,0.008\) is included
3 Two-component model fit in low-\(m_\mathrm{inv}\) region
In what follows, we illustrate a fit method to potentially identify the possible CME at low \(m_\mathrm{inv}\). Still use \(\rho \rightarrow \pi ^{+}\pi ^{-}\) as an example, and consider the event to be composed of primordial pions containing CME signals (\(\gamma _\mathrm{CME}\)) and common (charge-independent) backgrounds, such as momentum conservation (\(\gamma _\mathrm{m.c.}\)) [16, 18], and decay pions containing correlations from the decay [9, 17, 24]. We have
(If one normalized \(\gamma _\mathrm{OS}\) by \(N_\mathrm{SS}\) instead, then Eq. (3) would become simpler, \(\Delta \gamma '=r'\gamma _{\rho }+\Delta \gamma _\mathrm{CME}\) with \(r'=(N_\mathrm{OS}-N_\mathrm{SS})/N_\mathrm{SS}\).) Considering Eq. (3), the \(\Delta \gamma \) can be expressed by two terms:
The first term is resonance contributions, where the response function
contains \(v_{2}\) of various resonances and is likely a smooth function of \(m_\mathrm{inv}\) while \(r(m_\mathrm{inv})\) contains resonance spectral profile (Fig. 3a). Consequently, the first term is not smooth but a peaked function of \(m_\mathrm{inv}\). The second term in Eq. (4) is the CME signal which should be a smooth function of \(m_\mathrm{inv}\) (note we have dropped the negligible r / 2). However, the exact functional form of \(\Delta \gamma _\mathrm{CME}(m_\mathrm{inv})\) is presently unknown and needs theoretical input. It is possible that the CME may possess some resonance shapes; in the extreme case where the CME has the same \(m_\mathrm{inv}\) shape as the background, then our method would obviously fail. Nevertheless, the \(m_\mathrm{inv}\) dependences of the two terms are likely different, and this can be exploited to identify CME signals at low \(m_\mathrm{inv}\). This is illustrated in Fig. 3c where the ratio of \(\Delta \gamma /r\) is depicted. If CME signal is present, as is the case in our toy MC, \(\Delta \gamma /r\) should not be smooth, but with a deviation resembling the inverse shape of r in Fig. 3a. This is clearly seen in Fig. 3c in the \(\rho \) mass region, although not as clear in the \(K_S\) mass region.
Toy model simulation of (a) inclusive \(\Delta \gamma \) and \(\Delta \gamma _A-\Delta \gamma _B\) as functions of \(m_\mathrm{inv}\), and b \(\Delta \gamma _A\) versus \(\Delta \gamma _B\). The simulation corresponds to the 40–50% centrality Au+Au collisions at \(\sqrt{s_{_\mathrm{NN}}}=200\) GeV. \(\Delta \gamma _A\) and \(\Delta \gamma _B\) are calculated in two event classes selected by \(q_2\), corresponding to the 50% high-\(q_2\) and 50% low-\(q_2\) events, respectively. Each data point in panel (b) corresponds to one \(m_\mathrm{inv}\) bin in panel (a)
In Eq. (4), \(\Delta \gamma (m_\mathrm{inv})\) and \(r(m_\mathrm{inv})\) are measured, and \(R(m_\mathrm{inv})\) results from known physics and can in principle be obtained from models. AMPT indicates that \(R(m_\mathrm{inv})\) is a first-order polynomial. We can thus take a step further to fit the \(\Delta \gamma (m_\mathrm{inv})\) in Fig. 3b by Eq. (4) taking \(R(m_\mathrm{inv})\) as a first-order polynomial fit function, treating CME as a \(m_\mathrm{inv}\)-independent fit parameter (our input CME signal is \(p_{T}\) independent). The fit result is superimposed as the red histogram in Fig. 3b, and in Fig. 3c after divided by \(r(m_\mathrm{inv})\) from Fig. 3a. The straight line in blue in Fig. 3c is the fit result for \(R(m_\mathrm{inv})\). The difference between the fit red histogram and the blue line is \(\Delta \gamma _\mathrm{CME}/r(m_\mathrm{inv})\), which shows the inverse shape of \(r(m_\mathrm{inv})\). It is found, with the simulated statistics, that the inverse-shape feature becomes hard to identify when the CME input signal is smaller than 10% of the inclusive \(\Delta \gamma \). The fit parameters are written in Fig. 3(b). The fit parameter for CME is \(\Delta \gamma _\mathrm{CME}=(4.2\pm 0.2)\times 10^{-5}\), not far away from the input CME signal of \(4.6\times 10^{-5}\). The fit \(\chi ^2/\mathrm{ndf}=108/75\) is not ideal because of the approximation for the \(m_\mathrm{inv}\)-dependence of \(R(m_\mathrm{inv})\), but it presents a potentially viable way to extract CME signals from data even at low \(m_\mathrm{inv}\).
Theoretically, the \(m_\mathrm{inv}\) dependence of the CME is unknown. The likely sphaleron or instanton mechanism for transitions between QCD vacuum states [2, 5, 6, 10], leading to the CME, might yield a broad \(m_\mathrm{inv}\) distribution around \(m_\mathrm{inv}\sim 1\) \(\hbox {GeV}/c\). With such a CME signal, assuming a \(m_\mathrm{inv}\)-independent CME in our fit would probably still yield a reasonable average CME signal. To illustrate this point, we simulate sphalerons/instantons by a broad Gaussian mass distribution at 1 \(\hbox {GeV}/c^2\) with width 0.5 \(\hbox {GeV}/c^2\). Each sphaleron/instanton is at rest and decays into a \(\pi ^{+}\pi ^{-}\) pair where the decay polar angle is uniform in \(\sin \theta \) and the azimuthal angles of \(\pi ^{\pm }\) are sampled according to \(dN/d\phi \propto 1\pm \sin \phi \). The number of sphalerons/instantons is Poisson and on average 0.7% (0.9% within \(|\eta |<1\)) of the event single charge pion multiplicity. The pion azimuthal distributions in the form of Eq. (2) are \(dN_{\pi ^{\pm }}/d\phi \propto 1+2v_2\cos 2\phi +0.009\times (1\pm \sin \phi )\). This gives an effective CME signal of \(2a_1^2\approx 4.0\times 10^{-5}\). We apply our fit method, still assuming a constant CME, and obtain \(\Delta \gamma _\mathrm{CME}=(3.7\pm 0.2)\times 10^{-5}\), consistent with the input signal, with \(\chi ^2/\mathrm{ndf}=187/75\).
4 Use ESE to determine background shape in two-component fit
In the TC fit in Sect. 3, one needs the functional form of \(R(m_\mathrm{inv})\) as input. The linear form used in the Fig. 3 fit was motivated by AMPT results, but is strongly model dependent. To lift this model dependency, one may resort to event-shape engineering (ESE) [32, 46, 65] where events in each narrow centrality bin are divided into two classes according to the flow vector \(q_2\):
where M is the particle multiplicity and \(\phi _j\) is the jth particle azimuth. The two \(q_2\) event classes will have different average \(v_2\) exploiting dynamical fluctuations of \(v_2\) [32, 46, 65]. (In our simulation we included dynamical fluctuations of 40% of the average \(v_2\) [24].) Since the magnetic fields are approximately equal for the two classes while the \(v_2\) backgrounds differ, the difference in \(\Delta \gamma \) between the two event classes is a good representation of the background shape, and can therefore be used to add to the TC fit. We refer to such a fit as TC+ESE fit. Note that in this fit model the background is not required to be strictly proportional to \(v_2\) [64].
We calculate \(q_2\) using particles from \(-1<\eta <-0.05\) and \(\Delta \gamma \) using particles from \(0.05<\eta <1\), and vice versa (which we refer to as the subevent method). Figure 4 left panel shows the \(m_\mathrm{inv}\) distributions of \(\Delta \gamma _A-\Delta \gamma _B\) (scaled by a factor of 5) together with the inclusive \(\Delta \gamma \). Note that, because of the different \(\eta \) acceptances, the \(\Delta \gamma \)’s in Fig. 4 and Fig. 3 are numerically different. The inclusive \(\Delta \gamma \) contains both background and CME. With the background shape given by \(\Delta \gamma _A-\Delta \gamma _B\), the CME can be extracted from a fit \(\Delta \gamma =k(\Delta \gamma _A-\Delta \gamma _B)+\Delta \gamma _\mathrm{CME}\). Since the same data are used in \(\Delta \gamma \) and \(\Delta \gamma _A-\Delta \gamma _B\), their statistical errors are somewhat correlated. To properly handle statistical errors, one can simply fit the independent measurements of \(\Delta \gamma _A\) versus \(\Delta \gamma _B\), namely \(\Delta \gamma _A=b\Delta \gamma _B+(1-b)\Delta \gamma _\mathrm{CME}\) where b and \(\Delta \gamma _\mathrm{CME}\) are the fit parameters. Figure 4 right panel shows such a fit to our toy model simulation.
Figure 5 shows the \(\Delta \gamma _\mathrm{CME}\) parameters from the TC fit and the TC+ESE fit as functions of the input CME strength. The TC+ESE fit uncertainties on the \(\Delta \gamma _\mathrm{CME}\) parameter are relatively large. This is because \(\Delta \gamma _A-\Delta \gamma _B\) is small (see Fig. 4 left panel), corresponding to a relative difference in \(v_2\) on the order of 10% in our toy model simulation representing mid-central Au+Au collisions at RHIC. At the LHC, this difference is larger, approximately 20% [32, 46], because of the larger event multiplicities than at RHIC. As seen from Fig. 5, the fits appear to faithfully reproduce the input CME signal.
5 Discussion and summary
The STAR experiment at RHIC has accumulated Au+Au minimum bias data samples of \(15\times 10^6\) events from Run-4 [25, 26], \(57\times 10^6\) events from Run-7 [29], and \(500\times 10^6\) events from Run-11 [66]. If the CME signal is 1/3 of the measured inclusive \(\Delta \gamma \) [25, 26] and independent of \(m_\mathrm{inv}\), these data samples (with the 20–60% centrality) could yield, based on our toy MC study, a better than \(5\sigma \) measurement of \(\Delta \gamma \)(\(m_\mathrm{inv}>2~\hbox {GeV}/c^2\)). If the CME signal is unobservable, then our analysis method could set, based on our AMPT result, an upper limit with 98% CL on the CME of 5% at \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\) relative to the measured inclusive \(\Delta \gamma \). It is likely that the CME contribution decreases with \(m_\mathrm{inv}\) and, depending on the detailed physics mechanism, may become difficult to observe at \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\). Our fit methods can be used to explore and extract CME signals at low \(m_\mathrm{inv}\). The methods rely on the rather robust assumption of different \(m_\mathrm{inv}\) dependences of peaked resonance contributions and smooth CME signal, lifting the major difficulty of similar dependences of the background and CME on experimental variables thus far. The ESE method can further help determine the background dependence on \(m_\mathrm{inv}\), thus improving the accuracy in the extraction of the CME signal.
In summary, topological charge fluctuations, resulting in the chiral magnetic effect (CME) and charge separation in relativistic heavy ion collisions, are fundamental properties of QCD. Experimental charge separation measurements by the azimuthal correlator (\(\Delta \gamma \)) suffer from major backgrounds from resonance decays (generally, local charge conservation) coupled with elliptic anisotropy. In this article, we propose to measure the \(\Delta \gamma \) differentially as a function of the particle pair invariant mass (\(m_\mathrm{inv}\)). By using the AMPT (A Multi-Phase Transport) model, we demonstrate that one can essentially eliminate resonance decay backgrounds to \(\Delta \gamma \) by applying a lower cut on \(m_\mathrm{inv}\). With a \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\) cut, an upper limit on the CME of 20% of the inclusive \(\Delta \gamma \) can be achieved with \(11\times 10^6\) AMPT events of 200 GeV Au+Au collisions with impact parameter \(b=6.6\)–8.2 fm. By using a toy Monte Carlo simulation with realistic resonance distributions and a \(p_{T}\)-independent input CME signal, we show that the resonance decay backgrounds are eliminated by the \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\) cut and the CME signal remains. With input CME signal of \(a_1=0.008\) (20% of the total \(\Delta \gamma \)) and \(200\times 10^6\) events corresponding to the 40–50% centrality of Au+Au collisions, a \(5\sigma \) CME measurement could be achieved at \(m_\mathrm{inv}>2~\hbox {GeV}/c^2\). We further show that one may be able to separate the presumably smooth CME signals from peaked resonance decay backgrounds in the low \(m_\mathrm{inv}\) region by exploiting their different \(m_\mathrm{inv}\) dependences. We show this by the toy MC with a \(p_{T}\)-independent CME signal as well as the signal from a broad sphaleron/instanton mass distribution. We demonstrate that one may use the ESE to determine the background shape in \(m_\mathrm{inv}\), thus help the extraction of the CME signal.
We note that our lower \(m_\mathrm{inv}\) cut may also remove the CME signal together with the background. A negative conclusion at large \(m_\mathrm{inv}\) does therefore not necessarily mean null CME also at low \(m_\mathrm{inv}\). A positive signal at large \(m_\mathrm{inv}\), however, would be a good indication of the possible CME. We also note that our two-component model fit in the low \(m_\mathrm{inv}\) region is not without assumptions. One uncertainty is the unknown \(m_\mathrm{inv}\) dependence of the CME, where theoretical guidance is much needed. Nevertheless, our proposed invariant mass method provides a valuable tool and should help the ongoing experimental search for the CME at RHIC and the LHC.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This manuscript uses simulation data that can be regenerated according to descriptions in the manuscript. Thus these simulation data will not be deposited.]
References
T.D. Lee, G.C. Wick, Vacuum stability and vacuum excitation in a spin 0 field theory. Phys. Rev. D 9, 2291–2316 (1974)
Dmitri Kharzeev, R.D. Pisarski, Michel H.G. Tytgat, Possibility of spontaneous parity violation in hot QCD. Phys.Rev.Lett., 81, 512–515 (1998)
D. Kharzeev, R.D. Pisarski, Pionic measures of parity and CP violation in high-energy nuclear collisions. Phys. Rev. D 61, 111901 (2000)
D. Kharzeev, A. Zhitnitsky, Charge separation induced by P-odd bubbles in QCD matter. Nucl. Phys. A 797, 67–79 (2007)
D.E. Kharzeev, L.D. McLerran, H.J. Warringa, The Effects of topological charge change in heavy ion collisions: ’Event by event P and CP violation’. Nucl. Phys. A 803, 227–253 (2008)
K. Fukushima, D.E. Kharzeev, H.J. Warringa, The chiral magnetic effect. Phys. Rev. D 78, 074033 (2008)
B. Muller, A. Schafer, Charge fluctuations from the chiral magnetic effect in nuclear collisions. Phys. Rev. C 82, 057902 (2010)
K.F. Liu, Charge-dependent azimuthal correlations in relativistic heavy-ion collisions and electromagnetic effects. Phys. Rev. C 85, 014909 (2012)
S.A. Voloshin, Parity violation in hot QCD: how to detect it. Phys. Rev. C 70, 057901 (2004)
D. Kharzeev, Parity violation in hot QCD: why it can happen, and how to look for it. Phys. Lett. B 633, 260–264 (2006)
D.E. Kharzeev, J. Liao, S.A. Voloshin, G. Wang, Chiral magnetic and vortical effects in high-energy nuclear collisions—a status report. Prog. Part. Nucl. Phys. 88, 1–28 (2016)
Li Q, Kharzeev DE, Zhang C, Huang Y, Pletikosic I, Fedorov AV, Zhong RD, Schneeloch JA, Gu GD, Valla T (2016) Observation of the chiral magnetic effect in ZrTe5. Nat. Phys. 12, 550–554 (2016)
F. Wang, Effects of cluster particle correlations on local parity violation observables. Phys. Rev. C 81, 064902 (2010)
A. Bzdak, V. Koch, J. Liao, Remarks on possible local parity violation in heavy ion collisions. Phys. Rev. C 81, 031901 (2010)
J. Liao, V. Koch, A. Bzdak, On the charge separation effect in relativistic heavy ion collisions. Phys. Rev. C 82, 054902 (2010)
A. Bzdak, V. Koch, J. Liao, Azimuthal correlations from transverse momentum conservation and possible local parity violation. Phys. Rev. C 83, 014905 (2011)
S. Schlichting, S. Pratt, Charge conservation at energies available at the BNL relativistic heavy ion collider and contributions to local parity violation observables. Phys. Rev. C 83, 014913 (2011)
S. Pratt, S. Schlichting, S. Gavin, Effects of momentum conservation and flow on angular correlations at RHIC. Phys. Rev. C 84, 024909 (2011)
H. Petersen, T. Renk, S.A. Bass, Medium-modified Jets and initial state fluctuations as sources of charge correlations measured at RHIC. Phys. Rev. C 83, 014916 (2011)
V.D. Toneev, V.P. Konchakovski, V. Voronyuk, E.L. Bratkovskaya, W. Cassing, Event-by-event background in estimates of the chiral magnetic effect. Phys. Rev. C 86, 064907 (2012)
J. Zhao, Search for the chiral magnetic effect in relativistic heavy-ion collisions. Int. J. Mod. Phys. A 33(13), 1830010 (2018)
J. Zhao, Z. Tu, F. Wang, Status of the chiral magnetic effect search in relativistic heavy-ion collisions. Nucl. Phys. Rev. 35, 225–242 (2018)
U. Heinz, R. Snellings, Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 63, 123–151 (2013)
F. Wang, J. Zhao, Challenges in flow background removal in search for the chiral magnetic effect. Phys. Rev. C 95(5), 051901 (2017)
B.I. Abelev, Azimuthal charged-particle correlations and possible local strong parity violation. Phys. Rev. Lett. 103, 251601 (2009)
B.I. Abelev, Observation of charge-dependent azimuthal correlations and possible local strong parity violation in heavy ion collisions. Phys. Rev. C 81, 054908 (2010)
Betty Abelev et al. Charge separation relative to the reaction plane in Pb-Pb collisions at \(\sqrt{s_{NN}}= 2.76~ \text{TeV}\). Phys.Rev.Lett., 110(1), 012301 (2013)
L. Adamczyk et al., Fluctuations of charge separation perpendicular to the event plane and local parity violation in \(\sqrt{s_{NN}}=200~ \text{ GeV }\) Au+Au collisions at the BNL Relativistic Heavy Ion Collider. Phys. Rev. C 88(6), 064911 (2013)
L. Adamczyk et al., Beam-energy dependence of charge separation along the magnetic field in Au+Au collisions at RHIC. Phys. Rev. Lett. 113, 052302 (2014)
2017. Quark Matter 2017 Conference, Chicago
V. Khachatryan et al., Observation of charge-dependent azimuthal correlations in \(p\)-Pb collisions and its implication for the search for the chiral magnetic effect. Phys. Rev. Lett. 118(12), 122301 (2017)
Sirunyan A.M, et al. Constraints on the chiral magnetic effect using charge-dependent azimuthal correlations in \(p{\rm Pb}\) and PbPb collisions at the CERN Large Hadron Collider. Phys. Rev. C97(4), 044912 (2018)
J. Zhao, Charge dependent particle correlations motivated by chiral magnetic effect and chiral vortical effect. EPJ Web Conf. 141, 01010 (2017)
J. Zhao. Separate measurements of physics background and the possible chiral magnetic effect in p+Au and d+Au collisions at RHIC. Poster given at Quark Matter 2017 Conference, Chicago (2017)
J. Zhao, Chiral magnetic effect search in p+Au, d+Au and Au+Au collisions at RHIC. EPJ Web Conf. 172, 01005 (2018)
J. Zhao, Chiral magnetic effect search in p(d)+Au, Au+Au collisions at RHIC. Int. J. Mod. Phys. Conf. Ser. 46, 1860010 (2018)
R. Belmont, J.L. Nagle, To CME or not to CME? Implications of p+Pb measurements of the chiral magnetic effect in heavy ion collisions. Phys. Rev. C 96(2), 024901 (2017)
A. Bzdak, V. Skokov, Event-by-event fluctuations of magnetic and electric fields in heavy ion collisions. Phys. Lett. B 710, 171–174 (2012)
W.-T. Deng, X.-G. Huang, Event-by-event generation of electromagnetic fields in heavy-ion collisions. Phys. Rev. C 85, 044907 (2012)
J. Bloczynski, X.-G. Huang, X. Zhang, J. Liao, Azimuthally fluctuating magnetic field and its impacts on observables in heavy-ion collisions. Phys. Lett. B 718, 1529–1535 (2013)
S. Chatterjee, P. Tribedy, Separation of flow from the chiral magnetic effect in U + U collisions using spectator asymmetry. Phys. Rev. C 92(1), 011902 (2015)
N.N. Ajitanand, R.A. Lacey, A. Taranenko, J.M. Alexander, A New method for the experimental study of topological effects in the quark-gluon plasma. Phys.Rev. C83,011901, (2011)
A. Bzdak, Suppression of elliptic flow induced correlations in an observable of possible local parity violation. Phys. Rev. C 85, 044919 (2012)
L. Adamczyk et al., Measurement of charge multiplicity asymmetry correlations in high-energy nucleus-nucleus collisions at \(\sqrt{{s}_{NN}} = 200~ \text{ GeV }\). Phys. Rev. C 89(4), 044908 (2014)
F. Wen, L. Wen, G. Wang, Event-shape-engineering study of charge separation in heavy-ion collisions. Chin. Phys. C 42(1), 014001 (2018)
Shreyasi Acharya et al. Constraining the magnitude of the chiral magnetic effect with event shape engineering in Pb-Pb collisions at \(\sqrt{s_{{\rm NN}}} = 2.76~ \text{ TeV }\). Phys. Lett., B777:151–162, (2018)
S.A. Voloshin, Testing the chiral magnetic effect with central U+U collisions. Phys. Rev. Lett. 105, 172301 (2010)
W.-T. Deng, X.-G. Huang, G.-L. Ma, G. Wang, Test the chiral magnetic effect with isobaric collisions. Phys. Rev. C 94, 041901 (2016)
H.-J. Xu, X. Wang, H. Li, J. Zhao, Z.-W. Lin, C. Shen, F. Wang, Importance of isobar density distributions on the chiral magnetic effect search. Phys. Rev. Lett. 121(2), 022301 (2018)
B. Zhang, C.M. Ko, B.-A. Li, Z.-W. Lin, A multiphase transport model for nuclear collisions at RHIC. Phys. Rev. C61, 067901 (2000)
K.A. Olive, Review of particle physics. Chin. Phys. C38, 090001 (2014)
Z.-W. Lin, Evolution of transverse flow and effective temperatures in the parton phase from a multi-phase transport model. Phys. Rev. C 90, 014904 (2014)
M. Gyulassy, X.-N. Wang. HIJING 1.0: A Monte Carlo program for parton and particle production in high-energy hadronic and nuclear collisions. Comput. Phys. Commun., 83, 307 (1994)
Z.-W. Lin, C.M. Ko, Partonic effects on the elliptic flow at RHIC. Phys. Rev., C65, 034904 (2002)
B. Zhang. ZPC 1.0.1: A Parton cascade for ultrarelativistic heavy ion collisions. Comput. Phys. Commun., 109, 193–206 (1998)
Z.-W. Lin, C.M. Ko, B.-A. Li, B. Zhang, S. Pal, A multi-phase transport model for relativistic heavy ion collisions. Phys. Rev., C72, 064901 (2005)
H. Li, L. He, Z.-W. Lin, D. Molnar, F. Wang, W. Xie, Origin of the mass splitting of elliptic anisotropy in a multiphase transport model. Phys. Rev. C 93, 051901 (2016)
H. Li, L. He, Z.-W. Lin, D. Molnar, F. Wang, W. Xie, Origin of the mass splitting of azimuthal anisotropies in a multiphase transport model. Phys. Rev. C 96(1), 014901 (2017)
G.-L. Ma, B. Zhang, Effects of final state interactions on charge separation in relativistic heavy ion collisions. Phys. Lett. B 700, 39–43 (2011)
B.I. Abelev et al., Systematic measurements of identified particle spectra in \(pp\), \(d+\text{ Au }\) and Au+Au collisions from STAR. Phys. Rev. C 79, 034909 (2009)
L. Adamczyk et al., Measurements of Dielectron Production in \(\text{ Au }+\text{ Au }\) Collisions at \(\sqrt{s_{\rm NN}} = 200~ \text{ GeV }\) from the STAR Experiment. Phys. Rev. C 92(2), 024912 (2015)
J. Adams et al., Rho0 production and possible modification in Au+Au and p+p collisions at S(NN)**1/2 = 200-GeV. Phys. Rev. Lett. 92, 092301 (2004)
S. Shi, Y. Jiang, E. Lilleskov, J. Liao, Anomalous chiral transport in heavy ion collisions from anomalous-viscous fluid dynamics. Ann. Phys. 394, 50–72 (2018)
H. Li, J. Zhao, F. Wang, A novel invariant mass method to isolate resonance backgrounds from the chiral magnetic effect. Nucl. Phys. A 982, 563–566 (2019)
J. Schukraft, A. Timmins, S.A. Voloshin, Ultra-relativistic nuclear collisions: event shape engineering. Phys. Lett. B 719, 394–398 (2013)
V. Koch, S. Schlichting, V. Skokov, P. Sorensen, J. Thomas, S. Voloshin, G. Wang, H.-U. Yee, Status of the chiral magnetic effect and collisions of isobars. Chin. Phys. C 41(7), 072001 (2017)
Acknowledgements
We thank Prof. Zi-Wei Lin for useful discussions. This work was supported in part by the National Natural Science Foundation of China Grant Nos. 11647306 and 11747312 and the U.S. Department of Energy Grant No. DE-SC0012910. HL acknowledges financial support from the China Scholarship Council.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Zhao, J., Li, H. & Wang, F. Isolating the chiral magnetic effect from backgrounds by pair invariant mass. Eur. Phys. J. C 79, 168 (2019). https://doi.org/10.1140/epjc/s10052-019-6671-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-019-6671-1