Abstract
The production of X(4350) in the \(\gamma \gamma \) interactions that occur in proton–proton, proton–nucleus and nucleus–nucleus collisions at the CERN Large Hadron Collider (LHC) is investigated and predictions for the kinematical ranges probed by the ALICE and LHCb Collaborations are presented. We focus on the \(\gamma \gamma \rightarrow \phi J/\Psi \) process, which have been measured by the Belle Collaboration, and present parameter free predictions for the total cross sections at the LHC energies. Our results demonstrate that the experimental study of this process is, in principle, feasible and can be used to confirm or not the existence of the X(4350) state. Finally, for completeness, we present predictions for the production of the X(3915) state in the \(\gamma \gamma \rightarrow \omega J/\Psi \) process and show that this exotic state can also be probed in \(\gamma \gamma \) interactions at the LHC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
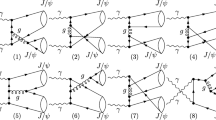
Over the last years the study of photon induced interactions at the LHC became a reality. The experimental results from the ALICE, ATLAS, CMS and LHCb Collaborations [1,2,3,4,5,6,7,8,9,10,11,12] are now being used to improve our understanding of the QCD dynamics as well to probe Beyond Standard Model Physics (For a recent review see Ref. [13]). The basic ideas present in the description of photon induced interactions are very simple: ultra-relativistic charged hadrons are an intense source of photons and in a collision at large impact parameters (\(b > R_{h_1} + R_{h_2}\), with \(R_i\) being the hadron radius), denoted hereafter ultra-peripheral collisions (UPCs), photon–photon and photon–hadron interactions become dominant over the strong hadron–hadron one. For photon–photon interactions, the total cross section for a given process can be factorized in terms of the equivalent flux of photons of the incident hadrons and the photon-photon production cross section [14,15,16,17]. The experimental separation for such events is relatively easy, as photon emission is coherent over the hadron and the photon is colorless we expect the events to be characterized by two intact recoiled hadrons (tagged hadrons) and the presence of two rapidity gaps. As pointed out in Refs. [18,19,20,21], photon-induced interactions can also be used to study the production and properties of exotic charmoniumlike states, which are a class of hadrons that decay to final states that contain a heavy quark and a heavy antiquark but cannot be easily accommodated in the remaining unfilled states in the \(c\bar{c}\) level scheme (For reviews see e.g. Refs. [22,23,24,25]). Our goal in this paper is to explore the possibility of producing the exotic X(4350) in two-photon interactions in UPCs with ultra-relativistic protons and nuclei. Such state have been observed by the Belle Collaboration [26] in the \(\gamma \gamma \rightarrow \phi J/\Psi \) process, but none of the \(\phi J/\Psi \) states observed by the LHCb Collaboration in the analysis of \(B^+\) decays is consistent with this state [27]. Therefore, the X(4350) awaits confirmation [25]. In what follows we use the values obtained by the Belle Collaboration for the product of the two-photon decay \(\Gamma _{X(4350) \rightarrow \gamma \gamma }\) and branching fraction \(\mathcal{{B}}(X(4350) \rightarrow \phi J/\Psi )\) to derive parameter free predictions for the X(4350) production in \(\gamma \gamma \) interactions at the LHC (Fig. 1). As we will show the resulting cross sections are large, which implies that a future experimental analysis is, in principle, feasible. Therefore, the study of this process can be used to confirm (or not) the existence and properties of this state. For completeness, we also demonstrate that a similar analysis can be performed for other exotic final states that have been observed in \(\gamma \gamma \) processes by the Belle and BaBar Collaborations. In particular, we also will present predictions for the production of the X(3915) state.
Initially, let’s present a brief review of the formalism need to describe the photon-induced interactions at hadronic colliders [14,15,16,17]. In the particular case of the X(4350) production in \(\gamma \gamma \) interactions at hadronic colliders, the cross section can be estimated using the equivalent photon approximation [14,15,16,17, 28]. In this approximation the cross section for the production of the exotic charmonium state, X(4350), in UPCs between two hadrons, \(h_{1}\) and \(h_{2}\), is given by (See e.g. [14,15,16,17])
where \(\sqrt{s}\) is center-of-mass energy for the \(h_1 h_2\) collision (\(h_i\) = p,A), \(\otimes \) characterizes a rapidity gap in the final state and \(W = \sqrt{4 \omega _1 \omega _2}\) is the invariant mass of the \(\gamma \gamma \) system. Moreover, \(N(\omega _i,b_i)\) is the equivalent photon spectrum generated by hadron (nucleus) i, which can be expressed as follows
where \(\omega _{i}\) is the energy of the photon emitted by the hadron (nucleus) \(h_{i}\) at an impact parameter, or distance, \(b_{i}\) from \(h_i\). Moreover, \(\gamma _L\) is the Lorentz factor and F is the nuclear form factor of the equivalent photon source. The factor \(S^2_{abs}({{\mathbf {b}}})\) is the absorption factor, given in what follows by [29]
where \(R_{h_i}\) is the radius of the hadron \(h_i\) (\(i = 1,2\)). In what follows we assume \(R_p = 0.7\) fm and \(R_{A} = 1.2 \, A^{1/3}\) fm. The presence of this factor in Eq. (1) excludes the overlap between the colliding hadrons and allows to take into account only ultraperipheral collisions. Finally, \( {\hat{\sigma }}_{\gamma \gamma \rightarrow X(4350)}(\omega _{1},\omega _{2})\) is the cross section for the production of a state X(4350) from two real photons with energies \(\omega _1\) and \(\omega _2\). Using the Low formula [30], the cross section for the production of the X(4350) state due to the two-photon fusion can be written in terms of the two-photon decay width \(\Gamma _{X(4350) \rightarrow \gamma \gamma }\) as follows
where \(M_{X}\) and J are, respectively, the mass and spin of the produced state. Using that the photon energies \(\omega _1\) and \(\omega _2\) are related to W and the rapidity Y of the outgoing resonance X(4350) by \( \omega _1 = \frac{W}{2} e^Y\) and \(\omega _2 = \frac{W}{2} e^{-Y}\) the total cross section can be expressed by (For details see e.g. Ref. [31])
Such expression allows to easily estimate the rapidity distribution as well as to calculate the cross sections for the restricted range of rapidities considered by the ALICE and LHCb Collaborations. In what follows the cross sections will be estimated assuming that the nucleus can be described by a monopole form factor given by [31]:
with \(\Lambda = 0.088\) GeV. On the other hand, for proton projectiles, the form factor will be assumed to be [32, 33]
A detailed discussion about the theoretical uncertainty associated to the model used for F is presented in Ref. [21].
One have that the cross section is directly dependent of the values for the decay width \(\Gamma _{X(4350) \rightarrow \gamma \gamma }\), mass and spin of the resonance. Such quantities can be taken from experiment or can be theoretically estimated (see Refs. [18, 19, 21]). In our analysis we will focus on the case in that the resonance decays into a \(\phi J/\Psi \) final state. As a consequence, the cross section will be proportional to \(\Gamma _{X(4350) \rightarrow \gamma \gamma } \times \mathcal{{B}}(X(4350) \rightarrow \phi J/\Psi )\), where \(\mathcal{{B}}(X(4350) \rightarrow \phi J/\Psi )\) is the branching fraction. Such product have been measured by the Belle Collaboration to be [26] \(\Gamma _{X(4350) \rightarrow \gamma \gamma } \times \mathcal{{B}}(X(4350) \rightarrow \phi J/\Psi ) = [6.7^{+3.2}_{-2.4} \, \text{(stat) } \pm 1.1 \, \text{(syst) }]\) eV for \(J^P = 0^+\), or \(\Gamma _{X(4350) \rightarrow \gamma \gamma } \times \mathcal{{B}}(X(4350) \rightarrow \phi J/\Psi ) = [1.5^{+0.7}_{-0.6} \, \text{(stat) } \pm 0.3 \, \text{(syst) }]\) eV for \(J^P = 2^+\). In what follows we will use these values as input in our calculations. Therefore, our predictions for LHC energies will be parameter free. A future experimental analysis of this process can be used to confirm (or not) the existence and properties of the X(4350) state observed by the Belle Collaboration.
In Table 1 we present our predictions for the total cross sections for the \(X(4350) \rightarrow \phi J/\Psi \) production in pp / pPb / PbPb collisions at the LHC energies considering the full LHC rapidity range as well as the rapidity ranges covered by the ALICE and LHCb detector. We consider the two possible values for \(J^P\). The lower (upper) limit of our predictions are calculated using the minimum (maximum) values for \(\Gamma _{X(4350) \rightarrow \gamma \gamma } \times \mathcal{{B}}(X(4350) \rightarrow \phi J/\Psi )\) obtained from the Belle data [26] by taking the central value and subtracting (adding) the total uncertainty, calculated in quadrature from the statistical and systematical uncertainties. Due to the \(Z^2\) dependence of the photon spectra, we have that the following hierarchy is approximately valid for the X(4350) production induced by \(\gamma \gamma \) interactions: \(\sigma _{PbPb} = Z^2 \cdot \sigma _{pPb} = Z^4 \cdot \sigma _{pp}\), with \(Z = 82\). In Fig. 2 the corresponding rapidity distributions for the \(X(4350)\,[2^{++}] \rightarrow \phi J/\psi \) production are presented. In the case of the \(X(4350)\,[0^{++}]\) resonance, the distributions are similar but with a smaller normalization. Due to the asymmetry in the proton and nuclear photon fluxes present in the initial state, we predict an asymmetric rapidity distribution in the case of pPb collisions. In Fig. 2 we also indicate the kinematical rapidity ranges probed by the ALICE (\(-1 \le Y \le +1\)) and LHCb (\(+2 \le Y \le +4.5\)) Collaborations. The resulting predictions for the total cross sections in the ALICE and LHCb rapidity ranges are also presented in Table 1. In comparison with the results for the full LHC rapidity range, one have that the predictions are reduced by a factor between 2.7 and 6.0 depending on the initial state and the rapidity range covered by the detector, with the larger reduction being for PbPb collisions at the LHCb. Although this reduction is nonnegligible, the final values are still large and imply a significant number of events if we consider that the expected integrated luminosity for the high luminosity run of the LHC is 50/fb (10/nb) for pp (PbPb) collisions. In particular, we predict that the number of events per year in pp (PbPb) collisions will be larger than 1850 (2300) at LHCb and 1970 (5200) at ALICE.
The analysis performed above can be directly extended for other exotic meson candidates. In particular, we can also provide predictions for the X(3915) production. A candidate for such state was observed in \(\gamma \gamma \) collisions by the Belle [34] and BaBar [35] Collaborations in the \(\gamma \gamma \rightarrow \omega J/\Psi \) process. Belle Collaboration obtained that [34] \(\Gamma _{X(3915) \rightarrow \gamma \gamma } \times \mathcal{{B}}(X(3915) \rightarrow \omega J/\Psi ) = [61 {\pm 17} \, \text{(stat) } \pm 8 \, \text{(syst) }]\) eV for \(J^P = 0^+\), or \(\Gamma _{X(3915) \rightarrow \gamma \gamma } \times \mathcal{{B}}(X(3915) \rightarrow \omega J/\Psi ) = [18 {\pm 5} \, \text{(stat) } \pm 2 \, \text{(syst) }]\) eV for \(J^P = 2^+\). Using these values as input in our calculations we can estimate the total cross sections for \(X(3915)[J^P] \rightarrow \omega J/\psi \) production in pp / pPb / PbPb collisions at the LHC energies. The predictions are presented in Table 2. In comparison to the results for the X(4350), the cross sections for the \(X(3915)[J^P] \rightarrow \omega J/\psi \) production are one order of magnitude larger.
Two important comments are in order here. First, the analysis of the final states considered in this paper can be limited by the need of a precise reconstruction of the meson masses, which is currently limited at the LHC. Second, the \(J/\Psi \) meson is usually observed through its decays into dileptons, with a branching fraction of the order of \(10 \%\). However, such decay mode is very small for the \(\phi \) and \( \omega \) mesons. Consequently, the study of the \(\phi J/\Psi \) and \(\omega J/\Psi \) only will be feasible if the hadronic decay modes, as e.g. \(\phi \rightarrow K^+ K^-\) and \(\omega \rightarrow \pi ^+ \pi ^- \pi ^0\), were effectively reconstructed. If these shortcomings are surpassed, our results indicate that the analysis of the X(4350) and X(3915) exotic mesons will be, in principle, feasible at the LHC considering the photon induced interactions that occur in hadronic collisions at large impact parameter.
Finally, let’s summarize our main results and conclusions. Over the last years the existence of exotic hadrons has been established and a large number of candidate have been proposed. In particular, the exotic X(4350) and X(3915) mesons have been observed in \(\gamma \gamma \) processes by the Belle Collaboration considering the production of the \(\phi J/\Psi \) and \(\omega J/\Psi \) final states, respectively. However, such states have not be observed at the LHC in the analysis of \(B^+\) decays. Consequently, these states still awaits confirmation. In this study we have proposed the search of these resonances in the \(\gamma \gamma \) interactions present in pp / pPb / PbPb collisions at the LHC. This is a clean process where the particles of the initial state are intact at the final state and can be detected at the forward direction as featured by the presence of two rapidity gaps between the projectiles and the produced resonance, which is assumed to decay in a pair of vector mesons. Our results indicate that the experimental analysis of this process is, in principle, feasible at the LHC and that its study is ideal to confirm (or not) the existence and properties from these resonances.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: All associated data have been presented in the paper.]
References
B. Abelev et al., [ALICE Collaboration]. Phys. Lett. B 718, 1273 (2013)
E. Abbas et al., [ALICE Collaboration]. Eur. Phys. J. C 73, 2617 (2013)
R. Aaij et al., [LHCb Collaboration]. J. Phys. G 40, 045001 (2013)
R. Aaij et al., [LHCb Collaboration]. J. Phys. G 41, 055002 (2014)
R. Aaij et al., [LHCb Collaboration]. JHEP 1509, 084 (2015)
S. Chatrchyan et al., [CMS Collaboration]. JHEP 01, 052 (2012)
S. Chatrchyan et al., [CMS Collaboration]. JHEP 11, 080 (2012)
S. Chatrchyan et al., [CMS Collaboration]. JHEP 07, 116 (2013)
G. Aad et al., [ATLAS Collaboration]. Phys. Lett. B 749, 242 (2015)
V. Khachatryan et al., [CMS Collaboration]. JHEP 1608, 119 (2016)
M. Aaboud et al., [ATLAS Collaboration], Phys. Rev. D 94, no. 3, 032011 (2016)
M. Aaboud et al., [ATLAS Collaboration]. Phys. Lett. B 777, 303 (2018)
K. Akiba et al., LHC Forward Physics Working Group Collaboration. J. Phys. G 43, 110201 (2016)
G. Baur, K. Hencken, D. Trautmann, S. Sadovsky, Y. Kharlov, Phys. Rep. 364, 359 (2002)
V.P. Goncalves, M.V.T. Machado, Mod. Phys. Lett. A 19, 2525 (2004)
C.A. Bertulani, S.R. Klein, J. Nystrand, Ann. Rev. Nucl. Part. Sci. 55, 271 (2005)
K. Hencken et al., Phys. Rept. 458, 1 (2008)
C.A. Bertulani, Phys. Rev. C 79, 047901 (2009)
V.P. Goncalves, D.T. Da Silva, W.K. Sauter, Phys. Rev. C 87, 028201 (2013)
V.P. Goncalves, M.L.L. da Silva, Phys. Rev. D 89, 114005 (2014)
B.D. Moreira, C.A. Bertulani, V.P. Goncalves, F.S. Navarra, Phys. Rev. D 94(9), 094024 (2016)
N. Brambilla, S. Eidelman, B.K. Heltsley, R. Vogt, G.T. Bodwin, E. Eichten, A.D. Frawley, A.B. Meyer et al., Eur. Phys. J. C 71, 1534 (2011)
M. Nielsen, F.S. Navarra, S.H. Lee, Phys. Rep. 497, 41 (2010)
M. Nielsen, F.S. Navarra, Mod. Phys. Lett. A 29, 1430005 (2014)
M. Karliner, J.L. Rosner, T. Skwarnicki, Ann. Rev. Nucl. Part. Sci. 68, 17 (2018)
C.P. Shen et al., [Belle Collaboration]. Phys. Rev. Lett. 104, 112004 (2010)
R. Aaij et al. [LHCb Collaboration], Phys. Rev. Lett. 118, no. 2, 022003 (2017)
V.M. Budnev, I.F. Ginzburg, G.V. Meledin, V.G. Serbo, Phys. Rept. 15, 181 (1975)
G. Baur, L.G. Ferreira Filho, Nucl. Phys. A 518, 786 (1990)
F.E. Low, Phys. Rev. 120, 582 (1960)
M. Klusek-Gawenda, A. Szczurek, Phys. Rev. C 82, 014904 (2010)
V.P. Goncalves, B.D. Moreira, F.S. Navarra, Eur. Phys. J. C 76, 103 (2016)
V.P. Goncalves, B.D. Moreira, F.S. Navarra, Eur. Phys. J. C 76, 388 (2016)
S. Uehara et al., Belle Collaboration. Phys. Rev. Lett. 104, 092001 (2010)
J.P. Lees et al., BaBar Collaboration. Phys. Rev. D 86, 072002 (2012)
Acknowledgements
One of the authors (VPG) is partially supported by the Brazil - U.S. Professorship given jointly by the Sociedade Brasileira de Física (SBF) and the American Physical Society (APS). This work was partially financed by the Brazilian funding agencies CNPq, CAPES, FAPERGS and INCT-FNA (process number 464898/2014-5).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Gonçalves, V.P., Moreira, B.D. Probing the X(4350) in \(\gamma \gamma \) interactions at the LHC. Eur. Phys. J. C 79, 7 (2019). https://doi.org/10.1140/epjc/s10052-018-6517-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6517-2