Abstract
An appealing candidate of the galactic dark matter is the axion, which was postulated to solve the strong CP (Charge-conjugation Parity) violation problem in the standard particle theory. A new experimental method is proposed to determine the axion mass. The method uses collectively and coherently excited atoms or molecules, the trigger laser inducing galactic axion absorption along with signal photon emission to be detected.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The galactic dark matter problem may be solved by the QCD (Quantum Chromo-Dynamics) axion [1,2,3,4,5,6,7], which provides simultaneously a solution to the conundrum of the strong CP problem [8,9,10,11] in the standard particle theory. The necessary galactic dark matter mass density is \(\rho _G \simeq (0.3\hbox {--}0.45) \,\)GeV/c\(^2\) cm\(^{-3}\) which implies by far the largest ambient number density \(n_a \sim 10^{13}\) cm\(^{-3}\) (its precise value depending on the Peceei-Quinn (PQ) symmetry breaking scale \(f_a\)). The current parameter region explored in major experiments is in the range, \(f_a = 10^8 -10^{13}\)GeV, the corresponding axion mass in the range, \(m_a = 10^{2}-10^{-3}\) meV (inversely proportional to \(f_a\)).
The cosmological origin of the galactic axion is traced back to the QCD epoch of cosmic temperature \(100 \,\mathrm{MeV}/k_B\) \(\sim 10^{12} \mathrm{K }\), since the axion mass is generated by the QCD chiral symmetry breaking. Its couplings to ordinary quarks, leptons, and gauge bosons are all suppressed by the PQ symmetry breaking scale \(\propto 1/f_a\), hence axions are born in cold, namely their initial velocities at creation are much less than the velocity of light. Cold axions decouple from radiation and matter throughout the later epoch of cosmological evolution [5,6,7]. After the radiation energy density drops below the axion matter density, gravitational self-interaction begins to dominate and axions become virialized (process of violent relaxation [12]), leaving a velocity dispersion of order \(10^{-3} \times \) the light velocity.
The PQ-symmetry breaking scale may be raised if it is higher than the reheat temperature due to inflation [13]. This widens the parameter space to be explored up to \(f_a \sim 10^{16}\) GeV.
Ongoing and proposed experiments [14,15,16,17], of galactic axion search sensitive to low mass axions use magnetic axion conversion into microwave in cavity [18, 19]. In this paper we propose an entirely new experimental method of axion detection using atoms or molecules, which is sensitive to the axion mass. It provides a powerful tool to directly link physics beyond the standard theory and the dark matter cosmology/astrophysics.
We use the natural unit of \(\hbar = c = 1\) unless otherwise stated.
2 Microscopic process of galactic axion detection
Our method proposed here uses atomic or molecular process, \(a_G +\gamma _t + | i\rangle \rightarrow | f \rangle + \gamma _s\): a galactic axion (\(a_G\)) collides against an atom or a molecule in an excited state \(|i \rangle \), which then de-excites to a lower energy state \(| f \rangle \), emitting a signal photon \( \gamma _s\) under the trigger photon \(\gamma _t\). The process is called TRiggered Absorption of Cosmic Axion (TRACA for short). Relevant diagrams are depicted in Fig. 1.
The virtual photon of four momentum k may be off or on the mass shell, depending on its invariant mass squared \(k^2= k_0^2 - \mathbf {k}^2 \ne 0\) or 0. The two cases have different experimental merits. In the on-shell case one may view TRACA occurring in two steps of real processes: the triggered decay axion produces a real photon, which is inelastically scattered off excited atom/molecule to generate a signal photon \(\gamma _s\). The on-shell TRACA may occur in the trigger photon frequency \(\omega _t\) at \( m_a/2\), hence in the rf (radio frequency) or microwave region, while the trigger frequency of the off-shell TRACA may be in the optical to the infrared (IR) range depending on the level spacing \(\epsilon _{if}\).
We also considered TRACA arising from diagrams containing direct electron coupling with the axion (both trigger laser and axion are connected to atomic line directly). In most axion parameter region we found that rates of axion emission are smaller than those of Fig. 1 even for DFSZ model [3, 4] of large axion-electron coupling.
The method can be applied to axion-like particles [20] as well.
In laboratory experiments on Earth, axions collide with its momentum around \(m_a \mathbf {\beta }_a = -\,m_a \mathbf {\beta }_e\), where \(\mathbf {\beta }_a (\mathbf {\beta }_e)\) is the velocity of axion (Earth). The axion momentum distribution function \(F_a(\mathbf {q})\) is assumed to have a momentum dispersion \(\displaystyle m_a \beta _0 \simeq 8 \,\mathrm{neV} (\frac{m_a}{10 \mu \mathrm{eV}})\), allowing for a possible BEC component [21], this component being separately detectable. The uniform \(-\,\mathbf {\beta }_e\) wind is superimposed by diurnal and sidereal modulation, which can be detected, too. One of our ultimate objectives of the proposed experiment is to determine these important parameters of cosmology.
To maximize TRACA rates, we fully utilize effects of large axion occupation and coherence (denoted by \(\rho _{if}\)) between the initial and final states: the total TRACA rate for entire atoms is proportional to the product of three factors, (1) axion number density \(n_a\), giving the enhancement \(\displaystyle 3 \times 10^{13} (\frac{m_a}{10 \mu \mathrm{eV}})\), (2) field power \(|E_t|^2 = \omega _t n_t\) (its photon number density denoted by \(n_t\)) driving the axion decay, (3) macro-coherently prepared atomic or molecular target number squared \( N_T^2\rho _{if}^2/V\) with \(N_T\) the total number of excited atoms within a volume V. The principle of amplification by macro-coherence [22, 23] related to the second and the third issues has been experimentally demonstrated in [24,25,26] for a weak QED (Quantum ElectroDynamics) process of two-photon emission in para-hydrogen (p-H\(_2\)) vibrational transition (the quantum number change of \(v=1 \rightarrow 0\)). The process was amplified by a factor \(\sim 10^{18}\) in rate, with a realization of atomic coherence \(\rho _{if} \sim 0.03\) [26]. The degree of achievable coherence was limited by various de-coherence effects including Doppler and pressure broadenings as well as laser line width. The process was termed PSR (Paired Super-Radiance) in an obvious analogy to Dicke’s super-radiance [27,28,29,30].
TRACA diagram of axion detection. Virtual or real photon emitted by the axion \(a_G\) decay due to trigger \(\gamma _t\) induces inelastic photon or Raman scattering producing a signal photon \(\gamma _s\). Diagram of exchanged atomic/molecular vertexes (s-channel \(|n\rangle \) here being replaced by u-channel \(|n\rangle \) not depicted here) adds coherently to this contribution. This diagram is further doubled by \( \gamma _t \leftrightarrow \gamma _s\) exchange. The quantities in \((\cdot \cdot )\) denote the 4-vector symbols used in the text
3 Derivation of rate formula
We shall first treat the off mass shell case and later discuss briefly the on mass shell case. Suppose that the intermediate atomic state \(|n \rangle \) related by electric dipole transitions to \(|i \rangle \) and \(|f \rangle \) is far away in energy from these states; both of \(\epsilon _{ni}\,, \epsilon _{nf} \gg \epsilon _{if}\). This holds for the example of p-H\(_2\). We further assume the frequency relation, both of \( \omega _t, \omega _s\)(trigger and signal frequencies) \( \gg m_a\) for the off-shell TRACA.
The axion–photon–photon vertex in Fig. 1 has a form \(g_{a\gamma \gamma } a\mathbf {E}\cdot \mathbf {B}\) in terms of electric \(\mathbf {E}\) and magnetic \(\mathbf {B}\) field operators, since the axion field a is a pseudo-scalar. Its coupling constant is suppressed by \(g_{a\gamma \gamma } \simeq \alpha /(\pi f_a) \,, \alpha = 1/137\). The dominant atomic couping along the electron line is of the usual electric dipole form \(\mathbf {d}\cdot \mathbf {E}'\), giving rise to an effective, external field coupling of the form, \(\mathbf {B}_t \cdot \langle 0 | T(\mathbf {E}' \mathbf {E}) | 0\rangle \cdot \mathbf {d}\) with propagation taken into account (\(\mathbf {B}_t:\) the trigger photon magnetic field). The central part of the probability amplitude is thus
Here \(\mathbf {d}_{nf}, \mathbf {d}_{ni}\) are dipole operators and their product divided by the energy denominator is related to if off-diagonal polarizabiity when summed over states \(| n \rangle \). The propagator factor is approximately \((k_t - q)_0^2/(k_t- q)^2 \sim - \omega _t/(2 m_a) \) with q the 4-vector of axion. Model dependent coefficient \( c_{a\gamma \gamma }\) [31,32,33] is typically \(- 0.97\) for KSVZ-model [1, 2], and 0.36 for DFSZ-model [3, 4].
For simplicity we take the atomic transition of no spin parity change, \(0^+ \rightarrow 0^+\). Excluding the squared probability amplitude given above, the rate contains a product of coherence and position-dependent phase factor of the target system integrated over a target volume V prior to taking the square,
with \( \mathbf {Q} = \mathbf {k}_t + \mathbf {k}_s - \mathbf {p}_{if} \) and \(\mathbf {p}_{if}\) the phase imprinted at the excitation to \(|i \rangle \)[34]. The coherence \(\rho _{if}\) and the excited target number density \(n_T =N_T/V\) may in principle be a function of target atom positions, but we take its averaged constant values within the entire target. We perform the axion momentum integration first, and use the fact that \(\displaystyle q_0 = m_a \beta _0 = 10 \,\mathrm{neV} (\frac{m_a}{ 10 \mu \mathrm{eV}})\) much smaller than the inverse of linear size of target volume. The infinite target volume limit then gives Eq. (1) \(\sim \rho _{if}^2 n_T N_T (2\pi )^3 \delta (\mathbf {k}_t + \mathbf {k}_s - \mathbf {p}_{if} - \mathbf {q}_e )\,, \mathbf {q}_e = - m_a \mathbf {\beta }_e\), which cannot be used however due to the following reason.
Due to kinematic reasons one needs to calculate TRACA rates in a finite target volume, for which we take a cylinder of radius R and length L along excitation lasers. This gives the geometric factor defined in Eq. (1),
with \(J_1(x)\) the Bessel function of the first order. In our parameter range the dimensionless \(\mathcal{A}\) is of order \(10^{-7}\) when we integrate over all solid angles.
The differential off-shell TRACA rate is thus calculated as
\(\mu _{if}\) the atomic or molecular polarizability. The relation \(E_t^2 = \omega _t n_t\) of the trigger field power to the photon number density \(n_t\) and various level spacings, \(\epsilon _{ab} = \epsilon _a - \epsilon _b\) were used. We assumed that only one dominant upper level \(|n \rangle \) contributes, but extension to include many contributing levels is straightforward.
A striking feature of the off-shell TRACA formula (3) is the dependence \(\sin ^2 \theta _{\mathrm{pol}}\) with the relative angle \(\theta _{\mathrm{pol}}\) between polarizations of two photons, \(\gamma _t\) and \(\gamma _s\). The rate is maximal at the perpendicular \(\theta _{\mathrm{pol}} =\pi /2\) and vanishes at the parallel configuration.
We shall make an order of magnitude estimate of on-shell rate. The easiest way of calculating the on-shell amplitude is to replace the real propagator of virtual photon by the imaginary part in the zero-width approximation, to give
for \( (k_t- q)_0^2/ (k_t- q)^2 + (t \rightarrow s )\). In practice, the squared delta-function in the rate of on-shell amplitude should be convoluted with the trigger frequency distribution of a finite width \(\Delta \). Moreover, \((2\pi )^2 \times \) the squared delta-function is replaced by \(2\pi T \times \) the delta-function where T is the time of trigger irradiation. This time T is equal to the target length/2. The procedure ends up in replacing the previous \(- \epsilon _{if}/( 2m_a)\) by \( i \frac{\pi }{ 4} m_a \sqrt{L/\Delta } \). The on-shell contribution thus dominates over the off-shell contribution for the axion mass above a threshold; \(m_a > O( \sqrt{ \epsilon _{if}\sqrt{\Delta /L}})\) if \(\omega _t \simeq m_a/2\) or \(\omega _s \simeq m_a/2\). The axion mass dependence \(\propto m_a^2\) in the on-shell formula thus derived differs from the off-shell rate \(\propto 1/m_a^2\).
4 TRACA rates for p-H\(_2\) vibrational transition
A typical experimental scheme we consider uses two excitation lasers and a trigger field, all of which may be irradiated near the same axis direction. The target is of a cylindrical shape whose length and volume are denoted by L, V.
Consider para-hydrogen molecule as a high density target, its gas density at the liquid nitrogen temperature 77 K being \(\sim 5 \times 10^{19}\) cm\(^{-3}\). Solid p-H\(_2\) target is also promising from a number of reasons [25]; (1) a larger molecule density like \(2.6 \times 10^{22}\) cm\(^{-3}\), (2) expected small relaxation caused by phonon emission. Relevant phonon emission involves the axion-proton coupling predominantly of the spin operator. The spatial extension of axion wave function is of order 1 cm for 10 \(\mu \)eV mass, hence the axion field feels a collective body of para-hydrogen molecule. Since the molecule has a total nuclear spin 0, this coupling, hence the phonon relaxation, is highly suppressed. The vibrational transition of electronically ground state, \(v=1 \rightarrow 0\) of level spacing 0.52 eV, may be used. The electronically excited level (1s)(2p) is far away from the ground vibrational levels, separated by \(\sim 10\,\) eV.
To calculate the signal rate for molecules, we need to take into account vibrational modes associated with electronically excited states such as (1s)(2p). The effect of Franck–Condon factor related to the molecular potential curve of this first electronically excited state may be automatically avoided by using p-H\(_2\) off-diagonal polarizability \(\mu _{if} \sim 1.43 \times 10^{-24}\)cm\(^3\) [35].
The off-shell TRACA rate for solid p-H\(_2\) is numerically
The on-shell TRACA rate is obtained by multiplying \(\displaystyle \sim 2 \times 10^{-8} (\frac{m_a}{10 \mu \mathrm{eV}})^4 (\frac{L}{\mathrm{cm}})^2 (\frac{100 \mathrm{MHz}}{\Delta })^2\) to the off-shell rate.
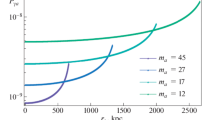
We illustrate total rates of the off-shell and the on-shell TRACA contributions in Fig. 2. There are higher sensitivities for smaller axion masses less than 100 \(\mu \)eV.
TRACA rate for p-H\(_2\). Assumed parameters are the target number density \(n_T=2.6 \times 10^{22}\, \mathrm{cm}^{-3}\), the target volume \(V=1\) cm\(^3\), the target length \(L=10\) cm, the coherence \(\rho _{if}=0.1\), \(\omega _t =\) 0.124 eV trigger for the off-shell case and \(\omega _t = m_a/2, \Delta = 300\) MHz for the on-shell case and of a common photon number density \(n_t=10^{18}\, \mathrm{cm}^{-3}\) and a common \(\mathcal{A} = 1\). Experimental parameters such as detection efficiency or duty factor (if a pulsed laser is used) are not included. We used \(c_{a\gamma \gamma }\) values for the KSVZ and DFSZ models, and the perpendicular polarization of the trigger and the signal was taken, using the formula (5)
5 Raman excitation and trigger
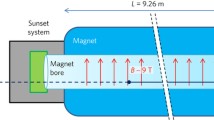
We consider Raman-type of excitation from the ground \(v=0\) to \(v=1\) state, with frequencies, \(\omega _1 > \omega _2\,, \omega _1 - \omega _2 = 0.52\)eV. In the on-shell process the trigger frequency must coincide with the axion mass in search (in the rf or microwave frequency range with photon density of \(n_t=10^{18}\) cm\(^{-3}\)), and the momentum conservation dictates the signal photon emission very near the excitation axis. On the other hand, in the off-shell case it can be in a near infra-red range. For example, using CO\(_2\) laser of \(\omega _t = 0.124\)eV for the trigger, one can relate the angles of trigger irradiation and signal emission as functions of the axion mass: \(\displaystyle \theta _t = 11 \,\mathrm{mrad}\sqrt{\frac{m_a}{10 \mu \mathrm{eV}}}\) and \(\displaystyle \theta _s = - 3.5 \,\mathrm{mrad}\sqrt{\frac{m_a}{10 \mu \mathrm{eV}}}\) (formulas valid for small axion mass less than of order 1 meV) away from both the trigger and the excitation lasers.
The off-axis configuration and its kinematic constraint is illustrated in Fig. 3. This much of the off-axis configuration may be crucial in rejecting various QED backgrounds (see below on more of this).
Kinematic configuration of initial Raman excitation in the left, the final decay processes in the right. Both energy and momentum conservations are satisfied for PSR only when the trigger (\(\omega _t^{\prime }\)) is injected colinearly with the excitation lasers, while they are satisfied for TRACA when the trigger (\(\omega _t\)) is injected with angle due to the axion absorption. These different configurations help separate two processes
6 Backgrounds
By far the largest background may arise from (macro-coherently amplified) PSR process. The ratio of the signal (off-shell part) to this PSR rate is found to be \(\displaystyle \sim 10^{-27} \left( \frac{10 \mu \mathrm{eV}}{m_a} \right) ^2 \frac{\mathcal{A}(m_a)}{\mathcal{A}(m_a=0)} \frac{\cos ^2 \theta _{pol}}{\sin ^2 \theta _{pol}}\), taking the same set of target and trigger parameters as indicated in Fig(2). The last factor comes from the fact that polarization vectors of \(\gamma _t\) and \(\gamma _s\) must be parallel in the case of the PSR process. The geometric factor \(\mathcal{A}\) would suppress the background (since \(\mathcal{A}(m_a)\gg \mathcal{A}(m_a=0)\)), but not entirely due to diffuseness of the finite-size volume effects. Reduction of the background is also possible by choosing \(\theta _{pol}\simeq \pi /2\), but not enough with current technologies. It is crucial to devise a clever method of PSR background rejection for a realistic experimental proposal.
7 Summary
In summary, we proposed a novel experimental method of axion detection using macro-coherently excited atoms or molecules which can be implemented in small scale laboratories. The method may clarify how the galactic axion dark matter is distributed and serve to determine the fundamental symmetry breaking scale beyond the standard particle theory.
References
J.E. Kim, Phys. Rev. Lett. 43, 103 (1979)
M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Nucl. Phys. B 166, 493 (1980)
M. Dine, W. Fischler, M. Srednicki, Phys. Lett. B 104, 199 (1981)
A.R. Zhitnitsky, Sov. J. Nucl. Phys. 31, 260 (1980)
J. Preskill, M.B. Wise, F. Wilczek, Phys. Lett. 120B, 127 (1983)
L. Abbott, P. Sikivie, Phys. Lett. 120B, 133 (1983)
M. Dine, W. Fischler, Phys. Lett. 120B, 137 (1983)
R.D. Peccei, H.R. Quinn, Phys. Rev. Lett. 38, 1440 (1977)
R.D. Peccei, H.R. Quinn, Phys. Rev. D 16, 1791 (1977)
S. Weinberg, Phys. Rev. Lett. 40, 223 (1978)
F. Wilczek, Phys. Rev. Lett. 40, 279 (1978)
D. Lynden-Bell, Mon. Not. R. Astro. Soc. 136, 101 (1967)
M.P. Hertzberg, M. Tegmark, F. Wilczek, Phys. Rev. D 78, 083507 (2008). and references therein
S. Asztalos et al., Phys. Rev. Lett. 104, 041301 (2010)
N. Du et al., Phys. Rev. Lett. 120, 151301 (2018)
J. Choi et al. arXiv:1704.07957v2 [hep-ex] (2017)
R. Bradley et al., Rev. Mod. Phys. 75, 777 (2003). and references therein
P. Sikivie, Phys. Rev. Lett. 51, 1415 (1983)
P. Sikivie, Phys. Rev. D 32, 2988 (1985)
J. Jaeckel, A. Ringwald, Annu. Rev. Nucl. Part. Sci. 60, 405 (2010)
P. Sikivie, Q. Yang, Phys. Rev. Lett. 103, 111301 (2009)
M. Yoshimura, N. Sasao, M. Tanaka, Phys. Rev. A 86, 013812 (2012)
A. Fukumi et al., Prog. Theor. Exp. Phys. 2012, 04D002 (2012)
Y. Miyamoto, Externally triggered coherent two-photon emission from hydrogen molecules. Prog. Theor. Exp. Phys. 2015, 081C01 (2015)
Y. Miyamoto et al., Vibrational Two-Photon Emission from Coherently Excited Solid Parahydrogen. J. Phys. Chem. A 121, 3943 (2017)
Y. Miyamoto et al., Observation of coherent two-photon emission from the first vibrationally-excited state of hydrogen molecules. Prog. Theor. Exp. Phys. 2014, 113C01 (2014)
R.H. Dicke, Phys. Rev. 93, 99 (1954)
D. Polder, M.F.H. Schuurmans, Q.H.F. Vrehen, Phys. Rev. A 19, 1192 (1979)
F. Haake, H. King, G. Schroeder, J. Haus, R. Glauber, Phys. Rev. A 20, 2047 (1979)
M. Benedict, A.M. Ermolaev, V.A. Malyshev, I.V. Sokolov, E.D. Trifonov, Super-radiance: multiatomic coherent emission (Taylor and Francis, New York, 1996)
D. B. Kaplan, B260, 215 (1985)
M. Srednicki, Nucl. Phys. B 260, 689 (1985)
C. Patrignani et al., Particle Data Group. Chin. Phys. C 40, 100001 (2016)
M. Tanaka, K. Tsumura, N. Sasao, S. Uetake, M. Yoshimura, Phys. Rev. D 96, 113005 (2017)
W. Kolos, L. Wolmiewicz, J. Chem. Phys. 46, 1426 (1967)
Acknowledgements
We appreciate discussions with Y. Miyamoto, M. Tanaka, K. Tsumura, and S. Uetake. This work is supported in part by JSPS KAKENHI Grant numbers JP 15H02093, 15K13486 and 17H02895.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Sasao, N., Yoshimura, M. New method of galactic axion search. Eur. Phys. J. C 78, 949 (2018). https://doi.org/10.1140/epjc/s10052-018-6412-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6412-x