Operation and performance of the ATLAS Tile Calorimeter in Run 1

1.1 The ATLAS Tile Calorimeter structure and read-out electronics

The light generated in each plastic scintillator is collected at two edges, and then transported to photomultiplier tubes (PMTs) by wavelength shifting (WLS) fibres [5]. The read-out cell geometry is defined by grouping the fibres from individual tiles on the corresponding PMT. A typical cell is read out on each side (edge) by one PMT, each corresponding to one channel. The dimensions of the cells are \(\Delta \eta \times \Delta \phi = 0.1 \times 0.1\) in the first two radial layers, called layers A and BC (just layer B in the EB), and \(\Delta \eta \times \Delta \phi = 0.2 \times 0.1\) in the third layer, referred to as layer D. The projective layout of cells and naming convention are shown in Fig. 1. The so-called ITC cells (D4, C10 and E-cells) are located between the LB and EB, and provide coverage in the range \(0.8< |\eta | < 1.6\). Some of the C10 and D4 cells have reduced thickness or special geometry in order to accommodate services and read-out electronics for other ATLAS detector systems [3, 6]. The gap (E1–E2) and crack (E3–E4) cells are only composed of scintillator and are exceptionally read out by only one PMT. For Run 1, eight crack scintillators were removed per side, to allow for routing of fibres for 16 Minimum Bias Trigger Scintillators (MBTS), used to trigger on events from colliding particles, as well as to free up the necessary electronics channels for read-out of the MBTS. The MBTS scintillators are also read out by the TileCal EB electronics.

Open image in new window

The PMTs and front-end electronics are housed in a steel girder at the outer radius of each module in 1.4 m long aluminium units that can be fully extracted while leaving the remaining module in place, and hence are given the name of electronics drawers. Each drawer holds a maximum of 24 channels, two of which form a super-drawer. There are nominally 45 and 32 active channels per super-drawer in the LB and EB, respectively. Each channel consists of a unit called a PMT block, which contains the light-mixer, PMT tube and voltage divider, and a so-called 3-in-1 card [7, 8]. This card is responsible for fast signal shaping in two gains (with a bi-gain ratio of 1:64), the slow integration of the PMT signal, and provides an input for a charge injection calibration system.

The maximum height of the analogue pulse in a channel is proportional to the amount of energy deposited by the incident particle in the corresponding cell. The shaped signals are sampled and digitised every 25 ns by 10-bit ADCs [9]. The sampled data are temporarily stored in a pipeline memory until a trigger Level-1 signal is received. Seven samples, centred around the pulse peak, are obtained. A gain switch is used to determine which gain information is sent to the back-end electronics for event processing. By default the high-gain signal is used, unless any of the seven samples saturates the ADC, at which point the low-gain signal is transmitted.

Adder boards receive the analogue low-gain signal from the 3-in-1 cards and sum the signal from six 3-in-1 cards within \(\Delta \eta \times \Delta \phi = 0.1 \times 0.1\) before transmitting it to the ATLAS hardware-based trigger system as a trigger tower.

The integrator circuit measures PMT currents (0.01 nA to 1.4 \(\upmu \)A) over a long time window of 10–20 ms with one of the six available gains, and is used for calibration with a radioactive caesium source and to measure the rate of soft interactions during collisions at the LHC [10]. It is a low-pass DC amplifier that receives less than 1% of the PMT current, which is then digitised by a 12-bit ADC card (which saturates at 5 V) [11].

Power is supplied to the front-end electronics of a single super-drawer by means of a low-voltage power supply (LVPS) source, which is positioned in an external steel box mounted just outside the electronics super-drawer. The high voltage is set and distributed to each individual PMT using dedicated boards positioned inside the super-drawers located with the front-end electronics.

The back-end electronics is located in a counting room approximately 100 m away from the ATLAS detector. The data acquisition system of the Tile Calorimeter is split into four partitions, the ATLAS A-side (\(\eta > 0\)) and C-side (\(\eta < 0\)) for both the LB and EB, yielding four logical partitions: LBA, LBC, EBA, and EBC. Optical fibres transmit signals between each super-drawer and the back-end trigger, timing and control (TTC) and read-out driver (ROD [12]) crates. There are a total of four TTC and ROD crates, one for each physical partition. The ATLAS TTC system distributes the LHC clock, trigger decisions, and configuration commands to the front-end electronics. If the TTC system sends the trigger acceptance command to the front-end electronics, the corresponding digital signals for all channels of the calorimeter are sent to the ROD via optical links, where the signal is reconstructed for each channel.

2.1 ATLAS experimental data

The full ATLAS detector started recording events from cosmic-ray muons in 2008 as a part of the detector commissioning [6, 18]. Cosmic-ray muon data from 2008–2010 are used to validate test beam and in situ calibrations, and to study the full calorimeter in the ATLAS environment; these results are presented in Sect. 6.1.1.

ATLAS also recorded data during these years with lower-energy proton collisions (at \(\sqrt{s}\) = 900 GeV, 2.76 TeV), and data containing lead ion collisions. Nevertheless, this paper focuses on the results obtained in pp collisions at \(\sqrt{s} = 7\) and 8 TeV.

2.2 Monte Carlo simulations

Monte Carlo (MC) simulated data are frequently used by performance and physics groups to predict the behaviour of the detector. It is crucial that the MC simulation closely matches the actual data, so those relying on simulation for algorithm optimisations and/or searches for new physics are not misled in their studies.

The MC process is divided into four steps: event generation, simulation, digitisation, and reconstruction. Various event generators were used in the analyses as described in each subsection. The ATLAS MC simulation [19] relies on the Geant4 toolkit [20] to model the detector and interactions of particles with the detector material. During Run 1, ATLAS used the so-called QGSP_BERT physics model to describe the hadronic interactions with matter, where at high energies the hadron showers are modelled using the Gluon String Plasma model, and the Bertini intra-nuclear cascade model is used for lower-energy hadrons [21]. The input to the digitisation is a collection of hits in the active scintillator material, characterised by the energy, time, and position. The amount of energy deposited in scintillator is divided by the calorimeter sampling fraction to obtain the channel energy [22]. In the digitisation step, the channel energy in GeV is converted into its equivalent charge using the electromagnetic scale constant (Sect. 4) measured in the beam tests. The charge is subsequently translated into the signal amplitude in ADC counts using the corresponding calibration constant (Sect. 4.3). The amplitude is convolved with the pulse shape and digitised each 25 ns as in real data. The electronic noise is emulated and added to the digitised samples as described in Sect. 3.2. Pile-up (i.e. contributions from additional minimum-bias interactions occurring in the same bunch crossing as the hard-scattering collision or in nearby ones), are simulated with Pythia 6  [23] in 2010–2011 and Pythia 8  [24] in 2012, and mixed at realistic rates with the hard-scattering process of interest during the digitisation step. Finally, the same reconstruction methods, detailed in Sect. 3, as used for the data are applied to the digitised samples of the simulations.

3.1 Channel time calibration and corrections

Correct channel time is essential for energy reconstruction, object selection, and for time-of-flight analyses searching for hypothetical long-lived particles entering the calorimeter. Initial channel time calibrations are performed with laser and cosmic-ray muon events, and are later refined using beam-splash events from a single LHC beam [6]. A laser calibration system pulses laser light directly into each PMT. The system is used to calibrate the time of all channels in one super-drawer such that the laser signal is sampled simultaneously. These time calibrations are used to account for time delays due to the physical location of the electronics. Finally, the time calibration is set with collision data, considering in each event only channels that belong to a reconstructed jet. This approach mitigates the bias from pile-up noise (Sect. 3.3) and non-collision background. Since the reconstructed time slightly depends on the energy deposited by the jet in a cell (Fig. 5 left), the channel energy is further required to be in a certain range (2–4 GeV) for the time calibration. An example of the reconstructed time spectrum in a channel satisfying these conditions is shown in Fig. 5(right). The distribution shows a clear Gaussian core (the Gaussian mean determines the time calibration constant) with a small fraction of events at both high- and low-time tails. The higher-time tails are more evident for low-energy bins and are mostly due to the slow hadronic component of the shower development. Symmetric tails are due to out-of-time pile-up (see Sect. 3.3) and are not seen in 2010 data where pile-up is negligible. The overall time resolution is evaluated with jets and muons from collision data, and is described in Sect. 6.3.

Open image in new window

During Run 1 a problem was identified in which a digitiser could suddenly lose its time calibration settings. This problem, referred to as a “timing jump”, was later traced to the TTCRx chip in the digitiser board, which received clock configuration commands responsible for aligning that digitiser sampling clock with the LHC clock. During operation these settings are sent to all digitisers during configuration of the super-drawers, so a timing jump manifests itself at the beginning of a run or after a hardware failure requiring reconfiguration during a run. All attempts to avoid this feature at the hardware or configuration level failed, hence the detection and correction of faulty time settings became an important issue. Less than 15% of all digitisers were affected by these timing jumps, and were randomly distributed throughout the TileCal. All channels belonging to a given digitiser exhibit the same jump, and the magnitude of the shift for one digitiser is the same for every jump.

Laser and collision events are used to detect and correct for the timing jumps. Laser events are recorded in parallel to physics data in empty bunch crossings. The reconstructed laser times are studied for each channel as a function of luminosity block. As the reconstructed time phase is expected to be close to zero the monitoring algorithm searches for differences (\(> 3\) ns) from this baseline. Identified cases are classified as potential timing jumps, and are automatically reported to a team of experts for manual inspection. The timing differences are saved in the database and applied as a correction in the offline data reconstruction.

Reconstructed jets from collision data are used as a secondary tool to verify timing jumps, but require completion of the full data reconstruction chain and constitute a smaller sample as a function of luminosity block. These jets are used to verify any timing jumps detected by the laser analysis, or used by default in cases where the laser is not operational. For the latter, problematic channels are identified after the full reconstruction, but are corrected in data reprocessing campaigns.

A typical case of a timing jump is shown in Fig. 6 before (left) and after (right) the time correction. Before the correction the time step is clearly visible and demonstrates good agreement between the times measured by the laser and physics collision data.

Open image in new window

The overall impact of the timing jump corrections on the reconstructed time is studied with jets using 1.3 fb\(^{-1}\) of collision data taken in 2012. To reduce the impact of the time dependence on the reconstructed energy, the channel energy is required to be \(E > 4\) GeV, and read out in high-gain mode. The results are shown in Fig. 7, where the reconstructed time is shown for all calorimeter channels with and without the timing jump correction. While the Gaussian core, corresponding to channels not affected by timing jumps, remains basically unchanged, the timing jump correction significantly reduces the number of events in the tails. The 95% quantile range around the peak position shrinks by 12% (from 3.3 ns to 2.9 ns) and the overall RMS improves by 9% (from 0.90 ns to 0.82 ns) after the corrections are applied. In preparation for Run 2, problematic digitisers were replaced and repaired. The new power supplies, discussed in the next section, also contribute to the significant reduction in the number of the timing jumps since the trips almost ceased (Sect. 5.4) and thus the module reconfigurations during the run are eliminated in Run 2.

Open image in new window

3.2 Electronic noise

The total noise per cell is calculated taking into account two components, electronic noise and a contribution from pile-up interactions (so-called pile-up noise). These two contributions are added in quadrature to estimate the total noise. Since the cell noise is directly used as input to the topological clustering algorithm [28] (see Sect. 6), it is very important to estimate the noise level per cell with good precision.

The electronic noise in the TileCal, measured by fluctuations of the pedestal, is largely independent of external LHC beam conditions. Electronic noise is studied using large samples of high- and low-gain pedestal calibration data, which are taken in dedicated runs without beam in the ATLAS detector. Noise reconstruction of pedestal data mirrors that of the data-taking period, using the OF technique with iterations for 2010 data and the non-iterative version from 2011 onward.

The electronic noise per channel is calculated as a standard deviation (RMS) of the energy distributions in pedestal events. The fluctuation of the digital noise as a function of time is studied with the complete 2011 dataset. It fluctuates by an average of 1.2% for high gain and 1.8% for low gain across all channels, indicating stable electronic noise constants.

As already mentioned in Sect. 1.1, a typical cell is read out by two channels. Therefore, the cell noise constants are derived for the four combinations of the two possible gains from the two input channels (high–high, high–low, low–high, and low–low). Figure 8 shows the mean cell noise (RMS) for all cells as a function of \(\eta \) for the high–high gain combinations. The figure also shows the variations with cell type, reflecting the variation with the cell size. The average cell noise is approximately 23.5 MeV. However, cells located in the highest \(|\eta |\) ranges show noise values closer to 40 MeV. These cells are formed by channels physically located near the LVPS. The influence of the LVPS on the noise distribution is discussed below. A typical electronic noise values for other combinations of gains are 400–700 MeV for high–low/low–high gain combinations and 600–1200 MeV for low–low gain case. Cells using two channels with high gain are relevant when the deposited energy in the cell is below about 15 GeV, above that both channels are often in low-gain mode, and if they fall somewhere in the middle range of energies (10–20 GeV) one channel is usually in high gain and the other in low gain.

During Run 1 the electronic noise of a cell is best described by a double Gaussian function, with a narrow central single Gaussian core and a second central wider Gaussian function to describe the tails [6]. A normalised double Gaussian template with three parameters (\(\sigma _1\), \(\sigma _2\), and the relative normalisation of the two Gaussian functions R) is used to fit the energy distribution:

$$\begin{aligned} f_{\mathrm {pdf}} = \frac{1}{1+R} \left( \frac{1}{\sqrt{2\pi }\sigma _1} \mathrm {e}^{-\frac{x^2}{2\sigma _1^2}} + \frac{R}{\sqrt{2\pi }\sigma _2} \mathrm {e}^{-\frac{x^2}{2\sigma _2^2}}\right) \end{aligned}$$

The means of the two Gaussian functions are set to \(\mu _1 = \mu _2 = 0\), which is a good approximation for the cell noise. As input to the topological clustering algorithm an equivalent \(\sigma _{\mathrm {eq}}(E)\) is introduced to measure the significance (\(S = |E| /\sigma _{\mathrm {eq}}(E)\)) of the double Gaussian probability distribution function in units of standard deviations of a normal distribution.³

Open image in new window

The double Gaussian behaviour of the electronic noise is believed to originate from the LVPS used during Run 1, as the electronic noise in test beam data followed a single Gaussian distribution, and this configuration used temporary power supplies located far from the detector. During December 2010, five original LVPS sources were replaced by new versions of the LVPS. During operation in 2011 these LVPSs proved to be more reliable by suffering virtually no trips, and resulted in lower and more single-Gaussian-like behaviour of channel electronic noise. With this success, 40 more new LVPS sources (corresponding to 16% of all LVPSs) were installed during the 2011–2012 LHC winter shutdown. Figure 9 shows the ratio of the RMS to the width of a single Gaussian fit to the electronic noise distribution for all channels averaged over the 40 modules before and after the replacement of the LVPS. It can be seen that the new LVPS have values of RMS\(/\sigma \) closer to unity, implying a shape similar to a single Gaussian function, across all channels. The average cell noise in the high–high gain case decreases to 20.6 MeV with the new LVPS.

Open image in new window

The coherent component of the electronic noise was also investigated. A considerable level of correlation was only found among channels belonging to the same motherboard,⁴ for other pairs of channels the correlations are negligible. Methods to mitigate the coherent noise were developed;⁵ they reduce the correlations from (\(-\,40\%\), \(+\,70\%\)) to (\(-\,20\%\), \(+\,10\%\)) and also decrease the fraction of events in the tails of the double Gaussian noise distribution.

Electronic noise in the Monte Carlo simulations

The emulation of the electronic noise, specific to each individual calorimeter cell, is implemented in the digitisation of the Monte Carlo signals. It is assumed that it is possible to convert the measured cell noise to an ADC noise in the digitisation step, as the noise is added to the individual samples in the MC simulation. The correlations between the two channels in the cell are not considered. As a consequence, the constants of the double Gaussian function, used to generate the electronic noise in the MC simulation, are derived from the cell-level constants used in the real data. As a closure test, after reconstruction of the cell energies in the MC simulation the cell noise constants are calculated using the same procedure as for real data. The reconstructed cell noise in the MC reconstruction is found to be in agreement with the original cell noise used as input from the real data. Good agreement between data and MC simulation of the energy of the TileCal cells, also for the low and negative amplitudes, is found (see Fig. 10). The measurement is performed using 2010 data where the pile-up contribution is negligible. The noise contribution can be compared with data collected using a random trigger.

Open image in new window

3.3 Pile-up noise

The pile-up effects consist of two contributions, in-time pile-up and out-of-time pile-up. The in-time pile-up originates from multiple interactions in the same bunch crossing. In contrast, the out-of-time pile-up comes from minimum-bias events from previous or subsequent bunch crossings. The out-of-time pile-up is present if the width of the electrical pulse (Fig. 2) is longer than the bunch spacing, which is the case in Run 1 where the bunch spacing in runs used for physics analyses is 50 ns. These results are discussed in the following paragraphs.

The pile-up in the TileCal is studied as a function of the detector geometry and the mean number of inelastic pp interactions per bunch crossing \(\left<\mu \right>\) (averaged over all bunch crossings within a luminosity block and depending on the actual instantaneous luminosity and number of colliding bunches). The data are selected using a zero-bias trigger. This trigger unconditionally accepts events from collisions occurring a fixed number of LHC bunch crossings after a high-energy electron or photon is accepted by the L1 trigger, whose rate scales linearly with luminosity. This triggering provides a data sample which is not biased by any residual signal in the calorimeter system. Minimum-bias MC samples for pile-up noise studies were generated using Pythia 8 and Pythia 6 for 2012 and 2011 simulations, respectively. The noise described in this section contains contributions from both electronic noise and pile-up, and is computed as the standard deviation (RMS) of the energy deposited in a given cell.

The total noise (electronic noise and contribution from pile-up) in different radial layers as a function of \(|\eta |\) for a medium pile-up run (average number of interactions per bunch crossing over the whole run \(\left<\mu _{\mathrm {run}}\right>=15.7\)) taken in 2012 is shown in Fig. 11. The plots make use of the \(\eta \) symmetry of the detector and use cells from both \(\eta \) sides in the calculation. In the EB standard cells (all except E-cells), where the electronic noise is almost flat (see Fig. 8), the amount of upstream material as a function of \(|\eta |\) increases [1], causing the contribution of pile-up to the total noise to visibly decrease. The special cells (E1–E4), representing the gap and crack scintillators, experience the highest particle flux, and have the highest amount of pile-up noise, with cell E4 (\(|\eta | = 1.55\)) exhibiting about 380 MeV of noise at \(\left<\mu _{\mathrm {run}}\right>=15.7\) (of which about 5 MeV is attributed to electronic noise). In general, the trends seen in the data for all layers as a function of \(|\eta |\) are reproduced by the MC simulation. The total noise observed in data exceeds that in the simulation, the differences are up to 20%.

Open image in new window

The energy spectrum in the cell A12 is shown in Fig. 12(left) for two different pile-up conditions with \(\left<\mu \right>=20\) and \(\left<\mu \right>=30\). The mean energy reconstructed in TileCal cells is centred around zero in minimum-bias events. Increasing pile-up widens the energy distribution both in data and MC simulation. Reasonable agreement between data and simulation is found above approximately 200 MeV. However, below this energy, the simulated energy distribution is narrower than in data. This results in lower total noise in simulation compared with that in experimental data as already shown in Fig. 11. Figure 12(right) displays the average noise for all cells in the A-layer as a function of \(\left<\mu \right>\). Since this layer is the closest to the beam pipe among LB and EB layers, it exhibits the largest increase in noise with increasing \(\left<\mu \right>\). When extrapolating \(\left<\mu \right>\) to zero, the noise values are consistent with the electronic noise.

Open image in new window

4.1 Caesium calibration

The TileCal exploits a radioactive \(^{137}\)Cs source to maintain the global EM scale and to monitor the optical and electrical response of each PMT in the ATLAS environment [30]. A hydraulic system moves this Cs source through the calorimeter using a network of stainless steel tubes inserted into small holes in each tile scintillator.⁷ The beta decay of the \(^{137}\)Cs source produces 0.665 MeV photons at a rate of \(\sim 10^6\) Hz, generating scintillation light in each tile.⁸ In order to collect a sufficient signal, the electrical read-out of the Cs calibration is performed using the integrator read-out path; therefore the response is a measure of the integrated current in a PMT. As is described in Sect. 4.3, dedicated calibration runs of the integrator system show that the stability of individual channels was better than 0.05% throughout Run 1.

In June 2009 the high voltage (HV) of each PMT was modified so that the Cs source response in the same PMTs was equal to that observed in the test beam. Corrections are applied to account for differences between these two environments, namely the activity of the different sources and half-life of \(^{137}\)Cs.

Three Cs sources are used to calibrate the three physical TileCal partitions in the ATLAS detector, one in the LB and one in each EB. A fourth source was used for beam tests and another is used in a surface research laboratory at CERN. The response to each of the five sources was measured in April 2009 [6] and again in March 2013 at the end of Run 1 using a test module for both the LB and EB. The relative response to each source measured on these two dates agrees to within 0.2% and confirms the expected \(^{137}\)Cs activity during Run 1.

A full Cs calibration scan through all tiles takes approximately six hours and was performed roughly once per month during Run 1. The precision of the Cs calibration in one typical cell is approximately 0.3%. For cells on the extreme sides of a partition the precision is 0.5% due to larger uncertainties associated with the source position. Similarly, the precision for the narrow C10 and D4 ITC cells is 3% and \(\sim \)1%, respectively, due to the absence of an iron end-plate between the tile and Cs pipe. It makes more challenging the distinction between the desired response when the Cs source is inside that particular tile of interest versus a signal detected when the source moves towards a neighbouring tile row.

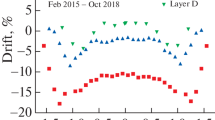
The Cs response as a function of time is shown in Fig. 14(left) averaged over all cells of a given radial layer. The solid line, enveloped by an uncertainty band, represents the expected response due to the reduced activity of the three Cs sources in the ATLAS detector (\(-2.3\%\)/year). The error bars on each point represent the RMS spread of the response in all cells within a layer. There is a clear deviation from this expectation line, with the relative difference between the measured and expected values shown in Fig. 14(right). The average up-drift of the response relative to the expectation was about 0.8%/year in 2009–2010. From 2010 when the LHC began operation, the upward and downward trends are correlated with beam conditions–the downward trends correspond to the presence of colliding beams, while the upward trends are evident in the absence of collisions. This effect is pronounced in the innermost layer A, while for layer D there is negligible change in response. This effect is even more evident when looking at pseudorapidity-dependent responses in individual layers. While in most LB-A cells a deviation of approximately 2.0% is seen (March 2012 to December 2012), in EB-A cells the deviation ranges from 3.5% (cell A13) to 0% (outermost cell A16). These results indicate the total effect, as seen by the Cs system, is due to the scintillator irradiation and PMT gain changes (see Sect. 4.5 for more details).

Open image in new window

The Cs calibration constants are derived using Cs calibration data taken with the full ATLAS magnetic field system on, as in the nominal physics configuration. The magnetic field effectively increases the light yield in scintillators approximately by 0.7% in the LB and 0.3% in the EB.

Since the response to the Cs source varies across the surface of each tile, additional layer-dependent weights are applied to maintain the EM scale across the entire calorimeter [27]. These weights reflect the different radial tile sizes in individual layers and the fact that the Cs source passes through tiles at their outer edge.

The total systematic uncertainty in applying the EM scale from the test beam environment to ATLAS was found to be 0.7%, with the largest contributions from variations in the response to the Cs sources in the presence of a magnetic field (0.5%) and the layer weights (0.3%) [27].

4.2 Laser calibration

A laser calibration system is used to monitor and correct for PMT response variations between Cs scans and to monitor channel timing during periods of collision data-taking [31, 32].

This laser calibration system consists of a single laser source, located off detector, able to produce short light pulses that are simultaneously distributed by optical fibres to all 9852 PMTs. The intrinsic stability of the laser light was found to be 2%, so to measure the PMT gain variations to a precision of better than 0.5% using the laser source, the response of the PMTs is normalised to the signal measured by a dedicated photodiode. The stability of this photodiode is monitored by an \(\alpha \)-source and, throughout 2012, its stability was shown to be 0.1%, and the linearity of the associated electronics response within 0.2%.

The calibration constants, \(C_{\mathrm {laser}}\) in Eq. (2), are calculated for each channel relative to a reference run taken just after a Cs scan, after new Cs calibration constants are extracted and applied. Laser calibration runs are taken for both gains approximately twice per week.

For the E3 and E4 cells, where the Cs calibration is not possible, the reference run is taken as the first laser run before data-taking of the respective year. A sample of the mean gain variation in the PMTs for each cell type averaged over \(\phi \) between 19 March 2012 (before the start of collisions) and 21 April 2012 is shown in Fig. 15. The observed down-drift of approximately 1% mostly affects cells at the inner radius with higher current draws.

Open image in new window

The laser calibration constants were not used during 2010. For data taken in 2011 and 2012 these constants were calculated and applied for channels with PMT gain variations larger than 1.5% (2%) in the LB (EB) as determined by the low-gain calibration run, with a consistent drift as measured in the equivalent high-gain run. In 2012 up to 5% of the channels were corrected using the laser calibration system. The laser calibration constants for E3 and E4 cells were applied starting in the summer of 2012, and were retroactively applied after the ATLAS data were reprocessed with updated detector conditions. The total statistical and systematic errors of the laser calibration constants are 0.4% for the LB and 0.6% for the EBs, where the EBs experience larger current draws due to higher exposure.

4.3 Charge injection calibration

The charge injection system is used to calculate the constant \(C_{{\mathrm {ADC}\rightarrow \mathrm {pC}},\mathrm {CIS}}\) in Eq. (2) and applied for physics signals and laser calibration data. A part of this system is also used to calibrate the gain conversion constant for the slow integrator read-out.

All 19704 ADC channels in the fast front-end electronics are calibrated by injecting a known charge from the 3-in-1 cards, repeated for a wide range of charge values (approximately 0–800 pC in low-gain and 0–12 pC in high-gain). A linear fit to the mean reconstructed signal (in ADC counts) yields the constant \(C_{{\mathrm {ADC}\rightarrow \mathrm {pC}},\mathrm {CIS}}\). During Run 1 the precision of the system was better than 0.7% for each ADC channel.

Charge injection calibration data are typically taken twice per week in the absence of colliding beams. For channels where the calibration constant varies by more than 1.0% the constant is updated for the energy reconstruction. Figure 16 shows the stability of the charge injection constants as a function of time in 2012 for the high-gain and low-gain ADC channels. Similar stability was seen throughout 2010 and 2011. At the end of Run 1 approximately 1% of all ADC channels were unable to be calibrated using the CIS mostly due to hardware problems evolving in time, so default \(C_{{\mathrm {ADC}\rightarrow \mathrm {pC}},\mathrm {CIS}}\) constants are used in such channels.

Open image in new window

The slow integrator read-out is used to measure the PMT current over \(\sim \!\!10\) ms. Dedicated runs are periodically taken to calculate the integrator gain conversion constant for each of the six gain settings, by fitting the linear relationship between the injected current and measured voltage response. The stability of individual channels is better than 0.05%, the average stability is better than 0.01%.

Open image in new window

4.4 Minimum-bias currents

Due to the distribution of upstream material and the distance of cells from the interaction point the MB signal seen in the TileCal is not expected to be uniform. Figure 17 shows the measured PMT current versus cell \(\eta \) (averaged over all modules) for a fixed instantaneous luminosity. As expected, the largest signal is seen for the A-layer cells which are closer to the interaction point, with cell A13 (\(|\eta | = 1.3\)) located in the EB and (with minimal upstream material) exhibiting the highest currents.

The currents induced in the PMTs due to MB activity are used to validate response changes observed by the Cs calibration system as well as for response monitoring during the physics runs. Moreover, they probe the response in the E3 and E4 cells, which are not calibrated by Cs.

4.5 Combination of calibration methods

The TileCal response is expected to vary over time, with particular sensitivity to changing LHC luminosity conditions. Figure 18 shows the variation of the response to MB, Cs, and laser calibration systems for cell A13 as a function of the time in 2012. Cell A13 is located in the EB, and due to the smaller amount of upstream material, it is exposed to one of the highest radiation doses of all cells as also seen in Fig. 17. To disentangle the effects of PMT and scintillator changes one can study the laser versus MB (or Cs) responses.

The PMT gain, as monitored with the laser, is known to decrease with increasing light exposure due to lower secondary emissions from the dynode surfaces [33].¹⁰ When a PMT is initially exposed to light after a long period of ‘rest’, its gain decreases rapidly and then a slow stabilisation occurs [34]. This behaviour is demonstrated in Fig. 18 – the data-taking in 2012 started after four months of inactivity, followed by the gain stabilisation after several weeks of LHC operation. The same trends were also observed in 2011. The periods of recovery, where the laser response tends towards initial conditions, coincide with times when LHC is not colliding protons. This is consistent with the known behaviour of ‘fatigued’ PMTs that gradually return towards original operating condition after the exposure is removed [35]. A global PMT gain increase of 0.9% per year is observed even without any exposure (e.g. between 2003 and 2009). This is consistent with Fig. 14(right) – after 3.5 years the total gain increase corresponds to approximately 3.5%. Throughout Run 1 the maximum loss of the PMT gain in A13 is approximately 3%, but at the end of 2012 after periods of inactivity the gain essentially recovered from this loss.

The responses to the Cs and MB systems, which are sensitive to both the PMT gain changes and scintillator irradiation show consistent behaviour. The difference between MB (or Cs) and laser response variations is interpreted as an effect of the scintillators’ irradiation. The transparency of scintillator tiles is reduced after radiation exposure [36]; in the TileCal this is evident in the continued downward response to MB events (and Cs) with increasing integrated luminosity of the collisions, despite the eventual slow recovery of the PMTs as described above. In the absence of the radiation source the annealing process is believed to slowly restore the scintillator material, hence improving the collected light yield. The rate and amount of scintillator damage and recovery are complicated combinations of factors, such as particle energies, temperatures, exposure rates and duration, and are difficult to quantify.

Open image in new window

The overlap between the different calibration systems allows calibration and monitoring of the complete hardware and read-out chain of the TileCal, and correct for response changes with fine granularity for effects such as changing luminosity conditions. These methods enable the identification of sources of response variations, and during data-taking, the correction of these variations to maintain the global EM scale throughout Run 1. When possible, problematic components are repaired or replaced during maintenance periods.

5.1 ATLAS detector control system

An ATLAS-wide Detector Control System (DCS) [37, 38] provides a common framework to continuously monitor, control, and archive the status of all hardware and infrastructure components for each subsystem. The status and availability of each hardware component is visually displayed in real time on a web interface. This web interface also provides a detailed history of conditions over time to enable tracking of the stability. The DCS infrastructure stores information about individual device properties in databases.

The TileCal DCS is responsible for tracking the low voltage, high voltage, front-end electronics cooling systems, and back-end crates. The DCS monitoring data are used by automatic scripts to generate alarms if the actual values are outside the expected operating conditions. Actions to address alarm states can be taken manually by experts, or subject to certain criteria the DCS system can automatically execute actions.

The TileCal DCS system monitors the temperature of the front-end electronics with seven probes at various locations in the super-drawer. A temperature variation of \(1\,^{\circ }\)C would induce a PMT gain variation of 0.2% [6]. Analyses done over several data periods within Run 1 indicated the temperature is maintained within \(0.2\,^{\circ }\)C.

The TileCal high-voltage system is based on remote HV bulk power supplies providing a single high voltage to each super-drawer. Each drawer is equipped with a regulator system (HVopto card) that provides fine adjustment of the voltage for each PMT. One controller (HVmicro card) manages two HVopto cards of the super-drawer. The HVmicro card reports actual HV values to the DCS through a CANbus network every few seconds.

Several studies were performed to quantify the stability of the HV of the PMTs and to identify unstable PMTs. One study compares the value of the measured HV with the expected HV for each PMT over the 2012 period. The difference between the measured and set high voltage (\(\Delta \mathrm {HV}\)) for each PMT is fitted with a Gaussian distribution, and the mean value is plotted for all good channels in a given partition. Good channels are all channels except those in modules that were turned off or in the so-called emergency state (described later). For each partition the mean value is approximately 0 V with an RMS spread of 0.44 V, showing good agreement. Another study investigates the time evolution of \(\Delta \mathrm {HV}\) for a given partition. The variation of the mean values versus time is lower than 0.05 V, demonstrating the stability of the HV system over the full period of the 2012 collision run.

In order to identify PMTs with unstable HV over time, \(\Delta \mathrm {HV}\) is computed every hour over the course of one day for each PMT. Plots showing the daily variation in HV over periods of several months are made. PMTs with \(\Delta \mathrm {HV} > 0.5\) V are classified as unstable. The gain variation for these unstable channels is calculated using Eq. (3) (with knowledge of the \(\beta \) value for that particular PMT), and compared with the gain variation as seen by the laser and Cs calibration systems. These calibration systems are insensitive to electrical failures associated with reading back the measured HV and provide a cross-check of apparent instabilities. Figure 19 shows the gain variation for one PMT that suffered from large instabilities in 2012, as measured by the HV and calibration systems. The gain variations agree between the three methods used. Only those channels that demonstrate instabilities in both the HV and calibration systems are classified as unstable. During 2012, a total of only 15 PMTs (0.15% of the total number of PMTs) were found to be unstable.

Open image in new window

5.2 Online data quality assessment and monitoring

During periods of physics collisions, the Tile Calorimeter has experts in the ATLAS control room 24 hours per day and a handful of remote experts available on call to assist in advanced interventions. The primary goal is to quickly identify and possibly correct any problem that cannot be fixed later in software, and that can result in overall data loss. The ATLAS data quality framework is designed to perform automatic checks of the data and to alert experts to potential problems that warrant further investigation [39].

Common problems identified by TileCal experts during the online shifts include hardware failures that do not automatically recover, or software configuration problems that might present themselves as data corruption flags from the ROD data integrity checks. The trigger efficiency and data acquisition, as well as higher-level reconstruction data quality, might be influenced by such problems.

5.3 Offline data quality review

Shortly after the data are taken, a small fraction is quickly reconstructed using the Tier-0 computing farm within the ATLAS Athena software framework [40]. Reconstructed data are then used by the offline data quality experts with more complex tools to evaluate the quality of the data. The experts are given 48 hours to identify, and, where possible, to correct problems, before the bulk reconstruction of the entire run is made. The TileCal offline experts can update the conditions database, where information such as the calibration constants and status of each channel is stored. Channels that suffer from high levels of noise have calibration constants in the database updated accordingly. For channels that suffer from intermittent data corruption problems, data quality flags are assigned to the affected data to exclude the channels in the full reconstruction during that period. This 48-hour period is also used to identify cases of digitiser timing jumps and to add the additional time phases to the time constants of the digitiser affected to account for the magnitude of the time jump.

Luminosity blocks can be flagged as defective to identify periods of time when the TileCal is not operating in its nominal configuration. These defects can either be tolerable whereby corrections are applied but additional caution should be taken while analysing these data, or intolerable in which case the data are not deemed suitable for physics analyses. Defects are entered into the ATLAS Data Quality Defect database [41] with the information propagating to analyses as well as to integrated luminosity calculations.

One luminosity block nominally spans one minute, and removing all data within that time can accumulate to a significant data loss. For rare situations where only a single event is affected by the data corruption, an additional error-state flag is introduced into the reconstruction data. This flag is used to remove such events from the analysis.

Once all offline teams review the run, it is sent to the Tier-0 computing farm for bulk reconstruction, where the entire run is reconstructed using the most up-to-date conditions database. Subsequently the data can be re-reconstructed when reconstruction algorithms are improved and/or the conditions database is further refined to improve the description of the detector.¹¹ These data reprocessing campaigns typically occur several months after the data are taken.

5.4 Overall Tile Calorimeter operation

Overall the TileCal operation was highly successful in Run 1, with an extremely high fraction of data acceptable for a physics analysis. A summary of the total integrated luminosity delivered to ATLAS and approved for analysis is shown in Table 2, along with the fraction of data passing the Tile Calorimeter data quality reviews.

In 2012, the total integrated luminosity lost after the first bulk reconstruction of the data due to TileCal data-quality-related problems was \(104\,\mathrm {pb}^{-1}\) out of \(21.7\,\mathrm {fb}^{-1}\), and is summarised in Fig. 20 as a function of time for various categories of intolerable defects.¹² The primary source of Tile luminosity losses are cases when a read-out link (ROL), which transmits data from the ROD to the subsequent chain in the trigger and data acquisition system, is removed from processing. It implies no data are received from the four corresponding modules. ROLs are disabled in situations when they are flooding the trigger with data (malfunctioning configuration or difficulty processing data), putting the trigger into a busy state where effectively no data can be read from any part of the detector. Removing a ROL during a run is done in a so-called stop-less recovery state, whereby the run is not stopped, as restarting a run can take several minutes. One role of the online experts is to identify these cases and to respond by correcting the source of the removal and re-enabling the ROL in the run. After a new run begins any ROLs that were previously removed are re-included. Improvements for handling ROL removals include adding monitoring plots counting the number of reconstructed Tile cells, where large drops can indicate a ROL removal, and an automatic ROL recovery procedure. With the automatic recovery in place, a single ROL removal lasts less than 30 seconds, and losses due to ROL removal dramatically dropped in the second half of 2012. As the removal of a ROL affects four consecutive modules, this defect is classified as intolerable, and it accounted for 45.2 pb\(^{-1}\) of data loss in 2012.

Power cuts or trips of the HV bulk power supply sources accounted for 22.6 pb\(^{-1}\) of lost integrated luminosity. The last 4.9 pb\(^{-1}\) of loss came from situations when the laser ROD became busy.¹³ During 2012 this was improved by prompting the online expert to disable the laser ROD.

Open image in new window

There are several operational problems with the LVPS sources that contribute to the list of tolerable defects. In some cases the LVPS fails entirely, implying an entire module is not analysed. The failure rate was one LVPS per month in 2011 and 0.5 LVPS per month in 2012. The faulty LVPS sources were replaced with spares during the maintenance campaigns in the ATLAS cavern at the end of each year.

In addition to overall failures, sometimes there are problems with the low voltage supplied to the HVopto card, which means the PMT HV can be neither controlled nor measured. In this case the applied HV is set to the minimum value, putting the module in an emergency state. The calibration and noise constants for all channels within a module in emergency mode are updated to reflect this non-nominal state.

Finally, the LVPS suffered from frequent trips correlated with the luminosity at a rate of 0.6 trips per 1 pb\(^{-1}\). Automatic recovery of these modules was implemented, to recover the lost drawer. During the maintenance period between 2011 and 2012, 40 new LVPS sources (version 7.5) with improved design [42] were installed on the detector. In 2012 there were a total of about 14,000 LVPS trips from all modules, only one of which came from the new LVPS version. After the LHC Run 1, all LVPS sources were replaced with version 7.5.

Figure 21 shows the percentage of the TileCal cells masked in the reconstruction as a function of time. These cells are located in all areas of the detector, with no one area suffering from a large number of failures. The main reasons for masking a cell are failures of LVPS sources, evident by the steep steps in the figure. Other reasons are severe data corruption problems or very large noise. The periods of maintenance, when faulty hardware components are repaired or replaced (when possible), are visible by the reduction of the number of faulty cells to near zero. For situations when cell energy reconstruction is not possible the energy is interpolated from neighbouring cells. The interpolation is linear in energy density (energy per cell volume) and is done independently in each layer, using all possible neighbours of the cell (i.e. up to a maximum of eight). In cases where only one of two channels defining a cell is masked the energy is taken to be twice that of the functioning channel.

Open image in new window

6.1 Energy response to single isolated muons

Muon energy loss in matter is a well-understood process [46], and can be used to probe the response of the Tile Calorimeter. For high-energy muons, up to muon energies of a few hundred GeV, the dominant energy loss process is ionisation. Under these conditions the muon energy loss per unit distance is approximately constant. This subsection studies the response to isolated muons from cosmic-ray sources and to \(W\rightarrow \mu \nu \) events from pp collisions.

Candidate muons are selected using the muon RPC and TGC triggering subsystems of the Muon Spectrometer. A muon track measured by the Pixel and SCT detectors is extrapolated through the calorimeter volume, taking into account the detector material and magnetic field [47]. A linear interpolation is performed to determine the exact entry and exit points of the muon in every crossed cell to compute the distance traversed by the muon in a given TileCal cell. The distance (\(\Delta x\)) together with the energy deposited in the cell (\(\Delta E\)) are used to compute the muon energy loss per unit distance, \(\Delta E/\Delta x\).

6.1.1 Cosmic-ray muon data

Muons from cosmic-ray showers, called cosmic muons, are used as a cross-check of energy reconstruction and calibration complementary to the collision data. At sea level, cosmic muons can have energies up to a TeV or more, but most of the muons are at lower energies, with the mean energy being approximately 4 GeV [46].

Candidate cosmic muons are triggered during empty bunch crossings in physics runs in a dedicated data stream allocated for muon candidates identified by the muon spectrometer trigger system if at least one track is matched to the inner detector tracking system. In total there are approximately one million such events triggered in each year studied (2008, 2009, 2010).

The energy in TileCal channels is reconstructed using the iterative OF method (see Sect. 3). The muon tracks, reconstructed using Pixel and SCT detectors with a dedicated algorithm, are extrapolated through the volume of the calorimeter in both upward and downward directions. This allows to study the response of the TileCal modules in top and bottom parts of the detector.

The event selection criteria used to select events for the cosmic muons analysis are summarised in Table 3. A candidate cosmic-muon event is required to have exactly one track associated with a reconstructed muon (Cut 1), with at least eight hits in the Pixel plus SCT detectors (Cut 2). A cut on the maximum distance of the reconstructed track from the origin of the coordinate system in both the transverse (\(d_0\)) and longitudinal (\(z_0\)) components (Cut 3) is used to select well-reconstructed tracks that follow the projective geometry of the calorimeter. Muons with a trajectory close to the vertical direction are poorly measured in the TileCal due to the vertical orientation of the scintillating tiles, hence Cut 4 is used to remove the very central cells located within the vertical coverage of the inner detector. The last two requirements (Cut 3 and Cut 4) effectively remove muons at very low pseudorapidities. The muon is required to have momentum in the range 10–30 GeV to minimise the effects of multiple scattering at low momentum, and to reduce radiative energy losses at higher momentum, which could produce large fluctuations in the results. The muon path length through a cell must be larger than 200 mm. An energy of at least 60 MeV¹⁴ has to be released in that cell to remove contributions from noise. Cut 8 is used to reduce contributions from multiple scattering, such that the track’s azimuthal impact point at the inner (outer) radial point of the cell, \(\phi _{\mathrm {inner}} (\phi _{\mathrm {outer}})\) is within 0.04 radians of the cell centre \(\phi _{\mathrm {c}}\) coordinate (with a cell width of \(\Delta \phi = 0.1\)).

Table 3

Selection criteria applied to the event, track, and muon used in the cosmic muons analysis. A description and motivation of each cut can be found in the text

Cut	Variable	Requirement
1	Number of muon tracks \(N_{\mu }\)	\(N_{\mu } = 1\)
2	Number of track hits in Pixel + SCT	\(\ge 8\)
3	Reconstructed track distance from origin	\(|d_0| \le 380\) mm (transverse),
		\(|z_0| \le 800\) mm (longitudinal)
4	Polar angle of track relative to vertical axis	\(|\theta _\mu | > 0.13\) rad
5	Muon momentum	\(10\,\mathrm {GeV}< p_\mu < 30\,\mathrm {GeV}\)
6	muon path length through cell	\(\Delta x > 200\) mm
7	cell energy	\(\Delta E > 60\) MeV
8	track impact point at inner and outer radial point of cell	\(|\phi _{c} - \phi _{\mathrm {inner}}| < 0.04\),
		\( |\phi _{c} - \phi _{\mathrm {outer}}| < 0.04\)

The response to cosmic muons in the calorimeter is also studied using MC simulated data. The cosmic-muon energy and flux spectra as measured at sea-level [48] are used as input into the simulation. The material between the surface and the ATLAS cavern is simulated, including the cavern volumes and detector access shafts. Air showers are not simulated but have negligible impact due to the selection requirements for single-track events. The \(\Delta E/\Delta x\) distributions for the 2008 cosmic-muon data and MC simulation are shown in Fig. 22 for cells A3 (left) and D2 (right) in the long barrel. The A3 (D2) cell covers the region \(0.2< |\eta | < 0.3\) (\(0.3< |\eta | < 0.5\)) and is located in the innermost (outermost) calorimeter layer. Differences between the experimental and simulated data are discussed in the following paragraphs.

Open image in new window

Verification of the radial layer intercalibration

The calibration between cells within the same layer is investigated using the double ratio formed by the ratio of the experimental and simulated truncated means, as shown in Eq. (4). The typical non-uniformity of all cells in a given layer is found to be approximately 2% for all layers every year. This can be explained by the variations in the optical and electrical components of the calorimeter.

Several sources of systematic uncertainty, summarised in Table 4, are considered in the studies of cosmic muons. The systematic variations 1–5 are related to the selection criteria. The results are assumed to be stable for different values used in the selection criteria. This assumption is checked by varying the values in the specified range and repeating the analysis for every variation, both for data and MC simulations. The resulting differences contribute to the total systematic uncertainty. Differences in the response along the muon path through the detector and due to signal evaluation method should be well described by MC. Two systematic variations, applied both to data and MC, are introduced to verify this assumption. Variation 6 compares the response in the upper part of the detector (\(\phi _{\mathrm {c}} > 0\)), where these muons enter the detector, and in the lower part (\(\phi _{\mathrm {c}} < 0\)), after the muons pass through a large fraction of the detector. The uncertainty of the method used to evaluate the detector’s response to cosmic muons is considered as source 7. Source 8 reflects the different spread of the experimental and simulated \(\Delta E/ \Delta x\) distributions. The effect on the determination of the truncated mean is estimated to be 0.3% using a toy MC simulation. The final classes of uncertainties, 9 and 10, concern the signal calibration procedures performed in the test beam and in situ in ATLAS (already discussed in Sect. 4). T