Abstract
A measurement of the electroweak (EW) production of two jets in association with a \(\mathrm {Z} \) boson in proton-proton collisions at \(\sqrt{s}=13\,\text {TeV} \) is presented, based on data recorded in 2016 by the CMS experiment at the LHC corresponding to an integrated luminosity of 35.9\(\,\text {fb}^{\text {--}1}\). The measurement is performed in the \(\ell \ell \mathrm {jj}\) final state with \(\ell \) including electrons and muons, and the jets j corresponding to the quarks produced in the hard interaction. The measured cross section in a kinematic region defined by invariant masses \(m_{\ell \ell } >50\,\text {GeV} \), \(m_{\mathrm {jj}} >120\,\text {GeV} \), and transverse momenta \(p_{\mathrm {T j}} > 25\,\text {GeV}\) is \(\sigma _\mathrm {EW}(\ell \ell \mathrm {jj})= 534 \pm 20\,\text {(stat)} \pm 57\,\text {(syst) fb} \), in agreement with leading-order standard model predictions. The final state is also used to perform a search for anomalous trilinear gauge couplings. No evidence is found and limits on anomalous trilinear gauge couplings associated with dimension-six operators are given in the framework of an effective field theory. The corresponding 95% confidence level intervals are \(-2.6< c_{WWW}/\varLambda ^2 < 2.6\,\text {TeV}^{-2}\) and \(-8.4< c_{W}/\varLambda ^2 < 10.1\,\text {TeV}^{-2}\). The additional jet activity of events in a signal-enriched region is also studied, and the measurements are in agreement with predictions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In proton-proton (pp) collisions at the CERN LHC, the production of dileptons (\(\ell \ell \)) consistent with the Z boson invariant mass in association with two jets (\(\mathrm {jj}\)) is dominated by events where the dilepton pair is produced by a Drell–Yan (DY) process, in association with jets from strong interactions. This production is governed by a mixture of electroweak (EW) and strong processes of order \(\alpha _\mathrm {EW}^2\alpha _\mathrm {S}^2\), where \(\alpha _\mathrm {S}\) is the strong coupling and \(\alpha _\mathrm {EW}\) is the EW coupling strength.
The pure electroweak production of the \(\ell \ell \mathrm {jj}\) final state, at order \(\alpha _\mathrm {EW}^4\), is less frequent [1], and includes production via the vector boson fusion (VBF) process, with its distinctive signature of two jets with both large energy and separation in pseudorapidity \(\eta \). In this paper the electroweak production is referred to as EW \(\mathrm {Z} \mathrm {jj}\), and the two jets produced through the fragmentation of the outgoing quarks are referred to as “tagging jets”.
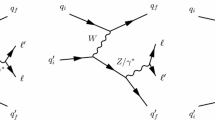
Figure 1 shows representative Feynman diagrams for the EW \(\mathrm {Z} \mathrm {jj}\) signal, namely VBF (left), bremsstrahlung-like (center), and multiperipheral (right) production. Gauge cancellations lead to a large negative interference between the VBF process and the other two processes, with the interferences from the bremsstrahlung-like production being larger. Interference with multiperipheral production is limited to cases where the dilepton mass is close to the Z boson peak mass [2].
In the inclusive production of \(\ell \ell \mathrm {jj}\) final states, some of the nonexclusive EW interactions with identical initial and final states can interfere with the exclusive EW interactions that are shown in Fig. 1. This interference effect between the signal production and the main background processes is much smaller than the interference effects among the EW production amplitudes, but needs to be taken into account when measuring the signal contribution [3, 4].
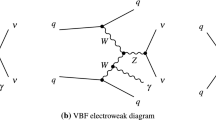
Figure 2 (left) shows one example of corrections to order \(\alpha _\mathrm {S}^2\) for DY production that have the same initial and final states as those in Fig. 1. A process at order \(\alpha _\mathrm {S}^2\) that does not interfere with the EW signal is shown in Fig. 2 (right).
The study of EW \(\mathrm {Z} \mathrm {jj}\) processes is part of a more general investigation of standard model (SM) vector boson fusion and scattering processes that include studies of Higgs boson production [5,6,7] and searches for physics beyond the SM [8,9,10,11]. When isolated from the backgrounds, the properties of EW \(\mathrm {Z} \mathrm {jj}\) events can be compared with SM predictions. Probing the additional hadronic activity in selected events can shed light on the modelling of additional parton radiation [12, 13], which is important for signal selection or vetoing of background events.
New physics could appear in the form of anomalous trilinear gauge couplings (ATGCs) [14, 15] that can be parameterized with higher-dimensional operators. Their measurements could provide an indirect search for new physics at mass scales not directly accessible at the LHC.
At the LHC, the EW \(\mathrm {Z} \mathrm {jj}\) process was first measured by the CMS experiment using pp collisions at \(\sqrt{s}=7\,\text {TeV} \) [3], and then at \(\sqrt{s}=8\,\text {TeV} \) by both the CMS [4] and ATLAS [16] experiments. The ATLAS experiment has also performed measurements at \(\sqrt{s}=13\,\text {TeV} \) [17], with a data sample corresponding to an integrated luminosity of 3.2\(\,\text {fb}^{\text {--}1}\). All results so far agree with the expectations of the SM within a precision of approximately 20%.
This paper presents a measurement with the CMS detector using pp collisions collected at \(\sqrt{s}=13\,\text {TeV} \) during 2016, corresponding to an integrated luminosity of 35.9\(\,\text {fb}^{\text {--}1}\). A multivariate analysis, based on the methods developed for the 7 and 8 TeV data results [3, 4], is used to separate signal events from the large DY + jets background. Analysis of the 13\(\,\text {TeV}\) data with larger integrated luminosity and larger predicted total cross section offers an opportunity to measure the cross section at a higher energy and reduce the uncertainties of the earlier measurements.
Section 2 describes the experimental apparatus and Sect. 3 the event simulations. Event selection procedures are described in Sect. 4, together with the selection efficiencies and background models in control regions. Section 5 details the strategy adopted to extract the signal from the data, and the corresponding systematic uncertainties are summarized in Sect. 6. The cross section and anomalous coupling results are presented in Sects. 7 and 8, respectively. Section 9 provides a study of the additional hadronic activity in an EW \(\mathrm {Z} \mathrm {jj}\)-enriched region. Finally, a brief summary of the results is given in Sect. 10.
2 The CMS detector
The central feature of the CMS apparatus is a superconducting solenoid of 6\(\text {\,m}\) internal diameter, providing a magnetic field of 3.8\(\text {\,T}\). Within the solenoid volume are a silicon pixel and strip tracker, a lead tungstate crystal electromagnetic calorimeter (ECAL), and a brass and scintillator hadron calorimeter (HCAL), each composed of a barrel and two endcap sections. Forward calorimeters extend the \(\eta \) coverage provided by the barrel and endcap detectors. Muons are measured in gas-ionization detectors embedded in the steel flux-return yoke outside the solenoid.
The tracker measures charged particles within the pseudorapidity range \(|\eta | < 2.5\). It consists of 1440 pixel and 15 148 strip detector modules. For nonisolated particles of \(1< p_{\mathrm {T}} < 10\,\text {GeV} \) and \(|\eta | < 1.4\), the track resolutions are typically 1.5% in \(p_{\mathrm {T}}\) and 25–90 (45–150)\(\,\mu \text {m}\) in the transverse (longitudinal) impact parameter [18].
The electron momenta are estimated by combining energy measurements in the ECAL with momentum measurements in the tracker [19]. The dielectron invariant mass resolution for \(\mathrm {Z} \rightarrow \mathrm {e}\mathrm {e}\) decays is 1.9% when both electrons are in the ECAL barrel, and 2.9% when both electrons are in the endcaps.
Muons are measured in the pseudorapidity range \(|\eta | < 2.4\) with detection planes made using three technologies: drift tubes, cathode strip chambers, and resistive-plate chambers. Matching muons to tracks measured in the silicon tracker results in a relative transverse momentum resolution for muons with \(20<p_{\mathrm {T}} < 100\,\text {GeV} \) of 1.3–2.0% in the barrel and better than 6% in the endcaps. The \(p_{\mathrm {T}}\) resolution in the barrel is better than 10% for muons with \(p_{\mathrm {T}}\) up to 1\(\,\text {TeV}\) [20].
The offline analysis uses reconstructed charged-particle tracks and candidates from the particle-flow (PF) algorithm [21]. In the PF event reconstruction, all stable particles in the event, i.e. electrons, muons, photons, charged and neutral hadrons, are reconstructed as PF candidates using information from all subdetectors to obtain an optimal determination of their direction, energy, and type. The PF candidates are then used to reconstruct the jets and the missing transverse momentum.
A more detailed description of the CMS detector, together with a definition of the coordinate system and the relevant kinematic variables, can be found in Ref. [22].
3 Simulation of signal and background events
Signal events are simulated at leading order (LO) using the MadGraph 5_amc@nlo (v2.3.3) Monte Carlo (MC) generator [23, 24], interfaced with pythia (v8.212) [25, 26] for parton showering (PS) and hadronization. The NNPDF30 (nlo_as0130) [27] parton distribution functions (PDF) are used to generate the events. The underlying event (UE) is modelled using the CUETP8M1 tune [28]. The simulation does not include extra partons at matrix element (ME) level. The signal is defined in the kinematic region with dilepton invariant mass \(m_{\ell \ell } >50\,\text {GeV} \), parton transverse momentum \(p_{\mathrm {T j}} > 25\,\text {GeV} \), and diparton invariant mass \(m_{\mathrm {jj}} >120\,\text {GeV} \). The cross section of the \(\ell \ell \mathrm {jj}\) final state (with \(\ell \) = e or \(\mu \)), applying the above fiducial cuts, is calculated to be \(\sigma _\mathrm {LO}(\mathrm {EW}~\ell \ell \mathrm {jj})=543^{+7}_{-9}\,\text {(scale)}\pm 22\,\text {(PDF) fb} \), where the first uncertainty is obtained by changing simultaneously the factorization (\(\mu _\mathrm{F}\)) and renormalization (\(\mu _\mathrm{R}\)) scales by factors of 2 and 1 / 2, and the second reflects the uncertainties in the NNPDF30 PDFs. The LO signal cross section and relevant kinematic distributions estimated with MadGraph 5_amc@nlo are found to be in agreement within 5% with the next-to-leading order (NLO) predictions of the vbfnlo generator (v.2.7.1) [29,30,31] that includes NLO QCD corrections. For additional comparisons, signal events have also been simulated with the herwig++ (v2.7.1) [32] PS, using the EE5C [33] tune.
Events coming from processes including ATGCs are generated with the same setting as the SM sample, but include additional information for reweighting in a three-dimensional effective field theory (EFT) parameter space, as described in more detail in Sect. 8.1.
Background DY events are also simulated with MadGraph 5_amc@nlo using (1) an NLO ME calculation with up to three final-state partons generated from quantum chromodynamics (QCD) interactions, and (2) an LO ME calculation with up to four partons. The ME-PS matching is performed following the FxFx prescription [34] for the NLO case, and the MLM prescription [35, 36] for the LO case. The NLO background simulation is used to extract the final results, while the independent LO samples are used to perform the multivariate discriminant training. The dilepton DY production for \(m_{\ell \ell }>50\,\text {GeV}\) is normalized to \(\sigma _\text {th}(\mathrm {DY})=5.765\text {\,nb} \), which is computed at next-to-next-to-leading order (NNLO) with fewz (v3.1) [37].
The evaluation of the interference between \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) and \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) processes relies on predictions obtained with MadGraph 5_amc@nlo. A dedicated sample of events arising from the interference terms is generated directly by selecting the contributions of order \(\alpha _\mathrm {S}\alpha _\mathrm {EW}^3\), and passing them through the full detector simulation to estimate the expected interference contribution.
Other backgrounds are expected from other sources of events with two opposite-sign and same-flavour leptons together with jets. Top quark pair events are generated with powheg (v2.0) [38,39,40] and normalized to the inclusive cross section calculated at NNLO together with next-to-next-to-leading logarithmic corrections [41, 42]. Single top quark processes are modelled at NLO with powheg [38,39,40, 43, 44] and normalized to cross sections of \(71.7\pm 2.0\text {\,pb} \), \(217\pm 3\text {\,pb} \), and \(10.32\pm 0.20\text {\,pb} \) respectively for the tW, t-, and s-channel production [41, 45]. The diboson production processes \(\mathrm {W}\mathrm {W}\), \(\mathrm {W}\mathrm {Z} \), and \(\mathrm {Z} \mathrm {Z} \) are generated with pythia and normalized to NNLO cross section computations obtained with mcfm (v8.0) [46]. The abbreviation VV is used in this document when referring to the sum of the processes that yield two vector bosons.
The contribution from diboson processes with \(\ell \ell \mathrm {jj}\) final states, such as ZW and ZZ, to the signal definition is small, and these contributions are not included in the background.
The production of a \(\mathrm {W}\) boson in association with jets, where the \(\mathrm {W}\) decays to a charged lepton and a neutrino, is also simulated with MadGraph 5_amc@nlo, and normalized to a total cross section of 61.53\(\text {\,nb}\), computed at NNLO with fewz. Multijet QCD processes are also studied in simulation, but are found to yield negligible contributions to the selected events. All background productions make use of the pythia PS model with the CUETP8M1 tune.
A detector simulation based on Geant4 (v.9.4p03) [47, 48] is applied to all the generated signal and background samples. The presence of multiple pp interactions in the same bunch crossing (pileup) is incorporated by simulating additional interactions (both in-time and out-of-time with respect to the hard interaction) with a multiplicity that matches the distribution observed in data. The additional events are simulated with pythia (v8.212) making use of the NNPDF23 (nlo_as0130) [49] PDF, and the CUETP8M1 tune. The average pileup is estimated to be about 27 additional interactions per bunch crossing.
4 Reconstruction and selection of events
Events containing two isolated, high-\(p_{\mathrm {T}}\) leptons, and at least two high-\(p_{\mathrm {T}}\) jets are selected. Isolated single-lepton triggers are used to acquire the data, where the lepton is required to have \(p_{\mathrm {T}} >27\,\text {GeV}\) for the electron trigger and \(p_{\mathrm {T}} >24\,\text {GeV} \) for the muon trigger [50].
In the offline reconstruction, electrons are reconstructed from clusters of energy deposits in the ECAL that match tracks extrapolated from the silicon tracker [19]. Offline muons are reconstructed by fitting trajectories based on hits in the silicon tracker and in the muon system [20]. Reconstructed electron or muon candidates are required to have \(p_{\mathrm {T}} >20\,\text {GeV} \). Electron candidates are required to be reconstructed within \(|\eta |\le 2.4\), excluding barrel-to-endcap \(1.444< |\eta | < 1.566\) transition regions of the ECAL [22]. Muon candidates are required to be reconstructed in the fiducial region \(|\eta |\le 2.4\) of the muon system. The track associated with a lepton candidate is required to have both its transverse and longitudinal impact parameters compatible with the position of the main primary vertex (PV) of the event. The reconstructed PV with the largest value of summed physics-object \(p_{\mathrm {T}} ^2\) is taken to be the primary \(\mathrm {p}\mathrm {p}\) interaction vertex. The physics objects are the objects returned by a jet finding algorithm [51, 52] applied to all charged particle tracks associated with the vertex, plus the corresponding associated missing transverse momentum.
The leptons are required to be isolated. The isolation is calculated from particle candidates reconstructed by the PF algorithm and is corrected for pileup on an event-by-event basis. The sum of scalar \(p_{\mathrm {T}}\) of all particle candidates reconstructed in an isolation cone with radius \(R=\sqrt{\smash [b]{(\varDelta \eta )^{2}+(\varDelta \phi )^{2}}}=0.4\) around the momentum vector of the lepton is required to be below 15 (25)% of the electron (muon) \(p_{\mathrm {T}}\) value. The two isolated leptons with opposite electric charge and highest \(p_{\mathrm {T}}\) are chosen to form the dilepton pair, and are required to have \(p_{\mathrm {T}} >30\,\text {GeV} \) and \(p_{\mathrm {T}} >20\,\text {GeV} \) for the \(p_{\mathrm {T}}\)-leading and subleading lepton, respectively. Events with additional leptons are kept in the event selection. Same-flavour dileptons (ee or \(\mu \mu \)) compatible with \(\mathrm {Z} \rightarrow \ell \ell \) decays are then selected by requiring \(|m_{\mathrm {Z}}-m_{\ell \ell }|<15\,\text {GeV} \), where \(m_{\mathrm {Z}}\) is the mass of the \(\mathrm {Z} \) boson [53].
Jets are reconstructed by clustering PF candidates with the anti-\(k_{\mathrm {T}}\) algorithm [51, 54] using a distance parameter of 0.4. The jet momentum is determined as the vector sum of all particle momenta in the jet, and is found from simulation to be within 5 to 10% of the true momentum over the whole \(p_{\mathrm {T}}\) spectrum and detector acceptance [21].
An offset correction is applied to jet energies to take into account the contribution from additional proton-proton interactions within the same or nearby bunch crossings. Jet energy corrections are derived from simulation, and are confirmed with in situ measurements of the energy balance in dijet, multijet, photon + jet, and leptonically decaying \(\mathrm {Z} \) + jet events [55]. Loose jet identification criteria are applied to reject misconstructed jets resulting from detector noise [56]. Loose criteria are also applied to remove jets heavily contaminated with pileup energy (clustering of energy deposits not associated with a parton from the primary \(\mathrm {p}\mathrm {p}\) interaction) [56, 57]. The efficiency of the jet identification criteria is greater than 99%, rejecting 90% of background pileup jets with \(p_{\mathrm {T}} \simeq 50\,\text {GeV} \). The jet energy resolution (JER) is typically \({\approx }15\%\) at 10\(\,\text {GeV}\), 8% at 100\(\,\text {GeV}\), and 4% at 1\(\,\text {TeV}\) [55]. Jets reconstructed with \(p_{\mathrm {T}} \ge 15\,\text {GeV} \) and \({|\eta |\le 4.7}\) are used in the analysis.
The two highest \(p_{\mathrm {T}}\) jets are defined as the tagging jets, and are required to have \(p_{\mathrm {T}} >50\,\text {GeV} \) and \(p_{\mathrm {T}} >30\,\text {GeV} \) for the \(p_{\mathrm {T}}\)-leading and subleading jet, respectively. The invariant mass of the two tagging jets is required to satisfy \(m_{\mathrm {jj}}>200\,\text {GeV} \).
A multivariate analysis technique, described in Sect. 5, is used to provide an optimal separation of the \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) and \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) components of the inclusive \(\ell \ell \mathrm {jj}\) spectrum. The main discriminating variables are the dijet invariant mass \(m_{\mathrm {jj}}\) and the pseudorapidity separation \(\varDelta \eta _{\mathrm {jj}}\). Other variables used in the multivariate analysis are described below.
Table 1 reports the expected and observed event yields after the initial selection and after imposing a minimum value for the final discriminator output that defines the signal-enriched region used for the studies of additional hadronic activity described in Sect. 9.
4.1 Discriminating gluons from quarks
Jets in signal events are expected to originate from quarks, while for background events it is more probable that jets are initiated by a gluon. A quark-gluon likelihood (QGL) discriminant [3] is evaluated for the two tagging jets with the intent of distinguishing the nature of each jet.
The QGL discriminant exploits differences in the showering and fragmentation of gluons and quarks by making use of the following internal jet composition observables: (1) the particle multiplicity of the jet, (2) the minor root-mean-square of distance between the jet constituents in the \(\eta \)-\(\phi \) plane, and (3) the \(p_{\mathrm {T}}\) distribution function of the jet constituents, as defined in Ref. [58].
The variables are used as inputs to a likelihood discriminant on gluon and quark jets constructed from simulated dijet events. The performance of this QGL discriminant is evaluated and validated using independent, exclusive samples of \(\mathrm {Z} \) + jet and dijet data [58]. Comparisons of simulation predictions and data distributions allow the derivation of corrections to the simulated QGL distributions and define a systematic uncertainty band.
4.2 Additional discriminating variables
An event balance variable, \(R(p_{\mathrm {T}} ^{\text {hard}})\), is used to separate the signal from the background, defined as
where \(\vec {p}_{\mathrm {T} \mathrm {j}_1}\), \(\vec {p}_{\mathrm {T} \mathrm {j}_2}\) and \(\vec {p}_{\mathrm {T} \mathrm {Z}}\) are, respectively, the transverse momenta of the two tagging jets and of the Z boson, and the numerator is the estimator of the \(p_{\mathrm {T}}\) for the hard process, i.e. \(p_{\mathrm {T}} ^{\,\text {hard}}\).
Angular variables useful for signal discrimination include the difference between the rapidity of the \(\mathrm {Z} \) boson \(y_{\mathrm {Z}}\) and the average rapidity of the two tagging jets, i.e.
and the \(z^*\) Zeppenfeld variable [13] defined as
Data and simulated event distributions for the dielectron event selection: \(m_{\mathrm {jj}}\) (top left), \(R(p_{\mathrm {T}} ^{\,\text {hard}})\) (top right), and \(z^*\) (bottom). The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations, as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties
Data and simulated event distributions for the dimuon event selection: \(m_{\mathrm {jj}}\) (top left), \(R(p_{\mathrm {T}} ^{\,\text {hard}})\) (top right), and \(z^*\) (bottom). The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties
The distributions for data and simulated samples of the \(m_{\mathrm {jj}}\), \(R(p_{\mathrm {T}} ^{\,\text {hard}})\) and \(z^*\) variables, after the initial selection, are shown in Figs. 3 and 4, for the dielectron and dimuon channels, respectively. The distributions for data and simulated samples of the dijet transverse momentum (\(p_{\mathrm {T jj}} \)), pseudorapidity separation (\(\varDelta \eta _{\mathrm {jj}}\)), and of the QGL output values of each jet, after the initial selection, are shown in Figs. 5 and 6, respectively, for the dielectron and dimuon channels. Good agreement between the data and the MC expectations is observed in both channels. In the lower panels of these plots the experimental uncertainties in the jet energy scales (JES) (dotted envelope) and the uncertainties due to the choice of QCD factorisation and normalization scales defined in Sec. 6 (dashed envelope) are shown.
5 Signal discriminants and extraction procedure
The \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) signal is characterized by a large separation in pseudorapidity between the tagging jets, due to the small scattering-angle of the two initial partons. Because of both the topological configuration and the large energy of the outgoing partons, \(m_{\mathrm {jj}}\) is also expected to be large. The evolution of \(\varDelta \eta _{\mathrm {jj}}\) with \(m_{\mathrm {jj}}\) is expected to be different for signal and background events, and therefore these characteristics are expected to yield a high separation power between the \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) and the \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) productions. In addition, in signal events it is expected that the Z boson candidate is produced centrally in the rapidity region defined by the two tagging jets and that the \(\mathrm {Z} \mathrm {jj}\) system is approximately balanced in the transverse plane. As a consequence signal events are expected to yield lower values of both \(z^*\) and \(p_{\mathrm {T}} ^{\,\text {hard}}\) than the DY background. Other variables that are used to enhance the signal-to-background separation are related to the kinematics of the event (\(p_{\mathrm {T}}\), rapidity, and distance between the jets and/or the \(\mathrm {Z} \) boson) or to the properties of the jets that are expected to be initiated by quarks. The variables that are used in the multivariate analysis are: (1) \(m_\mathrm{jj}\); (2) \(\varDelta \eta _\mathrm{jj}\); (3) the dijet transverse momentum \(p_{\mathrm {T jj}}\); (iv) the QGL values of the two tagging jets; (v) \(R\left( p_{\mathrm {T}} ^{\,\text {hard}}\right) \) and \(z^*\).
Data and simulated event distributions for the dielectron event selection: dijet system transverse momentum (top left), dijet pseudorapidity opening (top right), \(p_{\mathrm {T}}\)-leading jet QGL (bottom left), and \(p_{\mathrm {T}}\)-subleading jet QGL (bottom right). The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations, as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties
Data and simulated event distributions for the dimuon event selection: dijet system transverse momentum (top left), dijet pseudorapidity opening (top right), \(p_{\mathrm {T}}\)-leading jet QGL (bottom left), and \(p_{\mathrm {T}}\)-subleading jet QGL (bottom right). The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations, as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties
The output of the discriminator is built by training a boosted decision tree (BDT) from the tmva package [59] to achieve an optimal separation between the \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) and \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) processes, independently in the dielectron and dimuon channels.
In order to improve the sensitivity for the extraction of the signal component, the transformation that originally projects the BDT output value in the [\(-1\),\(+1\)] interval is changed into \(\mathrm{BDT'} = \tanh ^{-1}((\mathrm{BDT}+1)/2)\). This allows the purest signal region of the BDT output to be better sampled while keeping an equal-width binning of the BDT variable.
Figure 7 shows the distributions of the discriminants for the two leptonic channels. Good overall agreement between simulation and data is observed in all distributions, and the signal presence is visible at high BDT′ values.
Distributions for transformed BDT discriminants in dielectron (left) and dimuon (right) events. The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations, as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties
A binned maximum likelihood calculation, which is used to fit simultaneously the strength modifiers for the \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) and \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) processes, \(\mu = \sigma ({\mathrm {EW}\,\mathrm {Z} \mathrm {jj}}) / \sigma _\mathrm {LO}({\mathrm {EW}\,\ell \ell \mathrm {jj}})\) and \(\upsilon = \sigma ({\mathrm {DY}})/\sigma _\text {th}({\mathrm {DY}})\), is built from the expected rates for each process. Nuisance parameters are added to modify the expected rates and shapes according to the estimate of the systematic uncertainties affecting the measurement.
The interference between the \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) and \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) processes is included in the fit procedure, and its strength scales as \(\sqrt{\mu \upsilon }\). The interference model is derived from the MadGraph 5_amc@nlo simulation described in Section 3.
The parameters of the model (\(\mu \) and \(\upsilon \)) are determined by maximizing the likelihood. The statistical methodology follows the one used in other CMS analyses [6] using the asymptotic formulas [60]. In this procedure the systematic uncertainties affecting the measurement of the signal and background strengths (\(\mu \) and \(\upsilon \)) are constrained with log-normal probability distributions.
6 Systematic uncertainties
The main systematic uncertainties affecting the measurement are classified into experimental and theoretical sources. Some uncertainties affect only normalizations, while others affect both the normalization and shape of the BDT output distribution.
6.1 Experimental uncertainties
The following experimental uncertainties are considered.
Integrated luminosity A 2.5% uncertainty is assigned to the value of the integrated luminosity [61].
Trigger and selection efficiencies Uncertainties in the efficiency corrections based on control samples in data for the leptonic trigger and offline selections amount to a total of 2–3%, depending on the lepton \(p_{\mathrm {T}} \) and \(\eta \) for both the ee and \(\mu \mu \) channels. These uncertainties are estimated by comparing the lepton efficiencies expected in simulation and measured in data with a tag-and-probe method [62].
Jet energy scale and resolution The energy of the jets enters at the selection level and in the computation of the kinematic variables used to calculate the discriminants. Therefore the uncertainty in the JES affects both the expected event yields and the final shapes. The effect of the JES uncertainty is studied by scaling up and down the reconstructed jet energy by \(p_{\mathrm {T}}\)- and \(\eta \)-dependent scale factors [55]. An analogous approach is used for the JER. The final impact on the signal strength uncertainty amounts to about 3% for JES and 2% for JER.
QGL discriminator The uncertainty in the performance of the QGL discriminator is measured using independent \(\mathrm {Z} \) + jet and dijet data [58]. Shape variations corresponding to the full data versus simulation differences are implemented. The variations are of the order of 10% for lower QGL output values, corresponding to gluon-like jets, and of the order of 5% for larger QGL output values, corresponding to quark-like jets. The final impact on the signal strength uncertainty amounts to about 1%.
Pileup Pileup can affect the identification and isolation of the leptons or the corrected energy of the jets. When jet clustering is performed, pileup can induce a distortion of the reconstructed dijet system because of the contamination from tracks and calorimetric deposits. This uncertainty is evaluated by generating alternative distributions of the number of pileup interactions, corresponding to a 5% uncertainty in the total inelastic pp cross section at \(\sqrt{s}=13\,\text {TeV} \).
Limited number of simulated events For each signal and background simulation, shape variations for the distributions are created by shifting each bin content up or down by its statistical uncertainty. This generates alternatives to the nominal shapes that are used to describe the uncertainty from the limited number of simulated events. Depending on the BDT output bin, the impact on the signal strength uncertainty can be up to 3%.
6.2 Theoretical uncertainties
The following theoretical uncertainties are considered in the analysis.
PDF The PDF uncertainties are evaluated by comparing the nominal distributions to those obtained when using the alternative PDFs of the NNPDF set, including \(\alpha _\mathrm {S}\) variations. The final impact on the signal strength uncertainty is less than 1%.
Factorization and renormalization scales To account for theoretical uncertainties, signal and background shape variations are built by changing the values of \(\mu _\mathrm{F}\) and \(\mu _\mathrm{R}\) from their defaults by factors of 2 or 1/2 in the ME calculation, simultaneously for \(\mu _\mathrm{F}\) and \(\mu _\mathrm{R}\), but independently for each simulated sample. The final impact on the signal strength uncertainty amounts to 6% and 4% respectively for the signal and background variations.
Normalization of top quark and diboson backgrounds Diboson and top quark production processes are modelled with MC simulations. An uncertainty in the normalization of these backgrounds is assigned based on the PDF and \(\mu _\mathrm{F}\), \(\mu _\mathrm{R}\) uncertainties, following calculations in Refs. [41, 42, 46]. The final impact on the signal strength uncertainty amounts to less than 1%.
Interference between \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) and \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) An overall normalization uncertainty and a shape uncertainty are assigned to the interference term in the fit, based on an envelope of prediction with different \(\mu _\mathrm{F}\), \(\mu _\mathrm{R}\) scales. The final impact on the signal strength uncertainty amounts to 2–3%.
Parton showering model The uncertainty in the signal PS model and the event tune is assessed as the full difference of the acceptance and shape predictions using pythia and herwig++. The final impact on the signal strength uncertainty amounts to about 4%.
The largest sources of experimental uncertainty come from the JES and the limited statistics of simulated events; the largest source of theoretical uncertainty comes from the \(\mu _\mathrm{F}\), \(\mu _\mathrm{R}\) scale uncertainties.
7 Measurement of the EW Zjj production cross section
The signal strength, defined for the \(\ell \ell \mathrm {jj}\) final state in the kinematic region described in Sect. 3, is extracted from the fit to the BDT output distribution as discussed in Sect. 5.
In the dielectron channel, the signal strength is measured to be
corresponding to a measured signal cross section
In the dimuon channel, the signal strength is measured to be
corresponding to a measured signal cross section
The results obtained for the different dilepton channels are compatible with each other, and in agreement with the SM predictions.
From the combined fit of the two channels, the signal strength is measured to be
corresponding to a measured signal cross section
in agreement with the SM prediction \(\sigma _\mathrm {LO}(\mathrm {EW}\,\ell \ell \mathrm {jj})=543\pm 24\text {\,fb} \). In the combined fit, the DY strength is \(\upsilon = 0.988 \pm 0.031\). Using the statistical methodology described in Ref. [60], the background-only hypotheses in the dielectron, dimuon, and combined channels are all excluded with significance well above \(5\sigma \).
8 Limits on anomalous gauge couplings
In the framework of EFT, new physics can be described as an infinite series of new interaction terms organized as an expansion in the mass dimension of the operators.
In the EW sector of the SM, the first higher-dimensional operators containing bosons are six-dimensional [15]:
where, as is customary, group indices are suppressed and the mass scale \(\varLambda \) is factorized from the coupling constants c. In Eq. (4), \(W_{\mu \nu }\) is the SU(2) field strength, \(B_{\mu \nu }\) is the U(1) field strength, \(\varPhi \) is the Higgs doublet, and operators with a tilde are the magnetic duals of the field strengths. The first three operators are charge and parity conserving, whereas the two last ones are not. In this paper, models with operators that preserve charge conjugation and parity symmetries can be included in the calculation either individually or in pairs. With these assumptions, the value of coupling constants divided by the mass scale \(c/\varLambda ^2\) are measured.
These operators have a rich phenomenology since they contribute to many multiboson scattering processes at tree level. The operator \(\mathcal {O}_{WWW}\) modifies vertices with 3 to 6 vector bosons, whereas the operators \(\mathcal {O}_{W}\) and \(\mathcal {O}_{B}\) modify both HVV vertices and vertices with 3 or 4 vector bosons. A more detailed description of the phenomenology of these operators can be found in Ref. [63]. Modifications to the ZWW vertex are investigated in this case, since this modifies the \( \mathrm {p}\mathrm {p}\rightarrow \mathrm {Z} \mathrm {jj} \) cross section.
Previously, modifications to these vertices have been studied using anomalous trilinear gauge couplings [64]. The relationship between the dimension-6 operators in Eq. (4) and ATGCs can be found in Ref. [15].
8.1 ATGC signal simulation
ATGC signal events are simulated at LO using MadGraph 5_amc@nlo with the NNPDF3.0 PDF set for signal generation. Showering and hadronization of the events is performed with pythia using the CUETP8M1 tune [28], using the same configuration as in the SM signal sample. The ’EWdim6NLO’ model [15, 24] is used for the generation of anomalous couplings.
For each event, 125 weights are assigned that correspond to a \(5{\times } 5{\times } 5\) grid in \(c_{WWW}/\varLambda ^2 \times c_{W}/\varLambda ^2 \times c_{B}/\varLambda ^2\). Equal bins are used in the interval \([-15, 15]\,\text {TeV}^{-2}\) for \(c_{WWW}/\varLambda ^2\), \([-50, 50]\,\text {TeV}^{-2}\) for \(c_{W}/\varLambda ^2\), and equal bins in the interval \([-500, 500]\,\text {TeV}^{-2}\) for \(c_{B}/\varLambda ^2\).
8.2 Statistical analysis
The measurement of the coupling constants uses templates in the transverse momentum of the dilepton system (\(p_{\mathrm {T} \mathrm {Z}}\)). Because this is well-measured and longitudinally Lorentz invariant, this variable is robust against mismodelling and, in principle, ideal for this purpose. In the electron channel 15 equal bins for \( 0< p_{\mathrm {T} \mathrm {Z}} < 900 \,\text {GeV}\) are used, and 20 equal bins for \(0< p_{\mathrm {T} \mathrm {Z}} < 1200 \,\text {GeV}\) are used in the muon channel, where the last bin contains overflow.
In order to construct the \(p_{\mathrm {T} \mathrm {Z}}\) templates, the associated weights calculated for each event are used to construct a parametrized model of the expected yield in each bin as a function of the values of the dimension-six operators’ coupling constants. For each bin, the ratios of the expected signal yield with dimension-6 operators to the one without (leaving only the SM contribution) are fitted at each point of the grid to a quadratic polynomial. The highest bin is the one with the largest statistical power to detect the presence of higher dimensional operators. Figure 8 shows examples of the final templates, with the expected signal overlaid on the background expectation, for two different hypotheses of dimension-6 operators. The SM distribution is normalized to the expected cross section.
A simultaneous binned fit for the values of the ATGCs is performed in the two lepton channels. A profile likelihood method, the Wald Gaussian approximation and Wilks’ theorem [60] are used to derive one-dimensional and two-dimensional limits at 95% confidence level (CL) on each of the three ATGC parameters and each combination of two ATGC parameters, respectively, while all other parameters are set to their SM values. Systematic and theoretical uncertainties are represented by individual nuisance parameters with log-normal distributions and are profiled in the fit.
8.3 Results
No significant deviation from the SM expectation is observed. Limits on ATGC parameters were previously set by LEP [65], ATLAS [66, 67], and CMS [68, 69]. The LHC semileptonic diboson analyses using 8\(\,\text {TeV}\) data currently set the most stringent limits.
Limits on the EFT parameters are reported and also translated into the equivalent parameters defined in an effective Lagrangian (LEP parametrization) in Ref. [70], without form factors: \(\lambda ^{\gamma } = \lambda ^{\mathrm {Z}} = \lambda \), \(\varDelta {\kappa ^{\mathrm {Z}}} = \varDelta {g_1^{\mathrm {Z}}}-\varDelta {\kappa ^\gamma } \, \tan ^2\theta _{{\mathrm {W}}}\). The parameters \(\lambda \), \(\varDelta {\kappa ^{Z}}\), and \(\varDelta {g_1^{\mathrm {Z}}}\) are considered, where the \(\varDelta \) symbols represents deviations from their respective SM values.
This analysis shows high sensitivity to \(c_{WWW}/\varLambda ^2\) and \(c_{W}/\varLambda ^2\) parameters (equivalently \(\lambda ^{Z}\) and \(\varDelta g_{1}^{Z}\)). The sensitivity to \(c_{B}/\varLambda ^2\) (equivalently \(\varDelta \kappa ^{Z}\)) parameter is very low since the contribution of this operator to the WWZ vertex is suppressed by the weak mixing angle.
Results for 1D limits on \(c_{WWW}\) and \(c_W\) (\(\lambda \) and \(\varDelta g_{1}^{\mathrm {Z}}\)) can be found in Table 2 (Table 3) respectively, and 2D limits are shown in Fig. 9. Results are dominated by the sensitivity in the muon channel due to the larger acceptance for muons. An ATGC signal is not included in the interference between EW and DY production. The effect on the limits is small (\({<}3\%\)).
9 Study of the hadronic and jet activity in Z + jet events
Now that the presence of an SM signal is established, the properties of the hadronic activity in the selected events can be examined. The production of additional jets in a region with a larger contribution from \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) processes is explored in Sect. 9.1. Studies of the region in rapidity with expected low hadron activity (rapidity gap), using track-only observables, are presented in Sect. 9.2. Finally a study of hadronic activity vetoes, using both PF jets and track-only observables, is presented in Sect. 9.3. A significant suppression of the hadronic activity in signal events is expected because the final-state objects originate from pure electroweak interactions, in contrast with the radiative QCD production of jets in \(\mathrm {DY}\,\mathrm {Z} \mathrm {jj}\) events. The reconstructed distributions are compared directly to the prediction obtained with a full simulation of the CMS detector.
In the following studies, event distributions are shown with a selection \(\mathrm {BDT}>0.92\), which allows a signal-enriched region to be selected with a similar fraction of signal and background events. The \(\mathrm {BDT}>0.92\) selection corresponds approximately to a selection \(\mathrm {BDT'}>1.946\) on the transformed BDT′ discriminants shown in Fig. 7.
9.1 Jet activity studies in a high-purity region
In this study, aside from the two tagging jets used in the preselection, all PF jets with a \(p_{\mathrm {T}} >15\,\text {GeV} \) found within the pseudorapidity gap of the tagging jets, \(\eta ^\text {tag jet}_\text {min}< \eta < \eta ^\text {tag jet}_\text {max}\), are used. The background contribution uses the normalizations obtained from the fit discussed in Sect. 7.
The \(p_{\mathrm {T}}\) of the \(p_{\mathrm {T}}\)-leading additional jet, as well as the scalar \(p_{\mathrm {T}}\) sum (\(H_{\mathrm {T}} \)) of all additional jets, are shown in Fig. 10. Data and expectations are generally in reasonable agreement for all distributions in the signal-enriched regions, with some deficit of the simulation predictions for the rate of events with no additional jet activity. A suppression of the emission of additional jets is observed in data, when taking into account the background-only predictions. In the simulation of the signal, the additional jets are produced by the PS (see Sect. 3), so studying these distributions provides insight on the PS model in the rapidity-gap region.
Transverse momentum of the third highest \(p_{\mathrm {T}}\) jet (top row), and \(H_{\mathrm {T}} \) of all additional jets (bottom row) within the pseudorapidity interval of the two tagging jets in dielectron (left) and dimuon (right) events with \(\mathrm {BDT}>0.92\). The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations, as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties. In all distributions the first bin contains events where no additional jet with \( p_{\mathrm {T}} >15\,\text {GeV} \) is present
9.2 Study of the charged-hadron activity
For this study, a collection is formed of high-purity tracks [71] with \(p_{\mathrm {T}} > 0.3\,\text {GeV} \) that are uniquely associated with the main PV in the event. Tracks associated with the two leptons or with the tagging jets are excluded from the selection. The association between the selected tracks and the reconstructed PVs is carried out by minimizing the longitudinal impact parameter, which is defined as the z-distance between the PV and the point of closest approach of the track helix to the PV, labelled \(d_z^\mathrm {PV}\). The association is required to satisfy \(d_z^\mathrm {PV}<2\text {\,mm} \) and \(d_z^\mathrm {PV}<3\delta d_z^\mathrm {PV}\), where \(\delta d_z^\mathrm {PV}\) is the uncertainty in \(d_z^\mathrm {PV}\).
A collection of “soft track jets” is defined by clustering the selected tracks using the anti-\(k_{\mathrm {T}}\) clustering algorithm [51] with a distance parameter of \(R=0.4\). The use of track jets represents a clean and well-understood method [72] to reconstruct jets with energy as low as a few \(\,\text {GeV}\). These jets are not affected by pileup because of the association of the constituent tracks with the hard-scattering vertex [73].
Track jets of low \(p_{\mathrm {T}}\) and within \(\eta ^\text {tag jet}_\text {min}< \eta < \eta ^\text {tag jet}_\text {max} \) are considered for the study of the central hadronic activity between the tagging jets. For each event, the scalar \(p_{\mathrm {T}}\) sum of the soft-track jets with \(p_{\mathrm {T}} >1\,\text {GeV} \) is computed, and referred to as “soft \(H_{\mathrm {T}} \)”. Figure 11 shows the distribution of the soft \(H_{\mathrm {T}}\) in the signal-enriched region (\(\mathrm {BDT}>0.92\)), for the dielectron and dimuon channels, compared to predictions from pythia and herwig++ PS models.
Overall, a reasonable agreement is observed between data and the simulation.
\(H_{\mathrm {T}} \) of additional soft track-jets with \(p_{\mathrm {T}} >1\,\text {GeV}\) in dielectron (left) and dimuon (right) events with \(\mathrm {BDT}>0.92\). Data are compared to MC expectations with the pythia PS model (top row), or the herwig++ PS model (bottom row). The contributions from the different background sources and the signal are shown stacked, with data points superimposed. The expected signal-only contribution is also shown as an unfilled histogram. The lower panels show the relative difference between the data and expectations, as well as the uncertainty envelopes for JES and \(\mu _\mathrm{F,R}\) scale uncertainties
9.3 Study of gap activity vetoes
The efficiency of a gap activity veto corresponds to the fraction of events with a measured gap activity below a given threshold. This efficiency can be studied as a function of the applied threshold, and for different gap activity observables. The veto thresholds studied here start at 15\(\,\text {GeV}\) for gap activities measured with standard PF jets, while they go down to 1\(\,\text {GeV}\) for gap activities measured with soft track jets.
Figure 12 shows the gap activity veto efficiency of combined dielectron and dimuon events in the signal-enriched region when placing an upper threshold on the \(p_{\mathrm {T}}\) of the additional third jet, or on the total \(H_{\mathrm {T}}\) of all additional jets. The observed efficiency in data is compared to expected efficiencies for background-only events, and efficiencies for background plus signal events where the signal is modeled with pythia or herwig++. Data points disfavour the background-only predictions and are in reasonable agreement with the presence of the signal for both PS predictions.
Efficiency of a gap activity veto in dielectron and dimuon events with \(\mathrm {BDT}>0.92\), as a function of the additional jet \(p_{\mathrm {T}}\) (left), and of the total \(H_{\mathrm {T}}\) of additional jets (right). Data points are compared to MC expectations with only DY events, including signal with the pythia PS model, or the herwig++ PS model. The bands represent the MC statistical uncertainty
Figure 13 shows the gap activity veto efficiency of combined dielectron and dimuon events in the signal-enriched region when placing an upper threshold on the \(p_{\mathrm {T}}\) of the leading soft jet, or on the total soft \(H_{\mathrm {T}}\). The data points disfavour the background-only predictions and are in reasonable agreement with the presence of the signal with both PS predictions. Comparisons between the signal gap activity predictions obtained with pythia PS model and the herwig++ PS model have been previously studied [13], and are consistent with the predictions found here. Among the two considered signal models, the data seem to prefer the signal model with herwig++ PS at low gap activity values, whereas the pythia (v8.212) PS predictions seem to be preferred by the data in the case of larger gap activities.
Efficiency of a gap activity veto in dielectron and dimuon events with \(\mathrm {BDT}>0.92\), as a function of the leading soft track-jet \(p_{\mathrm {T}}\) (left), and of the total soft \(H_{\mathrm {T}}\) (right). Data points are compared to MC expectations with only DY events, including signal with the pythia PS model, or the herwig++ PS model. The bands represent the MC statistical uncertainty
10 Summary
The cross section for the electroweak (EW) production of a Z boson in association with two jets in the \(\ell \ell \mathrm {jj}\) final state is measured in proton-proton collisions at \(\sqrt{s}=13\,\hbox {TeV}\) in the kinematic region defined by \(m_{\ell \ell } >50\,\text {GeV} \), \(m_{\mathrm {jj}} >120\,\text {GeV} \), and transverse momenta \(p_\mathrm {T j} > 25\,\text {GeV} \). The result
agrees with the standard model prediction.
The increased cross section and integrated luminosity recorded at \(13\,\hbox {TeV}\), as well as the more precise NLO modelling of background processes, have led to a more precise measurement of the \(\mathrm {EW}\,\mathrm {Z} \mathrm {jj}\) process, relative to earlier CMS and ATLAS results, where the relative precision was approximately 20% [3, 4, 16, 17].
No evidence for anomalous trilinear gauge couplings is found. The following one-dimensional limits at 95% CL are obtained: \(-2.6< c_{WWW}/\varLambda ^2 < 2.6\,\hbox {TeV}^{-2}\) and \(-8.4< c_{W}/\varLambda ^2 < 10.1\,\hbox {TeV}^{-2}\). These results provide the most stringent constraints on \(c_{WWW}\) to date.
In events from a signal-enriched region, the additional hadron activity is also studied, as well as the efficiencies for a gap-activity veto, and generally good agreement is found between data and quantum chromodynamics predictions with either the pythia or herwig++ parton shower and hadronization model.
References
C. Oleari, D. Zeppenfeld, QCD corrections to electroweak \(\ell \nu _\ell \text{ jj }\) and \(\ell ^+\ell ^-\text{ jj }\) production. Phys. Rev. D 69, 093004 (2004). https://doi.org/10.1103/PhysRevD.69.093004. arXiv:hep-ph/0310156
H. Chehime, D. Zeppenfeld, Single W and Z boson production as a probe for rapidity gaps at the SSC. Phys. Rev. D 47, 3898 (1993). https://doi.org/10.1103/PhysRevD.47.3898
CMS Collaboration, Measurement of the hadronic activity in events with a Z and two jets and extraction of the cross section for the electroweak production of a Z with two jets in pp collisions at \(\sqrt{s} = 7\,\text{ TeV }\). JHEP 10 062, (2013). https://doi.org/10.1007/JHEP10(2013)062. arXiv:1305.7389
CMS Collaboration, Measurement of electroweak production of two jets in association with a Z boson in proton-proton collisions at \(\sqrt{s} = 8\,\text{ TeV }\). Eur. Phys. J. C 75 66, (2015). https://doi.org/10.1140/epjc/s10052-014-3232-5. arXiv:1410.3153
ATLAS Collaboration, Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716 1, (2012). https://doi.org/10.1016/j.physletb.2012.08.020. arXiv:1207.7214
CMS Collaboration, Observation of a new boson at a mass of \(125\,\text{ GeV }\) with the CMS experiment at the LHC. Phys. Lett. B 716 30, (2012). https://doi.org/10.1016/j.physletb.2012.08.021. arXiv:1207.7235
CMS Collaboration, Observation of a new boson with mass near \(125\,\text{ GeV }\) in pp collisions at \(\sqrt{s} = 7\) and \(8\,\text{ TeV }\). JHEP 06 081, (2013). https://doi.org/10.1007/JHEP06(2013)081. arXiv:1303.4571
G.-C. Cho et al., Weak boson fusion production of supersymmetric particles at the CERN LHC. Phys. Rev. D 73, 054002 (2006). https://doi.org/10.1103/PhysRevD.73.054002. arXiv:hep-ph/0601063
B. Dutta et al., Vector boson fusion processes as a probe of supersymmetric electroweak sectors at the LHC. Phys. Rev. D 87, 035029 (2013). https://doi.org/10.1103/PhysRevD.87.035029. arXiv:1210.0964
CMS Collaboration, Search for supersymmetry in the vector-boson fusion topology in proton-proton collisions at \( \sqrt{s}=8 \) TeV. JHEP 11 189, (2015). https://doi.org/10.1007/JHEP11(2015)189. arXiv:1508.07628
CMS Collaboration, Search for dark matter and supersymmetry with a compressed mass spectrum in the vector boson fusion topology in proton-proton collisions at \(\sqrt{s} =\) 8 TeV. Phys. Rev. Lett. 118 021802, (2017). https://doi.org/10.1103/PhysRevLett.118.021802. arXiv:1605.09305
J.D. Bjorken, Rapidity gaps and jets as a new physics signature in very high-energy hadron hadron collisions. Phys. Rev. D 47, 101 (1993). https://doi.org/10.1103/PhysRevD.47.101
F. Schissler, D. Zeppenfeld, Parton shower effects on W and Z production via vector boson fusion at NLO QCD. JHEP 04, 057 (2013). https://doi.org/10.1007/JHEP04(2013)057. arXiv:1302.2884
K. Hagiwara, S. Ishihara, R. Szalapski, D. Zeppenfeld, Low-energy effects of new interactions in the electroweak boson sector. Phys. Rev. D 48, 2182 (1993). https://doi.org/10.1103/PhysRevD.48.2182
C. Degrande et al., Effective field theory: a modern approach to anomalous couplings. Ann. Phys. 335, 21 (2013). https://doi.org/10.1016/j.aop.2013.04.016. arXiv:1205.4231
ATLAS Collaboration, Measurement of the electroweak production of dijets in association with a Z-boson and distributions sensitive to vector boson fusion in proton-proton collisions at \(\sqrt{s} = 8\,\text{ TeV }\) using the ATLAS detector. JHEP 04 031, (2014). https://doi.org/10.1007/JHEP04(2014)031. arXiv:1401.7610
ATLAS Collaboration, Measurement of the cross-section for electroweak production of dijets in association with a Z boson in pp collisions at \(\sqrt{s} = 13\,\text{ TeV }\) with the ATLAS detector. Phys. Lett.B 775 206, (2017). https://doi.org/10.1016/j.physletb.2017.10.040. arXiv:1709.10264
CMS Collaboration, Description and performance of track and primary-vertex reconstruction with the CMS tracker. JINST 9 P10009, (2014). https://doi.org/10.1088/1748-0221/9/10/P10009. arXiv:1405.6569
CMS Collaboration, Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at \(\sqrt{s} = 8\,\text{ TeV }\). JINST 10 P06005, (2015). https://doi.org/10.1088/1748-0221/10/06/P06005. arXiv:1502.02701
CMS Collaboration, Performance of CMS muon reconstruction in pp collision events at \(\sqrt{s} = 7\,\text{ TeV }\). JINST 7 P10002, (2012). https://doi.org/10.1088/1748-0221/7/10/P10002. arXiv:1206.4071
CMS Collaboration, Particle-flow reconstruction and global event description with the CMS detector. JINST 12 P10003, (2017). https://doi.org/10.1088/1748-0221/12/10/P10003. arXiv:1706.04965
CMS Collaboration, The CMS experiment at the CERN LHC. JINST 3 S08004, (2008). https://doi.org/10.1088/1748-0221/3/08/S08004
J. Alwall et al., MadGraph 5: going beyond. JHEP 06, 128 (2011). https://doi.org/10.1007/JHEP06(2011)128. arXiv:1106.0522
J. Alwall et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). https://doi.org/10.1007/JHEP07(2014)079. arXiv:1405.0301
T. Sjöstrand, S. Mrenna, P. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852 (2008). https://doi.org/10.1016/j.cpc.2008.01.036. arXiv:0710.3820
T. Sjöstrand et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159 (2015). https://doi.org/10.1016/j.cpc.2015.01.024. arXiv:1410.3012
NNPDF Collaboration, Parton distributions for the LHC Run II. JHEP 04 040, (2015). https://doi.org/10.1007/JHEP04(2015)040. arXiv:1410.8849
CMS Collaboration, Event generator tunes obtained from underlying event and multiparton scattering measurements. Eur. Phys. J. C 76 155, (2016). https://doi.org/10.1140/epjc/s10052-016-3988-x. arXiv:1512.00815
K. Arnold et al., VBFNLO: a parton level Monte Carlo for processes with electroweak bosons. Comput. Phys. Commun. 180, 1661 (2009). https://doi.org/10.1016/j.cpc.2009.03.006. arXiv:0811.4559
J. Baglio et al., VBFNLO: a parton level Monte Carlo for processes with electroweak bosons—manual for version 2.7.0. (2011). arXiv:1107.4038
K. Arnold et al., Release note—VBFNLO-2.6.0. (2012). arXiv:1207.4975
M. Bähr et al., Herwig++ physics and manual. Eur. Phys. J. C 58, 639 (2008). https://doi.org/10.1140/epjc/s10052-008-0798-9. arXiv:0803.0883
M.H. Seymour, A. Siodmok, Constraining MPI models using \(\sigma_{\text{ eff }}\) and recent Tevatron and LHC underlying event data. JHEP 10, 113 (2013). https://doi.org/10.1007/JHEP10(2013)113. arXiv:1307.5015
R. Frederix, S. Frixione, Merging meets matching in MC@NLO. JHEP 12, 061 (2012). https://doi.org/10.1007/JHEP12(2012)061. arXiv:1209.6215
M.L. Mangano, M. Moretti, F. Piccinini, M. Treccani, Matching matrix elements and shower evolution for top-quark production in hadronic collisions. JHEP 01, 013 (2007). https://doi.org/10.1088/1126-6708/2007/01/013. arXiv:hep-ph/0611129
J. Alwall et al., Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions. Eur. Phys. J. C 53, 473 (2008). https://doi.org/10.1140/epjc/s10052-007-0490-5. arXiv:0706.2569
K. Melnikov, F. Petriello, Electroweak gauge boson production at hadron colliders through \(\cal{O}(\alpha _S^2)\). Phys. Rev. D 74, 114017 (2006). https://doi.org/10.1103/PhysRevD.74.114017. arXiv:hep-ph/0609070
P. Nason, A new method for combining NLO QCD with shower Monte Carlo algorithms. JHEP 11, 040 (2004). https://doi.org/10.1088/1126-6708/2004/11/040. arXiv:hep-ph/0409146
S. Frixione, P. Nason, C. Oleari, Matching NLO QCD computations with parton shower simulations: the POWHEG method. JHEP 11, 070 (2007). https://doi.org/10.1088/1126-6708/2007/11/070. arXiv:0709.2092
S. Alioli, P. Nason, C. Oleari, E. Re, A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX. JHEP 06, 043 (2010). https://doi.org/10.1007/JHEP06(2010)043. arXiv:1002.2581
N. Kidonakis, Differential and total cross sections for top pair and single top production. in Proceedings of the XX International Workshop on Deep-Inelastic Scattering and Related Subjects. Bonn, Germany (2012). https://doi.org/10.3204/DESY-PROC-2012-02/251. arXiv:1205.3453
M. Czakon, P. Fiedler, A. Mitov, Total top-quark pair-production cross section at hadron colliders through \(\cal{O}(\alpha_S^4)\). Phys. Rev. Lett. 110, 252004 (2013). https://doi.org/10.1103/PhysRevLett.110.252004. arXiv:1303.6254
S. Alioli, P. Nason, C. Oleari, E. Re, NLO single-top production matched with shower in POWHEG: \(s\)- and \(t\)-channel contributions. JHEP 09, 111 (2009). https://doi.org/10.1088/1126-6708/2009/09/111. arXiv:0907.4076. [Erratum: 10.1007/JHEP02(2010) 011]
E. Re, Single-top Wt-channel production matched with parton showers using the POWHEG method. Eur. Phys. J. C 71, 1547 (2011). https://doi.org/10.1140/epjc/s10052-011-1547-z. arXiv:1009.2450
N. Kidonakis, Top quark production, in Proceedings, Helmholtz International Summer School on Physics of Heavy Quarks and Hadrons (HQ 2013): JINR, Dubna, Russia, July 15–28, 2013, p. 139. (2014). https://doi.org/10.3204/DESY-PROC-2013-03/Kidonakis. arXiv:1311.0283
J.M. Campbell, R.K. Ellis, MCFM for the Tevatron and the LHC. Nucl. Phys. B Proc. Suppl. 205–206, 10 (2010). https://doi.org/10.1016/j.nuclphysbps.2010.08.011. arXiv:1007.3492
GEANT4 Collaboration, GEANT4—a simulation toolkit. Nucl. Instrum. Meth. A 506 250, (2003). https://doi.org/10.1016/S0168-9002(03)01368-8
J. Allison et al., GEANT4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270 (2006). https://doi.org/10.1109/TNS.2006.869826
NNPDF Collaboration, Parton distributions with LHC data. Nucl. Phys. B 867 244, (2013). https://doi.org/10.1016/j.nuclphysb.2012.10.003. arXiv:1207.1303
CMS Collaboration, The CMS trigger system. JINST 12 P01020, (2017). https://doi.org/10.1088/1748-0221/12/01/P01020. arXiv:1609.02366
M. Cacciari, G.P. Salam, G. Soyez, The anti-\(k_t\) jet clustering algorithm. JHEP 04, 063 (2008). https://doi.org/10.1088/1126-6708/2008/04/063. arXiv:0802.1189
M. Cacciari, G.P. Salam, G. Soyez, FastJet user manual. Eur. Phys. J. C 72, 1896 (2012). https://doi.org/10.1140/epjc/s10052-012-1896-2. arXiv:1111.6097
Particle Data Group, C. Patrignani et al., Review of particle physics. Chin. Phys. C 40 100001 (2016). https://doi.org/10.1088/1674-1137/40/10/100001
M. Cacciari, G.P. Salam, Dispelling the \(N^{3}\) myth for the \(k_{t}\) jet-finder. Phys. Lett. B 641, 57 (2006). https://doi.org/10.1016/j.physletb.2006.08.037. arXiv:hep-ph/0512210
CMS Collaboration, Determination of jet energy calibration and transverse momentum resolution in CMS. JINST 6 P11002 (2011). https://doi.org/10.1088/1748-0221/6/11/P11002. arXiv:1107.4277
CMS Collaboration, Jet algorithms performance in \(13\,\text{ TeV }\) data. CMS Physics Analysis Summary CMS-PAS-JME-16-003 (2017)
CMS Collaboration, Pileup jet identification. CMS Physics Analysis Summary (2013)
CMS Collaboration, Performance of quark/gluon discrimination using pp collision data at \(\sqrt{s} = 8\,\text{ TeV }\). CMS Physics Analysis Summary CMS-PAS-JME-13-002 (2013)
H. Voss, A. Höcker, J. Stelzer, F. Tegenfeldt, TMVA, the toolkit for multivariate data analysis with ROOT, in XIth International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT), p. 40. (2007). arXiv:physics/0703039
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011). https://doi.org/10.1140/epjc/s10052-011-1554-0. arXiv:1007.1727. [Erratum: 10.1140/epjc/s10052-013-2501-z]
CMS Collaboration, CMS luminosity measurements for the 2016 data taking period. CMS Physics Analysis Summary CMS-PAS-LUM-17-001 (2017)
CMS Collaboration, Measurements of inclusive W and Z cross sections in pp collisions at \(\sqrt{s}=7\,\text{ TeV }\). JHEP 01 080, (2011). https://doi.org/10.1007/JHEP01(2011)080. arXiv:1012.2466
C. Degrande et al., Studies of vector boson scattering and triboson production with DELPHES parametrized fast simulation for Snowmass 2013. (2013). arXiv:1309.7452
Particle Data Group, Review of particle physics. J. Phys. G 37 075021 (2010). https://doi.org/10.1088/0954-3899/37/7A/075021
The LEP Electroweak Working Group, Electroweak measurements in electron-positron collisions at W-boson-pair energies at LEP. Phys. Rept. 532 119 (2013). https://doi.org/10.1016/j.physrep.2013.07.004. arXiv:1302.3415
ATLAS Collaboration, Measurement of \(\rm WW/WZ\rightarrow \ell \nu \rm q q^{\prime } \rm \) production with the hadronically decaying boson reconstructed as one or two jets in pp collisions at \(\sqrt{s}=8\,\text{ TeV }\) with ATLAS, and constraints on anomalous gauge couplings. Eur. Phys. J. C 77 563 (2017). https://doi.org/10.1140/epjc/s10052-017-5084-2. arXiv:1706.01702
ATLAS Collaboration, Measurements of \(\rm W^{\pm }\rm Z\rm \) production cross sections in pp collisions at \(\sqrt{s} = 8\,\text{ TeV }\) with the ATLAS detector and limits on anomalous gauge boson self-couplings. Phys. Rev. D 93 092004 (2016). https://doi.org/10.1103/PhysRevD.93.092004. arXiv:1603.02151
CMS Collaboration, Search for anomalous couplings in boosted \(\rm WW/WZ\rightarrow \ell \nu \rm q \overline{q} \rm \) production in proton-proton collisions at \(\sqrt{s} = 8\,\text{ TeV }\). Phys. Lett. B 772 21 (2017). https://doi.org/10.1016/j.physletb.2017.06.009. arXiv:1703.06095
CMS Collaboration, Measurement of the WZ production cross section in pp collisions at \(\sqrt{s} = 7\) and \(8\,\text{ TeV }\) and search for anomalous triple gauge couplings at \(\sqrt{s} = 8\,\text{ TeV }\). Eur. Phys. J. C 77 236 (2017). https://doi.org/10.1140/epjc/s10052-017-4730-z. arXiv:1609.05721
K. Hagiwara, R.D. Peccei, D. Zeppenfeld, Probing the weak boson sector in \(\rm e^{+} e^{-} \rightarrow W^{+} W^{-} \). Nucl. Phys. B 282, 253 (1987). https://doi.org/10.1016/0550-3213(87)90685-7
CMS Collaboration, Tracking and primary vertex results in first \(7\,\text{ TeV }\) collisions. CMS Physics Analysis Summary CMS-PAS-TRK-10-005, (2010)
CMS Collaboration, Commissioning of trackjets in pp collisions at \(\sqrt{s} = 7\,\text{ TeV }\)., CMS Physics Analysis Summary CMS-PAS-JME-10-006 (2010)
CMS Collaboration, Performance of jet reconstruction with charged tracks only. CMS Physics Analysis Summary CMS-PAS-JME-08-001 (2009)
Acknowledgements
We congratulate our colleagues in the CERN accelerator departments for the excellent performance of the LHC and thank the technical and administrative staffs at CERN and at other CMS institutes for their contributions to the success of the CMS effort. In addition, we gratefully acknowledge the computing centers and personnel of the Worldwide LHC Computing Grid for delivering so effectively the computing infrastructure essential to our analyses. Finally, we acknowledge the enduring support for the construction and operation of the LHC and the CMS detector provided by the following funding agencies: the Austrian Federal Ministry of Science, Research and Economy and the Austrian Science Fund; the Belgian Fonds de la Recherche Scientifique, and Fonds voor Wetenschappelijk Onderzoek; the Brazilian Funding Agencies (CNPq, CAPES, FAPERJ, and FAPESP); the Bulgarian Ministry of Education and Science; CERN; the Chinese Academy of Sciences, Ministry of Science and Technology, and National Natural Science Foundation of China; the Colombian Funding Agency (COLCIENCIAS); the Croatian Ministry of Science, Education and Sport, and the Croatian Science Foundation; the Research Promotion Foundation, Cyprus; the Secretariat for Higher Education, Science, Technology and Innovation, Ecuador; the Ministry of Education and Research, Estonian Research Council via IUT23-4 and IUT23-6 and European Regional Development Fund, Estonia; the Academy of Finland, Finnish Ministry of Education and Culture, and Helsinki Institute of Physics; the Institut National de Physique Nucléaire et de Physique des Particules / CNRS, and Commissariat à l’Énergie Atomique et aux Énergies Alternatives / CEA, France; the Bundesministerium für Bildung und Forschung, Deutsche Forschungsgemeinschaft, and Helmholtz-Gemeinschaft Deutscher Forschungszentren, Germany; the General Secretariat for Research and Technology, Greece; the National Scientific Research Foundation, and National Innovation Office, Hungary; the Department of Atomic Energy and the Department of Science and Technology, India; the Institute for Studies in Theoretical Physics and Mathematics, Iran; the Science Foundation, Ireland; the Istituto Nazionale di Fisica Nucleare, Italy; the Ministry of Science, ICT and Future Planning, and National Research Foundation (NRF), Republic of Korea; the Lithuanian Academy of Sciences; the Ministry of Education, and University of Malaya (Malaysia); the Mexican Funding Agencies (BUAP, CINVESTAV, CONACYT, LNS, SEP, and UASLP-FAI); the Ministry of Business, Innovation and Employment, New Zealand; the Pakistan Atomic Energy Commission; the Ministry of Science and Higher Education and the National Science Centre, Poland; the Fundação para a Ciência e a Tecnologia, Portugal; JINR, Dubna; the Ministry of Education and Science of the Russian Federation, the Federal Agency of Atomic Energy of the Russian Federation, Russian Academy of Sciences, the Russian Foundation for Basic Research and the Russian Competitiveness Program of NRNU “MEPhI”; the Ministry of Education, Science and Technological Development of Serbia; the Secretaría de Estado de Investigación, Desarrollo e Innovación, Programa Consolider-Ingenio 2010, Plan de Ciencia, Tecnología e Innovación 2013-2017 del Principado de Asturias and Fondo Europeo de Desarrollo Regional, Spain; the Swiss Funding Agencies (ETH Board, ETH Zurich, PSI, SNF, UniZH, Canton Zurich, and SER); the Ministry of Science and Technology, Taipei; the Thailand Center of Excellence in Physics, the Institute for the Promotion of Teaching Science and Technology of Thailand, Special Task Force for Activating Research and the National Science and Technology Development Agency of Thailand; the Scientific and Technical Research Council of Turkey, and Turkish Atomic Energy Authority; the National Academy of Sciences of Ukraine, and State Fund for Fundamental Researches, Ukraine; the Science and Technology Facilities Council, UK; the US Department of Energy, and the US National Science Foundation.
Individuals have received support from the Marie-Curie program and the European Research Council and Horizon 2020 Grant, contract No. 675440 (European Union); the Leventis Foundation; the A. P. Sloan Foundation; the Alexander von Humboldt Foundation; the Belgian Federal Science Policy Office; the Fonds pour la Formation à la Recherche dans l’Industrie et dans l’Agriculture (FRIA-Belgium); the Agentschap voor Innovatie door Wetenschap en Technologie (IWT-Belgium); the Ministry of Education, Youth and Sports (MEYS) of the Czech Republic; the Council of Scientific and Industrial Research, India; the HOMING PLUS program of the Foundation for Polish Science, cofinanced from European Union, Regional Development Fund, the Mobility Plus program of the Ministry of Science and Higher Education, the National Science Center (Poland), contracts Harmonia 2014/14/M/ST2/00428, Opus 2014/13/B/ST2/02543, 2014/15/B/ST2/03998, and 2015/19/B/ST2/02861, Sonata-bis 2012/07/E/ST2/01406; the National Priorities Research Program by Qatar National Research Fund; the Programa Severo Ochoa del Principado de Asturias; the Thalis and Aristeia programs cofinanced by EU-ESF and the Greek NSRF; the Rachadapisek Sompot Fund for Postdoctoral Fellowship, Chulalongkorn University and the Chulalongkorn Academic into Its 2nd Century Project Advancement Project (Thailand); the Welch Foundation, contract C-1845; and the Weston Havens Foundation (USA).
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Sirunyan, A.M., Tumasyan, A., Adam, W. et al. Electroweak production of two jets in association with a Z boson in proton–proton collisions at \(\sqrt{s}= \) 13\(\,\text {TeV}\). Eur. Phys. J. C 78, 589 (2018). https://doi.org/10.1140/epjc/s10052-018-6049-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-6049-9