1 Introduction

One of the remarkable properties of non-Abelian gauge theories (NAGTs) is the Reggeization of elementary particles in perturbation theory. In contrast to Quantum Electrodynamics (QED), where the electron does Reggeize [1], but the photon remains elementary [2], the criteria of Reggeization formulated in [2] are fulfilled in NAGTs for all particles [3, 4]. In Ref. [5, 6], by direct two-loop calculations in the leading logarithmic approximation (LLA), when in each order of perturbation theory only terms with the highest powers of the logarithm of c.m.s. energy \(\sqrt{s}\) are retained, it was shown that the gauge bosons of NAGTs do Reggeize and give the main contribution to the scattering amplitudes with the quantum numbers of the gauge bosons and negative signature (symmetry with respect to the replacement \(s\leftrightarrow u\simeq s\) ) in the t-channel. Then, based on the three-loop calculations, it was assumed that the Regge form of such amplitudes is valid in the LLA in all orders of perturbation theory, and self-consistency of this assumption was checked [7,8,9]. A little bit later, the same was done for the amplitudes with the quark quantum numbers and positive signature in the t-channel [10, 11]. Therefore, in Quantum Chromodynamics (QCD), which is a particular case of NAGTs, all elementary particles, i.e. quarks and gluons, do Reggeize.

Reggeization of elementary particles is very important for the theoretical description of high energy processes. The gluon Reggeization is especially important because it determines the high energy behaviour of non-decreasing with energy cross sections in perturbative QCD. In particular, it appears to be the basis of the famous BFKL (Balitskii–Fadin–Kuraev–Lipatov) equation, which was first derived in non-Abelian theories with spontaneously broken symmetry [7,8,9, 12, 13] and whose applicability in QCD was then shown [14, 15]. In the BFKL approach the primary Reggeon is the Reggeized gluon. The Pomeron, which determines the high energy behaviour of cross sections, appears as a compound state of two Reggeized gluons, and the Odderon, responsible for the difference of particle and antiparticle cross sections, as a compound state of three Reggeized gluons.

The Reggeization allows to express an infinite number of amplitudes through several Reggeon vertices and the Reggeized gluon trajectory. It means definite form not only of elastic amplitudes, but of inelastic amplitudes in the multi-Regge kinematics (MRK) as well. This kinematics is very important because it gives dominant contributions to cross sections and to discontinuities of amplitudes with fixed momentum transfer in the unitarity relations. In this kinematics all particles have fixed (not growing with s) transverse momenta and are combined into jets with limited invariant mass of each jet and large (growing with s) invariant masses of any pair of the jets. In the LLA each jet contains only one gluon; in the next-to-leading logarithmic approximation (NLLA), where the eldest of non-leading terms are also retained, one has to account production of \(Q\bar{Q}\) and GG jets.

It is extremely important that in these approximations elastic amplitudes and real parts of inelastic amplitudes in the MRK with negative signature in cross-channels are determined by the Regge pole contributions and have a simple factorized form (we will call it pole Regge form). Due to this, the Reggeization provides a simple derivation of the BFKL equation in the LLA and in the NLLA.

Validity of this form is proved now in all orders of perturbation theory in the coupling constant g both in the LLA [16], and in the NLLA (see [17, 18] and references therein).

The pole Regge form is violated in the NNLLA. The first observation of the violation was done [19] at consideration of the high-energy limit of the two-loop amplitudes for gg, gq and qq scattering. The discrepancy appears in non-logarithmic terms. If the pole Regge form would be correct in the NNLLA, they should satisfy a definite condition (factorization condition), because three amplitudes should be expressed in terms of two Reggeon–Particle–Particle vertices.

Detailed consideration of the terms responsible for breaking of the pole Regge form in two-loop and three-loop amplitudes of elastic scattering in QCD was performed in [20,21,22]. In particular, the non-logarithmic terms violating the pole Regge form at two-loops were recovered and not satisfying the factorization condition single-logarithmic terms at three loops were found using the techniques of infrared factorization.

It is necessary to say that, in general, breaking the pole Regge form is not a surprise. It is well known that Regge poles in the complex angular momenta plane generate Regge cuts. Moreover, in amplitudes with positive signature the Regge cuts appear already in the LLA. In particular, the BFKL Pomeron is the two-Reggeon cut in the complex angular momenta plane. But in amplitudes with negative signature Regge cuts appear only in the NNLLA. It is natural to expect that the observed violation of the pole Regge form can be explained by their contributions. As it is shown in [23, 24], this is actually so.

Here the results on which the report [23] at the workshop “Diffraction 2016” was based are presented. Since for violation of the pole Regge form only amplitudes with the gluon quantum numbers in the t-channel and negative signature are important, only such amplitudes are considered below. The three-Reggeon cuts in other channels with negative signature are discussed in [24, 25]

2 Lowest order contribution

Let us consider parton (quark and gluon) elastic scattering amplitudes with negative signature in the two-loop approximation, and try to find the contribution of the Regge cut in them. Due to the signature conservation the cut with negative signature has to be a three-Reggeon one. Since our Reggeon is the Reggeized gluon, the cut starts with the diagrams with three t-channels gluons. They are presented in Fig. 1, where particles \(A, A'\) and \(B, B'\) can be quarks or gluons.

Fig. 1
figure 1

Three-gluon exchange diagrams

Full size image

The colour structures of the diagrams in Fig. 1 can be decomposed into irreducible representations of the colour group in the t-channel. Since we confine ourselves to amplitudes with the gluon quantum numbers in the t-channel, we need to consider only the adjoint representations. Moreover, since we are interested in the negative signature, for gluon scattering we need to consider only the antisymmetric adjoint representation. In other words, in the colour decomposition we need only the same structure as in the one-gluon exchange,

$$\begin{aligned} C_{AB}^{A'B'} =\langle A'|\mathcal{T}^a|A\rangle \langle B'|\mathcal{T}^a|B\rangle , \end{aligned}$$
(1)

where \(\mathcal{T}^a\) are the colour group generators in the corresponding representations, \([\mathcal{T}^a, \mathcal{T}^b] =if_{abc} \mathcal{T}^c\); \(\mathcal{T}^a_{bc} = T^a_{bc} = -if_{abc} \) for gluons and \(\mathcal{T}^a_{bc} = -t^a_{bc}\) for quarks.

Matrix elements corresponding to the diagrams in Fig. 1 contain this colour structure with the coefficients \(C^\alpha _{ij}\), where \(\alpha =a, b, c,d,e,f\) and \(ij=gg, gq\) and qq for gluon–gluon, gluon–quark and quark–quark scattering correspondingly. They are given by the convolutions \(\text{ Tr }(\mathcal{T}^a\mathcal{T}^b\mathcal{T}^c\mathcal{T}^d)\text{ Tr }(\mathcal{T}^{a_1}\mathcal{T}^{b_1}\mathcal{T}^{c_1}\mathcal{T}^d)\), where \(a_1b_1c_1\) are obtained from abc by all possible permutations.

Using the equalities

$$\begin{aligned} \text{ Tr }(t^a t^b)=\frac{1}{2} \delta ^{ab} , \quad t^a t^b{=}\frac{1}{2N_c}\delta ^{ab} I {+} \frac{1}{2} (d^{abc}+if^{abc})t^c ,\nonumber \\ \end{aligned}$$
(2)

one easily finds

$$\begin{aligned} \text{ Tr }(t^at^bt^ct^d)= & {} \frac{1}{{N_c}}\delta ^{ad}\delta ^{bc}+\frac{1}{8}\left( d^{adi}d^{bci} \right. \nonumber \\&\left. +f^{adi}f^{bci} +id^{adi}f^{bci}-if^{adi}d^{bci}\right) . \end{aligned}$$
(3)

As it follows from (2), the tensor \(\text{ Tr }(T^aT^bT^cT^d)\) can be written as

$$\begin{aligned} \text{ Tr }(T^aT^bT^cT^d) = 4 \text{ Tr }([t^a,t^i][t^j, t^b])\text{ Tr }([t^c,t^j][t^i, t^d]) . \nonumber \\ \end{aligned}$$
(4)

Using this representation, the completeness condition for the matrices \(t^a\) and the identity matrix I in the form

$$\begin{aligned} \text{ Tr }(t^i A) \text{ Tr }(t^i B) = -\frac{1}{2N_c}\text{ Tr }(A) \text{ Tr }(B) +\frac{1}{2}\text{ Tr }(AB) , \end{aligned}$$
(5)

and the relations (which are easily obtained from the completeness condition)

$$\begin{aligned} t^at^a= & {} C_F I, \quad t^at^bt^a=\left( C_F-\frac{C_A}{2}\right) t^b, \nonumber \\ t^at^bt^ct^a= & {} \frac{1}{4}\delta ^{bc}I +\left( C_F-\frac{C_A}{2}\right) t^bt^c , \end{aligned}$$
(6)

where \(C_F\) and \(C_A\) are the values of the Casimir operators in the fundamental and adjoint representations,

$$\begin{aligned} C_F=\frac{N_c^2-1}{2N_c} , \quad C_A=N_c , \end{aligned}$$
(7)

we obtain

$$\begin{aligned} \text{ Tr }(T^aT^bT^cT^d)= & {} \delta ^{ad}\delta ^{bc}+\frac{1}{2}(\delta ^{ab}\delta ^{cd}+\delta ^{ac}\delta ^{bd}) \nonumber \\&+\frac{{N_c}}{4}(f^{adi}f^{bci}+d^{adi}d^{bci}) . \end{aligned}$$
(8)

The convolutions can be performed with the help of the relations

$$\begin{aligned} \text{ Tr } (T^aD^b )= & {} 0 , \quad \text{ Tr } (T^aT^b )=N_c\delta ^{ab}, \text{ Tr } (D^aD^b )=\frac{N^2_c-4}{N_c}\delta ^{ab}, \nonumber \\\end{aligned}$$
(9)
$$\begin{aligned} \text{ Tr } (T^aT^bT^c )= & {} i\frac{N_c}{2}f^{abc}, \text{ Tr } (T^aT^bD^c )=\frac{N_c}{2}d^{abc} , \end{aligned}$$
(10)
$$\begin{aligned} \text{ Tr } (D^aD^bT^c )= & {} i\frac{N^2_c-4}{2N_c}f^{abc}, \nonumber \\ \text{ Tr } (D^aD^bD^c )= & {} \frac{N^2_c-12}{2N_c}d^{abc}, \end{aligned}$$
(11)

where \(D^a_{bc}= d_{abc}\). They can be derived analogously to (4). As the result, one obtains

$$\begin{aligned} C^a_{gg}= & {} \frac{3}{2}+\frac{N_c^2}{8} , \; C^a_{gq} =\frac{1}{4}+\frac{N_c^2}{8} , \quad C^a_{qq} =\frac{1}{4}\left( 1+\frac{3}{N_c^2}\right) , \nonumber \\ \end{aligned}$$
(12)
$$\begin{aligned} C^b_{gg}= & {} C^c_{gg}=C^d_{gg} =C^e_{gg} =C_{gg} =\frac{3}{2} , \nonumber \\ C^b_{gq}= & {} C^c_{gq}=C^d_{gq} =C^e_{gq}= C_{gq} =\frac{1}{4} , \end{aligned}$$
(13)
$$\begin{aligned} C^b_{qq}= & {} C^c_{qq}=C^d_{qq} =C^e_{qq} = C_{qq} =\frac{1}{4}\left( -1+\frac{3}{N_c^2}\right) , \end{aligned}$$
(14)
$$\begin{aligned} C^f_{gg}= & {} \frac{3}{2}+\frac{N_c^2}{8} , C^f_{gq} =\frac{1}{4}+\frac{N_c^2}{8} , \nonumber \\ C^f_{qq}= & {} \frac{1}{4}\left( N_c^2-3+\frac{3}{N_c^2}\right) . \end{aligned}$$
(15)

The contribution \(A^{Fig.1}\) of the diagrams in Fig. 1 to the scattering amplitudes with the colour structures (1) can be written as

$$\begin{aligned} A_{ij}^{Fig.1}= & {} \langle A'|\mathcal{T}^a|A\rangle \langle B'|\mathcal{T}^a|B\rangle \left[ C_{ij} A^{eik} + \frac{N_c^2}{8} (A_{ij}^{a}+A_{ij}^{f} ) \right. \nonumber \\&\left. + \delta _{i,q}\delta _{j,q}\frac{4-N_c^2}{8} (A_{ij}^{a}-A_{ij}^{f} )\right] , \end{aligned}$$
(16)

where \(A_{ij}^{\alpha }\) is the contribution of the diagram \(\alpha \) with omitted colour factors and \(A_{ij}^{eik} = \sum _\alpha A_{ij}^{\alpha }\). Note that \(A^{eik}\) is gauge invariant. It can be easily found:

$$\begin{aligned} A^{eik} = g^2\frac{s}{t}\left( \frac{-4\pi ^2}{3}\right) g^4\,\vec {q}^{\;2}\, A^{(3)}_\perp , \end{aligned}$$
(17)

where \(A^{(3)}_\perp \) is presented by the diagram in Fig. 2 in the transverse momentum space, and is given by the integral

Fig. 2
figure 2

Diagrammatic representation of \(A^{(3)}_\perp \) in the transverse momentum space

Full size image
$$\begin{aligned} A^{(3)}_\perp= & {} \int \frac{{d^{2+2\epsilon }l_1}{d^{2+2\epsilon } l_2}}{(2\pi )^{2(3+2\epsilon )}\vec l_1^{\, 2}\vec l_2^{\, 2}(\vec q -\vec l_1-\vec l_2)^2} \nonumber \\= & {} 3C_{\Gamma }^2\frac{4}{\epsilon ^2}\frac{(\vec q^{\, 2})^{2\epsilon }}{\vec q^{\, 2}} \frac{\Gamma ^2(1+2\epsilon )\Gamma (1-2\epsilon )}{\Gamma (1+\epsilon )\Gamma ^2(1-\epsilon )\Gamma (1+3\epsilon )} , \end{aligned}$$
(18)

where

$$\begin{aligned}&C_{\Gamma }= \frac{\Gamma (1-\epsilon )\Gamma ^2(1+\epsilon )}{(4\pi )^{2+\epsilon }\Gamma (1+2\epsilon )} = \frac{\Gamma (1-\epsilon )\Gamma ^2(1+\epsilon )}{(4\pi )^{2+\epsilon }}\nonumber \\&\qquad \left( 1-\epsilon ^2 \zeta (2)+2\epsilon ^3 \zeta (3)-\frac{9}{4}\epsilon ^4 \zeta (4)+ \cdots \right) , \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\Gamma ^2(1+2\epsilon )\Gamma (1-2\epsilon )}{\Gamma (1+\epsilon )\Gamma ^2(1-\epsilon )\Gamma (1+3\epsilon )} \nonumber \\&\quad =1+ 6\epsilon ^3 \zeta (3)-9\epsilon ^4 \zeta (4)+ \cdots ) . \end{aligned}$$
(20)

Note that we use the ”infrared” \(\epsilon \), \(\epsilon = (D-4)/2\), D is the space-time dimension.

The last term in (16) is not relevant; it is the contribution of positive signature in the quark–quark scattering. The second term does not violate the pole factorization and can be assigned to the Reggeized gluon contribution. This is not true for the first term, because

$$\begin{aligned} 2C_{gq}\ne & {} C_{qq}+C_{gg} , \quad 2C_{gq} - C_{qq} - C_{gg} \nonumber \\= & {} -\frac{1}{4}\left( 1+\frac{1}{N_c^2}\right) , \end{aligned}$$
(21)

which means violation of the pole factorization. It is not difficult to see that the nonvanishing in the limit \(\epsilon \rightarrow 0\) part of the amplitudes \(C_{ij}A^{(eik)}\) coincides with \(g^2(s/t)(\alpha _s/\pi )^2 \mathcal{R}_{ij}^{(2), 0, [8]}\) of the paper [22]. The values \(\mathcal{R}_{ij}^{(2), 0, [8]}\) are given there in Eq. (4.35), \((\alpha _s/\pi )^2 \mathcal{R}_{ij}^{(2), 0, [8]}\) is the first (two-loop, non-logarithmic) contributions to the ”non-factorizing remainder function” \(\mathcal{R}^{[8]}_{ij}\) introduced in Eq. (3.1) of [22]. This means that the violation of the pole factorization discovered in [19] and analysed in [20,21,22] is due to the eikonal part of the contribution of the diagrams with three-gluon exchange.

However, one can not affirm that this part is given entire by the three-Reggeon cut. Indeed, it can contain also the Reggeized gluon contribution. In fact, a non-factorizing remainder function is not uniquely defined. The definition used in [22] was chosen for convenience of comparison of the high energy and infrared factorizations.

3 Radiative corrections

The problem of separation of the pole and cut contributions can be solved by consideration of logarithmic radiative corrections to them. In the case of the Reggeized gluon contribution the correction comes solely from the Regge factor, so that the first order correction (more strictly, its relative value; this is assumed also in the following) is \(\omega (t)\ln s\), where \(\omega (t)\) is the gluon trajectory,

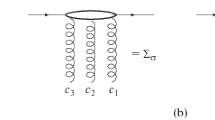
$$\begin{aligned} \omega (t)= & {} -g^2 N_c {\vec q^{\, 2}} \int \frac{d^{2+2\epsilon }l}{2(2\pi )^{(3+2\epsilon )}\vec l^{\, 2}(\vec q -\vec l)^2} \nonumber \\= & {} -g^2 N_c C_{\Gamma }\frac{2}{\epsilon }(\vec q^{\, 2})^{\epsilon } . \end{aligned}$$
(22)

In the case of the three-Reggeon cut, one has to take into account the Reggeization of each of three gluons and the interaction between them. The Reggeization gives \(\ln s\) with the coefficient \(3C_R\), where \(A^{(3)}_\perp C_R\) is represented by the diagram in Fig. 3 in the transverse momentum space, and is given by the integral

$$\begin{aligned} A^{(3)}_\perp C_R= & {} -g^2 N_c C_{\Gamma }\frac{2}{\epsilon } \int \frac{d^{2+2\epsilon }l_1\,d^{2+2\epsilon } l_2}{(2\pi )^{2(3+2\epsilon )}\vec l_1^{\, 2}\vec l_2^{\, 2}(\vec q -\vec l_1-\vec l_2)^{2(1-\epsilon )}}\nonumber \\= & {} -g^2 N_c C_{\Gamma }\frac{4}{3\epsilon } (\vec q^{\, 2})^{\epsilon }\nonumber \\&\times \frac{\Gamma (1-3\epsilon )\Gamma (1+2\epsilon )\Gamma (1+3\epsilon )}{\Gamma (1-\epsilon )\Gamma (1-2\epsilon )\Gamma (1+\epsilon ) \Gamma (1+4\epsilon )}A^{(3)}_\perp .\nonumber \\ \end{aligned}$$
(23)
Fig. 3
figure 3

Diagrammatic representation of \(A^{(3)}_\perp C_R\)

Full size image

Interaction between two Reggeons with transverse momenta \(\vec {l}_1\) and \(\vec {l}_2\) and colour indices \(c_1\) and \(c_2\) defined by the real part of the BFKL kernel

$$\begin{aligned}&[\mathcal{K}_r(\vec {q}_1, \vec {q}_{2}; \vec {k}) ]^{c'_1c'_2}_{c_1c_2} \nonumber \\&\quad = -T_{c_1c'_1}^{a}T_{c_2c'_2}^{a}\frac{g^2}{(2\pi )^{D-1}} \left[ \frac{\vec {q}^{\;2}_{1}\vec {q}^{\;\prime \; 2}_{2}+\vec {q}^{\;2}_{2}\vec {q}^{\;\prime \; 2}_{1}}{\vec {k}^{\;2}}-\vec {q}^{\;2}\right] , \end{aligned}$$
(24)

where \(\vec {k}\) is the momentum transferred from one Reggeon to another in the interaction, \(\vec {q}^{\;\prime }_1\) and \(\vec {q}^{\;\prime }_2\) (\(c'_1\) and \(c'_2\)) are the Reggeon momenta (colour indices) after the interaction, \(\vec {q}^{\;\prime }_1=\vec {q}_1 -\vec {k}, \quad \vec {q}^{\;\prime }_2=\vec {q}_2 +\vec {k}, \) and \(\vec {q}=\vec {q}_1+\vec {q}_2=\vec {q}^{\;\prime }_1+\vec {q}^{\;\prime }_2\).

For the colour structure which we are interested in, account of the interactions between all pairs of Reggeons leads in the sum to the colour coefficients which differ from the coefficients \(C^{\alpha }_{ij}\) (15) only by the common factor \(N_c\). It can be easily obtained using invariance of \(\text{ Tr }( \mathcal{T}^{a_1}\mathcal{T}^{a_2}\mathcal{T}^{a_3}\mathcal{T}^{a_4})\) under the colour group transformation

$$\begin{aligned} \mathcal{T}^{a_i}\rightarrow e^{i\theta ^c \mathcal{T}^{c} } \mathcal{T}^{a_i}e^{-i\theta ^c \mathcal{T}^{c} } , \end{aligned}$$
(25)

which takes the form

$$\begin{aligned} \mathcal{T}^{a_i}\rightarrow \mathcal{T}^{a_i} -i \theta ^c \hat{T}^c(i)\mathcal{T}^{a_i} , \quad \hat{T}^c(i)\mathcal{T}^{a_i} = T^c_{a_ia'_i}\mathcal{T}^{a'_i} \end{aligned}$$
(26)

at small \(\theta ^c \). It means that we can put

$$\begin{aligned} {\hat{R}}^{c} = \sum _i {\hat{T}}^{c} (i) =0 , \end{aligned}$$
(27)

if \(\hat{R}^c\) acts on \(\text{ Tr }( \mathcal{T}^{a_1}\mathcal{T}^{a_2}\mathcal{T}^{a_3}\mathcal{T}^{a_4})\). Using (27) and \(\hat{R}^c \hat{R}^c =0 \) one has

$$\begin{aligned} -\sum _{i>j =2}^4 \hat{T}^c (i) \hat{T}^c (j) = \frac{1}{2} \left( \sum _{i=2}^4 \hat{T}^c (i) \hat{T}^c (i) - \hat{T}^c (1) \hat{T}^c (1)\right) .\nonumber \\ \end{aligned}$$
(28)

Here on the left side we have the sum of the colours factors of the BFKL kernel (24) for interactions between all pairs of Reggeons, and the right side is equal \(N_c\).

Now about the kinematic part of the kernel (24). The first two terms in the square brackets in (24) correspond to the same diagrams as in (3), and their total contribution to the coefficient of \(\ln s\) in the first order correction is \(-4C_R\). The last term corresponds to the diagram in Fig. 4 and its contribution to the coefficient of \(\ln s\) in the first order correction is \(-C_3\), where

Fig. 4
figure 4

Diagrammatic representation of \(A^{(3)}_\perp C_3\)

Full size image
$$\begin{aligned} C_3= & {} g^{2} N_{c} C_{\Gamma }\frac{4}{\epsilon }\int \frac{d^{2+2\epsilon }l_{1}\,d^{2+2\epsilon } l_{2}(l_{1}+l_{2})^{2\epsilon }}{(2\pi )^{2(3+2\epsilon )}\vec {l}_{1}^{2}\vec {l}_{2}^{2}(\vec {q} -\vec {l}_{1}-\vec {l}_{2})^{2}}\nonumber \\&\times \left( A^{(3)}_{\perp }\right) ^{-1}\nonumber \\= & {} g^{2} N_{c} C_{\Gamma }\frac{32}{9\epsilon } (\vec {q}^{2})^{\epsilon }\frac{\Gamma (1-3\epsilon )\Gamma (1-\epsilon )\Gamma ^{2}(1+3\epsilon )}{\Gamma ^{2}(1-2\epsilon )\Gamma (1+2\epsilon )\Gamma (1+4\epsilon )}.\nonumber \\ \end{aligned}$$
(29)

Therefore, the first order correction in the case of Reggeized gluon is \(\omega (t)\ln s\), where \(\omega (t)\) is given by (22), and in the case of the three-Reggeon cut is \((-C_R -C_3)\ln s\), where \(C_R\) and \(C_3\) are given by (23) and (29) respectively. If to present the coefficients \(C_{ij}\) in (15) as the sum

$$\begin{aligned} C_{ij} = C^R_{ij}+C^C_{ij} , \end{aligned}$$
(30)

where \(C^R_{ij}\) correspond to the pole, so that

$$\begin{aligned} 2C^R_{gq} = C^R_{qq}+C^R_{gg} , \end{aligned}$$
(31)

and \(C^C_{ij}\) correspond to the cut, we obtain that with the logarithmic accuracy the total three-loop contributions to the coefficient of \(\ln s\) are

$$\begin{aligned} A^{eik}\left( C^R_{ij} \omega (t)-C^C_{ij}(C_R+C_3)\right) \ln s . \end{aligned}$$
(32)

The infrared divergent part of these contributions must be compared with the functions \(g^2(s/t)\mathcal{R}_{ij}^{(3), 1, [8]} \ln s\) of the paper [22]. The values \(\mathcal{R}_ij^{(3), 1, [8]}\) are given there in Eq. (4.59), \(\mathcal{R}_ij^{(3), 1, [8]}\ln s\) are the three-loop logarithmic contributions to the non-factorizing remainder function \(\mathcal{R}^{[8]}_{ij}\). It is not difficult to see that with the accuracy with which the values \(\mathcal{R}_ij^{(2), 1, [8]}\) are known the equality

$$\begin{aligned} g^2(s/t)\mathcal{R}_{ij}^{(3), 1, [8]} = A^{eik} (C^R_{ij} \omega (t)-C^C_{ij}(C_R+C_3) ) \end{aligned}$$
(33)

can be fulfilled if

$$\begin{aligned} C^C_{gg} = -\frac{3}{2} , \quad C^C_{gq} =-\frac{3}{2} , \quad C^C_{qq} =\frac{3(1-N_c^2)}{4N_c^2} , \end{aligned}$$
(34)

and

$$\begin{aligned} C^R_{gg} = 3 , \quad C^R_{gq} =\frac{7}{4} , \quad C^R_{qq} =\frac{1}{2} . \end{aligned}$$
(35)

It means that the restrictions imposed by the infrared factorization on the parton scattering amplitudes with the adjoint representation of the colour group in the t-channel and negative signature can be fulfilled in the NNLLA at two and three loops if besides the Regge pole contribution there is the Regge cut contribution

$$\begin{aligned} A^{eik}C^C_{ij} (1-(C_R+C_3)\ln s ) . \end{aligned}$$
(36)

Here the coefficients \(C^C_{ij}, \; C_R\) and \(C_3\) are given by Eqs. (23), (29) and (34) respectively.

4 On the derivation of the BFKL equation in the NNLLA

The BFKL equation was derived [7,8,9] for summation of radiative corrections in the LLA to amplitudes of elastic scattering processes. These amplitudes were calculated using the s-channel unitarity and analyticity. The unitarity was used for calculation of discontinuities of elastic amplitudes, and analyticity for their full restoration. Use of the s-channel unitarity requires knowledge of multiple production amplitudes in the MRK. The assumption was made that all amplitudes in the unitarity relations for elastic amplitudes, both elastic and inelastic, are determined by the Regge pole contributions. With this assumption, the s-channel discontinuities of the elastic amplitudes can be presented as the convolution in the transverse momentum space of energy independent impact factors of colliding particles, describing their interaction with Reggeons, and the Green’s function G for two interacting Reggeons, which is universal (process independent). The BFKL equation looks as

$$\begin{aligned} \frac{d\;G}{d\ln s} = \hat{\mathcal {K}} \; G , \end{aligned}$$
(37)

where \({\hat{\mathcal {K}}}\) is the kernel of the BFKL equation. It consists of virtual and real parts; the first of them is expressed through the Regge trajectories and the second through effective vertices for s-channel production of particles in Reggeon interaction.

The assumption that all amplitudes in the unitarity relations are determined by the Regge pole contributions is very strong, and it should have been proven. The first check of this assumption was made already in [8, 9]. Here it should be recalled that the BFKL equation is written for all t-channel colour states, which a system of two Reggeons can have, in particular, for the colour octet. Therefore, there is the bootstrap requirement: solution of the BFKL equation for the colour octet in the t-channel and negative signature must reproduce the pole Regge form, which was assumed in its derivation. It was shown in [8, 9] that this requirement is satisfied. Of course, it was not a proof of the assumption, but only verification in a very particular case. Later it was realized that it is possible to formulate the bootstrap conditions for amplitudes of multiple production in the MRK and to give a complete proof of the hypothesis on their basis [16]. A similar (although much more complicated) proof for elastic amplitudes and for real parts of inelastic ones was carried out in the NLLA (see [17, 18] and references therein).

It turns out that all amplitudes in the unitarity relations are determined by the Regge pole contributions also in the NNLLA. The reason is that in this approximation one of two amplitudes in the unitarity relations can lose \(\ln s\), while the second one must be taken in the LLA. The LLA amplitudes are real, so that only real parts of the NLLA amplitudes are important in the unitarity relations. Since they have a simple pole Regge form, the scheme of deviation of the BFKL equation in the NLLA remains unchanged. The only difference is that we have to know the Reggeon trajectory and Reggeon–Reggeon–gluon production vertex with higher accuracy and to know also effective Reggeon–Reggeon \(\rightarrow \) gluon–gluon and Reggeon–Reggeon \(\rightarrow \) quark-antiquark vertices.

Unfortunately, this scheme is violated in the NNLLA. In this approximation two powers of \(\ln s\) can be lost compared with the LLA in the product of two amplitudes in the unitarity relations. It can be done losing either one \(\ln s\) in each of the amplitudes or \(\ln ^2 s\) in one of them. In the first case, discontinuities receive contributions from products of real parts of amplitudes with negative signature in the NLLA, products of imaginary parts of amplitudes with negative signature in the LLA, and products of amplitudes with positive signature in the LLA. Of course, account of these contributions greatly complicates derivation of the BFKL equation. In particular, since for amplitudes with positive signature there are different colour group representations in the t-channel for quark–quark, quark–gluon and gluon–gluon scattering, their account violates unity of consideration.

However, these complications do not seem to be as great as in the second case, when \(\ln ^2 s\) is lost in one of the amplitudes in the unitarity relations. In this case one of the amplitudes must be taken in the NNLLA and the other in the LLA. Since the amplitudes in the LLA are real, only real parts of the NNLLA amplitudes are important. But even for these parts the pole Regge form becomes inapplicable because of the contributions of the three-Reggeon cuts which appear in this approximation. Note that account of these contributions also violates unity of consideration of quark–quark, quark–gluon and gluon–gluon scattering because the cuts give contributions to amplitudes with different representations of the colour group in the t-channel for these processes. But even worse is that we actually do not know the contributions of the cuts.

We showed that the non-factorizing terms in the parton’s elastic scattering amplitudes with the colour octet in the t-channel and negative signature calculated using the infrared factorization [22] in two and three loops (non-logarithmic terms nonvanishing at \(\epsilon \rightarrow 0\) in two loops and one-logarithmic terms singular at \(\epsilon \rightarrow 0\) in three loops) can be explained by the contribution of the three-Reggeon cut. But these terms may have other explanations. In particular, in [24] for their explanation, along with the three-Reggeon cut, mixing of the pole and the cut is used. In this paper, the coupling of the cut with partons and the Reggeon-cut mixing were introduced using effective theory of Wilson lines.

If we compare our current understanding of the cuts with the history of investigation of the gluon Reggeization, it seems that we are even in the worse position than after [5, 6], because the Regge form of elastic amplitudes was confirmed there by direct calculation in two loops with power accuracy. Remind that to prove this form in all orders of perturbation theory it was firstly generalized for multiple production amplitudes in the multi-Regge kinematics, then the bootstrap conditions for elastic and inelastic amplitudes were derived, after which it was proved that their fulfilment is sufficient for justification of the form, and finally it was shown that they are fulfilled.

5 Conclusions

The gluon Reggeization is one of the remarkable properties of QCD. The Reggeization means existence of the Regge pole with the gluon quantum numbers and negative signature with the trajectory \(j(t) = 1+\omega (t)\) with \(\omega (0)=1\). It is important that this pole gives the main contribution to QCD amplitudes with octet representation of the colour group in cross channels and negative signature. Thereby these amplitudes have a simple factorized form (pole Regge form) in the leading and next-to-leading logarithmic approximations (LLA and NLLA). This is true not only for elastic amplitudes, but also for real parts of multiparticle production amplitudes in the multi-Regge-kinematics.

Regge cuts, generated by the Regge poles, appear in the amplitudes with the colour octet and negative signature in the next-to-next-to-leading logarithmic approximation (NNLLA). Strictly speaking, one can not assert that these amplitudes are completely given by contributions of the pole and the cut. A direct proof of such assertion could be coincidence of these contributions with results of calculation of the amplitudes in the perturbation theory. Here we showed that for elastic scattering amplitudes the coincidence exists for the non-logarithmic terms nonvanishing at \(\epsilon \rightarrow 0\) in two loops and the one-logarithmic terms singular at \(\epsilon \rightarrow 0\) in three loops.

Contributions of the Regge cuts greatly complicates derivation of the BFKL equation in the NNLLA. There are another complication: the need to consider in the unitarity relations products of real parts of amplitudes with negative signature in the NLLA, products of imaginary parts of amplitudes with negative signature in the LLA, and products of amplitudes with positive signature in the LLA. But they do not seem as significant as the need to take into account Regge cuts.