Abstract
A search is performed for new phenomena in events having a photon with high transverse momentum and a jet collected in \(36.7~\text {fb}^{-1} \) of proton–proton collisions at a centre-of-mass energy of \(\sqrt{s}\) = 13 TeV recorded with the ATLAS detector at the Large Hadron Collider. The invariant mass distribution of the leading photon and jet is examined to look for the resonant production of new particles or the presence of new high-mass states beyond the Standard Model. No significant deviation from the background-only hypothesis is observed and cross-section limits for generic Gaussian-shaped resonances are extracted. Excited quarks hypothesized in quark compositeness models and high-mass states predicted in quantum black hole models with extra dimensions are also examined in the analysis. The observed data exclude, at 95% confidence level, the mass range below 5.3 TeV for excited quarks and 7.1 TeV (4.4 TeV) for quantum black holes in the Arkani-Hamed–Dimopoulos–Dvali (Randall–Sundrum) model with six (one) extra dimensions.
Similar content being viewed by others

Study of $$Z \rightarrow ll\gamma $$ decays at $$\sqrt{s}$$ = 8 TeV with the ATLAS detector
Avoid common mistakes on your manuscript.
1 Introduction
This paper reports a search for new phenomena in events with a photon and a jet produced from proton–proton (\(pp\)) collisions at \(\sqrt{s}\) = 13 TeV, collected with the ATLAS detector at the Large Hadron Collider (LHC). Prompt photons in association with jets are copiously produced at the LHC, mainly through quark–gluon scattering (\(qg \rightarrow q\gamma \)). The \(\gamma \) + jet(s) final state provides a sensitive probe for a class of phenomena beyond the Standard Model (SM) that could manifest themselves in the high invariant mass (\(m_{\gamma j}\)) region of the \(\gamma \) + jet system. The search is performed by looking for localized excesses of events in the \(m_{\gamma j}\) distribution with respect to the SM prediction. Two classes of benchmark signal models are considered.
The first class of benchmark models is based on a generic Gaussian-shaped mass distribution with different values of its mean and standard deviation. This provides a generic interpretation for the presence of signals with different Gaussian widths, ranging from a resonance with a width similar to the reconstructed \(m_{\gamma j}\) resolution of \(\sim 2\)% to wide resonances with a width up to 15%. The second class of benchmark models is based on signals beyond the SM that are implemented in Monte Carlo (MC) simulation and appear as broad peaks in the \(m_{\gamma j}\) spectrum. This paper considers two scenarios for physics beyond the SM: quarks as composite particles and extra spatial dimensions. In the first case, if quarks are composed of more fundamental constituents bound together by some unknown interaction, new effects should appear depending on the value of the compositeness scale \(\Lambda \). In particular, if \(\Lambda \) is sufficiently smaller than the centre-of-mass energy, excited quark (\(q^*\)) states may be produced in high-energy \(pp\) collisions at the LHC [1,2,3]. The \(q^*\) production at the LHC could result in a resonant peak at the mass of the \(q^*\) (\(m_{q^*}\)) in the \(m_{\gamma j}\) distribution if the \(q^*\) can decay into a photon and a quark (\(qg \rightarrow q^* \rightarrow q\gamma \)). In the present search, only the SM gauge interactions are considered for \(q^*\) production. In the second scenario, the existence of extra spatial dimensions (EDs) is assumed to provide a solution to the hierarchy problem [4,5,6]. Certain types of ED models predict the fundamental Planck scale \(M^*\) in the \(4+n\) dimensions (n being the number of extra spatial dimensions) to be at the TeV scale, and thus accessible in \(pp\) collisions at \(\sqrt{s}\) = 13 TeV at the LHC. In such a TeV-scale \(M^*\) scenario of the extra dimensions, quantum black holes (QBHs) may be produced at the LHC as a continuum above the threshold mass (\(M_{\text {th}}\)) and then decay into a small number of final-state particles including photon–quark/gluon pairs before they are able to thermalize [7,8,9,10]. In this case a broad resonance-like structure could be observed just above \(M_{\text {th}}\) on top of the SM \(m_{\gamma j}\) distribution. The \(M_{\text {th}}\) value for QBH production is taken to be equal to \(M^*\) while the maximum allowed QBH mass is set to either \(3M^* \) or the LHC \(pp\) centre-of-mass energy of 13 TeV, whichever is smaller. The upper bound on the mass ensures that the QBH production is far from the “thermal” regime, where the classical description of the black hole and its decay into high-multiplicity final states should be used. In this paper, the extra-dimensions model proposed by Arkani-Hamed, Dimopoulous and Dvali (ADD) [11] with \(n=6\) flat EDs and the one by Randall and Sundrum (RS1) [12] with \(n=1\) warped ED are considered.
The ATLAS and CMS experiments at the LHC have performed searches for excited quarks in the \(\gamma +\text {jet}\) final state using \(pp\) collision data recorded at \(\sqrt{s}\) = 7 TeV [13], 8 TeV [14, 15] and 13 TeV [16]. In the ATLAS searches, limits for generic Gaussian-shaped resonances were obtained at 7, 8 and 13 TeV while a limit for QBHs in the ADD model (\(n=6\)) was first obtained at 8 TeV. The ATLAS search at 13 TeV with data taken in 2015 was further extended to constrain QBHs in the RS1 model (\(n=1\)). No significant excess of events was observed in any of these searches, and the lower mass limits of 4.4 TeV for the \(q^*\) and 6.2 (3.8) TeV for QBHs in the ADD (RS1) model were set, currently representing the most stringent limits for the decay into a photon and a jet. For a Gaussian-shaped resonance a cross-section upper limit of 0.8 (1.0) fb at \(\sqrt{s}\) = 13 TeV was obtained, for example, for a mass of 5 TeV and a width of 2% (15%).
The dijet resonance searches at ATLAS [17, 18] and CMS [19] using \(pp\) collisions at \(\sqrt{s}\) = 13 TeV also set limits on the production cross-sections of excited quarks and QBHs. The search in the \(\gamma +\text {jet}\) final state presented here complements the dijet results and provides an independent check for the presence of these signals in different decay channels.
This paper presents the search based on the full 2015 and 2016 data set recorded with the ATLAS detector, corresponding to \(36.7~\text {fb}^{-1} \) of \(pp\) collisions at \(\sqrt{s}\) = 13 TeV. The analysis strategy is unchanged from the one reported in Ref. [16], focusing on the region where the \(\gamma \) + jet system has a high invariant mass.
The paper is organized as follows. In Sect. 2 a brief description of the ATLAS detector is given. Section 3 summarizes the data and simulation samples used in this study. The event selection is discussed in Sect. 4. The signal and background modelling are presented in Sect. 5 together with the signal search and limit-setting strategies. Finally the results are discussed in Sect. 6 and the conclusions are given in Sect. 7.
2 ATLAS detector
The ATLAS detector at the LHC is a multi-purpose, forward-backward symmetric detectorFootnote 1 with almost full solid angle coverage, and is described in detail elsewhere [20, 21]. Most relevant for this analysis are the inner detector (ID) and the calorimeter system composed of electromagnetic (EM) and hadronic calorimeters. The ID consists of a silicon pixel detector, a silicon microstrip tracker and a transition radiation tracker, all immersed in a 2 T axial magnetic field, and provides charged-particle tracking in the range \(|\eta |<2.5\). The electromagnetic calorimeter is a lead/liquid-argon (LAr) sampling calorimeter with accordion geometry. The calorimeter is divided into a barrel section covering \(|\eta |<1.475\) and two endcap sections covering \(1.375<|\eta |<3.2\). For \(|\eta |<2.5\) it is divided into three layers in depth, which are finely segmented in \(\eta \) and \(\phi \). In the region \(|\eta |<1.8\), an additional thin LAr presampler layer is used to correct for fluctuations in the energy losses in the material upstream of the calorimeters. The hadronic calorimeter is a sampling calorimeter composed of steel/scintillator tiles in the central region (\(|\eta |<1.7\)), while copper/LAr modules are used in the endcap (\(1.5<|\eta |<3.2\)) regions. The forward regions (\(3.1<|\eta |<4.9\)) are instrumented with copper/LAr and tungsten/LAr calorimeter modules optimized for electromagnetic and hadronic measurements, respectively. Surrounding the calorimeters is a muon spectrometer that includes three air-core superconducting toroidal magnets and multiple types of tracking chambers, providing precision tracking for muons within \(|\eta |<2.7\) and trigger capability within \(|\eta |<2.4\).
A dedicated two-level trigger system is used for the online event selection [22]. Events are selected using a first-level trigger implemented in custom electronics, which reduces the event rate to a design value of 100 kHz using a subset of the detector information. This is followed by a software-based trigger that reduces the accepted event rate to 1 kHz on average by refining the first-level trigger selection.
3 Data and Monte Carlo simulations
The data sample used in this analysis was collected from \(pp\) collisions in the 2015–2016 LHC run at a centre-of-mass energy of 13 TeV, and corresponds to an integrated luminosity of \(36.7\pm 1.2~\text {fb}^{-1} \). The uncertainty was derived, following a methodology similar to that detailed in Ref. [23], from a preliminary calibration of the luminosity scale using x–y beam-separation scans performed in August 2015 and May 2016. The data are required to satisfy a number of quality criteria ensuring that the relevant detectors were operational while the data were recorded.
Monte Carlo samples of simulated events are used to study the background modelling for the dominant \(\gamma +\text {jet}\) processes, to optimize the selection criteria and to evaluate the acceptance and selection efficiencies for the signals considered in the search. Events from SM processes containing a photon with associated jets were simulated using the Sherpa 2.1.1 [24] event generator, requiring a photon transverse energy \(E_{\text {T}} ^{\gamma }\) above 70 GeV at the generator level. The matrix elements were calculated with up to four final state partons at leading order (\(\text {LO}\)) in quantum chromodynamics (QCD) and merged with the parton shower [25] using the ME+PS@LO prescription [26]. The CT10 [27] parton distribution function (PDF) set was used in conjunction with dedicated parton shower tuning developed by the Sherpa authors. A second sample of SM \(\gamma +\text {jet}\) events was generated using the LO Pythia 8.186 [28] event generator with the LO NNPDF 2.3 PDFs [29] and the A14 tuning of the underlying-event parameters [30]. The Pythia simulation includes leading-order \(\gamma \) + jet events from both the direct processes (the hard subprocesses \(qg \rightarrow q\gamma \) and \(q\bar{q} \rightarrow g\gamma \)) and bremsstrahlung photons in QCD dijet events. To estimate the systematic uncertainty associated with the background modelling, a large sample of events was generated with the next-to-leading-order (NLO) Jetphox v1.3.1_2 [31] program. Events were generated at parton level for both the direct and fragmentation photon contributions using the NLO photon fragmentation functions [32] and the NLO NNPDF 2.3 PDFs, and setting the renormalization, factorization and fragmentation scales to the photon \(E_{\text {T}} ^{\gamma }\). Jets of partons are reconstructed using the anti-\(k_{t}\) algorithm [33, 34] with a radius parameter of \(R=0.4\). The generated photon is required to be isolated by ensuring that the total transverse energy of partons inside a cone of size \(\Delta R =0.4\) around the photon is smaller than 7.07 GeV + \(0.03\times E_{\text {T}} ^{\gamma }\), equivalentFootnote 2 to the photon selection for the data described in Sect. 4.
Samples of excited quark events were produced using Pythia 8.186 with the LO NNPDF 2.3 PDFs and the A14 set of tuned parameters for the underlying event. The Standard Model gauge interactions and the magnetic-transition type couplings [1,2,3] to gauge bosons were considered in the production processes of the excited states of the first-generation quarks (\(u^*\), \(d^*\)) with degenerate masses. The compositeness scale \(\Lambda \) was taken to be equal to the mass \(m_{q^*}\) of the excited quark, and the coefficients \(f_\mathrm {s}\), f and \(f'\) of magnetic-transition type couplings to the respective SU(3), SU(2) and U(1) gauge bosons were chosen to be unity. The \(q^*\) samples were generated with \(m_{q^*}\) values between 0.5 and 6.0 TeV in steps of 0.5 TeV.
The QBH samples were generated using the QBH 2.02 [35] event generator with the CTEQ6L1 [36] PDF set and Pythia 8.186 for the parton shower and underlying event tuned with the A14 parameter set. The \(M_{\text {th}}\) values were chosen to vary between 3.0 (1.0) and 9.0 (7.0) TeV in steps of 0.5 TeV for the QBH signals in the ADD (RS1) model. All the qg, \(\bar{q}g\), gg and \(q\bar{q}\) processes were included in the QBH signal production while only final states with a photon and a quark/gluon were considered for the decay. All six quark flavours were included together with their anti-quark counterparts in both the production and decay processes.
Apart from the sample generated with Jetphox which is a parton-level calculator, all the simulated samples include the effects of multiple \(pp\) interactions in the same and neighbouring bunch crossings (pile-up) and were processed through the ATLAS detector simulation [37] based on Geant4 [38]. Pile-up effects were emulated by overlaying simulated minimum-bias events from Pythia 8.186, generated with the A2 tune [39] for the underlying event and the MSTW2008LO PDF set [40]. The number of overlaid minimum-bias events was adjusted to match the one observed in data. All the MC samples except for the Jetphox sample were reconstructed with the same software as that used for collision data.
4 Event selection
Photons are reconstructed from clusters of energy deposits in the EM calorimeter as described in Ref. [41]. A photon candidate is classified depending on whether the EM cluster is associated with a conversion track candidate reconstructed in the ID. If no ID track is matched, the candidate is considered as an unconverted photon. If the EM cluster is matched to either a conversion vertex formed from two tracks constrained to originate from a massless particle or a single track with its first hit after the innermost layer of the pixel detector, the candidate is considered to be a converted photon. Both the converted and unconverted photon candidates are used in the analysis. The energy of each photon candidate is corrected using MC simulation and data as described in Ref. [42]. The EM energy clusters are calibrated separately for converted and unconverted photons, based on their properties including the longitudinal shower development. The energy scale and resolution of the photon candidates after the MC-based calibration are further adjusted based on a correction derived using \(Z \rightarrow e^{+} e^{-} \) events from data and MC simulation. Photon candidates are required to have \(E_{\text {T}} ^{\gamma } >25\) GeV and \(|\eta ^{\gamma } |<2.37\) and satisfy the “tight” identification criteria defined in Ref. [41]. Photons are identified based on the profile of the energy deposits in the first two layers of the EM calorimeter and the energy leakage into the hadronic calorimeter. To further reduce the contamination from \(\pi ^{0}\) \(\rightarrow \gamma \gamma \) or other neutral hadrons decaying into photons, the photon candidates are required to be isolated from other energy deposits in an event. The calorimeter isolation variable \(E_{\text {T,\,iso}}\) is defined as the sum of the \(E_{\mathrm {T}}\) of all positive-energy topological clusters [43] reconstructed within a cone of \(\Delta R = 0.4\) around the photon direction excluding the energy deposits in an area of size \(\Delta \eta \times \Delta \phi =0.125 \times 0.175\) centred on the photon cluster. The photon energy expected outside the excluded area is subtracted from the isolation energy while the contributions from pile-up and the underlying event are subtracted event by event [44]. The photon candidates are required to have \(E_{\text {T,\,iso}}^{\gamma } =E_{\text {T,\,iso}}-0.022\times E_{\text {T}} ^{\gamma } \) less than 2.45 GeV. This \(E_{\text {T}} ^{\gamma }\)-dependent selection requirement is used to guarantee an efficiency greater than 90% for signal photons in the \(E_{\text {T}} ^{\gamma }\) range relevant for this analysis. The efficiency for the signal photon selection varies from (\(90\pm 1\))% to (\(83\pm 1\))% for signal events with masses from 1 to 6 TeV. The dependency on the signal mass is mainly from the efficiency of the tight identification requirement while the isolation selection efficiency is approximately (\(99\pm 1\))% over the full mass range.
Jets are reconstructed from topological clusters calibrated at the electromagnetic scale using the anti-\(k_{t}\) algorithm with a radius parameter \(R=0.4\). The jets are calibrated to the hadronic energy scale by applying corrections derived from MC simulation and in situ measurements of relative jet response obtained from Z+jets, \(\gamma \)+jets and multijet events at \(\sqrt{s}\) = 13 TeV [45,46,47]. Jets from pile-up interactions are suppressed by applying the jet vertex tagger [48], using information about tracks associated with the hard-scatter and pile-up vertices, to jets with \(p_{\text {T}} ^\text {jet} <60\) GeV and \(|\eta ^{\text {jet}} |<2.4\). In order to remove jets due to calorimeter noise or non-collision backgrounds, events containing at least one jet failing to satisfy the loose quality criteria defined in Ref. [49] are discarded. Jets passing all the requirements and with \(p_{\text {T}} ^\text {jet} >20\) GeV and \(|\eta ^{\text {jet}} |<4.5\) are considered in the rest of the analysis. Since a photon is also reconstructed as a jet, jet candidates in a cone of \(\Delta R = 0.4\) around a photon are not considered.
This analysis selects events based on a single-photon trigger requiring at least one photon candidate with \(E_{\text {T}} ^{\gamma }>140\) GeV which satisfies loose identification conditions [41] based on the shower shape in the second sampling layer of the EM calorimeter and the energy leakage into the hadronic calorimeter. Selected events are required to contain at least one primary vertex with two or more tracks with \(p_{\text {T}} >400\) MeV. Photon candidates are required to satisfy the “tight” identification and isolation conditions discussed above. The kinematic requirements for the highest-\(E_{\text {T}}\) photon in the events are tightened to \(E_{\text {T}} ^{\gamma } >150\) GeV and \(|\eta ^{\gamma } |<1.37\). The \(E_{\text {T}} ^{\gamma }\) requirement is used to select events with nearly full trigger efficiency [50] while the \(\eta ^{\gamma }\) requirement is imposed to enhance the signal-to-background ratio. Moreover, an event is rejected if there is any jet with \(p_{\text {T}} ^\text {jet} >30\) GeV within \(\Delta R <0.8\) around the photon. The presence of additional tight and isolated photons with \(E_{\text {T}} ^{\gamma }>150\) GeV in events is negligible for both signal and background events, and therefore allowed. The \(\gamma +\text {jet}\) system is formed from the highest-\(E_{\text {T}}\) photon and the highest-\(p_{\text {T}}\) jet in the event. Finally, the highest-\(p_{\text {T}}\) jet in the event is required to have \(p_{\text {T}} ^\text {jet} >60\) GeV and the pseudorapidity difference between the photon and the jet (\(\Delta \eta _{\gamma j} \equiv |\eta ^{\gamma }-\eta ^{\text {jet}} |\)) must be less than 1.6 to enhance signals over the \(\gamma +\text {jet}\) background, which typically has a large \(\Delta \eta _{\gamma j}\) value. After applying all the selection requirements, \(6.34\times 10^{5}\) events with an invariant mass (\(m_{\gamma j}\)) of the selected \(\gamma +\text {jet}\) system greater than 500 GeV remain in the data sample.
5 Statistical analysis
The data are examined for the presence of a significant deviation from the SM prediction using a test statistic based on a profile likelihood ratio [51]. Limits on the visible cross-section for generic Gaussian-shaped signals and limits on the cross-section times branching ratio for specific benchmark models are computed using the CL\(_{\text {S}}\) prescription [52]. The details of the signal and background modelling used for the likelihood function construction are discussed in Sects. 5.1 and 5.2 while a summary of the statistical procedures used to establish the presence of a signal or set limits on the production cross-sections for new phenomena is given in Sect. 5.3.
5.1 Signal modelling
The signal model is built starting from the probability density function (pdf), \(f_{\text {sig}}(m_{\gamma j})\), of the \(m_{\gamma j}\) distribution at the reconstruction level. For a Gaussian-shaped resonance with mass \(m_{\text {G}}\), the \(m_{\gamma j}\) pdf is modelled by a normalized Gaussian distribution with the mean located at \(m_{\gamma j} = m_{\text {G}} \). The standard deviation of the Gaussian distribution is chosen to be 2, 7 or 15% of \(m_{\text {G}}\), where 2% approximately corresponds to the effect of the detector resolution on the reconstruction of the photon–jet invariant mass. For the \(q^*\) and QBH signals, the \(m_{\gamma j}\) pdfs are created from the normalized reconstructed \(m_{\gamma j}\) distributions after applying the selection requirements described in Sect. 4 using the simulated MC events, and a kernel density estimation technique [53] is applied to smooth the distributions. The signal pdfs for intermediate mass points at which signal events were not generated are obtained from the simulated signal samples by using a moment-morphing method [54]. The signal template for the \(q^*\) and QBH signals is then constructed as \(f_{\text {sig}}(m_{\gamma j}) \times (\sigma \cdot B \cdot A \cdot \varepsilon ) \times \mathcal {L}_{\text {int}} \), where the \(f_{\text {sig}}\) is scaled by the product of the cross-section times branching ratio to a photon and a quark or gluon (\(\sigma \cdot {B}\)), acceptance (A), selection efficiency (\(\varepsilon \)) and the integrated luminosity (\(\mathcal {L}_{\text {int}}\)) for the data sample. The product of the acceptance times efficiency (\(A \cdot \varepsilon \)) is found to be about 50% for all the \(q^*\) and QBH models, varying only by a few percent with \(m_{q^*}\) or \(M_{\text {th}}\). This dependence is accounted for in the model by interpolating between the generated mass points using a third-order spline. For the \(q^*\) and QBH signals, limits are set on \(\sigma \cdot {B}\) after correcting for the acceptance and efficiency \(A \cdot \varepsilon \) of the selection criteria.
Experimental uncertainties in the signal yield arise from uncertainties in the luminosity (\(\pm 3.2\%\)), photon identification efficiency (\(\pm 2\%\)), trigger efficiency (\(\pm 1\%\) as measured in Ref. [50] ) and pile-up dependence (\(\pm 1\%\)). The impact of the uncertainties in the photon isolation efficiency, photon and jet energy scales and resolutions is negligible. A 1% uncertainty in the signal yield is included to account for the statistical error in the acceptance and selection efficiency estimates due to the limited size of the MC signal samples. The impact of the PDF uncertainties on the signal acceptance is found to be negligible compared to the other uncertainties. The photon and jet energy resolution uncertainties (\(\pm 2\%\) of the mass) are accounted for as a variation of the width for the Gaussian-shaped signals. The impact of the resolution uncertainty on intrinsically large width signals is found to be negligible and thus not included in the signal models for the \(q^*\) and QBH. The typical difference between the peaks of the reconstructed and generator-level \(m_{\gamma j}\) distributions for the excited-quark signals is well below 1%.
A summary of systematic uncertainties in the signal yield and shape included in the statistical analysis is given in Table 1.
In order to facilitate the re-interpretation of the present results in alternative physics models, the fiducial acceptance and efficiency for events with the invariant mass of the \(\gamma \) + jet system around \(m_{q^*}\) or \(M_{\text {th}}\) (referred to as “on-shell” events hereafter) are also provided. The chosen \(m_{\gamma j}\) ranges are \(0.6m_{q^*}<m_{\gamma j} <1.2m_{q^*} \) for the \(q^*\) signal and \(0.8M_{\text {th}}<m_{\gamma j} <3.0M_{\text {th}} \) for the QBH signal. The fiducial region at particle level, as summarized in Table 2, is chosen to be close to the one used in the event selection at reconstruction level.
The fiducial acceptance \(A_\mathrm {f}\), defined as the fraction of generated on-shell signal events falling into the fiducial region, increases from 56 to 63% with increasing signal mass \(M_{\text {th}}\) from 1.0 to 6.5 (9.0) TeV for the QBH in the RS1 (ADD) model. The \(A_\mathrm {f}\) value for the \(q^*\) model varies very similarly to that for the RS1 QBH signal. The rise in the fiducial acceptance as a function of \(M_{\text {th}}\) (\(m_{q^*}\)) is driven mainly by the increase of the efficiency for the photon \(\eta \) requirement since the photons tend to be more central as \(M_{\text {th}}\) (\(m_{q^*}\)) becomes larger.
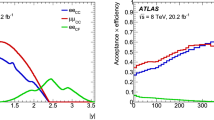
The fiducial selection efficiency \(\varepsilon _\mathrm {f}\) is defined as the ratio of the number of on-shell events in the particle-level fiducial region passing the selection at the reconstruction level, including photon identification, isolation and jet quality criteria, to the number of generated on-shell events in the particle-level fiducial region. The migration of generated on-shell events outside the particle-level fiducial region into the selected sample at the reconstruction level is found to be negligible. The fiducial selection efficiency decreases from 88 (86) to 82 (80)% within the same \(M_{\text {th}}\) ranges as above for the RS1 (ADD) QBH model and is not highly dependent on the kinematics of the assumed signal production processes. The \(\varepsilon _\mathrm {f}\) for the \(q^*\) model behaves very similarly to that for the RS1 QBH model. The reduction in the fiducial selection efficiency is caused mainly by the inefficiency of the shower shape requirements used in the photon identification for high-\(E_{\text {T}}\) photons. The fiducial acceptance and selection efficiencies for the three benchmark signal models are shown in Fig. 1 as functions of \(m_{q^*}\) or \(M_{\text {th}}\).
a Fiducial acceptance and b selection efficiencies for the three signal models considered in the analysis as a function of the excited-quark mass \(m_{q^*}\) or the QBH threshold mass \(M_{\text {th}}\). The fiducial region definition is detailed in Table 2. The description of the selection criteria can be found in the text
5.2 Background modelling
The \(m_{\gamma j}\) distribution of the background is modelled using a functional form. A family of functions, similar to the ones used in the previous searches for \(\gamma +\text {jet}\) [13, 14, 16] and \(\gamma \gamma \) resonances [55] as well as dijet resonances [17] is considered:
where x is defined as \(m_{\gamma j}/\sqrt{s}\), p and \(a_{i}\) are free parameters, and N is a normalization factor. The number of free parameters describing the normalized mass distribution is thus \(k+2\) with a fixed N, where k is the stopping point of the summation in Eq. (1). The normalization N as well as the shape parameters p and \(a_{i}\) are simultaneously determined by the final fit of the signal plus background model to data. The goodness of a given functional form in describing the background is quantified based on the potential bias introduced in the fitted number of signal events. To quantify this bias the functional form under test is used to perform a signal + background fit to a large sample of background events built from the Jetphox prediction. The large Jetphox event sample is used for this purpose as the shape of the background prediction can be extracted with sufficiently small statistical uncertainty.
The parton-level Jetphox calculations do not account for effects from hadronization, the underlying event and the detector resolution. Therefore, the nominal Jetphox prediction is corrected by calculating the ratio of reconstructed jet \(p_{\text {T}}\) to parton \(p_{\text {T}}\) in the Sherpa \(\gamma +\text {jet}\) sample and applying the parameterized ratio to the Jetphox parton \(p_{\text {T}}\). In addition, an \(m_{\gamma j}\)-dependent correction is applied to the Jetphox prediction to account for the contribution from multijet events where one of the jets is misidentified as a photon (fake photon events). This correction is estimated from data as the inverse of the purity, defined as the fraction of real \(\gamma +\text {jet}\) events in the selected sample. The purity is measured in bins of \(m_{\gamma j}\) by exploiting the difference between the shapes of the \(E_{\text {T,\,iso}}^{\gamma }\) distributions of real photons and jets faking photons; the latter typically have a large \(E_{\text {T,\,iso}}^{\gamma }\) value due to nearby particles produced in the jet fragmentation. The purity is estimated by performing a two-component template fit to the \(E_{\text {T,\,iso}}^{\gamma }\) distribution in bins of \(m_{\gamma j}\). The templates of real- and fake-photon isolation distributions are obtained from MC (Sherpa) simulation and from data control samples, respectively. The \(E_{\text {T,\,iso}}^{\gamma }\) variable for real photons from Sherpa simulation is corrected to account for the observed mis-modelling in the description of isolation profiles between data and MC events in a separate control sample. The template for fake photons is derived in a data sample where the photon candidate fails to satisfy the tight identification criteria but fulfils a looser set of identification criteria. Details about the correction to the real-photon template and the derivation of the fake-photon template are given in Ref. [56]. To reduce the bias in the \(E_{\text {T,\,iso}}^{\gamma }\) shape due to different kinematics, both the real- and fake-photon templates are obtained by applying the same set of kinematic requirements used in the main analysis. As an example, Fig. 2 shows the \(E_{\text {T,\,iso}}^{\gamma }\) distribution of events within the range \(1.0<m_{\gamma j} <1.1\) TeV, superimposed on the best-fit result. This procedure is repeated in every bin of the \(m_{\gamma j}\) distribution and the resulting estimate of the purity is shown as a function of \(m_{\gamma j}\) in Fig. 3. The uncertainty in the measured purity includes both the statistical and systematic uncertainties. The latter are estimated by recomputing the purity using different data control samples for the fake-photon template or alternative templates for real photons obtained from Pythia simulation or removing the data-to-MC corrections applied to \(E_{\text {T,\,iso}}^{\gamma }\) in the Sherpa sample and by symmetrizing the variations. The variation from different data control samples for the fake-photon template has the largest effect on the purity (4% at \(1.0< m_{\gamma j} < 1.1 \) TeV). The measured purity is approximately constant at 93% over the \(m_{\gamma j}\) range above 500 GeV, indicating that the fake-photon contribution does not depend significantly on \(m_{\gamma j}\). Figure 3 shows the \(m_{\gamma j}\) distribution in data compared to the corrected Jetphox \(\gamma +\text {jet}\) prediction normalized to data in the \(m_{\gamma j} > 500\) GeV region.
Theoretical uncertainties in the Jetphox prediction are computed by considering the variations induced by \(\pm 1\sigma \) of the NNPDF 2.3 PDF uncertainties, by switching between the nominal NNPDF 2.3 and CT10 or MSTW2008 PDFs, by the variation of the value of the strong coupling constant by \(\pm 0.002\) around the nominal value of 0.118 and by the variation of the renormalization, factorization and fragmentation scales between half and twice the photon transverse momentum. The differences between data and the corrected Jetphox prediction shown in Fig. 3 are well within the uncertainties associated with the perturbative QCD prediction.
Distribution of \(E_{\text {T,\,iso}}^{\gamma } =E_{\text {T,\,iso}}-0.022\times E_{\text {T}} ^{\gamma } \) for the photon candidates in events with \(1.0<m_{\gamma j} <1.1\) TeV, and the comparison with the result of the template fit. Real- and fake-photon components determined by the fit are shown by the green dashed and red dot-dashed histograms, respectively, and the sum of the two components is shown as the solid blue histogram. The blue band shows the systematic uncertainties in the real- plus fake-photon template. The last bin of the distribution includes overflow events. The vertical dashed line corresponds to the isolation requirement used in the analysis. The photon purity determined from the fit for the selected sample in the \(1.0<m_{\gamma j} <1.1\) TeV mass range is 93%
Distribution of the invariant mass of the \(\gamma \) + jet system as measured in the \(\gamma +\text {jet}\) data (dots), compared with the Jetphox (green histogram) \(\gamma +\text {jet}\) predictions. The Jetphox distribution is obtained after correcting the parton-level spectrum for showering, hadronization and detector resolution effects as described in the text. The distributions are divided by the bin width and the Jetphox spectrum is normalized to the data in the \(m_{\gamma j}\) range above 500 GeV. The ratio of the data to Jetphox prediction as a function of \(m_{\gamma j}\) is shown in the middle panel (green histogram): the theoretical uncertainty is shown as a shaded band. The statistical uncertainty from the data sample and the sum of the statistical uncertainty plus the systematic uncertainty from the background subtraction are shown as inner and outer bars respectively. The measured \(\gamma +\text {jet}\) purity as a function of \(m_{\gamma j}\) is presented in the bottom panel (black histogram): the statistical uncertainty of the purity measurement is reported as the inner error bar while the total uncertainty is shown as the outer error bar
The number of signal events extracted by the signal + background fit to the pure background model described above is called the spurious signal [57] and it is used to select the optimal functional form and the \(m_{\gamma j}\) range of the fit. In order to account for the assumption that the corrected Jetphox prediction itself is a good representation of the data, the fit is repeated on modified samples obtained by changing the nominal shape to account for several effects: firstly, the nominal distribution is corrected to follow the envelope of the changes induced by \(\pm 1\sigma \) variations of the NNPDF 2.3 PDF uncertainty, the variations between the nominal NNPDF 2.3 and CT10 or MSTW2008 PDFs, the variation of the value of the strong coupling constant by \(\pm 0.002\) around the nominal value of 0.118 and the variation of the renormalization, factorization and fragmentation scales between half and twice the photon transverse momentum; secondly the corrections for the hadronization, underlying event and detector effects are removed; and finally the corrections for the photon purity are changed within their estimated uncertainty. The largest absolute fitted signal from all variations of the nominal background sample discussed above is taken to be the spurious signal.
The spurious signal is evaluated at a number of hypothetical masses over a large search range. It is required to be less than 40% of the background’s statistical uncertainty, as quantified by the statistical uncertainty of the fitted spurious signal, anywhere in the investigated search range. In this way the impact of the systematic uncertainties due to background modelling on the analysis sensitivity is expected to be subdominant with respect to the statistical uncertainty. Functional forms that cannot meet this requirement are rejected. For different signal models, the functional form and fit range are determined separately. All considered functions with k up to two (four parameters) are found to fulfil the spurious-signal requirement when fitting in the range \(1.1<m_{\gamma j} <6.0\) TeV for the \(q^*\) signal and \(1.5~(2.5)<m_{\gamma j} <6.0~(8.0)\) TeV for the RS1 (ADD) QBH signal. To further consolidate the choice of nominal background functional form, an F test [58] is performed to determine if the change in the \(\chi ^2\) value obtained by fitting the Jetphox sample with an additional parameter is significant. The test indicates that the \(k=0\) (1) functional form with two (three) parameters can describe the present data sufficiently well over the entire fit range for the QBH (\(q^*\)) signal search, and there is no improvement by adding more parameters to the background fit function.
Given the fit range determined by the spurious signal test, the search is performed for the \(q^*\) (RS1 and ADD QBH) signal within the \(m_{\gamma j}\) range above 1.5 (2.0 and 3.0) TeV, to account for the width of the expected signal. The estimated spurious signal for the selected functional form is converted into a spurious-signal cross-section (\(\sigma _{\text {spur}}\)), which is included as the uncertainty due to background modelling in the statistical analysis. The spurious-signal cross-section, and the ratio of the spurious-signal cross-section to its uncertainty (\(\delta \sigma _{\mathrm {spur}}\)) and to the signal cross-section (\(\sigma _{\text {model}}\)) for the three benchmark models under investigation are given in Table 3 in the different search ranges. While both \(\sigma _{\text {spur}}\) and \(\sigma _{\text {spur}}\)/\(\delta \sigma _{\mathrm {spur}}\) decrease with the hypothesized signal mass, the ratio \(\sigma _{\text {spur}}\)/\(\sigma _{\text {model}}\) increases with \(m_{q^*}\) or \(M_{\text {th}}\), becoming as large as 15% in the case of excited quarks with \(m_{q^*}\) = 6 TeV.
A similar test is performed to determine the functional form and fit ranges for the Gaussian-shaped signal with a 15% width. The test indicates that the same functional form and fit range as those used for the \(q^*\) signal are optimal for a wide-width Gaussian signal. The same functional form and mass range is used for all the Gaussian signals.
5.3 Statistical tests
A profile-likelihood-ratio test statistic is used to quantify the compatibility between the data and the SM prediction, and to set limits on the presence of possible signal contributions in the \(m_{\gamma j}\) distribution. The likelihood function \(\mathcal {L}\) is built from a Poisson probability for the numbers of observed events, n, and expected events, N, in the selected sample:
where \(N(\varvec{\theta })\) is the expected number of candidates, \(f(m_{\gamma j} ^i, \varvec{\theta })\) is the value of the probability density function of the invariant mass distribution evaluated for each candidate event i and \(\varvec{\theta }\) are nuisance parameters. The \(G(\varvec{\theta })\) term collects the set of constraints on the nuisance parameters associated with the systematic uncertainties in the signal yield, in the spurious signal and in the resolution (only for Gaussian signals) and it is represented by normal distributions centred at zero and with unit variance.
The pdf of the \(m_{\gamma j}\) distribution is given as the normalized sum of the signal and background pdfs:
where \(f_{\text {sig}}\) and \(f_{\text {bg}}\) are the normalized signal and background \(m_{\gamma j}\) distributions described in the previous sections. The \(\varvec{\theta } _{\mathrm {yield}}\) are nuisance parameters associated with the signal yield uncertainties (constrained) while \(\varvec{\theta } _{\mathrm {bkg}}\) are the nuisance parameters of the background shape (unconstrained). The expected number of events N is given by the sum of the expected numbers of signal events (\(N_{\text {sig}}\)) and background events (\(N_{\text {bg}}\)). The \(N_{\text {sig}}\) term can be expressed as
where \(\sigma _{\text {spur}}\) and \(\theta _{\text {spur}}\) are the spurious-signal cross-section described in Sect. 5.2 and its nuisance parameter while \(\mathcal {L}_{\text {int}}\) and \(F(\delta _{\mathcal {L}},\theta _{\mathcal {L}})\) are the integrated luminosity and its uncertainty. Apart from the spurious signal, systematic uncertainties with an estimated size \(\delta _{X}\) are incorporated into the likelihood by multiplying the relevant parameter of the statistical model by a factor \(F(\delta _{X},\theta _{X})=\mathrm {e}^{\delta _{X} \theta _{X}}\). The parameter of interest in the fit to Gaussian-shaped resonances is the visible cross-section \(\sigma _{\text {model}} \cdot B \cdot A \cdot \varepsilon \) while that in the fit to \(q^*\) and QBH signals is \(\sigma _{\text {model}} \cdot B\). For the latter case, the additional nuisance parameters for the signal efficiency uncertainties \(F(\varvec{\delta }_{\varepsilon },\varvec{\theta }_{\varepsilon })\) are included.
The significance of a possible deviation from the SM prediction is estimated by computing the \(p_0\) value, defined as the probability to observe, under the background model hypothesis, an excess at least as large as the one observed in data. Upper limits are set at 95% confidence level (CL) with a modified frequentist CL\(_{\text {S}}\) method on the visible cross-section (\(\sigma _{\text {model}} \cdot B \cdot A \cdot \varepsilon \)) for the Gaussian-shaped resonances or on the signal cross-section times branching ratio (\(\sigma _{\text {model}} \cdot B\)) for the \(q^*\) and QBH signals by identifying the value for which the CL\(_{\text {S}}\) value is equal to 0.05.
6 Results
The photon–jet invariant mass distributions obtained from the selected data are shown in Fig. 4, together with the background-only fits using the model described in Sect. 5.2 and expected distributions from the signal models under test. No significant deviation from the background prediction is observed in any of the distributions. The most significant excess is observed at 1.8 TeV with the assumption of the 2%-width Gaussian model for a local significance of 2.1 standard deviations.
Distributions of the invariant mass of the \(\gamma \) + jet system of the observed events (dots) in \(36.7~\text {fb}^{-1} \) of data at \(\sqrt{s}\) = 13 TeV and fits to the data (solid lines) under the background-only hypothesis for searches in the a excited quarks, b QBH (RS1) with \(n=1\) and c QBH (ADD) with \(n=6\) models. The \(\pm 1\sigma \) uncertainty in the background prediction originating from the uncertainties in the fit function parameter values is shown as a shaded band around the fit. The predicted signal distributions (dashed lines) for the \(q^*\) model with \(m_{q^*}\) = 5.5 TeV and the QBH model with \(M_{\text {th}}\) = 4.5 (7.0) TeV based on RS1 (ADD) are shown on top of the background predictions. The bottom panels show the bin-by-bin significances of the data–fit differences, considering only statistical uncertainties
Limits are placed at 95% CL on the visible cross-section in the case of generic Gaussian-shaped resonances and on the production cross-section times branching ratio to a photon and a quark or gluon for the excited-quark and QBH signals. The results are shown in Fig. 5 for the Gaussian signals with the width varying between 2 and 15%, and in Fig. 6 for the benchmark signal models. The Gaussian signals are excluded for visible cross-sections above 0.25–1.1 fb (0.08–0.2 fb), depending on the width, at a mass \(m_{\text {G}}\) of 3 TeV (5 TeV). In the case of the benchmark signal models considered in this analysis, the presence of a signal with a mass below 5.3, 4.4 and 7.1 TeV for the excited quarks, RS1 and ADD QBHs, can be excluded at 95% CL. The limits improve on those in Ref. [16] by about 0.9, 0.6 and 0.9 TeV for the excited quarks, RS1 and ADD QBHs, respectively.
Observed (solid lines) and expected (dotted lines) 95% CL upper limits on the visible cross-sections \(\sigma \cdot B \cdot A \cdot \varepsilon \) in \(36.7~\text {fb}^{-1} \) of data at \(\sqrt{s}\) = 13 TeV as a function of the mass \(m_{\text {G}}\) of the Gaussian resonances with three different Gaussian widths between 2 and 15%. The calculation is performed using ensemble tests at mass points separated by 100 GeV over the search range
Observed 95% CL upper limits (solid line with dots) on the production cross-section times branching ratio \(\sigma \cdot {B}\) to a photon and a quark or gluon in \(36.7~\text {fb}^{-1} \) of data at \(\sqrt{s}\) = 13 TeV for the a excited-quarks, b QBH (RS1) with \(n=1\) and c QBH (ADD) with \(n=6\) models. The limits are placed as a function of \(m_{q^*}\) for the excited quarks and \(M_{\text {th}}\) for the QBH signals. The calculation is performed using ensemble tests at mass points separated by 200 (500) GeV for the RS1 (ADD) model over the search range. For the \(q^*\) model the step size is 250 GeV up to 5 TeV and then 200 GeV up to 6 TeV. The limits expected if a signal is absent (dashed lines) are shown together with the \(\pm 1\sigma \) and \(\pm 2\sigma \) intervals represented by the green and yellow bands, respectively. The theoretical predictions of \(\sigma \cdot {B}\) for the respective benchmark signals are shown by the red solid lines.
7 Conclusion
A search is performed for new phenomena in events having a photon with high transverse momentum and a jet collected in \(36.7~\text {fb}^{-1} \) of \(pp\) collision data at a centre-of-mass energy of \(\sqrt{s}\) = 13 TeV recorded with the ATLAS detector at the LHC. The invariant mass distribution of the \(\gamma \) + jet system above 1.1 TeV is used in the search for localized excesses of events. No significant deviation is found. Limits are set on the visible cross-section for generic Gaussian-shaped resonances and on the production cross-section times branching ratio for signals predicted in models of excited quarks or quantum black holes. The data exclude, at 95% CL, the mass range below 5.3 TeV for the excited quarks and 7.1 (4.4) TeV for the quantum black holes with six (one) extra dimensions in the Arkani-Hamed–Dimopoulos–Dvali (Randall–Sundrum) model. These limits supersede the previous ATLAS exclusion limits for excited quarks and quantum black holes in the \(\gamma +\text {jet}\) final state.
Notes
ATLAS uses a right-handed coordinate system with its origin at the nominal interaction point (IP) in the centre of the detector and the z-axis along the beam pipe. The x-axis points from the IP to the centre of the LHC ring, and the y-axis points upwards. Cylindrical coordinates \((r,\phi )\) are used in the transverse plane, \(\phi \) being the azimuthal angle around the z-axis. The pseudorapidity is defined in terms of the polar angle \(\theta \) as \(\eta = -\ln \tan (\theta /2)\). Angular distance is measured in units of \(\Delta R \equiv \sqrt{(\Delta \eta )^{2} + (\Delta \phi )^{2}}\).
The parton-level isolation requirement takes into account the correlation between reconstruction-level isolation energies and particle-level isolation energies, as a proxy for the parton-level isolation, as evaluated using \(\gamma +\text {jet}\) events simulated by Pythia 8.186.
References
U. Baur, I. Hinchliffe, D. Zeppenfeld, Excited quark production at hadron colliders. Int. J. Mod. Phys. A 2, 1285 (1987)
U. Baur, M. Spira, P.M. Zerwas, Excited-quark and -lepton production at hadron colliders. Phys. Rev. D 42, 815 (1990)
S. Bhattacharya, S.S. Chauhan, B.C. Choudhary, D. Choudhury, Quark excitations through the prism of direct photon plus jet at the LHC. Phys. Rev. D 80, 015014 (2009). arXiv:0901.3927 [hep-ph]
S. Weinberg, Gauge hierarchies. Phys. Lett. B 82, 387 (1979)
M.J.G. Veltman, The infrared-ultraviolet connection. Acta Phys. Polon. B 12, 437 (1981)
C.H. Llewellyn Smith, G.G. Ross, The real Gauge hierarchy problem. Phys. Lett. B 105, 38 (1981)
S. Dimopoulos, G.L. Landsberg, Black holes at the large hadron collider. Phys. Rev. Lett. 87, 161602 (2001). arXiv:hep-ph/0106295
S.B. Giddings, S.D. Thomas, High energy colliders as black hole factories: the end of short distance physics. Phys. Rev. D 65, 056010 (2002). arXiv:hep-ph/0106219
D.M. Gingrich, Quantum black holes with charge, colour, and spin at the LHC. J. Phys. G 37, 105008 (2010). arXiv:0912.0826 [hep-ph]
X. Calmet, W. Gong, S.D. Hsu, Colorful quantum black holes at the LHC. Phys. Lett. B 668, 20 (2008). arXiv:0806.4605 [hep-ph]
N. Arkani-Hamed, S. Dimopoulos, G. Dvali, The hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 429, 263 (1998). arXiv:hep-ph/9803315
L. Randall, R. Sundrum, A large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 83, 3370 (1999). arXiv:hep-ph/9905221
ATLAS Collaboration, Search for production of resonant states in the photon-jet mass distribution using \(pp\) collisions at at \(\sqrt{s} = 7\;\text{TeV}\) collected by the ATLAS detector. Phys. Rev. Lett. 108, 211802 (2012). arXiv:1112.3580 [hep-ex]
ATLAS Collaboration, Search for new phenomena in photon+jet events collected in proton–proton collisions at \(\sqrt{s} = 8\;\text{ TeV }\) with the ATLAS detector. Phys. Lett. B 728, 562 (2014). arXiv:1309.3230 [hep-ex]
CMS Collaboration, Search for excited quarks in the \(\gamma \)+jet final state in proton–proton collisions at \(\sqrt{s} = 8\;\text{ TeV }\). Phys. Lett. B 738, 274 (2014). arXiv:1406.5171 [hep-ex]
ATLAS Collaboration, Search for new phenomena with photon+jet events in proton–proton collisions at \(\sqrt{s} = 13\;\text{ TeV }\) with the ATLAS detector. JHEP 03, 041 (2016). arXiv:1512.05910 [hep-ex]
ATLAS Collaboration, Search for new phenomena in dijet mass and angular distributions from \(pp\) collisions at \(\sqrt{s} = 13\;\text{ TeV }\) with the ATLAS detector. Phys. Lett. B 754, 302 (2016). arXiv:1512.01530 [hep-ex]
ATLAS Collaboration, Search for new phenomena in dijet events using \(37\;\text{ fb }^{-1}\) of \(pp\) collision data collected at \(\sqrt{s} = 13\;\text{ TeV }\) with the ATLAS detector. Phys. Rev. D 96, 052004 (2017). arXiv:1703.09127 [hep-ex]
CMS Collaboration, Search for dijet resonances in proton–proton collisions at \(\sqrt{s} = 13\;\text{ TeV }\) and constraints on dark matter and other models. Phys. Lett. B 769, 520 (2017). arXiv:1611.03568 [hep-ex]
ATLAS Collaboration, The ATLAS experiment at the CERN large hadron collider. JINST 3, S08003 (2008)
ATLAS Collaboration, Atlas insertable b-layer technical design report. ATLAS-TDR-19 (2010). https://cds.cern.ch/record/1291633. ATLAS Insertable B-Layer Technical Design Report Addendum, ATLAS-TDR-19-ADD-1 (2012). https://cds.cern.ch/record/1451888
ATLAS Collaboration, Performance of the ATLAS trigger system in 2015. Eur. Phys. J. C 77, 317 (2017). arXiv:1611.09661 [hep-ex]
ATLAS Collaboration, Luminosity determination in \(pp\) collisions at \(\sqrt{s} = 8\;\text{ TeV }\) using the ATLAS detector at the LHC. Eur. Phys. J. C 76, 653 (2016). arXiv:1608.03953 [hep-ex]
T. Gleisberg, S. Höche, F. Krauss, M. Schönherr, S. Schumann et al., Event generation with SHERPA1.1. JHEP 02, 007 (2009). arXiv:0811.4622 [hep-ph]
S. Schumann, F. Krauss, A parton shower algorithm based on Catani–Seymour dipole factorisation. JHEP 03, 038 (2008). arXiv:0709.1027 [hep-ph]
S. Höche, F. Krauss, S. Schumann, F. Siegert, QCD matrix elements and truncated showers. JHEP 05, 053 (2009). arXiv:0903.1219 [hep-ph]
H.L. Lai et al., New parton distributions for collider physics. Phys. Rev. D 82, 074024 (2010). arXiv:1007.2241 [hep-ph]
T. Sjöstrand et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159–177 (2015). arXiv:1410.3012 [hep-ph]
R.D. Ball et al., Parton distributions with LHC data. Nucl. Phys. B 867, 244–289 (2013). arXiv:1207.1303 [hep-ph]
S. Catani, M. Fontannaz, J.P. Guillet, E. Pilon, Cross-section of isolated prompt photons in hadron hadron collisions. JHEP 05, 028 (2002). arXiv:hep-ph/0204023
ATLAS Collaboration, ATLAS Pythia 8 tunes to \(7\;\text{ TeV }\) data. ATL-PHYS-PUB-2014-021 (2014). https://cds.cern.ch/record/1966419
L. Bourhis, M. Fontannaz, J. Guillet, M. Werlen, Next-to-leading order determination of fragmentation functions. Eur. Phys. J. C 19, 89 (2001). arXiv:hep-ph/0009101
M. Cacciari, G.P. Salam, G. Soyez, The anti-\(k_t\) jet clustering algorithm. JHEP 04, 063 (2008). arXiv:0802.1189 [hep-ph]
M. Cacciari, G.P. Salam, G. Soyez, FastJet user manual. Eur. Phys. J. C 72, 1896 (2012). arXiv:1111.6097 [hep-ph]
D.M. Gingrich, Monte Carlo event generator for black hole production and decay in proton-proton collisions. Comput. Phys. Commun. 181, 1917 (2010). arXiv:0911.5370 [hep-ph]
J. Pumplin et al., New generation of parton distributions with uncertainties from global QCD analysis. JHEP 07, 012 (2002). arXiv:hep-ph/0201195
ATLAS Collaboration, The ATLAS Simulation Infrastructure. Eur. Phys. J. C 70, 823 (2010). arXiv:1005.4568 [hep-ex]
S. Agostinelli et al., GEANT4—a simulation toolkit. Nucl. Instrum. Methods A 506, 250 (2003)
ATLAS Collaboration, Summary of ATLAS Pythia 8 tunes. ATL-PHYS-PUB-2012-003 (2012). https://cds.cern.ch/record/1474107
A.D. Martin, W.J. Stirling, R.S. Thorne, G. Watt, Parton distributions for the LHC. Eur. Phys. J. C 63, 189 (2009). arXiv:0901.0002 [hep-ph]
ATLAS Collaboration, Measurement of the photon identification efficiencies with the ATLAS detector using LHC Run-1 data. Eur. Phys. J. C 76(12), 666 (2016). arXiv:1606.01813 [hep-ex]
ATLAS Collaboration, Electron and photon energy calibration with the ATLAS detector using LHC Run 1 data. Eur. Phys. J. C 74, 3071 (2014). arXiv:1407.5063 [hep-ex]
ATLAS Collaboration, Topological cell clustering in the ATLAS calorimeters and its performance in LHC Run 1. Eur. Phys. J. C 77, 490 (2017). arXiv:1603.02934 [hep-ex]
ATLAS Collaboration, Measurement of the inclusive isolated prompt photon cross section in \(pp\) collisions at \(\sqrt{s} = 7\;\text{ TeV }\) with the ATLAS detector. Phys. Rev. D 83, 052005 (2011). arXiv:1012.4389 [hep-ex]
ATLAS Collaboration, Performance of pile-up mitigation techniques for jets in \(pp\) collisions at \(\sqrt{s} = 8\;\text{ TeV }\) using the ATLAS detector. Eur. Phys. J. C 76, 581 (2016). arXiv:1510.03823 [hep-ex]
ATLAS Collaboration, Jet energy scale measurements and their systematic uncertainties in proton–proton collisions at \(\sqrt{s} = 13\;\text{ TeV }\) with the ATLAS detector. Phys. Rev. D 96, 072002 (2017). arXiv:1703.09665 [hep-ex]
ATLAS Collaboration, Jet global sequential corrections with the ATLAS detector in proton–proton collisions at \(\sqrt{s} = 8\;\text{ TeV }\). ATLAS-CONF-2015-002 (2015). https://cds.cern.ch/record/2001682
ATLAS Collaboration, Tagging and suppression of pileup jets with the ATLAS detector. ATLAS-CONF-2014-018 (2014). https://cds.cern.ch/record/1700870
ATLAS Collaboration, Selection of jets produced in \(13\;\text{ TeV }\) proton–proton collisions with the ATLAS detector. ATLAS-CONF-2015-029 (2015). https://cds.cern.ch/record/2037702
ATLAS Collaboration, Search for dark matter at \(\sqrt{s} = 13\;\text{ TeV }\) in final states containing an energetic photon and large missing transverse momentum with the ATLAS detector. Eur. Phys. J. C 77, 393 (2017). arXiv:1704.03848 [hep-ex]
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011). arXiv:1007.1727 [physics.data-an]. Erratum: Eur. Phys. J. C 73, 2501 (2013)
A.L. Read, Presentation of search results: the \(CL_S\) technique. J. Phys. G 28, 2693 (2002)
K.S. Cranmer, Kernel estimation in high-energy physics. Comput. Phys. Commun. 136, 198 (2001). arXiv:hep-ex/0011057
M. Baak, S. Gadatsch, R. Harrington, W. Verkerke, Interpolation between multi-dimensional histograms using a new non-linear moment morphing method. Nucl. Instrum. Methods A 771, 39 (2015). arXiv:1410.7388 [physics.data-an]
ATLAS Collaboration, Search for resonances in diphoton events at \(\sqrt{s}\)=13 TeV with the ATLAS detector. JHEP 09, 001 (2016). arXiv:1606.03833 [hep-ex]
ATLAS Collaboration, High-\(E_{{\rm T}}\) isolated-photon plus jets production in \(pp\) collisions at \(\sqrt{s} = 8\;\text{ TeV }\) with the ATLAS detector. Nucl. Phys. B 918, 257 (2017). arXiv:1611.06586 [hep-ex]
ATLAS Collaboration, Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1 (2012). arXiv:1207.7214 [hep-ex]
R.A. Fisher, On the interpretation of \(\chi ^2\) from contingency tables, and the calculation of p. J. R. Stat. Soc. 85, 87 (1922)
ATLAS Collaboration, ATLAS computing acknowledgements 2016–2017. ATL-GEN-PUB-2016-002 (2016). https://cds.cern.ch/record/2202407
Acknowledgements
We thank CERN for the very successful operation of the LHC, as well as the support staff from our institutions without whom ATLAS could not be operated efficiently.
We acknowledge the support of ANPCyT, Argentina; YerPhI, Armenia; ARC, Australia; BMWFW and FWF, Austria; ANAS, Azerbaijan; SSTC, Belarus; CNPq and FAPESP, Brazil; NSERC, NRC and CFI, Canada; CERN; CONICYT, Chile; CAS, MOST and NSFC, China; COLCIENCIAS, Colombia; MSMT CR, MPO CR and VSC CR, Czech Republic; DNRF and DNSRC, Denmark; IN2P3-CNRS, CEA-DRF/IRFU, France; SRNSF, Georgia; BMBF, HGF, and MPG, Germany; GSRT, Greece; RGC, Hong Kong SAR, China; ISF, I-CORE and Benoziyo Center, Israel; INFN, Italy; MEXT and JSPS, Japan; CNRST, Morocco; NWO, Netherlands; RCN, Norway; MNiSW and NCN, Poland; FCT, Portugal; MNE/IFA, Romania; MES of Russia and NRC KI, Russian Federation; JINR; MESTD, Serbia; MSSR, Slovakia; ARRS and MIZŠ, Slovenia; DST/NRF, South Africa; MINECO, Spain; SRC and Wallenberg Foundation, Sweden; SERI, SNSF and Cantons of Bern and Geneva, Switzerland; MOST, Taiwan; TAEK, Turkey; STFC, United Kingdom; DOE and NSF, United States of America. In addition, individual groups and members have received support from BCKDF, the Canada Council, CANARIE, CRC, Compute Canada, FQRNT, and the Ontario Innovation Trust, Canada; EPLANET, ERC, ERDF, FP7, Horizon 2020 and Marie Skłodowska-Curie Actions, European Union; Investissements d’Avenir Labex and Idex, ANR, Région Auvergne and Fondation Partager le Savoir, France; DFG and AvH Foundation, Germany; Herakleitos, Thales and Aristeia programmes co-financed by EU-ESF and the Greek NSRF; BSF, GIF and Minerva, Israel; BRF, Norway; CERCA Programme Generalitat de Catalunya, Generalitat Valenciana, Spain; the Royal Society and Leverhulme Trust, United Kingdom.
The crucial computing support from all WLCG partners is acknowledged gratefully, in particular from CERN, the ATLAS Tier-1 facilities at TRIUMF (Canada), NDGF (Denmark, Norway, Sweden), CC-IN2P3 (France), KIT/GridKA (Germany), INFN-CNAF (Italy), NL-T1 (Netherlands), PIC (Spain), ASGC (Taiwan), RAL (UK) and BNL (USA), the Tier-2 facilities worldwide and large non-WLCG resource providers. Major contributors of computing resources are listed in Ref. [59].
Author information
Authors and Affiliations
Department of Physics, University of Adelaide, Adelaide, Australia
A. Artamonov, D. Duvnjak, P. Jackson, A. Petridis & M. J. White
Physics Department, SUNY Albany, Albany, NY, USA
J. Bouffard, A. Fischer, V. Jain & S. P. Swift
Department of Physics, University of Alberta, Edmonton, AB, Canada
J. Dassoulas, N. Dehghanian, D. M. Gingrich, S. Jabbar, R. W. Moore, J. L. Pinfold, X. Sun & H. Wang
Department of Physics, Ankara University, Ankara, Turkey
O. Cakir, A. K. Ciftci & H. Duran Yildiz
Istanbul Aydin University, Istanbul, Turkey
S. Kuday & I. Turk Cakir
Division of Physics, TOBB University of Economics and Technology, Ankara, Turkey
S. Sultansoy
LAPP, CNRS/IN2P3 and Université Savoie Mont Blanc, Annecy-le-Vieux, France
N. Berger, A. M. Burger, M. Delmastro, L. Di Ciaccio, S. Elles, K. Grevtsov, T. Guillemin, T. Hryn’ova, S. Jézéquel, O. Kivernyk, I. Koletsou, R. Lafaye, J. Levêque, N. Lorenzo Martinez, P. Mastrandrea, S. Raspopov, E. Sauvan, B. H. Smart, S. Todorova-Nova, A. Vallier, I. Wingerter-Seez & E. Yatsenko
High Energy Physics Division, Argonne National Laboratory, Argonne, IL, USA
R. E. Blair, S. Chekanov, T. LeCompte, J. Love, D. Malon, J. Metcalfe, A. Paramonov, J. Proudfoot, S. Ryu, R. W. Stanek, P. van Gemmeren, R. Wang, J. S. Webster & J. Zhang
Department of Physics, University of Arizona, Tucson, AZ, USA
E. Cheu, C. M. Delitzsch, K. A. Johns, S. Jones, W. Lampl, X. Lei, R. Leone, P. Loch, R. Nayyar, J. P. Rutherfoord, M. A. Shupe, E. W. Varnes & V. Veeraraghavan
Department of Physics, The University of Texas at Arlington, Arlington, TX, USA
A. Brandt, D. Bullock, S. Darmora, K. De, A. Farbin, L. Feremenga, J. Griffiths, H. K. Hadavand, L. Heelan, H. Y. Kim, N. Ozturk, A. R. Stradling, G. Usai, A. Vartapetian, A. White & J. Yu
Physics Department, National and Kapodistrian University of Athens, Athens, Greece
D. Fassouliotis, I. Gkialas, P. Ioannou, C. Kourkoumelis, K. Papageorgiou & N. Tsirintanis
Physics Department, National Technical University of Athens, Zografou, Greece
T. Alexopoulos, N. Benekos, M. Dris, E. N. Gazis, P. Gkountoumis, K. Karakostas, N. Karastathis, E. Karentzos, A. Koulouris, S. Maltezos, P. Moschovakos, E. St. Panagiotopoulou, I. Panagoulias, Th. D. Papadopoulou, G. Tsipolitis, S. Vlachos & G. Zacharis
Department of Physics, The University of Texas at Austin, Austin, TX, USA
T. Andeen, Y. Ilchenko, R. Narayan, N. Nikiforou, P. U. E. Onyisi, H. Potti & A. F. Webb
Institute of Physics, Azerbaijan Academy of Sciences, Baku, Azerbaijan
O. Abdinov & F. Khalil-zada
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology, Barcelona, Spain
N. Anjos, M. Bosman, M. P. Casado, M. Casolino, E. Cavallaro, M. Cavalli-Sforza, S. Fernandez Perez, C. Fischer, F. A. Förster, D. Gerbaudo, E. L. Gkougkousis, J. Glatzer, S. Grinstein, A. Juste Rozas, I. Korolkov, J. C. Lange, I. Lopez Paz, M. Martinez, L. M. Mir, A. Pacheco Pages, C. Padilla Aranda, I. Riu, C. Rizzi, A. Rodriguez Perez, S. Terzo, M. F. Tripiana, S. Tsiskaridze, L. Valéry, D. Vazquez Furelos, G. Volpi & R. Zaidan
Institute of Physics, University of Belgrade, Belgrade, Serbia
T. Agatonovic-Jovin, A. Dimitrievska, J. Krstic, Dj. Sijacki, N. Vranjes, M. Vranjes Milosavljevic & L. Živković
Department for Physics and Technology, University of Bergen, Bergen, Norway
T. Buanes, O. Dale, G. Eigen, W. Liebig, A. Lipniacka, S. Maeland, B. Martin dit Latour, B. Stugu, Z. Yang & J. Zalieckas
Physics Division, Lawrence Berkeley National Laboratory, University of California, Berkeley, CA, USA
B. T. Amadio, B. Axen, R. M. Barnett, J. Beringer, J. Brosamer, P. Calafiura, F. Cerutti, A. Ciocio, R. N. Clarke, M. Cooke, E. M. Duffield, K. Einsweiler, S. Farrell, A. Gabrielli, M. Garcia-Sciveres, M. Gilchriese, H. M. Gray, C. Haber, T. Heim, I. Hinchliffe, L. Jeanty, K. Krizka, W. Lavrijsen, C. Leggett, Z. Marshall, B. P. Nachman, S. Pagan Griso, A. Pranko, M. Shapiro, M. J. Tibbetts, M. Trottier-McDonald, V. Tsulaia, S. Viel, H. Wang, H. Yang & W-M. Yao
Department of Physics, Humboldt University, Berlin, Germany
D. Biedermann, J. Dietrich, S. Grancagnolo, G. H. Herbert, I. Hristova, O. M. Kind, H. Lacker, T. Lohse, S. Mergelmeyer, F. Peri, L. Rehnisch, H. Schulz, D. Sperlich, S. Stamm & M. zur Nedden
Albert Einstein Center for Fundamental Physics, Laboratory for High Energy Physics, University of Bern, Bern, Switzerland
H. P. Beck, A. Ereditato, S. Haug, F. Meloni, C. Merlassino, A. Miucci, G. A. Mullier, M. Rimoldi, M. E. Stramaglia, M. S. Weber & T. D. Weston
School of Physics and Astronomy, University of Birmingham, Birmingham, UK
P. P. Allport, N. Andari, M. J. Baca, J. Bracinik, D. L. Briglin, J. H Broughton, D. Casadei, D. G. Charlton, A. C. Daniells, A. G. Foster, L. Gonella, C. M. Hawkes, S. J. Head, S. J. Hillier, J Kendrick, M. Levy, P. R. Newman, K. Nikolopoulos, R. E. Owen, E. Reynolds, M. Slater, J. P. Thomas, P. D. Thompson, P. M. Watkins, A. T. Watson, M. F. Watson, J. A. Wilson & S. D. Worm
Department of Physics, Bogazici University, Istanbul, Turkey
M. Arik, S. Gurbuz, S. Istin & V. E. Ozcan
Department of Physics Engineering, Gaziantep University, Gaziantep, Turkey
A. Beddall & A. Bingul
Faculty of Engineering and Natural Sciences, Istanbul Bilgi University, Istanbul, Turkey
E. Celebi & S. A. Cetin
Faculty of Engineering and Natural Sciences, Bahcesehir University, Istanbul, Turkey
A. J. Beddall
Centro de Investigaciones, Universidad Antonio Narino, Bogotá, Colombia
M. Losada, D. Moreno, G. Navarro & C. Sandoval
INFN Sezione di Bologna, Bologna, Italy
G. L. Alberghi, L. Bellagamba, S. Biondi, D. Boscherini, A. Bruni, G. Bruni, M. Bruschi, A. Cervelli, G. D’amen, S. De Castro, F. Fabbri, L. Fabbri, M. Franchini, A. Gabrielli, B. Giacobbe, N. Giangiacomi, F. M. Giorgi, F. Lasagni Manghi, A. Mengarelli, M. Negrini, A. Polini, L. Rinaldi, M. Romano, C. Sbarra, A. Sbrizzi, N. Semprini-Cesari, A. Sidoti, M. Sioli, R. Spighi, G. Ucchielli, S. Valentinetti, M. Villa, C. Vittori & A. Zoccoli
Dipartimento di Fisica e Astronomia, Università di Bologna, Bologna, Italy
G. L. Alberghi, S. Biondi, A. Cervelli, G. D’amen, S. De Castro, F. Fabbri, L. Fabbri, M. Franchini, A. Gabrielli, N. Giangiacomi, F. Lasagni Manghi, A. Mengarelli, M. Romano, A. Sbrizzi, N. Semprini-Cesari, A. Sidoti, M. Sioli, G. Ucchielli, S. Valentinetti, M. Villa, C. Vittori & A. Zoccoli
Physikalisches Institut, University of Bonn, Bonn, Germany
O. Arslan, A. Bandyopadhyay, P. Bechtle, F. U. Bernlochner, I. Brock, J. Caudron, I. A. Cioara, M. Cristinziani, W. Davey, K. Desch, J. Dingfelder, G. Gaycken, M. Ghneimat, C. A. Gottardo, C. Grefe, S. Hageböck, M. C. Hansen, S. Heer, D. Hohn, F. Huegging, R. M. Jacobs, J. Janssen, T. Klingl, V. V. Kostyukhin, J. Kroseberg, H. Krüger, K. Lantzsch, T. Lenz, J. Liebal, A. Melzer, R. Moles-Valls, T. Obermann, D. Pohl, O. Ricken, B. Sarrazin, S. Schaepe, L. K. Schildgen, E. Schopf, M. J. Schultens, A. Sciandra, P. Seema, E. von Toerne, P. Wagner, N. Wermes, B. T. Winter, K. H. Yau Wong, S. P. Y. Yuen & R. Zhang
Department of Physics, Boston University, Boston, MA, USA
S. P. Ahlen, K. M. Black, J. M. Butler, L. Dell’Asta, B. A. Long, J. T. Shank, Z. Yan & E. Yigitbasi
Department of Physics, Brandeis University, Waltham, MA, USA
C. Amelung, G. Amundsen, G. Barone, J. R. Bensinger, C. Blocker, S. Dhaliwal, D. Dodsworth, M. Goblirsch-Kolb, H. Herde, K. M. Loew, K. O’connor, G. Sciolla & A. Venturini
Universidade Federal do Rio De Janeiro COPPE/EE/IF, Rio de Janeiro, Brazil
Y. Amaral Coutinho, V. Araujo Ferraz, M. Begalli, L. P. Caloba, R. Goncalves Gama, C. Maidantchik, F. Marroquim & J. M. Seixas
Electrical Circuits Department, Federal University of Juiz de Fora (UFJF), Juiz de Fora, Brazil
A. S. Cerqueira, L. Manhaes de Andrade Filho & B. S. Peralva
Federal University of Sao Joao del Rei (UFSJ), Sao Joao del Rei, Brazil
M. A. B. do Vale
Instituto de Fisica, Universidade de Sao Paulo, São Paulo, Brazil
M. Donadelli, J. L. La Rosa Navarro & M. A. L. Leite
Physics Department, Brookhaven National Laboratory, Upton, NY, USA
K. Assamagan, M. Begel, W. Buttinger, H. Chen, R. Debbe, J. Elmsheuser, M. Ernst, H. A. Gordon, G. Iakovidis, A. Klimentov, V. Kouskoura, E. Lançon, F. Lanni, C. A. Lee, H. Liu, D. Lynn, H. Ma, T. Maeno, E. Mountricha, P. Nilsson, M. A. Nomura, D. Oliveira Damazio, F. Paige, S. Panitkin, D. V. Perepelitsa, M.-A. Pleier, V. Polychronakos, S. Protopopescu, V. Radeka, S. Rajagopalan, G. Redlinger, S. Snyder, P. Steinberg, S. A. Stucci, H. Takai, A. Tricoli, A. Undrus, T. Wenaus, L. Xu & S. Ye
Transilvania University of Brasov, Brasov, Romania
T. T. Tulbure
Horia Hulubei National Institute of Physics and Nuclear Engineering, Bucharest, Romania
C. Alexa, I. Caprini, M. Caprini, A. Chitan, M. Ciubancan, S. Constantinescu, P. Dita, S. Dita, M. Dobre, A. E. Dumitriu, A. Jinaru, V. S. Martoiu, J. Maurer, A. Olariu, D. Pantea, M. Rotaru, G. Stoicea, A. Tudorache & V. Tudorache
Department of Physics, Alexandru Ioan Cuza University of Iasi, Iasi, Romania
C. Agheorghiesei
Physics Department, National Institute for Research and Development of Isotopic and Molecular Technologies, Cluj-Napoca, Romania
G. A. Popeneciu
West University in Timisoara, Timisoara, Romania
P. M. Gravila
Departamento de Física, Universidad de Buenos Aires, Buenos Aires, Argentina
J. D. Bossio Sola, M. F. Daneri, M. R. Devesa, G. Marceca, G. Otero y Garzon, R. Piegaia & S. Sacerdoti
Cavendish Laboratory, University of Cambridge, Cambridge, UK
M. Arratia, N. Barlow, J. R. Batley, F. M. Brochu, BH Brunt, J. D. Chapman, G. Cottin, J. C. Hill, C. G. Lester, C. Malone, M. A. Parker, C. J. Potter, D. Robinson, J. H. N. Rosten, C. P. Ward & I. Yusuff
Department of Physics, Carleton University, Ottawa, ON, Canada
A. Bellerive, C. C. Chau, G. Cree, D. Di Valentino, D. Gillberg, R. F. H. Hunter, J. S. Keller, T. Koffas, I. Nomidis, F. G. Oakham, A. Ruiz-Martinez, N. Sherafati, M. G. Vincter & S. A. Weber
CERN, Geneva, Switzerland
M. Aleksa, B. Alvarez Gonzalez, S. Amoroso, L. Aperio Bella, A. J. Armbruster, G. Avolio, M-S Barisits, T. A. Beermann, O. Beltramello, J. Bortfeldt, J. Boyd, P. Butti, S. Camarda, S. Campana, M. D. M. Capeans Garrido, T. Carli, G. D. Carrillo-Montoya, A. Catinaccio, A. Cattai, M. A. Chelstowska, A. S. Chisholm, G. Conti, A. Cortes-Gonzalez, P. Czodrowski, A. Dell’Acqua, P. O. Deviveiros, A. Di Girolamo, B. Di Girolamo, R. Di Nardo, F. Dittus, D. Dobos, A. Dudarev, M. Dührssen, T. Eifert, N. Ellis, M. Elsing, J. Faltova, P. Farthouat, P. Fassnacht, E. J. Feng, D. Francis, S. M. Fressard-Batraneanu, D. Froidevaux, S. Gadatsch, L. Goossens, B. Gorini, J. Guenther, S. Guindon, C. Gumpert, R. J. Hawkings, L. Helary, C. Helsens, A. M. Henriques Correia, L. Hervas, A. Hoecker, J. Hrdinka, M. Huhtinen, P. Iengo, T. Klioutchnikova, A. Krasznahorkay, S. Kuehn, R. J. Langenberg, M. Lassnig, G. Lehmann Miotto, B. Lenzi, S. Malyukov, A. Manousos, L. Mapelli, C. A. Marin Tobon, A. Marzin, J. A. Mcfayden, J. Montejo Berlingen, M. Moreno Llácer, S. Morgenstern, A. K. Morley, G. Mornacchi, H. Musheghyan, A. M. Nairz, M. Nessi, M. Nordberg, S. Palestini, P. Pani, T. Pauly, H. Pernegger, B. A. Petersen, R. Polifka, K. Pommès, J. Poveda, M. E. Pozo Astigarraga, M. Raymond, C. Rembser, B. Ristić, E. Ritsch, S. Roe, N. Ruthmann, A. Salzburger, S. Schlenker, K. Schmieden, J. Schovancova, C. A. Solans Sanchez, G. Spigo, S. Stärz, H. J. Stelzer, H. Ten Kate, G. Unal, W. Vandelli, N. Venturi, R. Voss, R. Vuillermet, P. S. Wells, T. Wengler, S. Wenig, P. Werner, H. G. Wilkens, J. Wotschack, C. J. S. Young & L. Zwalinski
Enrico Fermi Institute, University of Chicago, Chicago, IL, USA
J. Alison, K. J. Anderson, P. Bryant, R. Camacho Toro, R. W. Gardner, K. Hildebrand, T. R. Holmes, Y. K. Kim, F. S. Merritt, D. W. Miller, M. J. Oreglia, J. E. Pilcher, J. Saxon, D. Schaefer, M. J. Shochet, G. H. Stark, M. Swiatlowski, I. Vukotic, M. Wu & R. Zou
Departamento de Física, Pontificia Universidad Católica de Chile, Santiago, Chile
S. Blunier, M. A. Diaz, F. M. Garay Walls, G. R. Lee, J. P. Ochoa-Ricoux & S. A. Olivares Pino
Departamento de Física, Universidad Técnica Federico Santa María, Valparaiso, Chile
W. K. Brooks, E. Carquin, S. Kuleshov, J. A. Lopez, R. Pezoa, F. Prokoshin, J. E. Salazar Loyola, S. Tapia Araya, G. A. Vasquez, N. Viaux Maira & R. White
Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China
M. K. Ayoub, J. Barreiro Guimarães da Costa, C. Bertella, H. J. Cheng, Y. Fang, J. A. García Pascual, S. Han, Y. Huang, S. Jin, M. G. Kurth, Q. Li, Z. Liang, J. Llorente Merino, X. Lou, F. Lyu, J. D. Mansour, Q. Ouyang, C. Peng, H. Ren, L. Y. Shan, D. Xu, Y. Zhang, M. Zhou, H. Zhu & X. Zhuang
Department of Physics, Nanjing University, Nanjing, Jiangsu, China
S. Chen, C. Wang & P. Zhang
Physics Department, Tsinghua University, Beijing, 100084, China
X. Chen & L. Xia
Department of Modern Physics and State Key Laboratory of Particle Detection and Electronics, University of Science and Technology of China, Hefei, Anhui, China
Z. Barnovska-Blenessy, C. Chen, J. Chen, Y. Guo, L. Han, Q. Hu, Y. Jiang, B. Li, Changqiao Li, Q. Li, J. B. Liu, M. Liu, Y. L. Liu, Y. Liu, R. Ospanov, H. Peng, W. Wang, G. Zhang, L. Zhang, R. Zhang, Z. Zhao & Y. Zhu
School of Physics, Shandong University, Jinan, Shandong, China
Y. Du, C. Feng, J. Liu, L. L. Ma, Y. Ma, C. Wang, D. Zhang, X. Zhang, Y. Zhao & C. G. Zhu
Department of Physics and Astronomy, Key Laboratory for Particle Physics, Astrophysics and Cosmology, Ministry of Education, Shanghai Key Laboratory for Particle Physics and Cosmology, Shanghai Jiao Tong University, Shanghai (also at PKU-CHEP), Shanghai, China
S. L. Barnes, M. Cano Bret, J. Guo, S. Hu, N. Kondrashova, L. Li, X. Li, N. Nishu, Z. Wang, H. Yang & N. Zhou
Université Clermont Auvergne, CNRS/IN2P3, LPC, Clermont-Ferrand, France
S. Angelidakis, D. Boumediene, E. Busato, D. Calvet, S. Calvet, A. R. Chomont, J. Donini, S. Ganguly, Ph. Gris, R. Madar, M. Marjanovic, D. Pallin, S. M. Romano Saez, C. Santoni, S. Senkin & F. Vazeille
Nevis Laboratory, Columbia University, Irvington, NY, USA
S. P. Alkire, A. Angerami, G. Brooijmans, R. M. Carbone, M. R. Clark, B. Cole, L. B. Havener, E. W. Hughes, K. Iordanidou, S. Mohapatra, I. Ochoa, J. A. Parsons, M. N. K. Smith, R. W. Smith, Y. Tian, P. M. Tuts & T. Wang
Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark
A. Alonso, M. Bajic, G. J. Besjes, M. Dam, F. A. Dias, G. Galster, J. B. Hansen, J. D. Hansen, P. H. Hansen, J. Monk, T. C. Petersen, S. H Stark, F. Thiele, C. Wiglesworth & S. Xella
INFN Gruppo Collegato di Cosenza, Laboratori Nazionali di Frascati, Frascati, Italy
V. M. Cairo, G. Callea, M. Capua, G. Crosetti, M. Del Gaudio, L. La Rotonda, F. La Ruffa, A. Mastroberardino, E. Meoni, S. Palazzo, A. Policicchio, D. Salvatore, M. Schioppa, M. Scornajenghi & E. Tassi
Dipartimento di Fisica, Università della Calabria, Rende, Italy
V. M. Cairo, G. Callea, M. Capua, G. Crosetti, M. Del Gaudio, L. La Rotonda, F. La Ruffa, A. Mastroberardino, E. Meoni, S. Palazzo, A. Policicchio, D. Salvatore, M. Schioppa, M. Scornajenghi & E. Tassi
Faculty of Physics and Applied Computer Science, AGH University of Science and Technology, Kraków, Poland
L. Adamczyk, T. Bold, W. Dabrowski, G. P. Gach, I. Grabowska-Bold, M. P. Guzik, P. A. Janus, D. Kisielewska, S. Koperny, T. Z. Kowalski, J. A. Kremer, B. Mindur, M. Przybycien & A. Zemla
Marian Smoluchowski Institute of Physics, Jagiellonian University, Kraków, Poland
M. Palka & E. Richter-Was
Institute of Nuclear Physics, Polish Academy of Sciences, Kraków, Poland
M. Bahmani, E. Banas, P. A. Bruckman de Renstrom, K. Burka, J. J. Chwastowski, S. Czekierda, D. Derendarz, B. S. Dziedzic, J. Godlewski, A. Kaczmarska, K. Korcyl, A. B. Kowalewska, Pa. Malecki, A. Olszewski, J. Olszowska, M. Slawinska, E. Stanecka, R. Staszewski, M. Trzebinski, A. Trzupek, M. W. Wolter, B. K. Wosiek, K. W. Wozniak & B. Zabinski
Physics Department, Southern Methodist University, Dallas, TX, USA
R. Gupta, J. W. Hetherly, S. Kama, R. Kehoe, F. Lo Sterzo, S. J. Sekula, R. Stroynowski, T. Varol, J. Ye, X. Zhao & L. Zhou
Physics Department, University of Texas at Dallas, Richardson, TX, USA
J. M. Izen, B. Meirose & K. Reeves
DESY, Hamburg and Zeuthen, Germany
N. Asbah, J. K. Behr, C. Bertsche, M. Bessner, I. Bloch, F. Braren, K. Brendlinger, D. Britzger, L. Bryngemark, T. Daubney, C. David, C. Deterre, S. Díez Cornell, B. Dutta, M. Dyndal, C. Eckardt, J. Ferrando, M. Filipuzzi, N. Flaschel, A. Gascon Bravo, K. Gasnikova, P. C. F. Glaysher, A. Glazov, I. M. Gregor, M. Haleem, P. G. Hamnett, S. Heim, B. Heinemann, K. H. Hiller, J. Katzy, V. Kitali, T. Kuhl, J. Lacey, V. S. Lang, W. A. Leight, E. M. Lobodzinska, A. Madsen, K. Mönig, R. F. Naranjo Garcia, T. Naumann, A. A. O’Rourke, K. A. Parker, R. Peschke, K. Peters, H. Pirumov, A. Poley, K. Potamianos, M. Queitsch-Maitland, D. M. Rauch, J. E. M. Robinson, M. Saimpert, C. O. Sander, R. Schaefer, S. Schmitt, D. South, M. M. Stanitzki, M. Stegler, N. A. Styles, K. Tackmann, A. Trofymov, A. Vishwakarma, J. Wang, C. Wanotayaroj, Y. C. Yap & N. Zakharchuk
Lehrstuhl für Experimentelle Physik IV, Technische Universität Dortmund, Dortmund, Germany
I. Burmeister, D. Cinca, J. Erdmann, G. Geßner, C. Gössling, M. Homann, R. Klingenberg, K. Kroeninger, T. Kupfer & I. Nitsche
Institut für Kern- und Teilchenphysik, Technische Universität Dresden, Dresden, Germany
C. Bittrich, D. Duschinger, L. Hauswald, M. Hils, F. Iltzsche, D. Kirchmeier, M. Kobel, W. F. Mader, J. Manjarres Ramos, O. Novgorodova, F. Siegert, F. Socher, A. Straessner, S. Todt, H. Torres & S. Wahrmund
Department of Physics, Duke University, Durham, NC, USA
A. T. H. Arce, D. P. Benjamin, D. M. Bjergaard, A. Bocci, D. R. Davis, M. B. Epland, A. T. Goshaw, A. Kotwal, M. C. Kruse, S. Li & S. H. Oh
SUPA-School of Physics and Astronomy, University of Edinburgh, Edinburgh, UK
T. M. Bristow, P. J. Clark, M. Faucci Giannelli, A. Hasib, X. Hoad, C. Leonidopoulos, V. J. Martin, L. Mijović, C. Mills, A. Søgaard, A. Strubig, A. J. Taylor, A. Washbrook & B. M. Wynne
INFN e Laboratori Nazionali di Frascati, Frascati, Italy
P. Albicocco, M. Antonelli, M. Beretta, H. Bilokon, V. Chiarella, M. Curatolo, B. Esposito, C. Gatti, P. Laurelli, G. Maccarrone, G. Mancini, A. Sansoni, M. Testa & E. Vilucchi
Fakultät für Mathematik und Physik, Albert-Ludwigs-Universität, Freiburg, Germany
H. Arnold, M. Boehler, F. Buehrer, C. D. Burgard, D. Büscher, F. Cardillo, E. Coniavitis, A. Di Simone, G. Gonella, K. K. Heidegger, G. Herten, M. Hirose, K. Jakobs, T. Javůrek, M. Javurkova, P. Jenni, T. Klapdor-Kleingrothaus, K. Köneke, A. K. Kopp, U. Landgraf, A. Loesle, C. Luedtke, V. Magerl, T. J. Megy, P. Mogg, M. Nagel, U. Parzefall, M. Ronzani, K. Rosbach, F. Rühr, Z. Rurikova, D. Sammel, C. Schillo, U. Schnoor, M. Schumacher, P. Sommer, D. Ta, P. Tornambe, V. Tsiskaridze, C. Weiser, L. A. M. Wiik-Fuchs, L. Zhang & S. Zimmermann
Departement de Physique Nucleaire et Corpusculaire, Université de Genève, Geneva, Switzerland
E. Akilli, L. S. Ancu, M. Benoit, N. Calace, A. Clark, A. Coccaro, D. della Volpe, F. A. Di Bello, A. Dubreuil, D. Ferrere, T. Golling, S. Gonzalez-Sevilla, G. Iacobucci, R. Jansky, A. Katre, T. J. Khoo, M. C. Lanfermann, A. E. Lionti, L. March, P. Mermod, O. Nackenhorst, C. E. Pandini, L. Paolozzi, S. Schramm, A. Sfyrla, M. Valente & X. Wu
INFN Sezione di Genova, Genoa, Italy
D. Barberis, G. Darbo, A. Favareto, G. Gagliardi, A. Gaudiello, C. Gemme, E. Guido, A. Lapertosa, S. Miglioranzi, P. Morettini, H. Oide, B. Osculati, F. Parodi, S. Passaggio, L. P. Rossi, M. Sannino, C. Schiavi & C. Varni
Dipartimento di Fisica, Università di Genova, Genoa, Italy
D. Barberis, A. Favareto, G. Gagliardi, A. Gaudiello, E. Guido, A. Lapertosa, S. Miglioranzi, H. Oide, B. Osculati, F. Parodi, M. Sannino, C. Schiavi & C. Varni
E. Andronikashvili Institute of Physics, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia
J. Jejelava & E. G. Tskhadadze
High Energy Physics Institute, Tbilisi State University, Tbilisi, Georgia
T. Djobava, A. Durglishvili, J. Khubua, I. A. Minashvili & M. Mosidze
II Physikalisches Institut, Justus-Liebig-Universität Giessen, Giessen, Germany
M. Düren, C. Heinz, K. Kreutzfeldt & H. Stenzel
SUPA-School of Physics and Astronomy, University of Glasgow, Glasgow, UK
A. A. Alshehri, R. L. Bates, A. Blue, S. K. Boutle, W. D. Breaden Madden, D. Britton, A. G. Buckley, P. Bussey, C. M. Buttar, S. J. Crawley, S. D’Auria, A. T. Doyle, A. K. Duncan, M. J. Fenton, C. Gray, U. Gul, P. Mullen, V. O’Shea, M. Owen, C. S. Pollard, G. Qin, D. Quilty, A. Robson, R. D. St. Denis, G. A. Stewart & A. S. Thompson
II Physikalisches Institut, Georg-August-Universität, Göttingen, Germany
H. C. Beck, M. Bindi, T. Bisanz, G. Brandt, A. De Maria, E. Drechsler, J. Geisen, J. Grosse-Knetter, M. Janus, G. Kawamura, S. Lai, B. Lemmer, M. Mantoani, G. Mchedlidze, J. D. Mellenthin, C. Nellist, I. Pokharel, A. Quadt, J. Rieger, N.-A. Rosien, G. F. Rzehorz, E. Shabalina, J. W. Smith, P. Stolte, J. Veatch & J. Weingarten
Laboratoire de Physique Subatomique et de Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, Grenoble, France
S. Berlendis, C. Camincher, J. Collot, S. Crépé-Renaudin, P. A. Delsart, M. H. Genest, J-Y. Hostachy, F. Ledroit-Guillon, A. Lleres, A. Lucotte, F. Malek, T. Meideck, E. Petit, N. P. Readioff, J. Stark & B. Trocmé
Laboratory for Particle Physics and Cosmology, Harvard University, Cambridge, MA, USA
S. K. Chan, B. L. Clark, K. F. Di Petrillo, M. Franklin, P. Giromini, J. Huth, V. Ippolito, T. Lazovich, L. Lee, M. Morii, C. S. Rogan, J. Roloff, S. Sun, E. Tolley, B. Tong, A. N. Tuna & S. Zambito
Kirchhoff-Institut für Physik, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
V. Andrei, C. Antel, A. E. Baas, O. Brandt, J. I. Djuvsland, M. Dunford, S. Franchino, M. P. Geisler, P. Hanke, J. Jongmanns, E.-E. Kluge, A. Kugel, K. Meier, H. Meyer Zu Theenhausen, D. I. Narrias Villar, M. Sahinsoy, H.-C. Schultz-Coulon, T. M. Spieker, R. Stamen, P. Starovoitov, S. Suchek, S. M. Weber & M. Wessels
Physikalisches Institut, Ruprecht-Karls-Universität Heidelberg, Heidelberg, Germany
C. F. Anders, A. E. Bolz, D. E. Ferreira de Lima, M. Giulini, M. Kolb, M. Lisovyi, S. Schaetzel, A. Schoening & D. Sosa
Faculty of Applied Information Science, Hiroshima Institute of Technology, Hiroshima, Japan
Y. Nagasaka
Department of Physics, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong
V. Bortolotto, Y. L. Chan, Y. S. Chow, M. C. Chu, L. R. Flores Castillo, J. M. Iturbe Ponce, T. S. Lau, H. Lu, A. Salvucci & K. W. Tsang
Department of Physics, The University of Hong Kong, Hong Kong, China
V. Bortolotto, C. Y. Lo, N. Orlando, A. Salvucci & Y. Tu
Department of Physics, Institute for Advanced Study, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, China
V. Bortolotto, K. Lie, T. Y. Ng, K. Prokofiev & A. Salvucci
Department of Physics, National Tsing Hua University, Taiwan, Taiwan
K. Cheung, P. J. Hsu & Y. J. Lu
Department of Physics, Indiana University, Bloomington, IN, USA
P. Calfayan, K. Choi, H. Evans, C. A. Johnson, R. Kopeliansky, S. Lammers, R. A. Linck, F. Luehring, G. Palacino, J. Penwell, B. Weinert & D. Zieminska
Institut für Astro- und Teilchenphysik, Leopold-Franzens-Universität, Innsbruck, Austria
S. Jakobsen, E. Kneringer & W. Lukas
University of Iowa, Iowa City, IA, USA
S. Argyropoulos, J. Benitez & U. Mallik
Department of Physics and Astronomy, Iowa State University, Ames, IA, USA
C. Chen, J. Cochran, F. De Lorenzi, H. Jiang, N. Krumnack, B. Liu, D. Pluth, S. Prell, M. D. Werner & J. Yu
Joint Institute for Nuclear Research, JINR Dubna, Dubna, Russia
F. Ahmadov, I. N. Aleksandrov, V. A. Bednyakov, I. R. Boyko, I. A. Budagov, G. A. Chelkov, A. Cheplakov, M. V. Chizhov, D. V. Dedovich, M. Demichev, A. Gongadze, M. I. Gostkin, N. Huseynov, N. Javadov, S. N. Karpov, Z. M. Karpova, E. Khramov, U. Kruchonak, V. Kukhtin, E. Ladygin, V. Lyubushkin, M. Mineev, V. D. Peshekhonov, E. Plotnikova, I. N. Potrap, N. A. Rusakovich, R. Sadykov, A. Sapronov, M. Shiyakova, Lj. Simic, A. Soloshenko, S. Turchikhin, V. B. Vinogradov, I. Yeletskikh, A. Zhemchugov & N. I. Zimine
KEK, High Energy Accelerator Research Organization, Tsukuba, Japan
M. Aoki, Y. Arai, K. Hanagaki, S. Higashino, T. Honda, Y. Ikegami, M. Ikeno, H. Iwasaki, J. Kanzaki, T. Kondo, T. Kono, Y. Makida, A. Mizukami, R. Nagai, K. Nagano, K. Nakamura, M. Nozaki, S. Odaka, T. Okuyama, O. Sasaki, S. Suzuki, Y. Takubo, S. Tanaka, S. Terada, K. Tokushuku, S. Tsuno, I. Ueda, Y. Unno, J. Usui, A. Yamamoto & Y. Yasu
Graduate School of Science, Kobe University, Kobe, Japan
Y. Chen, K. Kawade, S. Kido, H. Kurashige, J. Maeda, A. Ochi, S. Shimizu, K. Takeda, R. Tanioka, F. Yamane & Y. Yamazaki
Faculty of Science, Kyoto University, Kyoto, Japan
S. Akatsuka, T. Kunigo, Y. Noguchi, T. Sumida & T. Tashiro
Kyoto University of Education, Kyoto, Japan
R. Takashima
Research Center for Advanced Particle Physics and Department of Physics, Kyushu University, Fukuoka, Japan
K. Kawagoe, D. Kobayashi, S. Oda, H. Otono, S. Shirabe & J. Tojo
Instituto de Física La Plata, Universidad Nacional de La Plata and CONICET, La Plata, Argentina
M. J. Alconada Verzini, F. Alonso, F. A. Arduh, M. T. Dova, J. Hoya, F. Monticelli & H. Wahlberg
Physics Department, Lancaster University, Lancaster, UK
A. E. Barton, M. D. Beattie, I. A. Bertram, G. Borissov, E. V. Bouhova-Thacker, H. Fox, K. Grimm, R. C. W. Henderson, G. Hughes, R. W. L. Jones, V. Kartvelishvili, R. E. Long, P. A. Love, D. Muenstermann, A. J. Parker, M. B. Skinner, M. Smizanska, J. Walder, A. M. Wharton & B. W. Whitmore
INFN Sezione di Lecce, Lecce, Italy
M. Aliev, K. Bachas, G. Chiodini, E. Gorini, L. Longo, A. Mirto, M. Primavera, M. Reale, S. Spagnolo & A. Ventura
Dipartimento di Matematica e Fisica, Università del Salento, Lecce, Italy
M. Aliev, K. Bachas, E. Gorini, L. Longo, A. Mirto, M. Reale, S. Spagnolo & A. Ventura
Oliver Lodge Laboratory, University of Liverpool, Liverpool, UK
J. K. Anders, S. Burdin, M. D’Onofrio, P. Dervan, Y. Gao, C. B. Gwilliam, H. S. Hayward, T. J. Jones, E. F. Kay, B. T. King, M. Klein, U. Klein, J. Kretzschmar, P. Laycock, S. J. Maxfield, A. Mehta, L. Meng, N. Rompotis & J. H. Vossebeld
Department of Experimental Particle Physics, Jožef Stefan Institute and Department of Physics, University of Ljubljana, Ljubljana, Slovenia
V. Cindro, A. Filipčič, A. Gorišek, B. Hiti, L. Kanjir, B. P. Kerševan, G. Kramberger, B. Maček, I. Mandić, M. Mikuž, M. Muškinja, T. Sfiligoj & G. Sokhrannyi
School of Physics and Astronomy, Queen Mary University of London, London, UK
L. J. Armitage, A. J. Bevan, U. Blumenschein, M. Bona, J. M. Hays, M. P. J. Landon, D. Lewis, S. L. Lloyd, D. A. Millar, J. D. Morris, T. Nooney, E. Piccaro, E. Rizvi, R. L. Sandbach & E. Tahirovic
Department of Physics, Royal Holloway University of London, Surrey, UK
R. E. Ardell, T. Berry, V. Boisvert, A. J. Bozson, T. Brooks, G. Cowan, S. Gadomski, S. George, S. M. Gibson, J. J. Kempster, C. R. Kilby, J. G. Panduro Vazquez, Fr. Pastore, G. Savage, B. C. Sowden, F. Spanò, P. Teixeira-Dias & J. Thomas-Wilsker
Department of Physics and Astronomy, University College London, London, UK
A. S. Bell, J. M. Butterworth, M. Campanelli, V. Christodoulou, P. Davison, G. Facini, R. J. Falla, D. Freeborn, K. Gregersen, Z. J. Grout, N. G. Gutierrez Ortiz, C. Gutschow, G. G. Hesketh, S. Jiggins, N. Konstantinidis, A. Korn, H. Kucuk, K. J. C. Leney, A. C. Martyniuk, L. I. McClymont, E. Nurse, S. Richter, T. Scanlon, P. Sherwood, B. Simmons, A. Vaidya, D. R. Wardrope & B. M. Waugh
Louisiana Tech University, Ruston, LA, USA
Z. D. Greenwood, G. C. Grossi, D. K. Jana, L. Sawyer & M. Wobisch
Laboratoire de Physique Nucléaire et de Hautes Energies, UPMC and Université Paris-Diderot and CNRS/IN2P3, Paris, France
T. Beau, G. Bernardi, M. Bomben, G. Calderini, F. Crescioli, L. D’eramo, S. De Cecco, A. Demilly, F. Derue, A. Ducourthial, P. Francavilla, M. W. Krasny, D. Lacour, B. Laforge, S. Laplace, O. Le Dortz, G. Lefebvre, A. Lopez Solis, P. M. Luzi, B. Malaescu, G. Marchiori, I. Nikolic-Audit, J. Ocariz, D. M. Portillo Quintero, M. Ridel, L. Roos, S. Trincaz-Duvoid & R.-J. Wang
Fysiska institutionen, Lunds universitet, Lund, Sweden
T. P. A. Åkesson, S. S. Bocchetta, C. Doglioni, V. Hedberg, G. Jarlskog, C. W. Kalderon, E. Kellermann, E. Lytken, K. H. Mankinen, J. U. Mjörnmark, R. Poettgen, T. Poulsen, O. Smirnova & O. Viazlo
Departamento de Fisica Teorica C-15, Universidad Autonoma de Madrid, Madrid, Spain
F. Barreiro, S. Calvente Lopez, A. Cueto, J. Del Peso, C. Glasman & J. Terron
Institut für Physik, Universität Mainz, Mainz, Germany
S. Artz, M. Becker, P. Berta, K. Bierwagen, W. Blum, V. Büscher, J. Cúth, A. Chr. Dudder, O. C. Endner, F. Fiedler, M. Geisen, S. Groh, T. Heck, H. Herr, K. B. Jakobi, A. Kaluza, K. Kleinknecht, T. H. Lin, L. Masetti, S. Pataraia, V. Pleskot, S. Rave, A. Reiss, E. Rocco, J. Schaeffer, U. Schäfer, C. Schmitt, S. Schmitz, M. Schott, N. Schuh, A. Schulte, E. Simioni, M. Simon, S. Tapprogge, P. Urrejola, S. Webb, M. Weirich, E. Yildirim, C. Zimmermann & M. Zinser
School of Physics and Astronomy, University of Manchester, Manchester, UK
A. Bethani, R. Bielski, I. A. Connelly, B. E. Cox, C. Da Via, N. S. Dann, G. T. Forcolin, A. Forti, J. Howarth, D. P. J. Lack, F. K. Loebinger, S. P. Marsden, J. Masik, S. B. Menary, F. J. Munoz Sanchez, A. Oh, J. R. Pater, R. F. Y. Peters, A. D. Pilkington, D. Price, Y. Qin, J. A. Raine, J. H. Rawling, R. T. Roberts, H. Schweiger, S. M. Shaw, L. Tomlinson, S. Watts, F. Wilk & T. R. Wyatt
CPPM, Aix-Marseille Université and CNRS/IN2P3, Marseille, France
G. Aad, M. I. Alstaty, M. Barbero, A. Calandri, T. P. Calvet, Y. Coadou, K. De Vasconcelos Corga, C. Diaconu, F. Djama, A. Duperrin, R. El Kosseifi, V. Ellajosyula, L. Feligioni, A. Hadef, G. D. Hallewell, F. Hubaut, S. J. Kahn, E. B. F. G. Knoops, R. Kukla, E. Le Guirriec, K. Liu, E. Monnier, S. Muanza, E. Nagy, P. Pralavorio, Y. Rodina, A. Rozanov, M. Talby, T. Theveneaux-Pelzer, R. E. Ticse Torres, S. Tisserant, J. Toth, F. Touchard, L. Vacavant & R. Wolff
Department of Physics, University of Massachusetts, Amherst, MA, USA
N. R. Bernard, B. Brau, C. Dallapiccola, M. S. Lutz, E. J. W. Moyse, N. E. Pettersson, A. Picazio & S. Willocq
Department of Physics, McGill University, Montreal, QC, Canada
A. J. Chuinard, F. Corriveau, R. A. Keyes, B. Lefebvre, R. Mantifel, S. Prince, S. H. Robertson, A. Robichaud-Veronneau, H. L. Russell, M. Stoebe, B. Vachon, T. Vazquez Schroeder & A. Warburton
School of Physics, University of Melbourne, Victoria, Australia
E. L. Barberio, A. J. Brennan, E. Dawe, S. Goldfarb, T. Kubota, B. Le, L. H. Mason, E. F. McDonald, P. C. McNamara, M. Milesi, F. Nuti, P. Rados, F. Scutti, L. A. Spiller, G. N. Taylor, P. T. E. Taylor, F. C. Ungaro, P. Urquijo & D. Zanzi
Department of Physics, The University of Michigan, Ann Arbor, MI, USA
D. Amidei, H. C. Cheng, T. Dai, E. B. Diehl, R. C. Edgar, C. Ferretti, P. Fleischmann, C. Geng, L. Guan, W. Guo, R. Hyneman, M. H. Klein, D. Levin, H. Liu, N. Lu, D. E. Marley, S. P. Mc Kee, A. McCarn, X. T. Meng, H. A. Neal, J. Qian, T. A. Schwarz, J. Searcy, K. Sekhon, I. Siral, A. S. White, Y. Wu, Z. Xi, D. Zhang, B. Zhou & J. Zhu
Department of Physics and Astronomy, Michigan State University, East Lansing, MI, USA
G. Arabidze, R. Brock, A. Chegwidden, H. De la Torre, T. Farooque, W. C. Fisher, G. Halladjian, R. Hauser, D. Hayden, J. Huston, K. Lin, M. C. Mondragon, F. H. Phillips, I. Pogrebnyak, B. D. Schoenrock, R. Schwienhorst & C. Willis
INFN Sezione di Milano, Milan, Italy
G. Alimonti, A. Andreazza, A. Camplani, L. Carminati, S. Carrá, D. Cavalli, M. Citterio, G. Costa, M. Fanti, D. Giugni, T. Lari, M. Lazzaroni, S. Manzoni, S. M. Mazza, C. Meroni, S. Monzani, L. Perini, F. Ragusa, M. G. Ratti, S. Resconi, S. Shojaii, A. Stabile, G. F. Tartarelli, C. Troncon, R. Turra & M. Villaplana Perez
Dipartimento di Fisica, Università di Milano, Milan, Italy
A. Andreazza, A. Camplani, L. Carminati, S. Carrá, M. Fanti, M. Lazzaroni, S. Manzoni, S. M. Mazza, S. Monzani, L. Perini, F. Ragusa, M. G. Ratti, S. Shojaii & M. Villaplana Perez
B.I. Stepanov Institute of Physics, National Academy of Sciences of Belarus, Minsk, Republic of Belarus
S. Harkusha, Y. Kulchitsky, Y. A. Kurochkin & P. V. Tsiareshka
Research Institute for Nuclear Problems of Byelorussian State University, Minsk, Republic of Belarus
A. Hrynevich
Group of Particle Physics, University of Montreal, Montreal, QC, Canada
J-F. Arguin, G. Azuelos, T. R. V. Billoud, F. Dallaire, O. A. Ducu, B. Freund, L. G. Gagnon, C. Leroy, K. Mochizuki, T. Nguyen Manh, R. Rezvani & D. Shoaleh Saadi
P.N. Lebedev Physical Institute of the Russian Academy of Sciences, Moscow, Russia
A. V. Akimov, I. L. Gavrilenko, A. A. Komar, R. Mashinistov, P. Yu. Nechaeva, A. Shmeleva, A. A. Snesarev, V. V. Sulin, V. O. Tikhomirov & K. Zhukov
Institute for Theoretical and Experimental Physics (ITEP), Moscow, Russia
A. Artamonov, P. A. Gorbounov, V. Khovanskiy, P. B. Shatalov & I. I. Tsukerman
National Research Nuclear University MEPhI, Moscow, Russia
A. Antonov, K. Belotskiy, N. L. Belyaev, O. Bulekov, V. A. Kantserov, D. Krasnopevtsev, D. Ponomarenko, N. Proklova, A. Romaniouk, E. Shulga, N. Smirnov, S. Yu. Smirnov, Y. Smirnov, E. Yu. Soldatov, S. Timoshenko & K. Vorobev
D.V. Skobeltsyn Institute of Nuclear Physics, M.V. Lomonosov Moscow State University, Moscow, Russia
A. S. Boldyrev, L. K. Gladilin, V. A. Kramarenko, A. S. Maevskiy, S. Yu. Sivoklokov & L. N. Smirnova
Fakultät für Physik, Ludwig-Maximilians-Universität München, Munich, Germany
M. Adersberger, M. Bender, O. Biebel, C. Bock, D. Bogavac, G. Duckeck, B. M. Flierl, N. M. Hartmann, J. J. Heinrich, R. Hertenberger, F. Hoenig, F. Legger, J. Lorenz, P. J. Lösel, T. Maier, A. Mann, S. Mehlhase, J. Mitrevski, R. S. P. Mueller, F. Rauscher, B. M. Schachtner, D. Schaile, C. Unverdorben, C. Valderanis, J. Wagner-Kuhr & R. Walker
Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Munich, Germany
T. Barillari, S. Bethke, J. Beyer, K. M. Ecker, M. J. Flowerdew, C. Giuliani, A. E. Kiryunin, S. Kluth, A. Knue, N. M. Köhler, O. Kortner, S. Kortner, D. Krauss, H. Kroha, A. La Rosa, A. Macchiolo, T. G. McCarthy, S. Menke, F. Mueller, R. Nisius, H. Oberlack, B. Pearson, R. Richter, P. Rieck, D. Salihagic, N. Savic, P. Schacht, K. R. Schmidt-Sommerfeld, F. Spettel, S. Stonjek, E. H. Takasugi, H. von der Schmitt, A. Wildauer & Z. Zinonos
Nagasaki Institute of Applied Science, Nagasaki, Japan
T. Fusayasu & M. Shimojima
Graduate School of Science and Kobayashi-Maskawa Institute, Nagoya University, Nagoya, Japan
Y. Horii, Y. Nakahama, K. Onogi, Y. Sano & M. Tomoto
INFN Sezione di Napoli, Naples, Italy
A. Aloisio, M. G. Alviggi, V. Canale, G. Carlino, F. Cirotto, F. Conventi, R. de Asmundis, M. Della Pietra, C. Di Donato, A. Doria, V. Izzo, L. Merola, S. Perrella, E. Rossi & G. Sekhniaidze
Dipartimento di Fisica, Università di Napoli, Naples, Italy
A. Aloisio, M. G. Alviggi, V. Canale, F. Cirotto, M. Della Pietra, C. Di Donato, L. Merola, S. Perrella & E. Rossi
Department of Physics and Astronomy, University of New Mexico, Albuquerque, NM, USA
I. Gorelov, A. Grummer, M. R. Hoeferkamp, N. C. Mc Fadden, S. C. Seidel, A. C. Taylor & K. Toms
Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen/Nikhef, Nijmegen, The Netherlands
S. C. Alderweireldt, S. Caron, L. Colasurdo, N. De Groot, V. Fabiani, F. Filthaut, C. Galea, A. C. König, S. Nektarijevic & J. F. P. Schouwenberg
Nikhef National Institute for Subatomic Physics, University of Amsterdam, Amsterdam, The Netherlands
I. Angelozzi, P. J. Bakker, M. Bedognetti, S. Bentvelsen, D. Berge, G. J. Bobbink, L. Brenner, L. S. Bruni, R. Castelijn, W. S. Chan, A. P. Colijn, P. de Jong, I. Deigaard, D. Duda, P. Ferrari, O. Igonkina, P. Kluit, E. Koffeman, J. Meyer, K. P. Oussoren, G. Sabato, D. Salek, B. S. Stapf, W. Van Den Wollenberg, H. van der Graaf, I. van Vulpen, M. C. van Woerden, P. Vankov, W. Verkerke, A. T. Vermeulen, J. C. Vermeulen, M. Vreeswijk, H. Weits, S. Williams & T. M. H. Wolf
Department of Physics, Northern Illinois University, DeKalb, IL, USA
J. Adelman, E. Brost, T. J. Burch, B. Burghgrave, D. Chakraborty, P. Klimek & P. Saha
Budker Institute of Nuclear Physics, SB RAS, Novosibirsk, Russia
A. V. Anisenkov, E. M. Baldin, V. S. Bobrovnikov, A. G. Bogdanchikov, A. R. Buzykaev, V. F. Kazanin, A. G. Kharlamov, T. Kharlamova, A. A. Korol, A. L. Maslennikov, D. A. Maximov, S. V. Peleganchuk, P. Podberezko, O. L. Rezanova, A. M. Soukharev, A. A. Talyshev & Yu. A. Tikhonov
Department of Physics, New York University, New York, NY, USA
C. Becot, K. Cranmer, V. Croft, A. Haas, L. Heinrich, B. Kaplan, K. Karthik, R. Konoplich, A. I. Mincer, P. Nemethy & C. J. Treado
Ohio State University, Columbus, OH, USA
J. B. Beacham, A. Boveia, S. Che, K. K. Gan, B. Gui, H. Kagan, R. D. Kass, K. A. Looper, C. B. Martin, S. Shrestha & B. B. Tannenwald
Faculty of Science, Okayama University, Okayama, Japan
I. Nakano
Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, Norman, OK, USA
B. Abbott, M. Alhroob, D. Bertsche, A. De Benedetti, G. Gustavino, P. Gutierrez, O. Rifki, H. Severini, Y. Shen, D. R. Shope, P. Skubic, M. Strauss & Q. Wang
Department of Physics, Oklahoma State University, Stillwater, OK, USA
J. Cantero, J. Haley, D. O. Jamin, A. Khanov & F. Rizatdinova
Palacký University, RCPTM, Olomouc, Czech Republic
L. Chytka, P. Hamal, M. Hrabovsky, J. Kvita & L. Nozka
Center for High Energy Physics, University of Oregon, Eugene, OR, USA
R. Abreu, B. W. Allen, J. T. Barkeloo, J. E. Brau, A. Dattagupta, W. H. Hopkins, S. Majewski, P. Radloff, N. B. Sinev, I. M. Snyder, M. C. Stockton, D. M. Strom, E. Torrence, K. Whalen & F. Winklmeier
LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay, Orsay, France
B. Abeloos, A. Bassalat, C. Bourdarios, J. B. De Vivie De Regie, D. Delgove, C. Delporte, L. Duflot, M. Escalier, L. Fayard, D. Fournier, C. R. Goudet, J.-F. Grivaz, F. Hariri, S. Henrot-Versille, J. Hrivnac, L. Iconomidou-Fayard, M. Kado, A. Lounis, C. Maiani, N. Makovec, N. Morange, P. Petroff, L. Poggioli, P. Puzo, T. Rashid, D. Rousseau, G. Rybkin, A. C. Schaffer, L. Serin, S. Simion, R. Tanaka, D. Varouchas, D. Zerwas, H. Zhang & Z. Zhang
Graduate School of Science, Osaka University, Osaka, Japan
N. Ishijima, M. Nomachi, Y. Sugaya & J. J. Teoh
Department of Physics, University of Oslo, Oslo, Norway
M. K. Bugge, D. Cameron, J. R. Catmore, S. Feigl, L. Franconi, V. Garonne, B. K. Gjelsten, E. Gramstad, V. Morisbak, J. K. Nilsen, H. Oppen, F. Ould-Saada, S. Raddum, A. L. Read, O. Røhne, H. Sandaker, C. Serfon, S. Stapnes & K. O. H. Vadla
Department of Physics, Oxford University, Oxford, UK
G. Artoni, M. Backes, A. J. Barr, K. Becker, L. Beresford, D. Bortoletto, J. T. P. Burr, A. M. Cooper-Sarkar, W. J. Fawcett, J. A. Frost, E. J. Gallas, F. Giuli, S. Gupta, C. Gwenlan, C. P. Hays, T. B. Huffman, C. Issever, J. K. K. Liu, L. Marchese, K. Nagai, M. E. Nelson, R. B. Nickerson, N. Norjoharuddeen, M. Petrov, M. A. Pickering, V. Radescu, I. P. J. Shipsey, J. C-L. Tseng, G. H. A. Viehhauser, L. Vigani, A. R. Weidberg & G. Zemaityte
INFN Sezione di Pavia, Pavia, Italy
P. Dondero, E. M. Farina, R. Ferrari, M. Fraternali, G. Gaudio, G. Introzzi, A. Kourkoumeli-Charalampidi, A. Lanza, M. Livan, A. Negri, R. Poggi, G. Polesello, D. M. Rebuzzi, A. Rimoldi, S. Sottocornola & V. Vercesi
Dipartimento di Fisica, Università di Pavia, Pavia, Italy
P. Dondero, E. M. Farina, M. Fraternali, G. Introzzi, A. Kourkoumeli-Charalampidi, M. Livan, A. Negri, R. Poggi, D. M. Rebuzzi, A. Rimoldi & S. Sottocornola
Department of Physics, University of Pennsylvania, Philadelphia, PA, USA
W. K. Balunas, R. A. Creager, J. R. Dandoy, W. K. Di Clemente, R. R. M. Fletcher, B. Haney, T. C. Herwig, J. Kroll, E. Lipeles, J. Machado Miguens, C. Meyer, K. P. Mistry, J. Reichert, E. D. Resseguie, L. Schaefer, E. Thomson, H. H. Williams & K. Yoshihara
National Research Centre “Kurchatov Institute” B.P. Konstantinov Petersburg Nuclear Physics Institute, St. Petersburg, Russia
A. Basalaev, A. Ezhilov, O. L. Fedin, V. Gratchev, M. Levchenko, V. P. Maleev, I. Naryshkin, Y. F. Ryabov, V. A. Schegelsky & V. Solovyev
INFN Sezione di Pisa, Pisa, Italy
A. Annovi, N. V. Biesuz, V. Cavasinni, G. Chiarelli, M. Dell’Orso, S. Donati, P. Giannetti, S. Leone, C. Roda, F. Scuri, C. L. Sotiropoulou & M. Spalla
Dipartimento di Fisica E. Fermi, Università di Pisa, Pisa, Italy
A. Annovi, N. V. Biesuz, V. Cavasinni, G. Chiarelli, M. Dell’Orso, S. Donati, P. Giannetti, S. Leone, C. Roda, F. Scuri, C. L. Sotiropoulou & M. Spalla
Department of Physics and Astronomy, University of Pittsburgh, Pittsburgh, PA, USA
R. M. Bianchi, J. Boudreau, N. Bruscino, B. T. Carlson, C. Farina, T. M. Hong, J. Mueller & J. Su
Laboratório de Instrumentação e Física Experimental de Partículas-LIP, Lisbon, Portugal
J. A. Aguilar-Saavedra, S. P. Amor Dos Santos, J. P. Araque, N. F. Castro, P. Conde Muiño, M. J. Da Cunha Sargedas De Sousa, M. C. N. Fiolhais, B. Galhardo, A. Gomes, R. Gonçalo, P. M. Jorge, A. Maio, J. Maneira, L. F. Oleiro Seabra, A. Onofre, R. Pedro, H. Santos, J. G. Saraiva, J. Silva, A. Tavares Delgado, F. Veloso & H. Wolters
Faculdade de Ciências, Universidade de Lisboa, Lisbon, Portugal
P. Conde Muiño, M. J. Da Cunha Sargedas De Sousa, A. Gomes, P. M. Jorge, J. Machado Miguens, A. Maio, J. Maneira, R. Pedro & A. Tavares Delgado
Department of Physics, University of Coimbra, Coimbra, Portugal
S. P. Amor Dos Santos, M. C. N. Fiolhais, B. Galhardo, F. Veloso & H. Wolters
Centro de Física Nuclear da Universidade de Lisboa, Lisbon, Portugal
A. Gomes, A. Maio, J. G. Saraiva & J. Silva
Departamento de Fisica, Universidade do Minho, Braga, Portugal
A. Onofre
Departamento de Fisica Teorica y del Cosmos, Universidad de Granada, Granada, Spain
J. A. Aguilar-Saavedra
Institute of Physics, Academy of Sciences of the Czech Republic, Prague, Czech Republic
J. Chudoba, J. Hejbal, O. Hladik, T. Jakoubek, O. Kepka, J. Kroll, A. Kupco, M. Lokajicek, R. Lysak, M. Marcisovsky, M. Mikestikova, S. Nemecek, O. Penc, P. Sicho, P. Staroba, M. Svatos & M. Tasevsky
Czech Technical University in Prague, Prague, Czech Republic
B. Ali, K. Augsten, D. Caforio, P. Gallus, M. Havranek, Z. Hubacek, M. Myska, S. Pospisil, V. Simak, T. Slavicek, K. Smolek, M. Solar, A. Sopczak, M. Suk, V. Vacek, P. Vokac & V. Vrba
Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
I. Carli, T. Davidek, J. Dolejsi, Z. Dolezal, P. Kodys, T. Kosek, R. Leitner, M. Mlynarikova, P. Reznicek, D. Scheirich, R. Slovak, M. Spousta, T. Sykora, P. Tas, S. Valkar & V. Vorobel
State Research Center Institute for High Energy Physics (Protvino), NRC KI, Protvino, Russia
A. Borisov, E. Cheremushkina, S. P. Denisov, R. M. Fakhrutdinov, A. B. Fenyuk, D. Golubkov, A. Kamenshchikov, A. N. Karyukhin, A. S. Kozhin, A. A. Minaenko, A. G. Myagkov, V. Nikolaenko, A. Ryzhov, A. A. Solodkov, O. V. Solovyanov, E. A. Starchenko, A. M. Zaitsev & O. Zenin
Particle Physics Department, Rutherford Appleton Laboratory, Didcot, UK
T. Adye, J. T. Baines, B. M. Barnett, S. Burke, A. Dewhurst, J. Dopke, D. Emeliyanov, B. J. Gallop, C. N. P. Gee, S. J. Haywood, J. Kirk, S. Martin-Haugh, S. J. McMahon, R. P. Middleton, W. J. Murray, P. W. Phillips, D. P. C. Sankey, C. Sawyer, F. J. Wickens & M. Wielers
INFN Sezione di Roma, Rome, Italy
F. Anulli, P. Bagnaia, M. Bauce, C. Bini, M. Corradi, D. De Pedis, A. De Salvo, S. Falciano, S. Gentile, S. Giagu, M. Kuna, F. Lacava, C. Luci, L. Luminari, A. Messina, A. Nisati, E. Pasqualucci, E. Petrolo, L. Pontecorvo, M. Rescigno, S. Rosati, F. Safai Tehrani, R. Vari & S. Veneziano
Dipartimento di Fisica, Sapienza Università di Roma, Rome, Italy
P. Bagnaia, M. Bauce, C. Bini, M. Corradi, S. Gentile, S. Giagu, M. Kuna, F. Lacava, C. Luci & A. Messina
INFN Sezione di Roma Tor Vergata, Rome, Italy
G. Aielli, S. Bruno, P. Camarri, R. Cardarelli, L. Cerrito, U. De Sanctis, A. Di Ciaccio, B. Liberti, L. Massa, M. Pinamonti & M. Vanadia
Dipartimento di Fisica, Università di Roma Tor Vergata, Rome, Italy
G. Aielli, S. Bruno, P. Camarri, L. Cerrito, U. De Sanctis, A. Di Ciaccio, L. Massa, M. Pinamonti & M. Vanadia
INFN Sezione di Roma Tre, Rome, Italy
A. Baroncelli, M. Biglietti, F. Ceradini, B. Di Micco, A. Farilla, M. Iodice, D. Orestano, F. Petrucci, G. Salamanna, M. Sessa, C. Stanescu & M. Verducci
Dipartimento di Matematica e Fisica, Università Roma Tre, Rome, Italy
F. Ceradini, B. Di Micco, D. Orestano, F. Petrucci, G. Salamanna, M. Sessa & M. Verducci
Faculté des Sciences Ain Chock, Réseau Universitaire de Physique des Hautes Energies-Université Hassan II, Casablanca, Morocco
D. Benchekroun, A. Chafaq & A. Hoummada
Faculté des Sciences Semlalia, Université Cadi Ayyad, LPHEA-Marrakech, Marrakech, Morocco
M. El Kacimi & D. Goujdami
Faculté des Sciences, Université Mohamed Premier and LPTPM, Oujda, Morocco
M. Aaboud, J. E. Derkaoui & M. Ouchrif
Faculté des Sciences, Université Mohammed V, Rabat, Morocco
R. Cherkaoui El Moursli, M. Ezzi, F. Fassi, N. Haddad, Z. Idrissi & Y. Tayalati
DSM/IRFU (Institut de Recherches sur les Lois Fondamentales de l’Univers), CEA Saclay (Commissariat à l’Energie Atomique et aux Energies Alternatives), Gif-sur-Yvette, France
H. Bachacou, F. Balli, F. Bauer, N. Besson, M. Boonekamp, L. Chevalier, M. Dano Hoffmann, F. Deliot, D. Denysiuk, A. I. Etienvre, A. Formica, P. F. Giraud, J. Goncalves Pinto Firmino Da Costa, C. Guyot, S. Hassani, F. Jeanneau, W. Kozanecki, J. F. Laporte, E. P. Le Quilleuc, A. A. J. Lesage, B. Mansoulie, J-P. Meyer, T. J. Neep, R. Nicolaidou, A. Ouraou, L. Pacheco Rodriguez, M. M. Perego, A. Peyaud, L. Schoeffel, Ph. Schune, Ph. Schwemling, J. Schwindling & T. Xu
Santa Cruz Institute for Particle Physics, University of California Santa Cruz, Santa Cruz, CA, USA
O. S. AbouZeid, A. A. Affolder, M. Battaglia, C. Debenedetti, A. A. Grillo, M. Hance, A. T. Law, A. M. Litke, J. Nielsen, J. M. Pasner, R. Reece, P. Rose, H. F-W. Sadrozinski, S. Schier, B. A. Schumm, A. Seiden & N. L. Woods
Department of Physics, University of Washington, Seattle, WA, USA
C. Alpigiani, A. G. Goussiou, A. Hostiuc, S.-C. Hsu, W. J. Johnson, H. J. Lubatti, S. Meehan, R. Rosten, J. Rothberg, J. Schaarschmidt, E. Torró Pastor, G. Watts & N. L. Whallon
Department of Physics and Astronomy, University of Sheffield, Sheffield, UK
C. Anastopoulos, D. Costanzo, T. Cuhadar Donszelmann, I. Dawson, S. Fracchia, G. N. Hamity, M. C. Hodgkinson, P. Hodgson, P. Johansson, E. V. Korolkova, E. Kourlitis, D. Kyriazopoulos, K. Lohwasser, C. M. Macdonald, P. S. Miyagawa, H. J. Moss, D. R. Tovey, T. Vickey & O. E. Vickey Boeriu
Department of Physics, Shinshu University, Nagano, Japan
Y. Hasegawa & T. Takeshita
Department Physik, Universität Siegen, Siegen, Germany
N. B. Atlay, P. Buchholz, A. Campoverde, I. Fleck, S. Ghasemi, I. Ibragimov, Y. Li, W. Walkowiak & M. Ziolkowski
Department of Physics, Simon Fraser University, Burnaby, BC, Canada
H. Bahrasemani, Q. Buat, A. J. Horton, D. Mori, D. C. O’Neil, K. Pachal, B. Stelzer, D. Temple, J. Van Nieuwkoop & M. C. Vetterli
SLAC National Accelerator Laboratory, Stanford, CA, USA
T. Barklow, R. Bartoldus, H. S. Bawa, C. Bernius, J. E. Black, A. R. Cukierman, Y. S. Gao, N. Garelli, P. Grenier, N. Ilic, Z. Jiang, M. Kagan, M. Kocian, T. Koi, J. Moss, R. Mount, F. Rubbo, A. Salnikov, A. Schwartzman, D. Su, L. Tompkins, M. Wittgen, C. Young & Q. Zeng
Faculty of Mathematics, Physics and Informatics, Comenius University, Bratislava, Slovak Republic
R. Astalos, P. Bartos, T. Blazek, T. Dado, O. Majersky, M. Melo, L. Plazak, J. Smiesko, I. Sykora, S. Tokár & T. Ženiš
Department of Subnuclear Physics, Institute of Experimental Physics of the Slovak Academy of Sciences, Kosice, Slovak Republic
D. Bruncko, E. Kladiva, P. Strizenec & J. Urban
Department of Physics, University of Cape Town, Cape Town, South Africa
A. Hamilton & S. Yacoob
Department of Physics, University of Johannesburg, Johannesburg, South Africa
S. H. Connell, N. Govender & L. Truong
School of Physics, University of the Witwatersrand, Johannesburg, South Africa
Y. Hernández Jiménez, H. Jivan, D. Kar, B. R. Mellado Garcia, R. G. Reed, X. Ruan & E. Sideras Haddad
Department of Physics, Stockholm University, Stockholm, Sweden
Y. Abulaiti, H. Akerstedt, G. Bertoli, O. Bessidskaia Bylund, C. Bohm, R. M. D. Carney, C. Clement, W. A. Cribbs, K. Gellerstedt, S. Hellman, K. Jon-And, O. Lundberg, D. A. Milstead, T. Moa, S. Molander, N. W. Shaikh, A. Shcherbakova, S. B. Silverstein, J. Sjölin, S. Strandberg, M. Ughetto, E. Valdes Santurio & V. Wallangen
The Oskar Klein Centre, Stockholm, Sweden
Y. Abulaiti, H. Akerstedt, G. Bertoli, O. Bessidskaia Bylund, R. M. D. Carney, C. Clement, W. A. Cribbs, K. Gellerstedt, S. Hellman, K. Jon-And, O. Lundberg, D. A. Milstead, T. Moa, S. Molander, N. W. Shaikh, A. Shcherbakova, J. Sjölin, S. Strandberg, M. Ughetto, E. Valdes Santurio & V. Wallangen
Physics Department, Royal Institute of Technology, Stockholm, Sweden
A. Kastanas, B. Lund-Jensen, C. C. Ohm, G. Ripellino, P. E. Sidebo & J. Strandberg
Departments of Physics and Astronomy and Chemistry, Stony Brook University, Stony Brook, NY, USA
C. P. Bee, V. Dao, J. Hobbs, P. Huo, J. Jia, H. Li, B. E. Lindquist, R. L. McCarthy, A. Montalbano, L. Morvaj, G. Piacquadio, S. K. Radhakrishnan, M. Rijssenbeek, R. D. Schamberger, D. Tsybychev, A. Zaman & M. Zhou
Department of Physics and Astronomy, University of Sussex, Brighton, UK
N. L. Abraham, B. M. M. Allbrooke, L. Asquith, A. Cerri, C. A. Chavez Barajas, A. De Santo, S. D. Jones, G. Lerner, F. Miano, F. Salvatore, I. Santoyo Castillo, C. Y. Shehu, K. Suruliz, M. R. Sutton, F. Tresoldi, I. Vivarelli, E. Winkels & O. J. Winston
School of Physics, University of Sydney, Sydney, Australia
K. D. Finelli, A. Limosani, A. F. Saavedra, C. J. E. Suster, K. E. Varvell, J. Wang & B. Yabsley
Institute of Physics, Academia Sinica, Taipei, Taiwan
A. Buzatu, S. Hou, S. C. Lee, R. Mazini, L. Shi, D. A. Soh, P. K. Teng, S. M. Wang, W. Wang & Y. Yang
Department of Physics, Technion: Israel Institute of Technology, Haifa, Israel
H. Abreu, Y. Afik, M. Bellomo, O. Gabizon, E. Gozani, B. J. Gutelman, E. Kajomovitz, Y. Rozen & S. Tarem
Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
H. Abramowicz, G. Alexander, A. Ashkenazi, L. Barak, G. Bella, O. Benary, Y. Benhammou, T. Cao, J. Duarte-Campderros, E. Etzion, O. Gueta, O. Kuprash, Y. Oren, A. Soffer, J. Taenzer & N. Taiblum
Department of Physics, Aristotle University of Thessaloniki, Thessaloníki, Greece
S. Chouridou, C. Gentsos, S. Gkaitatzis, D. Iliadis, N. Kimura, K. Kordas, I. Maznas, C. Petridou, D. Sampsonidis & D. Sampsonidou
International Center for Elementary Particle Physics and Department of Physics, The University of Tokyo, Tokyo, Japan
S. Adachi, S. Asai, S. Chen, Y. Enari, K. Hanawa, M. Ishino, N. Kanaya, Y. Kataoka, C. Kato, T. Kawamoto, T. Kishimoto, A. Kobayashi, T. Kobayashi, C. Kozakai, T. Mashimo, T. Masubuchi, Y. Minami, Y. Minegishi, T. Mori, T. Nakamura, Y. Ninomiya, T. Nobe, Y. Okumura, M. Saito, T. Saito, H. Sakamoto, J. Tanaka, K. Terashi, S. Yamamoto, T. Yamanaka & M. Yamatani
Graduate School of Science and Technology, Tokyo Metropolitan University, Tokyo, Japan
U. Bratzler & C. Fukunaga
Department of Physics, Tokyo Institute of Technology, Tokyo, Japan
D. Hayakawa, M. Ishitsuka, O. Jinnouchi, M. Kuze, K. Motohashi, M. Tanaka, K. Todome, D. Yamaguchi & Y. Yamaguchi
Tomsk State University, Tomsk, Russia
A. Khodinov & A. Vaniachine
Department of Physics, University of Toronto, Toronto, ON, Canada
S. H. Abidi, O. Arnaez, S. J. Batista, K. J. R. Cormier, D. A. DeMarco, K. Dette, R. Di Sipio, M. Diamond, H. Keoshkerian, P. Krieger, R. Les, A. Liblong, G. Mc Goldrick, A. Milic, R. S. Orr, V. R. Pascuzzi, P. Savard, P. Sinervo, R. J. Teuscher, W. Trischuk & L. M. Veloce
INFN-TIFPA, Trento, Italy
R. Iuppa & DMS Sultan
University of Trento, Trento, Italy
R. Iuppa & DMS Sultan
TRIUMF, Vancouver, BC, Canada
S. V. Chekulaev, F. Guescini, N. P. Hessey, N. Hod, J. Jovicevic, L. L. Kurchaninov, O. Stelzer-Chilton, R. Tafirout & I. M. Trigger
Department of Physics and Astronomy, York University, Toronto, ON, Canada
M. J. Kareem & W. Taylor
Faculty of Pure and Applied Sciences, and Center for Integrated Research in Fundamental Science and Engineering, University of Tsukuba, Tsukuba, Japan
M. Hagihara, K. Hara, S. Honda, F. Ito, K. Kasahara, S. H. Kim, K. Nagata, H. Okawa, K. Sato & F. Ukegawa
Department of Physics and Astronomy, Tufts University, Medford, MA, USA
P. H. Beauchemin, F. Sforza, K. Sliwa & H. Son
Department of Physics and Astronomy, University of California Irvine, Irvine, CA, USA
D. J. Antrim, D. W. Casper, T. Colombo, M. Frate, J. Gramling, D. Guest, A. J. Lankford, A. S. Mete, A. Nelson, K. Ntekas, D. A. Scannicchio, M. Schernau, A. Taffard, G. Unel & D. Whiteson
INFN Gruppo Collegato di Udine, Sezione di Trieste, Udine, Italy
B. S. Acharya, S. Cheatham, M. Cobal, M. P. Giordani, G. Giugliarelli, A. Sanchez Pineda, L. Serkin, K. Shaw & R. Soualah
ICTP, Trieste, Italy
B. S. Acharya, L. Serkin & K. Shaw
Dipartimento di Chimica, Fisica e Ambiente, Università di Udine, Udine, Italy
S. Cheatham, M. Cobal, M. P. Giordani, G. Giugliarelli, A. Sanchez Pineda & R. Soualah
Department of Physics and Astronomy, University of Uppsala, Uppsala, Sweden
E. Bergeaas Kuutmann, P. Bokan, R. Brenner, T. Ekelof, M. Ellert, A. Ferrari, P. O. J. Gradin, M. F. Isacson, M. U. F Martensson, H. Ohman, C. Rangel-Smith & P. H. Sales De Bruin
Department of Physics, University of Illinois, Urbana, IL, USA
M. Atkinson, H. Cai, R. Caminal Armadans, V. Cavaliere, P. Chang, S. Errede, B. H. Hooberman, M. Khader, Y. P. Kulinich, T. M. Liss, L. Liu, J. D. Long, V. I. Martinez Outschoorn, M. S. Neubauer, A. Puri, M. Rybar, R. Shang, A. M. Sickles, I. Vichou, J. C. Zeng & M. Zhang
Instituto de Fisica Corpuscular (IFIC), Centro Mixto Universidad de Valencia-CSIC, Valencia, Spain
D. Álvarez Piqueras, L. Barranco Navarro, S. Cabrera Urbán, V. Castillo Gimenez, L. Cerda Alberich, M. J. Costa, C. Escobar, O. Estrada Pastor, P. Fernandez Martinez, A. Ferrer, L. Fiorini, J. Fuster, C. García, J. E. García Navarro, S. González de la Hoz, E. Higón-Rodriguez, J. Jimenez Pena, C. Lacasta, D. Madaffari, J. Mamuzic, S. Marti-Garcia, D. Melini, V. A. Mitsou, S. Pedraza Lopez, S. Rodriguez Bosca, D. Rodriguez Rodriguez, E. Romero Adam, J. Salt, J. Sánchez, V. Sanchez Martinez, U. Soldevila, A. Valero, J. A. Valls Ferrer & M. Vos
Department of Physics, University of British Columbia, Vancouver, BC, Canada
F. Cormier, M. Danninger, W. Fedorko, C. Gay, M. Gignac, A. Held, S. Henkelmann, A. Lister, S. Rettie & V. W. S. Wong
Department of Physics and Astronomy, University of Victoria, Victoria, BC, Canada
J. Albert, Y. H. Chiu, A. A. Elliot, M. Fincke-Keeler, K. Hamano, E. Hill, R. Keeler, R. Kowalewski, E. S. Kuwertz, T. Kwan, M. LeBlanc, M. Lefebvre, R. A. McPherson, R. Seuster, R. Sobie, M. Trovatelli & M. Venturi
Department of Physics, University of Warwick, Coventry, UK
J. S. Ennis, S. M. Farrington, P. F. Harrison, A. Jelinskas, C. Jeske, T. A. Martin, C. J. McNicol, W. J. Murray, E. Pianori & M. Spangenberg
Waseda University, Tokyo, Japan
T. Iizawa, T. Kaji, T. Mitani, M. Morinaga, T. Nitta, Y. Sakurai & K. Yorita
Department of Particle Physics, The Weizmann Institute of Science, Rehovot, Israel
P. Balek, S. Bressler, Z. H. Citron, E. Duchovni, M. Dumancic, E. Gross, M. K. Köhler, D. Lellouch, L. J. Levinson, G. Mikenberg, A. Milov, M. Pitt, I. Ravinovich, J. Shlomi, V. Smakhtin & D. Turgeman
Department of Physics, University of Wisconsin, Madison, WI, USA
Sw. Banerjee, N. P. Dang, W. Guan, A. S. Hard, Y. Heng, H. Ji, X. Ju, L. S. Kaplan, L. Kashif, Y. Ming, F. Wang, W. Wiedenmann, S. L. Wu, F. Zhang, C. Zhou & G. Zobernig
Fakultät für Physik und Astronomie, Julius-Maximilians-Universität, Würzburg, Germany
V. Herget, F. Kuger, A. Redelbach, O. Sidiropoulou, G. Siragusa, R. Ströhmer, T. Trefzger, S. W. Weber & A. Zibell
Fakultät für Mathematik und Naturwissenschaften, Fachgruppe Physik, Bergische Universität Wuppertal, Wuppertal, Germany
A. A. E. Bannoura, D. Boerner, C. Dulsen, F. Ellinghaus, J. Fischer, T. Flick, G. Gilles, K. Hamacher, T. Harenberg, D. Hirschbuehl, S. Kersten, J. T. Kuechler, P. Mättig, M. Neumann, C. J. Riegel, M. Sandhoff, F. Tepel, M. Vogel, W. Wagner & C. Zeitnitz
Department of Physics, Yale University, New Haven, CT, USA
O. K. Baker, E. Benhar Noccioli, J. Cummings, S. Demers, T. Lagouri, M. Paganini, D. Paredes Hernandez, C. O. Shimmin, S. J. Thais, L. A. Thomsen, P. Tipton & J. G. Vasquez
Yerevan Physics Institute, Yerevan, Armenia
H. Hakobyan, T. Mkrtchyan & G. Vardanyan
Centre de Calcul de l’Institut National de Physique Nucléaire et de Physique des Particules (IN2P3), Villeurbanne, France
G. Rahal
Academia Sinica Grid Computing, Institute of Physics, Academia Sinica, Taipei, Taiwan
S. C. Lin
- M. Aaboud
You can also search for this author in PubMed Google Scholar
- G. Aad
You can also search for this author in PubMed Google Scholar
- B. Abbott
You can also search for this author in PubMed Google Scholar
- O. Abdinov
You can also search for this author in PubMed Google Scholar
- B. Abeloos
You can also search for this author in PubMed Google Scholar
- S. H. Abidi
You can also search for this author in PubMed Google Scholar
- O. S. AbouZeid
You can also search for this author in PubMed Google Scholar
- N. L. Abraham
You can also search for this author in PubMed Google Scholar
- H. Abramowicz
You can also search for this author in PubMed Google Scholar
- H. Abreu
You can also search for this author in PubMed Google Scholar
- R. Abreu
You can also search for this author in PubMed Google Scholar
- Y. Abulaiti
You can also search for this author in PubMed Google Scholar
- B. S. Acharya
You can also search for this author in PubMed Google Scholar
- S. Adachi
You can also search for this author in PubMed Google Scholar
- L. Adamczyk
You can also search for this author in PubMed Google Scholar
- J. Adelman
You can also search for this author in PubMed Google Scholar
- M. Adersberger
You can also search for this author in PubMed Google Scholar
- T. Adye
You can also search for this author in PubMed Google Scholar
- A. A. Affolder
You can also search for this author in PubMed Google Scholar
- Y. Afik
You can also search for this author in PubMed Google Scholar
- T. Agatonovic-Jovin
You can also search for this author in PubMed Google Scholar
- C. Agheorghiesei
You can also search for this author in PubMed Google Scholar
- J. A. Aguilar-Saavedra
You can also search for this author in PubMed Google Scholar
- S. P. Ahlen
You can also search for this author in PubMed Google Scholar
- F. Ahmadov
You can also search for this author in PubMed Google Scholar
- G. Aielli
You can also search for this author in PubMed Google Scholar
- S. Akatsuka
You can also search for this author in PubMed Google Scholar
- H. Akerstedt
You can also search for this author in PubMed Google Scholar
- T. P. A. Åkesson
You can also search for this author in PubMed Google Scholar
- E. Akilli
You can also search for this author in PubMed Google Scholar
- A. V. Akimov
You can also search for this author in PubMed Google Scholar
- G. L. Alberghi
You can also search for this author in PubMed Google Scholar
- J. Albert
You can also search for this author in PubMed Google Scholar
- P. Albicocco
You can also search for this author in PubMed Google Scholar
- M. J. Alconada Verzini
You can also search for this author in PubMed Google Scholar
- S. C. Alderweireldt
You can also search for this author in PubMed Google Scholar
- M. Aleksa
You can also search for this author in PubMed Google Scholar
- I. N. Aleksandrov
You can also search for this author in PubMed Google Scholar
- C. Alexa
You can also search for this author in PubMed Google Scholar
- G. Alexander
You can also search for this author in PubMed Google Scholar
- T. Alexopoulos
You can also search for this author in PubMed Google Scholar
- M. Alhroob
You can also search for this author in PubMed Google Scholar
- B. Ali
You can also search for this author in PubMed Google Scholar
- M. Aliev
You can also search for this author in PubMed Google Scholar
- G. Alimonti
You can also search for this author in PubMed Google Scholar
- J. Alison
You can also search for this author in PubMed Google Scholar
- S. P. Alkire
You can also search for this author in PubMed Google Scholar
- B. M. M. Allbrooke
You can also search for this author in PubMed Google Scholar
- B. W. Allen
You can also search for this author in PubMed Google Scholar
- P. P. Allport
You can also search for this author in PubMed Google Scholar
- A. Aloisio
You can also search for this author in PubMed Google Scholar
- A. Alonso
You can also search for this author in PubMed Google Scholar
- F. Alonso
You can also search for this author in PubMed Google Scholar
- C. Alpigiani
You can also search for this author in PubMed Google Scholar
- A. A. Alshehri
You can also search for this author in PubMed Google Scholar
- M. I. Alstaty
You can also search for this author in PubMed Google Scholar
- B. Alvarez Gonzalez
You can also search for this author in PubMed Google Scholar
- D. Álvarez Piqueras
You can also search for this author in PubMed Google Scholar
- M. G. Alviggi
You can also search for this author in PubMed Google Scholar
- B. T. Amadio
You can also search for this author in PubMed Google Scholar
- Y. Amaral Coutinho
You can also search for this author in PubMed Google Scholar
- C. Amelung
You can also search for this author in PubMed Google Scholar
- D. Amidei
You can also search for this author in PubMed Google Scholar
- S. P. Amor Dos Santos
You can also search for this author in PubMed Google Scholar
- S. Amoroso
You can also search for this author in PubMed Google Scholar
- G. Amundsen
You can also search for this author in PubMed Google Scholar
- C. Anastopoulos
You can also search for this author in PubMed Google Scholar
- L. S. Ancu
You can also search for this author in PubMed Google Scholar
- N. Andari
You can also search for this author in PubMed Google Scholar
- T. Andeen
You can also search for this author in PubMed Google Scholar
- C. F. Anders
You can also search for this author in PubMed Google Scholar
- J. K. Anders
You can also search for this author in PubMed Google Scholar
- K. J. Anderson
You can also search for this author in PubMed Google Scholar
- A. Andreazza
You can also search for this author in PubMed Google Scholar
- V. Andrei
You can also search for this author in PubMed Google Scholar
- S. Angelidakis
You can also search for this author in PubMed Google Scholar
- I. Angelozzi
You can also search for this author in PubMed Google Scholar
- A. Angerami
You can also search for this author in PubMed Google Scholar
- A. V. Anisenkov
You can also search for this author in PubMed Google Scholar
- N. Anjos
You can also search for this author in PubMed Google Scholar
- A. Annovi
You can also search for this author in PubMed Google Scholar
- C. Antel
You can also search for this author in PubMed Google Scholar
- M. Antonelli
You can also search for this author in PubMed Google Scholar
- A. Antonov
You can also search for this author in PubMed Google Scholar
- D. J. Antrim
You can also search for this author in PubMed Google Scholar
- F. Anulli
You can also search for this author in PubMed Google Scholar
- M. Aoki
You can also search for this author in PubMed Google Scholar
- L. Aperio Bella
You can also search for this author in PubMed Google Scholar
- G. Arabidze
You can also search for this author in PubMed Google Scholar
- Y. Arai
You can also search for this author in PubMed Google Scholar
- J. P. Araque
You can also search for this author in PubMed Google Scholar
- V. Araujo Ferraz
You can also search for this author in PubMed Google Scholar
- A. T. H. Arce
You can also search for this author in PubMed Google Scholar
- R. E. Ardell
You can also search for this author in PubMed Google Scholar
- F. A. Arduh
You can also search for this author in PubMed Google Scholar
- J-F. Arguin
You can also search for this author in PubMed Google Scholar
- S. Argyropoulos
You can also search for this author in PubMed Google Scholar
- M. Arik
You can also search for this author in PubMed Google Scholar
- A. J. Armbruster
You can also search for this author in PubMed Google Scholar
- L. J. Armitage
You can also search for this author in PubMed Google Scholar
- O. Arnaez
You can also search for this author in PubMed Google Scholar
- H. Arnold
You can also search for this author in PubMed Google Scholar
- M. Arratia
You can also search for this author in PubMed Google Scholar
- O. Arslan
You can also search for this author in PubMed Google Scholar
- A. Artamonov
You can also search for this author in PubMed Google Scholar
- G. Artoni
You can also search for this author in PubMed Google Scholar
- S. Artz
You can also search for this author in PubMed Google Scholar
- S. Asai
You can also search for this author in PubMed Google Scholar
- N. Asbah
You can also search for this author in PubMed Google Scholar
- A. Ashkenazi
You can also search for this author in PubMed Google Scholar
- L. Asquith
You can also search for this author in PubMed Google Scholar
- K. Assamagan
You can also search for this author in PubMed Google Scholar
- R. Astalos
You can also search for this author in PubMed Google Scholar
- M. Atkinson
You can also search for this author in PubMed Google Scholar
- N. B. Atlay
You can also search for this author in PubMed Google Scholar
- K. Augsten
You can also search for this author in PubMed Google Scholar
- G. Avolio
You can also search for this author in PubMed Google Scholar
- B. Axen
You can also search for this author in PubMed Google Scholar
- M. K. Ayoub
You can also search for this author in PubMed Google Scholar
- G. Azuelos
You can also search for this author in PubMed Google Scholar
- A. E. Baas
You can also search for this author in PubMed Google Scholar
- M. J. Baca
You can also search for this author in PubMed Google Scholar
- H. Bachacou
You can also search for this author in PubMed Google Scholar
- K. Bachas
You can also search for this author in PubMed Google Scholar
- M. Backes
You can also search for this author in PubMed Google Scholar
- P. Bagnaia
You can also search for this author in PubMed Google Scholar
- M. Bahmani
You can also search for this author in PubMed Google Scholar
- H. Bahrasemani
You can also search for this author in PubMed Google Scholar
- J. T. Baines
You can also search for this author in PubMed Google Scholar
- M. Bajic
You can also search for this author in PubMed Google Scholar
- O. K. Baker
You can also search for this author in PubMed Google Scholar
- P. J. Bakker
You can also search for this author in PubMed Google Scholar
- E. M. Baldin
You can also search for this author in PubMed Google Scholar
- P. Balek
You can also search for this author in PubMed Google Scholar
- F. Balli
You can also search for this author in PubMed Google Scholar
- W. K. Balunas
You can also search for this author in PubMed Google Scholar
- E. Banas
You can also search for this author in PubMed Google Scholar
- A. Bandyopadhyay
You can also search for this author in PubMed Google Scholar
- Sw. Banerjee
You can also search for this author in PubMed Google Scholar
- A. A. E. Bannoura
You can also search for this author in PubMed Google Scholar
- L. Barak
You can also search for this author in PubMed Google Scholar
- E. L. Barberio
You can also search for this author in PubMed Google Scholar
- D. Barberis
You can also search for this author in PubMed Google Scholar
- M. Barbero
You can also search for this author in PubMed Google Scholar
- T. Barillari
You can also search for this author in PubMed Google Scholar
- M-S Barisits
You can also search for this author in PubMed Google Scholar
- J. T. Barkeloo
You can also search for this author in PubMed Google Scholar
- T. Barklow
You can also search for this author in PubMed Google Scholar
- N. Barlow
You can also search for this author in PubMed Google Scholar
- S. L. Barnes
You can also search for this author in PubMed Google Scholar
- B. M. Barnett
You can also search for this author in PubMed Google Scholar
- R. M. Barnett
You can also search for this author in PubMed Google Scholar
- Z. Barnovska-Blenessy
You can also search for this author in PubMed Google Scholar
- A. Baroncelli
You can also search for this author in PubMed Google Scholar
- G. Barone
You can also search for this author in PubMed Google Scholar
- A. J. Barr
You can also search for this author in PubMed Google Scholar
- L. Barranco Navarro
You can also search for this author in PubMed Google Scholar
- F. Barreiro
You can also search for this author in PubMed Google Scholar
- J. Barreiro Guimarães da Costa
You can also search for this author in PubMed Google Scholar
- R. Bartoldus
You can also search for this author in PubMed Google Scholar
- A. E. Barton
You can also search for this author in PubMed Google Scholar
- P. Bartos
You can also search for this author in PubMed Google Scholar
- A. Basalaev
You can also search for this author in PubMed Google Scholar
- A. Bassalat
You can also search for this author in PubMed Google Scholar
- R. L. Bates
You can also search for this author in PubMed Google Scholar
- S. J. Batista
You can also search for this author in PubMed Google Scholar
- J. R. Batley
You can also search for this author in PubMed Google Scholar
- M. Battaglia
You can also search for this author in PubMed Google Scholar
- M. Bauce
You can also search for this author in PubMed Google Scholar
- F. Bauer
You can also search for this author in PubMed Google Scholar
- H. S. Bawa
You can also search for this author in PubMed Google Scholar
- J. B. Beacham
You can also search for this author in PubMed Google Scholar
- M. D. Beattie
You can also search for this author in PubMed Google Scholar
- T. Beau
You can also search for this author in PubMed Google Scholar
- P. H. Beauchemin
You can also search for this author in PubMed Google Scholar
- P. Bechtle
You can also search for this author in PubMed Google Scholar
- H. P. Beck
You can also search for this author in PubMed Google Scholar
- H. C. Beck
You can also search for this author in PubMed Google Scholar
- K. Becker
You can also search for this author in PubMed Google Scholar
- M. Becker
You can also search for this author in PubMed Google Scholar
- C. Becot
You can also search for this author in PubMed Google Scholar
- A. J. Beddall
You can also search for this author in PubMed Google Scholar
- A. Beddall
You can also search for this author in PubMed Google Scholar
- V. A. Bednyakov
You can also search for this author in PubMed Google Scholar
- M. Bedognetti
You can also search for this author in PubMed Google Scholar
- C. P. Bee
You can also search for this author in PubMed Google Scholar
- T. A. Beermann
You can also search for this author in PubMed Google Scholar
- M. Begalli
You can also search for this author in PubMed Google Scholar
- M. Begel
You can also search for this author in PubMed Google Scholar
- J. K. Behr
You can also search for this author in PubMed Google Scholar
- A. S. Bell
You can also search for this author in PubMed Google Scholar
- G. Bella
You can also search for this author in PubMed Google Scholar
- L. Bellagamba
You can also search for this author in PubMed Google Scholar
- A. Bellerive
You can also search for this author in PubMed Google Scholar
- M. Bellomo
You can also search for this author in PubMed Google Scholar
- K. Belotskiy
You can also search for this author in PubMed Google Scholar
- O. Beltramello
You can also search for this author in PubMed Google Scholar
- N. L. Belyaev
You can also search for this author in PubMed Google Scholar
- O. Benary
You can also search for this author in PubMed Google Scholar
- D. Benchekroun
You can also search for this author in PubMed Google Scholar
- M. Bender
You can also search for this author in PubMed Google Scholar
- N. Benekos
You can also search for this author in PubMed Google Scholar
- Y. Benhammou
You can also search for this author in PubMed Google Scholar
- E. Benhar Noccioli
You can also search for this author in PubMed Google Scholar
- J. Benitez
You can also search for this author in PubMed Google Scholar
- D. P. Benjamin
You can also search for this author in PubMed Google Scholar
- M. Benoit
You can also search for this author in PubMed Google Scholar
- J. R. Bensinger
You can also search for this author in PubMed Google Scholar
- S. Bentvelsen
You can also search for this author in PubMed Google Scholar
- L. Beresford
You can also search for this author in PubMed Google Scholar
- M. Beretta
You can also search for this author in PubMed Google Scholar
- D. Berge
You can also search for this author in PubMed Google Scholar
- E. Bergeaas Kuutmann
You can also search for this author in PubMed Google Scholar
- N. Berger
You can also search for this author in PubMed Google Scholar
- J. Beringer
You can also search for this author in PubMed Google Scholar
- S. Berlendis
You can also search for this author in PubMed Google Scholar
- N. R. Bernard
You can also search for this author in PubMed Google Scholar
- G. Bernardi
You can also search for this author in PubMed Google Scholar
- C. Bernius
You can also search for this author in PubMed Google Scholar
- F. U. Bernlochner
You can also search for this author in PubMed Google Scholar
- T. Berry
You can also search for this author in PubMed Google Scholar
- P. Berta
You can also search for this author in PubMed Google Scholar
- C. Bertella
You can also search for this author in PubMed Google Scholar
- G. Bertoli
You can also search for this author in PubMed Google Scholar
- I. A. Bertram
You can also search for this author in PubMed Google Scholar
- C. Bertsche
You can also search for this author in PubMed Google Scholar
- D. Bertsche
You can also search for this author in PubMed Google Scholar
- G. J. Besjes
You can also search for this author in PubMed Google Scholar
- O. Bessidskaia Bylund
You can also search for this author in PubMed Google Scholar
- M. Bessner
You can also search for this author in PubMed Google Scholar
- N. Besson
You can also search for this author in PubMed Google Scholar
- A. Bethani
You can also search for this author in PubMed Google Scholar
- S. Bethke
You can also search for this author in PubMed Google Scholar
- A. J. Bevan
You can also search for this author in PubMed Google Scholar
- J. Beyer
You can also search for this author in PubMed Google Scholar
- R. M. Bianchi
You can also search for this author in PubMed Google Scholar
- O. Biebel
You can also search for this author in PubMed Google Scholar
- D. Biedermann
You can also search for this author in PubMed Google Scholar
- R. Bielski
You can also search for this author in PubMed Google Scholar
- K. Bierwagen
You can also search for this author in PubMed Google Scholar
- N. V. Biesuz
You can also search for this author in PubMed Google Scholar
- M. Biglietti
You can also search for this author in PubMed Google Scholar
- T. R. V. Billoud
You can also search for this author in PubMed Google Scholar
- H. Bilokon
You can also search for this author in PubMed Google Scholar
- M. Bindi
You can also search for this author in PubMed Google Scholar
- A. Bingul
You can also search for this author in PubMed Google Scholar
- C. Bini
You can also search for this author in PubMed Google Scholar
- S. Biondi
You can also search for this author in PubMed Google Scholar
- T. Bisanz
You can also search for this author in PubMed Google Scholar
- C. Bittrich
You can also search for this author in PubMed Google Scholar
- D. M. Bjergaard
You can also search for this author in PubMed Google Scholar
- J. E. Black
You can also search for this author in PubMed Google Scholar
- K. M. Black
You can also search for this author in PubMed Google Scholar
- R. E. Blair
You can also search for this author in PubMed Google Scholar
- T. Blazek
You can also search for this author in PubMed Google Scholar
- I. Bloch
You can also search for this author in PubMed Google Scholar
- C. Blocker
You can also search for this author in PubMed Google Scholar
- A. Blue
You can also search for this author in PubMed Google Scholar
- W. Blum
You can also search for this author in PubMed Google Scholar
- U. Blumenschein
You can also search for this author in PubMed Google Scholar
- S. Blunier
You can also search for this author in PubMed Google Scholar
- G. J. Bobbink
You can also search for this author in PubMed Google Scholar
- V. S. Bobrovnikov
You can also search for this author in PubMed Google Scholar
- S. S. Bocchetta
You can also search for this author in PubMed Google Scholar
- A. Bocci
You can also search for this author in PubMed Google Scholar
- C. Bock
You can also search for this author in PubMed Google Scholar
- M. Boehler
You can also search for this author in PubMed Google Scholar
- D. Boerner
You can also search for this author in PubMed Google Scholar
- D. Bogavac
You can also search for this author in PubMed Google Scholar
- A. G. Bogdanchikov
You can also search for this author in PubMed Google Scholar
- C. Bohm
You can also search for this author in PubMed Google Scholar
- V. Boisvert
You can also search for this author in PubMed Google Scholar
- P. Bokan
You can also search for this author in PubMed Google Scholar
- T. Bold
You can also search for this author in PubMed Google Scholar
- A. S. Boldyrev
You can also search for this author in PubMed Google Scholar
- A. E. Bolz
You can also search for this author in PubMed Google Scholar
- M. Bomben
You can also search for this author in PubMed Google Scholar
- M. Bona
You can also search for this author in PubMed Google Scholar
- M. Boonekamp
You can also search for this author in PubMed Google Scholar
- A. Borisov
You can also search for this author in PubMed Google Scholar
- G. Borissov
You can also search for this author in PubMed Google Scholar
- J. Bortfeldt
You can also search for this author in PubMed Google Scholar
- D. Bortoletto
You can also search for this author in PubMed Google Scholar
- V. Bortolotto
You can also search for this author in PubMed Google Scholar
- D. Boscherini
You can also search for this author in PubMed Google Scholar
- M. Bosman
You can also search for this author in PubMed Google Scholar
- J. D. Bossio Sola
You can also search for this author in PubMed Google Scholar
- J. Boudreau
You can also search for this author in PubMed Google Scholar
- J. Bouffard
You can also search for this author in PubMed Google Scholar
- E. V. Bouhova-Thacker
You can also search for this author in PubMed Google Scholar
- D. Boumediene
You can also search for this author in PubMed Google Scholar
- C. Bourdarios
You can also search for this author in PubMed Google Scholar
- S. K. Boutle
You can also search for this author in PubMed Google Scholar
- A. Boveia
You can also search for this author in PubMed Google Scholar
- J. Boyd
You can also search for this author in PubMed Google Scholar
- I. R. Boyko
You can also search for this author in PubMed Google Scholar
- A. J. Bozson
You can also search for this author in PubMed Google Scholar
- J. Bracinik
You can also search for this author in PubMed Google Scholar
- A. Brandt
You can also search for this author in PubMed Google Scholar
- G. Brandt
You can also search for this author in PubMed Google Scholar
- O. Brandt
You can also search for this author in PubMed Google Scholar
- F. Braren
You can also search for this author in PubMed Google Scholar
- U. Bratzler
You can also search for this author in PubMed Google Scholar
- B. Brau
You can also search for this author in PubMed Google Scholar
- J. E. Brau
You can also search for this author in PubMed Google Scholar
- W. D. Breaden Madden
You can also search for this author in PubMed Google Scholar
- K. Brendlinger
You can also search for this author in PubMed Google Scholar
- A. J. Brennan
You can also search for this author in PubMed Google Scholar
- L. Brenner
You can also search for this author in PubMed Google Scholar
- R. Brenner
You can also search for this author in PubMed Google Scholar
- S. Bressler
You can also search for this author in PubMed Google Scholar
- D. L. Briglin
You can also search for this author in PubMed Google Scholar
- T. M. Bristow
You can also search for this author in PubMed Google Scholar
- D. Britton
You can also search for this author in PubMed Google Scholar
- D. Britzger
You can also search for this author in PubMed Google Scholar
- F. M. Brochu
You can also search for this author in PubMed Google Scholar
- I. Brock
You can also search for this author in PubMed Google Scholar
- R. Brock
You can also search for this author in PubMed Google Scholar
- G. Brooijmans
You can also search for this author in PubMed Google Scholar
- T. Brooks
You can also search for this author in PubMed Google Scholar
- W. K. Brooks
You can also search for this author in PubMed Google Scholar
- J. Brosamer
You can also search for this author in PubMed Google Scholar
- E. Brost
You can also search for this author in PubMed Google Scholar
- J. H Broughton
You can also search for this author in PubMed Google Scholar
- P. A. Bruckman de Renstrom
You can also search for this author in PubMed Google Scholar
- D. Bruncko
You can also search for this author in PubMed Google Scholar
- A. Bruni
You can also search for this author in PubMed Google Scholar
- G. Bruni
You can also search for this author in PubMed Google Scholar
- L. S. Bruni
You can also search for this author in PubMed Google Scholar
- S. Bruno
You can also search for this author in PubMed Google Scholar
- BH Brunt
You can also search for this author in PubMed Google Scholar
- M. Bruschi
You can also search for this author in PubMed Google Scholar
- N. Bruscino
You can also search for this author in PubMed Google Scholar
- P. Bryant
You can also search for this author in PubMed Google Scholar
- L. Bryngemark
You can also search for this author in PubMed Google Scholar
- T. Buanes
You can also search for this author in PubMed Google Scholar
- Q. Buat
You can also search for this author in PubMed Google Scholar
- P. Buchholz
You can also search for this author in PubMed Google Scholar
- A. G. Buckley
You can also search for this author in PubMed Google Scholar
- I. A. Budagov
You can also search for this author in PubMed Google Scholar
- F. Buehrer
You can also search for this author in PubMed Google Scholar
- M. K. Bugge
You can also search for this author in PubMed Google Scholar
- O. Bulekov
You can also search for this author in PubMed Google Scholar
- D. Bullock
You can also search for this author in PubMed Google Scholar
- T. J. Burch
You can also search for this author in PubMed Google Scholar
- S. Burdin
You can also search for this author in PubMed Google Scholar
- C. D. Burgard
You can also search for this author in PubMed Google Scholar
- A. M. Burger
You can also search for this author in PubMed Google Scholar
- B. Burghgrave
You can also search for this author in PubMed Google Scholar
- K. Burka
You can also search for this author in PubMed Google Scholar
- S. Burke
You can also search for this author in PubMed Google Scholar
- I. Burmeister
You can also search for this author in PubMed Google Scholar
- J. T. P. Burr
You can also search for this author in PubMed Google Scholar
- E. Busato
You can also search for this author in PubMed Google Scholar
- D. Büscher
You can also search for this author in PubMed Google Scholar
- V. Büscher
You can also search for this author in PubMed Google Scholar
- P. Bussey
You can also search for this author in PubMed Google Scholar
- J. M. Butler
You can also search for this author in PubMed Google Scholar
- C. M. Buttar
You can also search for this author in PubMed Google Scholar
- J. M. Butterworth
You can also search for this author in PubMed Google Scholar
- P. Butti
You can also search for this author in PubMed Google Scholar
- W. Buttinger
You can also search for this author in PubMed Google Scholar
- A. Buzatu
You can also search for this author in PubMed Google Scholar
- A. R. Buzykaev
You can also search for this author in PubMed Google Scholar
- S. Cabrera Urbán
You can also search for this author in PubMed Google Scholar
- D. Caforio
You can also search for this author in PubMed Google Scholar
- H. Cai
You can also search for this author in PubMed Google Scholar
- V. M. Cairo
You can also search for this author in PubMed Google Scholar
- O. Cakir
You can also search for this author in PubMed Google Scholar
- N. Calace
You can also search for this author in PubMed Google Scholar
- P. Calafiura
You can also search for this author in PubMed Google Scholar
- A. Calandri
You can also search for this author in PubMed Google Scholar
- G. Calderini
You can also search for this author in PubMed Google Scholar
- P. Calfayan
You can also search for this author in PubMed Google Scholar
- G. Callea
You can also search for this author in PubMed Google Scholar
- L. P. Caloba
You can also search for this author in PubMed Google Scholar
- S. Calvente Lopez
You can also search for this author in PubMed Google Scholar
- D. Calvet
You can also search for this author in PubMed Google Scholar
- S. Calvet
You can also search for this author in PubMed Google Scholar
- T. P. Calvet
You can also search for this author in PubMed Google Scholar
- R. Camacho Toro
You can also search for this author in PubMed Google Scholar
- S. Camarda
You can also search for this author in PubMed Google Scholar
- P. Camarri
You can also search for this author in PubMed Google Scholar
- D. Cameron
You can also search for this author in PubMed Google Scholar
- R. Caminal Armadans
You can also search for this author in PubMed Google Scholar
- C. Camincher
You can also search for this author in PubMed Google Scholar
- S. Campana
You can also search for this author in PubMed Google Scholar
- M. Campanelli
You can also search for this author in PubMed Google Scholar
- A. Camplani
You can also search for this author in PubMed Google Scholar
- A. Campoverde
You can also search for this author in PubMed Google Scholar
- V. Canale
You can also search for this author in PubMed Google Scholar
- M. Cano Bret
You can also search for this author in PubMed Google Scholar
- J. Cantero
You can also search for this author in PubMed Google Scholar
- T. Cao
You can also search for this author in PubMed Google Scholar
- M. D. M. Capeans Garrido
You can also search for this author in PubMed Google Scholar
- I. Caprini
You can also search for this author in PubMed Google Scholar
- M. Caprini
You can also search for this author in PubMed Google Scholar
- M. Capua
You can also search for this author in PubMed Google Scholar
- R. M. Carbone
You can also search for this author in PubMed Google Scholar
- R. Cardarelli
You can also search for this author in PubMed Google Scholar
- F. Cardillo
You can also search for this author in PubMed Google Scholar
- I. Carli
You can also search for this author in PubMed Google Scholar
- T. Carli
You can also search for this author in PubMed Google Scholar
- G. Carlino
You can also search for this author in PubMed Google Scholar
- B. T. Carlson
You can also search for this author in PubMed Google Scholar
- L. Carminati
You can also search for this author in PubMed Google Scholar
- R. M. D. Carney
You can also search for this author in PubMed Google Scholar
- S. Caron
You can also search for this author in PubMed Google Scholar
- E. Carquin
You can also search for this author in PubMed Google Scholar
- S. Carrá
You can also search for this author in PubMed Google Scholar
- G. D. Carrillo-Montoya
You can also search for this author in PubMed Google Scholar
- D. Casadei
You can also search for this author in PubMed Google Scholar
- M. P. Casado
You can also search for this author in PubMed Google Scholar
- M. Casolino
You can also search for this author in PubMed Google Scholar
- D. W. Casper
You can also search for this author in PubMed Google Scholar
- R. Castelijn
You can also search for this author in PubMed Google Scholar
- V. Castillo Gimenez
You can also search for this author in PubMed Google Scholar
- N. F. Castro
You can also search for this author in PubMed Google Scholar
- A. Catinaccio
You can also search for this author in PubMed Google Scholar
- J. R. Catmore
You can also search for this author in PubMed Google Scholar
- A. Cattai
You can also search for this author in PubMed Google Scholar
- J. Caudron
You can also search for this author in PubMed Google Scholar
- V. Cavaliere
You can also search for this author in PubMed Google Scholar
- E. Cavallaro
You can also search for this author in PubMed Google Scholar
- D. Cavalli
You can also search for this author in PubMed Google Scholar
- M. Cavalli-Sforza
You can also search for this author in PubMed Google Scholar
- V. Cavasinni
You can also search for this author in PubMed Google Scholar
- E. Celebi
You can also search for this author in PubMed Google Scholar
- F. Ceradini
You can also search for this author in PubMed Google Scholar
- L. Cerda Alberich
You can also search for this author in PubMed Google Scholar
- A. S. Cerqueira
You can also search for this author in PubMed Google Scholar
- A. Cerri
You can also search for this author in PubMed Google Scholar
- L. Cerrito
You can also search for this author in PubMed Google Scholar
- F. Cerutti
You can also search for this author in PubMed Google Scholar
- A. Cervelli
You can also search for this author in PubMed Google Scholar
- S. A. Cetin
You can also search for this author in PubMed Google Scholar
- A. Chafaq
You can also search for this author in PubMed Google Scholar
- D. Chakraborty
You can also search for this author in PubMed Google Scholar
- S. K. Chan
You can also search for this author in PubMed Google Scholar
- W. S. Chan
You can also search for this author in PubMed Google Scholar
- Y. L. Chan
You can also search for this author in PubMed Google Scholar
- P. Chang
You can also search for this author in PubMed Google Scholar
- J. D. Chapman
You can also search for this author in PubMed Google Scholar
- D. G. Charlton
You can also search for this author in PubMed Google Scholar
- C. C. Chau
You can also search for this author in PubMed Google Scholar
- C. A. Chavez Barajas
You can also search for this author in PubMed Google Scholar
- S. Che
You can also search for this author in PubMed Google Scholar
- S. Cheatham
You can also search for this author in PubMed Google Scholar
- A. Chegwidden
You can also search for this author in PubMed Google Scholar
- S. Chekanov
You can also search for this author in PubMed Google Scholar
- S. V. Chekulaev
You can also search for this author in PubMed Google Scholar
- G. A. Chelkov
You can also search for this author in PubMed Google Scholar
- M. A. Chelstowska
You can also search for this author in PubMed Google Scholar
- C. Chen
You can also search for this author in PubMed Google Scholar
- C. Chen
You can also search for this author in PubMed Google Scholar
- H. Chen
You can also search for this author in PubMed Google Scholar
- J. Chen
You can also search for this author in PubMed Google Scholar
- S. Chen
You can also search for this author in PubMed Google Scholar
- S. Chen
You can also search for this author in PubMed Google Scholar
- X. Chen
You can also search for this author in PubMed Google Scholar
- Y. Chen
You can also search for this author in PubMed Google Scholar
- H. C. Cheng
You can also search for this author in PubMed Google Scholar
- H. J. Cheng
You can also search for this author in PubMed Google Scholar
- A. Cheplakov
You can also search for this author in PubMed Google Scholar
- E. Cheremushkina
You can also search for this author in PubMed Google Scholar
- R. Cherkaoui El Moursli
You can also search for this author in PubMed Google Scholar
- E. Cheu
You can also search for this author in PubMed Google Scholar
- K. Cheung
You can also search for this author in PubMed Google Scholar
- L. Chevalier
You can also search for this author in PubMed Google Scholar
- V. Chiarella
You can also search for this author in PubMed Google Scholar
- G. Chiarelli
You can also search for this author in PubMed Google Scholar
- G. Chiodini
You can also search for this author in PubMed Google Scholar
- A. S. Chisholm
You can also search for this author in PubMed Google Scholar
- A. Chitan
You can also search for this author in PubMed Google Scholar
- Y. H. Chiu
You can also search for this author in PubMed Google Scholar
- M. V. Chizhov
You can also search for this author in PubMed Google Scholar
- K. Choi
You can also search for this author in PubMed Google Scholar
- A. R. Chomont
You can also search for this author in PubMed Google Scholar
- S. Chouridou
You can also search for this author in PubMed Google Scholar
- Y. S. Chow
You can also search for this author in PubMed Google Scholar
- V. Christodoulou
You can also search for this author in PubMed Google Scholar
- M. C. Chu
You can also search for this author in PubMed Google Scholar
- J. Chudoba
You can also search for this author in PubMed Google Scholar
- A. J. Chuinard
You can also search for this author in PubMed Google Scholar
- J. J. Chwastowski
You can also search for this author in PubMed Google Scholar
- L. Chytka
You can also search for this author in PubMed Google Scholar
- A. K. Ciftci
You can also search for this author in PubMed Google Scholar
- D. Cinca
You can also search for this author in PubMed Google Scholar
- V. Cindro
You can also search for this author in PubMed Google Scholar
- I. A. Cioara
You can also search for this author in PubMed Google Scholar
- A. Ciocio
You can also search for this author in PubMed Google Scholar
- F. Cirotto
You can also search for this author in PubMed Google Scholar
- Z. H. Citron
You can also search for this author in PubMed Google Scholar
- M. Citterio
You can also search for this author in PubMed Google Scholar
- M. Ciubancan
You can also search for this author in PubMed Google Scholar
- A. Clark
You can also search for this author in PubMed Google Scholar
- B. L. Clark
You can also search for this author in PubMed Google Scholar
- M. R. Clark
You can also search for this author in PubMed Google Scholar
- P. J. Clark
You can also search for this author in PubMed Google Scholar
- R. N. Clarke
You can also search for this author in PubMed Google Scholar
- C. Clement
You can also search for this author in PubMed Google Scholar
- Y. Coadou
You can also search for this author in PubMed Google Scholar
- M. Cobal
You can also search for this author in PubMed Google Scholar
- A. Coccaro
You can also search for this author in PubMed Google Scholar
- J. Cochran
You can also search for this author in PubMed Google Scholar
- L. Colasurdo
You can also search for this author in PubMed Google Scholar
- B. Cole
You can also search for this author in PubMed Google Scholar
- A. P. Colijn
You can also search for this author in PubMed Google Scholar
- J. Collot
You can also search for this author in PubMed Google Scholar
- T. Colombo
You can also search for this author in PubMed Google Scholar
- P. Conde Muiño
You can also search for this author in PubMed Google Scholar
- E. Coniavitis
You can also search for this author in PubMed Google Scholar
- S. H. Connell
You can also search for this author in PubMed Google Scholar
- I. A. Connelly
You can also search for this author in PubMed Google Scholar
- S. Constantinescu
You can also search for this author in PubMed Google Scholar
- G. Conti
You can also search for this author in PubMed Google Scholar
- F. Conventi
You can also search for this author in PubMed Google Scholar
- M. Cooke
You can also search for this author in PubMed Google Scholar
- A. M. Cooper-Sarkar
You can also search for this author in PubMed Google Scholar
- F. Cormier
You can also search for this author in PubMed Google Scholar
- K. J. R. Cormier
You can also search for this author in PubMed Google Scholar
- M. Corradi
You can also search for this author in PubMed Google Scholar
- F. Corriveau
You can also search for this author in PubMed Google Scholar
- A. Cortes-Gonzalez
You can also search for this author in PubMed Google Scholar
- G. Costa
You can also search for this author in PubMed Google Scholar
- M. J. Costa
You can also search for this author in PubMed Google Scholar
- D. Costanzo
You can also search for this author in PubMed Google Scholar
- G. Cottin
You can also search for this author in PubMed Google Scholar
- G. Cowan
You can also search for this author in PubMed Google Scholar
- B. E. Cox
You can also search for this author in PubMed Google Scholar
- K. Cranmer
You can also search for this author in PubMed Google Scholar
- S. J. Crawley
You can also search for this author in PubMed Google Scholar
- R. A. Creager
You can also search for this author in PubMed Google Scholar
- G. Cree
You can also search for this author in PubMed Google Scholar
- S. Crépé-Renaudin
You can also search for this author in PubMed Google Scholar
- F. Crescioli
You can also search for this author in PubMed Google Scholar
- W. A. Cribbs
You can also search for this author in PubMed Google Scholar
- M. Cristinziani
You can also search for this author in PubMed Google Scholar
- V. Croft
You can also search for this author in PubMed Google Scholar
- G. Crosetti
You can also search for this author in PubMed Google Scholar
- A. Cueto
You can also search for this author in PubMed Google Scholar
- T. Cuhadar Donszelmann
You can also search for this author in PubMed Google Scholar
- A. R. Cukierman
You can also search for this author in PubMed Google Scholar
- J. Cummings
You can also search for this author in PubMed Google Scholar
- M. Curatolo
You can also search for this author in PubMed Google Scholar
- J. Cúth
You can also search for this author in PubMed Google Scholar
- S. Czekierda
You can also search for this author in PubMed Google Scholar
- P. Czodrowski
You can also search for this author in PubMed Google Scholar
- G. D’amen
You can also search for this author in PubMed Google Scholar
- S. D’Auria
You can also search for this author in PubMed Google Scholar
- L. D’eramo
You can also search for this author in PubMed Google Scholar
- M. D’Onofrio
You can also search for this author in PubMed Google Scholar
- M. J. Da Cunha Sargedas De Sousa
You can also search for this author in PubMed Google Scholar
- C. Da Via
You can also search for this author in PubMed Google Scholar
- W. Dabrowski
You can also search for this author in PubMed Google Scholar
- T. Dado
You can also search for this author in PubMed Google Scholar
- T. Dai
You can also search for this author in PubMed Google Scholar
- O. Dale
You can also search for this author in PubMed Google Scholar
- F. Dallaire
You can also search for this author in PubMed Google Scholar
- C. Dallapiccola
You can also search for this author in PubMed Google Scholar
- M. Dam
You can also search for this author in PubMed Google Scholar
- J. R. Dandoy
You can also search for this author in PubMed Google Scholar
- M. F. Daneri
You can also search for this author in PubMed Google Scholar
- N. P. Dang
You can also search for this author in PubMed Google Scholar
- A. C. Daniells
You can also search for this author in PubMed Google Scholar
- N. S. Dann
You can also search for this author in PubMed Google Scholar
- M. Danninger
You can also search for this author in PubMed Google Scholar
- M. Dano Hoffmann
You can also search for this author in PubMed Google Scholar
- V. Dao
You can also search for this author in PubMed Google Scholar
- G. Darbo
You can also search for this author in PubMed Google Scholar
- S. Darmora
You can also search for this author in PubMed Google Scholar
- J. Dassoulas
You can also search for this author in PubMed Google Scholar
- A. Dattagupta
You can also search for this author in PubMed Google Scholar
- T. Daubney
You can also search for this author in PubMed Google Scholar
- W. Davey
You can also search for this author in PubMed Google Scholar
- C. David
You can also search for this author in PubMed Google Scholar
- T. Davidek
You can also search for this author in PubMed Google Scholar
- D. R. Davis
You can also search for this author in PubMed Google Scholar
- P. Davison
You can also search for this author in PubMed Google Scholar
- E. Dawe
You can also search for this author in PubMed Google Scholar
- I. Dawson
You can also search for this author in PubMed Google Scholar
- K. De
You can also search for this author in PubMed Google Scholar
- R. de Asmundis
You can also search for this author in PubMed Google Scholar
- A. De Benedetti
You can also search for this author in PubMed Google Scholar
- S. De Castro
You can also search for this author in PubMed Google Scholar
- S. De Cecco
You can also search for this author in PubMed Google Scholar
- N. De Groot
You can also search for this author in PubMed Google Scholar
- P. de Jong
You can also search for this author in PubMed Google Scholar
- H. De la Torre
You can also search for this author in PubMed Google Scholar
- F. De Lorenzi
You can also search for this author in PubMed Google Scholar
- A. De Maria
You can also search for this author in PubMed Google Scholar
- D. De Pedis
You can also search for this author in PubMed Google Scholar
- A. De Salvo
You can also search for this author in PubMed Google Scholar
- U. De Sanctis
You can also search for this author in PubMed Google Scholar
- A. De Santo
You can also search for this author in PubMed Google Scholar
- K. De Vasconcelos Corga
You can also search for this author in PubMed Google Scholar
- J. B. De Vivie De Regie
You can also search for this author in PubMed Google Scholar
- R. Debbe
You can also search for this author in PubMed Google Scholar
- C. Debenedetti
You can also search for this author in PubMed Google Scholar
- D. V. Dedovich
You can also search for this author in PubMed Google Scholar
- N. Dehghanian
You can also search for this author in PubMed Google Scholar
- I. Deigaard
You can also search for this author in PubMed Google Scholar
- M. Del Gaudio
You can also search for this author in PubMed Google Scholar
- J. Del Peso
You can also search for this author in PubMed Google Scholar
- D. Delgove
You can also search for this author in PubMed Google Scholar
- F. Deliot
You can also search for this author in PubMed Google Scholar
- C. M. Delitzsch
You can also search for this author in PubMed Google Scholar
- A. Dell’Acqua
You can also search for this author in PubMed Google Scholar
- L. Dell’Asta
You can also search for this author in PubMed Google Scholar
- M. Dell’Orso
You can also search for this author in PubMed Google Scholar
- M. Della Pietra
You can also search for this author in PubMed Google Scholar
- D. della Volpe
You can also search for this author in PubMed Google Scholar
- M. Delmastro
You can also search for this author in PubMed Google Scholar
- C. Delporte
You can also search for this author in PubMed Google Scholar
- P. A. Delsart
You can also search for this author in PubMed Google Scholar
- D. A. DeMarco
You can also search for this author in PubMed Google Scholar
- S. Demers
You can also search for this author in PubMed Google Scholar
- M. Demichev
You can also search for this author in PubMed Google Scholar
- A. Demilly
You can also search for this author in PubMed Google Scholar
- S. P. Denisov
You can also search for this author in PubMed Google Scholar
- D. Denysiuk
You can also search for this author in PubMed Google Scholar
- D. Derendarz
You can also search for this author in PubMed Google Scholar
- J. E. Derkaoui
You can also search for this author in PubMed Google Scholar
- F. Derue
You can also search for this author in PubMed Google Scholar
- P. Dervan
You can also search for this author in PubMed Google Scholar
- K. Desch
You can also search for this author in PubMed Google Scholar
- C. Deterre
You can also search for this author in PubMed Google Scholar
- K. Dette
You can also search for this author in PubMed Google Scholar
- M. R. Devesa
You can also search for this author in PubMed Google Scholar
- P. O. Deviveiros
You can also search for this author in PubMed Google Scholar
- A. Dewhurst
You can also search for this author in PubMed Google Scholar
- S. Dhaliwal
You can also search for this author in PubMed Google Scholar
- F. A. Di Bello
You can also search for this author in PubMed Google Scholar
- A. Di Ciaccio
You can also search for this author in PubMed Google Scholar
- L. Di Ciaccio
You can also search for this author in PubMed Google Scholar
- W. K. Di Clemente
You can also search for this author in PubMed Google Scholar
- C. Di Donato
You can also search for this author in PubMed Google Scholar
- A. Di Girolamo
You can also search for this author in PubMed Google Scholar
- B. Di Girolamo
You can also search for this author in PubMed Google Scholar
- B. Di Micco
You can also search for this author in PubMed Google Scholar
- R. Di Nardo
You can also search for this author in PubMed Google Scholar
- K. F. Di Petrillo
You can also search for this author in PubMed Google Scholar
- A. Di Simone
You can also search for this author in PubMed Google Scholar
- R. Di Sipio
You can also search for this author in PubMed Google Scholar
- D. Di Valentino
You can also search for this author in PubMed Google Scholar
- C. Diaconu
You can also search for this author in PubMed Google Scholar
- M. Diamond
You can also search for this author in PubMed Google Scholar
- F. A. Dias
You can also search for this author in PubMed Google Scholar
- M. A. Diaz
You can also search for this author in PubMed Google Scholar
- E. B. Diehl
You can also search for this author in PubMed Google Scholar
- J. Dietrich
You can also search for this author in PubMed Google Scholar
- S. Díez Cornell
You can also search for this author in PubMed Google Scholar
- A. Dimitrievska
You can also search for this author in PubMed Google Scholar
- J. Dingfelder
You can also search for this author in PubMed Google Scholar
- P. Dita
You can also search for this author in PubMed Google Scholar
- S. Dita
You can also search for this author in PubMed Google Scholar
- F. Dittus
You can also search for this author in PubMed Google Scholar
- F. Djama
You can also search for this author in PubMed Google Scholar
- T. Djobava
You can also search for this author in PubMed Google Scholar
- J. I. Djuvsland
You can also search for this author in PubMed Google Scholar
- M. A. B. do Vale
You can also search for this author in PubMed Google Scholar
- D. Dobos
You can also search for this author in PubMed Google Scholar
- M. Dobre
You can also search for this author in PubMed Google Scholar
- D. Dodsworth
You can also search for this author in PubMed Google Scholar
- C. Doglioni
You can also search for this author in PubMed Google Scholar
- J. Dolejsi
You can also search for this author in PubMed Google Scholar
- Z. Dolezal
You can also search for this author in PubMed Google Scholar
- M. Donadelli
You can also search for this author in PubMed Google Scholar
- S. Donati
You can also search for this author in PubMed Google Scholar
- P. Dondero
You can also search for this author in PubMed Google Scholar
- J. Donini
You can also search for this author in PubMed Google Scholar
- J. Dopke
You can also search for this author in PubMed Google Scholar
- A. Doria
You can also search for this author in PubMed Google Scholar
- M. T. Dova
You can also search for this author in PubMed Google Scholar
- A. T. Doyle
You can also search for this author in PubMed Google Scholar
- E. Drechsler
You can also search for this author in PubMed Google Scholar
- M. Dris
You can also search for this author in PubMed Google Scholar
- Y. Du
You can also search for this author in PubMed Google Scholar
- J. Duarte-Campderros
You can also search for this author in PubMed Google Scholar
- A. Dubreuil
You can also search for this author in PubMed Google Scholar
- E. Duchovni
You can also search for this author in PubMed Google Scholar
- G. Duckeck
You can also search for this author in PubMed Google Scholar
- A. Ducourthial
You can also search for this author in PubMed Google Scholar
- O. A. Ducu
You can also search for this author in PubMed Google Scholar
- D. Duda
You can also search for this author in PubMed Google Scholar
- A. Dudarev
You can also search for this author in PubMed Google Scholar
- A. Chr. Dudder
You can also search for this author in PubMed Google Scholar
- E. M. Duffield
You can also search for this author in PubMed Google Scholar
- L. Duflot
You can also search for this author in PubMed Google Scholar
- M. Dührssen
You can also search for this author in PubMed Google Scholar
- C. Dulsen
You can also search for this author in PubMed Google Scholar
- M. Dumancic
You can also search for this author in PubMed Google Scholar
- A. E. Dumitriu
You can also search for this author in PubMed Google Scholar
- A. K. Duncan
You can also search for this author in PubMed Google Scholar
- M. Dunford
You can also search for this author in PubMed Google Scholar
- A. Duperrin
You can also search for this author in PubMed Google Scholar
- H. Duran Yildiz
You can also search for this author in PubMed Google Scholar
- M. Düren
You can also search for this author in PubMed Google Scholar
- A. Durglishvili
You can also search for this author in PubMed Google Scholar
- D. Duschinger
You can also search for this author in PubMed Google Scholar
- B. Dutta
You can also search for this author in PubMed Google Scholar
- D. Duvnjak
You can also search for this author in PubMed Google Scholar
- M. Dyndal
You can also search for this author in PubMed Google Scholar
- B. S. Dziedzic
You can also search for this author in PubMed Google Scholar
- C. Eckardt
You can also search for this author in PubMed Google Scholar
- K. M. Ecker
You can also search for this author in PubMed Google Scholar
- R. C. Edgar
You can also search for this author in PubMed Google Scholar
- T. Eifert
You can also search for this author in PubMed Google Scholar
- G. Eigen
You can also search for this author in PubMed Google Scholar
- K. Einsweiler
You can also search for this author in PubMed Google Scholar
- T. Ekelof
You can also search for this author in PubMed Google Scholar
- M. El Kacimi
You can also search for this author in PubMed Google Scholar
- R. El Kosseifi
You can also search for this author in PubMed Google Scholar
- V. Ellajosyula
You can also search for this author in PubMed Google Scholar
- M. Ellert
You can also search for this author in PubMed Google Scholar
- S. Elles
You can also search for this author in PubMed Google Scholar
- F. Ellinghaus
You can also search for this author in PubMed Google Scholar
- A. A. Elliot
You can also search for this author in PubMed Google Scholar
- N. Ellis
You can also search for this author in PubMed Google Scholar
- J. Elmsheuser
You can also search for this author in PubMed Google Scholar
- M. Elsing
You can also search for this author in PubMed Google Scholar
- D. Emeliyanov
You can also search for this author in PubMed Google Scholar
- Y. Enari
You can also search for this author in PubMed Google Scholar
- O. C. Endner
You can also search for this author in PubMed Google Scholar
- J. S. Ennis
You can also search for this author in PubMed Google Scholar
- M. B. Epland
You can also search for this author in PubMed Google Scholar
- J. Erdmann
You can also search for this author in PubMed Google Scholar
- A. Ereditato
You can also search for this author in PubMed Google Scholar
- M. Ernst
You can also search for this author in PubMed Google Scholar
- S. Errede
You can also search for this author in PubMed Google Scholar
- M. Escalier
You can also search for this author in PubMed Google Scholar
- C. Escobar
You can also search for this author in PubMed Google Scholar
- B. Esposito
You can also search for this author in PubMed Google Scholar
- O. Estrada Pastor
You can also search for this author in PubMed Google Scholar
- A. I. Etienvre
You can also search for this author in PubMed Google Scholar
- E. Etzion
You can also search for this author in PubMed Google Scholar
- H. Evans
You can also search for this author in PubMed Google Scholar
- A. Ezhilov
You can also search for this author in PubMed Google Scholar
- M. Ezzi
You can also search for this author in PubMed Google Scholar
- F. Fabbri
You can also search for this author in PubMed Google Scholar
- L. Fabbri
You can also search for this author in PubMed Google Scholar
- V. Fabiani
You can also search for this author in PubMed Google Scholar
- G. Facini
You can also search for this author in PubMed Google Scholar
- R. M. Fakhrutdinov
You can also search for this author in PubMed Google Scholar
- S. Falciano
You can also search for this author in PubMed Google Scholar
- R. J. Falla
You can also search for this author in PubMed Google Scholar
- J. Faltova
You can also search for this author in PubMed Google Scholar
- Y. Fang
You can also search for this author in PubMed Google Scholar
- M. Fanti
You can also search for this author in PubMed Google Scholar
- A. Farbin
You can also search for this author in PubMed Google Scholar
- A. Farilla
You can also search for this author in PubMed Google Scholar
- C. Farina
You can also search for this author in PubMed Google Scholar
- E. M. Farina
You can also search for this author in PubMed Google Scholar
- T. Farooque
You can also search for this author in PubMed Google Scholar
- S. Farrell
You can also search for this author in PubMed Google Scholar
- S. M. Farrington
You can also search for this author in PubMed Google Scholar
- P. Farthouat
You can also search for this author in PubMed Google Scholar
- F. Fassi
You can also search for this author in PubMed Google Scholar
- P. Fassnacht
You can also search for this author in PubMed Google Scholar
- D. Fassouliotis
You can also search for this author in PubMed Google Scholar
- M. Faucci Giannelli
You can also search for this author in PubMed Google Scholar
- A. Favareto
You can also search for this author in PubMed Google Scholar
- W. J. Fawcett
You can also search for this author in PubMed Google Scholar
- L. Fayard
You can also search for this author in PubMed Google Scholar
- O. L. Fedin
You can also search for this author in PubMed Google Scholar
- W. Fedorko
You can also search for this author in PubMed Google Scholar
- S. Feigl
You can also search for this author in PubMed Google Scholar
- L. Feligioni
You can also search for this author in PubMed Google Scholar
- C. Feng
You can also search for this author in PubMed Google Scholar
- E. J. Feng
You can also search for this author in PubMed Google Scholar
- M. J. Fenton
You can also search for this author in PubMed Google Scholar
- A. B. Fenyuk
You can also search for this author in PubMed Google Scholar
- L. Feremenga
You can also search for this author in PubMed Google Scholar
- P. Fernandez Martinez
You can also search for this author in PubMed Google Scholar
- S. Fernandez Perez
You can also search for this author in PubMed Google Scholar
- J. Ferrando
You can also search for this author in PubMed Google Scholar
- A. Ferrari
You can also search for this author in PubMed Google Scholar
- P. Ferrari
You can also search for this author in PubMed Google Scholar
- R. Ferrari
You can also search for this author in PubMed Google Scholar
- D. E. Ferreira de Lima
You can also search for this author in PubMed Google Scholar
- A. Ferrer
You can also search for this author in PubMed Google Scholar
- D. Ferrere
You can also search for this author in PubMed Google Scholar
- C. Ferretti
You can also search for this author in PubMed Google Scholar
- F. Fiedler
You can also search for this author in PubMed Google Scholar
- A. Filipčič
You can also search for this author in PubMed Google Scholar
- M. Filipuzzi
You can also search for this author in PubMed Google Scholar
- F. Filthaut
You can also search for this author in PubMed Google Scholar
- M. Fincke-Keeler
You can also search for this author in PubMed Google Scholar
- K. D. Finelli
You can also search for this author in PubMed Google Scholar
- M. C. N. Fiolhais
You can also search for this author in PubMed Google Scholar
- L. Fiorini
You can also search for this author in PubMed Google Scholar
- A. Fischer
You can also search for this author in PubMed Google Scholar
- C. Fischer
You can also search for this author in PubMed Google Scholar
- J. Fischer
You can also search for this author in PubMed Google Scholar
- W. C. Fisher
You can also search for this author in PubMed Google Scholar
- N. Flaschel
You can also search for this author in PubMed Google Scholar
- I. Fleck
You can also search for this author in PubMed Google Scholar
- P. Fleischmann
You can also search for this author in PubMed Google Scholar
- R. R. M. Fletcher
You can also search for this author in PubMed Google Scholar
- T. Flick
You can also search for this author in PubMed Google Scholar
- B. M. Flierl
You can also search for this author in PubMed Google Scholar
- L. R. Flores Castillo
You can also search for this author in PubMed Google Scholar
- M. J. Flowerdew
You can also search for this author in PubMed Google Scholar
- G. T. Forcolin
You can also search for this author in PubMed Google Scholar
- A. Formica
You can also search for this author in PubMed Google Scholar
- F. A. Förster
You can also search for this author in PubMed Google Scholar
- A. Forti
You can also search for this author in PubMed Google Scholar
- A. G. Foster
You can also search for this author in PubMed Google Scholar
- D. Fournier
You can also search for this author in PubMed Google Scholar
- H. Fox
You can also search for this author in PubMed Google Scholar
- S. Fracchia
You can also search for this author in PubMed Google Scholar
- P. Francavilla
You can also search for this author in PubMed Google Scholar
- M. Franchini
You can also search for this author in PubMed Google Scholar
- S. Franchino
You can also search for this author in PubMed Google Scholar
- D. Francis
You can also search for this author in PubMed Google Scholar
- L. Franconi
You can also search for this author in PubMed Google Scholar
- M. Franklin
You can also search for this author in PubMed Google Scholar
- M. Frate
You can also search for this author in PubMed Google Scholar
- M. Fraternali
You can also search for this author in PubMed Google Scholar
- D. Freeborn
You can also search for this author in PubMed Google Scholar
- S. M. Fressard-Batraneanu
You can also search for this author in PubMed Google Scholar
- B. Freund
You can also search for this author in PubMed Google Scholar
- D. Froidevaux
You can also search for this author in PubMed Google Scholar
- J. A. Frost
You can also search for this author in PubMed Google Scholar
- C. Fukunaga
You can also search for this author in PubMed Google Scholar
- T. Fusayasu
You can also search for this author in PubMed Google Scholar
- J. Fuster
You can also search for this author in PubMed Google Scholar
- O. Gabizon
You can also search for this author in PubMed Google Scholar
- A. Gabrielli
You can also search for this author in PubMed Google Scholar
- A. Gabrielli
You can also search for this author in PubMed Google Scholar
- G. P. Gach
You can also search for this author in PubMed Google Scholar
- S. Gadatsch
You can also search for this author in PubMed Google Scholar
- S. Gadomski
You can also search for this author in PubMed Google Scholar
- G. Gagliardi
You can also search for this author in PubMed Google Scholar
- L. G. Gagnon
You can also search for this author in PubMed Google Scholar
- C. Galea
You can also search for this author in PubMed Google Scholar
- B. Galhardo
You can also search for this author in PubMed Google Scholar
- E. J. Gallas
You can also search for this author in PubMed Google Scholar
- B. J. Gallop
You can also search for this author in PubMed Google Scholar
- P. Gallus
You can also search for this author in PubMed Google Scholar
- G. Galster
You can also search for this author in PubMed Google Scholar
- K. K. Gan
You can also search for this author in PubMed Google Scholar
- S. Ganguly
You can also search for this author in PubMed Google Scholar
- Y. Gao
You can also search for this author in PubMed Google Scholar
- Y. S. Gao
You can also search for this author in PubMed Google Scholar
- F. M. Garay Walls
You can also search for this author in PubMed Google Scholar
- C. García
You can also search for this author in PubMed Google Scholar
- J. E. García Navarro
You can also search for this author in PubMed Google Scholar
- J. A. García Pascual
You can also search for this author in PubMed Google Scholar
- M. Garcia-Sciveres
You can also search for this author in PubMed Google Scholar
- R. W. Gardner
You can also search for this author in PubMed Google Scholar
- N. Garelli
You can also search for this author in PubMed Google Scholar
- V. Garonne
You can also search for this author in PubMed Google Scholar
- A. Gascon Bravo
You can also search for this author in PubMed Google Scholar
- K. Gasnikova
You can also search for this author in PubMed Google Scholar
- C. Gatti
You can also search for this author in PubMed Google Scholar
- A. Gaudiello
You can also search for this author in PubMed Google Scholar
- G. Gaudio
You can also search for this author in PubMed Google Scholar
- I. L. Gavrilenko
You can also search for this author in PubMed Google Scholar
- C. Gay
You can also search for this author in PubMed Google Scholar
- G. Gaycken
You can also search for this author in PubMed Google Scholar
- E. N. Gazis
You can also search for this author in PubMed Google Scholar
- C. N. P. Gee
You can also search for this author in PubMed Google Scholar
- J. Geisen
You can also search for this author in PubMed Google Scholar
- M. Geisen
You can also search for this author in PubMed Google Scholar
- M. P. Geisler
You can also search for this author in PubMed Google Scholar
- K. Gellerstedt
You can also search for this author in PubMed Google Scholar
- C. Gemme
You can also search for this author in PubMed Google Scholar
- M. H. Genest
You can also search for this author in PubMed Google Scholar
- C. Geng
You can also search for this author in PubMed Google Scholar
- S. Gentile
You can also search for this author in PubMed Google Scholar
- C. Gentsos
You can also search for this author in PubMed Google Scholar
- S. George
You can also search for this author in PubMed Google Scholar
- D. Gerbaudo
You can also search for this author in PubMed Google Scholar
- G. Geßner
You can also search for this author in PubMed Google Scholar
- S. Ghasemi
You can also search for this author in PubMed Google Scholar
- M. Ghneimat
You can also search for this author in PubMed Google Scholar
- B. Giacobbe
You can also search for this author in PubMed Google Scholar
- S. Giagu
You can also search for this author in PubMed Google Scholar
- N. Giangiacomi
You can also search for this author in PubMed Google Scholar
- P. Giannetti
You can also search for this author in PubMed Google Scholar
- S. M. Gibson
You can also search for this author in PubMed Google Scholar
- M. Gignac
You can also search for this author in PubMed Google Scholar
- M. Gilchriese
You can also search for this author in PubMed Google Scholar
- D. Gillberg
You can also search for this author in PubMed Google Scholar
- G. Gilles
You can also search for this author in PubMed Google Scholar
- D. M. Gingrich
You can also search for this author in PubMed Google Scholar
- M. P. Giordani
You can also search for this author in PubMed Google Scholar
- F. M. Giorgi
You can also search for this author in PubMed Google Scholar
- P. F. Giraud
You can also search for this author in PubMed Google Scholar
- P. Giromini
You can also search for this author in PubMed Google Scholar
- G. Giugliarelli
You can also search for this author in PubMed Google Scholar
- D. Giugni
You can also search for this author in PubMed Google Scholar
- F. Giuli
You can also search for this author in PubMed Google Scholar
- C. Giuliani
You can also search for this author in PubMed Google Scholar
- M. Giulini
You can also search for this author in PubMed Google Scholar
- B. K. Gjelsten
You can also search for this author in PubMed Google Scholar
- S. Gkaitatzis
You can also search for this author in PubMed Google Scholar
- I. Gkialas
You can also search for this author in PubMed Google Scholar
- E. L. Gkougkousis
You can also search for this author in PubMed Google Scholar
- P. Gkountoumis
You can also search for this author in PubMed Google Scholar
- L. K. Gladilin
You can also search for this author in PubMed Google Scholar
- C. Glasman
You can also search for this author in PubMed Google Scholar
- J. Glatzer
You can also search for this author in PubMed Google Scholar
- P. C. F. Glaysher
You can also search for this author in PubMed Google Scholar
- A. Glazov
You can also search for this author in PubMed Google Scholar
- M. Goblirsch-Kolb
You can also search for this author in PubMed Google Scholar
- J. Godlewski
You can also search for this author in PubMed Google Scholar
- S. Goldfarb
You can also search for this author in PubMed Google Scholar
- T. Golling
You can also search for this author in PubMed Google Scholar
- D. Golubkov
You can also search for this author in PubMed Google Scholar
- A. Gomes
You can also search for this author in PubMed Google Scholar
- R. Gonçalo
You can also search for this author in PubMed Google Scholar
- R. Goncalves Gama
You can also search for this author in PubMed Google Scholar
- J. Goncalves Pinto Firmino Da Costa
You can also search for this author in PubMed Google Scholar
- G. Gonella
You can also search for this author in PubMed Google Scholar
- L. Gonella
You can also search for this author in PubMed Google Scholar
- A. Gongadze
You can also search for this author in PubMed Google Scholar
- S. González de la Hoz
You can also search for this author in PubMed Google Scholar
- S. Gonzalez-Sevilla
You can also search for this author in PubMed Google Scholar
- L. Goossens
You can also search for this author in PubMed Google Scholar
- P. A. Gorbounov
You can also search for this author in PubMed Google Scholar
- H. A. Gordon
You can also search for this author in PubMed Google Scholar
- I. Gorelov
You can also search for this author in PubMed Google Scholar
- B. Gorini
You can also search for this author in PubMed Google Scholar
- E. Gorini
You can also search for this author in PubMed Google Scholar
- A. Gorišek
You can also search for this author in PubMed Google Scholar
- A. T. Goshaw
You can also search for this author in PubMed Google Scholar
- C. Gössling
You can also search for this author in PubMed Google Scholar
- M. I. Gostkin
You can also search for this author in PubMed Google Scholar
- C. A. Gottardo
You can also search for this author in PubMed Google Scholar
- C. R. Goudet
You can also search for this author in PubMed Google Scholar
- D. Goujdami
You can also search for this author in PubMed Google Scholar
- A. G. Goussiou
You can also search for this author in PubMed Google Scholar
- N. Govender
You can also search for this author in PubMed Google Scholar
- E. Gozani
You can also search for this author in PubMed Google Scholar
- I. Grabowska-Bold
You can also search for this author in PubMed Google Scholar
- P. O. J. Gradin
You can also search for this author in PubMed Google Scholar
- J. Gramling
You can also search for this author in PubMed Google Scholar
- E. Gramstad
You can also search for this author in PubMed Google Scholar
- S. Grancagnolo
You can also search for this author in PubMed Google Scholar
- V. Gratchev
You can also search for this author in PubMed Google Scholar
- P. M. Gravila
You can also search for this author in PubMed Google Scholar
- C. Gray
You can also search for this author in PubMed Google Scholar
- H. M. Gray
You can also search for this author in PubMed Google Scholar
- Z. D. Greenwood
You can also search for this author in PubMed Google Scholar
- C. Grefe
You can also search for this author in PubMed Google Scholar
- K. Gregersen
You can also search for this author in PubMed Google Scholar
- I. M. Gregor
You can also search for this author in PubMed Google Scholar
- P. Grenier
You can also search for this author in PubMed Google Scholar
- K. Grevtsov
You can also search for this author in PubMed Google Scholar
- J. Griffiths
You can also search for this author in PubMed Google Scholar
- A. A. Grillo
You can also search for this author in PubMed Google Scholar
- K. Grimm
You can also search for this author in PubMed Google Scholar
- S. Grinstein
You can also search for this author in PubMed Google Scholar
- Ph. Gris
You can also search for this author in PubMed Google Scholar
- J.-F. Grivaz
You can also search for this author in PubMed Google Scholar
- S. Groh
You can also search for this author in PubMed Google Scholar
- E. Gross
You can also search for this author in PubMed Google Scholar
- J. Grosse-Knetter
You can also search for this author in PubMed Google Scholar
- G. C. Grossi
You can also search for this author in PubMed Google Scholar
- Z. J. Grout
You can also search for this author in PubMed Google Scholar
- A. Grummer
You can also search for this author in PubMed Google Scholar
- L. Guan
You can also search for this author in PubMed Google Scholar
- W. Guan
You can also search for this author in PubMed Google Scholar
- J. Guenther
You can also search for this author in PubMed Google Scholar
- F. Guescini
You can also search for this author in PubMed Google Scholar
- D. Guest
You can also search for this author in PubMed Google Scholar
- O. Gueta
You can also search for this author in PubMed Google Scholar
- B. Gui
You can also search for this author in PubMed Google Scholar
- E. Guido
You can also search for this author in PubMed Google Scholar
- T. Guillemin
You can also search for this author in PubMed Google Scholar
- S. Guindon
You can also search for this author in PubMed Google Scholar
- U. Gul
You can also search for this author in PubMed Google Scholar
- C. Gumpert
You can also search for this author in PubMed Google Scholar
- J. Guo
You can also search for this author in PubMed Google Scholar
- W. Guo
You can also search for this author in PubMed Google Scholar
- Y. Guo
You can also search for this author in PubMed Google Scholar
- R. Gupta
You can also search for this author in PubMed Google Scholar
- S. Gupta
You can also search for this author in PubMed Google Scholar
- S. Gurbuz
You can also search for this author in PubMed Google Scholar
- G. Gustavino
You can also search for this author in PubMed Google Scholar
- B. J. Gutelman
You can also search for this author in PubMed Google Scholar
- P. Gutierrez
You can also search for this author in PubMed Google Scholar
- N. G. Gutierrez Ortiz
You can also search for this author in PubMed Google Scholar
- C. Gutschow
You can also search for this author in PubMed Google Scholar
- C. Guyot
You can also search for this author in PubMed Google Scholar
- M. P. Guzik
You can also search for this author in PubMed Google Scholar
- C. Gwenlan
You can also search for this author in PubMed Google Scholar
- C. B. Gwilliam
You can also search for this author in PubMed Google Scholar
- A. Haas
You can also search for this author in PubMed Google Scholar
- C. Haber
You can also search for this author in PubMed Google Scholar
- H. K. Hadavand
You can also search for this author in PubMed Google Scholar
- N. Haddad
You can also search for this author in PubMed Google Scholar
- A. Hadef
You can also search for this author in PubMed Google Scholar
- S. Hageböck
You can also search for this author in PubMed Google Scholar
- M. Hagihara
You can also search for this author in PubMed Google Scholar
- H. Hakobyan
You can also search for this author in PubMed Google Scholar
- M. Haleem
You can also search for this author in PubMed Google Scholar
- J. Haley
You can also search for this author in PubMed Google Scholar
- G. Halladjian
You can also search for this author in PubMed Google Scholar
- G. D. Hallewell
You can also search for this author in PubMed Google Scholar
- K. Hamacher
You can also search for this author in PubMed Google Scholar
- P. Hamal
You can also search for this author in PubMed Google Scholar
- K. Hamano
You can also search for this author in PubMed Google Scholar
- A. Hamilton
You can also search for this author in PubMed Google Scholar
- G. N. Hamity
You can also search for this author in PubMed Google Scholar
- P. G. Hamnett
You can also search for this author in PubMed Google Scholar
- L. Han
You can also search for this author in PubMed Google Scholar
- S. Han
You can also search for this author in PubMed Google Scholar
- K. Hanagaki
You can also search for this author in PubMed Google Scholar
- K. Hanawa
You can also search for this author in PubMed Google Scholar
- M. Hance
You can also search for this author in PubMed Google Scholar
- B. Haney
You can also search for this author in PubMed Google Scholar
- P. Hanke
You can also search for this author in PubMed Google Scholar
- J. B. Hansen
You can also search for this author in PubMed Google Scholar
- J. D. Hansen
You can also search for this author in PubMed Google Scholar
- M. C. Hansen
You can also search for this author in PubMed Google Scholar
- P. H. Hansen
You can also search for this author in PubMed Google Scholar
- K. Hara
You can also search for this author in PubMed Google Scholar
- A. S. Hard
You can also search for this author in PubMed Google Scholar
- T. Harenberg
You can also search for this author in PubMed Google Scholar
- F. Hariri
You can also search for this author in PubMed Google Scholar
- S. Harkusha
You can also search for this author in PubMed Google Scholar
- P. F. Harrison
You can also search for this author in PubMed Google Scholar
- N. M. Hartmann
You can also search for this author in PubMed Google Scholar
- Y. Hasegawa
You can also search for this author in PubMed Google Scholar
- A. Hasib
You can also search for this author in PubMed Google Scholar
- S. Hassani
You can also search for this author in PubMed Google Scholar
- S. Haug
You can also search for this author in PubMed Google Scholar
- R. Hauser
You can also search for this author in PubMed Google Scholar
- L. Hauswald
You can also search for this author in PubMed Google Scholar
- L. B. Havener
You can also search for this author in PubMed Google Scholar
- M. Havranek
You can also search for this author in PubMed Google Scholar
- C. M. Hawkes
You can also search for this author in PubMed Google Scholar
- R. J. Hawkings
You can also search for this author in PubMed Google Scholar
- D. Hayakawa
You can also search for this author in PubMed Google Scholar
- D. Hayden
You can also search for this author in PubMed Google Scholar
- C. P. Hays
You can also search for this author in PubMed Google Scholar
- J. M. Hays
You can also search for this author in PubMed Google Scholar
- H. S. Hayward
You can also search for this author in PubMed Google Scholar
- S. J. Haywood
You can also search for this author in PubMed Google Scholar
- S. J. Head
You can also search for this author in PubMed Google Scholar
- T. Heck
You can also search for this author in PubMed Google Scholar
- V. Hedberg
You can also search for this author in PubMed Google Scholar
- L. Heelan
You can also search for this author in PubMed Google Scholar
- S. Heer
You can also search for this author in PubMed Google Scholar
- K. K. Heidegger
You can also search for this author in PubMed Google Scholar
- S. Heim
You can also search for this author in PubMed Google Scholar
- T. Heim
You can also search for this author in PubMed Google Scholar
- B. Heinemann
You can also search for this author in PubMed Google Scholar
- J. J. Heinrich
You can also search for this author in PubMed Google Scholar
- L. Heinrich
You can also search for this author in PubMed Google Scholar
- C. Heinz
You can also search for this author in PubMed Google Scholar
- J. Hejbal
You can also search for this author in PubMed Google Scholar
- L. Helary
You can also search for this author in PubMed Google Scholar
- A. Held
You can also search for this author in PubMed Google Scholar
- S. Hellman
You can also search for this author in PubMed Google Scholar
- C. Helsens
You can also search for this author in PubMed Google Scholar
- R. C. W. Henderson
You can also search for this author in PubMed Google Scholar
- Y. Heng
You can also search for this author in PubMed Google Scholar
- S. Henkelmann
You can also search for this author in PubMed Google Scholar
- A. M. Henriques Correia
You can also search for this author in PubMed Google Scholar
- S. Henrot-Versille
You can also search for this author in PubMed Google Scholar
- G. H. Herbert
You can also search for this author in PubMed Google Scholar
- H. Herde
You can also search for this author in PubMed Google Scholar
- V. Herget
You can also search for this author in PubMed Google Scholar
- Y. Hernández Jiménez
You can also search for this author in PubMed Google Scholar
- H. Herr
You can also search for this author in PubMed Google Scholar
- G. Herten
You can also search for this author in PubMed Google Scholar
- R. Hertenberger
You can also search for this author in PubMed Google Scholar
- L. Hervas
You can also search for this author in PubMed Google Scholar
- T. C. Herwig
You can also search for this author in PubMed Google Scholar
- G. G. Hesketh
You can also search for this author in PubMed Google Scholar
- N. P. Hessey
You can also search for this author in PubMed Google Scholar
- J. W. Hetherly
You can also search for this author in PubMed Google Scholar
- S. Higashino
You can also search for this author in PubMed Google Scholar
- E. Higón-Rodriguez
You can also search for this author in PubMed Google Scholar
- K. Hildebrand
You can also search for this author in PubMed Google Scholar
- E. Hill
You can also search for this author in PubMed Google Scholar
- J. C. Hill
You can also search for this author in PubMed Google Scholar
- K. H. Hiller
You can also search for this author in PubMed Google Scholar
- S. J. Hillier
You can also search for this author in PubMed Google Scholar
- M. Hils
You can also search for this author in PubMed Google Scholar
- I. Hinchliffe
You can also search for this author in PubMed Google Scholar
- M. Hirose
You can also search for this author in PubMed Google Scholar
- D. Hirschbuehl
You can also search for this author in PubMed Google Scholar
- B. Hiti
You can also search for this author in PubMed Google Scholar
- O. Hladik
You can also search for this author in PubMed Google Scholar
- X. Hoad
You can also search for this author in PubMed Google Scholar
- J. Hobbs
You can also search for this author in PubMed Google Scholar
- N. Hod
You can also search for this author in PubMed Google Scholar
- M. C. Hodgkinson
You can also search for this author in PubMed Google Scholar
- P. Hodgson
You can also search for this author in PubMed Google Scholar
- A. Hoecker
You can also search for this author in PubMed Google Scholar
- M. R. Hoeferkamp
You can also search for this author in PubMed Google Scholar
- F. Hoenig
You can also search for this author in PubMed Google Scholar
- D. Hohn
You can also search for this author in PubMed Google Scholar
- T. R. Holmes
You can also search for this author in PubMed Google Scholar
- M. Homann
You can also search for this author in PubMed Google Scholar
- S. Honda
You can also search for this author in PubMed Google Scholar
- T. Honda
You can also search for this author in PubMed Google Scholar
- T. M. Hong
You can also search for this author in PubMed Google Scholar
- B. H. Hooberman
You can also search for this author in PubMed Google Scholar
- W. H. Hopkins
You can also search for this author in PubMed Google Scholar
- Y. Horii
You can also search for this author in PubMed Google Scholar
- A. J. Horton
You can also search for this author in PubMed Google Scholar
- J-Y. Hostachy
You can also search for this author in PubMed Google Scholar
- A. Hostiuc
You can also search for this author in PubMed Google Scholar
- S. Hou
You can also search for this author in PubMed Google Scholar
- A. Hoummada
You can also search for this author in PubMed Google Scholar
- J. Howarth
You can also search for this author in PubMed Google Scholar
- J. Hoya
You can also search for this author in PubMed Google Scholar
- M. Hrabovsky
You can also search for this author in PubMed Google Scholar
- J. Hrdinka
You can also search for this author in PubMed Google Scholar
- I. Hristova
You can also search for this author in PubMed Google Scholar
- J. Hrivnac
You can also search for this author in PubMed Google Scholar
- T. Hryn’ova
You can also search for this author in PubMed Google Scholar
- A. Hrynevich
You can also search for this author in PubMed Google Scholar
- P. J. Hsu
You can also search for this author in PubMed Google Scholar
- S.-C. Hsu
You can also search for this author in PubMed Google Scholar
- Q. Hu
You can also search for this author in PubMed Google Scholar
- S. Hu
You can also search for this author in PubMed Google Scholar
- Y. Huang
You can also search for this author in PubMed Google Scholar
- Z. Hubacek
You can also search for this author in PubMed Google Scholar
- F. Hubaut
You can also search for this author in PubMed Google Scholar
- F. Huegging
You can also search for this author in PubMed Google Scholar
- T. B. Huffman
You can also search for this author in PubMed Google Scholar
- E. W. Hughes
You can also search for this author in PubMed Google Scholar
- G. Hughes
You can also search for this author in PubMed Google Scholar
- M. Huhtinen
You can also search for this author in PubMed Google Scholar
- R. F. H. Hunter
You can also search for this author in PubMed Google Scholar
- P. Huo
You can also search for this author in PubMed Google Scholar
- N. Huseynov
You can also search for this author in PubMed Google Scholar
- J. Huston
You can also search for this author in PubMed Google Scholar
- J. Huth
You can also search for this author in PubMed Google Scholar
- R. Hyneman
You can also search for this author in PubMed Google Scholar
- G. Iacobucci
You can also search for this author in PubMed Google Scholar
- G. Iakovidis
You can also search for this author in PubMed Google Scholar
- I. Ibragimov
You can also search for this author in PubMed Google Scholar
- L. Iconomidou-Fayard
You can also search for this author in PubMed Google Scholar
- Z. Idrissi
You can also search for this author in PubMed Google Scholar
- P. Iengo
You can also search for this author in PubMed Google Scholar
- O. Igonkina
You can also search for this author in PubMed Google Scholar
- T. Iizawa
You can also search for this author in PubMed Google Scholar
- Y. Ikegami
You can also search for this author in PubMed Google Scholar
- M. Ikeno
You can also search for this author in PubMed Google Scholar
- Y. Ilchenko
You can also search for this author in PubMed Google Scholar
- D. Iliadis
You can also search for this author in PubMed Google Scholar
- N. Ilic
You can also search for this author in PubMed Google Scholar
- F. Iltzsche
You can also search for this author in PubMed Google Scholar
- G. Introzzi
You can also search for this author in PubMed Google Scholar
- P. Ioannou
You can also search for this author in PubMed Google Scholar
- M. Iodice
You can also search for this author in PubMed Google Scholar
- K. Iordanidou
You can also search for this author in PubMed Google Scholar
- V. Ippolito
You can also search for this author in PubMed Google Scholar
- M. F. Isacson
You can also search for this author in PubMed Google Scholar
- N. Ishijima
You can also search for this author in PubMed Google Scholar
- M. Ishino
You can also search for this author in PubMed Google Scholar
- M. Ishitsuka
You can also search for this author in PubMed Google Scholar
- C. Issever
You can also search for this author in PubMed Google Scholar
- S. Istin
You can also search for this author in PubMed Google Scholar
- F. Ito
You can also search for this author in PubMed Google Scholar
- J. M. Iturbe Ponce
You can also search for this author in PubMed Google Scholar
- R. Iuppa
You can also search for this author in PubMed Google Scholar
- H. Iwasaki
You can also search for this author in PubMed Google Scholar
- J. M. Izen
You can also search for this author in PubMed Google Scholar
- V. Izzo
You can also search for this author in PubMed Google Scholar
- S. Jabbar
You can also search for this author in PubMed Google Scholar
- P. Jackson
You can also search for this author in PubMed Google Scholar
- R. M. Jacobs
You can also search for this author in PubMed Google Scholar
- V. Jain
You can also search for this author in PubMed Google Scholar
- K. B. Jakobi
You can also search for this author in PubMed Google Scholar
- K. Jakobs
You can also search for this author in PubMed Google Scholar
- S. Jakobsen
You can also search for this author in PubMed Google Scholar
- T. Jakoubek
You can also search for this author in PubMed Google Scholar
- D. O. Jamin
You can also search for this author in PubMed Google Scholar
- D. K. Jana
You can also search for this author in PubMed Google Scholar
- R. Jansky
You can also search for this author in PubMed Google Scholar
- J. Janssen
You can also search for this author in PubMed Google Scholar
- M. Janus
You can also search for this author in PubMed Google Scholar
- P. A. Janus
You can also search for this author in PubMed Google Scholar
- G. Jarlskog
You can also search for this author in PubMed Google Scholar
- N. Javadov
You can also search for this author in PubMed Google Scholar
- T. Javůrek
You can also search for this author in PubMed Google Scholar
- M. Javurkova
You can also search for this author in PubMed Google Scholar
- F. Jeanneau
You can also search for this author in PubMed Google Scholar
- L. Jeanty
You can also search for this author in PubMed Google Scholar
- J. Jejelava
You can also search for this author in PubMed Google Scholar
- A. Jelinskas
You can also search for this author in PubMed Google Scholar
- P. Jenni
You can also search for this author in PubMed Google Scholar
- C. Jeske
You can also search for this author in PubMed Google Scholar
- S. Jézéquel
You can also search for this author in PubMed Google Scholar
- H. Ji
You can also search for this author in PubMed Google Scholar
- J. Jia
You can also search for this author in PubMed Google Scholar
- H. Jiang
You can also search for this author in PubMed Google Scholar
- Y. Jiang
You can also search for this author in PubMed Google Scholar
- Z. Jiang
You can also search for this author in PubMed Google Scholar
- S. Jiggins
You can also search for this author in PubMed Google Scholar
- J. Jimenez Pena
You can also search for this author in PubMed Google Scholar
- S. Jin
You can also search for this author in PubMed Google Scholar
- A. Jinaru
You can also search for this author in PubMed Google Scholar
- O. Jinnouchi
You can also search for this author in PubMed Google Scholar
- H. Jivan
You can also search for this author in PubMed Google Scholar
- P. Johansson
You can also search for this author in PubMed Google Scholar
- K. A. Johns
You can also search for this author in PubMed Google Scholar
- C. A. Johnson
You can also search for this author in PubMed Google Scholar
- W. J. Johnson
You can also search for this author in PubMed Google Scholar
- K. Jon-And
You can also search for this author in PubMed Google Scholar
- R. W. L. Jones
You can also search for this author in PubMed Google Scholar
- S. D. Jones
You can also search for this author in PubMed Google Scholar
- S. Jones
You can also search for this author in PubMed Google Scholar
- T. J. Jones
You can also search for this author in PubMed Google Scholar
- J. Jongmanns
You can also search for this author in PubMed Google Scholar
- P. M. Jorge
You can also search for this author in PubMed Google Scholar
- J. Jovicevic
You can also search for this author in PubMed Google Scholar
- X. Ju
You can also search for this author in PubMed Google Scholar
- A. Juste Rozas
You can also search for this author in PubMed Google Scholar
- M. K. Köhler
You can also search for this author in PubMed Google Scholar
- A. Kaczmarska
You can also search for this author in PubMed Google Scholar
- M. Kado
You can also search for this author in PubMed Google Scholar
- H. Kagan
You can also search for this author in PubMed Google Scholar
- M. Kagan
You can also search for this author in PubMed Google Scholar
- S. J. Kahn
You can also search for this author in PubMed Google Scholar
- T. Kaji
You can also search for this author in PubMed Google Scholar
- E. Kajomovitz
You can also search for this author in PubMed Google Scholar
- C. W. Kalderon
You can also search for this author in PubMed Google Scholar
- A. Kaluza
You can also search for this author in PubMed Google Scholar
- S. Kama
You can also search for this author in PubMed Google Scholar
- A. Kamenshchikov
You can also search for this author in PubMed Google Scholar
- N. Kanaya
You can also search for this author in PubMed Google Scholar
- L. Kanjir
You can also search for this author in PubMed Google Scholar
- V. A. Kantserov
You can also search for this author in PubMed Google Scholar
- J. Kanzaki
You can also search for this author in PubMed Google Scholar
- B. Kaplan
You can also search for this author in PubMed Google Scholar
- L. S. Kaplan
You can also search for this author in PubMed Google Scholar
- D. Kar
You can also search for this author in PubMed Google Scholar
- K. Karakostas
You can also search for this author in PubMed Google Scholar
- N. Karastathis
You can also search for this author in PubMed Google Scholar
- M. J. Kareem
You can also search for this author in PubMed Google Scholar
- E. Karentzos
You can also search for this author in PubMed Google Scholar
- S. N. Karpov
You can also search for this author in PubMed Google Scholar
- Z. M. Karpova
You can also search for this author in PubMed Google Scholar
- K. Karthik
You can also search for this author in PubMed Google Scholar
- V. Kartvelishvili
You can also search for this author in PubMed Google Scholar
- A. N. Karyukhin
You can also search for this author in PubMed Google Scholar
- K. Kasahara
You can also search for this author in PubMed Google Scholar
- L. Kashif
You can also search for this author in PubMed Google Scholar
- R. D. Kass
You can also search for this author in PubMed Google Scholar
- A. Kastanas
You can also search for this author in PubMed Google Scholar
- Y. Kataoka
You can also search for this author in PubMed Google Scholar
- C. Kato
You can also search for this author in PubMed Google Scholar
- A. Katre
You can also search for this author in PubMed Google Scholar
- J. Katzy
You can also search for this author in PubMed Google Scholar
- K. Kawade
You can also search for this author in PubMed Google Scholar
- K. Kawagoe
You can also search for this author in PubMed Google Scholar
- T. Kawamoto
You can also search for this author in PubMed Google Scholar
- G. Kawamura
You can also search for this author in PubMed Google Scholar
- E. F. Kay
You can also search for this author in PubMed Google Scholar
- V. F. Kazanin
You can also search for this author in PubMed Google Scholar
- R. Keeler
You can also search for this author in PubMed Google Scholar
- R. Kehoe
You can also search for this author in PubMed Google Scholar
- J. S. Keller
You can also search for this author in PubMed Google Scholar
- E. Kellermann
You can also search for this author in PubMed Google Scholar
- J. J. Kempster
You can also search for this author in PubMed Google Scholar
- J Kendrick
You can also search for this author in PubMed Google Scholar
- H. Keoshkerian
You can also search for this author in PubMed Google Scholar
- O. Kepka
You can also search for this author in PubMed Google Scholar
- B. P. Kerševan
You can also search for this author in PubMed Google Scholar
- S. Kersten
You can also search for this author in PubMed Google Scholar
- R. A. Keyes
You can also search for this author in PubMed Google Scholar
- M. Khader
You can also search for this author in PubMed Google Scholar
- F. Khalil-zada
You can also search for this author in PubMed Google Scholar
- A. Khanov
You can also search for this author in PubMed Google Scholar
- A. G. Kharlamov
You can also search for this author in PubMed Google Scholar
- T. Kharlamova
You can also search for this author in PubMed Google Scholar
- A. Khodinov
You can also search for this author in PubMed Google Scholar
- T. J. Khoo
You can also search for this author in PubMed Google Scholar
- V. Khovanskiy
You can also search for this author in PubMed Google Scholar
- E. Khramov
You can also search for this author in PubMed Google Scholar
- J. Khubua
You can also search for this author in PubMed Google Scholar
- S. Kido
You can also search for this author in PubMed Google Scholar
- C. R. Kilby
You can also search for this author in PubMed Google Scholar
- H. Y. Kim
You can also search for this author in PubMed Google Scholar
- S. H. Kim
You can also search for this author in PubMed Google Scholar
- Y. K. Kim
You can also search for this author in PubMed Google Scholar
- N. Kimura
You can also search for this author in PubMed Google Scholar
- O. M. Kind
You can also search for this author in PubMed Google Scholar
- B. T. King
You can also search for this author in PubMed Google Scholar
- D. Kirchmeier
You can also search for this author in PubMed Google Scholar
- J. Kirk
You can also search for this author in PubMed Google Scholar
- A. E. Kiryunin
You can also search for this author in PubMed Google Scholar
- T. Kishimoto
You can also search for this author in PubMed Google Scholar
- D. Kisielewska
You can also search for this author in PubMed Google Scholar
- V. Kitali
You can also search for this author in PubMed Google Scholar
- O. Kivernyk
You can also search for this author in PubMed Google Scholar
- E. Kladiva
You can also search for this author in PubMed Google Scholar
- T. Klapdor-Kleingrothaus
You can also search for this author in PubMed Google Scholar
- M. H. Klein
You can also search for this author in PubMed Google Scholar
- M. Klein
You can also search for this author in PubMed Google Scholar
- U. Klein
You can also search for this author in PubMed Google Scholar
- K. Kleinknecht
You can also search for this author in PubMed Google Scholar
- P. Klimek
You can also search for this author in PubMed Google Scholar
- A. Klimentov
You can also search for this author in PubMed Google Scholar
- R. Klingenberg
You can also search for this author in PubMed Google Scholar
- T. Klingl
You can also search for this author in PubMed Google Scholar
- T. Klioutchnikova
You can also search for this author in PubMed Google Scholar
- E.-E. Kluge
You can also search for this author in PubMed Google Scholar
- P. Kluit
You can also search for this author in PubMed Google Scholar
- S. Kluth
You can also search for this author in PubMed Google Scholar
- E. Kneringer
You can also search for this author in PubMed Google Scholar
- E. B. F. G. Knoops
You can also search for this author in PubMed Google Scholar
- A. Knue
You can also search for this author in PubMed Google Scholar
- A. Kobayashi
You can also search for this author in PubMed Google Scholar
- D. Kobayashi
You can also search for this author in PubMed Google Scholar
- T. Kobayashi
You can also search for this author in PubMed Google Scholar
- M. Kobel
You can also search for this author in PubMed Google Scholar
- M. Kocian
You can also search for this author in PubMed Google Scholar
- P. Kodys
You can also search for this author in PubMed Google Scholar
- T. Koffas
You can also search for this author in PubMed Google Scholar
- E. Koffeman
You can also search for this author in PubMed Google Scholar
- N. M. Köhler
You can also search for this author in PubMed Google Scholar
- T. Koi
You can also search for this author in PubMed Google Scholar
- M. Kolb
You can also search for this author in PubMed Google Scholar
- I. Koletsou
You can also search for this author in PubMed Google Scholar
- A. A. Komar
You can also search for this author in PubMed Google Scholar
- T. Kondo
You can also search for this author in PubMed Google Scholar
- N. Kondrashova
You can also search for this author in PubMed Google Scholar
- K. Köneke
You can also search for this author in PubMed Google Scholar
- A. C. König
You can also search for this author in PubMed Google Scholar
- T. Kono
You can also search for this author in PubMed Google Scholar
- R. Konoplich
You can also search for this author in PubMed Google Scholar
- N. Konstantinidis
You can also search for this author in PubMed Google Scholar
- R. Kopeliansky
You can also search for this author in PubMed Google Scholar
- S. Koperny
You can also search for this author in PubMed Google Scholar
- A. K. Kopp
You can also search for this author in PubMed Google Scholar
- K. Korcyl
You can also search for this author in PubMed Google Scholar
- K. Kordas
You can also search for this author in PubMed Google Scholar
- A. Korn
You can also search for this author in PubMed Google Scholar
- A. A. Korol
You can also search for this author in PubMed Google Scholar
- I. Korolkov
You can also search for this author in PubMed Google Scholar
- E. V. Korolkova
You can also search for this author in PubMed Google Scholar
- O. Kortner
You can also search for this author in PubMed Google Scholar
- S. Kortner
You can also search for this author in PubMed Google Scholar
- T. Kosek
You can also search for this author in PubMed Google Scholar
- V. V. Kostyukhin
You can also search for this author in PubMed Google Scholar
- A. Kotwal
You can also search for this author in PubMed Google Scholar
- A. Koulouris
You can also search for this author in PubMed Google Scholar
- A. Kourkoumeli-Charalampidi
You can also search for this author in PubMed Google Scholar
- C. Kourkoumelis
You can also search for this author in PubMed Google Scholar
- E. Kourlitis
You can also search for this author in PubMed Google Scholar
- V. Kouskoura
You can also search for this author in PubMed Google Scholar
- A. B. Kowalewska
You can also search for this author in PubMed Google Scholar
- R. Kowalewski
You can also search for this author in PubMed Google Scholar
- T. Z. Kowalski
You can also search for this author in PubMed Google Scholar
- C. Kozakai
You can also search for this author in PubMed Google Scholar
- W. Kozanecki
You can also search for this author in PubMed Google Scholar
- A. S. Kozhin
You can also search for this author in PubMed Google Scholar
- V. A. Kramarenko
You can also search for this author in PubMed Google Scholar
- G. Kramberger
You can also search for this author in PubMed Google Scholar
- D. Krasnopevtsev
You can also search for this author in PubMed Google Scholar
- M. W. Krasny
You can also search for this author in PubMed Google Scholar
- A. Krasznahorkay
You can also search for this author in PubMed Google Scholar
- D. Krauss
You can also search for this author in PubMed Google Scholar
- J. A. Kremer
You can also search for this author in PubMed Google Scholar
- J. Kretzschmar
You can also search for this author in PubMed Google Scholar
- K. Kreutzfeldt
You can also search for this author in PubMed Google Scholar
- P. Krieger
You can also search for this author in PubMed Google Scholar
- K. Krizka
You can also search for this author in PubMed Google Scholar
- K. Kroeninger
You can also search for this author in PubMed Google Scholar
- H. Kroha
You can also search for this author in PubMed Google Scholar
- J. Kroll
You can also search for this author in PubMed Google Scholar
- J. Kroll
You can also search for this author in PubMed Google Scholar
- J. Kroseberg
You can also search for this author in PubMed Google Scholar
- J. Krstic
You can also search for this author in PubMed Google Scholar
- U. Kruchonak
You can also search for this author in PubMed Google Scholar
- H. Krüger
You can also search for this author in PubMed Google Scholar
- N. Krumnack
You can also search for this author in PubMed Google Scholar
- M. C. Kruse
You can also search for this author in PubMed Google Scholar
- T. Kubota
You can also search for this author in PubMed Google Scholar
- H. Kucuk
You can also search for this author in PubMed Google Scholar
- S. Kuday
You can also search for this author in PubMed Google Scholar
- J. T. Kuechler
You can also search for this author in PubMed Google Scholar
- S. Kuehn
You can also search for this author in PubMed Google Scholar
- A. Kugel
You can also search for this author in PubMed Google Scholar
- F. Kuger
You can also search for this author in PubMed Google Scholar
- T. Kuhl
You can also search for this author in PubMed Google Scholar
- V. Kukhtin
You can also search for this author in PubMed Google Scholar
- R. Kukla
You can also search for this author in PubMed Google Scholar
- Y. Kulchitsky
You can also search for this author in PubMed Google Scholar
- S. Kuleshov
You can also search for this author in PubMed Google Scholar
- Y. P. Kulinich
You can also search for this author in PubMed Google Scholar
- M. Kuna
You can also search for this author in PubMed Google Scholar
- T. Kunigo
You can also search for this author in PubMed Google Scholar
- A. Kupco
You can also search for this author in PubMed Google Scholar
- T. Kupfer
You can also search for this author in PubMed Google Scholar
- O. Kuprash
You can also search for this author in PubMed Google Scholar
- H. Kurashige
You can also search for this author in PubMed Google Scholar
- L. L. Kurchaninov
You can also search for this author in PubMed Google Scholar
- Y. A. Kurochkin
You can also search for this author in PubMed Google Scholar
- M. G. Kurth
You can also search for this author in PubMed Google Scholar
- E. S. Kuwertz
You can also search for this author in PubMed Google Scholar
- M. Kuze
You can also search for this author in PubMed Google Scholar
- J. Kvita
You can also search for this author in PubMed Google Scholar
- T. Kwan
You can also search for this author in PubMed Google Scholar
- D. Kyriazopoulos
You can also search for this author in PubMed Google Scholar
- A. La Rosa
You can also search for this author in PubMed Google Scholar
- J. L. La Rosa Navarro
You can also search for this author in PubMed Google Scholar
- L. La Rotonda
You can also search for this author in PubMed Google Scholar
- F. La Ruffa
You can also search for this author in PubMed Google Scholar
- C. Lacasta
You can also search for this author in PubMed Google Scholar
- F. Lacava
You can also search for this author in PubMed Google Scholar
- J. Lacey
You can also search for this author in PubMed Google Scholar
- D. P. J. Lack
You can also search for this author in PubMed Google Scholar
- H. Lacker
You can also search for this author in PubMed Google Scholar
- D. Lacour
You can also search for this author in PubMed Google Scholar
- E. Ladygin
You can also search for this author in PubMed Google Scholar
- R. Lafaye
You can also search for this author in PubMed Google Scholar
- B. Laforge
You can also search for this author in PubMed Google Scholar
- T. Lagouri
You can also search for this author in PubMed Google Scholar
- S. Lai
You can also search for this author in PubMed Google Scholar
- S. Lammers
You can also search for this author in PubMed Google Scholar
- W. Lampl
You can also search for this author in PubMed Google Scholar
- E. Lançon
You can also search for this author in PubMed Google Scholar
- U. Landgraf
You can also search for this author in PubMed Google Scholar
- M. P. J. Landon
You can also search for this author in PubMed Google Scholar
- M. C. Lanfermann
You can also search for this author in PubMed Google Scholar
- V. S. Lang
You can also search for this author in PubMed Google Scholar
- J. C. Lange
You can also search for this author in PubMed Google Scholar
- R. J. Langenberg
You can also search for this author in PubMed Google Scholar
- A. J. Lankford
You can also search for this author in PubMed Google Scholar
- F. Lanni
You can also search for this author in PubMed Google Scholar
- K. Lantzsch
You can also search for this author in PubMed Google Scholar
- A. Lanza
You can also search for this author in PubMed Google Scholar
- A. Lapertosa
You can also search for this author in PubMed Google Scholar
- S. Laplace
You can also search for this author in PubMed Google Scholar
- J. F. Laporte
You can also search for this author in PubMed Google Scholar
- T. Lari
You can also search for this author in PubMed Google Scholar
- F. Lasagni Manghi
You can also search for this author in PubMed Google Scholar
- M. Lassnig
You can also search for this author in PubMed Google Scholar
- T. S. Lau
You can also search for this author in PubMed Google Scholar
- P. Laurelli
You can also search for this author in PubMed Google Scholar
- W. Lavrijsen
You can also search for this author in PubMed Google Scholar
- A. T. Law
You can also search for this author in PubMed Google Scholar
- P. Laycock
You can also search for this author in PubMed Google Scholar
- T. Lazovich
You can also search for this author in PubMed Google Scholar
- M. Lazzaroni
You can also search for this author in PubMed Google Scholar
- B. Le
You can also search for this author in PubMed Google Scholar
- O. Le Dortz
You can also search for this author in PubMed Google Scholar
- E. Le Guirriec
You can also search for this author in PubMed Google Scholar
- E. P. Le Quilleuc
You can also search for this author in PubMed Google Scholar
- M. LeBlanc
You can also search for this author in PubMed Google Scholar
- T. LeCompte
You can also search for this author in PubMed Google Scholar
- F. Ledroit-Guillon
You can also search for this author in PubMed Google Scholar
- C. A. Lee
You can also search for this author in PubMed Google Scholar
- G. R. Lee
You can also search for this author in PubMed Google Scholar
- S. C. Lee
You can also search for this author in PubMed Google Scholar
- L. Lee
You can also search for this author in PubMed Google Scholar
- B. Lefebvre
You can also search for this author in PubMed Google Scholar
- G. Lefebvre
You can also search for this author in PubMed Google Scholar
- M. Lefebvre
You can also search for this author in PubMed Google Scholar
- F. Legger
You can also search for this author in PubMed Google Scholar
- C. Leggett
You can also search for this author in PubMed Google Scholar
- G. Lehmann Miotto
You can also search for this author in PubMed Google Scholar
- X. Lei
You can also search for this author in PubMed Google Scholar
- W. A. Leight
You can also search for this author in PubMed Google Scholar
- M. A. L. Leite
You can also search for this author in PubMed Google Scholar
- R. Leitner
You can also search for this author in PubMed Google Scholar
- D. Lellouch
You can also search for this author in PubMed Google Scholar
- B. Lemmer
You can also search for this author in PubMed Google Scholar
- K. J. C. Leney
You can also search for this author in PubMed Google Scholar
- T. Lenz
You can also search for this author in PubMed Google Scholar
- B. Lenzi
You can also search for this author in PubMed Google Scholar
- R. Leone
You can also search for this author in PubMed Google Scholar
- S. Leone
You can also search for this author in PubMed Google Scholar
- C. Leonidopoulos
You can also search for this author in PubMed Google Scholar
- G. Lerner
You can also search for this author in PubMed Google Scholar
- C. Leroy
You can also search for this author in PubMed Google Scholar
- R. Les
You can also search for this author in PubMed Google Scholar
- A. A. J. Lesage
You can also search for this author in PubMed Google Scholar
- C. G. Lester
You can also search for this author in PubMed Google Scholar
- M. Levchenko
You can also search for this author in PubMed Google Scholar
- J. Levêque
You can also search for this author in PubMed Google Scholar
- D. Levin
You can also search for this author in PubMed Google Scholar
- L. J. Levinson
You can also search for this author in PubMed Google Scholar
- M. Levy
You can also search for this author in PubMed Google Scholar
- D. Lewis
You can also search for this author in PubMed Google Scholar
- B. Li
You can also search for this author in PubMed Google Scholar
- Changqiao Li
You can also search for this author in PubMed Google Scholar
- H. Li
You can also search for this author in PubMed Google Scholar
- L. Li
You can also search for this author in PubMed Google Scholar
- Q. Li
You can also search for this author in PubMed Google Scholar
- Q. Li
You can also search for this author in PubMed Google Scholar
- S. Li
You can also search for this author in PubMed Google Scholar
- X. Li
You can also search for this author in PubMed Google Scholar
- Y. Li
You can also search for this author in PubMed Google Scholar
- Z. Liang
You can also search for this author in PubMed Google Scholar
- B. Liberti
You can also search for this author in PubMed Google Scholar
- A. Liblong
You can also search for this author in PubMed Google Scholar
- K. Lie
You can also search for this author in PubMed Google Scholar
- J. Liebal
You can also search for this author in PubMed Google Scholar
- W. Liebig
You can also search for this author in PubMed Google Scholar
- A. Limosani
You can also search for this author in PubMed Google Scholar
- K. Lin
You can also search for this author in PubMed Google Scholar
- S. C. Lin
You can also search for this author in PubMed Google Scholar
- T. H. Lin
You can also search for this author in PubMed Google Scholar
- R. A. Linck
You can also search for this author in PubMed Google Scholar
- B. E. Lindquist
You can also search for this author in PubMed Google Scholar
- A. E. Lionti
You can also search for this author in PubMed Google Scholar
- E. Lipeles
You can also search for this author in PubMed Google Scholar
- A. Lipniacka
You can also search for this author in PubMed Google Scholar
- M. Lisovyi
You can also search for this author in PubMed Google Scholar
- T. M. Liss
You can also search for this author in PubMed Google Scholar
- A. Lister
You can also search for this author in PubMed Google Scholar
- A. M. Litke
You can also search for this author in PubMed Google Scholar
- B. Liu
You can also search for this author in PubMed Google Scholar
- H. Liu
You can also search for this author in PubMed Google Scholar
- H. Liu
You can also search for this author in PubMed Google Scholar
- J. K. K. Liu
You can also search for this author in PubMed Google Scholar
- J. Liu
You can also search for this author in PubMed Google Scholar
- J. B. Liu
You can also search for this author in PubMed Google Scholar
- K. Liu
You can also search for this author in PubMed Google Scholar
- L. Liu
You can also search for this author in PubMed Google Scholar
- M. Liu
You can also search for this author in PubMed Google Scholar
- Y. L. Liu
You can also search for this author in PubMed Google Scholar
- Y. Liu
You can also search for this author in PubMed Google Scholar
- M. Livan
You can also search for this author in PubMed Google Scholar
- A. Lleres
You can also search for this author in PubMed Google Scholar
- J. Llorente Merino
You can also search for this author in PubMed Google Scholar
- S. L. Lloyd
You can also search for this author in PubMed Google Scholar
- C. Y. Lo
You can also search for this author in PubMed Google Scholar
- F. Lo Sterzo
You can also search for this author in PubMed Google Scholar
- E. M. Lobodzinska
You can also search for this author in PubMed Google Scholar
- P. Loch
You can also search for this author in PubMed Google Scholar
- F. K. Loebinger
You can also search for this author in PubMed Google Scholar
- A. Loesle
You can also search for this author in PubMed Google Scholar
- K. M. Loew
You can also search for this author in PubMed Google Scholar
- T. Lohse
You can also search for this author in PubMed Google Scholar
- K. Lohwasser
You can also search for this author in PubMed Google Scholar
- M. Lokajicek
You can also search for this author in PubMed Google Scholar
- B. A. Long
You can also search for this author in PubMed Google Scholar
- J. D. Long
You can also search for this author in PubMed Google Scholar
- R. E. Long
You can also search for this author in PubMed Google Scholar
- L. Longo
You can also search for this author in PubMed Google Scholar
- K. A. Looper
You can also search for this author in PubMed Google Scholar
- J. A. Lopez
You can also search for this author in PubMed Google Scholar
- I. Lopez Paz
You can also search for this author in PubMed Google Scholar
- A. Lopez Solis
You can also search for this author in PubMed Google Scholar
- J. Lorenz
You can also search for this author in PubMed Google Scholar
- N. Lorenzo Martinez
You can also search for this author in PubMed Google Scholar
- M. Losada
You can also search for this author in PubMed Google Scholar
- P. J. Lösel
You can also search for this author in PubMed Google Scholar
- X. Lou
You can also search for this author in PubMed Google Scholar
- A. Lounis
You can also search for this author in PubMed Google Scholar
- J. Love
You can also search for this author in PubMed Google Scholar
- P. A. Love
You can also search for this author in PubMed Google Scholar
- H. Lu
You can also search for this author in PubMed Google Scholar
- N. Lu
You can also search for this author in PubMed Google Scholar
- Y. J. Lu
You can also search for this author in PubMed Google Scholar
- H. J. Lubatti
You can also search for this author in PubMed Google Scholar
- C. Luci
You can also search for this author in PubMed Google Scholar
- A. Lucotte
You can also search for this author in PubMed Google Scholar
- C. Luedtke
You can also search for this author in PubMed Google Scholar
- F. Luehring
You can also search for this author in PubMed Google Scholar
- W. Lukas
You can also search for this author in PubMed Google Scholar
- L. Luminari
You can also search for this author in PubMed Google Scholar
- O. Lundberg
You can also search for this author in PubMed Google Scholar
- B. Lund-Jensen
You can also search for this author in PubMed Google Scholar
- M. S. Lutz
You can also search for this author in PubMed Google Scholar
- P. M. Luzi
You can also search for this author in PubMed Google Scholar
- D. Lynn
You can also search for this author in PubMed Google Scholar
- R. Lysak
You can also search for this author in PubMed Google Scholar
- E. Lytken
You can also search for this author in PubMed Google Scholar
- F. Lyu
You can also search for this author in PubMed Google Scholar
- V. Lyubushkin
You can also search for this author in PubMed Google Scholar
- H. Ma
You can also search for this author in PubMed Google Scholar
- L. L. Ma
You can also search for this author in PubMed Google Scholar
- Y. Ma
You can also search for this author in PubMed Google Scholar
- G. Maccarrone
You can also search for this author in PubMed Google Scholar
- A. Macchiolo
You can also search for this author in PubMed Google Scholar
- C. M. Macdonald
You can also search for this author in PubMed Google Scholar
- B. Maček
You can also search for this author in PubMed Google Scholar
- J. Machado Miguens
You can also search for this author in PubMed Google Scholar
- D. Madaffari
You can also search for this author in PubMed Google Scholar
- R. Madar
You can also search for this author in PubMed Google Scholar
- W. F. Mader
You can also search for this author in PubMed Google Scholar
- A. Madsen
You can also search for this author in PubMed Google Scholar
- J. Maeda
You can also search for this author in PubMed Google Scholar
- S. Maeland
You can also search for this author in PubMed Google Scholar
- T. Maeno
You can also search for this author in PubMed Google Scholar
- A. S. Maevskiy
You can also search for this author in PubMed Google Scholar
- V. Magerl
You can also search for this author in PubMed Google Scholar
- C. Maiani
You can also search for this author in PubMed Google Scholar
- C. Maidantchik
You can also search for this author in PubMed Google Scholar
- T. Maier
You can also search for this author in PubMed Google Scholar
- A. Maio
You can also search for this author in PubMed Google Scholar
- O. Majersky
You can also search for this author in PubMed Google Scholar
- S. Majewski
You can also search for this author in PubMed Google Scholar
- Y. Makida
You can also search for this author in PubMed Google Scholar
- N. Makovec
You can also search for this author in PubMed Google Scholar
- B. Malaescu
You can also search for this author in PubMed Google Scholar
- Pa. Malecki
You can also search for this author in PubMed Google Scholar
- V. P. Maleev
You can also search for this author in PubMed Google Scholar
- F. Malek
You can also search for this author in PubMed Google Scholar
- U. Mallik
You can also search for this author in PubMed Google Scholar
- D. Malon
You can also search for this author in PubMed Google Scholar
- C. Malone
You can also search for this author in PubMed Google Scholar
- S. Maltezos
You can also search for this author in PubMed Google Scholar
- S. Malyukov
You can also search for this author in PubMed Google Scholar
- J. Mamuzic
You can also search for this author in PubMed Google Scholar
- G. Mancini
You can also search for this author in PubMed Google Scholar
- I. Mandić
You can also search for this author in PubMed Google Scholar
- J. Maneira
You can also search for this author in PubMed Google Scholar
- L. Manhaes de Andrade Filho
You can also search for this author in PubMed Google Scholar
- J. Manjarres Ramos
You can also search for this author in PubMed Google Scholar
- K. H. Mankinen
You can also search for this author in PubMed Google Scholar
- A. Mann
You can also search for this author in PubMed Google Scholar
- A. Manousos
You can also search for this author in PubMed Google Scholar
- B. Mansoulie
You can also search for this author in PubMed Google Scholar
- J. D. Mansour
You can also search for this author in PubMed Google Scholar
- R. Mantifel
You can also search for this author in PubMed Google Scholar
- M. Mantoani
You can also search for this author in PubMed Google Scholar
- S. Manzoni
You can also search for this author in PubMed Google Scholar
- L. Mapelli
You can also search for this author in PubMed Google Scholar
- G. Marceca
You can also search for this author in PubMed Google Scholar
- L. March
You can also search for this author in PubMed Google Scholar
- L. Marchese
You can also search for this author in PubMed Google Scholar
- G. Marchiori
You can also search for this author in PubMed Google Scholar
- M. Marcisovsky
You can also search for this author in PubMed Google Scholar
- C. A. Marin Tobon
You can also search for this author in PubMed Google Scholar
- M. Marjanovic
You can also search for this author in PubMed Google Scholar
- D. E. Marley
You can also search for this author in PubMed Google Scholar
- F. Marroquim
You can also search for this author in PubMed Google Scholar
- S. P. Marsden
You can also search for this author in PubMed Google Scholar
- Z. Marshall
You can also search for this author in PubMed Google Scholar
- M. U. F Martensson
You can also search for this author in PubMed Google Scholar
- S. Marti-Garcia
You can also search for this author in PubMed Google Scholar
- C. B. Martin
You can also search for this author in PubMed Google Scholar
- T. A. Martin
You can also search for this author in PubMed Google Scholar
- V. J. Martin
You can also search for this author in PubMed Google Scholar
- B. Martin dit Latour
You can also search for this author in PubMed Google Scholar
- M. Martinez
You can also search for this author in PubMed Google Scholar
- V. I. Martinez Outschoorn
You can also search for this author in PubMed Google Scholar
- S. Martin-Haugh
You can also search for this author in PubMed Google Scholar
- V. S. Martoiu
You can also search for this author in PubMed Google Scholar
- A. C. Martyniuk
You can also search for this author in PubMed Google Scholar
- A. Marzin
You can also search for this author in PubMed Google Scholar
- L. Masetti
You can also search for this author in PubMed Google Scholar
- T. Mashimo
You can also search for this author in PubMed Google Scholar
- R. Mashinistov
You can also search for this author in PubMed Google Scholar
- J. Masik
You can also search for this author in PubMed Google Scholar
- A. L. Maslennikov
You can also search for this author in PubMed Google Scholar
- L. H. Mason
You can also search for this author in PubMed Google Scholar
- L. Massa
You can also search for this author in PubMed Google Scholar
- P. Mastrandrea
You can also search for this author in PubMed Google Scholar
- A. Mastroberardino
You can also search for this author in PubMed Google Scholar
- T. Masubuchi
You can also search for this author in PubMed Google Scholar
- P. Mättig
You can also search for this author in PubMed Google Scholar
- J. Maurer
You can also search for this author in PubMed Google Scholar
- S. J. Maxfield
You can also search for this author in PubMed Google Scholar
- D. A. Maximov
You can also search for this author in PubMed Google Scholar
- R. Mazini
You can also search for this author in PubMed Google Scholar
- I. Maznas
You can also search for this author in PubMed Google Scholar
- S. M. Mazza
You can also search for this author in PubMed Google Scholar
- N. C. Mc Fadden
You can also search for this author in PubMed Google Scholar
- G. Mc Goldrick
You can also search for this author in PubMed Google Scholar
- S. P. Mc Kee
You can also search for this author in PubMed Google Scholar
- A. McCarn
You can also search for this author in PubMed Google Scholar
- R. L. McCarthy
You can also search for this author in PubMed Google Scholar
- T. G. McCarthy
You can also search for this author in PubMed Google Scholar
- L. I. McClymont
You can also search for this author in PubMed Google Scholar
- E. F. McDonald
You can also search for this author in PubMed Google Scholar
- J. A. Mcfayden
You can also search for this author in PubMed Google Scholar
- G. Mchedlidze
You can also search for this author in PubMed Google Scholar
- S. J. McMahon
You can also search for this author in PubMed Google Scholar
- P. C. McNamara
You can also search for this author in PubMed Google Scholar
- C. J. McNicol
You can also search for this author in PubMed Google Scholar
- R. A. McPherson
You can also search for this author in PubMed Google Scholar
- S. Meehan
You can also search for this author in PubMed Google Scholar
- T. J. Megy
You can also search for this author in PubMed Google Scholar
- S. Mehlhase
You can also search for this author in PubMed Google Scholar
- A. Mehta
You can also search for this author in PubMed Google Scholar
- T. Meideck
You can also search for this author in PubMed Google Scholar
- K. Meier
You can also search for this author in PubMed Google Scholar
- B. Meirose
You can also search for this author in PubMed Google Scholar
- D. Melini
You can also search for this author in PubMed Google Scholar
- B. R. Mellado Garcia
You can also search for this author in PubMed Google Scholar
- J. D. Mellenthin
You can also search for this author in PubMed Google Scholar
- M. Melo
You can also search for this author in PubMed Google Scholar
- F. Meloni
You can also search for this author in PubMed Google Scholar
- A. Melzer
You can also search for this author in PubMed Google Scholar
- S. B. Menary
You can also search for this author in PubMed Google Scholar
- L. Meng
You can also search for this author in PubMed Google Scholar
- X. T. Meng
You can also search for this author in PubMed Google Scholar
- A. Mengarelli
You can also search for this author in PubMed Google Scholar
- S. Menke
You can also search for this author in PubMed Google Scholar
- E. Meoni
You can also search for this author in PubMed Google Scholar
- S. Mergelmeyer
You can also search for this author in PubMed Google Scholar
- C. Merlassino
You can also search for this author in PubMed Google Scholar
- P. Mermod
You can also search for this author in PubMed Google Scholar
- L. Merola
You can also search for this author in PubMed Google Scholar
- C. Meroni
You can also search for this author in PubMed Google Scholar
- F. S. Merritt
You can also search for this author in PubMed Google Scholar
- A. Messina
You can also search for this author in PubMed Google Scholar
- J. Metcalfe
You can also search for this author in PubMed Google Scholar
- A. S. Mete
You can also search for this author in PubMed Google Scholar
- C. Meyer
You can also search for this author in PubMed Google Scholar
- J-P. Meyer
You can also search for this author in PubMed Google Scholar
- J. Meyer
You can also search for this author in PubMed Google Scholar
- H. Meyer Zu Theenhausen
You can also search for this author in PubMed Google Scholar
- F. Miano
You can also search for this author in PubMed Google Scholar
- R. P. Middleton
You can also search for this author in PubMed Google Scholar
- S. Miglioranzi
You can also search for this author in PubMed Google Scholar
- L. Mijović
You can also search for this author in PubMed Google Scholar
- G. Mikenberg
You can also search for this author in PubMed Google Scholar
- M. Mikestikova
You can also search for this author in PubMed Google Scholar
- M. Mikuž
You can also search for this author in PubMed Google Scholar
- M. Milesi
You can also search for this author in PubMed Google Scholar
- A. Milic
You can also search for this author in PubMed Google Scholar
- D. A. Millar
You can also search for this author in PubMed Google Scholar
- D. W. Miller
You can also search for this author in PubMed Google Scholar
- C. Mills
You can also search for this author in PubMed Google Scholar
- A. Milov
You can also search for this author in PubMed Google Scholar
- D. A. Milstead
You can also search for this author in PubMed Google Scholar
- A. A. Minaenko
You can also search for this author in PubMed Google Scholar
- Y. Minami
You can also search for this author in PubMed Google Scholar
- I. A. Minashvili
You can also search for this author in PubMed Google Scholar
- A. I. Mincer
You can also search for this author in PubMed Google Scholar
- B. Mindur
You can also search for this author in PubMed Google Scholar
- M. Mineev
You can also search for this author in PubMed Google Scholar
- Y. Minegishi
You can also search for this author in PubMed Google Scholar
- Y. Ming
You can also search for this author in PubMed Google Scholar
- L. M. Mir
You can also search for this author in PubMed Google Scholar
- A. Mirto
You can also search for this author in PubMed Google Scholar
- K. P. Mistry
You can also search for this author in PubMed Google Scholar
- T. Mitani
You can also search for this author in PubMed Google Scholar
- J. Mitrevski
You can also search for this author in PubMed Google Scholar
- V. A. Mitsou
You can also search for this author in PubMed Google Scholar
- A. Miucci
You can also search for this author in PubMed Google Scholar
- P. S. Miyagawa
You can also search for this author in PubMed Google Scholar
- A. Mizukami
You can also search for this author in PubMed Google Scholar
- J. U. Mjörnmark
You can also search for this author in PubMed Google Scholar
- T. Mkrtchyan
You can also search for this author in PubMed Google Scholar
- M. Mlynarikova
You can also search for this author in PubMed Google Scholar
- T. Moa
You can also search for this author in PubMed Google Scholar
- K. Mochizuki
You can also search for this author in PubMed Google Scholar
- P. Mogg
You can also search for this author in PubMed Google Scholar
- S. Mohapatra
You can also search for this author in PubMed Google Scholar
- S. Molander
You can also search for this author in PubMed Google Scholar
- R. Moles-Valls
You can also search for this author in PubMed Google Scholar
- M. C. Mondragon
You can also search for this author in PubMed Google Scholar
- K. Mönig
You can also search for this author in PubMed Google Scholar
- J. Monk
You can also search for this author in PubMed Google Scholar
- E. Monnier
You can also search for this author in PubMed Google Scholar
- A. Montalbano
You can also search for this author in PubMed Google Scholar
- J. Montejo Berlingen
You can also search for this author in PubMed Google Scholar
- F. Monticelli
You can also search for this author in PubMed Google Scholar
- S. Monzani
You can also search for this author in PubMed Google Scholar
- R. W. Moore
You can also search for this author in PubMed Google Scholar
- N. Morange
You can also search for this author in PubMed Google Scholar
- D. Moreno
You can also search for this author in PubMed Google Scholar
- M. Moreno Llácer
You can also search for this author in PubMed Google Scholar
- P. Morettini
You can also search for this author in PubMed Google Scholar
- S. Morgenstern
You can also search for this author in PubMed Google Scholar
- D. Mori
You can also search for this author in PubMed Google Scholar
- T. Mori
You can also search for this author in PubMed Google Scholar
- M. Morii
You can also search for this author in PubMed Google Scholar
- M. Morinaga
You can also search for this author in PubMed Google Scholar
- V. Morisbak
You can also search for this author in PubMed Google Scholar
- A. K. Morley
You can also search for this author in PubMed Google Scholar
- G. Mornacchi
You can also search for this author in PubMed Google Scholar
- J. D. Morris
You can also search for this author in PubMed Google Scholar
- L. Morvaj
You can also search for this author in PubMed Google Scholar
- P. Moschovakos
You can also search for this author in PubMed Google Scholar
- M. Mosidze
You can also search for this author in PubMed Google Scholar
- H. J. Moss
You can also search for this author in PubMed Google Scholar
- J. Moss
You can also search for this author in PubMed Google Scholar
- K. Motohashi
You can also search for this author in PubMed Google Scholar
- R. Mount
You can also search for this author in PubMed Google Scholar
- E. Mountricha
You can also search for this author in PubMed Google Scholar
- E. J. W. Moyse
You can also search for this author in PubMed Google Scholar
- S. Muanza
You can also search for this author in PubMed Google Scholar
- F. Mueller
You can also search for this author in PubMed Google Scholar
- J. Mueller
You can also search for this author in PubMed Google Scholar
- R. S. P. Mueller
You can also search for this author in PubMed Google Scholar
- D. Muenstermann
You can also search for this author in PubMed Google Scholar
- P. Mullen
You can also search for this author in PubMed Google Scholar
- G. A. Mullier
You can also search for this author in PubMed Google Scholar
- F. J. Munoz Sanchez
You can also search for this author in PubMed Google Scholar
- W. J. Murray
You can also search for this author in PubMed Google Scholar
- H. Musheghyan
You can also search for this author in PubMed Google Scholar
- M. Muškinja
You can also search for this author in PubMed Google Scholar
- A. G. Myagkov
You can also search for this author in PubMed Google Scholar
- M. Myska
You can also search for this author in PubMed Google Scholar
- B. P. Nachman
You can also search for this author in PubMed Google Scholar
- O. Nackenhorst
You can also search for this author in PubMed Google Scholar
- K. Nagai
You can also search for this author in PubMed Google Scholar
- R. Nagai
You can also search for this author in PubMed Google Scholar
- K. Nagano
You can also search for this author in PubMed Google Scholar
- Y. Nagasaka
You can also search for this author in PubMed Google Scholar
- K. Nagata
You can also search for this author in PubMed Google Scholar
- M. Nagel
You can also search for this author in PubMed Google Scholar
- E. Nagy
You can also search for this author in PubMed Google Scholar
- A. M. Nairz
You can also search for this author in PubMed Google Scholar
- Y. Nakahama
You can also search for this author in PubMed Google Scholar
- K. Nakamura
You can also search for this author in PubMed Google Scholar
- T. Nakamura
You can also search for this author in PubMed Google Scholar
- I. Nakano
You can also search for this author in PubMed Google Scholar
- R. F. Naranjo Garcia
You can also search for this author in PubMed Google Scholar
- R. Narayan
You can also search for this author in PubMed Google Scholar
- D. I. Narrias Villar
You can also search for this author in PubMed Google Scholar
- I. Naryshkin
You can also search for this author in PubMed Google Scholar
- T. Naumann
You can also search for this author in PubMed Google Scholar
- G. Navarro
You can also search for this author in PubMed Google Scholar
- R. Nayyar
You can also search for this author in PubMed Google Scholar
- H. A. Neal
You can also search for this author in PubMed Google Scholar
- P. Yu. Nechaeva
You can also search for this author in PubMed Google Scholar
- T. J. Neep
You can also search for this author in PubMed Google Scholar
- A. Negri
You can also search for this author in PubMed Google Scholar
- M. Negrini
You can also search for this author in PubMed Google Scholar
- S. Nektarijevic
You can also search for this author in PubMed Google Scholar
- C. Nellist
You can also search for this author in PubMed Google Scholar
- A. Nelson
You can also search for this author in PubMed Google Scholar
- M. E. Nelson
You can also search for this author in PubMed Google Scholar
- S. Nemecek
You can also search for this author in PubMed Google Scholar
- P. Nemethy
You can also search for this author in PubMed Google Scholar
- M. Nessi
You can also search for this author in PubMed Google Scholar
- M. S. Neubauer
You can also search for this author in PubMed Google Scholar
- M. Neumann
You can also search for this author in PubMed Google Scholar
- P. R. Newman
You can also search for this author in PubMed Google Scholar
- T. Y. Ng
You can also search for this author in PubMed Google Scholar
- T. Nguyen Manh
You can also search for this author in PubMed Google Scholar
- R. B. Nickerson
You can also search for this author in PubMed Google Scholar
- R. Nicolaidou
You can also search for this author in PubMed Google Scholar
- J. Nielsen
You can also search for this author in PubMed Google Scholar
- N. Nikiforou
You can also search for this author in PubMed Google Scholar
- V. Nikolaenko
You can also search for this author in PubMed Google Scholar
- I. Nikolic-Audit
You can also search for this author in PubMed Google Scholar
- K. Nikolopoulos
You can also search for this author in PubMed Google Scholar
- J. K. Nilsen
You can also search for this author in PubMed Google Scholar
- P. Nilsson
You can also search for this author in PubMed Google Scholar
- Y. Ninomiya
You can also search for this author in PubMed Google Scholar
- A. Nisati
You can also search for this author in PubMed Google Scholar
- N. Nishu
You can also search for this author in PubMed Google Scholar
- R. Nisius
You can also search for this author in PubMed Google Scholar
- I. Nitsche
You can also search for this author in PubMed Google Scholar
- T. Nitta
You can also search for this author in PubMed Google Scholar
- T. Nobe
You can also search for this author in PubMed Google Scholar
- Y. Noguchi
You can also search for this author in PubMed Google Scholar
- M. Nomachi
You can also search for this author in PubMed Google Scholar
- I. Nomidis
You can also search for this author in PubMed Google Scholar
- M. A. Nomura
You can also search for this author in PubMed Google Scholar
- T. Nooney
You can also search for this author in PubMed Google Scholar
- M. Nordberg
You can also search for this author in PubMed Google Scholar
- N. Norjoharuddeen
You can also search for this author in PubMed Google Scholar
- O. Novgorodova
You can also search for this author in PubMed Google Scholar
- M. Nozaki
You can also search for this author in PubMed Google Scholar
- L. Nozka
You can also search for this author in PubMed Google Scholar
- K. Ntekas
You can also search for this author in PubMed Google Scholar
- E. Nurse
You can also search for this author in PubMed Google Scholar
- F. Nuti
You can also search for this author in PubMed Google Scholar
- K. O’connor
You can also search for this author in PubMed Google Scholar
- D. C. O’Neil
You can also search for this author in PubMed Google Scholar
- A. A. O’Rourke
You can also search for this author in PubMed Google Scholar
- V. O’Shea
You can also search for this author in PubMed Google Scholar
- F. G. Oakham
You can also search for this author in PubMed Google Scholar
- H. Oberlack
You can also search for this author in PubMed Google Scholar
- T. Obermann
You can also search for this author in PubMed Google Scholar
- J. Ocariz
You can also search for this author in PubMed Google Scholar
- A. Ochi
You can also search for this author in PubMed Google Scholar
- I. Ochoa
You can also search for this author in PubMed Google Scholar
- J. P. Ochoa-Ricoux
You can also search for this author in PubMed Google Scholar
- S. Oda
You can also search for this author in PubMed Google Scholar
- S. Odaka
You can also search for this author in PubMed Google Scholar
- A. Oh
You can also search for this author in PubMed Google Scholar
- S. H. Oh
You can also search for this author in PubMed Google Scholar
- C. C. Ohm
You can also search for this author in PubMed Google Scholar
- H. Ohman
You can also search for this author in PubMed Google Scholar
- H. Oide
You can also search for this author in PubMed Google Scholar
- H. Okawa
You can also search for this author in PubMed Google Scholar
- Y. Okumura
You can also search for this author in PubMed Google Scholar
- T. Okuyama
You can also search for this author in PubMed Google Scholar
- A. Olariu
You can also search for this author in PubMed Google Scholar
- L. F. Oleiro Seabra
You can also search for this author in PubMed Google Scholar
- S. A. Olivares Pino
You can also search for this author in PubMed Google Scholar
- D. Oliveira Damazio
You can also search for this author in PubMed Google Scholar
- A. Olszewski
You can also search for this author in PubMed Google Scholar
- J. Olszowska
You can also search for this author in PubMed Google Scholar
- A. Onofre
You can also search for this author in PubMed Google Scholar
- K. Onogi
You can also search for this author in PubMed Google Scholar
- P. U. E. Onyisi
You can also search for this author in PubMed Google Scholar
- H. Oppen
You can also search for this author in PubMed Google Scholar
- M. J. Oreglia
You can also search for this author in PubMed Google Scholar
- Y. Oren
You can also search for this author in PubMed Google Scholar
- D. Orestano
You can also search for this author in PubMed Google Scholar
- N. Orlando
You can also search for this author in PubMed Google Scholar
- R. S. Orr
You can also search for this author in PubMed Google Scholar
- B. Osculati
You can also search for this author in PubMed Google Scholar
- R. Ospanov
You can also search for this author in PubMed Google Scholar
- G. Otero y Garzon
You can also search for this author in PubMed Google Scholar
- H. Otono
You can also search for this author in PubMed Google Scholar
- M. Ouchrif
You can also search for this author in PubMed Google Scholar
- F. Ould-Saada
You can also search for this author in PubMed Google Scholar
- A. Ouraou
You can also search for this author in PubMed Google Scholar
- K. P. Oussoren
You can also search for this author in PubMed Google Scholar
- Q. Ouyang
You can also search for this author in PubMed Google Scholar
- M. Owen
You can also search for this author in PubMed Google Scholar
- R. E. Owen
You can also search for this author in PubMed Google Scholar
- V. E. Ozcan
You can also search for this author in PubMed Google Scholar
- N. Ozturk
You can also search for this author in PubMed Google Scholar
- K. Pachal
You can also search for this author in PubMed Google Scholar
- A. Pacheco Pages
You can also search for this author in PubMed Google Scholar
- L. Pacheco Rodriguez
You can also search for this author in PubMed Google Scholar
- C. Padilla Aranda
You can also search for this author in PubMed Google Scholar
- S. Pagan Griso
You can also search for this author in PubMed Google Scholar
- M. Paganini
You can also search for this author in PubMed Google Scholar
- F. Paige
You can also search for this author in PubMed Google Scholar
- G. Palacino
You can also search for this author in PubMed Google Scholar
- S. Palazzo
You can also search for this author in PubMed Google Scholar
- S. Palestini
You can also search for this author in PubMed Google Scholar
- M. Palka
You can also search for this author in PubMed Google Scholar
- D. Pallin
You can also search for this author in PubMed Google Scholar
- E. St. Panagiotopoulou
You can also search for this author in PubMed Google Scholar
- I. Panagoulias
You can also search for this author in PubMed Google Scholar
- C. E. Pandini
You can also search for this author in PubMed Google Scholar
- J. G. Panduro Vazquez
You can also search for this author in PubMed Google Scholar
- P. Pani
You can also search for this author in PubMed Google Scholar
- S. Panitkin
You can also search for this author in PubMed Google Scholar
- D. Pantea
You can also search for this author in PubMed Google Scholar
- L. Paolozzi
You can also search for this author in PubMed Google Scholar
- Th. D. Papadopoulou
You can also search for this author in PubMed Google Scholar
- K. Papageorgiou
You can also search for this author in PubMed Google Scholar
- A. Paramonov
You can also search for this author in PubMed Google Scholar
- D. Paredes Hernandez
You can also search for this author in PubMed Google Scholar
- A. J. Parker
You can also search for this author in PubMed Google Scholar
- M. A. Parker
You can also search for this author in PubMed Google Scholar
- K. A. Parker
You can also search for this author in PubMed Google Scholar
- F. Parodi
You can also search for this author in PubMed Google Scholar
- J. A. Parsons
You can also search for this author in PubMed Google Scholar
- U. Parzefall
You can also search for this author in PubMed Google Scholar
- V. R. Pascuzzi
You can also search for this author in PubMed Google Scholar
- J. M. Pasner
You can also search for this author in PubMed Google Scholar
- E. Pasqualucci
You can also search for this author in PubMed Google Scholar
- S. Passaggio
You can also search for this author in PubMed Google Scholar
- Fr. Pastore
You can also search for this author in PubMed Google Scholar
- S. Pataraia
You can also search for this author in PubMed Google Scholar
- J. R. Pater
You can also search for this author in PubMed Google Scholar
- T. Pauly
You can also search for this author in PubMed Google Scholar
- B. Pearson
You can also search for this author in PubMed Google Scholar
- S. Pedraza Lopez
You can also search for this author in PubMed Google Scholar
- R. Pedro
You can also search for this author in PubMed Google Scholar
- S. V. Peleganchuk
You can also search for this author in PubMed Google Scholar
- O. Penc
You can also search for this author in PubMed Google Scholar
- C. Peng
You can also search for this author in PubMed Google Scholar
- H. Peng
You can also search for this author in PubMed Google Scholar
- J. Penwell
You can also search for this author in PubMed Google Scholar
- B. S. Peralva
You can also search for this author in PubMed Google Scholar
- M. M. Perego
You can also search for this author in PubMed Google Scholar
- D. V. Perepelitsa
You can also search for this author in PubMed Google Scholar
- F. Peri
You can also search for this author in PubMed Google Scholar
- L. Perini
You can also search for this author in PubMed Google Scholar
- H. Pernegger
You can also search for this author in PubMed Google Scholar
- S. Perrella
You can also search for this author in PubMed Google Scholar
- R. Peschke
You can also search for this author in PubMed Google Scholar
- V. D. Peshekhonov
You can also search for this author in PubMed Google Scholar
- K. Peters
You can also search for this author in PubMed Google Scholar
- R. F. Y. Peters
You can also search for this author in PubMed Google Scholar
- B. A. Petersen
You can also search for this author in PubMed Google Scholar
- T. C. Petersen
You can also search for this author in PubMed Google Scholar
- E. Petit
You can also search for this author in PubMed Google Scholar
- A. Petridis
You can also search for this author in PubMed Google Scholar
- C. Petridou
You can also search for this author in PubMed Google Scholar
- P. Petroff
You can also search for this author in PubMed Google Scholar
- E. Petrolo
You can also search for this author in PubMed Google Scholar
- M. Petrov
You can also search for this author in PubMed Google Scholar
- F. Petrucci
You can also search for this author in PubMed Google Scholar
- N. E. Pettersson
You can also search for this author in PubMed Google Scholar
- A. Peyaud
You can also search for this author in PubMed Google Scholar
- R. Pezoa
You can also search for this author in PubMed Google Scholar
- F. H. Phillips
You can also search for this author in PubMed Google Scholar
- P. W. Phillips
You can also search for this author in PubMed Google Scholar
- G. Piacquadio
You can also search for this author in PubMed Google Scholar
- E. Pianori
You can also search for this author in PubMed Google Scholar
- A. Picazio
You can also search for this author in PubMed Google Scholar
- E. Piccaro
You can also search for this author in PubMed Google Scholar
- M. A. Pickering
You can also search for this author in PubMed Google Scholar
- R. Piegaia
You can also search for this author in PubMed Google Scholar
- J. E. Pilcher
You can also search for this author in PubMed Google Scholar
- A. D. Pilkington
You can also search for this author in PubMed Google Scholar
- M. Pinamonti
You can also search for this author in PubMed Google Scholar
- J. L. Pinfold
You can also search for this author in PubMed Google Scholar
- H. Pirumov
You can also search for this author in PubMed Google Scholar
- M. Pitt
You can also search for this author in PubMed Google Scholar
- L. Plazak
You can also search for this author in PubMed Google Scholar
- M.-A. Pleier
You can also search for this author in PubMed Google Scholar
- V. Pleskot
You can also search for this author in PubMed Google Scholar
- E. Plotnikova
You can also search for this author in PubMed Google Scholar
- D. Pluth
You can also search for this author in PubMed Google Scholar
- P. Podberezko
You can also search for this author in PubMed Google Scholar
- R. Poettgen
You can also search for this author in PubMed Google Scholar
- R. Poggi
You can also search for this author in PubMed Google Scholar
- L. Poggioli
You can also search for this author in PubMed Google Scholar
- I. Pogrebnyak
You can also search for this author in PubMed Google Scholar
- D. Pohl
You can also search for this author in PubMed Google Scholar
- I. Pokharel
You can also search for this author in PubMed Google Scholar
- G. Polesello
You can also search for this author in PubMed Google Scholar
- A. Poley
You can also search for this author in PubMed Google Scholar
- A. Policicchio
You can also search for this author in PubMed Google Scholar
- R. Polifka
You can also search for this author in PubMed Google Scholar
- A. Polini
You can also search for this author in PubMed Google Scholar
- C. S. Pollard
You can also search for this author in PubMed Google Scholar
- V. Polychronakos
You can also search for this author in PubMed Google Scholar
- K. Pommès
You can also search for this author in PubMed Google Scholar
- D. Ponomarenko
You can also search for this author in PubMed Google Scholar
- L. Pontecorvo
You can also search for this author in PubMed Google Scholar
- G. A. Popeneciu
You can also search for this author in PubMed Google Scholar
- D. M. Portillo Quintero
You can also search for this author in PubMed Google Scholar
- S. Pospisil
You can also search for this author in PubMed Google Scholar
- K. Potamianos
You can also search for this author in PubMed Google Scholar
- I. N. Potrap
You can also search for this author in PubMed Google Scholar
- C. J. Potter
You can also search for this author in PubMed Google Scholar
- H. Potti
You can also search for this author in PubMed Google Scholar
- T. Poulsen
You can also search for this author in PubMed Google Scholar
- J. Poveda
You can also search for this author in PubMed Google Scholar
- M. E. Pozo Astigarraga
You can also search for this author in PubMed Google Scholar
- P. Pralavorio
You can also search for this author in PubMed Google Scholar
- A. Pranko
You can also search for this author in PubMed Google Scholar
- S. Prell
You can also search for this author in PubMed Google Scholar
- D. Price
You can also search for this author in PubMed Google Scholar
- M. Primavera
You can also search for this author in PubMed Google Scholar
- S. Prince
You can also search for this author in PubMed Google Scholar
- N. Proklova
You can also search for this author in PubMed Google Scholar
- K. Prokofiev
You can also search for this author in PubMed Google Scholar
- F. Prokoshin
You can also search for this author in PubMed Google Scholar
- S. Protopopescu
You can also search for this author in PubMed Google Scholar
- J. Proudfoot
You can also search for this author in PubMed Google Scholar
- M. Przybycien
You can also search for this author in PubMed Google Scholar
- A. Puri
You can also search for this author in PubMed Google Scholar
- P. Puzo
You can also search for this author in PubMed Google Scholar
- J. Qian
You can also search for this author in PubMed Google Scholar
- G. Qin
You can also search for this author in PubMed Google Scholar
- Y. Qin
You can also search for this author in PubMed Google Scholar
- A. Quadt
You can also search for this author in PubMed Google Scholar
- M. Queitsch-Maitland
You can also search for this author in PubMed Google Scholar
- D. Quilty
You can also search for this author in PubMed Google Scholar
- S. Raddum
You can also search for this author in PubMed Google Scholar
- V. Radeka
You can also search for this author in PubMed Google Scholar
- V. Radescu
You can also search for this author in PubMed Google Scholar
- S. K. Radhakrishnan
You can also search for this author in PubMed Google Scholar
- P. Radloff
You can also search for this author in PubMed Google Scholar
- P. Rados
You can also search for this author in PubMed Google Scholar
- F. Ragusa
You can also search for this author in PubMed Google Scholar
- G. Rahal
You can also search for this author in PubMed Google Scholar
- J. A. Raine
You can also search for this author in PubMed Google Scholar
- S. Rajagopalan
You can also search for this author in PubMed Google Scholar
- C. Rangel-Smith
You can also search for this author in PubMed Google Scholar
- T. Rashid
You can also search for this author in PubMed Google Scholar
- S. Raspopov
You can also search for this author in PubMed Google Scholar
- M. G. Ratti
You can also search for this author in PubMed Google Scholar
- D. M. Rauch
You can also search for this author in PubMed Google Scholar
- F. Rauscher
You can also search for this author in PubMed Google Scholar
- S. Rave
You can also search for this author in PubMed Google Scholar
- I. Ravinovich
You can also search for this author in PubMed Google Scholar
- J. H. Rawling
You can also search for this author in PubMed Google Scholar
- M. Raymond
You can also search for this author in PubMed Google Scholar
- A. L. Read
You can also search for this author in PubMed Google Scholar
- N. P. Readioff
You can also search for this author in PubMed Google Scholar
- M. Reale
You can also search for this author in PubMed Google Scholar
- D. M. Rebuzzi
You can also search for this author in PubMed Google Scholar
- A. Redelbach
You can also search for this author in PubMed Google Scholar
- G. Redlinger
You can also search for this author in PubMed Google Scholar
- R. Reece
You can also search for this author in PubMed Google Scholar
- R. G. Reed
You can also search for this author in PubMed Google Scholar
- K. Reeves
You can also search for this author in PubMed Google Scholar
- L. Rehnisch
You can also search for this author in PubMed Google Scholar
- J. Reichert
You can also search for this author in PubMed Google Scholar
- A. Reiss
You can also search for this author in PubMed Google Scholar
- C. Rembser
You can also search for this author in PubMed Google Scholar
- H. Ren
You can also search for this author in PubMed Google Scholar
- M. Rescigno
You can also search for this author in PubMed Google Scholar
- S. Resconi
You can also search for this author in PubMed Google Scholar
- E. D. Resseguie
You can also search for this author in PubMed Google Scholar
- S. Rettie
You can also search for this author in PubMed Google Scholar
- E. Reynolds
You can also search for this author in PubMed Google Scholar
- O. L. Rezanova
You can also search for this author in PubMed Google Scholar
- P. Reznicek
You can also search for this author in PubMed Google Scholar
- R. Rezvani
You can also search for this author in PubMed Google Scholar
- R. Richter
You can also search for this author in PubMed Google Scholar
- S. Richter
You can also search for this author in PubMed Google Scholar
- E. Richter-Was
You can also search for this author in PubMed Google Scholar
- O. Ricken
You can also search for this author in PubMed Google Scholar
- M. Ridel
You can also search for this author in PubMed Google Scholar
- P. Rieck
You can also search for this author in PubMed Google Scholar
- C. J. Riegel
You can also search for this author in PubMed Google Scholar
- J. Rieger
You can also search for this author in PubMed Google Scholar
- O. Rifki
You can also search for this author in PubMed Google Scholar
- M. Rijssenbeek
You can also search for this author in PubMed Google Scholar
- A. Rimoldi
You can also search for this author in PubMed Google Scholar
- M. Rimoldi
You can also search for this author in PubMed Google Scholar
- L. Rinaldi
You can also search for this author in PubMed Google Scholar
- G. Ripellino
You can also search for this author in PubMed Google Scholar
- B. Ristić
You can also search for this author in PubMed Google Scholar
- E. Ritsch
You can also search for this author in PubMed Google Scholar
- I. Riu
You can also search for this author in PubMed Google Scholar
- F. Rizatdinova
You can also search for this author in PubMed Google Scholar
- E. Rizvi
You can also search for this author in PubMed Google Scholar
- C. Rizzi
You can also search for this author in PubMed Google Scholar
- R. T. Roberts
You can also search for this author in PubMed Google Scholar
- S. H. Robertson
You can also search for this author in PubMed Google Scholar
- A. Robichaud-Veronneau
You can also search for this author in PubMed Google Scholar
- D. Robinson
You can also search for this author in PubMed Google Scholar
- J. E. M. Robinson
You can also search for this author in PubMed Google Scholar
- A. Robson
You can also search for this author in PubMed Google Scholar
- E. Rocco
You can also search for this author in PubMed Google Scholar
- C. Roda
You can also search for this author in PubMed Google Scholar
- Y. Rodina
You can also search for this author in PubMed Google Scholar
- S. Rodriguez Bosca
You can also search for this author in PubMed Google Scholar
- A. Rodriguez Perez
You can also search for this author in PubMed Google Scholar
- D. Rodriguez Rodriguez
You can also search for this author in PubMed Google Scholar
- S. Roe
You can also search for this author in PubMed Google Scholar
- C. S. Rogan
You can also search for this author in PubMed Google Scholar
- O. Røhne
You can also search for this author in PubMed Google Scholar
- J. Roloff
You can also search for this author in PubMed Google Scholar
- A. Romaniouk
You can also search for this author in PubMed Google Scholar
- M. Romano
You can also search for this author in PubMed Google Scholar
- S. M. Romano Saez
You can also search for this author in PubMed Google Scholar
- E. Romero Adam
You can also search for this author in PubMed Google Scholar
- N. Rompotis
You can also search for this author in PubMed Google Scholar
- M. Ronzani
You can also search for this author in PubMed Google Scholar
- L. Roos
You can also search for this author in PubMed Google Scholar
- S. Rosati
You can also search for this author in PubMed Google Scholar
- K. Rosbach
You can also search for this author in PubMed Google Scholar
- P. Rose
You can also search for this author in PubMed Google Scholar
- N.-A. Rosien
You can also search for this author in PubMed Google Scholar
- E. Rossi
You can also search for this author in PubMed Google Scholar
- L. P. Rossi
You can also search for this author in PubMed Google Scholar
- J. H. N. Rosten
You can also search for this author in PubMed Google Scholar
- R. Rosten
You can also search for this author in PubMed Google Scholar
- M. Rotaru
You can also search for this author in PubMed Google Scholar
- J. Rothberg
You can also search for this author in PubMed Google Scholar
- D. Rousseau
You can also search for this author in PubMed Google Scholar
- A. Rozanov
You can also search for this author in PubMed Google Scholar
- Y. Rozen
You can also search for this author in PubMed Google Scholar
- X. Ruan
You can also search for this author in PubMed Google Scholar
- F. Rubbo
You can also search for this author in PubMed Google Scholar
- F. Rühr
You can also search for this author in PubMed Google Scholar
- A. Ruiz-Martinez
You can also search for this author in PubMed Google Scholar
- Z. Rurikova
You can also search for this author in PubMed Google Scholar
- N. A. Rusakovich
You can also search for this author in PubMed Google Scholar
- H. L. Russell
You can also search for this author in PubMed Google Scholar
- J. P. Rutherfoord
You can also search for this author in PubMed Google Scholar
- N. Ruthmann
You can also search for this author in PubMed Google Scholar
- Y. F. Ryabov
You can also search for this author in PubMed Google Scholar
- M. Rybar
You can also search for this author in PubMed Google Scholar
- G. Rybkin
You can also search for this author in PubMed Google Scholar
- S. Ryu
You can also search for this author in PubMed Google Scholar
- A. Ryzhov
You can also search for this author in PubMed Google Scholar
- G. F. Rzehorz
You can also search for this author in PubMed Google Scholar
- A. F. Saavedra
You can also search for this author in PubMed Google Scholar
- G. Sabato
You can also search for this author in PubMed Google Scholar
- S. Sacerdoti
You can also search for this author in PubMed Google Scholar
- H. F-W. Sadrozinski
You can also search for this author in PubMed Google Scholar
- R. Sadykov
You can also search for this author in PubMed Google Scholar
- F. Safai Tehrani
You can also search for this author in PubMed Google Scholar
- P. Saha
You can also search for this author in PubMed Google Scholar
- M. Sahinsoy
You can also search for this author in PubMed Google Scholar
- M. Saimpert
You can also search for this author in PubMed Google Scholar
- M. Saito
You can also search for this author in PubMed Google Scholar
- T. Saito
You can also search for this author in PubMed Google Scholar
- H. Sakamoto
You can also search for this author in PubMed Google Scholar
- Y. Sakurai
You can also search for this author in PubMed Google Scholar
- G. Salamanna
You can also search for this author in PubMed Google Scholar
- J. E. Salazar Loyola
You can also search for this author in PubMed Google Scholar
- D. Salek
You can also search for this author in PubMed Google Scholar
- P. H. Sales De Bruin
You can also search for this author in PubMed Google Scholar
- D. Salihagic
You can also search for this author in PubMed Google Scholar
- A. Salnikov
You can also search for this author in PubMed Google Scholar
- J. Salt
You can also search for this author in PubMed Google Scholar
- D. Salvatore
You can also search for this author in PubMed Google Scholar
- F. Salvatore
You can also search for this author in PubMed Google Scholar
- A. Salvucci
You can also search for this author in PubMed Google Scholar
- A. Salzburger
You can also search for this author in PubMed Google Scholar
- D. Sammel
You can also search for this author in PubMed Google Scholar
- D. Sampsonidis
You can also search for this author in PubMed Google Scholar
- D. Sampsonidou
You can also search for this author in PubMed Google Scholar
- J. Sánchez
You can also search for this author in PubMed Google Scholar
- V. Sanchez Martinez
You can also search for this author in PubMed Google Scholar
- A. Sanchez Pineda
You can also search for this author in PubMed Google Scholar
- H. Sandaker
You can also search for this author in PubMed Google Scholar
- R. L. Sandbach
You can also search for this author in PubMed Google Scholar
- C. O. Sander
You can also search for this author in PubMed Google Scholar
- M. Sandhoff
You can also search for this author in PubMed Google Scholar
- C. Sandoval
You can also search for this author in PubMed Google Scholar
- D. P. C. Sankey
You can also search for this author in PubMed Google Scholar
- M. Sannino
You can also search for this author in PubMed Google Scholar
- Y. Sano
You can also search for this author in PubMed Google Scholar
- A. Sansoni
You can also search for this author in PubMed Google Scholar
- C. Santoni
You can also search for this author in PubMed Google Scholar
- H. Santos
You can also search for this author in PubMed Google Scholar
- I. Santoyo Castillo
You can also search for this author in PubMed Google Scholar
- A. Sapronov
You can also search for this author in PubMed Google Scholar
- J. G. Saraiva
You can also search for this author in PubMed Google Scholar
- B. Sarrazin
You can also search for this author in PubMed Google Scholar
- O. Sasaki
You can also search for this author in PubMed Google Scholar
- K. Sato
You can also search for this author in PubMed Google Scholar
- E. Sauvan
You can also search for this author in PubMed Google Scholar
- G. Savage
You can also search for this author in PubMed Google Scholar
- P. Savard
You can also search for this author in PubMed Google Scholar
- N. Savic
You can also search for this author in PubMed Google Scholar
- C. Sawyer
You can also search for this author in PubMed Google Scholar
- L. Sawyer
You can also search for this author in PubMed Google Scholar
- J. Saxon
You can also search for this author in PubMed Google Scholar
- C. Sbarra
You can also search for this author in PubMed Google Scholar
- A. Sbrizzi
You can also search for this author in PubMed Google Scholar
- T. Scanlon
You can also search for this author in PubMed Google Scholar
- D. A. Scannicchio
You can also search for this author in PubMed Google Scholar
- J. Schaarschmidt
You can also search for this author in PubMed Google Scholar
- P. Schacht
You can also search for this author in PubMed Google Scholar
- B. M. Schachtner
You can also search for this author in PubMed Google Scholar
- D. Schaefer
You can also search for this author in PubMed Google Scholar
- L. Schaefer
You can also search for this author in PubMed Google Scholar
- R. Schaefer
You can also search for this author in PubMed Google Scholar
- J. Schaeffer
You can also search for this author in PubMed Google Scholar
- S. Schaepe
You can also search for this author in PubMed Google Scholar
- S. Schaetzel
You can also search for this author in PubMed Google Scholar
- U. Schäfer
You can also search for this author in PubMed Google Scholar
- A. C. Schaffer
You can also search for this author in PubMed Google Scholar
- D. Schaile
You can also search for this author in PubMed Google Scholar
- R. D. Schamberger
You can also search for this author in PubMed Google Scholar
- V. A. Schegelsky
You can also search for this author in PubMed Google Scholar
- D. Scheirich
You can also search for this author in PubMed Google Scholar
- M. Schernau
You can also search for this author in PubMed Google Scholar
- C. Schiavi
You can also search for this author in PubMed Google Scholar
- S. Schier
You can also search for this author in PubMed Google Scholar
- L. K. Schildgen
You can also search for this author in PubMed Google Scholar
- C. Schillo
You can also search for this author in PubMed Google Scholar
- M. Schioppa
You can also search for this author in PubMed Google Scholar
- S. Schlenker
You can also search for this author in PubMed Google Scholar
- K. R. Schmidt-Sommerfeld
You can also search for this author in PubMed Google Scholar
- K. Schmieden
You can also search for this author in PubMed Google Scholar
- C. Schmitt
You can also search for this author in PubMed Google Scholar
- S. Schmitt
You can also search for this author in PubMed Google Scholar
- S. Schmitz
You can also search for this author in PubMed Google Scholar
- U. Schnoor
You can also search for this author in PubMed Google Scholar
- L. Schoeffel
You can also search for this author in PubMed Google Scholar
- A. Schoening
You can also search for this author in PubMed Google Scholar
- B. D. Schoenrock
You can also search for this author in PubMed Google Scholar
- E. Schopf
You can also search for this author in PubMed Google Scholar
- M. Schott
You can also search for this author in PubMed Google Scholar
- J. F. P. Schouwenberg
You can also search for this author in PubMed Google Scholar
- J. Schovancova
You can also search for this author in PubMed Google Scholar
- S. Schramm
You can also search for this author in PubMed Google Scholar
- N. Schuh
You can also search for this author in PubMed Google Scholar
- A. Schulte
You can also search for this author in PubMed Google Scholar
- M. J. Schultens
You can also search for this author in PubMed Google Scholar
- H.-C. Schultz-Coulon
You can also search for this author in PubMed Google Scholar
- H. Schulz
You can also search for this author in PubMed Google Scholar
- M. Schumacher
You can also search for this author in PubMed Google Scholar
- B. A. Schumm
You can also search for this author in PubMed Google Scholar
- Ph. Schune
You can also search for this author in PubMed Google Scholar
- A. Schwartzman
You can also search for this author in PubMed Google Scholar
- T. A. Schwarz
You can also search for this author in PubMed Google Scholar
- H. Schweiger
You can also search for this author in PubMed Google Scholar
- Ph. Schwemling
You can also search for this author in PubMed Google Scholar
- R. Schwienhorst
You can also search for this author in PubMed Google Scholar
- J. Schwindling
You can also search for this author in PubMed Google Scholar
- A. Sciandra
You can also search for this author in PubMed Google Scholar
- G. Sciolla
You can also search for this author in PubMed Google Scholar
- M. Scornajenghi
You can also search for this author in PubMed Google Scholar
- F. Scuri
You can also search for this author in PubMed Google Scholar
- F. Scutti
You can also search for this author in PubMed Google Scholar
- J. Searcy
You can also search for this author in PubMed Google Scholar
- P. Seema
You can also search for this author in PubMed Google Scholar
- S. C. Seidel
You can also search for this author in PubMed Google Scholar
- A. Seiden
You can also search for this author in PubMed Google Scholar
- J. M. Seixas
You can also search for this author in PubMed Google Scholar
- G. Sekhniaidze
You can also search for this author in PubMed Google Scholar
- K. Sekhon
You can also search for this author in PubMed Google Scholar
- S. J. Sekula
You can also search for this author in PubMed Google Scholar
- N. Semprini-Cesari
You can also search for this author in PubMed Google Scholar
- S. Senkin
You can also search for this author in PubMed Google Scholar
- C. Serfon
You can also search for this author in PubMed Google Scholar
- L. Serin
You can also search for this author in PubMed Google Scholar
- L. Serkin
You can also search for this author in PubMed Google Scholar
- M. Sessa
You can also search for this author in PubMed Google Scholar
- R. Seuster
You can also search for this author in PubMed Google Scholar
- H. Severini
You can also search for this author in PubMed Google Scholar
- T. Sfiligoj
You can also search for this author in PubMed Google Scholar
- F. Sforza
You can also search for this author in PubMed Google Scholar
- A. Sfyrla
You can also search for this author in PubMed Google Scholar
- E. Shabalina
You can also search for this author in PubMed Google Scholar
- N. W. Shaikh
You can also search for this author in PubMed Google Scholar
- L. Y. Shan
You can also search for this author in PubMed Google Scholar
- R. Shang
You can also search for this author in PubMed Google Scholar
- J. T. Shank
You can also search for this author in PubMed Google Scholar
- M. Shapiro
You can also search for this author in PubMed Google Scholar
- P. B. Shatalov
You can also search for this author in PubMed Google Scholar
- K. Shaw
You can also search for this author in PubMed Google Scholar
- S. M. Shaw
You can also search for this author in PubMed Google Scholar
- A. Shcherbakova
You can also search for this author in PubMed Google Scholar
- C. Y. Shehu
You can also search for this author in PubMed Google Scholar
- Y. Shen
You can also search for this author in PubMed Google Scholar
- N. Sherafati
You can also search for this author in PubMed Google Scholar
- P. Sherwood
You can also search for this author in PubMed Google Scholar
- L. Shi
You can also search for this author in PubMed Google Scholar
- S. Shimizu
You can also search for this author in PubMed Google Scholar
- C. O. Shimmin
You can also search for this author in PubMed Google Scholar
- M. Shimojima
You can also search for this author in PubMed Google Scholar
- I. P. J. Shipsey
You can also search for this author in PubMed Google Scholar
- S. Shirabe
You can also search for this author in PubMed Google Scholar
- M. Shiyakova
You can also search for this author in PubMed Google Scholar
- J. Shlomi
You can also search for this author in PubMed Google Scholar
- A. Shmeleva
You can also search for this author in PubMed Google Scholar
- D. Shoaleh Saadi
You can also search for this author in PubMed Google Scholar
- M. J. Shochet
You can also search for this author in PubMed Google Scholar
- S. Shojaii
You can also search for this author in PubMed Google Scholar
- D. R. Shope
You can also search for this author in PubMed Google Scholar
- S. Shrestha
You can also search for this author in PubMed Google Scholar
- E. Shulga
You can also search for this author in PubMed Google Scholar
- M. A. Shupe
You can also search for this author in PubMed Google Scholar
- P. Sicho
You can also search for this author in PubMed Google Scholar
- A. M. Sickles
You can also search for this author in PubMed Google Scholar
- P. E. Sidebo
You can also search for this author in PubMed Google Scholar
- E. Sideras Haddad
You can also search for this author in PubMed Google Scholar
- O. Sidiropoulou
You can also search for this author in PubMed Google Scholar
- A. Sidoti
You can also search for this author in PubMed Google Scholar
- F. Siegert
You can also search for this author in PubMed Google Scholar
- Dj. Sijacki
You can also search for this author in PubMed Google Scholar
- J. Silva
You can also search for this author in PubMed Google Scholar
- S. B. Silverstein
You can also search for this author in PubMed Google Scholar
- V. Simak
You can also search for this author in PubMed Google Scholar
- Lj. Simic
You can also search for this author in PubMed Google Scholar
- S. Simion
You can also search for this author in PubMed Google Scholar
- E. Simioni
You can also search for this author in PubMed Google Scholar
- B. Simmons
You can also search for this author in PubMed Google Scholar
- M. Simon
You can also search for this author in PubMed Google Scholar
- P. Sinervo
You can also search for this author in PubMed Google Scholar
- N. B. Sinev
You can also search for this author in PubMed Google Scholar
- M. Sioli
You can also search for this author in PubMed Google Scholar
- G. Siragusa
You can also search for this author in PubMed Google Scholar
- I. Siral
You can also search for this author in PubMed Google Scholar
- S. Yu. Sivoklokov
You can also search for this author in PubMed Google Scholar
- J. Sjölin
You can also search for this author in PubMed Google Scholar
- M. B. Skinner
You can also search for this author in PubMed Google Scholar
- P. Skubic
You can also search for this author in PubMed Google Scholar
- M. Slater
You can also search for this author in PubMed Google Scholar
- T. Slavicek
You can also search for this author in PubMed Google Scholar
- M. Slawinska
You can also search for this author in PubMed Google Scholar
- K. Sliwa
You can also search for this author in PubMed Google Scholar
- R. Slovak
You can also search for this author in PubMed Google Scholar
- V. Smakhtin
You can also search for this author in PubMed Google Scholar
- B. H. Smart
You can also search for this author in PubMed Google Scholar
- J. Smiesko
You can also search for this author in PubMed Google Scholar
- N. Smirnov
You can also search for this author in PubMed Google Scholar
- S. Yu. Smirnov
You can also search for this author in PubMed Google Scholar
- Y. Smirnov
You can also search for this author in PubMed Google Scholar
- L. N. Smirnova
You can also search for this author in PubMed Google Scholar
- O. Smirnova
You can also search for this author in PubMed Google Scholar
- J. W. Smith
You can also search for this author in PubMed Google Scholar
- M. N. K. Smith
You can also search for this author in PubMed Google Scholar
- R. W. Smith
You can also search for this author in PubMed Google Scholar
- M. Smizanska
You can also search for this author in PubMed Google Scholar
- K. Smolek
You can also search for this author in PubMed Google Scholar
- A. A. Snesarev
You can also search for this author in PubMed Google Scholar
- I. M. Snyder
You can also search for this author in PubMed Google Scholar
- S. Snyder
You can also search for this author in PubMed Google Scholar
- R. Sobie
You can also search for this author in PubMed Google Scholar
- F. Socher
You can also search for this author in PubMed Google Scholar
- A. Soffer
You can also search for this author in PubMed Google Scholar
- A. Søgaard
You can also search for this author in PubMed Google Scholar
- D. A. Soh
You can also search for this author in PubMed Google Scholar
- G. Sokhrannyi
You can also search for this author in PubMed Google Scholar
- C. A. Solans Sanchez
You can also search for this author in PubMed Google Scholar
- M. Solar
You can also search for this author in PubMed Google Scholar
- E. Yu. Soldatov
You can also search for this author in PubMed Google Scholar
- U. Soldevila
You can also search for this author in PubMed Google Scholar
- A. A. Solodkov
You can also search for this author in PubMed Google Scholar
- A. Soloshenko
You can also search for this author in PubMed Google Scholar
- O. V. Solovyanov
You can also search for this author in PubMed Google Scholar
- V. Solovyev
You can also search for this author in PubMed Google Scholar
- P. Sommer
You can also search for this author in PubMed Google Scholar
- H. Son
You can also search for this author in PubMed Google Scholar
- A. Sopczak
You can also search for this author in PubMed Google Scholar
- D. Sosa
You can also search for this author in PubMed Google Scholar
- C. L. Sotiropoulou
You can also search for this author in PubMed Google Scholar
- S. Sottocornola
You can also search for this author in PubMed Google Scholar
- R. Soualah
You can also search for this author in PubMed Google Scholar
- A. M. Soukharev
You can also search for this author in PubMed Google Scholar
- D. South
You can also search for this author in PubMed Google Scholar
- B. C. Sowden
You can also search for this author in PubMed Google Scholar
- S. Spagnolo
You can also search for this author in PubMed Google Scholar
- M. Spalla
You can also search for this author in PubMed Google Scholar
- M. Spangenberg
You can also search for this author in PubMed Google Scholar
- F. Spanò
You can also search for this author in PubMed Google Scholar
- D. Sperlich
You can also search for this author in PubMed Google Scholar
- F. Spettel
You can also search for this author in PubMed Google Scholar
- T. M. Spieker
You can also search for this author in PubMed Google Scholar
- R. Spighi
You can also search for this author in PubMed Google Scholar
- G. Spigo
You can also search for this author in PubMed Google Scholar
- L. A. Spiller
You can also search for this author in PubMed Google Scholar
- M. Spousta
You can also search for this author in PubMed Google Scholar
- R. D. St. Denis
You can also search for this author in PubMed Google Scholar
- A. Stabile
You can also search for this author in PubMed Google Scholar
- R. Stamen
You can also search for this author in PubMed Google Scholar
- S. Stamm
You can also search for this author in PubMed Google Scholar
- E. Stanecka
You can also search for this author in PubMed Google Scholar
- R. W. Stanek
You can also search for this author in PubMed Google Scholar
- C. Stanescu
You can also search for this author in PubMed Google Scholar
- M. M. Stanitzki
You can also search for this author in PubMed Google Scholar
- B. S. Stapf
You can also search for this author in PubMed Google Scholar
- S. Stapnes
You can also search for this author in PubMed Google Scholar
- E. A. Starchenko
You can also search for this author in PubMed Google Scholar
- G. H. Stark
You can also search for this author in PubMed Google Scholar
- J. Stark
You can also search for this author in PubMed Google Scholar
- S. H Stark
You can also search for this author in PubMed Google Scholar
- P. Staroba
You can also search for this author in PubMed Google Scholar
- P. Starovoitov
You can also search for this author in PubMed Google Scholar
- S. Stärz
You can also search for this author in PubMed Google Scholar
- R. Staszewski
You can also search for this author in PubMed Google Scholar
- M. Stegler
You can also search for this author in PubMed Google Scholar
- P. Steinberg
You can also search for this author in PubMed Google Scholar
- B. Stelzer
You can also search for this author in PubMed Google Scholar
- H. J. Stelzer
You can also search for this author in PubMed Google Scholar
- O. Stelzer-Chilton
You can also search for this author in PubMed Google Scholar
- H. Stenzel
You can also search for this author in PubMed Google Scholar
- G. A. Stewart
You can also search for this author in PubMed Google Scholar
- M. C. Stockton
You can also search for this author in PubMed Google Scholar
- M. Stoebe
You can also search for this author in PubMed Google Scholar
- G. Stoicea
You can also search for this author in PubMed Google Scholar
- P. Stolte
You can also search for this author in PubMed Google Scholar
- S. Stonjek
You can also search for this author in PubMed Google Scholar
- A. R. Stradling
You can also search for this author in PubMed Google Scholar
- A. Straessner
You can also search for this author in PubMed Google Scholar
- M. E. Stramaglia
You can also search for this author in PubMed Google Scholar
- J. Strandberg
You can also search for this author in PubMed Google Scholar
- S. Strandberg
You can also search for this author in PubMed Google Scholar
- M. Strauss
You can also search for this author in PubMed Google Scholar
- P. Strizenec
You can also search for this author in PubMed Google Scholar
- R. Ströhmer
You can also search for this author in PubMed Google Scholar
- D. M. Strom
You can also search for this author in PubMed Google Scholar
- R. Stroynowski
You can also search for this author in PubMed Google Scholar
- A. Strubig
You can also search for this author in PubMed Google Scholar
- S. A. Stucci
You can also search for this author in PubMed Google Scholar
- B. Stugu
You can also search for this author in PubMed Google Scholar
- N. A. Styles
You can also search for this author in PubMed Google Scholar
- D. Su
You can also search for this author in PubMed Google Scholar
- J. Su
You can also search for this author in PubMed Google Scholar
- S. Suchek
You can also search for this author in PubMed Google Scholar
- Y. Sugaya
You can also search for this author in PubMed Google Scholar
- M. Suk
You can also search for this author in PubMed Google Scholar
- V. V. Sulin
You can also search for this author in PubMed Google Scholar
- DMS Sultan
You can also search for this author in PubMed Google Scholar
- S. Sultansoy
You can also search for this author in PubMed Google Scholar
- T. Sumida
You can also search for this author in PubMed Google Scholar
- S. Sun
You can also search for this author in PubMed Google Scholar
- X. Sun
You can also search for this author in PubMed Google Scholar
- K. Suruliz
You can also search for this author in PubMed Google Scholar
- C. J. E. Suster
You can also search for this author in PubMed Google Scholar
- M. R. Sutton
You can also search for this author in PubMed Google Scholar
- S. Suzuki
You can also search for this author in PubMed Google Scholar
- M. Svatos
You can also search for this author in PubMed Google Scholar
- M. Swiatlowski
You can also search for this author in PubMed Google Scholar
- S. P. Swift
You can also search for this author in PubMed Google Scholar
- I. Sykora
You can also search for this author in PubMed Google Scholar
- T. Sykora
You can also search for this author in PubMed Google Scholar
- D. Ta
You can also search for this author in PubMed Google Scholar
- K. Tackmann
You can also search for this author in PubMed Google Scholar
- J. Taenzer
You can also search for this author in PubMed Google Scholar
- A. Taffard
You can also search for this author in PubMed Google Scholar
- R. Tafirout
You can also search for this author in PubMed Google Scholar
- E. Tahirovic
You can also search for this author in PubMed Google Scholar
- N. Taiblum
You can also search for this author in PubMed Google Scholar
- H. Takai
You can also search for this author in PubMed Google Scholar
- R. Takashima
You can also search for this author in PubMed Google Scholar
- E. H. Takasugi
You can also search for this author in PubMed Google Scholar
- K. Takeda
You can also search for this author in PubMed Google Scholar
- T. Takeshita
You can also search for this author in PubMed Google Scholar
- Y. Takubo
You can also search for this author in PubMed Google Scholar
- M. Talby
You can also search for this author in PubMed Google Scholar
- A. A. Talyshev
You can also search for this author in PubMed Google Scholar
- J. Tanaka
You can also search for this author in PubMed Google Scholar
- M. Tanaka
You can also search for this author in PubMed Google Scholar
- R. Tanaka
You can also search for this author in PubMed Google Scholar
- S. Tanaka
You can also search for this author in PubMed Google Scholar
- R. Tanioka
You can also search for this author in PubMed Google Scholar
- B. B. Tannenwald
You can also search for this author in PubMed Google Scholar
- S. Tapia Araya
You can also search for this author in PubMed Google Scholar
- S. Tapprogge
You can also search for this author in PubMed Google Scholar
- S. Tarem
You can also search for this author in PubMed Google Scholar
- G. F. Tartarelli
You can also search for this author in PubMed Google Scholar
- P. Tas
You can also search for this author in PubMed Google Scholar
- M. Tasevsky
You can also search for this author in PubMed Google Scholar
- T. Tashiro
You can also search for this author in PubMed Google Scholar
- E. Tassi
You can also search for this author in PubMed Google Scholar
- A. Tavares Delgado
You can also search for this author in PubMed Google Scholar
- Y. Tayalati
You can also search for this author in PubMed Google Scholar
- A. C. Taylor
You can also search for this author in PubMed Google Scholar
- A. J. Taylor
You can also search for this author in PubMed Google Scholar
- G. N. Taylor
You can also search for this author in PubMed Google Scholar
- P. T. E. Taylor
You can also search for this author in PubMed Google Scholar
- W. Taylor
You can also search for this author in PubMed Google Scholar
- P. Teixeira-Dias
You can also search for this author in PubMed Google Scholar
- D. Temple
You can also search for this author in PubMed Google Scholar
- H. Ten Kate
You can also search for this author in PubMed Google Scholar
- P. K. Teng
You can also search for this author in PubMed Google Scholar
- J. J. Teoh
You can also search for this author in PubMed Google Scholar
- F. Tepel
You can also search for this author in PubMed Google Scholar
- S. Terada
You can also search for this author in PubMed Google Scholar
- K. Terashi
You can also search for this author in PubMed Google Scholar
- J. Terron
You can also search for this author in PubMed Google Scholar
- S. Terzo
You can also search for this author in PubMed Google Scholar
- M. Testa
You can also search for this author in PubMed Google Scholar
- R. J. Teuscher
You can also search for this author in PubMed Google Scholar
- S. J. Thais
You can also search for this author in PubMed Google Scholar
- T. Theveneaux-Pelzer
You can also search for this author in PubMed Google Scholar
- F. Thiele
You can also search for this author in PubMed Google Scholar
- J. P. Thomas
You can also search for this author in PubMed Google Scholar
- J. Thomas-Wilsker
You can also search for this author in PubMed Google Scholar
- P. D. Thompson
You can also search for this author in PubMed Google Scholar
- A. S. Thompson
You can also search for this author in PubMed Google Scholar
- L. A. Thomsen
You can also search for this author in PubMed Google Scholar
- E. Thomson
You can also search for this author in PubMed Google Scholar
- Y. Tian
You can also search for this author in PubMed Google Scholar
- M. J. Tibbetts
You can also search for this author in PubMed Google Scholar
- R. E. Ticse Torres
You can also search for this author in PubMed Google Scholar
- V. O. Tikhomirov
You can also search for this author in PubMed Google Scholar
- Yu. A. Tikhonov
You can also search for this author in PubMed Google Scholar
- S. Timoshenko
You can also search for this author in PubMed Google Scholar
- P. Tipton
You can also search for this author in PubMed Google Scholar
- S. Tisserant
You can also search for this author in PubMed Google Scholar
- K. Todome
You can also search for this author in PubMed Google Scholar
- S. Todorova-Nova
You can also search for this author in PubMed Google Scholar
- S. Todt
You can also search for this author in PubMed Google Scholar
- J. Tojo
You can also search for this author in PubMed Google Scholar
- S. Tokár
You can also search for this author in PubMed Google Scholar
- K. Tokushuku
You can also search for this author in PubMed Google Scholar
- E. Tolley
You can also search for this author in PubMed Google Scholar
- L. Tomlinson
You can also search for this author in PubMed Google Scholar
- M. Tomoto
You can also search for this author in PubMed Google Scholar
- L. Tompkins
You can also search for this author in PubMed Google Scholar
- K. Toms
You can also search for this author in PubMed Google Scholar
- B. Tong
You can also search for this author in PubMed Google Scholar
- P. Tornambe
You can also search for this author in PubMed Google Scholar
- E. Torrence
You can also search for this author in PubMed Google Scholar
- H. Torres
You can also search for this author in PubMed Google Scholar
- E. Torró Pastor
You can also search for this author in PubMed Google Scholar
- J. Toth
You can also search for this author in PubMed Google Scholar
- F. Touchard
You can also search for this author in PubMed Google Scholar
- D. R. Tovey
You can also search for this author in PubMed Google Scholar
- C. J. Treado
You can also search for this author in PubMed Google Scholar
- T. Trefzger
You can also search for this author in PubMed Google Scholar
- F. Tresoldi
You can also search for this author in PubMed Google Scholar
- A. Tricoli
You can also search for this author in PubMed Google Scholar
- I. M. Trigger
You can also search for this author in PubMed Google Scholar
- S. Trincaz-Duvoid
You can also search for this author in PubMed Google Scholar
- M. F. Tripiana
You can also search for this author in PubMed Google Scholar
- W. Trischuk
You can also search for this author in PubMed Google Scholar
- B. Trocmé
You can also search for this author in PubMed Google Scholar
- A. Trofymov
You can also search for this author in PubMed Google Scholar
- C. Troncon
You can also search for this author in PubMed Google Scholar
- M. Trottier-McDonald
You can also search for this author in PubMed Google Scholar
- M. Trovatelli
You can also search for this author in PubMed Google Scholar
- L. Truong
You can also search for this author in PubMed Google Scholar
- M. Trzebinski
You can also search for this author in PubMed Google Scholar
- A. Trzupek
You can also search for this author in PubMed Google Scholar
- K. W. Tsang
You can also search for this author in PubMed Google Scholar
- J. C-L. Tseng
You can also search for this author in PubMed Google Scholar
- P. V. Tsiareshka
You can also search for this author in PubMed Google Scholar
- G. Tsipolitis
You can also search for this author in PubMed Google Scholar
- N. Tsirintanis
You can also search for this author in PubMed Google Scholar
- S. Tsiskaridze
You can also search for this author in PubMed Google Scholar
- V. Tsiskaridze
You can also search for this author in PubMed Google Scholar
- E. G. Tskhadadze
You can also search for this author in PubMed Google Scholar
- I. I. Tsukerman
You can also search for this author in PubMed Google Scholar
- V. Tsulaia
You can also search for this author in PubMed Google Scholar
- S. Tsuno
You can also search for this author in PubMed Google Scholar
- D. Tsybychev
You can also search for this author in PubMed Google Scholar
- Y. Tu
You can also search for this author in PubMed Google Scholar
- A. Tudorache
You can also search for this author in PubMed Google Scholar
- V. Tudorache
You can also search for this author in PubMed Google Scholar
- T. T. Tulbure
You can also search for this author in PubMed Google Scholar
- A. N. Tuna
You can also search for this author in PubMed Google Scholar
- S. Turchikhin
You can also search for this author in PubMed Google Scholar
- D. Turgeman
You can also search for this author in PubMed Google Scholar
- I. Turk Cakir
You can also search for this author in PubMed Google Scholar
- R. Turra
You can also search for this author in PubMed Google Scholar
- P. M. Tuts
You can also search for this author in PubMed Google Scholar
- G. Ucchielli
You can also search for this author in PubMed Google Scholar
- I. Ueda
You can also search for this author in PubMed Google Scholar
- M. Ughetto
You can also search for this author in PubMed Google Scholar
- F. Ukegawa
You can also search for this author in PubMed Google Scholar
- G. Unal
You can also search for this author in PubMed Google Scholar
- A. Undrus
You can also search for this author in PubMed Google Scholar
- G. Unel
You can also search for this author in PubMed Google Scholar
- F. C. Ungaro
You can also search for this author in PubMed Google Scholar
- Y. Unno
You can also search for this author in PubMed Google Scholar
- C. Unverdorben
You can also search for this author in PubMed Google Scholar
- J. Urban
You can also search for this author in PubMed Google Scholar
- P. Urquijo
You can also search for this author in PubMed Google Scholar
- P. Urrejola
You can also search for this author in PubMed Google Scholar
- G. Usai
You can also search for this author in PubMed Google Scholar
- J. Usui
You can also search for this author in PubMed Google Scholar
- L. Vacavant
You can also search for this author in PubMed Google Scholar
- V. Vacek
You can also search for this author in PubMed Google Scholar
- B. Vachon
You can also search for this author in PubMed Google Scholar
- K. O. H. Vadla
You can also search for this author in PubMed Google Scholar
- A. Vaidya
You can also search for this author in PubMed Google Scholar
- C. Valderanis
You can also search for this author in PubMed Google Scholar
- E. Valdes Santurio
You can also search for this author in PubMed Google Scholar
- M. Valente
You can also search for this author in PubMed Google Scholar
- S. Valentinetti
You can also search for this author in PubMed Google Scholar
- A. Valero
You can also search for this author in PubMed Google Scholar
- L. Valéry
You can also search for this author in PubMed Google Scholar
- S. Valkar
You can also search for this author in PubMed Google Scholar
- A. Vallier
You can also search for this author in PubMed Google Scholar
- J. A. Valls Ferrer
You can also search for this author in PubMed Google Scholar
- W. Van Den Wollenberg
You can also search for this author in PubMed Google Scholar
- H. van der Graaf
You can also search for this author in PubMed Google Scholar
- P. van Gemmeren
You can also search for this author in PubMed Google Scholar
- J. Van Nieuwkoop
You can also search for this author in PubMed Google Scholar
- I. van Vulpen
You can also search for this author in PubMed Google Scholar
- M. C. van Woerden
You can also search for this author in PubMed Google Scholar
- M. Vanadia
You can also search for this author in PubMed Google Scholar
- W. Vandelli
You can also search for this author in PubMed Google Scholar
- A. Vaniachine
You can also search for this author in PubMed Google Scholar
- P. Vankov
You can also search for this author in PubMed Google Scholar
- G. Vardanyan
You can also search for this author in PubMed Google Scholar
- R. Vari
You can also search for this author in PubMed Google Scholar
- E. W. Varnes
You can also search for this author in PubMed Google Scholar
- C. Varni
You can also search for this author in PubMed Google Scholar
- T. Varol
You can also search for this author in PubMed Google Scholar
- D. Varouchas
You can also search for this author in PubMed Google Scholar
- A. Vartapetian
You can also search for this author in PubMed Google Scholar
- K. E. Varvell
You can also search for this author in PubMed Google Scholar
- J. G. Vasquez
You can also search for this author in PubMed Google Scholar
- G. A. Vasquez
You can also search for this author in PubMed Google Scholar
- F. Vazeille
You can also search for this author in PubMed Google Scholar
- D. Vazquez Furelos
You can also search for this author in PubMed Google Scholar
- T. Vazquez Schroeder
You can also search for this author in PubMed Google Scholar
- J. Veatch
You can also search for this author in PubMed Google Scholar
- V. Veeraraghavan
You can also search for this author in PubMed Google Scholar
- L. M. Veloce
You can also search for this author in PubMed Google Scholar
- F. Veloso
You can also search for this author in PubMed Google Scholar
- S. Veneziano
You can also search for this author in PubMed Google Scholar
- A. Ventura
You can also search for this author in PubMed Google Scholar
- M. Venturi
You can also search for this author in PubMed Google Scholar
- N. Venturi
You can also search for this author in PubMed Google Scholar
- A. Venturini
You can also search for this author in PubMed Google Scholar
- V. Vercesi
You can also search for this author in PubMed Google Scholar
- M. Verducci
You can also search for this author in PubMed Google Scholar
- W. Verkerke
You can also search for this author in PubMed Google Scholar
- A. T. Vermeulen
You can also search for this author in PubMed Google Scholar
- J. C. Vermeulen
You can also search for this author in PubMed Google Scholar
- M. C. Vetterli
You can also search for this author in PubMed Google Scholar
- N. Viaux Maira
You can also search for this author in PubMed Google Scholar
- O. Viazlo
You can also search for this author in PubMed Google Scholar
- I. Vichou
You can also search for this author in PubMed Google Scholar
- T. Vickey
You can also search for this author in PubMed Google Scholar
- O. E. Vickey Boeriu
You can also search for this author in PubMed Google Scholar
- G. H. A. Viehhauser
You can also search for this author in PubMed Google Scholar
- S. Viel
You can also search for this author in PubMed Google Scholar
- L. Vigani
You can also search for this author in PubMed Google Scholar
- M. Villa
You can also search for this author in PubMed Google Scholar
- M. Villaplana Perez
You can also search for this author in PubMed Google Scholar
- E. Vilucchi
You can also search for this author in PubMed Google Scholar
- M. G. Vincter
You can also search for this author in PubMed Google Scholar
- V. B. Vinogradov
You can also search for this author in PubMed Google Scholar
- A. Vishwakarma
You can also search for this author in PubMed Google Scholar
- C. Vittori
You can also search for this author in PubMed Google Scholar
- I. Vivarelli
You can also search for this author in PubMed Google Scholar
- S. Vlachos
You can also search for this author in PubMed Google Scholar
- M. Vogel
You can also search for this author in PubMed Google Scholar
- P. Vokac
You can also search for this author in PubMed Google Scholar
- G. Volpi
You can also search for this author in PubMed Google Scholar
- H. von der Schmitt
You can also search for this author in PubMed Google Scholar
- E. von Toerne
You can also search for this author in PubMed Google Scholar
- V. Vorobel
You can also search for this author in PubMed Google Scholar
- K. Vorobev
You can also search for this author in PubMed Google Scholar
- M. Vos
You can also search for this author in PubMed Google Scholar
- R. Voss
You can also search for this author in PubMed Google Scholar
- J. H. Vossebeld
You can also search for this author in PubMed Google Scholar
- N. Vranjes
You can also search for this author in PubMed Google Scholar
- M. Vranjes Milosavljevic
You can also search for this author in PubMed Google Scholar
- V. Vrba
You can also search for this author in PubMed Google Scholar
- M. Vreeswijk
You can also search for this author in PubMed Google Scholar
- R. Vuillermet
You can also search for this author in PubMed Google Scholar
- I. Vukotic
You can also search for this author in PubMed Google Scholar
- P. Wagner
You can also search for this author in PubMed Google Scholar
- W. Wagner
You can also search for this author in PubMed Google Scholar
- J. Wagner-Kuhr
You can also search for this author in PubMed Google Scholar
- H. Wahlberg
You can also search for this author in PubMed Google Scholar
- S. Wahrmund
You can also search for this author in PubMed Google Scholar
- J. Walder
You can also search for this author in PubMed Google Scholar
- R. Walker
You can also search for this author in PubMed Google Scholar
- W. Walkowiak
You can also search for this author in PubMed Google Scholar
- V. Wallangen
You can also search for this author in PubMed Google Scholar
- C. Wang
You can also search for this author in PubMed Google Scholar
- C. Wang
You can also search for this author in PubMed Google Scholar
- F. Wang
You can also search for this author in PubMed Google Scholar
- H. Wang
You can also search for this author in PubMed Google Scholar
- H. Wang
You can also search for this author in PubMed Google Scholar
- J. Wang
You can also search for this author in PubMed Google Scholar
- J. Wang
You can also search for this author in PubMed Google Scholar
- Q. Wang
You can also search for this author in PubMed Google Scholar
- R.-J. Wang
You can also search for this author in PubMed Google Scholar
- R. Wang
You can also search for this author in PubMed Google Scholar
- S. M. Wang
You can also search for this author in PubMed Google Scholar
- T. Wang
You can also search for this author in PubMed Google Scholar
- W. Wang
You can also search for this author in PubMed Google Scholar
- W. Wang
You can also search for this author in PubMed Google Scholar
- Z. Wang
You can also search for this author in PubMed Google Scholar
- C. Wanotayaroj
You can also search for this author in PubMed Google Scholar
- A. Warburton
You can also search for this author in PubMed Google Scholar
- C. P. Ward
You can also search for this author in PubMed Google Scholar
- D. R. Wardrope
You can also search for this author in PubMed Google Scholar
- A. Washbrook
You can also search for this author in PubMed Google Scholar
- P. M. Watkins
You can also search for this author in PubMed Google Scholar
- A. T. Watson
You can also search for this author in PubMed Google Scholar
- M. F. Watson
You can also search for this author in PubMed Google Scholar
- G. Watts
You can also search for this author in PubMed Google Scholar
- S. Watts
You can also search for this author in PubMed Google Scholar
- B. M. Waugh
You can also search for this author in PubMed Google Scholar
- A. F. Webb
You can also search for this author in PubMed Google Scholar
- S. Webb
You can also search for this author in PubMed Google Scholar
- M. S. Weber
You can also search for this author in PubMed Google Scholar
- S. M. Weber
You can also search for this author in PubMed Google Scholar
- S. W. Weber
You can also search for this author in PubMed Google Scholar
- S. A. Weber
You can also search for this author in PubMed Google Scholar
- J. S. Webster
You can also search for this author in PubMed Google Scholar
- A. R. Weidberg
You can also search for this author in PubMed Google Scholar
- B. Weinert
You can also search for this author in PubMed Google Scholar
- J. Weingarten
You can also search for this author in PubMed Google Scholar
- M. Weirich
You can also search for this author in PubMed Google Scholar
- C. Weiser
You can also search for this author in PubMed Google Scholar
- H. Weits
You can also search for this author in PubMed Google Scholar
- P. S. Wells
You can also search for this author in PubMed Google Scholar
- T. Wenaus
You can also search for this author in PubMed Google Scholar
- T. Wengler
You can also search for this author in PubMed Google Scholar
- S. Wenig
You can also search for this author in PubMed Google Scholar
- N. Wermes
You can also search for this author in PubMed Google Scholar
- M. D. Werner
You can also search for this author in PubMed Google Scholar
- P. Werner
You can also search for this author in PubMed Google Scholar
- M. Wessels
You can also search for this author in PubMed Google Scholar
- T. D. Weston
You can also search for this author in PubMed Google Scholar
- K. Whalen
You can also search for this author in PubMed Google Scholar
- N. L. Whallon
You can also search for this author in PubMed Google Scholar
- A. M. Wharton
You can also search for this author in PubMed Google Scholar
- A. S. White
You can also search for this author in PubMed Google Scholar
- A. White
You can also search for this author in PubMed Google Scholar
- M. J. White
You can also search for this author in PubMed Google Scholar
- R. White
You can also search for this author in PubMed Google Scholar
- D. Whiteson
You can also search for this author in PubMed Google Scholar
- B. W. Whitmore
You can also search for this author in PubMed Google Scholar
- F. J. Wickens
You can also search for this author in PubMed Google Scholar
- W. Wiedenmann
You can also search for this author in PubMed Google Scholar
- M. Wielers
You can also search for this author in PubMed Google Scholar
- C. Wiglesworth
You can also search for this author in PubMed Google Scholar
- L. A. M. Wiik-Fuchs
You can also search for this author in PubMed Google Scholar
- A. Wildauer
You can also search for this author in PubMed Google Scholar
- F. Wilk
You can also search for this author in PubMed Google Scholar
- H. G. Wilkens
You can also search for this author in PubMed Google Scholar
- H. H. Williams
You can also search for this author in PubMed Google Scholar
- S. Williams
You can also search for this author in PubMed Google Scholar
- C. Willis
You can also search for this author in PubMed Google Scholar
- S. Willocq
You can also search for this author in PubMed Google Scholar
- J. A. Wilson
You can also search for this author in PubMed Google Scholar
- I. Wingerter-Seez
You can also search for this author in PubMed Google Scholar
- E. Winkels
You can also search for this author in PubMed Google Scholar
- F. Winklmeier
You can also search for this author in PubMed Google Scholar
- O. J. Winston
You can also search for this author in PubMed Google Scholar
- B. T. Winter
You can also search for this author in PubMed Google Scholar
- M. Wittgen
You can also search for this author in PubMed Google Scholar
- M. Wobisch
You can also search for this author in PubMed Google Scholar
- T. M. H. Wolf
You can also search for this author in PubMed Google Scholar
- R. Wolff
You can also search for this author in PubMed Google Scholar
- M. W. Wolter
You can also search for this author in PubMed Google Scholar
- H. Wolters
You can also search for this author in PubMed Google Scholar
- V. W. S. Wong
You can also search for this author in PubMed Google Scholar
- N. L. Woods
You can also search for this author in PubMed Google Scholar
- S. D. Worm
You can also search for this author in PubMed Google Scholar
- B. K. Wosiek
You can also search for this author in PubMed Google Scholar
- J. Wotschack
You can also search for this author in PubMed Google Scholar
- K. W. Wozniak
You can also search for this author in PubMed Google Scholar
- M. Wu
You can also search for this author in PubMed Google Scholar
- S. L. Wu
You can also search for this author in PubMed Google Scholar
- X. Wu
You can also search for this author in PubMed Google Scholar
- Y. Wu
You can also search for this author in PubMed Google Scholar
- T. R. Wyatt
You can also search for this author in PubMed Google Scholar
- B. M. Wynne
You can also search for this author in PubMed Google Scholar
- S. Xella
You can also search for this author in PubMed Google Scholar
- Z. Xi
You can also search for this author in PubMed Google Scholar
- L. Xia
You can also search for this author in PubMed Google Scholar
- D. Xu
You can also search for this author in PubMed Google Scholar
- L. Xu
You can also search for this author in PubMed Google Scholar
- T. Xu
You can also search for this author in PubMed Google Scholar
- B. Yabsley
You can also search for this author in PubMed Google Scholar
- S. Yacoob
You can also search for this author in PubMed Google Scholar
- D. Yamaguchi
You can also search for this author in PubMed Google Scholar
- Y. Yamaguchi
You can also search for this author in PubMed Google Scholar
- A. Yamamoto
You can also search for this author in PubMed Google Scholar
- S. Yamamoto
You can also search for this author in PubMed Google Scholar
- T. Yamanaka
You can also search for this author in PubMed Google Scholar
- F. Yamane
You can also search for this author in PubMed Google Scholar
- M. Yamatani
You can also search for this author in PubMed Google Scholar
- Y. Yamazaki
You can also search for this author in PubMed Google Scholar
- Z. Yan
You can also search for this author in PubMed Google Scholar
- H. Yang
You can also search for this author in PubMed Google Scholar
- H. Yang
You can also search for this author in PubMed Google Scholar
- Y. Yang
You can also search for this author in PubMed Google Scholar
- Z. Yang
You can also search for this author in PubMed Google Scholar
- W-M. Yao
You can also search for this author in PubMed Google Scholar
- Y. C. Yap
You can also search for this author in PubMed Google Scholar
- Y. Yasu
You can also search for this author in PubMed Google Scholar
- E. Yatsenko
You can also search for this author in PubMed Google Scholar
- K. H. Yau Wong
You can also search for this author in PubMed Google Scholar
- J. Ye
You can also search for this author in PubMed Google Scholar
- S. Ye
You can also search for this author in PubMed Google Scholar
- I. Yeletskikh
You can also search for this author in PubMed Google Scholar
- E. Yigitbasi
You can also search for this author in PubMed Google Scholar
- E. Yildirim
You can also search for this author in PubMed Google Scholar
- K. Yorita
You can also search for this author in PubMed Google Scholar
- K. Yoshihara
You can also search for this author in PubMed Google Scholar
- C. Young
You can also search for this author in PubMed Google Scholar
- C. J. S. Young
You can also search for this author in PubMed Google Scholar
- J. Yu
You can also search for this author in PubMed Google Scholar
- J. Yu
You can also search for this author in PubMed Google Scholar
- S. P. Y. Yuen
You can also search for this author in PubMed Google Scholar
- I. Yusuff
You can also search for this author in PubMed Google Scholar
- B. Zabinski
You can also search for this author in PubMed Google Scholar
- G. Zacharis
You can also search for this author in PubMed Google Scholar
- R. Zaidan
You can also search for this author in PubMed Google Scholar
- A. M. Zaitsev
You can also search for this author in PubMed Google Scholar
- N. Zakharchuk
You can also search for this author in PubMed Google Scholar
- J. Zalieckas
You can also search for this author in PubMed Google Scholar
- A. Zaman
You can also search for this author in PubMed Google Scholar
- S. Zambito
You can also search for this author in PubMed Google Scholar
- D. Zanzi
You can also search for this author in PubMed Google Scholar
- C. Zeitnitz
You can also search for this author in PubMed Google Scholar
- G. Zemaityte
You can also search for this author in PubMed Google Scholar
- A. Zemla
You can also search for this author in PubMed Google Scholar
- J. C. Zeng
You can also search for this author in PubMed Google Scholar
- Q. Zeng
You can also search for this author in PubMed Google Scholar
- O. Zenin
You can also search for this author in PubMed Google Scholar
- T. Ženiš
You can also search for this author in PubMed Google Scholar
- D. Zerwas
You can also search for this author in PubMed Google Scholar
- D. Zhang
You can also search for this author in PubMed Google Scholar
- D. Zhang
You can also search for this author in PubMed Google Scholar
- F. Zhang
You can also search for this author in PubMed Google Scholar
- G. Zhang
You can also search for this author in PubMed Google Scholar
- H. Zhang
You can also search for this author in PubMed Google Scholar
- J. Zhang
You can also search for this author in PubMed Google Scholar
- L. Zhang
You can also search for this author in PubMed Google Scholar
- L. Zhang
You can also search for this author in PubMed Google Scholar
- M. Zhang
You can also search for this author in PubMed Google Scholar
- P. Zhang
You can also search for this author in PubMed Google Scholar
- R. Zhang
You can also search for this author in PubMed Google Scholar
- R. Zhang
You can also search for this author in PubMed Google Scholar
- X. Zhang
You can also search for this author in PubMed Google Scholar
- Y. Zhang
You can also search for this author in PubMed Google Scholar
- Z. Zhang
You can also search for this author in PubMed Google Scholar
- X. Zhao
You can also search for this author in PubMed Google Scholar
- Y. Zhao
You can also search for this author in PubMed Google Scholar
- Z. Zhao
You can also search for this author in PubMed Google Scholar
- A. Zhemchugov
You can also search for this author in PubMed Google Scholar
- B. Zhou
You can also search for this author in PubMed Google Scholar
- C. Zhou
You can also search for this author in PubMed Google Scholar
- L. Zhou
You can also search for this author in PubMed Google Scholar
- M. Zhou
You can also search for this author in PubMed Google Scholar
- M. Zhou
You can also search for this author in PubMed Google Scholar
- N. Zhou
You can also search for this author in PubMed Google Scholar
- C. G. Zhu
You can also search for this author in PubMed Google Scholar
- H. Zhu
You can also search for this author in PubMed Google Scholar
- J. Zhu
You can also search for this author in PubMed Google Scholar
- Y. Zhu
You can also search for this author in PubMed Google Scholar
- X. Zhuang
You can also search for this author in PubMed Google Scholar
- K. Zhukov
You can also search for this author in PubMed Google Scholar
- A. Zibell
You can also search for this author in PubMed Google Scholar
- D. Zieminska
You can also search for this author in PubMed Google Scholar
- N. I. Zimine
You can also search for this author in PubMed Google Scholar
- C. Zimmermann
You can also search for this author in PubMed Google Scholar
- S. Zimmermann
You can also search for this author in PubMed Google Scholar
- Z. Zinonos
You can also search for this author in PubMed Google Scholar
- M. Zinser
You can also search for this author in PubMed Google Scholar
- M. Ziolkowski
You can also search for this author in PubMed Google Scholar
- L. Živković
You can also search for this author in PubMed Google Scholar
- G. Zobernig
You can also search for this author in PubMed Google Scholar
- A. Zoccoli
You can also search for this author in PubMed Google Scholar
- R. Zou
You can also search for this author in PubMed Google Scholar
- M. zur Nedden
You can also search for this author in PubMed Google Scholar
- L. Zwalinski
You can also search for this author in PubMed Google Scholar
Consortia
ATLAS Collaboration
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Aaboud, M., Aad, G., Abbott, B. et al. Search for new phenomena in high-mass final states with a photon and a jet from \(pp\) collisions at \(\sqrt{s}\) = 13 TeV with the ATLAS detector. Eur. Phys. J. C 78, 102 (2018). https://doi.org/10.1140/epjc/s10052-018-5553-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5553-2
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative







