Abstract
We consider the production of \(J/\psi \) and \(\psi (2S)\) mesons originating from the decays of b-flavored hadrons at the LHC using the \(k_T\)-factorization approach. Our analysis covers both inclusive charmonia production and production of \(J/\psi \) mesons in association with Z bosons. We apply the transverse momentum dependent (or unintegrated) gluon density in a proton derived from Catani–Ciafaloni–Fiorani–Marchesini (CCFM) evolution equation and adopt fragmentation functions based on the non-relativistic QCD factorization to describe the inclusive b-hadron decays into the different charmonium states. Our predictions agree well with latest experimental data taken by the CMS, ATLAS and LHCb Collaborations at \(\sqrt{s} = 7\), 8 and 13 TeV. The contributions from double parton scattering to the associated non-prompt \(J/\psi + Z\) production are estimated and found to be small.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A few years ago, the CMS, ATLAS and LHCb Collaborations reported the measurements of the inclusive production of \(J/\psi \) and \(\psi (2S)\) mesons originating from b-hadron decays (so called “non-prompt” production) at the LHC energies \(\sqrt{s} = 7\) and 8 TeV [1,2,3,4]. More recently, the LHCb Collaboration has measured [5] the total and differential cross sections of the inclusive non-prompt \(J/\psi \) production at \(\sqrt{s} = 13\) TeV. Additionally, first experimental data on the associated non-prompt \(J/\psi \) meson and Z boson production have been presented by the ATLAS Collaboration at \(\sqrt{s} = 8\) TeV [6]. These measurements provide a new opportunity for studying b-flavor production in pp collisions at the LHC. A special point of interest because it involves both weak and strong interactions and therefore serves as a complex test of electroweak theory, perturbative Quantum Chromodynamics (pQCD) and our knowledge of parton distributions in a proton. The fixed-order next-to-leading-log (FONLL) approach [7, 8] and the general-mass variable-flavor-number scheme (GM-VFNS) [9, 10] are able to describe the inclusive production of non-prompt \(J/\psi \) and \(\psi (2S)\) mesons over the whole charmonia transverse momentum range. The role of the next-to-leading (NLO) pQCD corrections to the associated non-prompt \(J/\psi + Z\) production and contributions from the double parton scattering (DPS) mechanism were investigated very recently [11] using the MadGraph tool [12]. The main goal of our present study is to obtain first predictions for non-prompt \(J/\psi \) and \(\psi (2S)\) production, both inclusively and in association with a Z boson, employing the \(k_T\)-factorization approach [13,14,15,16] and to give a systematic self-consistent analysis of recent CMS, ATLAS and LHCb data [1,2,3,4,5,6]. The \(k_T\)-factorization approach has certain technical advantages in the ease of including higher-order radiative corrections that can be taken into account in the form of transverse momentum dependent (TMD) parton distributions.Footnote 1
The double differential cross sections of inclusive non-prompt \(J/\psi \) meson production at \(\sqrt{s} = 7\) TeV as a function of \(J/\psi \) transverse momentum. The solid histograms represent our predictions obtained with the JH’2013 set 2 gluon density at the default hard scales. The shaded bands represent the scale uncertainties of the calculations, as it is described in the text. The experimental data are from CMS [1]

The calculations involve two main ingredients: the cross sections of b-hadron production and the partial widths of their subsequent decays into the different charmonia states. In our previous papers [21,22,23], we paid attention to the first of them, describing the inclusive production of b-hadrons and production of Z bosons in association with one or two b-jets (or rather b-hadrons) within the \(k_T\)-factorization formalism. Our consideration below continues this line and extends to the second ingredient. In addition to the previously tested components of the theory, here we further inspect the evolution details of b-quarks fragmenting and decaying into the final state charmonia.
The outline of our paper is following. In Sect. 2 we briefly describe our theoretical input and calculation steps. In Sect. 3 we present a numerical results and a discussion. Section 4 contains our conclusions.
2 The model
In the present note we strictly follow the approach described earlier [21,22,23]. Here we only briefly recall the main points of the theoretical scheme.
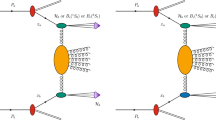
First, to calculate the cross sections of inclusive b-hadron production and associated \(Z + b\) production in pp collisions the \(k_T\)-factorization approach was applied, mainly based on the off-shell gluon–gluon fusion subprocesses:
where the Z boson further decays into a lepton pair. The corresponding gauge-invariant off-shell (dependent on the transverse momenta of initial gluons) production amplitudes were calculated earlier (see [21,22,23] and references therein) and implemented into the Monte-Carlo event generator cascade [24]. Then, b-flavor production cross sections were calculated as a convolution of the off-shell partonic cross sections and TMD gluon distributions in a proton.
In addition to the off-shell gluon–gluon fusion, several subprocesses involving quarks in the initial state are taken into account. These are the flavor excitation, quark–antiquark annihilation and quark-gluon scattering subprocesses:
with subsequent decays of Z bosons into a lepton pair. These processes become important at large transverse momenta \(p_T\) (or, respectively, at large parton longitudinal momentum fraction x, which is needed to produce high \(p_T\) events) where the quarks are less suppressed or can even dominate over the gluon density. We find it reasonable to rely upon the collinear Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) factorization scheme [25,26,27,28], which provides better theoretical grounds in the large-x region. We consider a combination of two techniques where each of them being used at the kinematic conditions where it is best suitable (off-shell gluon–gluon fusion subprocesses at small x and quark-induced subprocesses at large x values).
An essential point of our consideration is using a numerical solution of the Ciafaloni–Catani–Fiorani–Marchesini (CCFM) evolution equation [29,30,31,32] to derive the TMD gluon density in a proton. The CCFM equation provides a suitable tool since it smoothly interpolates between the small-x Balitsky–Fadin–Kuraev–Lipatov (BFKL) [33,34,35] gluon dynamics and high-x DGLAP dynamics. Following [23], we adopt the latest JH’2013 parametrization [36], taking JH’2013 set 2 as the default choice. This TMD gluon density was fitted to high-precision DIS data on the proton structure functions \(F_2(x,Q^2)\) and \(F_2^c(x,Q^2)\). For the conventional quark and gluon densities we use the MSTW’2008 (LO) set [37]. The fragmentation of the produced b quarks into b-hadrons is described with the Peterson fragmentation function with \(\epsilon _b = 0.0126\) [38]. Using these parameters, we successfully reproduce the latest CMS experimental data on inclusive \(B^+\) meson productionFootnote 2 at \(\sqrt{s} = 13~\hbox {TeV}\) [40].
The approach above provides the necessary starting point for the theoretical description of \(J/\psi \) or \(\psi (2S)\) production from b-hadrons. At the next step, the obtained b-hadron cross sections have to be convoluted with \(b\rightarrow J/\psi \) and \(b\rightarrow \psi (2S)\) fragmentation functions. These fragmentation functions are the longitudinal momentum distributions of the \(J/\psi \) and \(\psi (2S)\) mesons from b-hadron decay, appropriately boosted along the b-hadron flight direction. The latter have been calculated [41, 42] in the framework of nonrelativistic QCD (NRQCD) factorization [43,44,45] using the approach [46]. In this approach, the decays of b-hadrons into the final charmonia are represented by a sum of products. Each of them consists of a perturbative coefficient for the production of a \(c\bar{c}\) pair in a specific angular-momentum and color state and nonperturbative NRQCD matrix element (NME). It parametrizes the subsequent transition of this intermediate \(c \bar{c}\) state into the final physical charmonium with the help of nonperturbative soft gluon radiation and it has to be extracted from the experimental data. The resulting predictions [41, 42] for the \(b \rightarrow J/\psi + X\) and \(b \rightarrow \psi (2S) + X\) three-momentum distributions reasonably agree with the measurements performed by the CLEO [47] and BABAR [48] Collaborations. Then, the developed formalism [41, 42] is implemented into our calculations without any changes.Footnote 3 To be precise, we employ the asymptotic expression [41, 42] for the b-hadron decay distribution differential in the longitudinal momentum fraction z carried by the produced charmonium state, obtained in the limit \(|{\mathbf p}_b| \gg m_b\), where \(p_b\) and \(m_b\) are the momentum and the mass of decaying b-hadron. This approximation is valid within 11 and 5% accuracy for \(|{\mathbf p}_b| = 10\) and 20 GeV, respectively, that is suitable for our phenomenological study.
According to the experimental setup [1,2,3,4,5,6], we also included the feed-down contributions to \(J/\psi \) production from the \(b \rightarrow \chi _{cJ} + X\) with \(J = 0, 1, 2\) and \(b \rightarrow \psi (2S) + X\) decays (followed by their subsequent radiative decays \(\chi _{cJ} \rightarrow J/\psi + \gamma \) and \(\psi (2S) \rightarrow J/\psi + \gamma \)), taking them into account using the same approach [41, 42]. The \(\psi (2S)\) mesons are produced with no significant contributions from decays of higher-mass quarkonia. Following [49], we set the branching fractions \(B(b \rightarrow J/\psi + X) = 0.68\)%, \(B(b \rightarrow \psi (2S) + X) = 0.18\)%, \(B(b \rightarrow \chi _{c0} + X) = 0.015\)%, \(B(b \rightarrow \chi _{c1} + X) = 0.21\)%, \(B(b \rightarrow \chi _{c2} + X) = 0.026\)%, \(B(\psi (2S) \rightarrow J/\psi + \gamma ) = 61\)%, \(B(\chi _{c0} \rightarrow J/\psi + \gamma ) = 1.27\)%, \(B(\chi _{c1} \rightarrow J/\psi + \gamma ) = 33.9\)%, \(B(\chi _{c2} \rightarrow J/\psi + \gamma ) = 19.2\)%. Numerically, we set \(m_{J/\psi } = 3.097\) GeV, \(m_{\psi (2S)} = 3.686\) GeV, \(m_{\chi _{c0}} = 3.415\) GeV, \(m_{\chi _{c1}} = 3.511\) GeV, \(m_{\chi _{c2}} = 3.556\) GeV [49]. Other essential parameters, such as renormalization and factorization scales, masses of produced particles are taken exactly the same as in our previous studies [21,22,23].
3 Numerical results
Now we are in a position to present numerical results and a discussion. We consider first the inclusive non-prompt \(J/\psi \) and \(\psi (2S)\) production. The latest measurements have been carried out by the CMS [1], ATLAS [2] and LHCb [3,4,5] Collaborations. The CMS Collaboration presented non-prompt \(J/\psi \) transverse momentum \(p_T\) distributions at \(\sqrt{s} = 7\) TeV for three subdivisions in \(J/\psi \) rapidity: \(|y| < 1.2\), \(1.2< |y| < 1.6\) and \(1.6< |y| < 2.4\). The ATLAS Collaboration measured both \(J/\psi \) and \(\psi (2S)\) transverse momentum distributions at \(\sqrt{s} = 7\) and 8 TeV for eight rapidity subdivisions. The LHCb Collaboration presented the data on the inclusive non-prompt \(J/\psi \) production in the range \(p_T < 14\) GeV and \(2< y < 4.5\) at different energies \(\sqrt{s} = 7\), 8 and 13 TeV. The \(J/\psi \) and \(\psi (2S)\) cross sections measured by the CMS and ATLAS Collaborations were multiplied by the corresponding branching fractions \(B(J/\psi \rightarrow \mu ^+ \mu ^-) = 5.961\)% and \(B(\psi (2S) \rightarrow \mu ^+ \mu ^-) = 0.79\)% [49], respectively.
We confront our predictions with the available data in Figs. 1, 2, 3 and 4. The solid histograms represent our central predictions by fixing both the renormalization \(\mu _R\) and factorization \(\mu _F\) scales at their default values (see [21,22,23] for the detailed description of our input), while the shaded regions correspond to the scale uncertainties of our predictions. To estimate the latter we used the JH’2013 set 2\(+\) and JH’2013 set 2− sets instead of default one JH’2013 set 2. These two sets represent a variation of the renormalization scale used in the off-shell production amplitude [36]. We achieve good agreement with the LHC data on the transverse momentum distributions for both \(J/\psi \) and \(\psi (2S)\) mesons within the experimental and theoretical uncertainties. The slight disagreement is only observed at low transverse momenta, \(p_T \le 10\) GeV. It could be attributed to the finite \(|{\mathbf p}_b|\) terms in the longitudinal momentum distributions of the charmonia (important at \(|{\mathbf p}_b| \sim m_b\)), which are not taken into account in our calculations. The rapidity distributions of \(J/\psi \) mesons measured by the LHCb Collaboration at different energies are well reproduced. Our results are consistently close to the FONLL [7, 8] predictions presented in [1,2,3,4,5], which is explained by the fact that the main part of collinear QCD higher-order corrections (namely, NLO + NNLO + N\(^3\)LO + \(\cdots \) contributions which correspond to the \(\log 1/x\) enhanced terms in the perturbative series) are effectively taken into account as a part of the CCFM gluon evolution. Here we demonstrate again the main advantage of the \(k_T\)-factorization approach, which gives us the possibility to estimate the size of these higher-order corrections and reproduce in a straightforward manner the main features of rather cumbersome higher-order pQCD calculations.
The estimated non-prompt \(J/\psi \) production fiducial cross sections at \(\sqrt{s} = 7\), 8 and 13 TeV are listed in Table 1 in comparison with the available LHC data. One can see that our predictions agree well with these data within the theoretical and experimental uncertainties.
The differential cross sections of associated non-prompt \(J/\psi + Z\) production at \(\sqrt{s} = 8\) TeV as functions of \(J/\psi \) transverse momentum and rapidity. Notation of curves is the same as in Fig. 1. The estimated DPS contributions are shown separately and not summed with SPS ones. The experimental data are from ATLAS [6]
Now we turn to associated non-prompt \(J/\psi + Z\) production. First experimental data were obtained recently by the ATLAS Collaboration at \(\sqrt{s} = 8\) TeV [6]. The leptons originating from the Z boson decay are required to have pseudorapidities \(|\eta ^l| < 2.5\), transverse momenta \(p_T^l > 25\) GeV (leading lepton) and \(p_T^l > 15\) GeV (sub-leading lepton) and invariant mass of the lepton pair \(M^{ll}\) should lie within the interval \(|M^{ll} - m_Z| < 10\) GeV. The produced \(J/\psi \) meson is required to have the transverse momentum \(8.5< p_T < 100\) GeV and rapidity \(|y| < 2.1\). Fiducial cross sections were measured as ratios to the inclusive Z boson production rate in the same fiducial volume. We implemented this experimental setup into our numerical program. The results of our calculations are shown in Fig. 5. One can see that, similar to inclusive \(J/\psi \) production case, our predictions for associated \(J/\psi + Z\) production reasonably agree with the ATLAS data [6]. We find that both the transverse momentum and rapidity distributions of the produced \(J/\psi \) mesons are described within the theoretical and experimental uncertainties. However, we note that the overall description could be even improved if additional contributions from the DPS mechanism are taken into account. To estimate the latter we apply a simple factorization formula (for details see the reviews [50,51,52] and references therein):
where \(\sigma _\mathrm{eff}\) is a normalization constant which incorporates all “DPS unknowns” into a single phenomenological parameter. A numerical value of \(\sigma _\mathrm{eff} \simeq 15\) mb was obtained from fits to pp and \(p\bar{p}\) data (see, for example, [53]). We find that the DPS mechanism gives \(\sim 10\)% contribution to the production cross section in the considered kinematical region and populates mainly at low transverse momenta (see Fig. 5). Being added to the predictions of usual single parton scattering (SPS) mechanism, the DPS contributions slightly improve the description of the \(J/\psi \) rapidity distribution in a whole y range. Some reasonable variations in \(\sigma _\mathrm{eff} \simeq 15 \pm 5\) mb would affect DPS predictions, though without changing our basic conclusion.Footnote 4 The presented DPS estimation coincides with the earlier one performed by the ATLAS Collaboration [6].
4 Conclusions
We investigated the production of \(J/\psi \) and \(\psi (2S)\) mesons, originating from the decays of b-flavored hadrons, both inclusively and in association with Z bosons, at the LHC conditions using the \(k_T\)-factorization approach. Our consideration was mainly based on the dominant off-shell gluon–gluon fusion subprocesses where the transverse momenta of initial gluons are taken into account. In the case of associated non-prompt \(J/\psi + Z\) production, a number of subleading quark-induced subprocesses have been considered in the conventional collinear scheme. To describe the inclusive b-hadron decays into the different charmonium states, we applied fragmentation functions, based on the NRQCD factorization. The feed-down contributions from \(\chi _{cJ}\) (with \(J = 0, 1, 2\)) and \(\psi (2S)\) decays to \(J/\psi \) meson production were taken into account.
Using the TMD gluon densities derived from the CCFM gluon evolution equation, we achieved a good agreement between our predictions and latest CMS, ATLAS and LHCb data collected at \(\sqrt{s} = 7\), 8 and 13 TeV. We provided first theoretical expectations for the associated non-prompt \(J/\psi + Z\) production and estimated the contribution of the double parton scattering mechanism to the production cross sections. The latter is found to be of order of \(\sim 10\)%.
Notes
In particular, we took the NMEs from [41, 42]. It is well-known that these NMEs depend on the minimal charmonia transverse momentum used in the fits and are incompatible with each other when obtained from fitting the different sets of data. However, it was argued [41, 42] that the fine details of the developed formalism, like as exact values of the NMEs, are almost irrelevant (at least at large \(p_T\)) due to the Lorentz boost from the b-hadron rest frame to the laboratory one, so that the corresponding branching fraction becomes the key parameter.
The lower limit of \(\sigma _\mathrm{eff} \sim 5\) mb was established [11] using the MadGraph tool.
References
CMS Collaboration, Eur. Phys. J. C 71, 1575 (2011)
ATLAS Collaboration, Eur. Phys. J. C 76, 283 (2016)
LHCb Collaboration, Eur. Phys. J. C 71, 1645 (2011)
LHCb Collaboration, JHEP 06, 064 (2013)
LHCb Collaboration, JHEP 10, 172 (2015)
ATLAS Collaboration, Eur. Phys. J. C 75, 229 (2015)
M. Cacciari, M. Greco, P. Nason, JHEP 05, 007 (1998)
M. Cacciari, S. Frixione, M.L. Mangano, P. Nason, G. Ridolfi, JHEP 07, 033 (2004)
B.A. Kniehl, G. Kramer, I. Schienbein, H. Spiesberger, Phys. Rev. D 77, 014011 (2008)
B.A. Kniehl, G. Kramer, I. Schienbein, H. Spiesberger, Phys. Rev. D 84, 094026 (2011)
J.P. Lansberg, H.S. Shao, Nucl. Phys. B 916, 132 (2017)
J. Alwal, R. Frederix, S. Frixione, V. Hirschi, F. Maltoni, O. Mattelaer, H.S. Shao, T. Stelzer, P. Torielli, M. Zaro, JHEP 07, 079 (2014)
L.V. Gribov, E.M. Levin, M.G. Ryskin, Phys. Rep. 100, 1 (1983)
E.M. Levin, M.G. Ryskin, Yu.M. Shabelsky, A.G. Shuvaev, Sov. J. Nucl. Phys. 53, 657 (1991)
S. Catani, M. Ciafaloni, F. Hautmann, Nucl. Phys. B 366, 135 (1991)
J.C. Collins, R.K. Ellis, Nucl. Phys. B 360, 3 (1991)
B. Andersson et al. (Small-\(x\) Collaboration), Eur. Phys. J. C 25, 77 (2002)
J. Andersen et al. (Small-\(x\) Collaboration), Eur. Phys. J. C 35, 67 (2004)
J. Andersen et al. (Small-\(x\) Collaboration), Eur. Phys. J. C 48, 53 (2006)
R. Angeles-Martinez, A. Bacchetta, I.I. Balitsky, D. Boer, M. Boglione, R. Boussarie, F.A. Ceccopieri, I.O. Cherednikov, P. Connor, M.G. Echevarria, G. Ferrera, J. Grados Luyando, F. Hautmann, H. Jung, T. Kasemets, K. Kutak, J.P. Lansberg, A. Lelek, G. Lykasov, J.D. Madrigal Martinez, P.J. Mulders, E.R. Nocera, E. Petreska, C. Pisano, R. Placakyte, V. Radescu, M. Radici, G. Schnell, I. Scimemi, A. Signori, L. Szymanowski, S. Taheri Monfared, F.F. van der Veken, H.J. van Haevermaet, P. van Mechelen, A.A. Vladimirov, S. Wallon, Acta Phys. Pol. B 46, 2501 (2015)
H. Jung, M. Kraemer, A.V. Lipatov, N.P. Zotov, JHEP 01, 085 (2011)
H. Jung, M. Kraemer, A.V. Lipatov, N.P. Zotov, Phys. Rev. D 85, 0340 (2012)
S.P. Baranov, H. Jung, A.V. Lipatov, M.A. Malyshev, Eur. Phys. J. C 77, 772 (2017)
H. Jung, S.P. Baranov, M. Deak, A. Grebenyuk, F. Hautmann, M. Hentschinski, A. Knutsson, M. Kraemer, K. Kutak, A.V. Lipatov, N.P. Zotov, Eur. Phys. J. C 70, 1237 (2010)
V.N. Gribov, L.N. Lipatov, Sov. J. Nucl. Phys. 15, 438 (1972)
L.N. Lipatov, Sov. J. Nucl. Phys. 20, 94 (1975)
G. Altarelli, G. Parisi, Nucl. Phys. B 126, 298 (1977)
Yu.L. Dokshitzer, Sov. Phys. JETP 46, 641 (1977)
M. Ciafaloni, Nucl. Phys. B 296, 49 (1988)
S. Catani, F. Fiorani, G. Marchesini, Phys. Lett. B 234, 339 (1990)
S. Catani, F. Fiorani, G. Marchesini, Nucl. Phys. B 336, 18 (1990)
G. Marchesini, Nucl. Phys. B 445, 49 (1995)
E.A. Kuraev, L.N. Lipatov, V.S. Fadin, Sov. Phys. JETP 44, 443 (1976)
E.A. Kuraev, L.N. Lipatov, V.S. Fadin, Sov. Phys. JETP 45, 199 (1977)
I.I. Balitsky, L.N. Lipatov, Sov. J. Nucl. Phys. 28, 822 (1978)
F. Hautmann, H. Jung, Nucl. Phys. B 883, 1 (2014)
A.D. Martin, W.J. Stirling, R.S. Thorne, G. Watt, Eur. Phys. J. C 63, 189 (2009)
C. Peterson, D. Schlatter, I. Schmitt, P. Zerwas, Phys. Rev. D 27, 105 (1983)
H. Jung, arXiv:hep-ph/0411287
CMS Collaboration, Phys. Lett. B 771, 435 (2017)
P. Bolzoni, B.A. Kniehl, G. Kramer, Phys. Rev. D 88, 074035 (2013)
B.A. Kniehl, G. Kramer, Phys. Rev. D 60, 014006 (1999)
G. Bodwin, E. Braaten, G. Lepage, Phys. Rev. D 51, 1125 (1995)
P. Cho, A.K. Leibovich, Phys. Rev. D 53, 150 (1996)
P. Cho, A.K. Leibovich, Phys. Rev. D 53, 6203 (1996)
W.F. Palmer, E.A. Paschos, P.H. Soldan, Phys. Rev. D 56, 5794 (1997)
CLEO Collaboration, Phys. Rev. D 52, 2661 (1995)
BABAR Collaboration, Phys. Rev. D 67, 032002 (2003)
PDG Collaboration, Chin. Phys. C 40, 100001 (2016)
P. Bartalini, E.L. Berger, B. Blok, G. Calucci, R. Corke, M. Diehl, Yu. Dokshitzer, L. Fano, L. Frankfurt, J.R. Gaunt, S. Gieseke, G. Gustafson, D. Kar, C.-H. Kom, A. Kulesza, E. Maina, Z. Nagy, Ch. Roehr, A. Siodmok, M. Schmelling, W.J. Stirling, M. Strikman, D. Treleani, arXiv:1111.0469 [hep-ph]
H. Abramowicz, P. Bartalini, M. Baehr, N. Cartiglia, R. Ciesielski, E. Dobson, F. Ferro, K. Goulianos, B. Guiot, X. Janssen, H. Jung, Yu. Karpenko, J. Kaspar, J. Katzy, F. Krauss, P. Laycock, E. Levin, M. Mangano, Ch. Mesropian, A. Moraes, M. Myska, D. Moran, R. Muresan, Z. Nagy, T. Pierog, A. Pilkington, M. Poghosyan, T. Rogers, S. Sen, M.H. Seymour, A. Siodmok, M. Strikman, P. Skands, D. Treleani, D. Volyanskyy, K. Werner, P. Wijeratne, arXiv:1306.5413 [hep-ph]
S. Bansal, P. Bartalini, B. Blok, D. Ciangottini, M. Diehl, F.M. Fionda, J.R. Gaunt, P. Gunnellini, T. Du Pree, T. Kasemets, D. Ostermeier, S. Scopetta, A. Siodmok, A.M. Snigirev, A. Szczurek, D. Treleani, W.J. Waalewijn, arXiv:1410.6664 [hep-ph]
ATLAS Collaboration, New J. Phys. 15, 033038 (2012)
Acknowledgements
We thank F. Hautmann for very useful discussions and remarks. This research was supported by RFBR grant 16-32-00176-mol-a and grant of the President of Russian Federation NS-7989.2016.2. We are grateful to DESY Directorate for the support in the framework of Moscow – DESY project on Monte-Carlo implementation for HERA – LHC. M.A.M. was also supported by a grant of the foundation for the advancement of theoretical physics “Basis” 17-14-455-1.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Lipatov, A.V., Baranov, S.P., Jung, H. et al. Charmonia production from b-hadron decays at LHC with \(k_T\)-factorization: \(J/\psi \), \(\psi (2S)\) and \(J/\psi + Z\). Eur. Phys. J. C 78, 2 (2018). https://doi.org/10.1140/epjc/s10052-017-5489-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5489-y