Abstract
Observables sensitive to the anomalous production of events containing hadronic jets and missing momentum in the plane transverse to the proton beams at the Large Hadron Collider are presented. The observables are defined as a ratio of cross sections, for events containing jets and large missing transverse momentum to events containing jets and a pair of charged leptons from the decay of a \(Z/\gamma ^*\) boson. This definition minimises experimental and theoretical systematic uncertainties in the measurements. This ratio is measured differentially with respect to a number of kinematic properties of the hadronic system in two phase-space regions; one inclusive single-jet region and one region sensitive to vector-boson-fusion topologies. The data are found to be in agreement with the Standard Model predictions and used to constrain a variety of theoretical models for dark-matter production, including simplified models, effective field theory models, and invisible decays of the Higgs boson. The measurements use 3.2 fb\(^{-1}\) of proton–proton collision data recorded by the ATLAS experiment at a centre-of-mass energy of 13 \(\text {TeV}\) and are fully corrected for detector effects, meaning that the data can be used to constrain new-physics models beyond those shown in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Standard Model of particle physics (SM) is an extremely successful theory, describing the fundamental building blocks of nature and the interactions between them. Despite its many successes, it is known that the SM does not provide a complete description: for example it does not explain the abundance of dark matter in our universe, known to exist from astrophysical observations [1,2,3]. One of the main aims of the physics programme at the Large Hadron Collider (LHC) [4] is to find evidence of new phenomena, either via directly searching for the signatures predicted by specific scenarios beyond the Standard Model (BSM) or, as is the case in this paper, by performing a more general search for deviations from SM predictions.
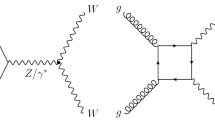
New physics phenomena at the LHC may manifest themselves as events with jets of collimated, mostly hadronic, particles and a momentum imbalance in the plane transverse to the LHC beams, known as missing transverse momentum, \(p_\mathrm {T}^\mathrm {miss}\). The \(p_\mathrm {T}^\mathrm {miss}\) may indicate the presence of particles that do not interact via the strong or electromagnetic interactions and therefore cannot be directly detected in the LHC detectors. These particles are referred to as invisible. In particular, new-physics models predicting the existence of weakly interacting massive particles (WIMPs), dark-matter candidates that could be produced at the LHC, could lead to such a signature [5]. As an example, a Feynman diagram is shown in Fig. 1a, where a mediator, A, is produced in association with a gluon-initiated jet and decays to a WIMP pair (\(\chi \bar{\chi }\)). Limits have previously been placed in such models by comparing the number of events in \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) final states in LHC data with the number of background events expected to be seen in the detector (the detector level) [6, 7]. Another possible production mechanism for the experimental observation of weakly interacting BSM particles is vector-boson fusion (VBF) [8], as shown in Fig. 1b. This is a topology similar to that in the invisible decay of a VBF-produced Higgs boson [9,10,11], for which limits have previously been set [12, 13] using detector-level data. The dominant SM process leading to the same final states is the production of a \(Z\) boson in association with jets, where the \(Z\) boson decays to a pair of neutrinos. Example diagrams are shown in Fig. 1c, d.
This paper presents a measurement of differential observables that are sensitive to the anomalous production of events containing one or more hadronic jets with high transverse momentum, \(p_{\text {T}}\), produced in association with a large \(p_\mathrm {T}^\mathrm {miss}\). The measurements are performed using data corresponding to an integrated luminosity of 3.2 fb\(^{-1}\) of proton–proton collisions at \(\sqrt{s}=13\) \(\text {TeV}\), collected by the ATLAS detector [14] in 2015. The observables are corrected for detector inefficiencies and resolutions and are presented at the particle level. They are constructed from a ratio of cross-sections,
defined in a fiducial phase space. The numerator is the fiducial cross-section for \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events, which corresponds to the fiducial cross-section for inclusive \(Z(\rightarrow \nu \bar{\nu })+\) jets production in the SM. The denominator is the fiducial cross-section for \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events, where the unobserved system that produces the \(p_\mathrm {T}^\mathrm {miss}\) in the numerator is replaced by an observed, opposite-sign, same-flavour pair of charged leptons consistent with originating from a \(Z/\gamma ^*\) boson. The lepton pair can be either a pair of electrons or muons. The jet system is required to satisfy very similar selection criteria in both the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) samples of events so as to significantly reduce experimental and theoretical uncertainties in the ratio measurement. The presence of BSM physics in the numerator would lead to a discrepancy between the measured ratio and that predicted by the SM.
The approach used in this paper allows for direct comparison of SM and BSM predictions at the particle level, without the need to simulate the effects of the ATLAS detector. This is computationally efficient and enables those without access to a precise simulation of the ATLAS detector to compare the data with predictions from alternative BSM models as they become available. Since each alternative BSM model may predict event signatures with different kinematic properties, the publication of the kinematic distributions enhances the usefulness and longevity of the data. Furthermore, future improvements in the predictions of the SM processes that contribute to the ratio can be compared to the particle-level data and limits in BSM models can be updated accordingly.
Particle-level measurements of SM processes are common in collider physics and have, on occasion, been used to set limits in BSM models (see e.g. [15]), although not to search for new physics in the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) final state. Moreover, a measurement of the particle-level ratio allows the denominator to provide a constraint on the dominant SM process contributing to the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) final state. Many sources of systematic uncertainty cancel in the ratio because the requirements on the hadronic system and the definition of the measured kinematic variables, determined from the hadronic system, are similar in the numerator \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and denominator \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events. This is made possible by treating the identified charged leptons in \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events as invisible when calculating the \(p_\mathrm {T}^\mathrm {miss}\). This cancellation occurs, for example, for phenomenological uncertainties in the prediction of initial-state parton radiation and experimental uncertainties in the jet reconstruction, energy scale and resolution.
The ratio measurements are presented in two phase-space regions: the \(\ge 1 \, \mathrm {jet}\) region, containing at least one high-\(p_{\text {T}}\) jet, and the VBF region, containing at least two high-\(p_{\text {T}}\) jets, and satisfying additional selection criteria to enhance the VBF process. This ratio is measured as a function of a number of kinematic properties of the hadronic system of the event and the statistical and systematic correlations between the different distributions are determined. The data and correlation information are made publicly available.
The remainder of this paper is laid out as follows. The ATLAS detector and event reconstruction are described in Sect. 2. The fiducial regions defined by particle-level objects and event selections, together with the measured variables, are detailed in Sect. 3. The \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) event samples are selected as described in Sect. 4. Samples of events were produced with Monte Carlo event generators and are used to correct the data for detector effects, to estimate background and signal contributions, and to assign systematic uncertainties to the results. Details of these samples are given in Sect. 5. Predicted backgrounds, explained in Sect. 6, are subtracted from the selected data and the ratio is computed. A correction for detector effects is applied to the ratios, as described in Sect. 7, so that they are defined at particle level with the definitions from Sect. 3. Systematic uncertainties in the measurement and theoretical predictions are summarised in Sect. 8. The detector-corrected events in the electron and muon channels are combined to form particle-level ratios to \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events, as described in Sect. 9. These are compared to the expected SM ratios and to the expected ratios including example BSM models in Sect. 10. The results are discussed in Sect. 11 and example limits are placed on BSM model parameters. Finally, conclusions are given in Sect. 12.
2 ATLAS detector and event reconstruction
The ATLAS detector [14, 16, 17] is a multipurpose particle detector with a cylindrical geometry. ATLAS consists of layers of tracking detectors, calorimeters, and muon chambers. The inner detector (ID) covers the pseudorapidity range \(|\eta | < 2.5\).Footnote 1 The ID is immersed in a 2 T magnetic field and measures the trajectories and momenta of charged particles. The calorimeter covers the pseudorapidity range \(|\eta | < 4.9\). Within \(|\eta | <2.47\), the finely segmented electromagnetic calorimeter identifies electromagnetic showers and measures their energy and position, providing electron identification together with the ID. The muon spectrometer (MS) surrounds the calorimeters and provides muon identification and measurement in the region \(|\eta | < 2.7\).
Jets are reconstructed from energy deposits in the calorimeters, using the anti-\(k_t\) jet algorithm [18, 19], with a jet-radius parameter of 0.4. The measured jet \(p_{\text {T}}\) is corrected [20] for the detector response and contributions to the jet energy from multiple proton–proton interactions (pileup). Jet quality selection criteria [21] are applied. Track-based variables are then used to suppress jets with \(|\eta |<2.4\) and \(p_{\text {T}} < 50\) \(\text {GeV}\) by requiring that a significant fraction of the tracks associated with each jet must have an origin compatible with the primary vertex in the event, which further suppresses jets from pileup interactions.
A muon is reconstructed by matching a track (or track segment) reconstructed in the MS to a track reconstructed in the ID. Its momentum is calculated by combining the information from the two systems and correcting for energy deposited in the calorimeters. Quality requirements are applied using the loose working point as described in Ref. [22]. An electron is reconstructed from an energy deposit (cluster) in the electromagnetic calorimeter matched to a track in the ID. Its momentum is computed from the cluster energy and the direction of the track. Electrons are distinguished from other particles using several identification criteria that rely on the shapes of electromagnetic showers as well as tracking and track-to-cluster matching quantities. The output of a likelihood function taking these quantities as input, similar to that described in Ref. [23], and using the loose working point described therein, is used to identify electrons. Data-driven energy/momentum scale corrections [22] are applied to both reconstructed muons and electrons. Leptons are required to be associated with the primary vertex, defined as the vertex with the highest \(\Sigma p_{\text {T}} ^2\) of its associated tracks, in order to suppress leptons originating from pileup and secondary decays. Hadronic decays of \(\tau \) leptons (\(\tau \rightarrow \) hadrons \(+ \nu \)) are predominantly characterised by the presence of one or three charged particles and possibly neutral pions. A multivariate boosted decision tree identification, based on calorimetric shower shape and track multiplicity of the \(\tau \) candidates, is used to reject jets faking \(\tau \) leptons. More details are given in Ref. [24], with the loose working point being used in this analysis.
The \(p_\mathrm {T}^\mathrm {miss}\) is reconstructed as the magnitude of the negative vector sum of the transverse momenta of all detected particles, as described in Ref. [25]. The \(p_\mathrm {T}^\mathrm {miss}\) calculation uses a soft term that is calculated using tracks within the ID which are not associated with jets or with leptons that are being treated as invisible particles. The momenta of calibrated jets with \(p_{\text {T}} > 20\) \(\text {GeV}\) are used.
Events in the numerator and the
 denominator are selected by a trigger that requires \(p_\mathrm {T}^\mathrm {miss}> 70\) \(\text {GeV}\), as computed in the final stage of the two-level trigger system. Since the momenta from muons are not included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation in this trigger, the muons appear to the trigger as invisible particles and hence the trigger can also be used to select
denominator are selected by a trigger that requires \(p_\mathrm {T}^\mathrm {miss}> 70\) \(\text {GeV}\), as computed in the final stage of the two-level trigger system. Since the momenta from muons are not included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation in this trigger, the muons appear to the trigger as invisible particles and hence the trigger can also be used to select
 events. This trigger is 100% efficient for the offline \(p_\mathrm {T}^\mathrm {miss}> 200\) \(\text {GeV}\) requirement used in the analysis. Events in the
events. This trigger is 100% efficient for the offline \(p_\mathrm {T}^\mathrm {miss}> 200\) \(\text {GeV}\) requirement used in the analysis. Events in the
 denominator are selected by a single-electron trigger, with an efficiency ranging between 93% and more than 99% for electrons with \(p_{\text {T}} >80\) \(\text {GeV}\), depending on their pseudorapidity.
denominator are selected by a single-electron trigger, with an efficiency ranging between 93% and more than 99% for electrons with \(p_{\text {T}} >80\) \(\text {GeV}\), depending on their pseudorapidity.
3 Particle-level objects, event selections and measured variables
The detector-corrected data are presented in fiducial regions defined in this section. The definition of the measured variables is also given. The final state of an event is defined using all particles with \(c\tau \) longer than 10 mm. Final-state particles that interact via the strong or electromagnetic interactions are referred to as visible particles, whereas those that interact via neither are referred to as invisible particles.
At particle level, the \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events for the denominator of \(R^{\mathrm {miss}}\) are required to have exactly one opposite-sign, same-flavour pair of promptFootnote 2 leptons: an \(e^+e^-\) or \(\mu ^+\mu ^-\) pair. The four-momenta of prompt photons within a cone of \(\Delta R= \sqrt{(\Delta \eta )^2 + (\Delta \phi )^2} = 0.1\) around each lepton are added to the four-momenta of the leptons and then removed from the final state, as motivated in Ref. [26]. These so-called ‘dressed’ leptons are required to satisfy the kinematic criteria detailed below.
Both the numerator and denominator of \(R^{\mathrm {miss}}\) are required to satisfy a number of phase-space-dependent criteria, summarised in Table 1. The fiducial phase-space definitions are motivated by the acceptance of the detector and the trigger [27], background reduction and, in the case of the VBF phase space, by the enhancement of the contribution from VBF processes. The \(p_\mathrm {T}^\mathrm {miss}\) value is defined as the magnitude of the negative vector sum of the transverse momenta of all visible final-state particles with \(|\eta |<4.9\), as this corresponds to the edge of the calorimeter. Muons with \(|\eta | > 2.5\) are excluded as they contribute only negligibly to the calculation of \(p_\mathrm {T}^\mathrm {miss}\) in this analysis, via a small energy deposition in the calorimeter. For the denominator, the \(p_\mathrm {T}^\mathrm {miss}\) variable is modified: the selected dressed leptons are excluded from the vector sum, making the variable very similar between numerator and denominator. Jets are reconstructed with the anti-\(k_t\) jet algorithm with jet radius parameter 0.4, excluding invisible particles and muons.
The event-level veto on (additional) leptons is applied to reduce the contribution from background processes. In particular, this requirement significantly reduces the background to \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events from \(W\) bosons produced in association with jets. The requirement on the difference in azimuthal angle between \(p_\mathrm {T}^\mathrm {miss}\) and any of the leading four jets with \(p_{\text {T}} > 30\) \(\text {GeV}\), \( \Delta \phi _{\mathrm {jet_{i},p_\mathrm {T}^\mathrm {miss}}}\) , suppresses backgrounds from multijet events, as is discussed in Sect. 6. For the denominator, the minimum \(p_{\text {T}}\) requirement for the leading lepton is much larger than the subleading lepton as events with a large \(p_\mathrm {T}^\mathrm {miss}\) tend to have one very high \(p_{\text {T}}\) lepton. The subleading lepton \(p_{\text {T}}\) can be much lower, in particular if it is in the direction opposite the decaying \(Z\) boson. The leading lepton \(p_{\text {T}} \) tends to be lower in \(t\bar{t}\) events, motivating the choice to make an asymmetric requirement. The requirement on the dilepton invariant mass to be between 66 and 116 \(\text {GeV}\) is implemented to minimise the contribution of the photon propagator and interference terms in the denominator, making it as similar as possible to the numerator.
In VBF, at least two jets are in the final state and, due to the colourless exchange, less hadronic activity in the rapidity space between the two jets is expected, which motivates the central-jet veto. The dijet invariant mass (\( m_{\mathrm {jj}}\) ) requirement suppresses the contribution from diboson events where one boson decays hadronically.
In order to increase the sensitivity to a range of targeted BSM scenarios, four differential measurements of \(R^{\mathrm {miss}}\) are made with respect to: \(p_\mathrm {T}^\mathrm {miss}\) in the \(\ge 1 \, \mathrm {jet}\) and VBF phase spaces, as well as \( m_{\mathrm {jj}}\) and \( \Delta \phi _{\mathrm {jj}}\) in the VBF phase space, where \( \Delta \phi _{\mathrm {jj}}\) is the difference in azimuthal angle between the two leading jets. Due to the larger mediator mass and higher energy scale of the interaction, many BSM signatures tend to have harder \(p_\mathrm {T}^\mathrm {miss}\) distributions than the SM processes, meaning that sensitivity to these models is enhanced in the high-\(p_\mathrm {T}^\mathrm {miss}\) region. Since the VBF process leads to events with a harder \( m_{\mathrm {jj}}\) spectrum than processes involving the strong production of dijets, the high-\( m_{\mathrm {jj}}\) region gives more discriminating power for VBF models. The expected \( \Delta \phi _{\mathrm {jj}}\) distribution varies between different BSM theories and could therefore give additional sensitivity and possibly help to distinguish between models, should a signal be seen.
4 Detector-level event selection
Events are required to contain a primary vertex with at least two associated tracks, each with \(p_{\text {T}} > 400\) \(\text {MeV}\). Events containing a jet with \(p_{\text {T}} > 20\) \(\text {GeV}\) not originating from a proton–proton interaction are rejected. Such jets are identified by jet quality selection criteria involving quantities such as the pulse shape of the energy depositions in the cells of the calorimeters, electromagnetic fraction in the calorimeter, calorimeter sampling fraction, or the fraction of energy coming from charged particles.
The kinematic selection criteria given in Table 1 are identically applied to detector-level objects, with an additional exclusion of electrons in the region \(1.37< |\eta | < 1.52\), which corresponds to the calorimeter barrel–endcap transition region, and in the region \(2.47< |\eta | < 2.5\), since electrons are identified only for \(|\eta | <2.47\). All electrons, as well as muons used for the lepton veto, are required to be isolated from other particles. In both cases, the LooseTrackOnly isolation working points described in Refs. [22, 23] are used. A veto on events containing an identified hadronically decaying \(\tau \) lepton, with the total \(p_{\text {T}} \) of the visible decay products being greater than 20 \(\text {GeV}\), is also applied to reduce the contribution from
 events to \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events. This veto is not applied at the particle level due to the complication of defining a hadronically decaying \(\tau \) lepton in terms of stable final-state particles.
events to \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events. This veto is not applied at the particle level due to the complication of defining a hadronically decaying \(\tau \) lepton in terms of stable final-state particles.
In this analysis, identified charged leptons are either vetoed or treated as invisible particles in the \(p_\mathrm {T}^\mathrm {miss}\) calculation. In particular, for the \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) denominator, the measured momenta of selected electrons, muons, and jets close to muons which are consistent with being associated with final-state radiation photons clustered close to the muon ID track, are treated as invisible. A jet is considered to be consistent with a final-state photon if its transverse momentum is less than twice the transverse momentum of the associated muon and it has fewer than five associated ID tracks. This makes \(p_\mathrm {T}^\mathrm {miss}\) very similar between numerator and denominator.
5 Monte Carlo simulation
Events containing \(Z\) and \(W\) bosons (collectively termed V) were generated using Monte Carlo (MC) event generators. Samples contributing to inclusive \(Z+\)jets production (\(Z \rightarrow \nu \bar{\nu }\) , \(Z/\gamma ^* \rightarrow \ell ^{+}\ell ^{-}\) and diboson ZV, where the \(Z\) decays to a \(\nu \bar{\nu }\), \(e^+e^-\) or \(\mu ^+\mu ^-\) pair and V is a hadronically decaying \(W\) or \(Z\) boson) are used for the detector corrections. Samples of
 (including WV where the \(W\) decays leptonically and the V decays hadronically), top–antitop quark pairs, single-top-quark and leptonically decaying diboson (WW, WZ, ZZ) events are used to estimate backgrounds.
(including WV where the \(W\) decays leptonically and the V decays hadronically), top–antitop quark pairs, single-top-quark and leptonically decaying diboson (WW, WZ, ZZ) events are used to estimate backgrounds.
Events containing single \(Z\) and \(W\) bosons in association with jets were simulated using the Sherpa v2.2.0 event generator [28]. Matrix elements were calculated for up to two additional parton emissions at next-to-leading-order (NLO) accuracy and up to four additional parton emissions at leading-order (LO) accuracy using the Comix [29] and OpenLoops [30] matrix element generators and merged with the Sherpa parton shower [31], which is based on Catani–Seymour subtraction terms. The merging of multi-parton matrix elements with the parton shower is achieved using an improved CKKW matching procedure [32, 33], which is extended to NLO accuracy using the MEPS@NLO prescription [34]. The NNPDF3.0nnlo parton distribution function (PDF) set [35] was used in conjunction with the dedicated parton-shower tuning developed by the Sherpa authors. These \(V+\)jets samples were produced with a simplified scale-setting prescription in the multi-parton matrix elements to improve the event generation speed. A theory-based reweighting of the jet-multiplicity distribution is applied, derived from event generation with the strict scale prescription. The samples are normalised to a next-to-next-to-leading-order (NNLO) prediction [36]. The full set-up is described in detail in Ref. [37]. Electroweakly produced \(V+\)jets as well as diboson production were generated using Sherpa v2.1.1 in conjunction with the CT10nlo [38] PDF set and the dedicated parton-shower tuning developed by the Sherpa authors. The full set-up is described in detail in Ref. [39].
Alternative samples of events with \(V+\)jets simulated using MG5_aMC@NLO v2.2.2 [40] at LO and interfaced to the Pythia v8.186 [41] parton shower are used for cross-checks and for the determination of systematic uncertainties. The ATLAS A14 set of tuned parameters [42] is used together with the NNPDF3.0nlo PDF set. These samples are also normalised to the NNLO prediction.
Top–antitop pair production [43], as well as single-top-quark production in the Wt [44] and s-channels [45, 46], were generated using the Powheg-Box v2 [47,48,49] event generator with the CT10nlo PDF set for the matrix element calculations. Single-top t-channel events were generated using the Powheg-Box v1 event generator. Parton showering, hadronisation, and the underlying event were provided by Pythia v6.428 [50] using the CTEQ6L1 PDF set [51] and the Perugia 2012 (P2012) set of tuned parton-shower parameters [52]. The full set-up of these top-quark samples is described in detail in Ref. [53]. The top-pair samples are normalised to a calculation at NNLO accuracy including soft-gluon resummation at next-to-next-to-leading logarithmic (NNLL) accuracy [54]. The single-top samples are normalised using an NLO calculation including the resummation of soft gluon terms at NNLL accuracy [55,56,57].
WIMP simplified signal models were simulated using Powheg-Box v2 (r3049) using the model described in Ref. [58]. This model implements the production of WIMP pairs with s-channel spin-1 mediator exchange at NLO precision. Events were generated with the NNPDF3.0nlo PDF set with parton showering using Pythia v8.205 [59] with the A14 [42] parameter set. This model has a coupling \(g_q\) of the SM quarks to the mediator, and a coupling \(g_{\chi }\) of dark-matter particles to the mediator. Couplings were set to a constant value of \(g_q = 0.25\) and \(g_{\chi }=1\), as recommended in Ref. [60]. A grid of samples was produced for WIMP masses ranging from 1 \(\text {GeV}\) to 1 \(\text {TeV}\) and axial-vector mediator masses between 10 \(\text {GeV}\) and 2 \(\text {TeV}\). More details of the samples are given in Ref. [6].
In order to assess the sensitivity to invisible decays of the Higgs boson, \(H \rightarrow ZZ \rightarrow 4\nu \) events were simulated using Powheg-Box v1 [61,62,63] with CT10 PDFs, and Pythia v8.165 simulating the parton shower, hadronisation and underlying event. The cross-sections and their uncertainties for Higgs boson production via vector-boson fusion, gluon–gluon fusion, and associated production are taken from Ref. [64].
In order to search for general signatures of Dirac-fermion dark-matter coupling to weak bosons, an implementation [65] of an effective field theory [8] (EFT) in FeynRules v2.3.1 [66] was used, with MadGraph5 v2.2.3 [40] used to simulate the hard interaction. This EFT includes ten possible dimension-five to dimension-seven operators with a range of possible Lorentz structures, including some with different charge-parity (CP) properties for the effective interaction between weak bosons and a dark matter candidate. This model was interfaced to Pythia v8.212 with the A14 parameter set and the NNPDF23LO [67] PDF to simulate the effects of parton showering, hadronisation and the underlying event.
All SM MC simulation samples were passed through GEANT4 [68, 69] for a full simulation [70] of the detector and are then reconstructed using the same analysis chain as the data. Scale factors are applied to the simulated events to correct for the small differences from data in the trigger, reconstruction, identification, isolation, and impact parameter efficiencies for leptons [22, 23]. Furthermore, the lepton and jet momentum scales and resolutions are adjusted to match the data. Additional proton–proton collisions in the same bunch crossing are overlaid. These are based on soft strong-interaction processes simulated with Pythia v8.186 using the MSTW2008lo PDF set [71] along with the A2 set of tuned parton-shower parameters [72]. The average number of proton–proton interactions per bunch crossing in this data set is 13.7.
6 Backgrounds
The dominant background in the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) numerator is from events containing a leptonically decaying \(W\) boson produced in association with jets, which contain \(p_\mathrm {T}^\mathrm {miss}\) associated with an invisible particle: in this case the neutrino in the \(W\) decay. Such events would pass the veto on additional leptons if the charged lepton (\(e, \mu \) or \(\tau \)) is not reconstructed or is outside the acceptance of the detector. This background includes contributions where the \(W\) boson originates from a top-quark decay or diboson events. The top-quark decay contribution to the \(W\) background amounts to approximately 18% (14%) in the \(\ge 1 \, \mathrm {jet}\) (VBF) phase spaces. The three lepton decay channels of the \(W\) background contribute approximately 18% (
 ), 12% (
), 12% (
 ) and 15% (
) and 15% (
 ) to the numerator. The size of the combined \(W\) background is similar to the SM \(Z \rightarrow \nu \bar{\nu }\) contribution to the numerator at low \(p_\mathrm {T}^\mathrm {miss}\), becoming less important at high \(p_\mathrm {T}^\mathrm {miss}\).
) to the numerator. The size of the combined \(W\) background is similar to the SM \(Z \rightarrow \nu \bar{\nu }\) contribution to the numerator at low \(p_\mathrm {T}^\mathrm {miss}\), becoming less important at high \(p_\mathrm {T}^\mathrm {miss}\).
The contribution from this background is estimated using two \(W\) control regions. A
 (
(
 ) control region is selected by requiring a muon (electron) that is isolated from other particles, with \(p_{\text {T}} {} > 25\) \(\text {GeV}\). The requirements on the jets, \(p_\mathrm {T}^\mathrm {miss}\), and the veto on additional leptons are identical to those of the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) signal region. In the
) control region is selected by requiring a muon (electron) that is isolated from other particles, with \(p_{\text {T}} {} > 25\) \(\text {GeV}\). The requirements on the jets, \(p_\mathrm {T}^\mathrm {miss}\), and the veto on additional leptons are identical to those of the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) signal region. In the
 control region, the muon is treated as an invisible particle in the \(p_\mathrm {T}^\mathrm {miss}\) calculation, in order to make the region as similar as possible to the signal region. This is because the signal region has a veto on reconstructed muons and so the muon is often not included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation. In the
control region, the muon is treated as an invisible particle in the \(p_\mathrm {T}^\mathrm {miss}\) calculation, in order to make the region as similar as possible to the signal region. This is because the signal region has a veto on reconstructed muons and so the muon is often not included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation. In the
 control region, the energy of the electron is included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation, calibrated as a jet. This is because the electron is usually included in the signal region for
control region, the energy of the electron is included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation, calibrated as a jet. This is because the electron is usually included in the signal region for
 events, where the electron is generally inside the acceptance of the calorimeter, but is not identified, as a veto on identified electrons is applied in the signal region.
events, where the electron is generally inside the acceptance of the calorimeter, but is not identified, as a veto on identified electrons is applied in the signal region.
 events, where the \(\tau \) decay includes a muon (electron), are included in the
events, where the \(\tau \) decay includes a muon (electron), are included in the
 (
(
 ) control regions so that the contribution of these events to the signal region is also included in this estimate.
) control regions so that the contribution of these events to the signal region is also included in this estimate.
The data in the
 and
and
 control regions are collected using the \(p_\mathrm {T}^\mathrm {miss}\) and single-electron triggers discussed in Sect. 4 and are corrected for lepton inefficiencies on an event-by-event basis using \(p_{\text {T}}\)- and \(\eta \)-dependent lepton reconstruction, identification and isolation efficiencies, \(\epsilon \), that were previously determined from data [22, 23]. The data in the
control regions are collected using the \(p_\mathrm {T}^\mathrm {miss}\) and single-electron triggers discussed in Sect. 4 and are corrected for lepton inefficiencies on an event-by-event basis using \(p_{\text {T}}\)- and \(\eta \)-dependent lepton reconstruction, identification and isolation efficiencies, \(\epsilon \), that were previously determined from data [22, 23]. The data in the
 control region are also corrected for the single-electron trigger inefficiency. A small background contribution from multijet events in the control region is estimated using dedicated MC simulation and subtracted from the data. The efficiency- and multijet-corrected data are then used to predict the contribution from
control region are also corrected for the single-electron trigger inefficiency. A small background contribution from multijet events in the control region is estimated using dedicated MC simulation and subtracted from the data. The efficiency- and multijet-corrected data are then used to predict the contribution from
 and
and
 events in the signal, which contains two types of events: those for which the lepton is inside the detector acceptance with \(p_{\text {T}} {} > 7\) \(\text {GeV}\) but does not pass the lepton reconstruction and identification criteria, and those with a lepton that is outside of the detector acceptance or has \(p_{\text {T}} {} < 7\) \(\text {GeV}\). The in-acceptance contribution is determined for each bin of a given distribution from the efficiency-corrected data in the control region by applying an additional weight of \(\left( 1 - \epsilon \right) \) per event as well as correcting for the small difference in lepton fiducial acceptance between the control region and the signal region, using an acceptance-correction factor that is estimated using MC simulation. The out-of-acceptance contribution is obtained by extrapolating efficiency-corrected in-acceptance data using again acceptance corrections derived from simulation. As a cross-check, the \(W\) background estimate is also determined using an alternative method, described in Ref. [6], where no efficiency weights are applied to data and the simulation is used to extrapolate from the control region to the signal region. Compatible results are found.
events in the signal, which contains two types of events: those for which the lepton is inside the detector acceptance with \(p_{\text {T}} {} > 7\) \(\text {GeV}\) but does not pass the lepton reconstruction and identification criteria, and those with a lepton that is outside of the detector acceptance or has \(p_{\text {T}} {} < 7\) \(\text {GeV}\). The in-acceptance contribution is determined for each bin of a given distribution from the efficiency-corrected data in the control region by applying an additional weight of \(\left( 1 - \epsilon \right) \) per event as well as correcting for the small difference in lepton fiducial acceptance between the control region and the signal region, using an acceptance-correction factor that is estimated using MC simulation. The out-of-acceptance contribution is obtained by extrapolating efficiency-corrected in-acceptance data using again acceptance corrections derived from simulation. As a cross-check, the \(W\) background estimate is also determined using an alternative method, described in Ref. [6], where no efficiency weights are applied to data and the simulation is used to extrapolate from the control region to the signal region. Compatible results are found.
There is no specific
 control region for hadronically decaying taus, as it is difficult to obtain a pure sample of
control region for hadronically decaying taus, as it is difficult to obtain a pure sample of
 events in data. Instead, background predictions for
events in data. Instead, background predictions for
 with hadronically decaying \(\tau \) leptons are obtained by reweighting the simulated
with hadronically decaying \(\tau \) leptons are obtained by reweighting the simulated
 events, in each bin of each distribution, by the ratio of efficiency-corrected data to simulation determined in the
events, in each bin of each distribution, by the ratio of efficiency-corrected data to simulation determined in the
 or
or
 control regions. The midpoint of the two predictions, obtained using the two control regions, is taken as the final
control regions. The midpoint of the two predictions, obtained using the two control regions, is taken as the final
 prediction and the difference between the midpoint and the two predictions is taken as a systematic uncertainty. This choice is made because a hadronically decaying \(\tau \) lepton is often included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation, calibrated as a jet, which is similar to the
prediction and the difference between the midpoint and the two predictions is taken as a systematic uncertainty. This choice is made because a hadronically decaying \(\tau \) lepton is often included in the \(p_\mathrm {T}^\mathrm {miss}\) calculation, calibrated as a jet, which is similar to the
 control region. However, the \(\tau \) decay includes a neutrino, meaning that some part of it is invisible, which is similar to the
control region. However, the \(\tau \) decay includes a neutrino, meaning that some part of it is invisible, which is similar to the
 control region.
control region.
A much smaller background to the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events arises from multijet events in which one or more jets are mismeasured leading to a large measured \(p_\mathrm {T}^\mathrm {miss}\). This implies that the \(p_\mathrm {T}^\mathrm {miss}\) direction is likely to point towards one of the jets and so most of this background is removed by the \( \Delta \phi _{\mathrm {jet_{i},p_\mathrm {T}^\mathrm {miss}}}\) requirement. The remaining background is estimated using a control region where at least one of the four leading jets satisfies the criterion \( \Delta \phi _{\mathrm {jet_{i},p_\mathrm {T}^\mathrm {miss}}} < 0.1\). A large multijet data sample is obtained from events selected with single-jet triggers. These control events are required to be well measured, meaning that the \(p_\mathrm {T}^\mathrm {miss}\) is low. In order to obtain a sample of events that pass the \(p_\mathrm {T}^\mathrm {miss}\) selection, the jets in these events are smeared 25,000 times per multijet control event, according to the full jet response distribution. This sample is used to extrapolate between the control region and the signal region. The multijet background amounts to 2% in the first \(p_\mathrm {T}^\mathrm {miss}\) bin, rapidly becoming negligible in the higher \(p_\mathrm {T}^\mathrm {miss}\) bins. The small (0.5%) \(Z/\gamma ^* \rightarrow \ell ^{+}\ell ^{-}\) background to the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events is estimated using MC simulation.
The background to \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events is dominated by top–antitop quark pairs, with smaller contributions from diboson, single-top-quark, \(W\) + jet and \(Z\rightarrow \tau ^{+}\tau ^{-}\) events. These backgrounds are all estimated with MC simulation together with a control region that selects differently flavoured \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events (an \(e^{\pm }\mu ^{\mp }\) pair). All other selection criteria are the same. This control region removes the contribution from same-flavour \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events but retains contributions from the background processes. Discrepancies between data and simulation of up to 50% are seen in the control region, depending on the phase space and the kinematic region. A reweighting factor is found by fitting a polynomial to the ratio of data to simulation in the control region and is applied to the background contribution in the signal region. The full difference between the background prediction with and without this reweighting is taken as a systematic uncertainty.
Figures 2 and 3 compare detector-level data to MC simulation of \(Z \rightarrow \nu \bar{\nu }\) and
 events, plus estimated backgrounds for selected \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and selected \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events in the signal region. Distributions of \(p_\mathrm {T}^\mathrm {miss}\) in the \(\ge 1 \, \mathrm {jet}\) and VBF phase spaces and for \( m_{\mathrm {jj}}\) and \( \Delta \phi _{\mathrm {jj}}\) in the VBF phase space are compared. For both the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) event rates, the data are above the predictions from MC simulation and estimated backgrounds. However, they are consistent within the systematic uncertainties, which are discussed in Sect. 8 in more detail.
events, plus estimated backgrounds for selected \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and selected \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events in the signal region. Distributions of \(p_\mathrm {T}^\mathrm {miss}\) in the \(\ge 1 \, \mathrm {jet}\) and VBF phase spaces and for \( m_{\mathrm {jj}}\) and \( \Delta \phi _{\mathrm {jj}}\) in the VBF phase space are compared. For both the \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) and \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) event rates, the data are above the predictions from MC simulation and estimated backgrounds. However, they are consistent within the systematic uncertainties, which are discussed in Sect. 8 in more detail.
Comparisons between detector-level distributions for data and MC simulation of \(Z \rightarrow \nu \bar{\nu }\) and
 events plus predicted backgrounds in selected a, c
\(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events and b, d
\(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events as a function of the \(p_\mathrm {T}^\mathrm {miss}\) variable in the a, b
\(\ge 1 \, \mathrm {jet}\) phase space and c, d VBF phase space. The lower panel shows the ratio of data to the Standard Model prediction. The error bars show the statistical uncertainty of the data. Uncertainties in the predictions are shown as hatched bands and include the statistical component as well as systematic contributions from theoretical predictions, lepton efficiencies and jet energy scales and resolutions to the MC predictions and uncertainties in the data-driven background estimates, explained in Sect. 8
events plus predicted backgrounds in selected a, c
\(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events and b, d
\(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events as a function of the \(p_\mathrm {T}^\mathrm {miss}\) variable in the a, b
\(\ge 1 \, \mathrm {jet}\) phase space and c, d VBF phase space. The lower panel shows the ratio of data to the Standard Model prediction. The error bars show the statistical uncertainty of the data. Uncertainties in the predictions are shown as hatched bands and include the statistical component as well as systematic contributions from theoretical predictions, lepton efficiencies and jet energy scales and resolutions to the MC predictions and uncertainties in the data-driven background estimates, explained in Sect. 8
Comparisons between detector-level distributions for data and MC simulation of \(Z \rightarrow \nu \bar{\nu }\) and
 events plus predicted backgrounds in selected a, c
\(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events and b, d
\(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events as a function of a, b
\( m_{\mathrm {jj}}\) and c, d
\( \Delta \phi _{\mathrm {jj}}\) in the VBF phase space. The lower panel shows the ratio of data to the Standard Model prediction. The error bars show the statistical uncertainty of the data. Uncertainties in the predictions are shown as hatched bands and include the statistical component as well as systematic contributions from theoretical predictions, lepton efficiencies and jet energy scales and resolutions to the MC predictions and uncertainties in the data-driven background estimates, explained in Sect. 8
events plus predicted backgrounds in selected a, c
\(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) events and b, d
\(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events as a function of a, b
\( m_{\mathrm {jj}}\) and c, d
\( \Delta \phi _{\mathrm {jj}}\) in the VBF phase space. The lower panel shows the ratio of data to the Standard Model prediction. The error bars show the statistical uncertainty of the data. Uncertainties in the predictions are shown as hatched bands and include the statistical component as well as systematic contributions from theoretical predictions, lepton efficiencies and jet energy scales and resolutions to the MC predictions and uncertainties in the data-driven background estimates, explained in Sect. 8
7 Detector corrections
The data are corrected for the inefficiencies and resolutions of the detector and trigger and are presented in terms of particle-level variables as defined in Sect. 3. Due to the similarity in the \(p_\mathrm {T}^\mathrm {miss}\) and jet selections between numerator and denominator, corrections for the \(p_\mathrm {T}^\mathrm {miss}\) and jet-based variables arising from the jet energy resolutions and scales almost completely cancel in the ratio. Similarly, the correction factors related to the lepton veto efficiencies cancel in the ratio. The dominant remaining correction factor arises from the inefficiency of reconstructing the charged leptons in the denominator of the ratio. The correction factor is defined as the ratio of \(R^{\mathrm {miss}}\) at particle level to \(R^{\mathrm {miss}}\) at detector level using \(Z \rightarrow \nu \bar{\nu }\) and \(Z/\gamma ^{*} \rightarrow \ell ^{+}\ell ^{-}\) MC simulation, in bins of the measured variables. The correction factor decreases with \(p_\mathrm {T}^\mathrm {miss}\) from 0.9 to 0.85 in the muon channel and increases with \(p_\mathrm {T}^\mathrm {miss}\) from 0.7 to 0.8 in the electron channel. The number is larger for muons than for electrons because the reconstruction efficiency for muons is higher for the selection criteria used in this analysis.
Event migration between bins in the distributions, due to differences in the particle-level and detector-level variables, is small due to the relatively wide bins and therefore ignored. In the absence of a BSM signal, dependencies of the migrations on the underlying distributions are very similar for the numerator and denominator and therefore systematic uncertainties arising from this source cancel in the ratio. The possible impact of signals on the correction factors has been studied and found to be small. The presence of a large BSM component in the numerator due to WIMP production with an axial-vector mediator mass of 1 \(\text {TeV}\) and a WIMP mass of 150 \(\text {GeV}\) (which has very different event kinematics to the SM processes) changes the correction factor by less than 0.5%. The injected BSM model events have a \(p_\mathrm {T}^\mathrm {miss}\) distribution that is much harder than the \(Z \rightarrow \nu \bar{\nu }\) contribution to the numerator, leading to changes in \(R^{\mathrm {miss}}\) of 4% at low \(p_\mathrm {T}^\mathrm {miss}\) and 50% at high \(p_\mathrm {T}^\mathrm {miss}\). Such a variation is much larger than the differences seen between data and SM simulation. Furthermore, injecting a Gaussian BSM contribution that adds events to a single bin (but remains consistent with the data) is also found to have a very small impact; the largest change in the correction factor is 2%, in the second bin of the \(p_\mathrm {T}^\mathrm {miss}\) distribution, which is small compared to the systematic uncertainties. This test is an extreme example, where it is assumed that the full difference between the SM prediction and data in the \(R^{\mathrm {miss}}\) ratio is due to BSM physics in the numerator. It is therefore concluded that the presence of any BSM model consistent with the data would lead to only small changes in the correction factors and that these models can be constrained by the detector-corrected results. Larger BSM contributions that could cause more significant changes in the correction factors have already been excluded with the detector-level data.
8 Systematic and statistical uncertainties
Uncertainties in the measured detector-corrected ratios are discussed in this section and summarised in Table 2. The dominant experimental systematic uncertainties come from the reconstruction and isolation efficiency of muons and the reconstruction, isolation and trigger efficiency of electrons. These uncertainties affect the detector corrections, the \(W\) background predictions from leptonic control regions and the backgrounds to \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events. A smaller uncertainty in the \(\tau \) reconstruction efficiency, affecting the \(\tau \) veto, is also included. These are collectively labelled “Lepton efficiency” in the table. Uncertainties in the jet energy scale and resolution, labelled “Jets” in the table, affect the background predictions as well as the detector corrections. The latter arises due to small differences between the selected events for the numerator and denominator, such as the removal of jets close to leptons. The uncertainty from the difference in the choice of control region for the
 background prediction, described in Sect. 6, is also included. For the multijet background estimation a 50% uncertainty in the number of predicted events, together with a smaller uncertainty found by varying the selection criteria for events used as input for the smearing method, is assumed. The difference between the reweighted and nominal MC simulation background prediction of \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events is taken as an uncertainty. The reweighting factor is obtained from an \(e^{\pm }\mu {\mp }\) control region, described in Sect. 6. Statistical uncertainties from the finite size of the MC simulation samples used to determine the detector corrections, in the \(W\) control region data, and MC simulation samples used for extrapolations are also included.
background prediction, described in Sect. 6, is also included. For the multijet background estimation a 50% uncertainty in the number of predicted events, together with a smaller uncertainty found by varying the selection criteria for events used as input for the smearing method, is assumed. The difference between the reweighted and nominal MC simulation background prediction of \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events is taken as an uncertainty. The reweighting factor is obtained from an \(e^{\pm }\mu {\mp }\) control region, described in Sect. 6. Statistical uncertainties from the finite size of the MC simulation samples used to determine the detector corrections, in the \(W\) control region data, and MC simulation samples used for extrapolations are also included.
Three categories of theoretical uncertainties are considered. Firstly, an uncertainty of 30% in the cross-section of processes involving top quarks in the numerator is assigned. This indirectly affects the extrapolation of \(W\) events to the signal region by altering the number of top quark events in the control regions. The uncertainty value is motivated by top-quark-enhanced control regions constructed using the same criteria as the \(W\) control regions but in addition requiring either one or two jets consistent with containing a b-hadron. Discrepancies between MC simulation and data of up to 30% are seen in these control regions, which justifies the large uncertainty. Secondly, theoretical uncertainties that affect the extrapolations between the control and signal regions for \(W\) backgrounds are included. These are estimated by varying the factorisation, renormalisation, resummation scales (each scale varied by factors of 0.5 and 2) and the CKKW matching [32, 33] scale between 30 \(\text {GeV}\) and 15 \(\text {GeV}\) (the nominal being 20 \(\text {GeV}\)). These variations were found to affect the control and signal regions in the same way and the resulting uncertainties are therefore treated as fully correlated between the two. PDF uncertainties are derived for the nominal NNPDF3.0nnlo PDF set [35] as well as the MMHT2014 [73] and CT14 [74] PDF sets using their recommended PDF uncertainty prescription. A combined PDF uncertainty is then obtained from the envelope of the three PDF families and their respective uncertainties. An uncertainty from the strong coupling constant \(\alpha _{\mathrm {S}} \left( m_{\mathrm {Z}}\right) \) is derived using up and down variations to 0.117 and 0.119, respectively (the nominal value being 0.118). Thirdly, the change in the \(W\) background predictions when using Sherpa [28] v2.1.1 (which uses the CT10nlo [38] PDF set and has some technical differences in the parton shower compared to v2.2.0) or MG5_aMC@NLO v2.2.2 [40] instead of Sherpa v2.2.0 is considered. The second and third theoretical sources are included as “W theory” in Table 2. The correction factors do not change significantly when varying the SM MC event generator.
For each of the three data samples (\(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\), \(e^+e^- + \mathrm {jets}\) and \(\mu ^+\mu ^- + \mathrm {jets}\)), the statistical uncertainty is taken as the Poisson error. For bins containing a small number of events, this uncertainty in the denominator leads to an asymmetric uncertainty in the ratio. Table 2 summarises the size of each systematic uncertainty and the statistical uncertainty from the data for the lowest and highest \(p_\mathrm {T}^\mathrm {miss}\) bins in the \(\ge 1 \, \mathrm {jet}\) phase space and the lowest and highest \( m_{\mathrm {jj}}\) bins in the VBF phase space of the combined ratio. The uncertainties vary monotonically as a function of the respective observable.
9 Combination
After subtracting the estimated backgrounds from the selected \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) event sample in the data, and applying the bin-by-bin detector correction factor, the electron and muon denominators are combined using the best linear unbiased estimate (BLUE) combination method [75], which takes into account the relative precision of the two measurements. The technique correlates the statistical and systematic uncertainties between the two measurements and between all bins in all distributions. The combined result produces an average for \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) of one flavour in the denominator. The combination is iterated once, replacing the statistical uncertainty in the observed number of \(Z \rightarrow \mu \mu \) and
 events with that obtained from the expected number of events after the first combination. This removes the effect of undue weight being given to the channel in which the number of events has fluctuated down. In the combination, statistical correlations between bins are accounted for using a bootstrap method [76]. The
events with that obtained from the expected number of events after the first combination. This removes the effect of undue weight being given to the channel in which the number of events has fluctuated down. In the combination, statistical correlations between bins are accounted for using a bootstrap method [76]. The
 background uncertainty is assumed to be fully correlated or anti-correlated between bins, depending on whether the fit to estimate
background uncertainty is assumed to be fully correlated or anti-correlated between bins, depending on whether the fit to estimate
 background events increases or decreases the result from MC simulation in a given bin. The correlation between bins for the electron and muon efficiency uncertainties is found by considering the separate sources that contribute to the total uncertainties. All other sources of systematic uncertainty are assumed to be fully correlated across bins in the combination. The p-value for the compatibility of the two channels for all four distributions is 74%. The ratio is then formed by subtracting the estimated backgrounds from the selected \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) event sample in the data and dividing by the combined denominator. Again, each source of systematic uncertainty is assumed to be fully correlated between numerator and denominator. A cross-check using a maximum-likelihood fitting method gives consistent results.
background events increases or decreases the result from MC simulation in a given bin. The correlation between bins for the electron and muon efficiency uncertainties is found by considering the separate sources that contribute to the total uncertainties. All other sources of systematic uncertainty are assumed to be fully correlated across bins in the combination. The p-value for the compatibility of the two channels for all four distributions is 74%. The ratio is then formed by subtracting the estimated backgrounds from the selected \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) event sample in the data and dividing by the combined denominator. Again, each source of systematic uncertainty is assumed to be fully correlated between numerator and denominator. A cross-check using a maximum-likelihood fitting method gives consistent results.
10 Results
Figure 4 shows the four combined differential measurements of \(R^{\mathrm {miss}}\) compared to the average of the Sherpa v2.2.0 SM particle-level predictions for the muon and electron channels. The measurement is consistent with the SM prediction within statistical uncertainties. The uncertainty in the SM prediction, found from the factorisation and renormalisation scale variations as well as the NNPDF3.0nnlo PDF uncertainty, explained in Sect. 8, is shown as a red hatched band in the figure. The SM predictions do not include NLO electroweak corrections beyond final-state photon radiation. These corrections were studied in Ref. [77] for the \(Z\) boson production at a centre-of-mass energy of 8 \(\text {TeV}\) and are very similar for the numerator and denominator with a residual effect of up to 1% on the ratio.
Measured \(R^{\mathrm {miss}}\) as a function of a \(p_\mathrm {T}^\mathrm {miss}\) in the \(\ge 1 \, \mathrm {jet}\) region, b \(p_\mathrm {T}^\mathrm {miss}\) in the VBF region, c \( m_{\mathrm {jj}}\) in the VBF region and d \( \Delta \phi _{\mathrm {jj}}\) in the VBF region. Statistical uncertainties are shown as error bars and the total statistical and systematic uncertainties are shown as solid grey bands. The results are compared to the SM prediction and to SM+BSM for four BSM models. One is a simplified model of WIMP production with an s-channel exchange of an axial-vector mediator with mass of 1 \(\text {TeV}\) coupling to quarks and a WIMPs with a mass of 10 \(\text {GeV}\), another represents the Higgs boson decaying to invisible particles with 50% branching fraction, and another two represent the predictions of two EFT operators allowing the production of WIMP dark matter through interactions with vector bosons (with differing charge-parity properties in the interaction). The \(R^{\mathrm {miss}}\) values of the third and fourth models in the highest \(p_\mathrm {T}^\mathrm {miss}\) bin in the \(\ge 1 \, \mathrm {jet}\) region are 18.8 and 38.3, respectively, and in the highest \(p_\mathrm {T}^\mathrm {miss}\) bin in the VBF region the fourth model has an \(R^{\mathrm {miss}}\) value of 19.4. The red hatched error bars correspond to the uncertainty in the SM prediction. The bottom panel shows the ratio of data to the SM prediction
Also shown in the Fig. 4 is a comparison with SM+BSM for four BSM models. These four models comprise a simplified model for WIMP production with an s-channel exchange of an axial-vector mediator with a mass of 1 \(\text {TeV}\) and a WIMP mass of 10 \(\text {GeV}\), a Higgs boson decaying to invisible particles with 50% branching fraction, and two examples of effective field theory operators (each with different charge-parity properties) involving couplings of WIMP dark-matter candidates with vector bosons. These models are described in Sect. 5.
11 Discussion
In Fig. 4a, b, both the measurements and the SM predictions show a ratio \(R^{\mathrm {miss}}\) of approximately 7.5 at \(p_\mathrm {T}^\mathrm {miss}{} = 200\) \(\text {GeV}\), decreasing with \(p_\mathrm {T}^\mathrm {miss}\) to approximately 6, which is very close to the SM ratio of branching fractions in the numerator and denominator of 5.9 [78].Footnote 3 The ratio is larger at lower \(p_\mathrm {T}^\mathrm {miss}\) values due to the fiducial requirements on the charged leptons in the denominator. At higher \(p_\mathrm {T}^\mathrm {miss}\) values the leptons are more central and have larger \(p_{\text {T}}\) , and are therefore more likely to pass the fiducial requirements. The removal of jets overlapping with charged leptons, described in Sect. 3, is only relevant to the denominator. In particular, a slight increase in the ratio towards large \( \Delta \phi _{\mathrm {jj}}\) values is seen, indicating that jets with this topology are more likely to be removed in the denominator. The data and SM predictions are in agreement with an overall p-value including all distributions of 22% taking into account statistical and systematic correlations. In addition to the measured ratios, a covariance matrix for all four distributions, taking into account the statistical and systematic correlations between all bins in the data, is produced using a bootstrap procedure. When forming the covariance matrix the uncertainties are symmetrised by taking the maximum of the upward and downward uncertainties.
The detector-corrected ratio for all four distributions, together with the covariance matrix for the statistical and systematic uncertainties, as well as model uncertainties in the SM prediction for the numerator and denominator, and acceptance uncertainties in the WIMP model, are used to set limits on the mass of the axial-vector mediator (\(m_A\)) and WIMP candidate (\(m_\chi \)). Factors affecting the WIMP model signal acceptance include uncertainties in the modelling of initial- and final-state radiation in simulated samples, uncertainties in PDFs and the choice of \(\alpha _{\mathrm {S}}\left( m_{\mathrm {Z}}\right) \), and the choice of renormalisation and factorisation scales.
Limits on dark-matter production models are set by first constructing the \(\chi ^2\) function
where \(\mathbf {y}_\mathrm {data}\) and \(\mathbf {y}_\mathrm {pred}\) are the vectors of the measured \(R^{\mathrm {miss}}\) values and the predicted \(R^{\mathrm {miss}}\) values for the hypothesis under test across the four distributions under study, C is the total covariance matrix defined as the sum of the statistical, experimental systematic and theoretical systematic covariances. The \(\mathrm {CL}_\mathrm {s}\) technique [79, 80] evaluated using the asymptotic approximation [81] is used to derive upper limits.
The overall rate and kinematic properties of events in the axial-vector mediator WIMP model under study are defined by four parameters: the WIMP candidate mass, the mediator mass and the strengths of the mediator interaction with quarks and WIMPs. The expected and observed 95% confidence level (CL) exclusion limits as a function of mediator and WIMP mass are shown in Fig. 5, for fixed mediator couplings of \(g_q = 0.25\) and \(g_\chi = 1\). Expected limits are shown with \(\pm 1\sigma \) bands indicating the range of the expected limit in the absence of a signal. Observed limits are shown with a band including the effect of \(\pm 1\sigma \) theoretical uncertainties in the WIMP model cross-section. Also highlighted is the region where perturbative unitarity is violated (where \(m_\chi >\sqrt{\pi /2}\,m_A\)) [82]. The points in the mass plane compatible with the relic density measured by Planck [83] and WMAP [84] are represented by a red continuous line, with WIMP masses below this line or mediator masses to the right of this line corresponding to dark-matter overproduction. The highest mediator mass observed (expected) to be excluded at 95% CL is 1.24 \(\text {TeV}\) (1.09 \(\text {TeV}\)). For comparison, limits set using detector-level observables [6] are also shown. For high mediator masses, the expected limits in the present analysis are slightly weaker, due to the limited number of events in the denominator, whereas the observed limits are slightly stronger compared to the detector-level analysis. This difference between expected and observed limits is driven entirely by systematic uncertainty correlations between bins of the corrected distributions. Switching between using the default correlation model and a simple correlation model assuming 100% correlation between bins for each source of experimental systematic uncertainty changes the observed limit in mediator mass by approximately 10 \(\text {GeV}\). The measurements presented in this paper have enhanced sensitivity to models with large WIMP masses and low mediator masses, with respect to the detector-level analysis presented in Ref. [6], due to the use of a larger fiducial volume and the use of differential information with associated correlations.
Exclusion contours (at 95% CL) in the WIMP–mediator mass plane for a simplified model with an axial-vector mediator and couplings \(g_q = 0.25\) and \(g_{\chi }=1\). The solid purple (green) curve shows the observed (expected) limit. The yellow filled region around the expected limit indicates the effect of \(\pm 1\sigma \) experimental uncertainties in the expected limit. The red curve corresponds to the expected relic density. The grey hatched region shows the region of non-perturbativity defined by WIMP mass greater than \(\sqrt{\pi /2}\) times the mediator mass. Also shown, for comparison, are limits set using detector-level event counts from Ref. [6]. The exclusion is based on the global fit to the \(p_\mathrm {T}^\mathrm {miss}\) distributions in the \(\ge 1 \, \mathrm {jet}\) and VBF phase spaces, and the \( m_{\mathrm {jj}}\) and \( \Delta \phi _{\mathrm {jj}}\) distributions in the VBF phase space
The detector-corrected data are also used to search for Higgs boson decays to invisible particles in the same manner. Limits are placed on the production rate of the Higgs boson multiplied by its branching fraction to invisible particles relative to the total Higgs boson production rate as predicted by the SM [85]. The expected 95% CL upper limit for a Higgs boson with a mass of 125 \(\text {GeV}\) is found to be 0.59 with a range of [0.47, 1.13] from \(\pm 1\sigma \) experimental uncertainties. The observed upper limit at 95% CL is 0.46. The most important distribution for setting limits in this model is \( m_{\mathrm {jj}}\) , although some additional expected sensitivity is achieved from \( \Delta \phi _{\mathrm {jj}}\) . The observed limits are stronger than expected due to systematic uncertainty correlations between bins in the corrected ratios. This is to be compared with an exclusion limit of 0.28 (0.31 expected) at 95% CL using a 20 fb\(^{-1}\) 8 \(\text {TeV}\) data set [12], with an event selection optimised for this particular process.
The detector-corrected data are further used to set limits on the production of Dirac-fermion dark matter in a generalised effective field theory (EFT) where dark matter interacts only with electroweak bosons. Limits are set as a function of the invariant mass of the dark-matter candidate and the EFT scale, \(\Lambda \), which can be related to a UV-complete model by the relationship \(1/\Lambda ^2 \sim g_\mathrm {SM}\, g_\chi /M^2\) where \(g_\mathrm {SM}\) and \(g_\chi \) would be couplings of the SM and dark-matter particles to some hypothetical heavy mediating particle with mass M. The scenario where production is dominated by two specific dimension-seven effective operators, \(\bar{\chi }\chi V^{\mu \nu }V_{\mu \nu }\) and \(\bar{\chi }\chi \varepsilon ^{\mu \nu \rho \sigma } V_{\mu \nu }V_{\rho \sigma }\), with differing CP properties in the interaction between two electroweak bosons (\(V=W/Z\)) and two dark-matter particles is considered. This EFT is described in Ref. [8] where an assessment of the EFT validity for these operators is also conducted. These operators are particularly interesting as sensitivity benchmarks since they are insensitive to constraints from Z-boson invisible-width measurements.
Figure 6 shows the 95% CL expected and observed limits extracted from the fit to all four measured distributions, compared to indirect-detection limits. For the CP-conserving operator, expected (observed) limits on the EFT scale range from 0.78 (0.89) \(\text {TeV}\) at low (\(<200\) \(\text {GeV}\)) dark-matter mass to 0.61 (0.71) TeV at dark-matter masses of 1 \(\text {TeV}\). Limits for the CP-violating operator are stronger than for the CP-conserving equivalent, ranging from 0.99 (1.14) \(\text {TeV}\) at low dark-matter masses to 0.77 (0.89) \(\text {TeV}\) at dark-matter masses of 1 \(\text {TeV}\). Limits from indirect dark matter detection experiment results [8, 86, 87] interpreted in terms of these effective operators overlaid on Fig. 6 are sensitive up to EFT scales of 100–200 \(\text {GeV}\).
Exclusion contours (at 95% CL) for Dirac-fermion dark matter produced via a contact interaction with two electroweak bosons as described in an effective field theory with two dimension-seven operators (described in text) with different charge-parity properties. Limits are set as a function of dark-matter mass and the effective field theory scale, \(\Lambda \). The solid purple (green) curve shows the median of the observed (expected) limit. Also shown are limits on these operators from indirect-detection experiments. The yellow filled region around the expected limit indicates the effect of \(\pm 1\sigma \) experimental uncertainties in the expected limit. The exclusion is based on the global fit to the \(p_\mathrm {T}^\mathrm {miss}\) distributions in the \(\ge 1 \, \mathrm {jet}\) and VBF phase spaces, and the \( m_{\mathrm {jj}}\) and \( \Delta \phi _{\mathrm {jj}}\) distributions in the VBF phase space
The limits presented above assume a single operator would dominate the dark-matter production rate, but the detector-corrected data and covariance information can be used to explore more complex scenarios where multiple operators could contribute to the observed production rate with arbitrary relative rates and induce interference contributions between processes that would introduce non-trivial shapes and correlations between all three observables presented in this paper. The impact on the ratios in such an EFT model is demonstrated in Fig. 4 and is unlike the axial-vector mediator WIMP model and Higgs model presented above which predominantly modify only the \(p_\mathrm {T}^\mathrm {miss}\) and \( m_{\mathrm {jj}}\) distribution shapes, respectively.
The data have been corrected for detector effects and can be compared to any SM prediction or a combination of SM and BSM predictions at particle level, where the BSM model produces \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) final states. Models that also produce final states with at least one prompt lepton and \(p_\mathrm {T}^\mathrm {miss}\) cannot be accurately compared to the data. This is because they will have been included in the \(W\) background estimation, for which the extrapolation factors from control regions to the signal regions, determined using SM MC simulation, would be incorrect. Similarly, new-physics models with two leptons, entering the denominator, can only be reliably constrained by the data if the leptons have kinematics that are qualitatively similar to those in SM events, otherwise differences in the lepton efficiency correction factors may be observed. The data, together with the full covariance matrix for the uncertainties, are stored in HepData [88] and the analysis is included as a routine in the Rivet [89] software framework, in order to ease comparisons. Also stored in HepData are the SM numerator and denominator predicted by Sherpa, together with the covariance matrix for their uncertainties, such that these can be used when comparing to BSM models without having to simulate the SM contributions.
12 Conclusions
Observables sensitive to the anomalous production of events containing one or more hadronic jets with high transverse momentum produced in association with a large \(p_\mathrm {T}^\mathrm {miss}\) have been measured differentially with respect to a number of properties of the hadronic system. The results are presented as a measurement of the ratio of \(p_\mathrm {T}^\mathrm {miss}{} + \mathrm {jets}\) to \(\ell ^{+}\ell ^{-} + \mathrm {jets}\) events and are fully corrected for detector effects. This is the first detector-corrected measurement of observables specifically designed to be sensitive to dark-matter production.
The analysis uses 3.2 fb\(^{-1}\) of proton–proton collision data recorded by the ATLAS experiment at the LHC at a centre-of-mass energy of 13 \(\text {TeV}\). The results are presented in two phase-space regions defined by the hadronic system: a \(\ge 1 \, \mathrm {jet}\) inclusive sample and a VBF topology. The particle-level differential ratio measurements are found to be consistent with the SM expectations.
Using this infrastructure, limits are placed in three BSM scenarios: a simplified model of pair production of weakly interacting dark-matter candidates, a model with an invisibly decaying Higgs boson, and an effective field theory with general interactions of electroweak bosons with a dark-matter candidate. Limits in simplified models are competitive with previous approaches and the use of shape information in the differential spectra measured in this paper provides improved sensitivity to models where the dark-matter candidate mass is close to half the mediator mass. For the specific effective field theory operators considered in the interpretation, the dark-matter interactions would evade direct-detection experiments. The results presented here represent the most stringent constraints to date on such interactions, with an order-of-magnitude improvement over previous limits from indirect-detection experiments.
The detector-corrected data are published along with the statistical and systematic uncertainty correlations so that they can easily be used in the future to place limits in a wide range of new-physics models that predict final states with jets and missing transverse momentum.
Notes
ATLAS uses a right-handed coordinate system with its origin at the nominal interaction point in the centre of the detector and the z-axis along the beam pipe. The x-axis points to the centre of the LHC ring, and the y-axis points upward. Cylindrical coordinates \((r,\phi )\) are used in the transverse plane, \(\phi \) being the azimuthal angle around the beam pipe. The pseudorapidity is defined in terms of the polar angle \(\theta \) as \(\eta =-\ln [\tan (\theta /2)]\). Rapidity is defined as \(y=0.5 \ln [(E+p_z)/(E-p_z)]\) where E denotes the energy and \(p_z\) is the momentum component along the beam direction.
Prompt refers to particles not coming from the decay of a hadron or from the decay of a \(\tau \) lepton.
The denominator also includes the presence of the \(\gamma ^*\) mediator, which is not present in the numerator and would influence the \(R^{\mathrm {miss}} \) ratio in the SM; however, this contribution is small as the dilepton invariant mass is required to be close to the \(Z\) mass.
References
G. Bertone, D. Hooper, J. Silk, Particle dark matter: evidence, candidates and constraints. Phys. Rep. 405, 279 (2005). arXiv:hep-ph/0404175
J. de Swart, G. Bertone, J. van Dongen, How dark matter came to matter. Nat. Astron. 1, 0059 (2017). arXiv:1703.00013 [astro-ph.CO]
J. Conrad, O. Reimer, Indirect dark matter searches in gamma and cosmic rays. Nat. Phys. 13, 224 (2017). arXiv:1705.11165 [astro-ph.HE]
L. Evans, P. Bryant, LHC machine. JINST 3, S08001 (2008)
J. Abdallah et al., Simplified models for dark matter searches at the LHC. Phys. Dark Univ. 9–10, 8 (2015). arXiv:1506.03116 [hep-ph]
ATLAS Collaboration, Search for new phenomena in final states with an energetic jet and large missing transverse momentum in \(pp\) collisions at \(\sqrt{s} = 13\;\text{TeV}\) using the ATLAS detector. Phys. Rev. D 94, 032005 (2016). arXiv:1604.07773 [hep-ex]
CMS Collaboration, Search for dark matter, extra dimensions, and unparticles in monojet events in proton-proton collisions at \(\sqrt{s} = 8\;\text{ TeV }\). Eur. Phys. J. C 75, 235 (2015). arXiv:1408.3583 [hep-ex]
R.C. Cotta, J.L. Hewett, M.P. Le, T.G. Rizzo, Bounds on dark matter interactions with electroweak gauge bosons. Phys. Rev. D 88, 116009 (2013). arXiv:1210.0525 [hep-ph]
R.E. Shrock, M. Suzuki, Invisible decays of Higgs bosons. Phys. Lett. B 110, 250 (1982)
D. Choudhury, D.P. Roy, Signatures of an invisibly decaying Higgs particle at LHC. Phys. Lett. B 322, 368 (1994). arXiv:hep-ph/9312347
O.J.P. Eboli, D. Zeppenfeld, Observing an invisible Higgs boson. Phys. Lett. B 495, 147–154 (2000). arXiv:hep-ph/0009158
ATLAS Collaboration, Search for invisible decays of a Higgs boson using vector-boson fusion in \(pp\) collisions at \(\sqrt{s} = 8\;\text{ TeV }\) with the ATLAS detector. JHEP 01, 172 (2016). arXiv:1508.07869 [hep-ex]
CMS Collaboration, Searches for invisible decays of the Higgs boson in \(pp\) collisions at \(\sqrt{s} = 7, 8\), and 13 TeV. JHEP 02, 135 (2017). arXiv:1610.09218 [hep-ex]
ATLAS Collaboration, The ATLAS experiment at the CERN large hadron collider. JINST 3, S08003 (2008)
ATLAS Collaboration, Measurement of dijet cross sections in \(pp\) collisions at \(7\;\text{ TeV }\) centre-of-mass energy using the ATLAS detector. JHEP 05, 059 (2014). arXiv:1312.3524 [hep-ex]
ATLAS Collaboration, ATLAS insertable B-layer technical design report. ATLAS-TDR-19 (2010). https://cds.cern.ch/record/1291633
ATLAS Collaboration, ATLAS insertable B-layer technical design report addendum. ATLAS-TDR-19-ADD-1 (2012). https://cds.cern.ch/record/1451888
M. Cacciari, G.P. Salam, G. Soyez, The anti-\(k_t\) jet clustering algorithm. JHEP 04, 063 (2008). arXiv:0802.1189 [hep-ph]
M. Cacciari, G.P. Salam, G. Soyez, FastJet user manual. Eur. Phys. J. C 72, 1896 (2012). arXiv:1111.6097 [hep-ph]
ATLAS Collaboration, Jet energy scale measurements and their systematic uncertainties in proton-proton collisions at \(\sqrt{s} = 13\) TeV with the ATLAS detector, (2017), arXiv:1703.09665 [hep-ex]
ATLAS Collaboration, Selection of jets produced in \(13\;\text{ TeV }\) proton–proton collisions with the ATLAS detector. ATLAS-CONF-2015-029 (2015). https://cds.cern.ch/record/2037702
ATLAS Collaboration, Muon reconstruction performance of the ATLAS detector in proton–proton collision data at \(\sqrt{s} = 13\;\text{ TeV }\). Eur. Phys. J. C 76, 292 (2016). arXiv:1603.05598 [hep-ex]
ATLAS Collaboration, Electron efficiency measurements with the ATLAS detector using 2012 LHC proton-proton collision data. Eur. Phys. J. C 77, 195 (2017). arXiv:1612.01456 [hep-ex]
ATLAS Collaboration, Reconstruction, energy calibration, and identification of hadronically decaying tau leptons in the ATLAS Experiment for run-2 of the LHC. ATL-PHYS-PUB-2015-045 (2015). https://cds.cern.ch/record/2064383
ATLAS Collaboration, Performance of algorithms that reconstruct missing transverse momentum in \(\sqrt{s}=\) 8 TeV proton-proton collisions in the ATLAS detector. Eur. Phys. J. C 77, 241 (2017). arXiv:1609.09324 [hep-ex]
ATLAS Collaboration, Proposal for particle-level object and observable definitions for use in physics measurements at the LHC. ATL-PHYS-PUB-2015-013 (2015). https://cds.cern.ch/record/2022743
ATLAS Collaboration, Performance of the ATLAS trigger system in 2015. Eur. Phys. J. C 77, 317 (2017). arXiv:1611.09661 [hep-ex]
T. Gleisberg, S. Höche, F. Krauss, M. Schönherr, S. Schumann et al., Event generation with SHERPA 1.1. JHEP 02, 007 (2009). arXiv:0811.4622 [hep-ph]
T. Gleisberg, S. Höche, Comix, a new matrix element generator. JHEP 12, 039 (2008). arXiv:0808.3674 [hep-ph]
F. Cascioli, P. Maierhofer, S. Pozzorini, Scattering amplitudes with open loops. Phys. Rev. Lett. 108, 111601 (2012). arXiv:1111.5206 [hep-ph]
S. Schumann, F. Krauss, A Parton shower algorithm based on Catani–Seymour dipole factorisation. JHEP 03, 038 (2008). arXiv:0709.1027 [hep-ph]
S. Catani, F. Krauss, R. Kuhn, B.R. Webber, QCD matrix elements + parton showers. JHEP 11, 063 (2001). arXiv:hep-ph/0109231
S. Höche, F. Krauss, S. Schumann, F. Siegert, QCD matrix elements and truncated showers. JHEP 05, 053 (2009). arXiv:0903.1219 [hep-ph]
S. Höche, F. Krauss, M. Schönherr, F. Siegert, QCD matrix elements + parton showers: the NLO case. JHEP 04, 027 (2013). arXiv:1207.5030 [hep-ph]
NNPDF Collaboration, R.D. Ball et al., Parton distributions for the LHC Run II. JHEP 04, 040 (2015). arXiv:1410.8849 [hep-ph]
C. Anastasiou, L.J. Dixon, K. Melnikov, F. Petriello, High precision QCD at hadron colliders: electroweak gauge boson rapidity distributions at NNLO. Phys. Rev. D 69, 094008 (2004). arXiv:hep-ph/0312266
ATLAS Collaboration, Monte Carlo generators for the production of a \(W\) or \(Z/\gamma ^*\) boson in association with jets at ATLAS in run 2. ATL-PHYS-PUB-2016-003 (2016). https://cds.cern.ch/record/2120133
H.L. Lai, M. Guzzi, J. Huston, Z. Li, P.M. Nadolsky, J. Pumplin, C.P. Yuan, New parton distributions for collider physics. Phys. Rev. D 82, 074024 (2010). arXiv:1007.2241 [hep-ph]
ATLAS Collaboration, Multi-boson simulation for \(13\;\text{ TeV }\) ATLAS analyses. ATL-PHYS-PUB-2016-002 (2016). https://cds.cern.ch/record/2119986
J. Alwall et al., The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP 07, 079 (2014). arXiv:1405.0301 [hep-ph]
T. Sjöstrand, S. Mrenna, P.Z. Skands, A. Brief, Introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852–867 (2008). arXiv:0710.3820 [hep-ph]
ATLAS Collaboration, ATLAS Pythia 8 tunes to \(7\;\text{ TeV }\) data. ATL-PHYS-PUB-2014-021 (2014). https://cds.cern.ch/record/1966419
S. Alioli, S.O. Moch, P. Uwer, Hadronic top-quark pair-production with one jet and parton showering. JHEP 01, 137 (2012). arXiv:1110.5251 [hep-ph]
E. Re, Single-top Wt-channel production matched with parton showers using the POWHEG method. Eur. Phys. J. C 71, 1547 (2011). arXiv:1009.2450 [hep-ph]
R. Frederix, E. Re, P. Torrielli, Single-top t-channel hadroproduction in the four-flavour scheme with POWHEG and aMC@NLO. JHEP 09, 130 (2012). arXiv:1207.5391 [hep-ph]
S. Alioli, P. Nason, C. Oleari, E. Re, NLO single-top production matched with shower in POWHEG: s- and t-channel contributions. JHEP 09, 111 (2009). arXiv:0907.4076 [hep-ph]. Erratum: JHEP 02, 011 (2010)
S. Frixione, P. Nason, C. Oleari, Matching NLO QCD computations with Parton Shower simulations: the POWHEG method. JHEP 11, 070 (2007). arXiv:0709.2092 [hep-ph]
P. Nason, A New method for combining NLO QCD with shower Monte Carlo algorithms. JHEP 11, 040 (2004). arXiv:hep-ph/0409146
S. Frixione, P. Nason, G. Ridolfi, A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction. JHEP 09, 126 (2007). arXiv:0707.3088 [hep-ph]
T. Sjöstrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. JHEP 05, 026 (2006). arXiv:hep-ph/0603175
J. Pumplin et al., New generation of parton distributions with uncertainties from global QCD analysis. JHEP 07, 012 (2002). arXiv:hep-ph/0201195
P.Z. Skands, Tuning Monte Carlo generators: the Perugia tunes. Phys. Rev. D 82, 074,018 (2010). arXiv:1005.3457 [hep-ph]
ATLAS Collaboration, Simulation of top-quark production for the ATLAS experiment at \(\sqrt{s} = 13\;\text{ TeV }\). ATL-PHYS-PUB-2016-004 (2016). https://cds.cern.ch/record/2120417
M. Czakon, A. Mitov, Top++: a program for the calculation of the top-pair cross-section at hadron colliders. Comput. Phys. Commun. 185, 2930 (2014). arXiv:1112.5675 [hep-ph]
N. Kidonakis, Two-loop soft anomalous dimensions for single top quark associated production with a W- or H-. Phys. Rev. D 82, 054018 (2010). arXiv:1005.4451 [hep-ph]
N. Kidonakis, NNLL resummation for s-channel single top quark production. Phys. Rev. D 81, 054028 (2010). arXiv:1001.5034 [hep-ph]
N. Kidonakis, Next-to-next-to-leading-order collinear and soft gluon corrections for t-channel single top quark production. Phys. Rev. D 83, 091503 (2011). arXiv:1103.2792 [hep-ph]
U. Haisch, F. Kahlhoefer, E. Re, QCD effects in mono-jet searches for dark matter. JHEP 12, 007 (2013). arXiv:1310.4491 [hep-ph]
T. Sjöstrand et al., An introduction to PYTHIA 8.2. Comput. Phys. Commun. 191, 159 (2015). arXiv:1410.3012 [hep-ph]
D. Abercrombie et al., Dark matter benchmark models for early LHC run-2 searches: report of the ATLAS/CMS dark matter forum (2015). arXiv:1507.00966 [hep-ex]
S. Alioli, P. Nason, C. Oleari, E. Re, NLO Higgs boson production via gluon fusion matched with shower in POWHEG. JHEP 04, 002 (2009). arXiv:0812.0578 [hep-ph]
P. Nason, C. Oleari, NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG. JHEP 02, 037 (2010). arXiv:0911.5299 [hep-ph]
E. Bagnaschi, G. Degrassi, P. Slavich, A. Vicini, Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM. JHEP 02, 088 (2012). arXiv:1111.2854 [hep-ph]
J.R. Andersen et al., Handbook of LHC Higgs cross sections: 3. Higgs properties. arXiv:1307.1347 [hep-ph]
J. Brooke et al., Vector boson fusion searches for dark matter at the LHC. Phys. Rev. D 93(11), 113013 (2016). arXiv:1603.07739 [hep-ph]
A. Alloul, N.D. Christensen, C. Degrande, C. Duhr, B. Fuks, FeynRules 2.0—a complete toolbox for tree-level phenomenology. Comput. Phys. Commun. 185, 2250 (2014). arXiv:1310.1921 [hep-ph]
R.D. Ball et al., Parton distributions with LHC data. Nucl. Phys. B 867, 244 (2013). arXiv:1207.1303 [hep-ph]
S. Agostinelli et al., GEANT4: a simulation toolkit. Nucl. Instrum. Methods 506, 250 (2003) http://geant4.cern.ch/
J. Allison et al., GEANT4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270 (2006). http://geant4.cern.ch/
ATLAS Collaboration, The ATLAS simulation infrastructure. Eur. Phys. J. C 70, 823 (2010). arXiv:1005.4568 [hep-ex]
A. Martin, W. Stirling, R. Thorne, G. Watt, Parton distributions for the LHC. Eur. Phys. J. C 63, 189 (2009). arXiv:0901.0002 [hep-ph]
ATLAS Collaboration, Further ATLAS tunes of Pythia 6 and Pythia 8. ATL-PHYS-PUB-2011-014 (2011). https://cds.cern.ch/record/1400677
L.A. Harland-Lang, A.D. Martin, P. Motylinski, R.S. Thorne, Parton distributions in the LHC era: MMHT 2014 PDFs. Eur. Phys. J. C 75(5), 204 (2015). arXiv:1412.3989 [hep-ph]
S. Dulat et al., New parton distribution functions from a global analysis of quantum chromodynamics. Phys. Rev. D 93(3), 033,006 (2016). arXiv:1506.07443 [hep-ph]
R. Nisius, On the combination of correlated estimates of a physics observable. Eur. Phys. J. C 74(8), 3004 (2014). arXiv:1402.4016 [physics.data-an]
K.G. Hayes, M.L. Perl, B. Efron, Application of the bootstrap statistical method to the tau-decay-mode problem. Phys. Rev. D 39, 274(1989). https://link.aps.org/doi/10.1103/PhysRevD.39.274
A. Denner, S. Dittmaier, T. Kasprzik, A. Mück, Electroweak corrections to monojet production at the LHC. Eur. Phys. J. C 73(2), 2297 (2013). arXiv:1211.5078 [hep-ph]
C. Patrignani et al. (Particle Data Group), Review of particle physics. Chin. Phys. C 40(10), 100001 (2016)
A.L. Read, Presentation of search results: the CL(s) technique. J. Phys. G 28, 2693–2704 (2002)
T. Junk, Confidence level computation for combining searches with small statistics. Nucl. Instrum. Methods A 434, 435–443 (1999). arXiv:hep-ex/9902006 [hep-ex]
G. Cowan, K. Cranmer, E. Gross, O. Vitells, Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011). arXiv:1007.1727 [physics.data-an]. Erratum. Eur. Phys. J. C 73, 2501 (2013)
F. Kahlhoefer, K. Schmidt-Hoberg, T. Schwetz, S. Vogl, Implications of unitarity and gauge invariance for simplified dark matter models. JHEP 02, 016 (2016). arXiv:1510.02110 [hep-ph]
Planck Collaboration, R. Adam et al., Planck 2015 results. I. Overview of products and scientific results. Astron. Astrophys. 594, A1 (2016). arXiv:1502.01582 [astro-ph.CO]
G. Hinshaw et al., Nine-year Wilkinson microwave anisotropy probe (WMAP) observations: cosmological parameter results. Astrophys. J. Suppl. Ser. 208, 19 (2013). arXiv:1212.5226
D. de Florian et al., Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector (2016). arXiv:1610.07922 [hep-ph]
Fermi-LAT Collaboration, M. Ackermann et al., Constraining dark matter models from a combined analysis of milky way satellites with the fermi large area telescope. Phys. Rev. Lett. 107, 241302 (2011). arXiv:1108.3546 [astro-ph.HE]
VERITAS Collaboration, E. Aliu et al., VERITAS deep observations of the dwarf spheroidal galaxy segue 1. Phys. Rev. D 85, 062001 (2012). arXiv:1202.2144 [astro-ph.HE]. Erratum: Phys. Rev. D 91, 129903 (2015)
A. Buckley, M. Whalley, HepData reloaded: reinventing the HEP data archive. arXiv:1006.0517 [hep-ex]
A. Buckley et al., Rivet user manual. Comput. Phys. Commun. 184, 2803 (2013). arXiv:1003.0694 [hep-ph]
ATLAS Collaboration, ATLAS computing acknowledgements 2016–2017, ATL-GEN-PUB-2016-002. https://cds.cern.ch/record/2202407
Acknowledgements
We thank CERN for the very successful operation of the LHC, as well as the support staff from our institutions without whom ATLAS could not be operated efficiently. We acknowledge the support of ANPCyT, Argentina; YerPhI, Armenia; ARC, Australia; BMWFW and FWF, Austria; ANAS, Azerbaijan; SSTC, Belarus; CNPq and FAPESP, Brazil; NSERC, NRC and CFI, Canada; CERN; CONICYT, Chile; CAS, MOST and NSFC, China; COLCIENCIAS, Colombia; MSMT CR, MPO CR and VSC CR, Czech Republic; DNRF and DNSRC, Denmark; IN2P3-CNRS, CEA-DSM/IRFU, France; SRNSF, Georgia; BMBF, HGF, and MPG, Germany; GSRT, Greece; RGC, Hong Kong SAR, China; ISF, I-CORE and Benoziyo Center, Israel; INFN, Italy; MEXT and JSPS, Japan; CNRST, Morocco; NWO, Netherlands; RCN, Norway; MNiSW and NCN, Poland; FCT, Portugal; MNE/IFA, Romania; MES of Russia and NRC KI, Russian Federation; JINR; MESTD, Serbia; MSSR, Slovakia; ARRS and MIZŠ, Slovenia; DST/NRF, South Africa; MINECO, Spain; SRC and Wallenberg Foundation, Sweden; SERI, SNSF and Cantons of Bern and Geneva, Switzerland; MOST, Taiwan; TAEK, Turkey; STFC, United Kingdom; DOE and NSF, United States of America. In addition, individual groups and members have received support from BCKDF, the Canada Council, CANARIE, CRC, Compute Canada, FQRNT, and the Ontario Innovation Trust, Canada; EPLANET, ERC, ERDF, FP7, Horizon 2020 and Marie Skłodowska-Curie Actions, European Union; Investissements d’Avenir Labex and Idex, ANR, Région Auvergne and Fondation Partager le Savoir, France; DFG and AvH Foundation, Germany; Herakleitos, Thales and Aristeia programmes co-financed by EU-ESF and the Greek NSRF; BSF, GIF and Minerva, Israel; BRF, Norway; CERCA Programme Generalitat de Catalunya, Generalitat Valenciana, Spain; the Royal Society and Leverhulme Trust, United Kingdom.
The crucial computing support from all WLCG partners is acknowledged gratefully, in particular from CERN, the ATLAS Tier-1 facilities at TRIUMF (Canada), NDGF (Denmark, Norway, Sweden), CC-IN2P3 (France), KIT/GridKA (Germany), INFN-CNAF (Italy), NL-T1 (Netherlands), PIC (Spain), ASGC (Taiwan), RAL (UK) and BNL (USA), the Tier-2 facilities worldwide and large non-WLCG resource providers. Major contributors of computing resources are listed in Ref. [90].
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Aaboud, M., Aad, G., Abbott, B. et al. Measurement of detector-corrected observables sensitive to the anomalous production of events with jets and large missing transverse momentum in \(\varvec{pp}\) collisions at \(\mathbf {\sqrt{s}=13}\) TeV using the ATLAS detector. Eur. Phys. J. C 77, 765 (2017). https://doi.org/10.1140/epjc/s10052-017-5315-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5315-6