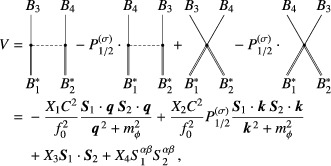Scattering of decuplet baryons in chiral effective field theory

Abstract

A formalism for treating the scattering of decuplet baryons in chiral effective field theory is developed. The minimal Lagrangian and potentials in leading-order SU(3) chiral effective field theory for the interactions of octet baryons ($B$) and decuplet baryons ($D$) for the transitions $\mathrm{BB}\rightarrow \mathrm{BB}$, $\mathrm{BB}\leftrightarrow \mathrm{DB}$, $\mathrm{DB}\rightarrow \mathrm{DB}$, $\mathrm{BB}\leftrightarrow \mathrm{DD}$, $\mathrm{DB}\leftrightarrow \mathrm{DD}$, and $\mathrm{DD}\rightarrow \mathrm{DD}$ are provided. As an application of the formalism we compare with results from lattice QCD simulations for ${\varOmega }{\varOmega }$ and $N{\varOmega }$ scattering. Implications of our results pertinent to the quest for dibaryons are discussed.

1 Introduction

An important and basically timeless topic in hadron physics is the possible existence of dibaryons [1, 2]. Historically, the so-called dibaryons have primarily been conceived as tightly bound six-quark objects. However, the terminology is also frequently adopted for shallow (or not so shallow) bound states of two baryons, as in practice it might be difficult to distinguish between these six-quark and two-baryon configurations. We note that methods to disentangle compact multi-quark states from loosely bound molecular systems have recently been reviewed in Ref. [3].

A famous dibaryon proposed to be of the first category is the H-particle, predicted by Jaffe within the bag model as a compact $|uuddss\rangle$ state [4]. The H-dibaryon has the quantum numbers of the ${\varLambda }{\varLambda }$ system in an S-wave state, namely strangeness ${S}=-\,2$, isospin $I=0$, and $J^P=0^+$. After decades of failed efforts to establish its existence experimentally, it regained popularity a few years ago due to lattice simulations that provided evidence for its presence [5, 6], though only for quark masses that are larger than the physical ones.

Definitely of the second category is the deuteron, a bound state in the coupled $^3S_1$–$^3D_1$ partial waves of the neutron–proton (np) system. Also of that category is a possible (unstable) quasibound state in the $^3S_1$–$^3D_1$ partial waves of the ${\varSigma }N$ channel with isospin $I=1/2$, which appears as a pronounced cusp-like enhancement in the ${\varLambda }p$ invariant-mass spectrum of reactions like $K^-d \rightarrow \pi ^-{\varLambda }p$ and $pp\rightarrow K^+{\varLambda }p$ very close to the ${\varSigma }N$ threshold; see the review [7].

In Refs. [8, 9] it has been shown that chiral effective field theory (EFT), an approach initially suggested for deriving and describing the forces between nucleons [10,11,12,13,14], can be straightforwardly extended to the interaction of baryons with strangeness. In this framework the symmetries of QCD together with the appropriate low-energy degrees of freedom are exploited to construct the baryon–baryon interactions. Moreover, there is an underlying power counting that allows one to improve the results systematically by going progressively to higher orders in a perturbative expansion. This approach is well suited to shed light on the H–dibaryon, should it indeed exist, and on other possible dibaryons in the strangeness $S=-\,3$ and $-\,4$ sectors, as demonstrated in Refs. [15, 16]. In particular, one can study implications of the imposed (approximate) SU(3) symmetry and further explore the dependence of the properties of such dibaryons on the pion¹ and baryon masses. The latter aspect is important since, as mentioned, the pertinent lattice QCD (LQCD) calculations were not performed for physical quark masses.

In the present paper we extend the investigations of Refs. [8, 15, 16] to decuplet baryons. The main goal is to provide the basic elements for treating the scattering of octet baryons with decuplet baryons ($\mathrm{BD}$) and of two decuplet baryons ($\mathrm{DD}$) within SU(3) chiral EFT. Here we restrict ourselves, as a first step, to leading order (LO) in the Weinberg counting [13]. In this case the interaction potential is given by single pseudoscalar-meson ($\pi$, $\eta$, K) exchange plus four-baryon contact terms without derivatives [8]. The latter represent the short-ranged part of the baryon–baryon force and involve low-energy constants (LECs), parameters to be fixed by fits to data. The resulting potential is then used in a regularized Lippmann–Schwinger (LS) equation to generate possible bound states and to evaluate two-body scattering amplitudes. As in Refs. [8, 15, 16] we assume the (approximate) validity of SU(3) flavor symmetry for the coupling strengths involved.² This assumption allows one to establish relations between the forces in channels with different isospin and strangeness, and we recapitulate the implications of SU(3) symmetry for the interactions in the $\mathrm{BD}$ and $\mathrm{DD}$ systems. In addition we investigate the consequences of SU(3) symmetry for transitions from these systems to states composed of two octet baryons ($\mathrm{BB}$). Note that a work in similar spirit but aiming at the charm and beauty sector, where instead heavy quark spin symmetry plays a fundamental role, has been presented recently [17].

A primary motivation for our study comes from recent LQCD calculations for ${{\varOmega }}{{\varOmega }}$ and $N{{\varOmega }}$ scattering [18,19,20,21]. In some of those computations signals for possible dibaryons were found [19,20,21]. Thus, as a first application of our formalism we analyze the results for ${{\varOmega }}{{\varOmega }}$ and $N{{\varOmega }}$ scattering presented in those works. We also discuss implications on possible other dibaryon states, notably in the ${{\varSigma }^*}{{\varDelta }}$, ${{\varOmega }}{{\varXi }^*}$, and ${{\varDelta }}{{\varDelta }}$ systems. Apart from indications for dibaryons in the ${{\varOmega }}{{\varOmega }}$ and $N{{\varOmega }}$ systems from LQCD calculations, there are further longstanding claims for dibaryons in those channels from studies based on the constituent quark model; see Refs. [22,23,24] for more recent efforts. Possible bound states in ${\varXi }{{\varOmega }}$ and ${\varXi }^* {{\varOmega }}$ [25], and ${{\varDelta }}{{\varOmega }}$ [26, 27] have been discussed, too. And finally, there has been a noticeable revival of dibaryons in the ${{\varDelta }}{{\varDelta }}$ sector, in the context of measurements of the reactions $pn\rightarrow d \pi ^0\pi ^0$ and $pn\rightarrow d \pi ^+\pi ^-$ by the WASA-at-COSY collaboration in Jülich [28]. A resonance in the $^3D_3$–$^3G_3\,NN$ partial wave required to describe the data [29], termed $d^*(2380)$ dibaryon, could be a reflection of an S-wave quasibound state in the ${{\varDelta }}{{\varDelta }}$ system [30,31,32].

In the analysis of the LQCD simulations we follow closely the strategy of our previous work [15, 16]: (i) the LECs, i.e. the only free parameters in the potential, are determined by a fit to LQCD results (phase shifts, scattering lengths) employing the inherent baryon and meson masses of the lattice simulation; (ii) results at the physical point are obtained via a calculation in which the pertinent physical masses of the mesons are substituted in the evaluation of the potential and those of the baryons in the baryon–baryon propagators appearing in the LS equation. Certainly, Such an “extrapolation” can be expected to work only qualitatively, given the still unphysically large hadron masses in the LQCD simulations for ${{\varOmega }}{{\varOmega }}$, $N{{\varOmega }}$, and ${{\varDelta }}{{\varDelta }}$. Nonetheless recent (and still preliminary) lattice results for the H–dibaryon, and for ${{\varLambda }}{{\varLambda }}$ and $N{\varXi }$ phase shifts, respectively, close to the physical point [21, 33] reveal that the prediction/extrapolation in Refs. [15, 16], performed in the way described above, may be fairly realistic. In this context let us mention that also for other baryon–baryon channels LQCD simulations have been performed with almost physical quark masses [34,35,36] and preliminary results for phase shifts have become available³ for some channels.

This paper is structured as follows: A basic outline of our formalism is given in Sect. 2. Specifically, we establish the underlying Lagrangians for constructing the interactions in the $\mathrm{BB}$, $\mathrm{BD}$, and $\mathrm{DD}$ sectors at leading order in chiral EFT. Furthermore, the essentials of the imposed SU(3) flavor symmetry are described. Finally, explicit expressions for the potentials resulting from meson exchange and from the four-baryon contact terms are given. In Sect. 3, as exemplary applications of our formalism, results for selected $\mathrm{DD}$ and $\mathrm{BD}$ reactions are presented, where we focus on such reaction channels for which predictions from lattice QCD simulations for phase shifts and/or scattering lengths are available: ${{\varOmega }}{{\varOmega }}$ scattering in the $^1S_0$ partial wave and $N{{\varOmega }}$ in the $^5S_2$ partial wave. Furthermore, we explore the ${{\varDelta }}{{\varDelta }}$ system with total angular momentum $J=3$ and isospin $I=0$, and the possible emergence of a bound state that could be associated with the $d^*(2380)$ dibaryon. A brief summary and an outlook is presented in Sect. 4. Technical details of our calculation are summarized in three appendices.

2 Formalism

Our calculation is based on a non-relativistic approach in leading-order SU(3) chiral EFT. Possible (isospin-violating) $\pi ^0$–$\eta$ or ${\varSigma }^0$–${\varLambda }$ mixing is neglected. We use the conventional building blocks as laid down, e.g., in Refs. [8, 9], with the pseudoscalar-meson octet represented by the $3\times 3$ matrix in flavor space:

$$\begin{aligned} \phi = \begin{pmatrix} \pi ^0 + \frac{\eta }{\sqrt{3}} &{}\quad \sqrt{2} \pi ^+ &{}\quad \sqrt{2} K^+ \\ \sqrt{2} \pi ^- &{}\quad -\pi ^0 + \frac{\eta }{\sqrt{3}} &{}\quad \sqrt{2} K^0 \\ \sqrt{2} K^- &{}\quad \sqrt{2} \bar{K}^0 &{}\quad -\frac{2\eta }{\sqrt{3}} \end{pmatrix}. \end{aligned}$$

(1)

The octet baryons are represented by the $3\times 3$ matrix

$$\begin{aligned} B= \begin{pmatrix} \frac{{\varSigma }^0}{\sqrt{2}} + \frac{{\varLambda }}{\sqrt{6}} &{}\quad {\varSigma }^+ &{}\quad p \\ {\varSigma }^- &{}\quad -\frac{{\varSigma }^0}{\sqrt{2}} + \frac{{\varLambda }}{\sqrt{6}} &{}\quad n \\ {\varXi }^- &{}\quad {\varXi }^0 &{}\quad -\frac{2{\varLambda }}{\sqrt{6}} \end{pmatrix}. \end{aligned}$$

(2)

The decuplet baryons are represented by the totally symmetric three-index tensor $T$:

$$\begin{aligned} T_{111}&={\varDelta }^{++}, \quad T_{112}=\tfrac{1}{\sqrt{3}}{\varDelta }^{+}, \quad T_{122}=\tfrac{1}{\sqrt{3}}{\varDelta }^{0}, \quad T_{222}={\varDelta }^{-}, \nonumber \\ T_{113}&=\tfrac{1}{\sqrt{3}}{\varSigma }^{*+}, \quad T_{123}=\tfrac{1}{\sqrt{6}}{\varSigma }^{*0}, \quad T_{223}=\tfrac{1}{\sqrt{3}}{\varSigma }^{*-}, \nonumber \\ T_{133}&=\tfrac{1}{\sqrt{3}}{\varXi }^{*0}, \quad T_{233}=\tfrac{1}{\sqrt{3}}{\varXi }^{*-}, \nonumber \\ T_{333}&={\varOmega }^-. \end{aligned}$$

(3)

The construction of the chiral Lagrangian requires a complete set of spin operators, covering all combinations of spin 1/2 and spin 3/2 states. These have been established employing the Wigner–Eckart theorem. One obtains for spin 1/2 the identity matrix and $\sigma ^i$, i.e. the usual Pauli matrices, corresponding to scalar and vector operators. For the spin 1/2 to spin 3/2 transition operators, the resulting $4\times 2$ matrices connect the two-component spinors of octet baryons with the four-component spinors of decuplet baryons [37]. The corresponding vector and rank-2 tensor operators are $S^{i\dagger }$ and $S^{ij\dagger }$, respectively. The reverse transition, 3/2 to 1/2, is described by the Hermitian-conjugate spin transition operators $S^i$ and $S^{ij}$. Finally, the $4\times 4$ matrices , ${\varSigma }^i$, ${\varSigma }^{ij}$, ${\varSigma }^{ijk}$, corresponding in this order to scalar, vector, rank-2 and rank-3 tensor operators, are introduced for the description of the spin 3/2 sector. These sets of matrices for the different types of transitions form a basis. More details on the construction of the spin operators and their explicit expressions can be found in Appendix A.

For the two-body interactions considered in the following, tensor products of two of these spin operators are involved.

2.1 Lagrangians generating meson exchange

In this subsection we consider the meson–baryon Lagrangians for the construction of the leading-order meson exchange interactions of octet and decuplet baryons.

The SU(3) invariant Lagrangian for octet baryons coupled to the pseudoscalar-meson octet is given by [8, 40]

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{BB}\phi }&= -\frac{D}{2f_0} \mathrm{tr}( \bar{B} \varvec{\sigma }\cdot \lbrace \varvec{\nabla }\phi ,B\rbrace ) - \frac{F}{2f_0} \mathrm{tr}(\bar{B} \varvec{\sigma }\cdot \left[ \varvec{\nabla }\phi ,B\right] ), \end{aligned}$$

(4)

where $f_0$ is the weak pseudoscalar-meson decay constant $f_0 \approx f_\pi$. The coupling constants $F$ and $D$ satisfy $F + D = g_A$, with $g_A$ the axial-vector strength measured in neutron $\beta$-decay.⁴ Introducing standard isospin operators, the Lagrangian can be written in its well-known form [42]:

$$\begin{aligned} {\mathcal L}_\mathrm {\mathrm{BB}\phi }= & {} -f_{NN\pi }\bar{N}{\varvec{\tau }}N\cdot {\varvec{\pi }} +if_{{\varSigma }{\varSigma }\pi }\bar{{\varvec{{\varSigma }}}}\times {{\varvec{{\varSigma }}}}\cdot {\varvec{\pi }} \nonumber \\&-\,f_{{\varLambda }{\varSigma }\pi }\left[ \bar{{\varLambda }}{{\varvec{{\varSigma }}}}+ \bar{{\varvec{{\varSigma }}}} {\varLambda }\right] \cdot {\varvec{\pi }}-f_{{\varXi }{\varXi }\pi }\bar{{\varXi }}{\varvec{\tau }}{\varXi }\cdot {\varvec{\pi }} \nonumber \\&-\,f_{{\varLambda }NK}\left[ \bar{N}{\varLambda }K+\bar{{\varLambda }} N K^\dagger \right] \nonumber \\&-\,f_{{\varXi }{\varLambda }K}\left[ \bar{{\varXi }}{\varLambda }K_c+\bar{{\varLambda }}{\varXi }K_c^\dagger \right] \nonumber \\&-\,f_{{\varSigma }NK}\left[ \bar{{\varvec{{\varSigma }}}}\cdot K^\dagger {\varvec{\tau }}N+\bar{N}{\varvec{\tau }} K\cdot {{\varvec{{\varSigma }}}}\right] \nonumber \\&-\,f_{{\varXi }{\varSigma }K}\left[ \bar{{\varvec{{\varSigma }}}}\cdot K_c^\dagger {\varvec{\tau }}{\varXi }+\bar{{\varXi }} {\varvec{\tau }} K_c\cdot {{\varvec{{\varSigma }}}}\right] \nonumber \\&-\,f_{NN\eta _8}\bar{N} N\eta -f_{{\varLambda }{\varLambda }\eta _8}\bar{{\varLambda }}{\varLambda }\eta -f_{{\varSigma }{\varSigma }\eta _8}\bar{{\varvec{{\varSigma }}}}\cdot {{\varvec{{\varSigma }}}}\eta \nonumber \\&-\,f_{{\varXi }{\varXi }\eta _8}\bar{{\varXi }}{\varXi }\eta . \end{aligned}$$

(5)

Here, we have introduced the isospin doublets

$$\begin{aligned} N=\left( \begin{array}{l} p \\ n \end{array}\right) , \quad {\varXi }=\left( \begin{array}{l} {\varXi }^0 \\ {\varXi }^-\end{array}\right) , \quad K=\left( \begin{array}{l} K^+\\ K^0 \end{array}\right) , \quad K_c=\left( \begin{array}{l} {\bar{K}}^0 \\ -K^-\end{array}\right) . \end{aligned}$$

(6)

The signs have been chosen according to the conventions of Ref. [42]. With regard to isovectors the assignment ${{\varSigma }}^+ = -|1,1\rangle$, etc., is used so that the inner product of ${\varvec{{\varSigma }}}$ (or ${\varvec{\pi }}$) defined in spherical components reads

$$\begin{aligned} {\varvec{{\varSigma }}}\cdot {\varvec{{\varSigma }}}=\sum _m (-1)^m{\varSigma }_m{\varSigma }_{-m}= {\varSigma }^+{\varSigma }^-+{\varSigma }^0{\varSigma }^0+{\varSigma }^-{\varSigma }^+\ . \end{aligned}$$

(7)

Spin and momentum operators ($\varvec{\sigma \cdot \nabla }$) have been omitted in Eq. (5) to simplify the presentation. That structure is the same for all $B_iB_j\phi _k$ vertices. The coupling constants introduced in Eq. (5) are given by

$$\begin{aligned} \begin{array}{rlrl} f_{NN\pi } = &{} f, &{} f_{NN\eta _8} = &{} \frac{1}{\sqrt{3}}(4\alpha -1)f, \\ f_{{\varLambda }NK} = &{} -\frac{1}{\sqrt{3}}(1+2\alpha )f, &{} f_{{\varXi }{\varXi }\pi } = &{} -(1-2\alpha )f, \\ f_{{\varXi }{\varXi }\eta _8} = &{} -\frac{1}{\sqrt{3}}(1+2\alpha )f, &{} f_{{\varXi }{\varLambda }K} = &{} \frac{1}{\sqrt{3}}(4\alpha -1)f, \\ f_{{\varLambda }{\varSigma }\pi } = &{} \frac{2}{\sqrt{3}}(1-\alpha )f, &{} f_{{\varSigma }{\varSigma }\eta _8} = &{} \frac{2}{\sqrt{3}}(1-\alpha )f,\\ f_{{\varSigma }NK} = &{} (1-2\alpha )f, &{} f_{{\varSigma }{\varSigma }\pi } = &{} 2\alpha f, \\ f_{{\varLambda }{\varLambda }\eta _8} = &{} -\frac{2}{\sqrt{3}}(1-\alpha )f, &{} f_{{\varXi }{\varSigma }K} = &{} -f. \end{array} \end{aligned}$$

(8)

with $f\equiv g_A/(2f_0)$ and $\alpha \equiv F/(F+D)$. In the present work we use the same values as in our previous LO study of the YN system [8], namely $f_0=93$ MeV, $g_A = 1.26$, $\alpha =0.4$.

The Lagrangian involving an octet and a decuplet baryon is written in the form [43, 44]

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DB}\phi }&= \frac{C}{f_0} \sum _{a,b,c,d,e=1}^3 \epsilon _{abc} \Big ( \bar{T}_{ade} {\varvec{S}}^{\,\dagger } \cdot \left( \varvec{\nabla } \phi _{db}\right) B_{ec} \nonumber \\&\quad +\, \bar{B}_{ce} {\varvec{S}} \cdot \left( \varvec{\nabla }\phi _{bd}\right) T_{ade} \Big ). \end{aligned}$$

(9)

The coupling constant $C$ can be fixed from the decay ${\varDelta }\rightarrow \pi N$. One finds $C=\frac{3}{4}g_A$ [45]. The vector spin operator ${\varvec{S}}^{\,\dagger }$ consists of $4\times 2$ matrices representing the transition from spin 1 / 2 to 3 / 2. Their explicit forms are given in Appendix A.

Omitting again the spin–momentum dependent part of the Lagrangian, Eq. (9), one can cast the remainder into a simple form using isospin operators,

$$\begin{aligned} {\mathcal {L}}_\mathrm {\mathrm{DB}\phi }= & {} -f_{N{\varDelta }\pi }\bar{{\varDelta }} {\varvec{T}}^{\varvec{\dagger }} N\cdot {\varvec{\pi }} +if_{{\varSigma }{{\varSigma }^*}\pi }\bar{{\varvec{{{\varSigma }^*}}}}\times {{\varvec{{\varSigma }}}}\cdot {\varvec{\pi }} \nonumber \\&-f_{{\varLambda }{{\varSigma }^*}\pi }\bar{{\varvec{{{\varSigma }^*}}}} {\varLambda }\cdot {\varvec{\pi }}-f_{{\varXi }{{\varXi }^*}\pi }\bar{{{\varXi }^*}}{\varvec{\tau }}{\varXi }\cdot {\varvec{\pi }} \nonumber \\&-f_{N{{\varSigma }^*}K}\bar{{\varvec{{{\varSigma }^*}}}}\cdot K^\dagger {\varvec{\tau }}N -f_{{\varSigma }{\varDelta }K}\bar{{\varDelta }}{{\varvec{T}}}^{{\varvec{\dagger }}} K\cdot {{\varvec{{\varSigma }}}} \nonumber \\&-f_{{\varLambda }{{\varXi }^*}K}\bar{{{\varXi }^*}}{\varLambda }K_c -f_{{\varSigma }{{\varXi }^*}K}\bar{{{\varXi }^*}}{\varvec{\tau }} K_c\cdot {{\varvec{{\varSigma }}}} \nonumber \\&-f_{{\varXi }{{\varSigma }^*}K}\bar{{\varvec{{{\varSigma }^*}}}}\cdot K_c^\dagger {\varvec{\tau }}{\varXi }-f_{{\varXi }{{\varOmega }}K}\bar{{{\varOmega }}}{\varXi }K^\dagger \nonumber \\&-f_{{\varSigma }{{\varSigma }^*}\eta _8}\bar{{\varvec{{{\varSigma }^*}}}}\cdot {{\varvec{{\varSigma }}}}\eta -f_{{\varXi }{{\varXi }^*}\eta _8}\bar{{{\varXi }^*}}{\varXi }\eta \nonumber \\&+ \ \mathrm{h.c.} \ , \end{aligned}$$

(10)

where the ${\varDelta }$ isobar is represented by an isospin quartet, i.e. $({{\varDelta }}^{++},{{\varDelta }}^{+},{{\varDelta }}^{0},{{\varDelta }}^{-})^T$ and ${{\varXi }^*}$ and ${{\varSigma }^*}$ by isospin states analogous to those in Eqs. (6) and (7). The SU(3) relations for the coupling constants of octet to decuplet baryons are expressed in terms of the coupling constant $f_{\mathrm{BD}}$ and read

$$\begin{aligned}&f_{N{\varDelta }\pi } = f_{{\varXi }{{\varOmega }}K} = -f_{{\varSigma }{\varDelta }K} = f_{\mathrm{BD}}, \nonumber \\&f_{{\varSigma }{{\varSigma }^*}\pi } = f_{N{{\varSigma }^*}K} = f_{{\varSigma }{{\varXi }^*}K} = f_{{\varXi }{{\varSigma }^*}K} = -\frac{1}{\sqrt{6}} f_{\mathrm{BD}}, \nonumber \\&f_{{\varLambda }{{\varSigma }^*}\pi } = -f_{{\varLambda }{{\varXi }^*}K} = -f_{{\varSigma }{{\varSigma }^*}\eta _8} = f_{{\varXi }{{\varXi }^*}\eta _8} = \frac{1}{\sqrt{2}} f_{\mathrm{BD}}, \nonumber \\&f_{{\varXi }{{\varXi }^*}\pi } = \frac{1}{\sqrt{6}} f_{\mathrm{BD}}. \end{aligned}$$

(11)

The relation between the coupling constants in Eqs. (9) and (10) is $f_{\mathrm{BD}} = \sqrt{2}\,C/f_0$ and results from the different normalization of the isospin transition operator ${{\varvec{T}}}^{\varvec{\dagger }}$, cf. Eq. (35) in Appendix A, and the tensor representation for the decuplet baryons in Eq. (3). The $N{{\varDelta }}\pi$ coupling constant $h_A$, commonly used in studies of $\pi N$ scattering within chiral perturbation theory [46,47,48], coincides with $f_{\mathrm{BD}}$. Accordingly, the choice of C mentioned above is in line with the large-$N_c$ value $h_{A} = 3g_A/(2\sqrt{2})$.

The Lagrangian involving two decuplet baryons and a meson expressed in the conventional building blocks is given by

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\phi }&= \frac{H}{f_0} \sum _{a,b,c,d=1} (\bar{T}_{abc}\varvec{{\varSigma }} T_{abd}) \cdot (\varvec{\nabla }\phi _{cd}) \, , \end{aligned}$$

(12)

with a new coupling constant $H$ and the spin-3/2 operator ${\varvec{{\varSigma }}}$ (see Appendix A). Although the same symbol is used for the isotriplet of ${\varSigma }^{+,0,-}$ hyperons, the respective meaning of ${\varvec{{\varSigma }}}$ should be clear from the context. Casting the Lagrangian Eq. (12) into a simple form utilizing isospin operators leads to

$$\begin{aligned} {\mathcal {L}}_\mathrm {\mathrm{DD}\phi }= & {} -f_{{{\varDelta }}{{\varDelta }}\pi }\bar{{{\varDelta }}}{\varvec{\theta }}{{\varDelta }}\cdot {\varvec{\pi }} +if_{{{\varSigma }^*}{{\varSigma }^*}\pi }\bar{{\varvec{{{\varSigma }^*}}}}\times {{\varvec{{{\varSigma }^*}}}}\cdot {\varvec{\pi }} \nonumber \\&-\,f_{{{\varXi }^*}{{\varXi }^*}\pi }\bar{{{\varXi }^*}}{\varvec{\tau }}{{\varXi }^*}\cdot {\varvec{\pi }} \nonumber \\&-\,f_{{{\varSigma }^*}{{\varDelta }}K}\left[ \bar{{\varvec{{{\varSigma }^*}}}}\cdot K^\dagger {{\varvec{T}}}{{\varDelta }}+\bar{{{\varDelta }}}{{\varvec{T}}}^{{\varvec{\dagger }}} K\cdot {{\varvec{{{\varSigma }^*}}}}\right] \nonumber \\&-\,f_{{{\varXi }^*}{{\varSigma }^*}K}\left[ \bar{{\varvec{{{\varSigma }^*}}}}\cdot K_c^\dagger {\varvec{\tau }}{{\varXi }^*}+\bar{{{\varXi }^*}} {\varvec{\tau }} K_c\cdot {{\varvec{{{\varSigma }^*}}}}\right] \nonumber \\&-\,f_{{{\varOmega }}{{\varXi }^*}K}\left[ \bar{{{\varOmega }}}{{\varXi }^*}K^\dagger + \bar{{{\varXi }^*}}{{\varOmega }}K\right] \nonumber \\&-\,f_{{{\varDelta }}{{\varDelta }}\eta _8}\bar{{{\varDelta }}} {{\varDelta }}\eta -f_{{{\varSigma }^*}{{\varSigma }^*}\eta _8}\bar{{\varvec{{{\varSigma }^*}}}}\cdot {{\varvec{{{\varSigma }^*}}}}\eta \nonumber \\&-\,f_{{{\varXi }^*}{{\varXi }^*}\eta _8}\bar{{{\varXi }^*}}{{\varXi }^*}\eta -f_{{{\varOmega }}{{\varOmega }}\eta _8}\bar{{{\varOmega }}}{{\varOmega }}\eta \ , \end{aligned}$$

(13)

omitting once again the spin–momentum part. Here the SU(3) relations for the coupling constants are

$$\begin{aligned} f_{{{\varDelta }}{{\varDelta }}\pi }= & {} f_{{{\varXi }^*}{{\varXi }^*}\pi } = f_{\mathrm{DD}}, \nonumber \\ -f_{{{\varSigma }^*}{{\varDelta }}K}= & {} f_{{{\varOmega }}{{\varXi }^*}K} = \sqrt{6} f_{\mathrm{DD}}, \nonumber \\ f_{{{\varSigma }^*}{{\varSigma }^*}\pi }= & {} f_{{{\varXi }^*}{{\varSigma }^*}K} = 2f_{\mathrm{DD}}, \nonumber \\ f_{{{\varDelta }}{{\varDelta }}\eta _8}= & {} -f_{{{\varXi }^*}{{\varXi }^*}\eta _8} =-f_{{{\varOmega }}{{\varOmega }}\eta _8}/2 = \sqrt{3} f_{\mathrm{DD}}, \nonumber \\ f_{{{\varSigma }^*}{{\varSigma }^*}\eta _8}= & {} 0, \end{aligned}$$

(14)

where the normalization of the decuplet-baryon tensor and the definition of the isospin 3/2 operator ${\varvec{\theta }}$ as given in Appendix A imply $f_{\mathrm{DD}} = H / (3 f_0)$. We note that a remarkable correlation between the leading $\pi {\varDelta }N$ and $\pi {\varDelta }{\varDelta }$ couplings beyond the large-$N_C$ expansion has recently been found [49].

The general form of the LO meson-exchange potential is analogous to that for $\mathrm{BB}$ systems [8, 9], namely

$$\begin{aligned} V_{P}= & {} -\frac{\left( \mathcal {O}_1\cdot \mathbf{q}\right) \left( \mathcal {O}_2\cdot \mathbf{q}\right) }{\mathbf{q}^2+m^2_P}, \end{aligned}$$

(15)

where $m_P$ is the mass of the exchanged pseudoscalar meson P. The symbol $\mathcal {O}_i$ stands generically for the spin operators at the two vertices. For spin $1/2 \rightarrow 1/2$ it is given by ${\varvec{\sigma }}_{\varvec{i}}$, for $3/2 \rightarrow 3/2$ by ${\varvec{{\varSigma }}}_{\varvec{i}}$, for $1/2 \rightarrow 3/2$ by ${\varvec{S}}_{\varvec{i}}^{{\varvec{\dagger }}}$, and for $3/2 \rightarrow 1/2$ by ${\varvec{S}}_{\varvec{i}}$. The transferred momentum $\mathbf{q}$ is defined in terms of the final and initial center-of-mass (c.m.) momenta of the baryons, $\mathbf{p}'$ and $\mathbf{p}$, as $\mathbf{q}=\mathbf{p}'-\mathbf{p}$. As already mentioned in the Introduction, we use either the physical masses of the exchanged pseudoscalar mesons or masses corresponding to the lattice QCD simulations. Thus, the explicit $\mathrm{SU(3)}$ breaking reflected in the mass splitting between the pseudoscalar mesons is taken into account.

Following our previous works [8, 9] the $\eta$ meson is identified with the octet state ($\eta _8$) and its physical mass is used. A possible coupling of two octet baryons to a singlet meson ($\eta _0$) which would introduce a further coupling constant [42], is ignored in the present context. As far as the vertex of two decuplet baryons and a meson is concerned, since according to the decomposition $\mathbf {10}\otimes \mathbf {\overline{10}} = \mathbf {64} \oplus \mathbf {27} \oplus \mathbf {8} \oplus \mathbf {1}$ [42], obviously one can also couple the two decuplet baryons to a singlet and then with a singlet meson to obtain an SU(3) invariant. Again this would introduce a further coupling constant which we likewise ignore.

The actual LO meson-exchange potential is obtained by multiplying the spin–momentum part of the potential, Eq. (15) with the coupling constants as given in Eqs. (8), (11), or (14) and with the pertinent isospin factors, i.e.

$$\begin{aligned}&V^{\mathcal {B}_1\mathcal {B}_2\rightarrow \mathcal {B}_1'\mathcal {B}_2'}_{OBE} \nonumber \\&\quad = \sum _{\pi ,\eta ,K} f_{\mathcal {B}_1\mathcal {B}_1'P}f_{\mathcal {B}_2\mathcal {B}_2'P} \, \mathcal {I}_P^{\mathcal {B}_1\mathcal {B}_2\rightarrow \mathcal {B}_1'\mathcal {B}_2'} \, V_{P} \ , \end{aligned}$$

(16)

where $\mathcal {B}$ stands here for octet or decuplet baryons.

A complete list of isospin factors for the $\mathrm{DD}$ case is provided in Sect. 3 where $\mathrm{DD}$ scattering results are presented for various channels and partial waves. Here, we refrain from listing those for $\mathrm{BD}$ scattering and for the $\mathrm{BB}\rightarrow \mathrm{BD}$, $\mathrm{BB}\rightarrow \mathrm{DD}$, and $\mathrm{BD}\rightarrow \mathrm{DD}$ transitions. The ones for diagrams involving $\pi$ and/or $\eta$ exchange can be straightforwardly calculated by using Eq. (27) of Ref. [50]. Furthermore, many coefficients can also be inferred from the tables in Refs. [8, 38] since for transitions of baryons with the same isospins in the initial- and final states, the isospin coefficients are also the same. Note, however, that symmetrization factors ($\sqrt{2}$ and/or a $(-1)^{I-I_1-I_2}$ from recoupling) may differ and that has to be taken into account appropriately. Some isospin coefficients for $\mathrm{BB}\rightarrow \mathrm{BD}$ can be found in Refs. [51, 52].

An explicit representation of the potentials in the particle basis can be found in Appendix B. This form of the potential has been used, in particular, to obtain the SU(3) relations in Appendix C, starting from the contact term Lagrangians.

2.2 Partial-wave decomposition of the meson-exchange contribution

The partial-wave projection of the meson-exchange contribution to the potential is performed using the helicity basis; see Refs. [52, 53] or Appendix B of [51]. The partial-wave projected potential is given by

$$\begin{aligned}&\langle \lambda _1'\lambda _2'| V^J(p',p) |\lambda _1\lambda _2 \rangle \nonumber \\&\quad = 2\pi \int _{-1}^{+1} d(\cos \theta ) d^J_{\lambda ,\lambda '}(\theta ) \langle \lambda _1'\lambda _2'| V({\varvec{p}}',{\varvec{p}}) |\lambda _1\lambda _2 \rangle \ , \end{aligned}$$

(17)

with $\lambda =\lambda _1-\lambda _2$, $\lambda '=\lambda _1'-\lambda _2'$. Here $|\lambda _i\rangle$ and $|\lambda _i'\rangle$ represent the helicity states of the incoming and outgoing baryons. The total angular momentum is denoted by J. The quantities $d^J_{\lambda ,\lambda '}(\theta )$ are the reduced rotation matrices. We calculate those numerically based on the definition of the d-functions in terms of Jacobi polynomials [54]. Analytic expressions for the d-functions needed for J up to 2 can be found, e.g. in Ref. [55]. An incomplete set of the $d^J_{\lambda ,\lambda '}$ with $\lambda = 3$ is listed in Ref. [56].

The amplitudes in the standard JMLS basis are then constructed via a unitary transformation, also described in Appendix B of [51]:

$$\begin{aligned}&\langle JML'S'| V^J(p',p) |JMLS \rangle = \sum _{\lambda _1\lambda _2,\lambda _1'\lambda _2'} \nonumber \\&\quad \langle JML'S'| JM\lambda _1'\lambda _2' \rangle \langle \lambda _1'\lambda _2'| V^J(p',p) |\lambda _1\lambda _2 \rangle \nonumber \\&\quad \langle JM\lambda _1\lambda _2 |JMLS \rangle , \end{aligned}$$

(18)

with

$$\begin{aligned} \langle JMLS|JM\lambda _1\lambda _2\rangle = \sqrt{\frac{2L+1}{2J+1}} \langle L0S\lambda |J\lambda \rangle \langle s_1\lambda _1 s_2 -\lambda _2|S\lambda \rangle , \end{aligned}$$

(19)

where $\lambda = \lambda _1 -\lambda _2$ and $<s_1\lambda _1 s_1\lambda _1 | S\lambda>$ denotes a Clebsch-Gordan coefficient.

The wave function of the decuplet baryons is constructed from the standard Rarita–Schwinger spinor

$$\begin{aligned} \psi ^\mu ({\varvec{p}}, {\varLambda }) = \sum _{\lambda _1,\lambda _2} \left\langle 1\lambda _1 \frac{1}{2} \lambda _2 | \frac{3}{2} {\varLambda }\right\rangle \epsilon ^\mu ({\varvec{p}}, \lambda _1) u ({\varvec{p}}, \lambda _2). \end{aligned}$$

(20)

In the non-relativistic (static) approach that we follow here, the polarization vector $\epsilon ^\mu$ $(\mathbf {p}, \lambda _1)$ reduce to [46, 57]

$$\begin{aligned} \epsilon ^i ({\varvec{p}},\pm 1) = \frac{1}{\sqrt{2}} \left( \begin{array}{c} \mp 1 \\ -i \\ 0 \\ \end{array} \right) , \quad \epsilon ^i ({\varvec{p}},0) = \left( \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array} \right) \end{aligned}$$

(21)

and $u ({\varvec{p}}, \lambda _2)$ reduces to a two-component spinor $\chi (\lambda _2)$.

Then the matrix element of the operator ${\varvec{{\varSigma }}} \cdot {\varvec{q}}$ representing the spin structure of the $\mathrm{DD}\phi$ vertex required for the $\mathrm{DD}\rightarrow \mathrm{DD}$, $ND\rightarrow ND$ and $ND\rightarrow \mathrm{DD}$ transition potentials is given in the helicity basis by

$$\begin{aligned} \left\langle {\varLambda }' | \ {\varvec{{\varSigma }}} \cdot {{\varvec{q}}} \ | {\varLambda }\right\rangle= & {} 3\sum _{\lambda _{1'},\lambda _{2'},\lambda _1,\lambda _2} \left\langle 1\lambda _{1'} \frac{1}{2} \lambda _{2'} | \frac{3}{2} {\varLambda }'\right\rangle \left\langle 1\lambda _1 \frac{1}{2} \lambda _2 | \frac{3}{2} {\varLambda }\right\rangle \\&\times \,\epsilon ^* ({\varvec{p}} ', \lambda _{1'}) \epsilon ({\varvec{p}}, \lambda _1) \, \langle \lambda _{2'} | \ {\varvec{\sigma }}\cdot {{\varvec{q}}} \ | \lambda _{2} \rangle . \end{aligned}$$

The helicity matrix elements for ${\varvec{\sigma }} \cdot {\varvec{q}}$ can be found, e.g., in Ref. [53]. Analytic expressions of helicity amplitudes for the transitions $\mathrm{BB}\rightarrow \mathrm{BD}$ and $\mathrm{BB}\rightarrow \mathrm{DD}$ that involve the operators ${\varvec{S}} \cdot {\varvec{q}}$ and/or ${{\varvec{S}}}^{\varvec{\dagger }} \cdot {\varvec{q}}$ can easily be deduced from those in Refs. [52, 58]. Note that an alternative method to perform the partial-wave projections, which exploits rotational invariance by averaging over the total angular momentum projection M, has been formulated in Ref. [59].

2.3 Lagrangians involving contact terms

The construction of the minimal Lagrangian collecting the contact terms at leading order for the various combinations of octet and decuplet baryons is achieved by writing down all chirally invariant flavor structures combined with all possible spin structures. This minimal set is obtained by eliminating redundant terms until the rank of the matrix formed by all transitions matches the number of terms in the Lagrangian. Redundant terms are deleted in such a way that one obtains a maximal number of contact terms with different spin structures and a minimal number of terms with different flavor structures.⁵

In the following we present the minimal leading-order Lagrangians in the non-relativistic limit and rewritten in terms of particle fields, using conventional matrix notation. For the low-energy constants $c^f_{ij}$ of the contact terms, the subscript ij denotes the number of decuplet baryons in the initial and final state. Note that Lagrangian terms for $\mathcal {L}_\mathrm {\mathrm{BB}\mathrm{BB}}$ can be found in [8, 40] and the terms for $\mathcal {L}_\mathrm {D\mathrm{BB}B}$ have been constructed in [44]. We have

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{BB}\mathrm{BB}} = \,&c_{00}^1\sum _{a,b,c,d=1}^3 \left( \bar{B}_{ab} B_{bc}\right) \left( \bar{B}_{cd} B_{da}\right) \nonumber \\&+ c_{00}^2\sum _{a,b,c,d=1}^3 \left( \bar{B}_{ab} \varvec{\sigma } B_{bc}\right) \cdot \left( \bar{B}_{cd} \varvec{\sigma } B_{da}\right) \nonumber \\&+ c_{00}^3\sum _{a,b,c,d=1}^3 \left( \bar{B}_{ab} B_{cd}\right) \left( \bar{B}_{bc} B_{da}\right) \nonumber \\&+ c_{00}^4\sum _{a,b,c,d=1}^3 \left( \bar{B}_{ab} \varvec{\sigma } B_{cd}\right) \cdot \left( \bar{B}_{bc} \varvec{\sigma } B_{da}\right) \nonumber \\&+ c_{00}^5\sum _{a,b,c,d=1}^3 \left( \bar{B}_{ab} B_{ba}\right) \left( \bar{B}_{cd} B_{dc}\right) \nonumber \\&+ c_{00}^6\sum _{a,b,c,d=1}^3 \left( \bar{B}_{ab} \varvec{\sigma } B_{ba}\right) \cdot \left( \bar{B}_{cd} \varvec{\sigma } B_{dc}\right) , \end{aligned}$$

(22)

$$\begin{aligned} \mathcal {L}_\mathrm {D\mathrm{BB}B} =\,&c_{01}^1\sum _{a,b,c,d,e,f=1}^3 \epsilon _{abc} \big [\left( \bar{T}_{ade}{\varvec{S}}^\dagger B_{db}\right) \cdot \left( \bar{B}_{fc}\varvec{\sigma } B_{ef}\right) \nonumber \\&+ \left( \bar{B}_{bd}{\varvec{S}}\, T_{ade}\right) \cdot \left( \bar{B}_{fe}\varvec{\sigma } B_{cf}\right) \big ] \nonumber \\&+c_{01}^2 \sum _{a,b,c,d,e,f=1}^3 \epsilon _{abc} \big [\left( \bar{T}_{ade}{\varvec{S}}^\dagger B_{fb}\right) \cdot \left( \bar{B}_{dc}\varvec{\sigma } B_{ef}\right) \nonumber \\&+ \left( \bar{B}_{bf}{\varvec{S}}\, T_{ade}\right) \cdot \left( \bar{B}_{fe}\varvec{\sigma } B_{cd}\right) \big ]. \end{aligned}$$

(23)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DB}\mathrm{DB}} = \,&c_{11}^1\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} T_{abc}\right) \left( \bar{B}_{de} B_{ed}\right) \nonumber \\&+ c_{11}^2\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} \varvec{{\varSigma }}\, T_{abc}\right) \cdot \left( \bar{B}_{de} \varvec{\sigma }\, B_{ed}\right) \nonumber \\&+c_{11}^3\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} T_{abd}\right) \left( \bar{B}_{ce} B_{ed}\right) \nonumber \\&+ c_{11}^4\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} \varvec{{\varSigma }}\, T_{abd}\right) \cdot \left( \bar{B}_{ce} \varvec{\sigma }\, B_{ed}\right) \nonumber \\&+c_{11}^5\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} T_{abd}\right) \left( \bar{B}_{ed} B_{ce}\right) \nonumber \\&+ c_{11}^6\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} \varvec{{\varSigma }}\, T_{abd}\right) \cdot \left( \bar{B}_{ed} \varvec{\sigma }\, B_{ce}\right) \nonumber \\&+c_{11}^7\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} T_{ade}\right) \left( \bar{B}_{bd} B_{ce}\right) \nonumber \\&+ c_{11}^8\sum _{a,b,c,d,e=1}^3 \left( \bar{T}_{abc} \varvec{{\varSigma }}\, T_{ade}\right) \cdot \left( \bar{B}_{bd} \varvec{\sigma }\, B_{ce}\right) . \end{aligned}$$

(24)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\mathrm{BB}}&= c_{02}^1\sum _{a,b,c,d,e,f,g,h=1}^3 \epsilon _{abc}\epsilon _{def} \big [\left( \bar{T}_{adg}{\varvec{S}}^\dagger B_{gc}\right) \cdot \left( \bar{T}_{beh}{\varvec{S}}^\dagger B_{hf}\right) \nonumber \\&\quad \, +\, \left( \bar{B}_{cg}{\varvec{S}}\, T_{adg}\right) \cdot \left( \bar{B}_{fh}{\varvec{S}}\, T_{beh}\right) \big ] \nonumber \\&\quad \, +\, c_{02}^2 \sum _{a,b,c,d,e,f,g,h=1}^3 \epsilon _{abc}\epsilon _{def} \big [\left( \bar{T}_{adg}S^{\alpha \beta \dagger } B_{gc}\right) \left( \bar{T}_{beh}S^{\alpha \beta \dagger } B_{hf}\right) \nonumber \\&\quad \, +\, \left( \bar{B}_{cg}S^{\alpha \beta } T_{adg}\right) \left( \bar{B}_{fh}S^{\alpha \beta } T_{beh}\right) \big ], \end{aligned}$$

(25)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\mathrm{DB}}&= c_{12}^1\sum _{a,b,c,d,e,f,g=1}^3 \epsilon _{abc} \big [ \left( \bar{T}_{ade}\varvec{{\varSigma }} T_{def}\right) \cdot \left( \bar{T}_{bfg}{\varvec{S}}^\dagger B_{gc}\right) \nonumber \\&\quad \, +\, \left( \bar{T}_{def}\varvec{{\varSigma }} T_{ade}\right) \cdot \left( \bar{B}_{cg}{\varvec{S}}\, T_{bfg}\right) \big ] \nonumber \\&\quad \, +\, c_{12}^2\sum _{a,b,c,d,e,f,g=1}^3 \epsilon _{abc} \big [ \left( \bar{T}_{ade}{\varSigma }^{\alpha \beta } T_{def}\right) \left( \bar{T}_{bfg}S^{\alpha \beta \dagger } B_{gc}\right) \nonumber \\&\quad \, +\, \left( \bar{T}_{def}{\varSigma }^{\alpha \beta } T_{ade}\right) \left( \bar{B}_{cg}S^{\alpha \beta } T_{bfg}\right) \big ]. \end{aligned}$$

(26)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\mathrm{DD}}&= c_{22}^1\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} T_{abc}\right) \left( \bar{T}_{def} T_{def}\right) \nonumber \\&\quad \, +\, c_{22}^2\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} \varvec{{\varSigma }} T_{abc}\right) \cdot \left( \bar{T}_{def} \varvec{{\varSigma }} T_{def}\right) \nonumber \\&\quad \, +\, c_{22}^3\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} {\varSigma }^{\alpha \beta } T_{abc}\right) \left( \bar{T}_{def} {\varSigma }^{\alpha \beta } T_{def}\right) \nonumber \\&\quad \, +\, c_{22}^4\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} {\varSigma }^{\alpha \beta \gamma } T_{abc}\right) \left( \bar{T}_{def} {\varSigma }^{\alpha \beta \gamma } T_{def}\right) \nonumber \\&\quad \, +\, c_{22}^5\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} T_{abd}\right) \left( \bar{T}_{def} T_{cef}\right) \nonumber \\&\quad \, +\, c_{22}^6\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} \varvec{{\varSigma }} T_{abd}\right) \cdot \left( \bar{T}_{def} \varvec{{\varSigma }} T_{cef}\right) \nonumber \\&\quad \, +\, c_{22}^7\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} {\varSigma }^{\alpha \beta } T_{abd}\right) \left( \bar{T}_{def} {\varSigma }^{\alpha \beta } T_{cef}\right) \nonumber \\&\quad \, +\, c_{22}^8\sum _{a,b,c,d,f=1}^3 \left( \bar{T}_{abc} {\varSigma }^{\alpha \beta \gamma } T_{abd}\right) \left( \bar{T}_{def} {\varSigma }^{\alpha \beta \gamma } T_{cef}\right) . \end{aligned}$$

(27)

2.4 Group theoretical considerations

Group theory can be used to deduce the number of terms in the chiral contact Lagrangian. First of all we need to express the two-baryon states in terms of irreducible representations of SU(3) (flavor) and SU(2) (spin). For octet–octet baryon states $\mathrm{BB}$ the decompositions in flavor and spin space are, respectively:

$$\begin{aligned} \mathbf {8}\otimes \mathbf {8} = {\mathbf {27}}\oplus {\mathbf {8_s}}\oplus {\mathbf {1}}\oplus \mathbf {10}\oplus \mathbf {\overline{10}}\oplus \mathbf {8_a},\quad \mathbf {2} \otimes \mathbf {2} = \mathbf {1} \oplus \mathbf {3}, \end{aligned}$$

(28)

where in flavor space the representations $\mathbf {27},{\mathbf {8_s}},{\mathbf {1}}$ are symmetric and the representations $\mathbf {10},\mathbf {\overline{10}},\mathbf {8_a}$ are antisymmetric. In spin space $\mathbf {1}$ is antisymmetric and $\mathbf {3}$ is symmetric. For decuplet–octet baryon states $\mathrm{DB}$ one obtains

$$\begin{aligned} \mathbf {10}\otimes \mathbf {8} = {\mathbf {35}}\oplus {\mathbf {27}}\oplus \mathbf {10}\oplus \mathbf {8},\quad \mathbf {4} \otimes \mathbf {2} = \mathbf {3} \oplus \mathbf {5}. \end{aligned}$$

(29)

Decuplet–decuplet-baryon states $\mathrm{DD}$ take the form

$$\begin{aligned} \mathbf {10}\otimes \mathbf {10} = {\mathbf {35}}\oplus \mathbf {\overline{10}}\oplus {\mathbf {28}}\oplus \mathbf {27},\quad \mathbf {4} \otimes \mathbf {4} =\mathbf {1} \oplus \mathbf {5} \oplus \mathbf {3} \oplus \mathbf {7}. \end{aligned}$$

(30)

Combining this information with the Pauli principle (for $\mathbf {8}\otimes \mathbf {8}$ and $\mathbf {10}\otimes \mathbf {10}$) and the fact that, at leading order, only transitions between the same flavor and spin irreducible representations can occur, we can write down the possible combinations of flavor and spin representations (flavor,spin) in which the transition can occur:

$$\begin{aligned} \mathrm{BB}\rightarrow \mathrm{BB}:&\ (\mathbf {27},\mathbf {1}),(\mathbf {8_s},\mathbf {1}),(\mathbf {1},\mathbf {1}),(\mathbf {10},\mathbf {3}),(\mathbf {10^*},\mathbf {3}),(\mathbf {8_a},\mathbf {3}) ,\\ \mathrm{BB}\rightarrow \mathrm{DB}:&\ (\mathbf {10},\mathbf {3}),(\mathbf {8},\mathbf {3}) ,\\ \mathrm{BB}\rightarrow \mathrm{DD}:&\ (\mathbf {27},\mathbf {1}),(\mathbf {\overline{10}},\mathbf {3}), \\ \mathrm{DB}\rightarrow \mathrm{DB}:&\ (\mathbf {35},\mathbf {3}),(\mathbf {27},\mathbf {3}),(\mathbf {10},\mathbf {3}),(\mathbf {8},\mathbf {3}),(\mathbf {35},\mathbf {5}),(\mathbf {27},\mathbf {5}),\\&\, (\mathbf {10},\mathbf {5}),(\mathbf {8},\mathbf {5}) ,\\ \mathrm{DB}\rightarrow \mathrm{DD}:&\ (\mathbf {35},\mathbf {3}),(\mathbf {27},\mathbf {5}), \\ \mathrm{DD}\rightarrow \mathrm{DD}:&\ (\mathbf {35},\mathbf {3}),(\mathbf {35},\mathbf {7}),(\mathbf {\overline{10}},\mathbf {3}),(\mathbf {\overline{10}},\mathbf {7}),(\mathbf {28},\mathbf {1}),(\mathbf {28},\mathbf {5}), \\&\, (\mathbf {27},\mathbf {1}),(\mathbf {27},\mathbf {5}). \end{aligned}$$

The resulting number of different (flavor,spin) representations is six for $\mathrm{BB}\rightarrow \mathrm{BB}$, eight for $\mathrm{DB}\rightarrow \mathrm{DB}$, eight for $\mathrm{DD}\rightarrow \mathrm{DD}$, and two each for the transitions $\mathrm{BB}\rightarrow \mathrm{DB}$, $\mathrm{BB}\rightarrow \mathrm{DD}$, and $\mathrm{DB}\rightarrow \mathrm{DD}$. This fits well to the number of low-energy constants of the minimal Lagrangians in Sect. 2.3. It serves as a non-trivial check of our calculation.

The SU(3) relations for the various two-body $S$-wave contact interactions among octet and decuplet baryons are summarized in Appendix C. Furthermore, the relations between the LECs of the Lagrangians and the irreducible representations are given. The SU(3) relations for the decuplet-decuplet interaction can be found already in Table 1 as they are of prime interest for applications discussed in the following sections. All those relations are relevant for checking the consistent construction of the LO Lagrangian and potentials. By an approach analogous to the one in Ref. [60], we can establish which irreducible representations contribute to a specific strangeness-isospin channel. These relations have to conform with corresponding results that follow directly from the isoscalar factors of the $\mathbf {8} \otimes \mathbf {8}$, $\mathbf {10} \otimes \mathbf {8}$, and $\mathbf {10} \otimes \mathbf {10}$ representations given in Ref. [42].⁶ They are also important for actual calculations as they specify how different strangeness and isospin channels are connected with each other via SU(3) symmetry. This aspect will be further exploited in Sect. 3.

Table 1 SU(3) relations of $\mathrm{DD}\rightarrow \mathrm{DD}$ in non-vanishing partial waves. The subscript $\{22\}$ of the constants $C_{22}^r$ that denotes the $\mathcal {B}\mathcal {B}$ channel is omitted in the table

2.5 Partial-wave decomposition of contact spin structures

In the following we present the explicit forms of the contact potentials $V_\mathrm{cont}$ involving the most general two-body spin operators for the non-vanishing transitions between partial waves ${}^{2S+1}L_J$ at leading order. Following the method described in Ref. [61] one finds (with constants $a_i$):

$$\begin{aligned} \mathrm{BB}\leftarrow \mathrm{DB}: \ V_\mathrm{cont}&= a_1 {{\varvec{S}}}^\dagger _1 \cdot \varvec{\sigma }_2 ,\\ \mathrm{BB}\rightarrow \mathrm{DB}: \ V_\mathrm{cont}&= a_1 {{\varvec{S}}}_1\cdot \varvec{\sigma }_2 , \\ V_{^3S_1}&= \langle {}^3S_1|V_\mathrm{cont}|{}^3S_1\rangle = -2\sqrt{\frac{2}{3}}a_1, \end{aligned}$$

$$\begin{aligned} \mathrm{DB}\rightarrow \mathrm{BD}: \ V_\mathrm{cont}&= a_1{{\varvec{S}}}_1\cdot {{\varvec{S}}}^\dagger _2 + a_2S^{ij}_1S^{ij\dagger }_2 , \\ V_{^3S_1}&= \langle {}^3S_1|V_\mathrm{cont}|{}^3S_1\rangle = \frac{1}{3}a_1 - \frac{5}{3} a_2 ,\\ V_{^5S_2}&= \langle {}^5S_2|V_\mathrm{cont}|{}^5S_2\rangle = a_1 + \frac{1}{3} a_2, \end{aligned}$$

$$\begin{aligned} \mathrm{DB}\leftarrow \mathrm{DD}: \ V_\mathrm{cont}&= a_1{{\varvec{{\varSigma }}}}_1\cdot {{\varvec{S}}}^\dagger _2 + a_2{\varSigma }^{ij}_1S^{ij\dagger }_2\\ \mathrm{DB}\rightarrow \mathrm{DD}: \ V_\mathrm{cont}&=a_1{{\varvec{{\varSigma }}}}_1\cdot {{\varvec{S}}}_2 + a_2{\varSigma }^{ij}_1S^{ij}_2 ,\\ V_{^3S_1}&=\langle {}^3S_1|V_\mathrm{cont}|{}^3S_1\rangle = 2\sqrt{\frac{5}{3}} a_1 + \sqrt{10} a_2, \\ V_{^5S_2}&=\langle {}^5S_2|V_\mathrm{cont}|{}^5S_2\rangle = 2\sqrt{3} a_1 - \sqrt{2} a_2, \end{aligned}$$

The actual potential for a specific channel and partial wave is a combination of low-energy constants according to Tables 1 and Tables 6, 7, 8, 9, 10 in Appendix C.

3 Application to lattice QCD results

In this section we exemplify how the formalism developed above can be used to analyze results from lattice QCD computations. It should be understood that this study has primarily illustrative character. Lattice results for interactions involving decuplet baryons are so far restricted to unphysically large pion masses. It is obvious that LO chiral EFT can give only a qualitative (but nonetheless instructive) picture. More elaborate treatments, at next-to-leading order and beyond, will be feasible as lattice simulations proceed (close) to physical masses and become increasingly accurate.

The reaction amplitude for a specific potential $V=V_{OBE}+V_\mathrm{cont}$ is obtained by solving a corresponding LS equation in partial-wave projected form [8],

$$\begin{aligned} T^{L'' L'}(p'',p';E)= & {} V^{L''L'}(p'',p') \nonumber \\&+ \sum _{L}\int _0^\infty \frac{dpp^2}{(2\pi )^3} \, V^{L''L}(p'',p) \nonumber \\&\times \,\frac{2\mu }{k^2-p^2+i\eta }T^{LL'}(p,p';E), \end{aligned}$$

(31)

where the tensor coupling between different orbital angular momenta $L''$, $L'$ is taken into account. $\mu$ is the reduced mass, i.e. $\mu = M_1 M_2/(M_1+ M_2)$, with $M_1$, $M_2$ being the masses of the baryons in the intermediate state. The on-shell momentum in the intermediate state, k, and the kinetic energy E in the center-of-mass frame are given by the relation $\sqrt{s} = E + M_1 + M_2 = \sqrt{M^2_1+k^2}+\sqrt{M^2_2+k^2}$. The scattering equation (31) generally includes couplings between different $\mathcal {B}\mathcal {B}$ channels [8]. In the applications described in this section we consider systems without such coupled channels, hence corresponding indices and summations in Eq. (31) have been omitted. For the simulation of the lattice QCD results the respective baryon masses as given in the corresponding publications are employed. These will be given in each case considered as we proceed. In the calculations at the physical point we use the following (isospin averaged) baryon masses: $M_N=938.92$ MeV, $M_{{\varDelta }}=1232$ MeV, $M_{{\varSigma }^*}=1385$ MeV, $M_{{\varXi }^*}=1530$ MeV, and $M_{{\varOmega }}=1672.45$ MeV. The LS equation is solved in the isospin basis and the Coulomb interaction is ignored (as in the lattice QCD calculations).

The integral in the LS Eq. (31) is divergent for the chiral potentials specified above. A regularization needs to introduced. We utilize here the same prescription as in our YN studies, where the potentials in the LS equation are cut off in momentum space by multiplication with a regulator function, $f(p',p) = \exp \left[ -\left( p'^4+p^4\right) /{\varLambda }^4\right]$, so that the high-momentum components of the baryon and pseudoscalar-meson fields are removed. In the present study we employ the cut-off scales 500 and 700 MeV, in line with the range considered in our LO study of the ${{\varLambda }}N$ and ${{\varSigma }}N$ interactions [8]. The variation of the results with the cut-off reflect uncertainties that will be indicated by bands. Clearly, a better error analysis based e.g. on the approach advocated in Ref. [62] should be done once more lattice data and/or higher-order calculations are available.

At LO the only dependence of the potential V on the pion mass or on other meson masses comes from the meson propagators in Eq. (15). The SU(3) breaking manifested in the masses of the octet and/or decuplet baryons does not affect the potential itself at this order [8]. However, those masses enter the LS Eq. (31) and, therefore, influence the actual result for the reaction amplitude T. It is important to take this effect into account, as argued in Refs. [15, 16]. After all, the binding energy of a possible bound state results from a delicate interplay between the potential energy (that depends on the pion mass) and the kinetic energy in the baryon–baryon Green’s function (that is affected by the baryon masses).

At next-to-leading order the contact terms as well as the coupling constants depend on the quark masses or, equivalently, on the pion mass. For details, we refer to Refs. [63,64,65,66,67,68], where the quark mass dependence of the NN interaction has been investigated; see also Ref. [40]. However, as mentioned, for the present limited applications it is sufficient to stay at the LO level of single pseudoscalar-meson exchange plus contact term with a much restricted set of low-energy constants. For NN scattering [63,64,65,66,67,68] the pion-exchange contribution plays an essential role. In contrast, for some of the systems considered here such as ${{\varOmega }}{{\varOmega }}$ or $N{{\varOmega }}$, the only contributor to pseudoscalar-meson exchange is the $\eta$ meson. Variations of the pion mass (or the SU(3) breaking due to the small pion mass as compared to the K and $\eta$ masses) are expected to be less important for such systems.

In the present work we follow closely the strategy utilized in our study/analysis of lattice QCD simulations for the H–dibaryon [15] and other possible bound states of two-body systems involving octet baryons in the sectors with strangeness $S=-\,2$, $-\,3$ and $-\,4$ [16]. We aim at a reproduction of the phase shifts and/or scattering lengths from the LQCD calculation within LO chiral EFT. Thereby we employ the masses of the pseudoscalar mesons and the baryons corresponding to the lattice simulation in our calculation and fix the low-energy constant associated with the strength of the contact term by a fit to the lattice data. Results at the physical point are then obtained replacing the masses of the mesons in the potential by their physical values and correspondingly those of the baryons in the LS equation.

3.1 ${\varDelta }{\varDelta }\pi$ coupling constant

An essential ingredient of the calculation is the ${\varDelta }{\varDelta }\pi$ coupling constant. Its value, together with the imposed SU(3) symmetry relations, fixes the strengths of all contributions from pseudoscalar-meson exchange to the $\mathrm{DD}$ interaction. Unfortunately, unlike the $NN\pi$ and $N{\varDelta }\pi$ coupling constants, the value for $f_{{\varDelta }{\varDelta }\pi }$ is not constrained by experimental information. A wide range of values for the ${\varDelta }{\varDelta }\pi$ coupling constant can be found in the literature [47, 48, 57, 69,70,71,72]. In a variety of calculations the quark-model value [57] is used which amounts to $f_{{{\varDelta }}{{\varDelta }}\pi } = f_{NN\pi }/5$ [50] for the normalization of the spin and isospin operators as defined in Appendix A. Large $N_c$ arguments lead to $g_1 = 9g_A/5$ [47, 71], where $g_1$ is the ${{\varDelta }}{{\varDelta }}\pi$ coupling constant commonly used in chiral perturbation theory. Taking into account the different normalization of the spin- and isospin operators, this corresponds likewise to $f_{{{\varDelta }}{{\varDelta }}\pi } = f_{NN\pi }/5$. The result in [71] using QCD sum rules is $g_1 = 0.885\pm 0.15$ based on Eqs. (4) and (10) of that work, i.e. roughly half of the large $N_c$ prediction. Recent lattice QCD calculations indicate values around $g_1 \approx 0.6$ ($g_1 \simeq g_A/2$) [73] for $m_\pi \approx 300$ MeV. In a new study of pion–nucleon scattering within chiral perturbation theory up to third order that includes the ${\varDelta }$ resonance explicitly [48] a value $g_1 =1.21\pm 0.46 \pm 0.39$ was deduced. The large uncertainty indicates the difficulty to pin down the ${{{\varDelta }}{{\varDelta }}\pi }$ coupling constant reliably from such a calculation. See, however, Ref. [49].

Table 2 Partial waves for $\mathrm{BB}$, $\mathrm{BD}$, and $\mathrm{DD}$ scattering for angular momenta $J \le 3$

3.2 Partial waves and isospin factors

An overview of partial waves up to total angular momentum $J=3$ is provided in Table 2. In general, denoting the states as $|JMLS\rangle$, L being the orbital angular momentum and S the total spin, the $\mathrm{BD}$ system (spin $1/2 \otimes 3/2$) can be in the following two sets of four states:

$$\begin{aligned}&|JMJ1\rangle , \ |JMJ2\rangle , \ |JM(J\pm 2)2\rangle ; \nonumber \\&\quad |JM(J\pm 1)1\rangle , \ |JM(J\pm 1)2\rangle , \end{aligned}$$

(32)

which differ by parity and, therefore, do not couple. For $\mathrm{DD}$ ($3/2 \otimes 3/2$) there are four such sets,

$$\begin{aligned}&|JMJ0\rangle , \ |JMJ2\rangle , \ |JM(J\pm 2)2\rangle ; \nonumber \\&\quad |JMJ1\rangle , \ |JMJ3\rangle , \ |JM(J\pm 2)3\rangle ; \nonumber \\&\quad |JM(J\pm 1)1\rangle , \ |JM(J \pm 3)3\rangle , \ |JM(J \pm 1)3\rangle ; \nonumber \\&\quad |JM(J \pm 1)2\rangle , \end{aligned}$$

(33)

where again there is no coupling between states with different parity. The other sets decouple too, as long as the interaction is given only by pseudoscalar-meson exchange, Eq. (15).

We focus here on (coupled) partial waves that involve S-wave states, i.e., where contributions from contact terms at leading order arise. The $\mathrm{DD}$ system can be in the following S-wave states: $^1S_0$, $^3S_1$, $^5S_2$, $^7S_3$. In channels with identical particles the Pauli principle reduces the number of possible states. For example, in the ${{\varOmega }}{{\varOmega }}$ system only the S waves $^1S_0$ and $^5S_2$ are allowed. In the case of ${\varDelta }{\varDelta }$ the spin-space odd states ($^1S_0$, $^5S_2$) can have total isospin $I=1$ and 3 while the spin-space even states ($^3S_1$, $^7S_3$) can have total isospin $I=0$ and 2. There is no restriction from the Pauli principle for the $\mathrm{BD}$ system so that one has the S-wave states $^3S_1$ and $^5S_2$ in all channels.

Table 3 Decuplet–decuplet scattering: isospin factors $I_P$ for the various meson exchanges

In Table 3 the isospin factors that enter into the evaluation of the meson-exchange contribution to the $\mathrm{DD}$ potential are summarized. For strangeness $S=-\,2$ and $-\,4$ there are channels with non-identical and with identical particles which require special treatment. Specifically, a proper symmetrization is required which can be achieved by introducing the flavor-exchange operator $P_f$, cf. the procedure applied in the analogous $\mathrm{BB}$ case with $S=-\,2$ (${{\varSigma }}{{\varSigma }}$, ${\varXi }N$, etc.) described in Ref. [38].

3.3 ${{\varOmega }}{{\varOmega }}$ and SU(3) related channels

The Paul principle implies that the only allowed S-wave states for ${{\varOmega }}{{\varOmega }}$ are $^1S_0$ and $^5S_2$. Moreover, the associated potentials depend only on a single LEC for each partial wave, namely the one corresponding to the SU(3) irreducible representation 28; see Table 1. There are lattice QCD simulations for ${{\varOmega }}{{\varOmega }}$ scattering by two groups. The earlier one by Buchoff et al. [18] corresponds to a pion mass of $m_\pi \approx 390$ MeV and an ${{\varOmega }}$ mass close to the physical value. It suggests a fairly weak and repulsive interaction in the $^1S_0$ state with a scattering length of $a = (0.16\pm 0.22)$ fm in the $^1S_0$ partial wave. The results of the HAL QCD collaboration, published soon after, turned out to be qualitatively different [19]. That calculation suggests a strongly attractive interaction for the $^1S_0$ channel, with phase shifts comparable to those of the $^1S_0$ partial wave in neutron–proton scattering. Indeed, taking into account the large statistical errors, even an ${{\varOmega }}{{\varOmega }}$ bound state might be supported. The lattice set-up in Ref. [19] corresponds to the masses: $m_\pi = 701$ MeV, $m_K = 789$ MeV, $M_{{\varOmega }}= 1966$ MeV, quite far from the physical point.

Results of our analysis of the HAL QCD results are presented in Fig. 1 as a function of the kinetic energy in the center-of-mass frame. These are achieved by appropriately adjusting the LEC $C^{28,\,^1S_0}_{22}$ (denoted simply by $C^{28}$ in the following discussion) to the lattice data for each cut-off. The variation of the results with the cut-offs ${\varLambda }=500$–700 MeV is indicated by uncertainty bands. Figure 1a shows a fit to the central HAL QCD prediction (hatched/blue band) while (b) is based on a fit to the upper limit given for the $^1S_0$ phase shift. In this case an ${{\varOmega }}{{\varOmega }}$ bound state with binding energy around 1 MeV is produced. Since the $\eta$ mass is not given in Ref. [19], we assume that $m_\eta \approx m_K$. In principle, the GMO mass formula could have been used to fix $m_\eta$ based on the values of $m_K$ and $m_\pi$. However, we refrain from doing so in this illustrative study. Anyway, it should be said that variations of $m_\eta$ by 20 or 30 MeV have very little influence on the actual results and can be accommodated by a slight readjustment of $C^{28}$.

Fig. 1

${{\varOmega }}{{\varOmega }}^1S_0$ phase shift as a function of the kinetic energy in the center-of-mass system. The result of the HAL QCD collaboration is taken from Ref. [19]. Fits to the central value (a) and maximal value (b) of the lattice simulation are shown by hatched (blue) bands, corresponding to cut-off variations between 500 and 700 MeV. Corresponding results at the physical point are indicated by dark (red) bands. The gray (green) band is the result based on the lattice simulation by Buchoff et al. [18]

The extrapolation to the physical point is indicated by dark (red) bands in Fig. 1. Obviously, the interaction becomes less attractive and for neither of the two cases considered there is a bound state. It should be noted that preliminary results for ${{\varOmega }}{{\varOmega }}$ corresponding to a pion mass close to the physical point ($m_\pi \approx 145$ MeV) reported recently by the HAL QCD collaboration [21] suggest that there could be indeed a bound state, with a binding energy roughly comparable to that of the deuteron. However, the corresponding mass of the ${{\varOmega }}$ baryon is not specified so that it remains unclear how close the latter is to its physical value. In any case, it will be interesting to see the final result.

The results in Fig. 1 were obtained with a ${{\varDelta }}{{\varDelta }}\pi$ coupling constant corresponding to $g_1 =1.5$. In the course of fitting to the lattice predictions we varied $g_1$ and it turned out that values around 1.3–1.5 allowed for the best reproduction of the energy dependence suggested by the lattice calculation. For larger values, specifically for values close to the large $N_c$ prediction, $g_1 =9 g_A/5 \approx 2.3$, we observed a very strong energy dependence of the $^1S_0$ phase shift close to threshold that is not in line with the lattice data. It is caused by a dramatic increase in the coupling between the $^1S_0$ and $^5D_0$ partial waves. The larger coupling constant increases the strength of the tensor force due to $\eta$ exchange so that the mixing angle becomes larger than the $^1S_0$ phase shift itself already at small energies. We consider such a scenario as not realistic. But it should be noted at the same time that the conclusions of Ref. [19] are based on an effective purely central ${{\varOmega }}{{\varOmega }}$ potential, used for calculating the $^1S_0$ phase shift. Accordingly, the role of the coupling to the $^5D_0$ channel in the evaluation of the lattice data remains unclear.

Results based on the lattice calculation in Ref. [18] are indicated by the gray (green) band in Fig. 1, where we fixed the LEC by a fit to the scattering length $a = 0.16$ fm. Since the relevant masses in that study are already fairly close to the physical point ($M_{{\varOmega }}= 1632$ MeV [74], $m_\eta = 587$ MeV [75]) we show only the evaluation for physical masses. The obvious discrepancy between the predictions in Refs. [18] and [19] cannot be resolved by the present study.

Fig. 2

Prediction for the ${{\varDelta }}{{\varDelta }}$ $^1S_0$ phase shift with isospin $I=3$ based on the ${{\varOmega }}{{\varOmega }}$ result and SU(3) symmetry. The dark (red) band is based on the $C^{28}$ value fixed by a fit to the central HAL QCD result for ${{\varOmega }}{{\varOmega }}$, while the hatched (red) band corresponds to the maximum HAL QCD result, cf. Fig. 1. The gray (green) band corresponds to the lattice result of Ref. [18]. All results are for physical meson and baryon masses

Fig. 3

Prediction for the ${{\varSigma }^*}{{\varDelta }}$ $^1S_0$ phase shift with isospin $I=5/2$ based on the ${{\varOmega }}{{\varOmega }}$ result and SU(3) symmetry. Same description of curves as in Fig. 2

Fig. 4

Prediction for the ${{\varXi }^*}{{\varOmega }}^1S_0$ phase shift with isospin $I=1/2$ based on the ${{\varOmega }}{{\varOmega }}$ result and SU(3) symmetry. Same description of curves as in Fig. 2

Once the LEC $C^{28}$ is fixed by a fit to the ${{\varOmega }}{{\varOmega }}$ channel, SU(3) symmetry can be exploited to obtain corresponding $^1S_0$ results/predictions for ${{\varDelta }}{{\varDelta }}$ ($I=3$), ${{\varSigma }^*}{{\varDelta }}$ ($I=5/2$), and ${{\varOmega }}{{\varXi }^*}$ ($I=1/2$). The interaction in all those cases is determined by the same LEC, cf. Table 1, together with contributions from meson exchange. And in all those cases there is no coupling to $\mathrm{BB}$ or $\mathrm{BD}$ channels.

The corresponding phase shifts are presented in Figs. 2, 3, 4. They illustrate the amount of SU(3) breaking that arises in our calculation from the mass differences between $\pi$, $\eta$ and K, and between the decuplet baryons. Clearly, given that the ${{\varDelta }}$ and ${{\varSigma }^*}$ resonances are fairly broad, the ${{\varDelta }}{{\varDelta }}$ and ${{\varSigma }^*}{{\varDelta }}$ phase shifts are interesting just for purely academic reasons. This is different for the ${{\varXi }^*}$ because its width is only around 10 MeV, i.e. comparable to the one of the $\omega$ meson, so that one can view it practically as a stable particle.

While in the case of ${{\varOmega }}{{\varOmega }}$ scattering only the $\eta$-meson can contribute, $\eta$ as well as K exchange is possible for ${{\varOmega }}{{\varXi }^*}$; see Table 3. However, given that $m_K\approx m_\eta$ there is not much difference in the actual potentials. Since the reduced mass $\mu$ of the latter system is smaller we still expect that the attraction should be slightly weaker, cf. Fig. 4. Concerning ${{\varDelta }}{{\varDelta }}$ and ${{\varSigma }^*}{{\varDelta }}$ there is a sizable contribution from pion exchange so that the corresponding potentials are more strongly influenced by the SU(3) breaking due to the meson masses. At the same time the reduced masses for these systems are noticeably smaller. Both effects together lead to interactions that are appreciably less attractive, as can be seen from the phase shifts in Figs. 2 and 3. The predictions based on the lattice result of Ref. [18] (cf. green/gray bands) suggest a basically repulsive interaction for all considered systems. Only in the ${{\varDelta }}{{\varDelta }}$ and ${{\varSigma }^*}{{\varDelta }}$ channels and for energies close to the threshold does one observe slightly positive values for the $^1S_0$ phase shift signaling a weakly attractive tail of the potential.

In this context, let us mention that quark-model studies [30], but also Faddeev-type calculations [31], often suggest the existence of a ${{\varDelta }}{{\varDelta }}$ dibaryon with $I=3$. Recently, an experimental search for such a dibaryon state has been performed by the WASA-at-COSY collaboration in the reaction $pp\rightarrow pp\pi ^+\pi ^+\pi ^-\pi ^-$ [76]. However, no clear-cut evidence for such a state was found.

3.4 ${{\varDelta }}{{\varDelta }}$ with $J=3$ and $I=0$

Dibaryon candidates for the ${{\varDelta }}{{\varDelta }}$ state with $J=3$, $I=0$ are often mentioned together with the ones with $J=0$, $I=3$ discussed above. In particular, model studies point out a close connection between the ${{\varDelta }}{{\varDelta }}$ states with $I(J^P)=0(3^+)$ and its $I(J^P)=3(0^+)$ mirror state [30, 31]. Indeed, at least with regard to the S-wave interactions the product of the expectation values for the spin and isospin operators is identical for the two channels so that the corresponding potential due to pion exchange is the same. However, from Table 1 one can see that the states actually belong to different SU(3) irreducible representations, so that the interactions involve different LECs. Furthermore, for the state with $J=3$ there are many more coupled partial waves; see Table 2. And finally, the ${{\varDelta }}{{\varDelta }}$ state with $J=3$, $I=0$ couples to the NN system.

Nonetheless, the ${{\varDelta }}{{\varDelta }}$ state with $J=3$, $I=0$ is of special interest because, as discussed in the Introduction, the $d^*(2380)$ dibaryon candidate seen by the WASA-at-COSY collaboration [29] could be a quasibound state produced by this system. Indeed, the analysis of data on quasifree polarized np scattering presented in that paper suggests the $d^*(2380)$ dibaryon to be a resonance in the $^3D_3$–$^3G_3$ NN partial wave. This state can couple to the ${{\varDelta }}{{\varDelta }}$ system with the partial waves $^7S_3$–$^3D_3$–$^7D_3$–$^3G_3$–$^7G_3$–$^7I_3$; see Table 2. The position of the resonance pole given by the WASA-at-COSY collaboration is $2380\pm 10 - i (40\pm 5)$ MeV. Since the nominal ${{\varDelta }}{{\varDelta }}$ threshold is at 2464 MeV this would imply a binding energy in the order of $84\pm 10$ MeV. Of course this naive binding energy assignment ignores the width associated with the ${\varDelta }\rightarrow \pi N$ decay channels. For an overview of the rapidly growing literature on the $d^*(2380)$ dibaryons see for example Ref. [2].

Fig. 5

Prediction for the ${{\varDelta }}{{\varDelta }}$ $^7S_3$ phase shift with isospin $I=0$. The result of the HAL QCD collaboration is taken from Ref. [21]. Results of a fit to the lattice simulation is shown by a hatched band, corresponding to cut-off variations between 500 and 700 MeV. The corresponding results for physical masses are shown by solid (700 MeV) and dash-dotted (500 MeV) lines

Addressing the experimental results directly is beyond the scope of the present study. Fortunately, there are also lattice QCD calculations for the ${{\varDelta }}{{\varDelta }}$ system in question by the HAL QCD collaboration to which we can connect. It should be said, however, that so far only preliminary results are available that have been presented at conferences [21]. Accordingly, we emphasize that our considerations here have likewise preliminary character. The ${{\varDelta }}{{\varDelta }}$ lattice QCD calculation of the $^7S_3$ partial wave with $I=0$ corresponds to a pion mass of $m_\pi = 1015$ MeV [21]. Unfortunately, the pertinent value for $M_{{\varDelta }}$ is not given. Supposedly the lattice set-up with $m_\pi = 1015$ MeV corresponds to an SU(3) symmetric calculation where the octet baryon mass is $M_B=2030~\hbox {MeV}$ [6], and so we assume that using this mass is a meaningful option. The results of the HAL QCD collaboration for the $^7S_3$ ${{\varDelta }}{{\varDelta }}$ partial wave is shown in Fig. 5 together with our fits. The LEC is fixed in such a way that the results at low energies are well reproduced. The hypothesis of a ${{\varDelta }}{{\varDelta }}$ bound state [21] is taken over and imposed in the fitting procedure. Again the cut-off values ${\varLambda }=500$ and 700 MeV have been adopted.

Given that the lattice calculation is for a rather large pion mass, the phase shifts are basically determined by the contact term in $^7S_3$ alone. The binding energy implied by the fit is around 50–100 MeV. When physical masses are used the results for the two cut-offs show different trends; see Fig. 5. In one case, ${\varLambda }=500$ MeV (dash-dotted line), there is very little change and the binding energy is still around 75 MeV. This happens to be close to the $d^*(2380)$ but this coincidence should of course not be overinterpreted. In the other case (solid line), the attraction is strongly reduced and only a fairly shallow bound state with a binding energy of about 2.2 MeV survives. Lowering the ${{\varDelta }}$ mass to its physical value weakens the attraction because the reduced mass becomes smaller and along with it the contribution of the loop integral in the LS Eq. (31). At the same time, reducing the pion mass increases the tensor coupling to the other partial waves, in particular, to the two D waves. Thereby, the attraction is increased so that there is a compensating effect. Obviously, the details of this compensation depends strongly on the cut-off so that no clear trend emerges. One has to keep in mind that the $^7S_3$ state can couple to many other partial waves; see Table 2, which increases the sensitivity to the employed cut-off mass. A further complication is certainly the circumstance that the so far available lattice QCD calculation is for rather large masses. An extrapolation over a large mass region and, moreover, based on an LO calculation cannot be very reliable. Nevertheless, even for masses closer to the physical point it will be a challenge to perform an accurate extrapolation in view of the complicated angular-momentum structure of that state.

Anyway, based on the present results one might still conclude that the existence of a quasibound ${{\varDelta }}{{\varDelta }}$ state with $J=3$, $I=0$ is at least not totally implausible. We should add that, given the very preliminary character of the ${{\varDelta }}{{\varDelta }}$ LQCD calculation, we ignored here the coupling to NN (in the $^3D_3$–$^3G_3$ partial wave, cf. Table 2) and the fact that the ${\varDelta }$ has a sizable width, i.e. there is a coupling to the $NN\pi$ and $NN\pi \pi$ continuum [77]. Both should have a significant influence on the location of the state and certainly on its width.

3.5 $N {{\varOmega }}$ with $J=2$

Finally, let us consider the $N{{\varOmega }}$ interaction in the $^5S_2$ partial wave. Also for this case results from a lattice QCD calculation by the HAL QCD collaboration are available [20]. The lattice set-up corresponds to the masses: $M_{{\varOmega }}= 2105$ MeV, $M_N = 1806$ MeV $m_\pi = 875$ MeV, $m_K = 916$ MeV (again we assume that $m_\eta \approx m_K$).

The $N{{\varOmega }}$ system is interesting because it involves only stable particles (stable against hadronic decay) so that, in principle, even scattering experiments are feasible. However, unlike ${{\varOmega }}{{\varOmega }}$ discussed above, $N{{\varOmega }}$ can couple to various other $\mathrm{BB}$ and $\mathrm{BD}$ channels. Specifically, the $N{{\varOmega }}$ $^5S_2$ system (with threshold at $\sqrt{s}=2611$ MeV) can couple to ${\varLambda }{\varXi }$ ($^1D_2$, threshold at 2434 MeV), ${\varSigma }{\varXi }$ ($^1D_2$, threshold at 2511 MeV) and ${\varLambda }{\varXi }\pi$ ($^3P_2s$, threshold at 2574 MeV). In addition, and more unfavorable for a concrete calculation, it couples to ${\varLambda }{\varXi }^*$ (threshold at 2647 MeV), ${\varSigma }{\varXi }^*$ (threshold at 2725 MeV), and ${\varXi }{\varSigma }^*$ (threshold at 2703 MeV) in all partial waves; see Table 2. Thus all four LECs that contribute to $\mathrm{BD}$ scattering (cf. Table 9) are needed. There is no way to determine the individual values of those four LECs from the $N{{\varOmega }}$ results in Ref. [20]. Indeed, the only “selective” LEC in $\mathrm{BD}$ scattering is $C^{35}$ which, once fixed, could be used to relate the interactions for $N{{\varDelta }}$ ($I=2$), ${{\varSigma }}{{\varDelta }}$ ($I=5/2$), and ${\varXi }{{\varOmega }}$ ($I=1/2$). Unfortunately, lattice results are not available for any of these channels.

Fig. 6

$N{{\varOmega }}^5S_2$ phase shift. The result of the HAL QCD collaboration is taken from Ref. [20]. Results of a fit to the lattice simulation is shown by a hatched band, corresponding to cut-off variations between 500 and 700 MeV. The corresponding results for physical masses are shown by solid (700 MeV) and dash-dotted (500 MeV) lines

We focus in the following on the only $\mathrm{BD}$ lattice results available and ignore all couplings of $N{{\varOmega }}$ to other channels. Then only one specific combination of LECs enter; see Table 9, which can be fixed by a fit to the lattice predictions. Note that the interaction in the $N{{\varOmega }}$ system is particularly simple because, apart from the contact interaction, only $\eta$-meson exchange can contribute. For other $\mathrm{BD}$ reactions there are contributions from direct diagrams, involving $\mathrm{BB}\phi$ and $\mathrm{DD}\phi$ vertices, and from exchange diagrams that involve $\mathrm{BD}\phi$ and $\mathrm{DB}\phi$ vertices.

Fits to the lattice calculation are presented in Fig. 6. Again the standard cut-offs ${\varLambda }=500$ MeV and 700 MeV are adopted. The lattice results of Ref. [20] support the existence of a bound state in the $N{{\varOmega }}$ system. The binding energy estimated from our fits is in the range 9–11 MeV. When extrapolating to the physical point we observe the same difficulty as already in the ${{\varDelta }}{{\varDelta }}$ case above. There is no clear trend because the results depend significantly on the cut-off. In one case (${\varLambda }=500$ MeV, dash-dotted line) the bound state would survive, with a binding energy of around 2 MeV, while for the other cut-off (solid line) it disappears. Thus conclusions—even qualitative ones—are difficult to draw. This is even more the case if we recall the various other channels that can couple to $N{{\varOmega }}$ and that are open at the physical point. In view of these additional channels, it is to be expected that the dynamics in the $N{{\varOmega }}$-system is highly complex. It will therefore be challenging to establish the existence of a bound state in this system from a lattice calculation. Actually, the situation is even more involved than the one for the H–dibaryon, where there is a delicate interplay between the interactions in the ${{\varLambda }}{{\varLambda }}$, ${\varXi }N$, and ${{\varSigma }}{{\varSigma }}$ channels [15, 16, 33, 78, 79].

4 Summary and outlook

In this paper we have derived the general form of the baryon–baryon interaction involving octet and decuplet baryons in a chiral effective field theory approach based on the Weinberg power counting. The present work is an extension of earlier studies on the nucleon–nucleon [13], hyperon–nucleon [8, 9] and hyperon–hyperon [38, 39] systems within the same framework. Specific attention is paid to the connections between the interactions in the various baryon–baryon channels that follow from the underlying (approximate) SU(3) flavor symmetry. The leading-order potential presented in this paper consists of two components: (i) long-ranged one-pseudoscalar-meson exchanges ($\pi$, K, $\eta$) with coupling constants at the various baryon–baryon-meson vertices related via $\mathrm{SU(3)}$ symmetry; (ii) short-ranged four-baryon contact terms without derivatives. For the latter the most general, minimal and $\mathrm{SU(3)}$ invariant Lagrangian has been derived. The number of independent contact terms at LO amounts to: six for the scattering of two octet baryons (as already established in [8, 38]), eight for the scattering of two decuplet baryons, eight for the scattering of an octet baryon on a decuplet baryon, and two (each) for the transitions between these systems.

The low-energy constants associated with those contact terms need to be determined from scattering data. Given the lack of empirical information on the scattering of decuplet baryons we have illustrated how lattice QCD simulations [18,19,20,21] can be used to constrain or even fix some of the LECs. Admittedly, since the presently available lattice QCD calculations for scattering of decuplet baryons still involve large pion masses (in general $m_\pi \approx 700 - 1000$ MeV) and large baryon masses, the considered extrapolations to the physical point have to be taken with a grain of salt. Nonetheless, it is clear from the presented applications that chiral EFT provides a useful tool to analyze lattice results once calculations corresponding to masses closer to the physical point will become available.

Finally, since the ${{\varOmega }}$ can decay only through weak interactions, in principle, actual experiments where ${{\varOmega }}$ baryons are scattered on nucleons are feasible, analogous to those performed for the ${{\varLambda }}N$ and ${{\varSigma }}N$ systems. Indeed, there are plans for studying the $N{{\varOmega }}$ interaction experimentally at J-PARC [80], where it is intended to produce the ${{\varOmega }}$ in the reaction $K^-p \rightarrow {{\varOmega }}K^+ K^0$. There is also a proposal to establish a secondary $K^0_L$ beam at JLab that can then be used for producing ${{\varOmega }}$s [81]. ${{\varOmega }}$ baryons can also be produced in the reaction $\bar{p}p\rightarrow \bar{{\varOmega }}{{\varOmega }}$, a case for the $\bar{\mathrm{P}}$ANDA project at the FAIR facility in Darmstadt [82, 83]. Furthermore, heavy-ion collisions could allow one to access information on the $N{{\varOmega }}$ [84, 85] but also the ${{\varOmega }}{{\varOmega }}$ interaction.

Another and completely different field of application for our formalism might be in studies of pion production in NN collisions. Here, an explicit inclusion of the direct $N{{\varDelta }}$ and ${{\varDelta }}{{\varDelta }}$ interactions could be a sensible next step for refining the treatment of the reaction $NN \rightarrow NN\pi$ within chiral perturbation theory [86]. Furthermore, a better knowledge of the ${\varDelta }N$ and ${\varDelta }{\varDelta }$ interaction could shed light on the so-called ${\varDelta }$ puzzle in neutron star matter; see e.g. Ref. [87].

Appendices

A Spin matrices

In this appendix we summarize the spin transition operators involving spin 1/2 and spin 3/2 states. In order to construct these matrices (cf. Ref. [37]), we use the Wigner–Eckart theorem, which relates matrix elements of a spherical tensor operator to a reduced matrix element and Clebsch–Gordon coefficients. For writing a Cartesian tensor (up to rank 3) in terms of spherical tensors, we express the usual scalar , vector $x^i$, irreducible tensor of rank two $x^ix^j - {\varvec{r}}^{\,2}\delta ^{ij}/3$ and irreducible tensor of rank three $5x^ix^jx^k - (x^i\delta ^{jk}+x^j\delta ^{ik}+x^k\delta ^{ij}){\varvec{r}}^{\,2}$ into spherical harmonics of the same rank.

Following this approach, we obtain for the vector spin matrices (see also Refs. [37, 50]):⁷

$$\begin{aligned}&\sigma _1 = \begin{pmatrix}0 &{}\quad 1\\ 1 &{}\quad 0 \end{pmatrix}, \quad \sigma _2 =\begin{pmatrix}0 &{}\quad -\mathrm i \\ \mathrm i &{}\quad 0 \end{pmatrix}, \quad \sigma _3 =\begin{pmatrix}1 &{}\quad 0\\ 0 &{}\quad -1 \end{pmatrix}, \end{aligned}$$

(34)

$$\begin{aligned}&S_1 = \begin{pmatrix} -\frac{1}{\sqrt{2}} &{}\quad 0 &{}\quad \frac{1}{\sqrt{6}} &{}\quad 0 \\ 0 &{}\quad -\frac{1}{\sqrt{6}} &{}\quad 0 &{}\quad \frac{1}{\sqrt{2}} \end{pmatrix},\quad S_2 = \begin{pmatrix} -\frac{i}{\sqrt{2}} &{}\quad 0 &{}\quad -\frac{i}{\sqrt{6}} &{}\quad 0 \\ 0 &{}\quad -\frac{i}{\sqrt{6}} &{}\quad 0 &{}\quad -\frac{i}{\sqrt{2}} \end{pmatrix}, \nonumber \\&S_3 = \begin{pmatrix} 0 &{}\quad \sqrt{\frac{2}{3}} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad \sqrt{\frac{2}{3}} &{}\quad 0 \end{pmatrix}, \end{aligned}$$

(35)

$$\begin{aligned}&{\varSigma }_1 = \begin{pmatrix} 0 &{}\quad \sqrt{3} &{}\quad 0 &{}\quad 0 \\ \sqrt{3} &{}\quad 0 &{}\quad 2 &{}\quad 0 \\ 0 &{}\quad 2 &{}\quad 0 &{}\quad \sqrt{3} \\ 0 &{}\quad 0 &{}\quad \sqrt{3} &{}\quad 0 \end{pmatrix},\quad {\varSigma }_2 = \begin{pmatrix} 0 &{}\quad -i \sqrt{3} &{}\quad 0 &{}\quad 0 \\ i \sqrt{3} &{}\quad 0 &{}\quad -2 i &{}\quad 0 \\ 0 &{}\quad 2 i &{}\quad 0 &{}\quad -i \sqrt{3} \\ 0 &{}\quad 0 &{}\quad i \sqrt{3} &{}\quad 0 \end{pmatrix}, \nonumber \\&{\varSigma }_3 = \begin{pmatrix} 3 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad -3 \end{pmatrix}. \end{aligned}$$

(36)

The analogous isospin matrices corresponding to the spin matrices $\varvec{\sigma }$, ${\varvec{S}}$ and $\varvec{{\varSigma }}$ are denoted by ${\varvec{\tau }}$, ${\varvec{T}}$ and ${\varvec{\theta }}$.

The spin matrices with rank two and three can be expressed through vector and scalar spin matrices:

(37)

B Two-body potentials in particle representation

In this section, we show the two-body interaction potentials in particle basis for the transitions $\mathrm{BB}\rightarrow \mathrm{BB}$, $\mathrm{BB}\leftrightarrow \mathrm{DB}$, $\mathrm{DB}\rightarrow \mathrm{DB}$, $\mathrm{BB}\leftrightarrow \mathrm{DD}$, $\mathrm{DB}\leftrightarrow \mathrm{DD}$, and $\mathrm{DD}\rightarrow \mathrm{DD}$.

First, we write the Lagrangians presented in Sects. 2.1 and 2.3 in terms of their particle fields, as defined in Eqs. (1), (2) and (3). The physical fields comprise the sets:

$$\begin{aligned}&\phi _i \in \left\{ \pi ^0,\pi ^+,\pi ^-,K^+,K^-,K^0,\bar{K}^0,\eta \right\} ,\nonumber \\&B_i \in \left\{ n,p,{\varSigma }^0,{\varSigma }^+,{\varSigma }^-,{\varLambda },{\varXi }^0,{\varXi }^-\right\} , \nonumber \\&B^*_i \in \left\{ {\varDelta }^-,{\varDelta }^0,{\varDelta }^+,{\varDelta }^{++}, {\varSigma }^{*0},{\varSigma }^{*+},{\varSigma }^{*-},{\varXi }^{*0},{\varXi }^{*-},{\varOmega }^-\right\} . \end{aligned}$$

(38)

For the octet-baryon meson Lagrangian one obtains

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{BB}\phi } = -\frac{1}{2f_0}\sum _{i,j,k} N_{B_iB_j\phi _k} (\bar{B}_i \varvec{\sigma } B_j) \cdot (\varvec{\nabla } \phi _k) , \end{aligned}$$

(39)

where the sum over $i,j,k$ runs over all particles fields, specified in Eq. (38). Furthermore, we have introduced the SU(3) factors $N$. These factors can easily be obtained by multiplying the flavor matrices and taking the traces. For example $N_{{\varLambda }{\varLambda }\eta }$ can be calculated as (see Eq. (4))

$$\begin{aligned} N_{{\varLambda }{\varLambda }\eta } = D\, \mathrm{tr}\left( Y^\top _{\varLambda }\lbrace Y_\eta ,Y_{\varLambda }\rbrace \right) + F\, \mathrm{tr}\left( Y^\top _{\varLambda }\left[ Y_\eta ,Y_{\varLambda }\right] \right) = -{2D \over \sqrt{3}}, \end{aligned}$$

(40)

with the flavor matrices

$$\begin{aligned} Y_{\varLambda }:= \begin{pmatrix} \frac{1}{\sqrt{6}} &{} 0 &{} 0 \\ 0 &{} \frac{1}{\sqrt{6}} &{} 0 \\ 0 &{} 0 &{} -\frac{2}{\sqrt{6}} \end{pmatrix},\quad Y_\eta := \begin{pmatrix} {1\over \sqrt{3}} &{} 0 &{} 0 \\ 0 &{} {1\over \sqrt{3}} &{} 0 \\ 0 &{} 0 &{} -{2\over \sqrt{3}} \end{pmatrix}. \end{aligned}$$

(41)

We will use the representation in terms of SU(3) factors $N$ in the following, as it allows for a simple presentation of the two-baryon potentials.

For the corresponding Lagrangian terms involving decuplet baryons one obtains in the same way

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DB}\phi } =\,&\frac{C}{f_0} \sum _{i,j,k} N_{B_i^*B_j\phi _k} \Big [ (\bar{B}_i^* {\varvec{S}}^{\,\dagger } B_j) \cdot \left( \varvec{\nabla } \phi _k\right) \nonumber \\&\qquad \qquad \qquad \qquad \qquad +\, (\bar{B}_j {\varvec{S}} B_i^*) \cdot \left( \varvec{\nabla } \phi _k^\dagger \right) \Big ] , \end{aligned}$$

(42)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\phi } =\,&\frac{H}{f_0} \sum _{i,j,k} N_{B^*_iB^*_j\phi _k} (\bar{B}^*_i \varvec{{\varSigma }} B^*_j) \cdot (\varvec{\nabla } \phi _k) . \end{aligned}$$

(43)

The minimal set of contact Lagrangian terms of Sect. 2.3 can also be rewritten in terms of particle fields, with SU(3) factors $N$:

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{BB}\mathrm{BB}} =\,&\sum _{f=1,3,5} c_{00}^f\sum _{i,j,k,l} N^{f}_{B_iB_jB_kB_l} \left( \bar{B}_iB_j\right) \left( \bar{B}_kB_l\right) \nonumber \\&+\sum _{f=2,4,6} c_{00}^f\sum _{i,j,k,l} N^{f}_{B_iB_jB_kB_l} \left( \bar{B}_i{\varvec{\sigma }} B_j\right) \cdot \left( \bar{B}_k\varvec{\sigma } B_l\right) . \end{aligned}$$

(44)

$$\begin{aligned} \mathcal {L}_\mathrm {D\mathrm{BB}B} =\,&\sum _{f=1,2} c_{01}^f\sum _{i,j,k,l} N^f_{B_i^*B_jB_kB_l} \big [\left( \bar{B}_i^*{\varvec{S}}^\dagger B_j\right) \cdot \left( \bar{B}_k\varvec{\sigma } B_l\right) \nonumber \\&+\left( \bar{B}_j{\varvec{S}}\, B_i^*\right) \cdot \left( \bar{B}_l\varvec{\sigma } B_k\right) \big ]. \end{aligned}$$

(45)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DB}\mathrm{DB}} =\,&\sum _{f=1,3,5,7} c_{11}^f\sum _{i,j,k,l} N^{f}_{B^*_iB^*_jB_kB_l} \left( \bar{B}^*_i B^*_j\right) \left( \bar{B}_k B_l\right) \nonumber \\&+ \sum _{f=2,4,6,8} c_{11}^f\sum _{i,j,k,l} N^{f}_{B^*_iB^*_jB_kB_l} \left( \bar{B}^*_i\varvec{{\varSigma }} B^*_j\right) \cdot \left( \bar{B}_k\varvec{\sigma } B_l\right) . \end{aligned}$$

(46)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\mathrm{BB}} =\,&c_{02}^1\sum _{i,j,k,l} N^{1}_{B^*_iB_jB^*_kB_l} \big [\left( \bar{B}^*_i{\varvec{S}}^\dagger B_j\right) \cdot \left( \bar{B}^*_k{\varvec{S}}^\dagger B_l\right) \nonumber \\&+\, \left( \bar{B}_j{\varvec{S}} B^*_i\right) \cdot \left( \bar{B}_l{\varvec{S}} B^*_k\right) \big ] \nonumber \\&+ \, c_{02}^2\sum _{i,j,k,l} N^{2}_{B^*_iB_jB^*_kB_l} \big [\left( \bar{B}^*_iS^{\alpha \beta \dagger } B_j\right) \left( \bar{B}^*_kS^{\alpha \beta \dagger } B_l\right) \nonumber \\&+\, \left( \bar{B}_jS^{\alpha \beta } B^*_i\right) \left( \bar{B}_lS^{\alpha \beta } B^*_k\right) \big ]. \end{aligned}$$

(47)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\mathrm{DB}} =\,&c_{12}^1\sum _{i,j,k,l} N^{1}_{B^*_iB^*_jB^*_kB_l} \big [\left( \bar{B}^*_i\varvec{{\varSigma }} B^*_j\right) \cdot \left( \bar{B}^*_k{\varvec{S}}^\dagger B_l\right) \nonumber \\&+ \left( \bar{B}^*_j\varvec{{\varSigma }} B^*_i\right) \cdot \left( \bar{B}_l{\varvec{S}} B^*_k\right) \big ] \nonumber \\&+c_{12}^2\sum _{i,j,k,l} N^{2}_{B^*_iB^*_jB^*_kB_l} \big [\left( \bar{B}^*_i{\varSigma }^{\alpha \beta } B^*_j\right) \left( \bar{B}^*_k S^{\alpha \beta \dagger } B_l\right) \nonumber \\&+ \left( \bar{B}^*_j{\varSigma }^{\alpha \beta } B^*_i\right) \left( \bar{B}_l S^{\alpha \beta } B^*_k\right) \big ]. \end{aligned}$$

(48)

$$\begin{aligned} \mathcal {L}_\mathrm {\mathrm{DD}\mathrm{DD}} =\,&\sum _{f=1,5} c_{22}^f\sum _{i,j,k,l} N^{f}_{B^*_iB^*_jB^*_kB^*_l} \left( \bar{B}^*_iB^*_j\right) \left( \bar{B}^*_kB^*_l\right) \nonumber \\&+\sum _{f=2,6} c_{22}^f\sum _{i,j,k,l} N^{f}_{B^*_iB^*_jB^*_kB^*_l} \left( \bar{B}^*_i{\varvec{{\varSigma }}} B^*_j\right) \cdot \left( \bar{B}^*_k\varvec{{\varSigma }} B^*_l\right) \nonumber \\&+\sum _{f=3,7} c_{22}^f\sum _{i,j,k,l} N^{f}_{B^*_iB^*_jB^*_kB^*_l} \left( \bar{B}^*_i {\varSigma }^{\alpha \beta } B^*_j\right) \left( \bar{B}^*_k{\varSigma }^{\alpha \beta } B^*_l\right) \nonumber \\&+\sum _{f=4,8} c_{22}^f\sum _{i,j,k,l} N^{f}_{B^*_iB^*_jB^*_kB^*_l} \left( \bar{B}^*_i{\varSigma }^{\alpha \beta \gamma } B^*_j\right) \left( \bar{B}^*_k{\varSigma }^{\alpha \beta \gamma } B^*_l\right) . \end{aligned}$$

(49)

Let us now come to the calculation of the two-body interaction potentials based on the Lagrangian in particle basis as shown above. The calculation is done in the center-of-mass frame with momentum assignments $A({\varvec{p}}\,)B(-{\varvec{p}}\,)\rightarrow C({\varvec{p}}^{\,\prime })D(-{\varvec{p}}^{\,\prime })$. We use the common definitions ${\varvec{q}} = {\varvec{p}}^{\,\prime } - {\varvec{p}}$ and ${\varvec{k}} = {\varvec{p}}^{\,\prime } + {\varvec{p}}$, where ${\varvec{q}}$ appears in the direct one-meson exchange and ${\varvec{k}}$ appears in the exchanged one-meson exchange.⁸

For all considered transitions we show in the first line, how the potential is calculated from Feynman diagrams. In the Feynman diagrams themselves, particles that are vertically above each other are defined to be in the same baryon bilinear. Octet baryons are denoted by single lines, decuplet baryons by double lines, and mesons by dashed lines.

Below the Feynman diagrams, we provide the full potentials in particle basis, for a general assignment of baryons $B_i$, decuplet baryons $B_i^*$ and mesons $\phi$. For a clearer presentation, we introduce prefactors $X_i$, which are linear combinations of SU(3) coefficients $N$ and low-energy constants. The factor $X_1$ is always related to the direct one-meson exchange, $X_2$ is related to the exchanged one-meson exchange and the remaining $X_i$ concern contact interaction with various spin structures. The $X_i$ for the considered interactions are summarized in Tables 4 and 5.

For the construction of the potentials we also need various spin exchange operators, defined by $P^{(\sigma )} \vert \chi _1,\chi _2\rangle = \vert \chi _2,\chi _1\rangle$, where the first position in $\vert .,.\rangle$ is spin space 1 (or baryon bilinear 1) and the second position in $\vert .,.\rangle$ is in spin space 2 (or baryon bilinear 2). For two spin-1/2 states the well-known spin exchange operator is given by

(50)

For two spin-3/2 states, the spin exchange operator can be expressed through

(51)

The spin exchange operator exchanging a spin-1/2 state and a spin-3/2 state is given by⁹

$$\begin{aligned} P_{1/2,3/2}^{(\sigma )}= \frac{3}{4}\left( {\varvec{S}}_1^{\,\dagger }\cdot {\varvec{S}}_2 + S_1^{\dagger ij} S_2^{ij} \right) . \end{aligned}$$

(52)

Table 4 Coefficients $X_i$ for various interactions

Table 5 Coefficients $X_i$ for the transition $B^*_1B^*_2\rightarrow B^*_3B^*_4$

Let us now list all considered transitions and their potentials, starting with the well-known potential involving only octet baryons, and with an increasing number of involved decuplet baryons.

• $B_1B_2\rightarrow B_3B_4$ (with bilinears in spin space $B_1$–$B_3$ and $B_2$–$B_4$):

  

  (53)

• $B_1B_2\rightarrow B_3^*B_4$:

  

  (54)

• $B_1^*B_2\rightarrow B_3B_4$:

  

  (55)

• $B_1^*B_2\rightarrow B^*_3B_4$:

  

  (56)

• $B_1B_2\rightarrow B^*_3B^*_4$:

  

  (57)

• $B^*_1B^*_2\rightarrow B_3B_4$:

  

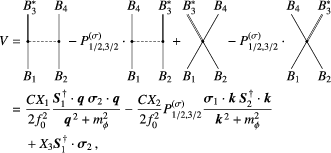
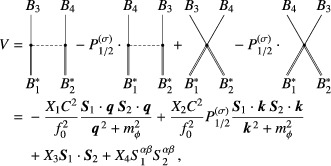  (58)

• $B^*_1B_2\rightarrow B^*_3B^*_4$:

  

  (59)

• $B^*_1B^*_2\rightarrow B^*_3B_4$:

  

  (60)

• $B^*_1B^*_2\rightarrow B^*_3B^*_4$:

  

  (61)

Analogous to Eq. (19) of Ref. [60], we obtain a representation of the potentials in the isospin basis, by applying the relation¹⁰

$$\begin{aligned}&\langle (i_{3}i_{4})IM|V|(i_1i_2)IM\rangle =\sum _{\begin{array}{c} m_1,m_2, \\ m_{3 },m_{4} \end{array}} \delta _{M,m_{3}+m_{4}} \delta _{M,m_1+m_2} \nonumber \\&\quad \times C^{i_{3}i_{4}I}_{m_{3}m_{4}M} C^{i_1i_2I}_{m_1m_2M} \langle i_{3}m_{3};i_{4}m_{4}|V|i_1m_1;i_2m_2\rangle \end{aligned}$$

(62)

to the potential $V$ in particle basis, where $I$ is the total isospin and $i_j$ is the isospin of the particles. This approach is used in order to obtain the SU(3) relations shown in appendix C.

In order to employ the transformation to the isospin basis, Eq. (62), with the conventional Clebsch–Gordan coefficients $C$, the following sign changes in identifying the isospin eigenstates with the particle fields are necessary:

$$\begin{aligned}&{\varSigma }^+=-\vert 1,+1\rangle ,\quad {\varXi }^-=-\vert 1/2,-1/2\rangle ,\ \nonumber \\&\pi ^+=-\vert 1,+1\rangle ,\quad K^-=-\vert 1/2,-1/2\rangle , \nonumber \\&{\varSigma }^{*+}=-\vert 1,+1\rangle ,\quad {\varSigma }^{*0}=-\vert 1,0\rangle ,\quad {\varSigma }^{*-}=-\vert 1,-1\rangle , \nonumber \\&{\varOmega }^-=-\vert 0,0\rangle . \end{aligned}$$

(63)

C SU(3) relations

In this appendix, we display our results for the SU(3) relations of the two-baryon interactions, following the approach described in Appendix B. In order to obtain the various SU(3) relations for the considered two-body interactions, we have projected the contact terms onto partial waves (see Sect. 2.5) and switched to the isospin basis (see Appendix B).

Table 6 SU(3) relations of $\mathrm{BB}\rightarrow \mathrm{BB}$ in non-vanishing partial waves. The subscript $\{00\}$ of the constants $C_{00}^r$ that denotes the $\mathcal {B}\mathcal {B}$ channel is omitted in the table

The low-energy constants $c^f_{ij}$ of the minimal contact Lagrangian terms have been redefined according to the group theoretical considerations in Sect. 2.4. One obtains the following relations.

• $\mathrm{BB}\rightarrow \mathrm{BB}$:

  $$\begin{aligned} C_{00}^{1}&= \frac{2}{3} \left( c_{00}^1 -3 c_{00}^2 -8 c_{00}^3 +24 c_{00}^4 -3 c_{00}^5 +9 c_{00}^6 \right) ,\nonumber \\ C_{00}^{8_s}&= \frac{4 c_{00}^1 }{3}-4 c_{00}^2 -\frac{5 c_{00}^3 }{3}+5 c_{00}^4 -2 c_{00}^5 +6 c_{00}^6 ,\nonumber \\ C_{00}^{8_a}&= 3 c_{00}^3 +3 c_{00}^4 -2 (c_{00}^5 +c_{00}^6 ) ,\nonumber \\ C_{00}^{10}&= 2 \left( c_{00}^1 +c_{00}^2 -c_{00}^5 -c_{00}^6 \right) ,\nonumber \\ C_{00}^{\overline{10}}&= -2 \left( c_{00}^1 +c_{00}^2 +c_{00}^5 +c_{00}^6 \right) ,\nonumber \\ C_{00}^{27}&= -2 \left( c_{00}^1 -3 c_{00}^2 +c_{00}^5 -3 c_{00}^6 \right) \end{aligned}$$

  (64)

• $\mathrm{BB}\rightarrow \mathrm{BD}$ and $\mathrm{BD}\rightarrow \mathrm{BB}$:

  $$\begin{aligned} C_{01}^{8}&= -\frac{1}{3} \sqrt{2} \left( c_{01}^1 +3 c_{01}^2 \right) ,\nonumber \\ C_{01}^{10}&= -\frac{2 \sqrt{2} c_{01}^1 }{3}, \end{aligned}$$

  (65)

• $\mathrm{DB}\rightarrow \mathrm{DB}$:

  $$\begin{aligned} C_{11}^{35,3S1}&= -\,c_{11}^1 +5 c_{11}^2 -c_{11}^5 +5 c_{11}^6 ,\nonumber \\ C_{11}^{27,3S1}&= \frac{1}{3} \left( -3 c_{11}^1 +15 c_{11}^2 +c_{11}^5 -5 c_{11}^6 \right) ,\nonumber \\ C_{11}^{10,3S1}&= \frac{1}{3} \left( -3 c_{11}^1 +15 c_{11}^2 -4 c_{11}^3 +20 c_{11}^4 \right. \nonumber \\&\quad \left. -\,c_{11}^5 +5 c_{11}^6 -4 c_{11}^7 +20 c_{11}^8 \right) ,\nonumber \\ C_{11}^{8,3S1}&= \frac{1}{6} \left( -6 c_{11}^1 +30 c_{11}^2 -10 c_{11}^3 +50 c_{11}^4 +2 c_{11}^5 \right. \nonumber \\&\quad \left. -\,10 c_{11}^6 +5 c_{11}^7 -25 c_{11}^8 \right) ,\nonumber \\ C_{11}^{35,5S2}&= -\,c_{11}^1 -3 c_{11}^2 -c_{11}^5 -3 c_{11}^6 ,\nonumber \\ C_{11}^{27,5S2}&= -\,c_{11}^1 -3 c_{11}^2 +\frac{c_{11}^5 }{3}+c_{11}^6 ,\nonumber \\ C_{11}^{10,5S2}&= \frac{1}{3} \left( -3 c_{11}^1 -9 c_{11}^2 -4 c_{11}^3 -12 c_{11}^4 -c_{11}^5 \right. \nonumber \\&\quad \left. -\,3 c_{11}^6 -4 c_{11}^7 -12 c_{11}^8 \right) ,\nonumber \\ C_{11}^{8,5S2}&= -\,c_{11}^1 -3 c_{11}^2 -\frac{5 c_{11}^3 }{3}-5 c_{11}^4 \nonumber \\&\quad \,+\,\frac{c_{11}^5 }{3}+c_{11}^6 +\frac{5 c_{11}^7 }{6} +\frac{5 c_{11}^8 }{2} \end{aligned}$$

  (66)

  Table 7 SU(3) relations of $\mathrm{BB}\rightarrow \mathrm{DB}$ (and $\mathrm{DB}\rightarrow \mathrm{BB}$) in non-vanishing partial waves. The subscript $\{01\}$ of the constants $C_{01}^r$ that denotes the $\mathcal {B}\mathcal {B}$ channel is omitted in the table

  Table 8 SU(3) relations of $\mathrm{BB}\rightarrow \mathrm{DD}$ (and $\mathrm{DD}\rightarrow \mathrm{BB}$) in non-vanishing partial waves. The subscript $\{02\}$ of the constants $C_{02}^r$ that denotes the $\mathcal {B}\mathcal {B}$ channel is omitted in the table

• $\mathrm{BB}\rightarrow \mathrm{DD}$ and $\mathrm{DD}\rightarrow \mathrm{BB}$:

  $$\begin{aligned} C_{02}^{27}&= \frac{4}{9} \sqrt{5} \left( 3 c_{02}^1 -5 c_{02}^2 \right) ,\nonumber \\ C_{02}^{\overline{10}}&= \frac{4}{3} \sqrt{5} \left( c_{02}^1 +c_{02}^2 \right) \end{aligned}$$

  (67)

• $\mathrm{DB}\rightarrow \mathrm{DD}$ and $\mathrm{DD}\rightarrow \mathrm{DB}$:

  $$\begin{aligned} C_{12}^{27}&= -\frac{2}{9} \sqrt{5} \left( 6 c_{12}^1 -\sqrt{6} c_{12}^2 \right) ,\nonumber \\ C_{12}^{35}&= -\frac{2}{3} \sqrt{5} \left( 2 c_{12}^1 +\sqrt{6} c_{12}^2 \right) , \end{aligned}$$

  (68)

• $\mathrm{DD}\rightarrow \mathrm{DD}$:

  $$\begin{aligned} C_{22}^{\overline{10},3S1}&= \frac{1}{3} \left( -6 c_{22}^1 +66 c_{22}^2 -9 c_{22}^3 -420 c_{22}^4 +2 c_{22}^5 \right. \nonumber \\&\quad \left. -22 c_{22}^6 +3 c_{22}^7 +140 c_{22}^8 \right) ,\nonumber \\ C_{22}^{\overline{10},7S3}&= -2 c_{22}^1 -18 c_{22}^2 -3 c_{22}^3 -\frac{20 c_{22}^4 }{3} \nonumber \\&\quad +\frac{2 c_{22}^5 }{3}+6 c_{22}^6 +c_{22}^7 +\frac{20 c_{22}^8 }{9} ,\nonumber \\ C_{22}^{27,1S0}&= \frac{1}{27} \left( -54 c_{22}^1 +810 c_{22}^2 -405 c_{22}^3 +6300 c_{22}^4 \right. \nonumber \\&\quad \left. +6 c_{22}^5 -90 c_{22}^6 +45 c_{22}^7 -700 c_{22}^8 \right) ,\nonumber \\ C_{22}^{27,5S2}&= -2 c_{22}^1 +6 c_{22}^2 +9 c_{22}^3 +\frac{140 c_{22}^4 }{3} \nonumber \\&\quad +\frac{2 c_{22}^5 }{9}-\frac{2 c_{22}^6 }{3}-c_{22}^7 -\frac{140 c_{22}^8 }{27} ,\nonumber \\ C_{22}^{35,3S1}&= \frac{1}{3} \left( -6 c_{22}^1 +66 c_{22}^2 -9 c_{22}^3 -420 c_{22}^4 \right. \nonumber \\&\quad \left. -2 c_{22}^5 +22 c_{22}^6 -3 c_{22}^7 -140 c_{22}^8 \right) ,\nonumber \\ C_{22}^{35,7S3}&= -2 c_{22}^1 -18 c_{22}^2 -3 c_{22}^3 -\frac{20 c_{22}^4 }{3} \nonumber \\&\quad -\frac{2 c_{22}^5 }{3}-6 c_{22}^6 -c_{22}^7 -\frac{20 c_{22}^8 }{9} ,\nonumber \\ C_{22}^{28,1S0}&= \frac{1}{3} \left( -6 c_{22}^1 +90 c_{22}^2 -45 c_{22}^3 +700 c_{22}^4 \right. \nonumber \\&\quad \left. -6 c_{22}^5 +90 c_{22}^6 -45 c_{22}^7 +700 c_{22}^8 \right) ,\nonumber \\ C_{22}^{28,5S2}&= -2 c_{22}^1 +6 c_{22}^2 +9 c_{22}^3 \nonumber \\&\quad +\frac{140 c_{22}^4 }{3}-2 c_{22}^5 +6 c_{22}^6 +9 c_{22}^7 +\frac{140 c_{22}^8 }{3} \end{aligned}$$

  (69)

The SU(3) tables of the two-body transitions (employing the redefined constants above) are given in Tables 1, 6, 7, 8, 9, 10.

Table 9 SU(3) relations of $\mathrm{DB}\rightarrow \mathrm{DB}$ in non-vanishing partial waves. The subscript $\{11\}$ of the constants $C_{11}^r$ that denotes the $\mathcal {B}\mathcal {B}$ channel is omitted in the table

Table 10 SU(3) relations of $\mathrm{DB}\rightarrow \mathrm{DD}$ (and $\mathrm{DD}\rightarrow \mathrm{DB}$) in non-vanishing partial waves. The subscript $\{12\}$ of the constants $C_{12}^r$ that denotes the $\mathcal {B}\mathcal {B}$ channel is omitted in the table