Abstract
Measurements of inclusive spectra and mean multiplicities of \(\pi ^\pm \), K\(^\pm \), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions at incident projectile momenta of 20, 31, 40, 80 and 158 \(\text{ GeV }/c\) (\(\sqrt{s} = \) 6.3, 7.7, 8.8, 12.3 and 17.3 \(\text{ GeV }\), respectively) were performed at the CERN Super Proton Synchrotron using the large acceptance NA61/SHINE hadron spectrometer. Spectra are presented as function of rapidity and transverse momentum and are compared to predictions of current models. The measurements serve as the baseline in the NA61/SHINE study of the properties of the onset of deconfinement and search for the critical point of strongly interacting matter.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This paper presents experimental results on inclusive spectra and mean multiplicities of \(\pi ^\pm \), K\(^\pm \), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions at 20, 31, 40, 80 and 158 \(\text{ GeV }/c\). The measurements were performed by the multi-purpose NA61/SHINE experiment [1, 2] at the CERN Super Proton Synchrotron (SPS). The new measurements complement previously published results from the same datasets on \(\pi ^-\) production [3] obtained without particle identification as well as on fluctuations of charged particles [4]. These studies form part of the NA61/SHINE strong interaction programme investigating the properties of the onset of deconfinement and searching for the critical point of strongly interacting matter. The programme is mainly motivated by the observation of rapid changes of hadron production properties in central Pb + Pb collisions at about 30\(A\,\text{ GeV }/c\) by the NA49 experiment [5, 6] which were interpreted as the onset of deconfinement. These findings were recently confirmed by the RHIC beam energy programme [7] and the interpretation is supported by the LHC results (see Ref. [8] and references therein). Clearly, a two dimensional scan in collision energy and size of colliding nuclei is required to explore systematically the phase diagram of strongly interacting matter [9].
Pursuing this programme NA61/SHINE already recorded data on p + p, Be + Be, Ar + Sc and p + pb collisions and data taking on Xe + La collisions is scheduled for 2017. Moreover, measurements of Pb + Pb interactions are planned for the coming years [10].
An interpretation of the rich experimental results on nucleus–nucleus collisions relies to a large extent on a comparison to the corresponding data on p + p and p + A interactions. However, the published measurements mainly refer to basic features of unidentified charged hadron production and are sparse. Results on identified hadron spectra, fluctuations and correlations are mostly missing. Detailed measurements of hadron spectra in a large acceptance in the beam momentum range covered by the data in this paper exist only from the NA49 experiment for inelastic p + p interactions at 158 \(\text{ GeV }/c\) [11,12,13]. Thus new high precision measurements of hadron production properties in p + p and p + A interactions are essential. They are performed by NA61/SHINE in parallel with the corresponding measurements on nucleus–nucleus collisions using the same detector and thus covering the same acceptance. Precise data on pion, kaon and proton production properties are crucial for constraining basic properties of models of strong interactions.
This publication presents two-dimensional spectra of positively and negatively charged pions, kaons, protons and antiprotons produced in p + p interactions in the SPS momentum range (20, 31, 40, 80, 158 \(\text{ GeV }/c\)). The paper is organized as follows: after this introduction the experiment is briefly described in Sect. 2. The analysis procedure is discussed in Sect. 3. Section 4 presents the results of the analysis. In Sect. 5 model calculations are compared to the new measurements. A summary in Sect. 6 closes the paper.
The following variables and definitions are used in this paper. The particle rapidity is calculated in the collision center of mass system (cms), \(y = a\tanh (\beta _\mathrm {L})\), where \(\beta _\mathrm {L} = cp_\mathrm {L}/E\) is the longitudinal component of the velocity and \(p_\mathrm {L}\) and E are the longitudinal momentum and energy given in the cms. The transverse component of the momentum is denoted as \(p_{{\mathrm {T}}} \) and the transverse mass \(m_{{\mathrm {T}}} \) is defined as \(m_{{\mathrm {T}}} = \sqrt{m^2 + (cp_{{\mathrm {T}}})^2}\), where m is the particle mass in GeV. The momentum in the laboratory frame is denoted \(p_{{\mathrm {lab}}}\) and electric charge in units of the electron charge as q. The collision energy per nucleon pair in the center of mass system is denoted as \(\sqrt{s_\mathrm {NN}}\).
2 NA61/SHINE experiment
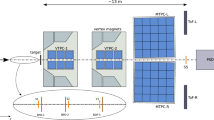
The schematic layout of the NA61/SHINE experiment at the CERN SPS (horizontal cut, not to scale). Alignment of the NA61/SHINE coordinate system is shown on the plot. The nominal beam direction is along the z axis. The magnetic field bends charged particle trajectories in the x–z plane. The electron drift direction in the TPCs is along the y (vertical) axis
NA61/SHINE is a fixed target experiment employing a large acceptance hadron spectrometer situated in the North Area H2 beam-line of the CERN SPS [1]. A schematic layout is shown in Fig. 1. The main components of the detection system used in the analysis are four large volume time projection chambers (TPC). Two of them, called vertex TPCs (VTPC), are located downstream of the target inside superconducting magnets with maximum combined bending power of 9 Tm. The TPCs are filled with Ar:CO\(_{2}\) gas mixtures in proportions 90:10 for the VTPCs and 95:5 for the Main TPCs. The MTPCs and two walls of pixel time-of-flight (ToF-L/R) detectors are placed symmetrically to the beamline downstream of the magnets. A GAP-TPC (GTPC) between VTPC-1 and VTPC-2 improves the acceptance for high-momentum forward-going tracks.
Individual beam particles are identified and precisely measured by a set of scintillation and Cherenkov counters, as well as three beam position detectors (BPDs) placed upstream of the target [1]. Secondary beams of positively charged hadrons at momenta of 20, 31, 40, 80 and 158 \(\text{ GeV }/c\) were used to collect the data for the analysis presented in this paper. These beams were produced from 400 \(\text{ GeV }/c\) protons extracted from the SPS in a slow extraction mode with a flat-top of 10 seconds. Protons from the secondary hadron beam are identified by two Cherenkov counters, a CEDAR [14] (either CEDAR-W or CEDAR-N) and a threshold counter (THC). A selection based on signals from the Cherenkov counters allowed to identify beam protons with a purity of about 99% [15]. The proton contamination in the secondary beam The beam momentum and intensity was adjusted by proper setting of the H2 beamline magnets and collimators. The precision of the setting of the beam magnet currents is approximately 0.5%. The beam momentum was verified by a direct measurement at 31 \(\text{ GeV }/c\) by bending the incoming beam particles into the TPCs with the maximum magnetic field. The properties of the beams used for obtaining the analysed data are summarized in Table 1.
A liquid hydrogen target (LHT) of 20.29 \(\text{ cm }\) length (2.8% interaction length) and 3 \(\text{ cm }\) diameter was placed 88.4 \(\text{ cm }\) upstream of VTPC-1. Data were taken with full (denoted as target inserted, I) and empty (denoted as target removed, R) LHT. The event statistics collected in the two configurations are summarised in Table 2.
Interactions in the target are selected with the trigger system by requiring an incoming beam proton and no signal from S4, a small 2 \(\text{ cm }\) diameter scintillation counter placed on the beam trajectory between the two vertex magnets. This minimum bias trigger is based on the disappearance of the beam proton downstream of the target.
3 Analysis procedure
This section starts with a brief overview of the data analysis procedure and the applied corrections. It also defines to which class of particles the final results correspond. A description of the calibration and the track and vertex reconstruction procedure can be found in Ref. [3].
The analysis procedure consists of the following steps:
-
(i)
application of event and track selection criteria,
-
(ii)
determination of spectra of identified hadrons using the selected events and tracks,
-
(iii)
evaluation of corrections to the spectra based on experimental data and simulations,
-
(iv)
calculation of the corrected spectra and mean multiplicities,
-
(v)
calculation of statistical and systematic uncertainties.
Corrections for the following biases were evaluated and applied:
-
(i)
geometrical acceptance,
-
(ii)
contribution from off-target interactions,
-
(iii)
contribution of particles other than primary (see below) hadrons produced in inelastic p + p interactions,
-
(iv)
losses of inelastic p + p interactions due to the trigger and the event and track selection criteria employed in the analysis as well as losses of produced hadrons in accepted interactions due to their decays and secondary interactions.
The final results refer to identified hadrons produced in inelastic p + p interactions by strong interaction processes and in electromagnetic decays of produced hadrons. Such hadrons are referred to as primary hadrons.
The analysis was performed independently in (y, \(p_{{\mathrm {T}}}\)) bins. The bin sizes were selected taking into account the statistical uncertainties and the resolution of the momentum reconstruction [3]. Corrections as well as statistical and systematic uncertainties were calculated for each bin.
3.1 Event and track selection
3.1.1 Event selection
Inelastic p + p events were selected using the following criteria:
-
(i)
no off-time beam particle detected within a time window of \(\pm 2~\upmu \hbox {s}\) around the trigger particle,
-
(ii)
beam particle trajectory measured in at least three planes out of four of BPD-1 and BPD-2 and in both planes of BPD-3,
-
(iii)
at least one track reconstructed in the TPCs and fitted to the interaction vertex,
-
(iv)
z position of the interaction vertex (fitted using the beam trajectory and TPC tracks) not farther away than 20 \(\text{ cm }\) from the center of the LHT,
-
(v)
events with a single, positively charged track with absolute momentum close to the beam momentum (see [3]) are removed in order to eliminate elastic scattering reactions.
3.1.2 Track selection
In order to select tracks of primary charged hadrons and to reduce the contamination of tracks from secondary interactions, weak decays and off-time interactions, the following track selection criteria were applied:
-
(i)
track momentum fit at the interaction vertex should have converged,
-
(ii)
fitted x component of particle rigidity \(\left( p_{lab,x}/q\right) \) is positive. This selection minimizes the angle between the track trajectory and the TPC pad direction for the chosen magnetic field direction, reducing uncertainties of the reconstructed cluster position, energy deposition and track parameters,
-
(iii)
total number of reconstructed points on the track should be greater than 30,
-
(iv)
sum of the number of reconstructed points in VTPC-1 and VTPC-2 should be greater than 15 or the number of reconstructed points in the GAP-TPC should be greater than 4,
-
(v)
the distance between the track extrapolated to the interaction plane and the interaction point (impact parameter) should be smaller than 4 \(\text{ cm }\) in the horizontal (bending) plane and 2 \(\text{ cm }\) in the vertical (drift) plane,
-
(vi)
the total number of reconstructed \({\mathrm {d}} E/{\mathrm {d}} x\) points on the track should be greater than 30,
-
(vii)
in case of tof-\({\mathrm {d}} E/{\mathrm {d}} x\) identification, three additional selection criteria were used:
-
(i)
the hit in the ToF pixel should be matched only with one TPC track,
-
(ii)
proper measurement of the hit in charge to digital converter (QDC) and time to digital converter (TDC)
-
(iii)
the last point of the track should be in the last 2 padrows of the MTPC to ensure good matching with the ToF hit.
-
(i)
The event and track statistics after applying the selection criteria are summarized in Table 2.
3.2 Identification techniques
Charged particle identification in the NA61/SHINE experiment is based on the measurement of the ionization energy loss \({\mathrm {d}} E/{\mathrm {d}} x\) in the gas of the TPCs and of the time of flight tof obtained from the ToF-L and ToF-R walls. In the region of the relativistic rise of the ionization at large momenta the measurement of \({\mathrm {d}} E/{\mathrm {d}} x\) alone allows identification. At lower momenta the \({\mathrm {d}} E/{\mathrm {d}} x\) bands for different particle species overlap and additional measurement of tof is required to remove the ambiguity. These two methods allow to cover most of the phase space in rapidity and transverse momentum which is of interest for the strong interaction program of NA61/SHINE. The acceptance of the two methods is shown in Figs. 2 and 3 for p + p interactions at 20 and 158 \(\text{ GeV }/c\), respectively. At low beam energies the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method extends the identification acceptance, while at top SPS energy it overlaps with the \({\mathrm {d}} E/{\mathrm {d}} x\) method.
3.2.1 Identification based on energy loss measurement (\({\mathrm {d}} E/{\mathrm {d}} x\))
Time projection chambers can provide measurements of energy loss \({\mathrm {d}} E/{\mathrm {d}} x\) of charged particles in the chamber gas along their trajectories. Simultaneous measurements of \({\mathrm {d}} E/{\mathrm {d}} x\) and \(p_{{\mathrm {lab}}}\) allow to extract information on particle mass. Here \({\mathrm {d}} E/{\mathrm {d}} x\) is calculated as the truncated mean (smallest 50%) of cluster charges measured along a track trajectory. As an example, \({\mathrm {d}} E/{\mathrm {d}} x\) measured in p + p interactions at 80 \(\text{ GeV }/c\), for positively and negatively charged particles, as a function of \(q \times p_{{\mathrm {lab}}}\) is presented in Fig. 4. The expected values of \({\mathrm {d}} E/{\mathrm {d}} x\) are shown by the Bethe–Bloch curves.
Distribution of charged particles in the \({\mathrm {d}} E/{\mathrm {d}} x\)-\(q \times p_{{\mathrm {lab}}}\) plane. The energy loss in the TPCs for different charged particles for events and tracks selected for the analysis of p + p interactions at 80 \(\text{ GeV }/c\) (the target inserted configuration). Expectations for the dependence of the mean \({\mathrm {d}} E/{\mathrm {d}} x\) on \(p_{{\mathrm {lab}}}\) for the considered particle types are shown by the curves calculated based on the Bethe–Bloch function
The contributions of e\(^{+}\), e\(^{-}\), \(\pi ^{+}\), \(\pi ^{-}\), K\(^{+}\), K\(^{-}\), p and \({\bar{\text {p}}}\) are obtained by fitting the \({\mathrm {d}} E/{\mathrm {d}} x\) distributions separately for positively and negatively charged particles in bins of \(p_{{\mathrm {lab}}}\) and \(p_{{\mathrm {T}}} \) with a sum of four functions [16, 17] each corresponding to the expected \({\mathrm {d}} E/{\mathrm {d}} x\) distribution for a given particle type.
In order to ensure similar particle multiplicities in each bin, 20 logarithmic bins are chosen in \(p_{{\mathrm {lab}}}\) in the range 1–100 \(\text{ GeV }/c\) to cover the full detector acceptance. Furthermore the data are binned in 20 equal \(p_{{\mathrm {T}}} \) intervals in the range 0–2 \(\text{ GeV }/c\).
The \({\mathrm {d}} E/{\mathrm {d}} x\) fits consider four particle types (\(i=\) p, K, \(\pi \), e). The signal shape for a given particle type is parametrised as the sum of asymmetric Gaussians with widths \(\sigma _{i,l}\) depending on the particle type i and the number of points l measured in the TPCs. Simplifying the notation in the fit formulae, the peak position of the \({\mathrm {d}} E/{\mathrm {d}} x\) distribution for particle type i is denoted as \(x_{i}\). The contribution of a reconstructed particle track to the fit function reads:
where x is the \({\mathrm {d}} E/{\mathrm {d}} x\) of the particle, \(n_{l}\) is the number of tracks with number of points l in the sample and \(A_{i}\) is the amplitude of the contribution of particles of type i. The second sum is the weighted average of the line-shapes from the different numbers of measured points (proportional to track-length) in the sample. The quantity \(\sigma _{l}\) is written as:
where the width parameter \(\sigma _{0}\) is assumed to be common for all particle types and bins. A \(1/\sqrt{l}\) dependence on number of points is assumed. The Gaussian peaks are allowed to be asymmetric (parameter \(\delta \) added/subtracted above/below the peak \(x_{i}\)) to describe the tail of the Landau distribution which may still be present after truncation.
The \({\mathrm {d}} E/{\mathrm {d}} x\) distributions for negatively (\(top{\text {-}}left\)) and positively (\(top{\text {-}}right\)) charged particles in the bin 12.6 \(< p_{{\mathrm {lab}}} \le \) 15.8 \(\text{ GeV }/c\) and 0.2 \(< p_{{\mathrm {T}}} \le \) 0.3 \(\text{ GeV }/c\) produced in p + p interactions at 158 \(\text{ GeV }/c\). The fit by a sum of contributions from different particle types is shown by solid lines. The corresponding residuals (the difference between the data and fit divided by the statistical uncertainty of the data) is shown in the bottom plots
The fit function has 10 parameters (4 amplitudes, 4 peak positions, width and asymmetry) which are very difficult to fit in each bin independently. Therefore the following simplifications were adopted:
-
(i)
relative positions of electrons, kaons and protons to pions were assumed to be \(p_{{\mathrm {T}}} \)-independent,
-
(ii)
in the analysed data, the asymmetry parameter \(\delta \) is smaller than 0.001 and thus was fixed to zero,
-
(iii)
the fitted amplitudes were required to be greater than or equal to 0,
-
(iv)
the electron amplitude was set to zero for total momentum \(p_{{\mathrm {lab}}}>\)23.4 \(\text{ GeV }/c\) (i.e. starting from the 13th bin), as the electron contribution vanishes at high \(p_{{\mathrm {lab}}}\),
-
(v)
if possible, the relative position of the positive kaon peak was taken to be the same as that of negative kaons determined from the negatively charged particles in the bin of the same \(p_{{\mathrm {lab}}}\) and \(p_{{\mathrm {T}}} \). This procedure helps to overcome the problem of the large overlap between K\(^+\) and protons in the \({\mathrm {d}} E/{\mathrm {d}} x\) distributions.
The simplifications reduce the number of independently fitted parameters in each bin from 10 to 6, i.e. the amplitudes of the four particle types, the pion peak position and the width parameter \(\sigma _{0}\).
Examples of fits are shown in Fig. 5 and the values of the fitted peak positions \(x_i\) are plotted in Fig. 6 versus momentum for different particle types i in p + p interactions at 158 \(\text{ GeV }/c\). As expected, the values of \(x_i\) increase with \(p_{{\mathrm {lab}}}\) but do not depend on \(p_{{\mathrm {T}}} \).
In order to ensure good fit quality, only bins with number of tracks grater than 300 are used for further analysis. The Bethe–Bloch curves for different particle types cross each other at low values of the total momentum. Thus, the proposed technique is not sufficient for particle identification at low \(p_{{\mathrm {lab}}}\) and bins with \(p_{{\mathrm {lab}}}<\) 3.98 \(\text{ GeV }/c\) (bins 1–5) are excluded from the analysis based solely on \({\mathrm {d}} E/{\mathrm {d}} x\).
3.2.2 Identification based on time of flight and energy loss measurements (tof-\({\mathrm {d}} E/{\mathrm {d}} x\))
Identification of \(\pi ^{+}\), \(\pi ^{-}\), K\(^{+}\), K\(^{-}\), p and \({\bar{\text {p}}}\) at low momenta (from 2 to 8 \(\text{ GeV }/c\)) is possible when measurement of \({\mathrm {d}} E/{\mathrm {d}} x\) is combined with time of flight (tof) information. Signals from the constant-fraction discriminators TDC and signal amplitude information from ADCs are recorded for each tile of the ToF-L/R walls. Only tof hits which satisfy quality criteria (see Ref. [18]) are selected for the analysis. Tracks reconstructed in the TPCs are extrapolated to the front face of ToF-L/R where they are matched to the selected hits. The position of the extrapolation point on the scintillator tile is used to correct the measured value of tof for the propagation time of the light signal. The distribution of the difference between the corrected tof measurement and the value predicted from the track momentum and the trajectory length can be well described by a Gaussian with standard deviation of 80 ps for ToF-R and 95 ps for ToF-L. These values represent the tof resolution including all detector effects.
The square of the particle mass \(m^2\) is obtained from tof, the momentum p and the fitted trajectory length l:
For illustration distributions of \(m^2\) versus \(p_{{\mathrm {lab}}}\) are plotted in Fig. 7 for negatively (left) and positively (right) charged hadrons produced in p + p interactions at 80 \(\text{ GeV }/c\). Bands which correspond to different particle types are visible. Separation between pions and kaons is possible up to momenta of about 5 \(\text{ GeV }/c\), between pions and protons up to about 8 \(\text{ GeV }/c\).
Example distributions of particles in the \(m^2\)-\({\mathrm {d}} E/{\mathrm {d}} x\) plane for p + p interactions at 40 \(\text{ GeV }/c\) are presented in Fig. 8. Simultaneous \({\mathrm {d}} E/{\mathrm {d}} x\) and tof measurements lead to improved separation between different hadron types. In this case a simple Gaussian parametrization of the \({\mathrm {d}} E/{\mathrm {d}} x\) distribution for a given hadron type can be used.
Particle number distribution in the \(m^2\)-\({\mathrm {d}} E/{\mathrm {d}} x\) plane for negatively (left) and positively (right) hadrons with momenta close to 4 \(\text{ GeV }/c\) for p + p interactions at 40 \(\text{ GeV }/c\). Electrons are not visible since their \({\mathrm {d}} E/{\mathrm {d}} x\) values are beyond the \({\mathrm {d}} E/{\mathrm {d}} x\) plot range
The tof-\({\mathrm {d}} E/{\mathrm {d}} x\) identification method proceeds by fitting the 2-dimensional distribution of particles in the \({\mathrm {d}} E/{\mathrm {d}} x\)-\(m^2\) plane. Fits were performed in 7 equal momentum bins from 1 to 8 \(\text{ GeV }/c\) and 20 equal bins in transverse momentum in the range 0–2 \(\text{ GeV }/c\). For positively charged particles the fit function included contributions of p, \(K^+\), \(\pi ^+\) and \(e^+\), whereas for negatively charged particles the corresponding anti-particles were considered. The fit function for a given particle type was assumed to be a product of a Gauss function in \({\mathrm {d}} E/{\mathrm {d}} x\) and the sum of two Gauss functions in \(m^2\). Then the full fitted function (for simplicity of notation \({\mathrm {d}} E/{\mathrm {d}} x\) is denoted by x and \(m^{2}\) by y) reads:
where \(A_{i}\) and f are the amplitude parameters, \(x_i\), \(\sigma _{x}\) and \(y_i\), \(\sigma _{y1}\), \(\sigma _{y2}\) are mean and width of the \({\mathrm {d}} E/{\mathrm {d}} x\) and \(m^2\) Gaussians, respectively. The total number of parameters in Eq. (4) is 16. The fits were performed imposing the following constraints:
-
(i)
\(y_i = m_i^2\), where \(m_i\) is a particle mass [19],
-
(ii)
relative \({\mathrm {d}} E/{\mathrm {d}} x\) positions of electrons, kaons and protons to pions were assumed to be \(p_{{\mathrm {T}}} \)-independent,
-
(iii)
the fitted amplitudes were required to be greater than or equal to 0,
-
(iv)
if possible, the relative \({\mathrm {d}} E/{\mathrm {d}} x\) position of the positive kaon peak was taken to be the same as that of negative kaons determined from the negatively charged particles in the bin of the same \(p_{{\mathrm {lab}}}\) and \(p_{{\mathrm {T}}} \). This procedure helps to overcome the problem of the large overlap between K\(^+\) and protons in the \({\mathrm {d}} E/{\mathrm {d}} x\) distributions,
-
(v)
\(\sigma _{y1} < \sigma _{y2} \) and \(f > 0.7 \), the ”core” distribution dominates the \(m^2\) fit.
The total number of fitted parameters is then reduced to 5.
An example of the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) fit obtained in a single phase-space bin for positively charged particles in p + p interactions at 158 \(\text{ GeV }/c\) is shown in Fig. 9.
Example of the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) fit (Eq. (4)) obtained in a single phase-space bin (3 \(< p_{{\mathrm {lab}}}<\) 4 \(\text{ GeV }/c\) and 0.2 \(< p_{{\mathrm {T}}}<\) 0.3 \(\text{ GeV }/c\)) for positively charged particles in p + p interactions at 158 \(\text{ GeV }/c\). Lines show projections of obtained fits for pions (red), kaons (blue) and protons (magenta)
The tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method allows to fit the kaon yield close to mid-rapidity. This is not possible using the \({\mathrm {d}} E/{\mathrm {d}} x\) method. Moreover, the kinematic domain in which pion and proton yields can be fitted is enlarged. The results from both methods partly overlap at the highest beam momenta. In these regions the results from the \({\mathrm {d}} E/{\mathrm {d}} x\) method were selected since they have smaller uncertainties.
3.2.3 Probability method
The probability method allows to transform fit results performed in (\(p_{{\mathrm {lab}}}\), \(p_{{\mathrm {T}}} \)) bins to results in (y, \(p_{{\mathrm {T}}} \)) bins. The fit results allow to calculate a probability \(P_i\) that a measured particle is of a given type \(i = \pi , K, {\text {p}}, e\), namely for the \({\mathrm {d}} E/{\mathrm {d}} x\) fits (see Eq. (1)) one gets:
where \(\rho _{i}\) is the value of the fitted function in a given (\(p_{{\mathrm {lab}}}\), \(p_{{\mathrm {T}}} \)) bin calculated for \({\mathrm {d}} E/{\mathrm {d}} x\) of the particle.
Similarly the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) fits (see Eq. (4)) give a particle type probability as
For illustration particle type probability distributions for positively and negatively charged particles produced in p + p interactions at 20 and 158 \(\text{ GeV }/c\) are presented in Fig. 10 for the \({\mathrm {d}} E/{\mathrm {d}} x\) fits and in Fig. 11 for the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) fits. Only in the case of perfect particle type discrimination the probability distributions in Figs. 10 and 11 will show peaks at 0 or 1. In the case of non-ideal discrimination (overlapping \({\mathrm {d}} E/{\mathrm {d}} x\) or tof-\({\mathrm {d}} E/{\mathrm {d}} x\) distributions) values between these extremes will be populated.
The numbers of identified particles in a given kinematical bin (e.g.,(\(p_{{\mathrm {lab}}}\), \(p_{{\mathrm {T}}} \))) are given by [20]:
where \(P_i\) is the probability of particle type i given by Eqs. (5) and (6) and n is the number of particles in the given kinematical bin.
Additionally the probability method allows to implement the efficiency correction particle by particle. The corrected number of identified particles in the given kinematical bin is:
where as in Eq. (7) \(P_i\) is the probability of particle type i given by Eqs. (5) and (6) and n is the number of particles in the given kinematical bin and \(\epsilon \) is the efficiency. Usually the efficiency is calculated with a different binning scheme. Thus the value of \(\epsilon \) has to be taken from the bin which corresponds to the kinematic quantities of particle i.
The probability method has some subtleties when the coverage of phase-space differs between identification and final variable. For example particles in bins selected for the identification (\(p_{{\mathrm {lab}}}\)) may not fully populate the edges of bins in the final variable (y) due to the non-orthogonal transformation between them. However, only the edges of the spectra are affected. For the \({\mathrm {d}} E/{\mathrm {d}} x\) analysis method bins could be selected in such a way that edges almost overlap. The remaining small effect was corrected by the overall Monte-Carlo correction factor. The mismatches are larger for the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method where identification had to be performed in linear, equal bins in total momentum due to the ToF acceptance. Therefore a separate correction factor \(\epsilon \) was calculated using the simulation based on the EPOS model (see below):
where \(n_{MC}^{{\mathrm {accepted}}}\) are the numbers of tracks accepted in a rapidity bin within the phase space covered by the identification technique and \(n_{MC}^{{\mathrm {generated}}}\) the number of tracks generated in the corresponding rapidity bin. Bins in which this correction exceeds 30% are rejected and the others are corrected by this factor.
3.3 Corrections
In order to determine the true number of each type of identified particle produced in inelastic p + p interactions a set of corrections was applied to the extracted raw results. The main effects for which corrections were introduced are the following: contribution of interactions outside the liquid hydrogen of the target (off-target events), detector effects (acceptance, efficiency) and particles from weak decays (feed-down). Note that the manner of application and the number of used correction factors depend on the particle identification technique (i.e. \({\mathrm {d}} E/{\mathrm {d}} x\) or tof-\({\mathrm {d}} E/{\mathrm {d}} x\))
3.3.1 Correction for off-target interactions
To estimate the off-target interactions about 10% of the data were collected without the liquid hydrogen in the target (so-called target removed data denoted as R). Before the identification procedure (see Sect. 3.2.1) a suitably normalized target removed yield was subtracted from target inserted data. This correction was applied for each bin of total momentum and transverse momentum.
The normalization of the target removed data was based on the fitted vertex z distribution. The ratio of the numbers of events with fitted vertex outside the target (in the range from −400 to −200 \(\text{ cm }\)) was calculated for target inserted and removed data and used subsequently as the normalization factor. The contamination of out of target events in the target inserted sample is given in Table 3 for p + p interactions at 20, 31, 40, 80 and 158 \(\text{ GeV }/c\).
3.3.2 Corrections for detector effects and particles from weak decays (feed-down)
A simulation of the NA61/SHINE detector is used to correct the data for reconstruction efficiency and acceptance. Only inelastic p + p interactions on the hydrogen in the target cell were simulated and reconstructed. The EPOS model [21] was selected to generate the primary interactions as it best describes the NA61/SHINE measurements. A Geant3 based program chain was used to track particles through the spectrometer, generate decays and secondary interactions and simulate the detector response (for more detail see Ref. [3]). The reconstructed tracks were matched to the simulated particles based on the cluster positions. The derived corrections can be applied only for inelastic events. The contribution of elastic events in the data was eliminated by the event and track selection cuts. Hadrons which were not produced in the primary interaction can amount to a significant fraction of the selected track sample. Thus a special effort was undertaken to evaluate and subtract this contribution (see above). As mentioned before correction factors depend on the particle identification technique and are described separately.
The \({\mathrm {d}} E/{\mathrm {d}} x\) method.
The correction factor C is defined as:
where:
-
\(\left( n_{i}\right) \ ^{MC}_{gen}\): multiplicity of particle type i \(\left( i=\pi ^{+/-},\ \text {K}^{+/-},\ {\text {p}},\ {\bar{\text {p}}} \right) \) generated by the EPOS model,
-
\(\left( n_{i}\right) \ ^{MC}_{sel}\): multiplicity of particle type i \(\left( i=\pi ^{+/-},\ \text {K}^{+/-},\ {\text {p}},\ {\bar{\text {p}}} \right) \) after applying the selection criteria described in the previous section,
The correction factor was calculated in the same bins of y and \(p_{T}\) as the particle spectra. Bins with correction factor lower than 0.5 and higher than 1.5 were rejected from the final results due to low acceptance or high contamination of particles from weak decays. Statistical uncertainties of the correction factors were calculated from the binomial distribution. The inverse correction factors for p + p interactions at 20 and 158 \(\text{ GeV }/c\) are presented in Figs. 12 and 13.
Correction factors \(C_{i}^{-1}\) for the \({\mathrm {d}} E/{\mathrm {d}} x\) identification method for positively and negatively charged pions, kaons and protons in p + p interactions at 20 \(\text{ GeV }/c\). The correction factor for antiprotons produced in inelastic p + p interactions is not presented due to insufficient statistics
The tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method.
Due to the lack of a simulation of the ToF system the corrections for the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) identification procedure had to be done in a different way than for the \({\mathrm {d}} E/{\mathrm {d}} x\) method, namely they partially employed a data based approach. Each simulated and reconstructed track was extrapolated to the ToF walls and if it crossed one of the ToF pixels it was classified as having a ToF hit. This defined the geometrical acceptance. The efficiency of the ToF pixels was estimated from data.
The correction factor for the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) identification method comprises the following components:
-
(i)
Correction for the detector efficiency and geometrical acceptance
Based on the event and detector simulation the combined geometrical and reconstruction efficiency \(C_i^{{\mathrm geo}}\) was calculated as:
$$\begin{aligned} C_i^{{\mathrm {geo}}} = \frac{\left( n_{i}\right) ^{MCrec}_{{\mathrm {geo}}}}{\left( n_{i}\right) ^{MCgen}}, \end{aligned}$$(11)where \(\left( n_{i}\right) ^{MCrec}_{{\mathrm {geo}}}\) is the multiplicity of particle type \(i=\pi ^{-},\ \pi ^{+}\), K\(^{-}\), K\(^{+}\), p, \({\bar{\text {p}}}\) after the TPC selection criteria and track extrapolation to the ToF wall resulting in a ToF hit, and \(\left( n_{i}\right) ^{MCgen}\) is the multiplicity of particle type i generated by the EPOS model. In addition, the last point on the track was required to be located in the last two padrows of a MTPC. The resulting geometrical correction factors for p + p interactions at 158 \(\text{ GeV }/c\) are presented in Fig. 46. Differences between efficiencies for pions, kaons and protons are due to the different particle lifetimes.
-
(ii)
Correction for the pixel efficiency of ToF-L and ToF-R detectors
The pixel efficiency was calculated from data as the ratio between \(\left( n_{i}\right) ^{tof}_{{\mathrm {hit}}}\), the number of tracks with ToF hits in working pixels (pixel efficiency from data higher than 50%) with correct TDC and QDC measurements and \(\left( n_{i}\right) ^{tof}_{{\mathrm {geo}}}\), the number of all tracks which were extrapolated to the particular pixel.
$$\begin{aligned} C_i^{pixel} = \frac{\left( n_{i}\right) ^{tof}_{{\mathrm {hit}}}}{\left( n_{i}\right) ^{tof}_{{\mathrm {geo}}}}, \end{aligned}$$(12)The pixel efficiency obtained for p + p interactions at 158 \(\text{ GeV }/c\) is shown in Fig. 47.
-
(iii)
Correction for decays and interactions between the last measured point in the MTPC and the ToF detectors
The probability of decays and interactions between the last measured point in the MTPC and the ToF detectors was estimated by simulations. The survival probability is defined in the following way:
$$\begin{aligned} C_i^{{\mathrm {survive}}}= \frac{\left( n_{i}\right) ^{MCrec}_{{\mathrm {survive}}}}{\left( n_{i}\right) ^{MCrec}_{{\mathrm {geo}}}}, \end{aligned}$$(13)where \(\left( n_{i}\right) ^{MCrec}_{{\mathrm {survive}}}\) is the number of particles which hit a working ToF pixel and which did not decay or interact between the last measured point in the MTPC and the ToF walls. The survival probability is lower than expected from decay only, due to interactions in the Forward Time of Flight detector. The survival probability \(C_i^{{\mathrm {survive}}}\) is presented in Fig. 48.
The combined efficiency factor \(C_{i}^{tof}\) was calculated as:
Combined efficiency factors \(C_{i}^{tof}\) for the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method calculated for each (p, \(p_{{\mathrm {T}}}\)) bin independently applied to p + p interactions at 20 and 158 \(\text{ GeV }/c\) are presented in Figs. 14 and 15.
3.4 Corrected spectra and uncertainties
3.4.1 Corrected spectra
The multiplicity of different types of hadrons from inelastic p + p interactions measured by the \({\mathrm {d}} E/{\mathrm {d}} x\) technique is defined as the sum of probabilities divided by the number of events corrected for detector effects, feed-down and contamination by target removed events. For particle type \(i=\pi ^{+}\), \(\pi ^{-}\), K\(^{+}\), K\(^{-}\), p, \({\bar{\text {p}}}\), the multiplicity is defined as:
where:
-
\(C_{i}\): correction factor defined in Eq. (10),
-
\(\sum \limits _{I} P_{i}(dE/dx)_{p_{{\mathrm {lab}}}, p_{{\mathrm {T}}}} \equiv \sum \limits _{I} P_{i}\): sum over probabilities \(P_{i}\) defined in Eq. (5) for all tracks for inserted target (abbreviated as “I”),
-
\(\sum \limits _{R} P_{i}(dE/dx)_{p_{{\mathrm {lab}}}, p_{{\mathrm {T}}}} \equiv \sum \limits _{R} P_{i}\): sum over probabilities \(P_{i}\) defined in Eq. (5) for all tracks for removed target (abbreviated as “R”),
-
B: the normalization factor applied to target removed events,
-
\(N_{I}\) and \(N_{R}\): the number of events of target inserted and removed, respectively.
Particle multiplicities for the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) technique can be calculated in a similar way:
where: \(P_{i}\) are the probabilities defined in Eq. (6), \(C_{i}^{tof}\) is the efficiency described by Eq. (14) and \(\epsilon \) is the correction for the non-orthogonal transformation between the phase spaces (momentum \(\rightarrow \) rapidity) described by Eq. (9). Sum over probabilities are the same like in Eq. (15).
3.4.2 Statistical uncertainties
Statistical uncertainties of multiplicities obtained by the \({\mathrm {d}} E/{\mathrm {d}} x\) method were calculated in the following way:
where \(\Delta \) denotes the statistical uncertainty of the quantities used to calculate the particle multiplicity. The uncertainty of the normalization factor (B) as well as of the number of events (\(N_{I}\) and \(N_{R}\)) are not taken into account in this calculation due to their negligible influence on the uncertainty value.
Calculation of statistical uncertainties of the multiplicities from the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) identification technique is more complicated. Assuming that the statistical uncertainty of \(C_{i}^{tof}\) is equal to the mean statistical uncertainty in the full \(y-p_{T}\) bin, it can be moved in front of the sums. The total statistical uncertainty can then be calculated according to the following formula:
3.4.3 Systematic uncertainties
Systematic biases to the measurements could result mainly from:
-
(i)
Methods of event selection.
The first uncertainty is related to the acceptance of events with additional tracks from off-time particles. This systematic uncertainty was estimated by changing the width of the time window in which no second beam particle is allowed by \(\pm ~1~\upmu s\) (variation by \(\pm \,50\)%) with respect to the nominal value of ±2\(~\upmu \)s. The maximal difference of the results was assigned as the systematic uncertainty of the selection.
The second source of possible systematic bias are losses of inelastic events due to the interaction trigger. The S4 detector veto mainly selects inelastic and removes elastic scattering events. However, it can also result in some losses of inelastic events. To estimate this effect, the analysis was done using correction factors calculated with and without applying the S4 trigger in the simulation. The difference between these two results was taken as a contribution to the systematic uncertainty.
The next source of systematic uncertainty related to the normalization came from the selection window for the z-position of the fitted vertex. To estimate the systematic uncertainty the selection criteria for the data and the EPOS model were varied in the range of ±10 \(\text{ cm }\) (50%) around the nominal value.
-
(ii)
Methods of track selection.
To estimate systematic uncertainty related to the track selection the following variations were performed independently: number of requested points on a track in all TPCs was changed by ± 5 (33% of the standard selection), number of requested points on a track in the VTPCs was reduced and increased by 5 (18% of the criterion).
-
(iii)
Identification techniques.
Moreover, uncertainties of the \({\mathrm {d}} E/{\mathrm {d}} x\) identification method were studied and estimated by a 10% variation of the parameter constraints for the function Eq. (1) used for particle identification. In case of tof-\({\mathrm {d}} E/{\mathrm {d}} x\) identification uncertainties were estimated by changing the selection criteria related to this technique – the last point of the track should be in the last 2 ± 1 padrows of the MTPC, the QDC signal is or is not required.
-
(iv)
Feeddown correction.
The determination of the feeddown correction is based on the EPOS model which describes well the available cross section data for strange particles (see e.g. for \(\Lambda \) at 158 \(\text{ GeV }/c\) Ref. [22] and at 40 \(\text{ GeV }/c\) Ref. [23] and Figs. 23 and 24 in this paper for K\(^{+}\) and K\(^{-}\)). Systematic uncertainty comes from the lack of precise knowledge of the production cross section of K\(^{+}\), K\(^{-}\), \(\Lambda \), \(\Sigma ^{+}\), \(\Sigma ^{-}\), K\(^{0}_{s}\) and \(\bar{\Lambda }\) in case of pions, and in addition of \(\Sigma ^{+}\) in case of protons, and \(\bar{\Lambda }\) in case of antiprotons. Since the corrections are only at the level of a few percent in the phase space region of the measurements a small additional systematic error of 1% was assumed in case of pions and 2% for protons and antiprotons.
The components of the systematic uncertainty and the total for the \({\mathrm {d}} E/{\mathrm {d}} x\) and tof-\({\mathrm {d}} E/{\mathrm {d}} x\) methods, for a selected \(p_{T}\) interval and beam momenta of 20 and 158 \(\text{ GeV }/c\) are presented in Figs. 16, 17, 18 and 19. Assuming independence of all systematic error sources, the total systematic uncertainty was calculated as the square root of the sum of squares of the described components.
Components of systematic uncertainty of particle spectra obtained from the \({\mathrm {d}} E/{\mathrm {d}} x\) method in inelastic p + p interaction at 20 \(\text{ GeV }/c\) as function of rapidity for the transverse momentum interval between 0.2–0.3 \(\text{ GeV }/c\). \(\sigma _{{\text {i}}}\) refers to acceptance of events with off-time beam tracks, \(\sigma _{{\text {ii}}}\) to possible bias of the S4 trigger, \(\sigma _{{\text {iii}}}\) to event vertex and track selection procedure and \(\sigma _{{\text {iv}}}\) to the identification technique. Black lines (Total) show the total systematic uncertainty calculated as the square root of the sum of squares of the components
Components of systematic uncertainty of particle spectra obtained from the \({\mathrm {d}} E/{\mathrm {d}} x\) method in inelastic p + p interaction at 158 \(\text{ GeV }/c\) as function of rapidity for the transverse momentum interval between 0.2–0.3 \(\text{ GeV }/c\). \(\sigma _{{\text {i}}}\) refers to removal of events with off-time beam tracks, \(\sigma _{{\text {ii}}}\) to possible bias of the S4 trigger, \(\sigma _{{\text {iii}}}\) to event vertex and track selection procedure and \(\sigma _{{\text {iv}}}\) to the identification technique. Black lines (Total) show the total systematic uncertainty calculated as the square root of the sum of squares of the components
Components of systematic uncertainty of particle spectra obtained from the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method in inelastic p + p interaction at 20 \(\text{ GeV }/c\) as function of rapidity for the transverse momentum interval between 0.2–0.3 \(\text{ GeV }/c\). \(\sigma _{{\text {i}}}\) refers to removal of events with off-time beam tracks, \(\sigma _{{\text {ii}}}\) to possible bias of the S4 trigger, \(\sigma _{{\text {iii}}}\) to event vertex and track selection procedure and \(\sigma _{{\text {iv}}}\) to the identification technique. Black lines (Total) show the total systematic uncertainty calculated as the square root of the sum of squares of the components
Components of systematic uncertainty of particle spectra obtained from the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method in inelastic p + p interaction at 158 \(\text{ GeV }/c\) as function of rapidity for the transverse momentum interval between 0.2–0.3 \(\text{ GeV }/c\). \(\sigma _{{\text {i}}}\) refers to removal of events with off-time beam tracks, \(\sigma _{{\text {ii}}}\) to possible bias of the S4 trigger, \(\sigma _{{\text {iii}}}\) to event vertex and track selection procedure and \(\sigma _{{\text {iv}}}\) to the identification technique. Black lines (Total) show the total systematic uncertainty calculated as the square root of the sum of squares of the components
Production of positive and negative pions, kaons and protons in p + p interactions at 158 \(\text{ GeV }/c\) was measured before by the NA49 experiment [11,12,13]. Comparison of NA61/SHINE and NA49 rapidity distributions is presented in Fig. 20. The results are consistent within the systematic uncertainty.
The NA61/SHINE experiment also published \(\pi ^{-}\) spectra obtained by the so-called \(h^{-}\) [3] analysis procedure. This technique is based on the fact that the majority of negatively charged particles are \(\pi ^{-}\) mesons. The contribution of the other particles was subtracted using predictions of the EPOS model. Comparison of rapidity spectra from the \(h^{-}\) method with those obtained in this publication using particle identification is shown in Fig. 21. Both methods give results for \(\pi ^{-}\) spectra which agree within uncertainties .
Comparison of \(\pi ^{-}\) rapidity distributions obtained by \({\mathrm {d}} E/{\mathrm {d}} x\) and tof-\({\mathrm {d}} E/{\mathrm {d}} x\) methods with results from the \(h^{-}\) technique [3]. The \(h^{-}\) results are presented with statistical uncertainty. Red shaded bands show the systematic uncertainty of particle multiplicities obtained by the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method
Spectra measured in p + p interactions should obey reflection symmetry with respect to mid-rapidity. As the NA61/SHINE acceptance extends somewhat below mid-rapidity a test of the reflection symmetry can be performed to check the consistency of the measurements. As examples these reflection tests are presented in Fig. 22 in selected \(p_{T}\) intervals for positively and negatively charged kaons, antiprotons and protons produced at 20 and 158 \(\text{ GeV }/c\). One observes that the yields measured for \(y < 0\) agree with those measured for \(y > 0\) in the reflected acceptance within uncertainties.
Rapidity spectra of K\(^{-}\), K\(^{+}\) and p measured (filled dots) and reflected with respect to mid-rapidity (open dots) obtained in inelastic p + p interactions in the interval \(p_{{\mathrm {T}}} = 0.2{-}0.3\) \(\text{ GeV }/c\) at 20 \(\text{ GeV }/c\) (upper row) and \(p_{{\mathrm {T}}} = 0.6{-}0.7\) \(\text{ GeV }/c\) at 158 \(\text{ GeV }/c\) (bottom row)
The EPOS model was chosen as the event generator in the simulation chain to calculate corrections. Figures 23 and 24 present EPOS model predictions and experimental results obtained in this analysis in selected rapidity intervals for inelastic p + p interactions at 20 and 158 \(\text{ GeV }/c\). The EPOS model describes well particle production in p + p interactions at 20 \(\text{ GeV }/c\) and at 158 \(\text{ GeV }/c\). Since the corrections were applied differentially in rapidity and transverse momentum bins the effect of minor discrepancies are not expected to cause significant biases.
Transverse momentum spectra of identified hadrons produced in inelastic p + p interactions at 20 \(\text{ GeV }/c\) in selected rapidity intervals in comparison to the EPOS model [21] (black line). Systematic uncertainties are shown as shaded bands
Transverse momentum spectra of identified hadrons produced in inelastic p + p interactions at 158 \(\text{ GeV }/c\) in selected rapidity intervals in comparison to the EPOS model [21] (black line). Systematic uncertainties are shown as shaded bands
4 Results
4.1 Spectra
Two dimensional distributions normalised per event (y vs. \(p_{T}\)) of \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions at different SPS energies are presented in Fig. 25. Where available, results from the \({\mathrm {d}} E/{\mathrm {d}} x\) methods were used because of their smaller statistical uncertainties. Results from the tof-\({\mathrm {d}} E/{\mathrm {d}} x\) method were taken to extend the phase space coverage. Anti-proton yields at 20 \(\text{ GeV }/c\) could not be determined due to the insufficient statistics of the collected data. Empty bins in phase-space (mostly for lower energies) are caused by insufficient acceptance for the methods used in the analysis. Yields for all particle types except protons are seen to increase with beam momentum in the SPS energy range.
Transverse momentum-rapidity spectrum of \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions at 20, 31, 40, 80 and 158 \(\text{ GeV }/c\). Color scale represents particle multiplicities normalized to the phase-space bin size (\(\frac{dn}{dydp_{T}}\))
The measurements shown in Fig. 25 were studied as a function of transverse momentum (\(p_{T}\)) in intervals of rapidity (y). Resulting double differential spectra of K\(^{-}\), K\(^{+}\), \(\pi ^{-}\), \(\pi ^{+}\), p and \({\bar{\text {p}}}\) produced in p + p interactions at 20, 31, 40, 80, 158 \(\text{ GeV }/c\) are plotted in Figs. 26, 27, 28, 29, 30 and 31, respectively. Spectra in successive rapidity intervals were scaled by appropriate factors for better visibility. Vertical bars on data points correspond to statistical, shaded bands to systematic uncertainties.
Results presented in Figs. 26, 27, 28, 29, 30 and 31 were parametrized by the exponential function [24, 25]:
where m is the particle mass and S and T are the yield integral and the inverse slope parameter, respectively. Examples of this parametrization fitted to K\(^{+}\) and K\(^{-}\) spectra at mid-rapidity are presented in Fig. 32. The obtained values of the inverse slope parameter for all spectra shown in Figs. 26, 27, 28, 29, 30 and 31 are plotted in Fig. 33 as function of the rapidity for four beam momenta 31, 40, 80 and 158 \(\text{ GeV }/c\). Note that results are only plotted for those rapidity intervals for which there were more than 6 data points in the \(p_{{\text {T}}}\)-distribution.
Transverse momentum spectra of \(K^{+}\) and \(K^{-}\) mesons produced at \(y\approx 0\) in inelastic \(p~+~p\) interactions. Colored lines represent the fitted function (Eq. (19))
Inverse slope parameter T obtained from fits with Eq. (19) to the \(p_{T}\) distributions of K\(^{+}\), K\(^{-}\), \(\pi ^{+}\), \(\pi ^{-}\), p and \({\bar{\text {p}}}\) as function of rapidity in inelastic p + p collisions at 30, 40, 80 and 158 \(\text{ GeV }/c\). Results are compared with EPOS model [21] predictions fitted in the same range. Bars show statistical uncertainties. Systematic uncertainties of about 10% are not shown
Rapidity distributions were then obtained by integrating the transverse momentum spectra also using reflection symmetry around mid-rapidity (\(y=0\)). Extrapolation to unmeasured regions in \(p_{{\mathrm {T}}} \) was performed in rapidity intervals using fits with function Eq. (19) where results were reliable (number of measured \(p_{{\mathrm {T}}}\) points higher than 6). In the other rapidity intervals the yield was obtained by summing the measured values and multiplying the result by an extrapolation factor calculated from the EPOS model. This factor was taken as the ratio of the integrated yield in the rapdity interval to that in the region of the measurements. The results are shown in Fig. 34. Statistical uncertainties, indicated by vertical bars, were calculated as the square root of the sum of the squares of statistical errors of the summed bins. Systematic uncertainties (shaded bands) were calculated by varying the uncertainty sources described in Sect. 3.4.3 and adding half of the extrapolated yield.
Rapidity spectra of K\(^{+}\), K\(^{-}\), \(\pi ^{+}\), \(\pi ^{-}\), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions at SPS energies, scaled by appropriate factors for better visibility. Vertical bars indicate statistical, shaded bands systematic uncertainties of the measurements. Curves depict Gaussian fits used to determine total multiplicities
4.2 Mean multiplicities
Next, mean multiplicities produced in the forward region \(y > 0\) were calculated by integrating the rapidity distributions shown in Fig. 34. The distributions are seen to be nearly Gaussian at all energies except for protons. In order to obtain a good description of the data points, fits were performed with a sum of two identical Gaussian functions with mean position symmetrically displaced around mid-rapidity. The integrated result was taken as the sum of measured values plus a contribution from the unmeasured region obtained from the fit function. The statistical uncertainty is obtained as the square root of the sum of squares of statistical uncertainties of the measured data points and the square of the statistical error of the extrapolation. The systematic uncertainty was estimated by repeating the complete analysis procedure by varying the components described in Sect. 3.4.3. Doubling of the results gives the \(4\pi \) multiplicities which are listed in Table 4 for \(\pi ^+\), K\(^+\) and p and in Table 5 for \(\pi ^-\), K\(^-\) and \({\bar{\text {p}}}\).
The determination of \(4\pi \) multiplicity is more complicated for protons due to the rapid rise of the yield towards beam rapidity and the lack of measurements in this region. A comparison of the rapidity distributions obtained in this analysis with measurements of the NA49 experiment [26] and calculations using the UrQMD [27, 28] and EPOS [21] models at 158 \(\text{ GeV }/c\) beam momentum is shown in Fig. 35. One observes that the models do not describe well the measurements at highest rapidities at this beam energy. Nevertheless, the models were used to extrapolate the proton yields into the unmeasured region since they provide predictions at all beam energies. Extrapolation factors were calculated from the models as the ratio of total multiplicity to that in the region covered by the measurements. The average of the two model results was then used for extrapolating the measured yield to \(4\pi \) phase space. The difference between results obtained using the UrQMD and EPOS models was added to the systematic uncertainty. Final results for protons are given in Table 4.
4.2.1 Energy dependence of mean multiplicities
The energy dependence of total charged kaon multiplicities produced in inelastic p + p collisions is presented in Fig. 36. One observes a steep threshold rise and a clear flattening above about 8 GeV for both K\(^{+}\) and K\(^{-}\). The new NA61/SHINE measurements (filled red squares) agree with the world data (open circles) and locate the change of slope due to the high precision of the actual measurement.
Mean K\(^+\) (left) and K\(^-\) (right) multiplicity produced in inelastic p + p interactions as function of collision energy. Measurements of NA61/SHINE are plotted as filled red squares, world data [13, 29,30,31,32,33,34,35,36] are shown by open circles. Statistical uncertainties are indicated by bars, systematic uncertainties of the NA61/SHINE measurements by shaded bands
The energy dependence of the NA61/SHINE measurements of charged pion multiplicities \(\left\langle \pi ^{+}\right\rangle \) and \(\left\langle \pi ^{-}\right\rangle \) produced in inelastic p + p collisions is compared in Fig. 37 to that of the world data [11, 37,38,39,40,41,42,43]. Clearly the NA61/SHINE results (filled red squares, filled blue dots) are consistent with measurements published in the literature (open squares). Also the NA61/SHINE measurements for \(\left\langle \pi ^{-}\right\rangle \) obtained with the identification method (filled red squares) and the \(h^{-}\) method [3] (blue dots) agree. It can be seen, that \(\left\langle \pi ^{+}\right\rangle \) and \(\left\langle \pi ^{-}\right\rangle \) increase smoothly with the collision energy. The rate of the increase gradually diminishes with increasing energy. The energy dependence of the charged pion multiplicity is qualitatively similar to that of charged kaons.
Mean \(\pi ^{+}\) (left) and \(\pi ^{-}\) (right) multiplicity produced in inelastic p + p interactions as function of collision energy. Measurements of NA61/SHINE for identified pions are plotted as filled red squares, whereas those obtained by the \(h^{-}\) method [3] by blue dots. Black open squares represent the world data [11, 37,38,39,40,41,42,43,44]. Statistical uncertainties are indicated by bars, systematic uncertainties of the NA61/SHINE measurements by shaded bands
For the determination of total proton multiplicities large acceptance over a full hemisphere of the reaction is particularly important. Due to this feature NA61/SHINE and NA49 were able to provide such measurements in the SPS energy range. The total proton multiplicity in inelastic p + p collisions is presented in Fig. 38 as function of collision energy. One observes that the proton yield is almost constant at SPS energies.
Mean proton multiplicities produced in inelastic p + p interactions as a function of collision energy. Filled red squares depict results from this analysis, the open black square shows the measurement of NA49 [12]. The dominating uncertainty of the NA61/SHINE measurements is systematic and is indicated by the shaded band
5 Comparison with hadron production models
This section compares the NA61/SHINE measurements with predictions from the publicly available codes of the microscopic models EPOS 1.99 [21] and UrQMD 3.4 [27, 28]. In EPOS the reaction proceeds via excitation of strings according to Gribov–Regge theory which subsequently fragment into hadrons. UrQMD generates a hadron cascade using elementary cross sections and supplements this process by string production and fragmentation at higher energies.
Two dimensional distributions \(d^{2}n/(dp_{T}dy)\) of \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions divided by the EPOS model prediction are presented in Fig. 39 at 20 \(\text{ GeV }/c\) and in Fig. 40 at 158 \(\text{ GeV }/c\) and divided by the UrQMD model calculations in Fig. 41 at 20 \(\text{ GeV }/c\) and in Fig. 42 at 158 \(\text{ GeV }/c\).
As demonstrated by Figs. 39 and 40 the EPOS model provides a good description of the measurements in most regions of phase space. Only at larger transverse momenta, where particle yields are low, some underprediction occurs. This conclusion is supported by Figs. 23 and 24 which show projected \(p_{T}\) distributions in selected rapidity intervals.
Comparison of the UrQMD 3.4 calculations with the NA61/SHINE measurements show larger discrepancies as seen in Figs. 41, 42 and 43. There are regions of underprediction for K\(^{+}\) at lower energies and overprediction for K\(^{-}\) at higher energies and especially \({\bar{\text {p}}}\) at all collision energies.
Two dimensional distributions \(d^{2}n/(dp_{T}dy)\) of \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\) and p produced in inelastic p + p interactions at 20 \(\text{ GeV }/c\) divided by the EPOS model [21] calculations
Two dimensional distributions \(d^{2}n/(dp_{T}dy)\) of \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\), p and \(\bar{{{\text {p}}}}\) produced in inelastic p + p interactions at 158 \(\text{ GeV }/c\) divided by the EPOS model [21] calculations
Comparison of the measured rapidity distributions with predictions of both models are shown in Fig. 43. The total multiplicities \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\) and \({\bar{\text {p}}}\) as function of collision energy are presented and compared in Fig. 44. The EPOS 1.99 model provides a reasonable description of the NA61/SHINE measurements, while significant discrepancies are evident for the UrQMD 3.4 calculations.
Mean multiplicity of \(\pi ^{-}\), \(\pi ^{+}\), K\(^{-}\), K\(^{+}\) and \({\bar{\text {p}}}\) multiplicity produced in inelastic p + p interactions as a function of collision energy. Measurements of NA61/SHINE are plotted as filled red squares, EPOS [21] and UrQMD [27, 28] models predictions are shown as dashed and dotted lines, respectively. Additionally, blue filled circles correspond to previously published results obtained by NA61/SHINE via the \(h^{-}\) method [3]. Statistical uncertainties are indicated by bars, systematic uncertainties of the NA61/SHINE measurements by shaded bands
Additionally the difference \(\left\langle \pi ^{+} \right\rangle - \left\langle \pi ^{-} \right\rangle \) is presented as function of collision energy in Fig. 45. It can be observed that this value is almost independent of collision energy. The NA61/SHINE results agree with the measurements of previous experiments. Both EPOS and UrQMD model predictions are consistent with the measurements.
Difference \(\left\langle \pi ^{+} \right\rangle - \left\langle \pi ^{-} \right\rangle \) in inelastic p + p interactions as function of collision energy. Solid red squares depict NA61/SHINE results from this analysis, open squares show previously published measurements [11, 37, 38, 44]. Statistical uncertainties of the NA61/SHINE results are indicated by bars, systematic uncertainties by the shaded band. The EPOS [21] and UrQMD [27, 28] model predictions are shown as dashed and dotted lines, respectively
6 Summary and outlook
Spectra and multiplicities of \(\pi ^{+}\), \(\pi ^{-}\), K\(^{+}\), K\(^{-}\), p and \({\bar{\text {p}}}\) produced in inelastic p + p interactions were measured with the NA61/SHINE spectrometer at beam momenta of 20, 31, 40, 80, 158 \(\text{ GeV }/c\) at the CERN SPS. New probabilistic analysis techniques based on the energy loss \({\mathrm {d}} E/{\mathrm {d}} x\) in the TPCs and the combination of the measurement of time of flight and energy loss tof-\({\mathrm {d}} E/{\mathrm {d}} x\) were employed. Statistical and systematic uncertainties were carefully evaluated. The NA61/SHINE results significantly improve the world data both in precision and momentum coverage. The EPOS 1.99 model [21] provides a good description of the measurements in the SPS energy range, while predictions of the UrQMD 3.4 model [27, 28] significantly differ from the data.
The new NA61/SHINE measurements of particle production in inelastic p + p collisions provide the baseline for the systematic study of the system size dependence of the onset of deconfinement observed by the NA49 experiment in central Pb + Pb collisions in the SPS energy range. In the nearest future the NA61/SHINE collaboration will extend the p + p energy scan by results from p + p interactions at 400 \(\text{ GeV }/c\) beam momentum.
References
N. Abgrall et al. [NA61/SHINE Collab.], JINST 9, P06005 (2014). arXiv:1401.4699 [physics.ins-det]
N. Antoniou et al. [NA61/SHINE Collab.], Study of hadron production in hadron nucleus and nucleus nucleus collisions at the CERN SPS. CERN-SPSC-2006-034 (2006)
N. Abgrall et al. [NA61/SHINE Collab.], Eur. Phys. J. C 74, 2794 (2014). arXiv:1310.2417 [hep-ex]
A. Aduszkiewicz et al. [NA61/SHINE Collab.], Eur. Phys. J. C 76(11), 635 (2016). arXiv:1510.00163 [hep-ex]
S. Afanasiev et al. [NA49 Collab.], Phys. Rev. C 66, 054902 (2002)
C. Alt et al. [NA49 Collab.], Phys. Rev. C 77, 024903 (2008)
L. Adamczyk et al. [STAR Collab.], arXiv:1701.07065 [nucl-ex]
A. Rustamov, Cent. Eur. J. Phys. 10, 1267–1270 (2012). arXiv:1201.4520 [nucl-ex]
M. Gazdzicki, M. Gorenstein, P. Seyboth, Int. J. Mod. Phys. E 23, 1430008 (2014). arXiv:1404.3567 [nucl-ex]
A. Aduszkiewicz [NA61/SHINE Collaboration Collab.], Beam momentum scan with Pb + Pb collisions. Tech. Rep. CERN-SPSC-2015-038. SPSC-P-330-ADD-8, CERN, Geneva (2015)
C. Alt et al. [NA49 Collab.], Eur. Phys. J. C 45, 343 (2006)
T. Anticic et al. [NA49 Collab.], Eur. Phys. J. C 65, 9 (2010)
T. Anticic et al. [NA49 Collab.], Eur. Phys. J. C 68, 1–73 (2010)
Bovet, C., Maleyran, R., Piemontese, L., Placci, A., Placidi, M.: TheCedar Counters for Particle Identification in the SPS Secondary Beams: A Description and an Operation Manual. Report Number: CERN-82-13, CERN-YELLOW-82-13 (1982). http://inspirehep.net/record/183384
N. Abgrall et al. [NA61/SHINE Collab.], in Eur. Phys. J. [3], p. 2794. arXiv:1310.2417 [hep-ex]
M. van Leeuwen [NA49 Collab.], Energy dependence of particle production in nucleus nucleus collisions at the CERN SPS. in Proceedings, 38th Rencontres de Moriond on QCD and High-Energy Hadronic Interactions. arXiv:nucl-ex/0306004 [nucl-ex] (2003)
M. van Leeuwen, A practical guide to de/dx analysis in na49. Note, CERN EDMS (2008)
T. Anticic et al. [NA49 Collab.], Phys. Rev. C 85, 044913 (2012). arXiv:1111.2588 [nucl-ex]
K.A. Olive et al. [Particle Data Group Collab.], Chin. Phys. C 38, 090001 (2014)
A. Rustamov, M. Gorenstein, Phys. Rev. C 86, 044906 (2012). arXiv:1204.6632 [nucl-th]
K. Werner, Nucl. Phys. Proc. Suppl. 175–176, 81–87 (2008)
A. Aduszkiewicz et al. [NA61/SHINE Collab.], Eur. Phys. J. C 76(4), 198 (2016). arXiv:1510.03720 [hep-ex]
H. Strobele, for the NA61/SHINE Collab. [NA61/SHINE Collab.]., New(s) from NA61: \(\Lambda \) in p + p and \(\pi ^{-}\) in Ar+Sc. Talk at the SQM 2016 (2016)
R. Hagedorn, Nuovo Cim. Suppl. 6, 311–354 (1968)
W. Broniowski, W. Florkowski, L.Y. Glozman, Phys. Rev. D 70, 117503 (2004). arXiv:hep-ph/0407290
B. Baatar et al. [NA49 Collaboration Collab.], Eur. Phys. J. C 73(4), 2364 (2013). arXiv:1207.6520 [hep-ex]
S. Bass et al., Prog. Part. Nucl. Phys. 41, 255–369 (1998). arXiv:nucl-th/9803035
M. Bleicher et al., J. Phys. G 25, 1859–1896 (1999). arXiv:hep-ph/9909407
M. Gazdzicki, D. Rohrich, Z. Phys. C 71, 55–64 (1996). arXiv:hep-ex/9607004
M. Gazdzicki, O. Hansen, Nucl. Phys. A 528, 754–770 (1991)
J. Bachler et al. [NA49 Collaboration Collab.], Nucl. Phys. A 661, 45–54 (1999)
F. Verbeure et al. [LEBC-EHS Collab.], Sov. J. Nucl. Phys. 54, 585–611 (1991)
A. Rossi, G. Vannini, A. Bussiere, E. Albini, D. D’Alessandro et al., Nucl. Phys. B 84, 269 (1975)
A. Golokhvastov, Phys. Atom. Nucl. 64, 1841–1855 (2001)
F. Becattini, U.W. Heinz, Z. Phys. C 76, 269–286 (1997). arXiv:hep-ph/9702274
B.B. Back et al. [PHOBOS Collab.], arXiv:nucl-ex/0301017
V. Blobel, H. Fesefeldt, P. Freund, D. Gall, K. von Holt, U. Idschok, D. Luers, W. Schrankel, B.M. Schwarzschild [Bonn-Hamburg-Munich Collab.], Nucl. Phys. B 103, 221–233 (1976)
M. Aguilar-Benitez et al., Z. Phys. C 50, 405–426 (1991)
A.C. Melissinos, T. Yamanouchi, G.G. Fazio, S.J. Lindenbaum, L.C.L. Yuan, Phys. Rev. 128, 2373–2381 (1962)
G. Alexander, O. Benary, G. Czapek, B. Haber, N. Kidron, B. Reuter, A. Shapira, E. Simopoulou, G. Yekutieli, Phys. Rev. 154, 1284–1304 (1967)
H.J. Mueck et al., Phys. Lett. B 39, 303–306 (1972)
C.W. Akerlof et al., Phys. Rev. D 3, 645–663 (1971)
M. Antinucci, A. Bertin, P. Capiluppi, M. D’Agostino-Bruno, A.M. Rossi, G. Vannini, G. Giacomelli, A. Bussiere et al., Lett. Nuovo Cim. 6, 121–128 (1973)
V.V. Ammosov et al. [French-Soviet Collab.], Nuovo Cim. A 40, 237 (1977)
Acknowledgements
We would like to thank the CERN EP, BE and EN Departments for the strong support of NA61/SHINE. This work was supported by the Hungarian Scientific Research Fund (Grants OTKA 68506 and 71989), the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, the Polish Ministry of Science and Higher Education (Grants 667/N-CERN/2010/0, NN 202 48 4339 and NN 202 23 1837), the Polish National Center for Science (Grants 2011/03/N/ST2/03691, 2013/11/N/ST2/03879, 2014/13/N/ST2/02565, 2014/14/E/ST2/00018, 2014/12/T/ST2/00692, 2015/18/M/ST2/00125, 2015/19/N/ST2 /01689 and 2014/15/B/ST2/02537) , the Foundation for Polish Science — MPD program, co-financed by the European Union within the European Regional Development Fund, the Federal Agency of Education of the Ministry of Education and Science of the Russian Federation (SPbSU research Grant 11.38.242.2015), the Russian Academy of Science and the Russian Foundation for Basic Research (Grants 08-02-00018, 09-02-00664 and 12-02-91503-CERN), the Ministry of Education, Culture, Sports, Science and Technology, Japan, Grant-in-Aid for Scientific Research (Grants 18071005, 19034011, 19740162, 20740160 and 20039012), the German Research Foundation (Grant GA 1480/2-2), the EU-funded Marie Curie Outgoing Fellowship, Grant PIOF-GA-2013-624803, the Bulgarian Nuclear Regulatory Agency and the Joint Institute for Nuclear Research, Dubna (bilateral contract No. 4418-1-15/17), Bulgarian National Science Fund (Grant DN08/11), Ministry of Education and Science of the Republic of Serbia (Grant OI171002), Swiss Nationalfonds Foundation (Grant 200020117913/1), ETH Research Grant TH-01 07-3 and the US Department of Energy, the National Research Nuclear University MEPhI in the framework of the Russian Academic Excellence Project (contract No. 02.a03.21.0005, 27.08.2013).
Author information
Authors and Affiliations
Corresponding author
A. ToF correction factors
A. ToF correction factors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Aduszkiewicz, A., Ali, Y., Andronov, E. et al. Measurements of \(\pi ^\pm \), K\(^\pm \), p and \({\bar{\text {p}}}\) spectra in proton-proton interactions at 20, 31, 40, 80 and 158 \(\text{ GeV }/c\) with the NA61/SHINE spectrometer at the CERN SPS. Eur. Phys. J. C 77, 671 (2017). https://doi.org/10.1140/epjc/s10052-017-5260-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5260-4