Abstract
Two-particle angular correlations were measured in pp collisions at \(\sqrt{s} = 7\) TeV for pions, kaons, protons, and lambdas, for all particle/anti-particle combinations in the pair. Data for mesons exhibit an expected peak dominated by effects associated with mini-jets and are well reproduced by general purpose Monte Carlo generators. However, for baryon–baryon and anti-baryon–anti-baryon pairs, where both particles have the same baryon number, a near-side anti-correlation structure is observed instead of a peak. This effect is interpreted in the context of baryon production mechanisms in the fragmentation process. It currently presents a challenge to Monte Carlo models and its origin remains an open question.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ultrarelativistic proton–proton collisions at the Large Hadron Collider (LHC) provide a unique opportunity to study Quantum Chromodynamics (QCD) at new energy scales. Two-particle angular correlations [1,2,3,4,5,6,7,8,9,10,11] are a robust tool which allows for exploration of the underlying physics phenomena of particle production in collisions of both protons and heavy ions by measuring the distributions of angles in \(\Delta \upeta \Delta \upvarphi \) space (where \(\Delta \upeta \) is the pseudorapidity difference and \(\Delta \upvarphi \) is the azimuthal angle difference between two particles). These correlations open up the possibility to study a number of mechanisms simultaneously. The baseline, the physics mechanism underlying all correlations, is the global conservation of energy and momentum as well as strangeness, baryon number, and electric charge. It results in a “\(-\cos (\Delta \upvarphi )\)”-like shape spanning the entire phase-space [12]. Other phenomena, including mini-jets, elliptic flow, Bose–Einstein correlations, resonance decays, are sources of additional correlations and each produces a characteristic distribution in \(\Delta \upeta \Delta \upvarphi \) space. Together with the baseline, they determine the final shape of the correlation function.
This work presents an extension to the traditional angular correlation measurements, which were studied at the LHC for all available collision systems [4, 7, 10, 13,14,15,16]. It is performed for identified particles, that is pions, kaons, protons, and lambda baryons, produced in proton–proton collisions at \(\sqrt{s}=7\) TeV recorded by ALICE [17]. The high collision energies provided by the LHC, leading to large cross-sections for production of (anti-)baryons, enable the measurement of correlations not only of primary protons, but also of lambdas and anti-lambdas with very high precision. Choosing specific particle types allows for the selection of a specific combination of quantum numbers (strangeness, baryon number) that may manifest in the measured correlation. As a consequence the angular correlations for identified particles may reveal new structures, which reflect the specific conservation laws for these quantum numbers. The correlations should also be sensitive to details of particle production mechanisms, including the parton fragmentation. In order to interpret the data in this context, dedicated Monte Carlo simulations using PYTHIA and PHOJET generators were performed.
The paper is organized as follows. Experimental setup, data taking conditions, and track selection criteria are presented in Sect. 2. Section 3 presents the analysis procedure and introduces the correlation function. In Sect. 4 systematic uncertainties are discussed. The experimental results are presented in Sect. 5. Detailed studies and the comparison of results to Monte Carlo simulations are shown in Sect. 6. Section 7 summarizes the paper.
2 Data taking and track reconstruction
This study was performed on a data sample of about \(2.5\times 10^8\) pp events at \(\sqrt{s}=7\) TeV recorded by ALICE [18] in 2010. The trigger system is described in details in Ref. [19]. The minimum-bias trigger required a signal in either V0 (a detector made of the two arrays of scintillating counters V0A and V0C; see Ref. [20] for details) or one of the two inner layers of the Silicon Pixel Detector (SPD), which cover pseudorapidity ranges of \(2.8<\upeta <5.1\) for V0C and \(-3.7<\upeta <-1.7\) for V0A and \(|\upeta |<1.4\) for the SPD. Each event (collision) consists of global properties and trajectories of particles (tracks).
Two main subsystems were used for particle trajectory reconstruction: the Inner Tracking System (ITS), a silicon-based tracker consisting of 6 layers, and the Time Projection Chamber (TPC). Their acceptance covers the full azimuth within the pseudorapidity range \(|\upeta |<0.9\). The collision-vertex position was determined with tracks reconstructed in the ITS and the TPC as described in Ref. [21]. Particle trajectories are reconstructed from a collection of space points. The ITS provides up to 6 points, one at each layer. The TPC provides up to 159 points (clusters), which also contain information on the ionization energy. This information is averaged over all clusters, giving a measurement of the specific ionization energy loss \(\langle {\mathrm {d}}E/{\mathrm {d}}x \rangle \) for the particle. For each track, the \(\langle {\mathrm {d}}E/{\mathrm {d}}x \rangle \) signal is computed as a truncated mean of the lowest 60% of the all measured points. The charged particle momentum is determined on the basis of the charged particle trajectories bent by the magnetic field of 0.5 T parallel to the beam axis.
ALICE provides a particle identification (PID) capability through the combination of the measurement of the specific ionization in the TPC and the timing signals in the Time-Of-Flight (TOF) detector [21, 22]. Particle trajectories are propagated from the TPC to the TOF and matched to hits in this detector. Each hit is associated with the time of its detection. The start-time of the event is determined by combining the time estimated using the particle arrival times at the TOF and the time measured by the T0 detector [20, 23]. This time, combined with the time of the detection of the particle and with the total length of the track enables the measurement of a particle’s velocity. This, combined with the momentum obtained from the TPC, enables the determination of particle’s mass and therefore its identity.
The protons analyzed here have a minimum transverse momentum of \(p_{\mathrm {T}}=0.5\) GeV/c, while the kaons and pions are measured for \(p_{\mathrm {T}}>0.3\) GeV/c and \(p_{\mathrm {T}}>0.2\) GeV/c, respectively. At lower values of transverse momenta, the sample can be contaminated by particles from the detector material and the PID procedures are also less reliable. The upper limit of \(p_\mathrm{{T}}\) for all particle species was set to 2.5 GeV/c; above this value the selected identification process was no longer able to efficiently distinguish pions from kaons and protons. In order to ensure that the sample of accepted tracks corresponds mostly to primary particles, a \(p_{\mathrm {T}}\)-dependent selection on the Distance of Closest Approach (DCA) to the primary vertex was applied. Accepted tracks were located at a distance in the transverse plane smaller than \((0.018+0.035 p_{\mathrm {T}}^{-1.01})\) cm, where \(p_\mathrm{{T}}\) is expressed in GeV/c (which corresponds to about \(7\upsigma \) of the track DCA resolution), and 2.0 cm in the beam direction. The contamination from secondary particles was estimated using PYTHIA Perugia-0 [24, 25] simulations and found to be below 1% for pions and kaons, and below 4% for protons. To ensure that only tracks with sufficient reconstruction quality were used in the analysis, they were required to have a minimum of 70 TPC clusters (maximum possible number is 159) associated to them; additionally, the maximum value of \(\chi ^2\) of the Kalman fit per TPC cluster was set to 4.0 (2 degrees of freedom per cluster) [26]. The selection criteria described above are summarized in Table 1.
The particle identification of pions, kaons, and protons was performed on a track by track basis using information from the TPC and TOF detectors; namely the measured values of \(\langle {\mathrm {d}}E/{\mathrm {d}}x \rangle \), the particle velocity \(\upbeta \), and their resolutions defined as standard deviations around the nominal signal, \(\upsigma _\mathrm{TPC}\) and \(\upsigma _\mathrm{TOF}\) respectively. Based on the difference (expressed in units of the resolution \(\upsigma \)) between the measured signal and the expected signal for pions, kaons, or protons in the TPC and TOF, three values of \({N_{\upsigma , \mathrm PID}^{a}}\) (where \({N_{\upsigma }}\) is the number of standard deviations of the observable away from the mean and “a” denotes one of the three particle type hypotheses) were used to select each track [26]. For particles with \(p_\mathrm{{T}}\) > 0.5 GeV/c, the values were calculated from the combined TPC–TOF information, \({N_{\upsigma , \mathrm PID}^{a}}^2 = {N_{\upsigma , \mathrm TPC}^{a}}^2 + {N_{\upsigma , \mathrm TOF}^{a}}^2\), resulting in a circular cut in the \(N_{\upsigma , \mathrm TPC}^{a}\) and \(N_{\upsigma , \mathrm TOF}^{a}\) space. For \(p_\mathrm{{T}}\) less than 0.5 GeV/c, only a few tracks have an associated signal in the TOF and information only from the TPC was used (\(N_{\upsigma , \mathrm PID}^{a} = N_{\upsigma , \mathrm TPC}^{a}\)). In order to form a sample consisting of particles of a species “a”, particles were selected with \(N_{\upsigma , \mathrm PID}^{a} < 2\). Additionally, to keep the purity of the sample above 96%, in regions where the areas of two species overlap, an exclusive identification was used. Specifically, tracks for which the \({N_{\upsigma , \mathrm PID}^{a}} < 3\) condition is fulfilled for more than one particle species hypothesis, were rejected. This procedure resulted in a purity above 99% for pions and protons and above 96% for kaons.
The weakly decaying lambda baryons were reconstructed using their distinctive V-shaped decay topology in the channel \(\Lambda (\overline{\Lambda })\rightarrow {\mathrm {p}}\uppi ^-(\overline{\mathrm {p}}\uppi ^+)\), which has a branching ratio of 63.9% [27]. The reconstruction method forms \(V^0\) decay candidatesFootnote 1; details are described in [28, 29]. The selection criteria used in this analysis are listed in Table 1. They were also varied to estimate the \(V^0\) selection systematic uncertainty. Only \(\Lambda \) candidates within an invariant mass window \(m_{\Lambda _\mathrm{PDG}}-0.0038< m_{V^0} < m_{\Lambda _\mathrm{PDG}}+0.0038\) GeV/\({c}^2\) and \(p_\mathrm{T}>0.6\) GeV/c were used. To calculate the \(\Lambda \) purity, the signal S was first approximated by a Gaussian superimposed on a second order polynomial background B [28]. The \(\Lambda \) purity (defined as S/\((S+B)\)), in the invariant mass range defined above, was found to be larger than 95%. With respect to the method used in Refs. [28, 29] an additional selection on maximum DCA of the \(\Lambda \) candidate to the primary vertex was applied to minimize the contribution of weak decays of the charged and neutral \(\Xi \). The resulting contamination was estimated using a data-driven approach, based on the fit of the \(V^0\) transverse DCA to the primary vertex distribution with the expected shapes for primary and secondary particles [22]. The contamination corresponds to 17% of the \(V^0\) candidates in the sample. Another cut was used to prevent two reconstructed \(V^0\)s from sharing the same daughter track. If two \(V^0\) candidates shared a daughter track, the \(V^0\) candidate with the lowest DCA to the primary vertex was chosen, while the other one was rejected from the analysis.
For pairs of pions, kaons and protons, a dedicated procedure (called share fraction rejection) was used to mitigate the effects of merging (two tracks reconstructed as one), and splitting (one track reconstructed as two). A share fraction value for a pair is obtained as a ratio of the number of times the two tracks share a cluster to the number of all clusters of both tracks in the TPC. All pairs for which this fraction was larger than \(5\%\) were rejected. In the \(\Lambda \) analysis, two main particle pair selection criteria were used. To resolve two-track inefficiencies associated with daughter tracks, such as the splitting or merging of tracks discussed above, a separation cut was employed (the share fraction cut is defined for primary tracks only): for each pair, the spatial separation between the same-sign daughters was measured at several points throughout the TPC (every 20 cm radially from 80 to 250 cm) and averaged. If the average separation of either pair of like-sign tracks was below 3 cm, the \(\Lambda \) pair was not used. Moreover, the process of photon conversions to \(e^{+}e^{-}\) pairs, which produce a very sharp peak at (0, 0), is usually treated as non-interesting in angular correlation analyses.Footnote 2 In this work their influence was intentionally minimized with dedicated experimental selection criteria, which remove electron–positron pairs with invariant mass \(m_{e^{+}e^{-}}<2\) MeV/c and polar angle difference \(\Delta \uptheta <0.008\) rad.
3 Analysis
The correlation function for two particles, of type “1” and type “2” (which in general may be non-identical), is expressed as the inclusive two-particle distribution \(P_{12}(\upvarphi _1,\upeta _1,\upvarphi _2,\upeta _2)\) divided by the product of the inclusive single-particle distributions \(P_1(\upvarphi _1,\upeta _1)\) and \(P_2(\upvarphi _2,\upeta _2)\) Footnote 3:
We can interpret the distribution \(P_{12}(\upvarphi _1,\upeta _1,\upvarphi _2,\upeta _2)\) as a conditional probability to observe a particle with azimuthal angle \(\upvarphi _1\) and pseudorapidity \(\upeta _1\) if a particle with azimuthal angle \(\upvarphi _2\) and pseudorapidity \(\upeta _2 \) is observed as well, and distributions \(P_1(\upvarphi _1,\upeta _1)\) and \(P_2(\upvarphi _2,\upeta _2)\) as probabilities of observing particles with \(\upvarphi _1\) and \(\upeta _1\), and \(\upvarphi _2\) and \(\upeta _2\), respectively. In the absence of correlations, the ratio should equal unity.
Therefore the experimental correlation function, including physical two-particle correlations as well as effects from single-particle acceptance, is constructed as
where \(\Delta \upeta =\upeta _1-\upeta _2\) is the difference in pseudorapidity, \(\Delta \upvarphi =\upvarphi _1 - \upvarphi _2\) is the difference in azimuthal angle, \(S(\Delta \upeta ,\Delta \upvarphi )\) is the distribution of correlated pairs and \(B(\Delta \upeta ,\Delta \upvarphi )\) is the reference distribution, reflecting the single-particle acceptance. S is constructed from particle pairs coming from the same event
where \(N_{{\textit{pairs}}}^{{\textit{signal}}}\) is the number of pairs of particles in S. B is constructed using an event mixing technique, where each particle in the pair comes from a different event and can be expressed as
where \(N_{{\textit{pairs}}}^{{\textit{mixed}}}\) is the number of pairs of particles in B. Given each of the S and B distributions are divided by the respective number of pairs, the reported distribution is a ratio of probabilities, as defined in Eq. (1).
In order to improve the reference estimation, particles from each event, selected according to Table 1, are combined with particles from other events, for which the multiplicities differ by no more than 5 tracks and primary vertex positions differ by no more than 2 cm in the beam direction. Each event is mixed with 10 events.
Each particle is weighted with a correction factor that accounts for detector acceptance, reconstruction and particle identification efficiencies, as well as contamination by secondary particles calculated using events from PYTHIA6 (Perugia-2011 tune) with particle transport performed via a GEANT3 [30] simulation of the ALICE detector. Applied corrections are \(p_\mathrm{{T}}\)-dependent and the correction method is validated on simulated events.Footnote 4 Therefore, the distributions are considered unfolded to the particle level. The contamination by secondary particles from weak decays (mostly charged and neutral \(\Xi \)) is estimated by varying the DCA cut and found to be relevant, after applying corrections, only for lambda particles. The related systematic uncertainty was calculated from the lambda sample in which the weak decay content was increased by 50%. The influence of misidentified particles was estimated by applying alternative PID methods for pions, kaons, and protons (i.e. by increasing the misidentification rate by 100%) and varying the invariant mass window for lambdas as well as by taking the misidentification fraction extracted from simulations into account.
4 Systematic uncertainty
In order to asses the systematic uncertainty connected to the measurement, the selection criteria discussed in Sect. 2 were modified and for each new set of them the analysis was repeated. The contribution from the different systematic sources were added in quadrature. The correlation functions were found to be rather insensitive to changes of selection criteria, yielding total uncertainty from about 1.5% for pions to 7.5% for lambdas. Due to different methods of particle reconstruction for neutral lambdas (\(V^0\)s) and charged pions, kaons, and protons (tracks) the calculation of systematic uncertainty for each of them was done separately.
In the case of evaluation of the tracking uncertainty for pions, kaons, and protons, an alternative track selection was used, where two classes of tracks are combined in order to avoid an azimuthally-dependent tracking efficiency due to inactive SPD modules [31]. The first class requires for tracks to have at least one hit in the SPD (as in the default track selection). For tracks which do not fulfill this criterion, in the second class, the primary vertex position is used as an additional constraint in the global track fit. To assess the systematic uncertainties related to the particle identification, the misidentification rate was doubled with respect to the values reported in Sect. 2. These uncertainties were found to be lower than 0.5% for pions, 1% for kaons, and 2% for protons. Finally, for pions, kaons, and protons separate analyses were performed for four the datasets collected, changing the single-track inefficiencies. For like-sign pairs the results were obtained separately for positive and negative particles.
The systematic uncertainty on \(V^0\) selection was evaluated by varying selection criteria discussed in Sect. 2; minimum DCA of \(V^0\) to the primary vertex, maximal DCA of daughters to the primary vertex, \(V^0\) decay length and cosine of pointing angle. Based on Pythia Perugia-2011 calculations, this increased or decreased the default content of fake \(V^0\)s in the sample of 0.7% by a factor of 2 or 3, respectively. The invariant mass window was varied in the systematic uncertainty estimation procedure to \({\pm } 0.0044\) GeV/\({c}^2\). To estimate the systematic uncertainty of feed-down from weak decays the selection on the DCA was removed, resulting in an increase in the contamination coming from secondary particles from 17 to 26%. The uncertainty of the correction procedure on PID efficiencies and contamination from secondary particles on both tracks and \(V^0\)s are discussed in Sect. 3.
Table 2 summarizes the main sources of systematic uncertainties of the measurement.
5 Results
The measured correlation functions for the four analyzed particle species (pions, kaons, protons, lambdas) are shown in Fig. 1. In the measurement of correlations in pp collisions at LHC energies a distinct near-side peak at \((\Delta \eta ,\Delta \varphi )\) about (0, 0) is observed [4, 32, 33], which is a combination of at least three effects: (i) fragmentation of hard-scattered partons, (ii) resonance decays, and (iii) femtoscopic correlations. (i) The fragmentation originating from low momentum-transfer scatterings, sometimes referred to as mini-jets [34], produces a broad structure extending at least over one unit in \(\Delta \eta \) and \(\Delta \varphi \). (ii) The decay of resonances contributes to the near-side peak of the correlation function or produces a ridge at \(\Delta \eta =0\) (extended in \(\Delta \varphi \) [4, 35, 36]), depending on the released kinetic energy of a given resonance. This effect plays a significant role only for correlation functions of unlike-sign particle pairs. (iii) The third effect, femtoscopic correlations (an enhancement due to Bose–Einstein quantum statistics for identical bosons, a suppression due to Fermi–Dirac quantum statistics for identical fermions, as well as Coulomb and strong final-state interactions), is present for particles at low relative momenta. The shape of this effect in \(\Delta \upeta \Delta \upvarphi \) depends strongly on the mass of the particle type considered, as well as on the size of the particle-emitting system. For pp collisions at ALICE this size was measured in great detail with pions [37] and kaons [38]. The expected width of the correlation peak produced by like-sign charged particles, e.g., pions, is comparable to the one for the mini-jet peak. In addition, by constraints on the energy–momentum conservation, an “away-side ridge” structure at \(\Delta \varphi =\pi \), with a magnitude only weakly changing with \(\Delta \eta \), is produced as well.
Correlation functions for identical-particle pairs: \(\pi ^{+}\pi ^{+}+\pi ^{-}\pi ^{-}\), \(\mathrm K^{+}K^{+}+K^{-}K^{-}\), \(\mathrm pp+\overline{p}\overline{p}\), \(\Lambda \Lambda +\overline{\Lambda }\overline{\Lambda }\) (left panel) and particle–anti-particle pairs: \(\pi ^{+}\pi ^{-}\), \(\mathrm K^{+}K^{-}\), \(\mathrm p\overline{p}\), \(\Lambda \overline{\Lambda }\) (right panel). Plots are mirrored around \(\Delta \eta =0\)
For correlation functions (a)–(f) in Fig. 1 the baseline reflecting the energy–momentum conservation is combined with several expected physics mechanisms. For same sign particle pairs of mesons (e)–(f), the near side peak is consistent with the mini-jet mechanism combined with the Bose–Einstein correlations. The away-side ridge is also prominent, consistent with a mini-jet origin.
The particle–anti-particle correlations (a)–(d) also show a mini-jet like structure on the near-side and a weak away-side one. For pairs of non-identical particles Bose–Einstein and Fermi–Dirac effects are not present; however, resonances play a significant role in shaping the correlation function. Baryon and meson correlations are qualitatively similar. The only difference is the magnitude and width of the near side peak, which is highest for kaons, lower for protons and lambdas, and lowest for pions. The shape and strength of the correlation functions (a distinct near-side peak) in (a)–(f) suggest that they might be dominated by significant mini-jet contributions.
In contrast to like-sign meson correlations, the baryon–baryon (combined with anti-baryon–anti-baryon) distributions for identical proton (g) and lambda (h) pairs show a qualitatively different effect of a wide near-side depression instead of the peak, combined with an away-side ridge. Such a structure resembles the one associated with the baseline global energy–momentum conservation. Thus, this strong near-side suppression means that the mechanisms which would produce a peak are either not present or produce a very different correlation shape. On the other hand, a clear correlation of particles with opposite baryon number (c) and (d) is observed, resembling the structures observed for unlike-sign mesons. Based on the results of these studies we can draw the following conclusion: if we consider a process of mini-jet fragmentation as the one producing a strong, positive near-side correlation then baryon–anti-baryon pairs are produced in mini-jets (see (c), (d)). However, producing more than one such a pair in a single fragmentation is strongly suppressed (see (g), (h)).
There are several hypotheses that could explain the depression observed for baryon–baryon pairs. First, it may be that we are seeing the effects of Fermi–Dirac statistics originating from the wave-function (anti-)symmetrization for identical baryon pairs for triplet (singlet) pair spin combinations [37, 39]. However, using an effective source size of about 1.5 fm (comparable to the measured source size for pions [37]), the repulsive effects of Fermi–Dirac statistics should be limited to baryon pairs with momentum differences of less than 200 MeV/c – a far too short range to explain our observations. The Coulomb and strong final-state interactions would also be convoluted with the quantum statistics effect (the combination of those three effects is referred to as a “femtoscopic” effect [37, 39]). In panel (g) an additional peak at (0, 0) with a height of \({\sim } 0.2\) and a width comparable to the size of a single bin is observed. The origin of that structure was studied by measuring the “femtoscopic” correlation function in momentum space and transforming it with a simple Monte Carlo procedure to \((\Delta \eta ,\Delta \varphi )\) space. Such procedure shows that this peak can be qualitatively and quantitatively reproduced by “femtoscopic” correlations mentioned above. Moreover, the Fermi–Dirac suppression cannot be present for non-identical baryon pairs, like \(\mathrm p\Lambda +\overline{p}\overline{\Lambda }\), which were also measured. The results are shown in Fig. 2. One observes that the characteristic shape of anti-correlation is preserved also in this case.
The comparison of all baryon pairs, shown as a function of \(\Delta \varphi \) and integrated over \(\Delta \eta \), can be seen in Fig. 3. The shape of the correlation function for all studied baryon–baryon (and baryon–anti-baryon) pairs is similar, regardless of particles’ electric charge. Therefore, we must reject the hypothesis that Fermi–Dirac quantum statistics is the cause of the observed depression for baryon–baryon pairs. Similar conclusions were reached based on observations of baryon production in \(\mathrm e^+e^-\) collisions, see Ref. [40]. The depression is a characteristic attribute connected solely to the baryonic nature of a particle.
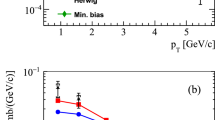
In order to check whether some fraction of the observed effect depends on the momentum transfer during the interaction, the \(\mathrm pp+\overline{p}\overline{p}\) sample was divided into two transverse momentum ranges. The correlation functions obtained with these selection criteria are shown in Fig. 4 and show even stronger anti-correlation for higher transverse momenta of particles in the pair.
An alternative interpretation of the observed depletion is that this structure is the manifestation of a local conservation of baryon number influencing the hadronization process, as argued in Ref. [40] in the analysis of \(\mathrm e^+e^-\) collisions at \(\sqrt{s}=29\) GeV. By “local” we denote the production of particles close together in the phase-space (e.g. in the same mini-jet), as opposed to “global” conservation which applies to all particles produced in an event. In string hadronization models, the “local” mechanism requires that two baryons produced in a single fragmentation are separated by at least one particle with a different baryon number [40]. The production of two baryons in a mini-jet would also be suppressed if the parton energy is small when compared with the minimum energy required to produce four baryons (2 particles + 2 anti-particles, the minimum amount to satisfy the law of local baryon number conservation when two baryons are produced in single mini-jet). At a collision energy of \(\sqrt{s}=29\) GeV it was reasonable to assume that the energy constraint would dominate. However, at LHC energies this constraint should have less of an impact on the observed structures. We tested this expectation by employing Monte Carlo generators which include local baryon number conservation: PYTHIA (6.4 and 8) and PHOJET (1.12). The results of MC simulations are discussed in the next section.
\(\Delta \eta \) integrated projections of correlation functions for combined pairs of (left) \(\mathrm pp+\overline{p}\overline{p}\), \(\mathrm p\Lambda +\overline{p}\overline{\Lambda }\), and \(\Lambda \Lambda +\overline{\Lambda }\overline{\Lambda }\) and (right) \(\mathrm p\overline{p}\), \(\mathrm p\overline{\Lambda }+\overline{p}\Lambda \), and \(\Lambda \overline{\Lambda }\). Statistical (bars) and systematic (boxes) uncertainties are plotted
Correlation functions for combined pairs of \(\mathrm pp+\overline{p}\overline{p}\) for two transverse momentum intervals a \(0.5<p_\mathrm{T} < 1.25\) GeV/c and b \(1.25<p_\mathrm{T} < 2.5\) GeV/c. Panel c shows \(\Delta \eta \) integrated projections. Statistical (bars) and systematic (boxes) uncertainties are plotted
6 Comparison to Monte Carlo models
The correlation functions measured in this work are compared to predictions of Monte Carlo (MC) models. The following MC event generators were used: PYTHIA6.4 tunes Perugia-0 and Perugia-2011 [24, 25], PYTHIA8 Monash tune [41, 42] and PHOJET version 1.12 [43]. PYTHIA, widely used for simulations of high-energy collisions, combines perturbative QCD for large momentum-transfer interactions and phenomenologically motivated models for the description of soft hadronic interactions; the Lund string fragmentation model [44] is used for hadronization. PYTHIA has many free parameters which are optimized to best describe specific measurements. These parameters are collected in predefined “tunes”. Perugia-0 was tuned for the best description of data up to \(\sqrt{s}=1.96\) TeV [25]. Perugia-2011 takes into account some of the early LHC results at \(\sqrt{s}=900\) GeV and 7 TeV, along with increased baryon production (especially of strange baryons) as well as removing suppression of strangeness in fragmentation models [25]. The PYTHIA8 Monash tune [41, 42] includes further improvements to the parameters by comparing them with both \(e^{+}e^{-}\) collisions and recent pp LHC data, including strange particle and baryon production rates. The PHOJET generator successfully describes experimental data measured at collision energies up to \(\sqrt{s}=1.8 \) TeV; however, it has not been updated to reproduce LHC data. PHOJET uses the Dual Parton Model [45] for the simulation of particle production in low-\(p_\mathrm{{T}}\) processes and thus it is interesting to consider in addition to PYTHIA. Similarly to PYTHIA, it incorporates the Lund string fragmentation model.
In Figs. 5 and 6 \(\Delta \eta \) integrated correlation function projections onto \(\Delta \varphi \), integrated over \(|\Delta \eta |<1.3\) for particle–anti-particle pairs and for particle–particle pairs (combined with anti-particle–anti-particle pairs) from four different MC calculations are compared to ALICE data.
The MC models reproduce the experimental results reasonably well for mesons. It should be noted that none of the models include quantum-statistics effects, therefore a smaller correlation strength in the near-side region is expected for correlation functions of identical particles in comparison to the experimental data. Both tunes of PYTHIA6.4, Perugia-0 and Perugia-2011, give the results which are close to the experimental data (Perugia-0 for pions and Perugia-2011 for kaons). They were also successfully used to describe the non-femtoscopic correlations underlying the Bose–Einstein statistics signal in femtoscopic measurements of identical pions [37] and identical kaons [38], respectively.
\(\Delta \eta \) integrated projections of correlation functions for a \(\pi ^+\pi ^-\), b \(\mathrm K^+K^-\), c \(\mathrm {p\overline{p}}\), and d \(\Lambda \overline{\Lambda }\) pairs obtained from ALICE data and four Monte Carlo models (PYTHIA6 Perugia-0, PYTHIA6 Perugia-2011, PYTHIA8 Monash, PHOJET) at \(\sqrt{s}=7~\hbox {TeV}\). Bottom panels show ratios of MC models to ALICE data. Statistical (bars) and systematic (boxes) uncertainties are plotted
\(\Delta \eta \) integrated projections of correlation functions for combined pairs of a \(\pi ^+\pi ^+ + \pi ^-\pi ^-\), b \(\mathrm K^+K^+ + K^-K^-\), c \(\mathrm {pp} + \overline{\mathrm{p}}\overline{\mathrm{p}}\) and d \(\Lambda \Lambda +\overline{\Lambda }\overline{\Lambda }\), obtained from ALICE data and four Monte Carlo models (PYTHIA6 Perugia-0, PYTHIA6 Perugia-2011, PYTHIA8 Monash, PHOJET). Bottom panels show ratios of MC models to ALICE data. Statistical (bars) and systematic (boxes) uncertainties are plotted
However, the models fail to reproduce baryon correlations (both particle–particle and particle–anti-particle pairs). No depression is observed for protons and lambdas for any of the studied models. Instead, a near-side peak is present for particle–particle pairs. Furthermore, additional studies were performed, concluding that the anti-correlation cannot be reproduced by tuning parameters of PYTHIA6.4. Apparently all models frequently produce two baryons close in phase-space (within the mini-jet peak). These results argue against the hypothesis that the combination of energy and baryon-number conservation is enough to explain the observed near-side anti-correlation, since both local baryon number and energy conservation laws are implemented in all studied models.
For baryons, pronounced differences are also seen for particle–anti-particle pairs; the magnitude of the near-side peak is much higher in all MC models than in ALICE data. The universality of this behaviour for all baryon pairs is further confirmed with the studies of the proton–lambda correlations, as shown in Fig. 7. The results show that \(\mathrm p\Lambda +\overline{p}\overline{\Lambda }\) correlation functions follow the trend common for all baryon–baryon pairs, and correlation functions of \(\mathrm p\overline{\Lambda }+\overline{p}\Lambda \) behave similarly to the baryon–anti-baryon correlations. The away-side correlation is similar to the experimental data for all pair combinations.
\(\Delta \eta \) integrated projection of correlation functions for combined pairs of (left) \(\mathrm p{\Lambda }+\overline{p}\overline{\Lambda }\) and (right) \(\mathrm p\overline{\Lambda }+\overline{p}\Lambda \) obtained from ALICE pp collision data and four Monte Carlo models (PYTHIA6 Perugia-0, PYTHIA6 Perugia-2011, PYTHIA8 Monash, PHOJET) at \(\sqrt{s}=7~\hbox {TeV}\). Clear anti-correlation is observed for all baryon pairs. Statistical (bars) and systematic (boxes) uncertainties are plotted
7 Conclusions
Angular correlations of identified particles were analyzed in pp collisions at \(\sqrt{s}=7\) TeV recorded with the ALICE experiment. The studies were done separately for particle/anti-particle pairs (for like-sign and unlike-sign pairs) and for four particle species (pions, kaons, protons, lambdas). A significant depression around \((\Delta \eta ,\Delta \varphi )\approx (0,0)\) is observed for the baryon–baryon and anti-baryon–anti-baryon pairs, which is not seen for baryon–anti-baryon pairs.
The analysis was complemented by Monte Carlo model calculations using the PYTHIA6.4 Perugia-0, Perugia-2011, PYTHIA8 and PHOJET (v. 1.12), two event generators designed to simulate high momentum fragmentation (i.e. jets). While the correlation functions of mesons are well-reproduced by the studied models, those of baryons in simulations are significantly different than those in collision data. The most surprising result is obtained for baryon–baryon (antibaryon–antibaryon) pairs where the models are unable to reproduce even qualitatively the depletion which is observed experimentally. In the case of baryon–antibaryon pairs the correlations are qualitatively comparable, however the simulated ones are much stronger than those observed in collision data.
The observed differences can therefore mean that either the models describe the hadronization process properly but the jet fragmentation is not the dominant mechanism involved in the production of particles found in the measured \(p_\mathrm{{T}}\) range (\(p_\mathrm{{T}}\) < 2.5 GeV/c), or the fragmentation mechanisms used in PYTHIA and PHOJET are incomplete. The latter scenario would further suggest that some additional, not yet identified mechanism must exist, which suppresses the production of more than one baryon–anti-baryon pair during a single fragmentation. Therefore, this may suggest the need to modify particle production mechanisms and/or the modification of fragmentation functions in Monte Carlo models.
Change history
10 December 2019
This document corrects two errors in Eur. Phys. J. C77 (2017) no. 8, 56: the incorrect referencing of Fig. 1 labels in three paragraphs in the results section and a missing acknowledgements section.
Notes
\(V^0\) candidate is a combination of two secondary tracks of opposite charge which have a sufficiently large impact parameter with respect to the primary vertex.
By the conservation of momentum and energy, electron positron pairs coming from gamma conversion move parallel to each other (both \(\Delta \eta \) and \(\Delta \varphi \) are equal to zero). The angular width of the peak is only slightly increased due to the detector resolution.
We note that the expression given by Eq. (1) is general and also applicable to all two-particle correlations by substituting \(\upvarphi \) and \(\upeta \) with the quantities of interest.
Correlation functions obtained from MC models after full ALICE reconstruction chain, with all corrections applied, were compared to the correlation functions obtained on the particle level. The correction procedure was tested on PYTHIA6 Perugia-0 and Perugia-2011 tunes.
References
PHOBOS Collaboration, B. Alver et al., System size dependence of cluster properties from two-particle angular correlations in Cu \(+\) Cu and Au \(+\) Au collisions at \(\sqrt{s_{{\rm {NN}}}} = 200\) GeV. Phys. Rev. C 81, 024904 (2010). doi:10.1103/PhysRevC.81.024904. arXiv:0812.1172 [nucl-ex]
STAR Collaboration, B.I. Abelev et al., Long range rapidity correlations and jet production in high energy nuclear collisions. Phys. Rev. C 80, 064912 (2009). doi:10.1103/PhysRevC.80.064912. arXiv:0909.0191 [nucl-ex]
PHOBOS Collaboration, B. Alver et al., High transverse momentum triggered correlations over a large pseudorapidity acceptance in Au \(+\) Au collisions at \(\sqrt{s_{{\rm {NN}}}}=200\) GeV. Phys. Rev. Lett. 104, 062301 (2010). doi:10.1103/PhysRevLett.104.062301. arXiv:0903.2811 [nucl-ex]
CMS Collaboration, V. Khachatryan et al., Observation of long-range near-side angular correlations in proton–proton collisions at the LHC. JHEP 09, 091 (2010). doi:10.1007/JHEP09(2010)091. arXiv:1009.4122 [hep-ex]
ATLAS Collaboration, M. Aaboud et al., Measurements of long-range azimuthal anisotropies and associated Fourier coefficients for \(pp\) collisions at \(\sqrt{s}=5.02\) and \(13\) TeV and \(p\) + Pb collisions at \(\sqrt{s_{\rm NN}}=5.02\) TeV with the ATLAS detector. arXiv:1609.06213 [nucl-ex]
CMS Collaboration, S. Chatrchyan et al., Long-range and short-range dihadron angular correlations in central PbPb collisions at a nucleon–nucleon center of mass energy of 2.76 TeV. JHEP 07, 076 (2011). doi:10.1007/JHEP07(2011)076. arXiv:1105.2438 [nucl-ex]
ATLAS Collaboration, G. Aad et al., Observation of associated near-side and away-side long-range correlations in \(\sqrt{s_{{\rm {NN}}}}=5.02\) TeV proton–lead collisions with the ATLAS detector. Phys. Rev. Lett. 110(18), 182302 (2013). doi:10.1103/PhysRevLett.110.182302. arXiv:1212.5198 [hep-ex]
ATLAS Collaboration, G. Aad et al., Measurement of long-range pseudorapidity correlations and azimuthal harmonics in \(\sqrt{s_{NN}}=5.02\) TeV proton–lead collisions with the ATLAS detector. Phys. Rev. C 90(4), 044906 (2014). doi:10.1103/PhysRevC.90.044906. arXiv:1409.1792 [hep-ex]
CMS Collaboration, S. Chatrchyan et al., Centrality dependence of dihadron correlations and azimuthal anisotropy harmonics in PbPb collisions at \(\sqrt{s_{NN}}=2.76\) TeV. Eur. Phys. J. C 72, 2012 (2012). doi:10.1140/epjc/s10052-012-2012-3. arXiv:1201.3158 [nucl-ex]
CMS Collaboration, S. Chatrchyan et al., Observation of long-range near-side angular correlations in proton–lead collisions at the LHC. Phys. Lett. B 718, 795–814 (2013). doi:10.1016/j.physletb.2012.11.025. arXiv:1210.5482 [nucl-ex]
CMS Collaboration, V. Khachatryan et al., Evidence for collectivity in pp collisions at the LHC. Phys. Lett. B 765, 193–220 (2017). doi:10.1016/j.physletb.2016.12.009. arXiv:1606.06198 [nucl-ex]
M.A. Janik, Ł.K. Graczykowski, A. Kisiel, Influence of quantum conservation laws on particle production in hadron collisions. Nucl. Phys. A 956, 886–889 (2016). doi:10.1016/j.nuclphysa.2016.02.018. arXiv:1606.09576 [hep-ph]
ALICE Collaboration, B. Abelev et al., Long-range angular correlations on the near and away side in \(p\)–Pb collisions at \(\sqrt{s_{{\rm {NN}}}}=5.02\) TeV. Phys. Lett. B 719, 29–41 (2013). doi:10.1016/j.physletb.2013.01.012. arXiv:1212.2001 [nucl-ex]
ALICE Collaboration, J. Adam et al., Forward-central two-particle correlations in p–Pb collisions at \(\sqrt{s_{\rm NN}}=5.02\) TeV. Phys. Lett. B 753, 126–139 (2016). doi:10.1016/j.physletb.2015.12.010. arXiv:1506.08032 [nucl-ex]
ALICE Collaboration, J. Adam et al., Anomalous evolution of the near-side jet peak shape in Pb–Pb collisions at \(\sqrt{s_{\rm NN}}=2.76\) TeV. arXiv:1609.06643 [nucl-ex]
ALICE Collaboration, J. Adam et al., Evolution of the longitudinal and azimuthal structure of the near-side jet peak in Pb–Pb collisions at \(\sqrt{s_{\rm NN}} = 2.76\) TeV. arXiv:1609.06667 [nucl-ex]
ALICE Collaboration, J. Adam et al., Measurement of pion, kaon and proton production in proton–proton collisions at \(\sqrt{s} = 7\) TeV. Eur. Phys. J. C 75(5), 226 (2015). doi:10.1140/epjc/s10052-015-3422-9. arXiv:1504.00024 [nucl-ex]
ALICE Collaboration, K. Aamodt et al., The ALICE experiment at the CERN LHC. JINST 3, S08002 (2008). doi:10.1088/1748-0221/3/08/S08002
M. Krivda et al., The ALICE trigger system performance for p-p and Pb-Pb collisions. JINST 7, C01057 (2012). doi:10.1088/1748-0221/7/01/C01057
ALICE Collaboration, P. Cortese et al., ALICE technical design report on forward detectors: FMD, T0 and V0
ALICE Collaboration, B.B. Abelev et al., Performance of the ALICE experiment at the CERN LHC. Int. J. Mod. Phys. A 29, 1430044 (2014). doi:10.1142/S0217751X14300440. arXiv:1402.4476 [nucl-ex]
ALICE Collaboration, B. Abelev et al., Centrality dependence of \(\pi \), K, p production in Pb–Pb collisions at \(\sqrt{s_{{\rm {NN}}}}=2.76\) TeV. Phys. Rev. C 88, 044910 (2013). doi:10.1103/PhysRevC.88.044910. arXiv:1303.0737 [hep-ex]
ALICE Collaboration, J. Adam et al., Determination of the event collision time with the ALICE detector at the LHC. Eur. Phys. J. Plus 132, 99 (2017). doi:10.1140/epjp/i2017-11279-1. arXiv:1610.03055 [physics.ins-det]
T. Sjostrand, S. Mrenna, P.Z. Skands, PYTHIA 6.4 physics and manual. JHEP 0605, 026 (2006). doi:10.1088/1126-6708/2006/05/026. arXiv:hep-ph/0603175
P.Z. Skands, Tuning Monte Carlo generators: the Perugia tunes. Phys. Rev. D 82, 074018 (2010). doi:10.1103/PhysRevD.82.074018. arXiv:1005.3457 [hep-ph]
ALICE Collaboration, B.B. Abelev et al., Long-range angular correlations of \(\uppi \), K and p in p–Pb collisions at \(\sqrt{s_{\rm NN}} = 5.02\) TeV. Phys. Lett. B 726, 164–177 (2013). doi:10.1016/j.physletb.2013.08.024. arXiv:1307.3237 [nucl-ex]
Particle Data Group Collaboration, C. Patrignani et al., Review of particle physics. Chin. Phys. C 40(10), 100001 (2016). doi:10.1088/1674-1137/40/10/100001
ALICE Collaboration, K. Aamodt et al., Strange particle production in proton–proton collisions at sqrt(s) \(=\) 0.9 TeV with ALICE at the LHC. Eur. Phys. J. C 71, 1594 (2011). doi:10.1140/epjc/s10052-011-1594-5. arXiv:1012.3257 [hep-ex]
ALICE Collaboration, B.B. Abelev et al., Multiplicity dependence of pion, kaon, proton and lambda production in p-Pb collisions at \(\sqrt{s_{NN}} = 5.02\) TeV. Phys. Lett. B 728, 25–38 (2014). doi:10.1016/j.physletb.2013.11.020. arXiv:1307.6796 [nucl-ex]
R. Brun, F. Bruyant, F. Carminati, S. Giani, M. Maire, A. McPherson, G. Patrick, L. Urban, GEANT detector description and simulation tool. CERN-W5013, CERN-W-5013, W5013, W-5013 (1994)
ALICE Collaboration, B. Abelev et al., Measurement of event background fluctuations for charged particle jet reconstruction in Pb–Pb collisions at \(\sqrt{s_{{\rm {NN}}}} = 2.76\) TeV. JHEP 03, 053 (2012). doi:10.1007/JHEP03(2012)053. arXiv:1201.2423 [hep-ex]
CMS Collaboration, V. Khachatryan et al., Measurement of long-range near-side two-particle angular correlations in pp collisions at \(\sqrt{s}=13\) TeV. Phys. Rev. Lett. 116(17), 172302 (2016). doi:10.1103/PhysRevLett.116.172302. arXiv:1510.03068 [nucl-ex]
ATLAS Collaboration, G. Aad et al., Observation of long-range elliptic anisotropies in \(\sqrt{s}=13\) and 2.76 TeV \(pp\) collisions with the ATLAS detector. Phys. Rev. Lett. 116(17), 172301 (2016). doi:10.1103/PhysRevLett.116.172301. arXiv:1509.04776 [hep-ex]
ALICE Collaboration, B.B. Abelev et al., Multiplicity dependence of jet-like two-particle correlation structures in pPb collisions at \(\sqrt{s_{{\rm {NN}}}}=5.02\) TeV. Phys. Lett. B 741, 38–50 (2015). doi:10.1016/j.physletb.2014.11.028. arXiv:1406.5463 [nucl-ex]
R. Eggert et al., Angular correlations between the charged particles produced in pp collisions at ISR energies. Nucl. Phys. B 86 (1975)
PHOBOS Collaboration, B. Alver et al., Cluster properties from two-particle angular correlations in p \(+\) p collisions at \(\sqrt{s}=200\) GeV and 410 GeV. Phys. Rev. C 75, 054913 (2007). doi:10.1103/PhysRevC.75.054913. arXiv:0704.0966 [nucl-ex]
ALICE Collaboration, K. Aamodt et al., Femtoscopy of \(pp\) collisions at \(\sqrt{s}=0.9\) and 7 TeV at the LHC with two-pion Bose–Einstein correlations. Phys. Rev. D 84, 112004 (2011). doi:10.1103/PhysRevD.84.112004. arXiv:1101.3665 [hep-ex]
ALICE Collaboration, B. Abelev et al., Charged kaon femtoscopic correlations in \(pp\) collisions at \(\sqrt{s}=7\) TeV. Phys. Rev. D 87(5), 052016 (2013). doi:10.1103/PhysRevD.87.052016. arXiv:1212.5958 [hep-ex]
STAR Collaboration, L. Adamczyk et al., Measurement of interaction between antiprotons. Nature 527, 345–348 (2015). doi:10.1038/nature15724. arXiv:1507.07158 [nucl-ex]
TPC/Two Gamma Collaboration, H. Aihara et al., Study of baryon correlations in \(e^+e^-\) annihilation at 29-GeV. Phys. Rev. Lett. 57, 3140 (1986)
T. Sjostrand, S. Mrenna, P.Z. Skands, A brief introduction to PYTHIA 8.1. Comput. Phys. Commun. 178, 852–867 (2008). doi:10.1016/j.cpc.2008.01.036. arXiv:0710.3820 [hep-ph]
P. Skands, S. Carrazza, J. Rojo, Tuning PYTHIA 8.1: the Monash 2013 tune. Eur. Phys. J. C 74(8), 3024 (2014). doi:10.1140/epjc/s10052-014-3024-y. arXiv:1404.5630 [hep-ph]
R. Engel, J. Ranft, S. Roesler, Hard diffraction in hadron hadron interactions and in photoproduction. Phys. Rev. D 52, 1459–1468 (1995)
B. Andersson, G. Gustafson, G. Ingelman, T. Sjostrand, Parton fragmentation and string dynamics. Phys. Rep. 97, 31 (1983)
A. Capella, U. Sukhatme, C.-I. Tan, J. Tran Thanh Van, Dual parton model. Phys. Rep. 236, 225–329 (1994). doi:10.1016/0370-1573(94)90064-7
Author information
Authors and Affiliations
Consortia
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Adam, J., Adamová, D., Aggarwal, M.M. et al. Insight into particle production mechanisms via angular correlations of identified particles in pp collisions at \(\sqrt{\mathrm{s}}=7\) TeV. Eur. Phys. J. C 77, 569 (2017). https://doi.org/10.1140/epjc/s10052-017-5129-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5129-6