Abstract
This study is conducted to examine the validity of the generalized second law of thermodynamics (GSLT) in flat FRW for modified teleparallel gravity involving coupling between a scalar field with the torsion scalar T and the boundary term \(B=2\nabla _{\mu }T^{\mu }\). This theory is very useful, since it can reproduce other important well-known scalar field theories in suitable limits. The validity of the first and second law of thermodynamics at the apparent horizon is discussed for any coupling. As examples, we have also explored the validity of those thermodynamics laws in some new cosmological solutions under the theory. Additionally, we have also considered the logarithmic entropy corrected relation and discuss the GSLT at the apparent horizon.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The rapid growth of observational measurements on expansion history reveals the expanding paradigm of the universe. This fact is based on accumulative observational evidence mainly from Type Ia supernova and other renowned sources [1,2,3]. The expanding phase implicates the presence of a repulsive force which compensates the attractiveness property of gravity on cosmological scales. This phenomenon may be translated as the existence of exotic matter components and most acceptable understanding for such enigma is termed dark energy (DE); it has a large negative pressure. Various DE models and modified theories of gravity have been proposed to incorporate the role of DE in cosmic expansion history (for reviews see [4,5,6]).
In contrast to Einstein’s relativity and its proposed modifications where the source of gravity is determined by curvature scalar terms, another formulation has been presented which comprises a torsional formulation as gravity source [7,8,9,10,11]. This theory is labeled TEGR (teleparallel equivalent of general relativity) and it is determined by a Lagrangian density involving a zero curvature Weitzenböck connection instead of a zero torsion Levi-Civita connection with the vierbein as a fundamental tool. The Weitzenböck connection is a specific connection which characterizes a globally flat space-time endowed with a non-zero torsion tensor. Using that connection, one can construct an alternative and equivalent theory of GR. The latter appears, since the scalar torsion only differs by a boundary term \(B=\frac{2}{e}\partial _\mu (eT^\mu )\) with the scalar curvature by the relationship \(R=-T+B\), making the two variations of the Einstein–Hilbert and TEGR actions the same. Thus, these two theories have the same field equations. However, these two theories have different geometrical interpretations, since in TEGR the torsion acts as a force; meanwhile in GR, the gravitational effects are understood due to the curved space-time. TEGR is then further extended to a generalized form by the inclusion of a f(T) function in the Lagrangian density (as f(R) is the extension of GR) and it has been tested cosmologically by numerous researchers [12,13,14]. It is important to mention that f(T) and f(R) are no longer equivalent theories, and in order to consider the equivalent teleparallel theory of f(R), one needs to consider a more generalized function f(T, B), incorporating the boundary term in the action [15]. In [16], the authors studied some cosmological features (reconstruction method, thermodynamics and stability) within f(T, B) gravity and, in [17], some cosmological solutions were found using the Noether symmetry approach. Additionally, it has been proved that when one considers Gauss–Bonnet higher order terms, an additional boundary term \(B_{G}\) (related to the contorsion tensor) needs to be introduced to find the equivalent teleparallel modified Gauss–Bonnet f(R, G) theory [18].
Later, Harko et al. [19] proposed a comprehensive form of this theory by involving a non-minimal torsion matter interaction in the Lagrangian density. In Ref. [20], Zubair and Waheed recently have investigated the validity of energy constraints for some specific f(T) models and discussed the feasible bounds of involved arbitrary parameters. They also discussed the validity of the generalized second law of thermodynamic in the cosmological constant regime [21].
Another very much studied approach in modified theories of gravity is to change the matter content of the universe by adding a scalar field in the matter sector. These models have been considered several times in cosmology, using different kinds of scalar fields such as quintessence, quintom, k-essence, etc. (see [22,23,24]). Moreover, we can also extend that idea by adding a coupling between the scalar field and the gravitational sector (see [25,26,27]) where, cosmologically speaking, we can have new interesting results such as the possibility of crossing the phantom barrier. Motivated by these theories, other interesting modified theories of gravity have also been discussed in the literature [28,29,30] on the cosmological landscape. Recently, Bahamonde and Wright [31] presented a new model of teleparallel gravity by introducing a scalar field non-minimally coupled to both the torsion T and the boundary term \(B=2\nabla _{\mu }T^{\mu }\). It is shown that such a theory can describe the non-minimal coupling to torsion and also the non-minimal coupling to scalar curvature under certain limits.
Black hole thermodynamics suggests that there is a fundamental connection between gravitation and thermodynamics [32]. Hawking radiation [33], the proportionality relation between the temperature and surface gravity, and also the connection between horizon entropy and the area of a black hole [34] support this idea. Jacobson [35] was the first to deduce the Einstein field equations from the Clausius relation, \(T_hd\hat{S}_h={\delta }\hat{Q}\), together with the fact that the entropy is proportional to the horizon area. In the case of a general spherically symmetric space-time, it was shown that the field equations can be constituted as the first law of thermodynamics (FLT) [36]. The relation between the FRW equations and the FLT was shown in [37] for \(T_h=1/2{\pi }R_A,~ S_h=\pi R_A^2/G\). The investigation of the validity of thermodynamical laws in GR as well as modified theories has been carried out by numerous researchers in the literature [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53].
In this work we focus on the validity of the thermodynamical laws in a modified teleparallel gravity involving a non-minimal coupling between both torsion scalar and the boundary term with a scalar field.
In Sect. 1, we give a brief introduction of this theory and then we derive the respective field equation for flat FRW geometry with a perfect fluid as the matter contents. In Sects. 2 and 3, we formulate the first and second law of thermodynamics at the apparent horizon for any coupling. Additionally, as examples, we study the validity of the thermodynamics laws using new cosmological solutions based on power-law and exponential-law cosmology (see Appendix A). In Sect. 4, we discuss the validity of GSLT for the entropy functional with quantum corrections. In each case, suitable limits of the parameters are chosen in order to visualize the validity of GSLT in quintessence, scalar field non-minimally coupled to torsion (known as teleparallel dark energy) and non-minimally coupled to the scalar curvature theories. Finally, in Sect. 5, a discussion of the work is presented.
In the following paper, the notation used is the same as in [31], where the tetrad and the inverse of the tetrad fields are denoted by a lower letter \(e^{a}_{\mu }\) and a capital letter \(E^{\mu }_{a}\), respectively, with the \((+,-,-,-)\) metric signature.
2 Teleparallel quintessence with a non-minimal coupling to a boundary term
In this study we consider the modified teleparallel model which involves a scalar field non-minimally coupled to the torsion T and a boundary term defined in terms of a divergence of the torsion vector, \(B=\frac{2}{e}\partial _\mu (eT^\mu )\), where \(e=\text {det}(e^{a}_{\mu })\). The action of this theory is given by
where \(L_{m}\) determines the matter contents, \(\kappa ^2=8\pi G\), \(V(\phi )\) is the energy potential and \(f(\phi )\) and \(g(\phi )\) are coupling functions. For simplicity, we will use the notation NMC-(B+T) to refer to this theory \((f(\phi )\ne g(\phi )\ne 0)\). In Ref. [31], the authors consider a special case of this action where \(f(\phi )=1+\kappa ^2\xi \phi ^2\) and \(g(\phi )=\kappa ^2\chi \phi ^2\). A non-minimally coupled scalar field with the boundary term B (NMC-B) is recovered if \(\xi =0\). Using dynamical system techniques, the cosmology in NMC-B was studied in [31]. If \(\chi =0\), we get the same action as in [25], which is known as “teleparallel dark-energy theory” (TDE). By choosing \(\chi =-\xi \) we obtain scalar field models non-minimally coupled to the Ricci scalar that hereafter, for simplicity we will label as NMC-R [26]. In addition, the so-called “Minimally coupled quintessence” theories arise when we take \(\chi =\xi =0\) [27].
Variation of the action (1) with respect to the tetrad field yields the following field equations:
where \({\Box }={\nabla }_{\alpha }{\nabla }^{\alpha };~{\nabla }_{\alpha }\) is the covariant derivative linked with the Levi-Civita connection symbol and \(\mathcal {T}^{\nu }_a\) is the matter-energy momentum tensor.
If we vary the action (1) with respect to the scalar field, that yields the following modified Klein–Gordon equation:
Throughout this paper, a prime denotes differentiation with respect to \(\phi \). We will assume the homogeneous and isotropic flat FRW metric in Euclidean coordinates defined by
where a(t) represents the scale factor and the corresponding tetrad components are \(e^i_\mu =(1,a(t),a(t),a(t))\). It is important to mention that despite f(T) gravity not being invariant under local Lorentz transformations, the latter tetrad is a “good tetrad” to consider, since it does not constrain its field equations [54]. Hence, this tetrad can be used safely within this scalar field theory too.
The energy-momentum tensor of matter is defined as
where \(u_{\mu }\) is the four velocity of the fluid and \(\rho _m\) and \(p_m\) define the matter energy density and pressure, respectively. Using the tetrad components for the flat FRW metric, the field Eq. (2) leads to
Here, \(H=\dot{a}(t)/a(t)\) is the Hubble parameter and dots and primes denote differentiation with respect to the time coordinate and the argument of the function, respectively. We can also rewrite these equations in a fluid representation,
where \(\kappa ^2_\text {eff}=\frac{\kappa ^2}{f(\phi )}\), \(\rho _\text {eff}=\rho _{m}+\rho _\phi \) is the total energy density and \(p_\text {eff}=p_{m}+p_\phi \) is the total pressure. The energy density and the pressure of the scalar field \(\rho _\phi \) and \(p_\phi \) are, respectively, defined as follows:
In this theory the standard continuity equation reads
Hereafter, we will assume a standard equation of state for the matter given by a barotropic equation \(p_{m}=w \rho _{m}\), with w being the state parameter. If we use the above equation, we can directly find that the energy density becomes
where \(\rho _{0}\) is an integration constant. It is proper to mention that, for a flat FRW metric, the torsion scalar and the boundary term are
and hence the Ricci scalar is recovered via \(R=-T+B=-12H^2-6\dot{H}\).
Finally, the equation for the scalar field, the so-called Klein–Gordon equation, takes the form
Note that the Klein–Gordon equation can also be obtained directly from the field equations (6) and (7), so that it is not an extra equation.
3 Thermodynamics in modified teleparallel theory
In this section we are interested to explore the general thermodynamic laws in the framework of the theory studied in [31], where the authors considered a quintessence theory non-minimally coupled between both a torsion scalar T and the boundary term B with the scalar field (NMC-B+T). The main aim of the next sections will be to formulate the first and second laws of thermodynamics in this theory. The complete and general thermodynamics law will be derived. After that, we will use the cosmological solutions found in Appendix A to study some interesting examples to visualize if they do or do not satisfy the thermodynamic laws.
3.1 First law of thermodynamics
This section is devoted to an investigation of the validity of the first law of thermodynamics in NMC-(B+T) at the apparent horizon for a flat FRW universe.
The condition \(h^{\alpha \beta }\partial _{\alpha }R_A\partial _{\beta }R_A=0\) gives the radius \(R_A\) of apparent horizon for flat FRW metric by
The associated temperature is \(T_h=\kappa _{sg}/2\pi \), where the surface gravity \(\kappa _{sg}\) is given by [55]
By using Eq. (9) and (III A) we easily get
Now, multiplying both sides of this equation by a factor \(-2\pi R_{A}T_{h}=1-\dot{R}_A/(2HR_A)\), we can rewrite the above equation as follows:
where we have used \(A=4\pi R_{A}^2\). Thus, we can identify the entropy as the quantity which is multiplied by \(T_{h}\), namely
Now, we define energy of the universe within the apparent horizon. The Misner–Sharp energy is defined as \(E=R_A/(2G_\mathrm{eff})\), which can be written as
In terms of the volume \(V=4\pi R_A^3/3\), we find that the energy density is given by
Taking the differential of the energy relation, we get
Combining Eqs. (19) and (17), it results in
By defining the work density, we get
Here \(\bar{T}^{(de)\alpha \beta }h_{\alpha \beta }\) is the energy density of the dark components. Using the above definition of the work density in Eq. (24), we obtain
which can be rewritten as
where \(\mathrm{d}S_p=-(R_{A}/(2GT_h))(2\pi R_AT_h-1)\mathrm{d}f(\phi )\), which is the first law of thermodynamics in this teleparallel theory. The extra term \(\mathrm{d}S_p\) defined in Eq. (27) can be treated as an entropy production term in non-equilibrium thermodynamics. In gravitational theories such as Einstein, Gauss–Bonnet and Lovelock gravities [56,57,58], the usual first law of thermodynamics is satisfied by the respective field equations. In fact, these theories do not involve any surplus term in universal form of the first law of thermodynamics, i.e., \(T\mathrm{d}S=\mathrm{d}E-W\mathrm{d}V\).
Initially Akbar and Cai used this approach to discuss thermodynamic laws in f(R) gravity [59]. It is shown that an additional entropy term is produced, to be compared to other modified theories. Later Bamba et al. [41, 42, 60, 61] developed the first law of thermodynamics in Palatini f(R), f(T), \(f(R,\phi ,X)\) (where \(X=-1/2g^{\mu \nu }\nabla _\mu \phi \nabla _\nu \phi \) is the kinetic term of a scalar field \(\phi \)) and \(f(R,\phi ,X,G)\) (where \(G=R^2-4R_{\mu \nu }R^{\mu \nu }+R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }\) is the Gauss–Bonnet invariant) theories and formulated an additional entropy production term. A similar approach is applied to discuss the thermodynamic laws in f(R, T), \(f(R,L_m)\) and \(f(R,T,R_{\mu \nu }T^{\mu \nu })\) theories, and one can see that the presence of non-equilibrium entropy production terms is necessary in such theories [46, 47, 62]. Bamba et al. [41, 42, 60, 61] have shown that one can manipulate the FRW equations in order to redefine the entropy relation, which results in an equilibrium description of thermodynamics so that the first law of thermodynamics takes the form \(T\mathrm{d}S=\mathrm{d}E-W\mathrm{d}V\). Moreover, in all these theories it has been the case that the usual form of the first law of thermodynamics, i.e., \(T\mathrm{d}S_\mathrm{eff}=\mathrm{d}E-W\mathrm{d}V\), can be obtained by defining the general entropy relation as a sum of an horizon entropy and an entropy production term.
Here, we may define the effective entropy term being the sum of horizon entropy and entropy production term as \(S_\text {eff}=S_h+S_p\) so that Eq. (27) can be rewritten as
where \(S_\text {eff}\) is the effective entropy related to the contributions involving a scalar field non-minimally coupled to the torsion T and a boundary term at the apparent horizon of FRW space-time.
3.2 Generalized second law of thermodynamics
According to the generalized second law of thermodynamic (GSLT), the entropy of matter and energy sources inside the horizon plus the entropy associated with a boundary of the horizon must be non-decreasing. In the previous section we have shown that the usual first law of thermodynamics does not hold in this theory. Therefore, to study GSLT, we would use the modified first law of thermodynamics. In fact the generalized entropy relation satisfies the condition
where \(\dot{S}_h\) represents the entropy associated with the horizon, \(\dot{S}_p\) represents the entropy production term and \(\dot{S}_\mathrm{in}\) is the sum of all entropy components inside the horizon.
Let us proceed with the modified first law of thermodynamics,
which can be represented as
where \(R_h\) represents the radius of the horizon, \(T_\mathrm{in}\) denotes the temperature for all the components inside the horizon and \(Q_i\) is an interaction term for the ith component. Summing up the total entropy inside the horizon, we find
Here,
Now, let us study the validity of GSLT at the apparent horizon. In de Sitter space-time \(R_A=1/H\) and the future event horizon becomes the same as the Hubble horizon. The time derivative of (20) results in
Here, we set the thermal equilibrium with \(T_\mathrm{in}=T_h\), so that Eq. (32) implies
After simplification, we get
Hence, Eq. (29) implies the relation of GSLT of the form
In the following sections we will see if the GSLT is satisfied for some interesting cosmological solutions that can be constructed from our solutions found before (see Sects. A.1–A.3).
3.2.1 Specific model: power-law solutions for \(f(\phi )=1+\xi \kappa ^2 \phi ^2\) and \(g(\phi )=\chi \kappa ^2\phi ^2\)
In this section we will analyze if the GSLT is valid for different power-law models. In Sect. A.1, we found some specific solutions to the specific coupling \(f(\phi )=1+\xi \kappa ^2 \phi ^2\) and \(g(\phi )=\chi \kappa ^2 \phi ^2\). Here, we will focus our study for quartic (\(m=-1\)) and inverse potentials (\(m=2/3\)). Additionally, by setting the coupling constants \(\xi \) and \(\chi \), we will also focus our study on different non-minimally coupled scalar–tensor theories.
(a) Power-law potential with \(\chi \ne \frac{1}{4}\)
For this case, the energy potential reads
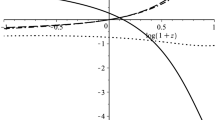
In Fig. 1, we present the evolution of energy density \(\rho \) and potential \(V(\phi )\) for the power-law case. It can be seen that \(V(\phi )\) is a decreasing function of time, where we set \(\xi \le 0\).
Here, we set the validity condition for GSLT in terms of the parameters m, \(\xi \) and \(\chi \). We choose m to show the particular representation of potential.
(b) Case \(m=-1\)
This choice of m corresponds to a quartic potential, \(V(\phi )\propto \phi ^4\). Here, we find the relation for n of the form \(n=\frac{1-6\chi }{6\xi +\chi }\) and the constraint \(n>1\) results in the following condition:
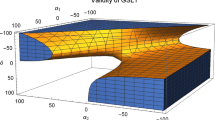
Here, we discuss the specific cases NMC-B (\(\xi =0\)) and TDE (\(\chi =0\)). The validity of GSLT for a quartic potential is shown in Fig. 2. For NMC-B theory, the GSLT is valid in the range \(0< \chi < \frac{1}{12}\) and in the case of TDE we need \(0<\xi <\frac{1}{6}\). These constraints are set in accordance with the condition of power-law solutions, \(n>1\).
We also the evolution of GSLT in Fig. 3, where we set \(n=2\) and choose the particular values for \(\chi \) and \(\xi \). The black curve corresponds to NMC-B with \(\chi =\frac{1}{18}\) and the blue curve represents the plot of GSLT for TDE with \(\xi =\frac{1}{18}\).
(c) Case \(m=2/3\)
In this case one can recover the inverse potential i.e., \(V(\phi )\propto \phi ^{-1}\). Here, we show the validity of GSLT in Figs. 4 and 5. In Fig. 4, the left plot corresponds to NMC-B, which shows the validity in the range \(-\frac{1}{8}< \chi < 0\) and the right plot corresponds to TDE with \(-\frac{2}{3}< \xi < 0\). It can be seen that GSLT is violated in case of TDE, whereas it is valid in both NMC-B and NMC-R.
Left plot shows the validity of GSLT in NMC-R for \(0< \xi < \frac{2}{13}\) and right plot sums up the validity in the case of inverse potential. The curves for NMC-B (\(\chi =\frac{-1}{17}\)), TDE (\(\xi =\frac{-1}{3}\)) and NMC-R (\(\xi =\frac{1}{14}\)) are represented by solid, dashed and dotted lines, respectively
(d) Power-law potential with \(\chi =\frac{1}{4}\)
For this case the potential takes the following form:
For this model, we have a fixed value of \(\chi \), so we cannot discuss the TDE and NMC-B theories. In the case of NMC-R (\(\chi =-\xi \)), we find that this representation does not show realistic results as we need to fix \(n<0\) for inverse and quadratic potentials.
Moreover, in the case of NMC-(B+R), we explore the validity for quartic potential, where we need to set \(\xi =\frac{-(3n+1)}{12n}\). Finally, we have GSLT dependence on n, and validity is shown in Fig. 6.
3.2.2 Specific model: exponential solutions for \(f(\phi )=1+\kappa ^2\alpha e^{m\phi }\) and \(g(\phi )=\kappa ^2\beta e^{k\phi }\)
This section is devoted to an analysis of the question if the GSLT is satisfied for some exponential solutions found in Sect. A.3. Since mostly all the solutions are similar, we will only analyze the case where \(w=\tfrac{2-\phi _{0}}{3n}-1\) (see Sect. A.3.2). In this case, the energy potential contains three exponentials that can represent different kind of potentials. For example, by taking \(m=\tfrac{\sqrt{3} \kappa \phi _0}{\sqrt{2(\phi _0-1)}}\), we find
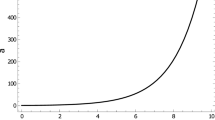
which is known as a double exponential potential. This kind of potential has been widely studied in the literature. From Fig. 7, it is observed that the scalar potential increases as the field increases. Thus the cosmic acceleration will be driven by the potential energy of the scalar field.
Another interesting example that can be constructed is by taking \(\phi _{0}=4\) and \(\alpha =\tfrac{24 \kappa ^2-m^2}{48 \kappa ^4}\), which gives us the following potential:
which is an interesting kind of potential studied in the literature (see [63, 64]). The exponential function models generally lead to an accelerating expansion behavior of the universe.
Let us now study the GSLT for this kind of potential. In this model, Eq. (36) becomes
where for simplicity we took \(\kappa =G=1\). Clearly, the above inequality will hold depending on the values of the parameters \(\phi _{0},n\) and \(\alpha \). Since \(n>1\), if \(\phi _{0}\ge -2\) and \(\alpha >0\), GSLT will be valid at any time. Additionally, if \(\phi _{0}\le -2\) and \(\alpha <0\), the GSLT will be always true. For all the other cases, the validity of GSLT will depend on time. Figures 8 and 9 show the behavior of the GSLT inequality for different values of the parameters. For \(\phi _{0}>0\) and \(\alpha <0\), the inequality will be more constrained for bigger \(|\phi _{0}|\). Additionally, it can be seen that GSLT will be always true at very late times for \(-2<\phi _{0}<0\).
4 Generalized second law of thermodynamics with logarithmic entropy corrections
The entropy–area relation involving quantum corrections leads to curvature corrections in the Einstein–Hilbert action [65, 66]. The logarithmic corrected entropy is defined through the relation [67,68,69,70]
where \(\alpha \), \(\beta \) and \(\gamma \) are dimensionless constants; however, the exact values of these constants are yet to be determined. These corrections arise in black hole entropy in loop quantum gravity due to thermal equilibrium fluctuations and quantum fluctuations [71, 72]. In [70] Sadjadi and Jamil investigated the validity of GSLT for FRW space-time with logarithmic correction. They found that in a (super-) accelerated universe the GSL is valid whenever \(\alpha (<)>0\), leading to a (negative) positive contribution from logarithmic correction to the entropy. In the following section, we will present the validity of the GSLT with modified entropy relations involving logarithmic corrections.
First note that the time derivative of Eq. (41) yields
In the case of the apparent horizon, Eq. (41) implies
Here, we used the fact that the Hubble horizon is \(R_A=1/H\). Now, by using Eqs. (35) and (43), we get
which can be represented in terms of effective components as follows:
The GSL with quantum corrections have natural implications in the studies of the very early universe since quantum corrections are directly linked with high energy and short distance scales.
5 Conclusions
The non-minimally coupling models in cosmology are frequently used to study guaranteed late time acceleration, phantom crossing and the existence of finite time future singularity. In this paper, the thermodynamic study is executed in modified teleparallel theory which involves scalar field non-minimally coupled to both the torsion and a boundary term [31]. One interesting factor in this theory is that in a suitable limit, one can recover very well-known theories of gravity such as quintessence, teleparallel dark energy and non-minimally coupled scalar field with the Ricci scalar R.
In this paper, we investigated the GSLT for an expanding universe with apparent horizon. The laws of thermodynamics are universally valid and hence they must apply in a modified form to the whole universe. The existence of an apparent horizon in a space-time provides the opportunity to formulate the first law and the generalized second law of thermodynamics. According to the laws of thermodynamics, the first law must always be true for a physical system (provided it is non-dissipative); however, the GSLT holds exactly using the apparent horizon. We obtained these laws in the non-minimal coupled teleparallel theory with a boundary term and a scalar field. Our results generalize many previous GSLT studies, while extending them to the logarithmic corrected entropy–area law. Moreover, GSLT with quantum corrections have natural implications in the studies of the very early universe, since quantum corrections are directly linked with high energy and short distance scales.
We explored the existence of power-law solutions for two different choices of Lagrangian coefficients, which are functions of the scalar field, \(f(\phi )\) and \(g(\phi )\). In the first case we set \(f(\phi )=1+\kappa ^2\xi \phi ^2\) and \(g(\phi )=\kappa ^2\chi \phi ^2\) and choose the power-law forms of scale factor and scalar field to discuss possible forms of the power-law potential \(V(\phi )\) (see [28]). Here, one can recover the quadratic, quartic, inverse and Ratra–Peebles potentials. We also discuss the Brans–Dicke theory as a particular case in power-law cosmology. Moreover, we also discuss the power-law solutions for the choice of \(f(\phi )=1+\kappa ^2\alpha e^{m\phi }\) and \(g(\phi )=\kappa ^2\beta e^{k\phi }\) with \(\phi (t)=\frac{\phi _0}{m}\log (t)\). Here, we explored different forms of \(V(\phi )\) depending on the equation of state parameter.
We showed the behavior of matter density \(\rho \) and potential \(V(\phi )\) for the power-law potential; it can be seen that both are decreasing functions of time as shown in Fig. 1. In our discussion of the validity of GSLT, we considered the quartic and inverse potentials in all the viable special cases like TDE, NMC-B, NMC-R and NMC-(B+R) and presented results in Figs. 2, 3, 4, 5 and 6. In Figs. 2 and 3, we found that GSLT is true for NMC-B (with \(0<\xi <\frac{1}{6}\)) and TDE (with \(0<\chi <\frac{1}{12}\)). For the inverse potential, we find that GSLT is valid for NMC-B (with \(\frac{-1}{8}<\chi <0\)) and TDE (with \(-\frac{2}{3}<\xi <0\)), whereas it is violated for TDE, as shown in Figs. 4 and 5. For the choice of \(\chi =\frac{1}{4}\), we found the validity region only in the case of NMC-(B+R) with \(n>\frac{1}{2}\) as shown in Fig. 6. For the exponential forms of the Lagrangian coefficients, we found that GSLT is always true for (\(\phi _0\le -2\) & \(\alpha <0\)) and (\(\phi _0\ge -2\) & \(\alpha >0\)), whereas for other choices of the parameters the validity of GSLT is time dependent. Finally, we also formulated the GSLT for logarithmic entropy corrections.
References
S. Perlmutter et al., Astrophys. J. 483, 565 (1997)
S. Perlmutter et al., Nature 391, 51 (1998)
A.G. Riess et al., Astrophys. J. 607, 665 (2004)
V. Sahni, Lect. Notes Phys. 653, 141 (2004)
M. Sharif, M. Zubair, Int. J. Mod. Phys. D 19, 1957 (2010)
K. Bamba, S. Capozziello, S. Nojiri, S.D. Odintsov, Astrophys. Space Sci. 342, 155 (2012)
Einstein, A., Sitzungsber. Preuss. Akad. Wiss. Phys. Math. KI. 217 (1928)
Einstein, A., Sitzungsber. Preuss. Akad. Wiss. Phys. Math. KI. 224 (1928)
K. Hayashi, Phys. Rev. D 19, 3524 (1979)
H.I. Arcos, J.G. Pereira, Int. J. Mod. Phys. D 13, 2193 (2004)
J.W. Maluf, Ann. Phys. 525, 339 (2013)
R. Ferraro, F. Fiorini, Phys. Rev. D 75, 084031 (2007)
G.R. Bengochea, R. Ferraro, Phys. Rev. D 79, 124019 (2009)
E.V. Linder, Phys. Rev. D 81, 127301 (2010)
S. Bahamonde, C.G. Böhmer, M. Wright, Phys. Rev. D 92(10), 104042 (2015)
S. Bahamonde, M. Zubair, G. Abbas. arXiv:1609.08373 [gr-qc]
S. Bahamonde, S. Capozziello. Eur. Phys. J. C 77, 107 (2017). doi:10.1140/epjc/s10052-017-4677-0
S. Bahamonde, C.G. Böhmer, Eur. Phys. J. C 76(10), 578 (2016)
T. Harko, F.S.N. Lobo, G. Otalora, E.N. Saridakis, Phys. Rev. D 89, 124036 (2014)
M. Zubair, S. Waheed, Astrophys. Space Sci. 355, 361 (2015)
M. Zubair, S. Waheed, Astrophys. Space Sci. 360, 68 (2015)
E.J. Copeland, M. Sami, S. Tsujikawa, Dynamics of dark energy. Int. J. Mod. Phys. D 15, 1753 (2006). arXiv:hep-th/0603057
C. Armendariz-Picon, V.F. Mukhanov, P.J. Steinhardt, Phys. Rev. D 63, 103510 (2001)
Y.F. Cai, E.N. Saridakis, M.R. Setare, J.Q. Xia, Phys. Rept. 493, 1 (2010)
C.Q. Geng, C.C. Lee, E.N. Saridakis, Y.P. Wu, Phys. Lett. B. 704, 384 (2011)
F. Perrotta, C. Baccigalupi, S. Matarrese, Phys. Rev. D 61, 023507 (1999)
O. Bertolami, P.J. Martins, Phys. Rev. D 61, 064007 (2000)
O. Chandia, J. Zanelli, Phys. Rev. D 55, 7580 (1997)
G. Kofinas, E.N. Saridakis, Phys. Rev. D 90, 084044 (2014)
G. Kofinas, E.N. Saridakis, Phys. Rev. D 90, 084045 (2014)
S. Bahamonde, M. Wright, Phys. Rev. D 92, 084034 (2015)
J.M. Bardeen, B. Carter, S.W. Hawking, Commun. Math. Phys. 31, 161 (1973)
S.W. Hawking, Commun. Math. Phys. 43, 199 (1975)
J.D. Bekenstein, Phys. Rev. D 7, 2333 (1973)
T. Jacobson, Phys. Rev. Lett. 75, 1260 (1995)
T. Padmanabhan, Phys. Rept. 406, 49 (2005)
R.G. Cai, S.P. Kim, JHEP 02, 050 (2005)
C. Eling, R. Guedens, T. Jacobson, Phys. Rev. Lett. 96, 121301 (2006)
M. Akbar, R.G. Cai, Phys. Lett. B 648, 243 (2007)
Y. Gong, A. Wang, Phys. Rev. Lett. 99, 211301 (2007)
K. Bamba, C.Q. Geng, JCAP 06, 014 (2010)
K. Bamba, C.Q. Geng, JCAP 11, 008 (2011)
S.-F. Wu, B. Wang, G.-H. Yang, P.-M. Zhang, Class. Quant. Gravit. 25, 235018 (2008)
M.R. Setare, Phys. Lett. B 641, 130 (2006)
M.R. Setare, JCAP 01, 123 (2007)
M. Sharif, M. Zubair, J. Cosmol. Astropart. Phys. 11, 042 (2013)
M. Sharif, M. Zubair, Adv. High Energy Phys. 2013, 947898 (2013)
Zubair, M., Jawad, A., 360, 11 (2015)
M. Zubair, F. Kousar, S. Bahamonde, Phys. Dark Univ. 14, 116 (2016)
H. Mohseni Sadjadi, Phys. Rev. D 76, 104024 (2007)
M. Jamil, E.N. Saridakis, M.R. Setare, JCAP 1011, 032 (2010)
K. Bamba, M. Jamil, D. Momeni, R. Myrzakulov, Astrophys. Space Sci. 344, 259 (2013)
U. Debnath, S. Chattopadhyay, I. Hussain, M. Jamil, R. Myrzakulov, Eur. Phys. J. C 72, 1875 (2012)
N. Tamanini, C.G. Boehmer, Phys. Rev. D 86, 044009 (2012)
R.G. Cai, S.P. Kim, JHEP 02, 050 (2005)
M. Akbar, R.G. Cai, Phys. Rev. D 75, 084003 (2007)
R.G. Cai, L.M. Cao, Nucl. Phys. B 785, 135 (2007)
R.G. Cai, L.M. Cao, Y.P. Hu, JHEP 08, 090 (2008)
M. Akbar, R.G. Cai, Phys. Lett. B 635, 7 (2006)
K. Bamba, C.Q. Geng, S. Tsujikawa, Phys. Lett. B 688, 101109 (2010)
K. Bamba, C.Q. Geng, S. Nojiri, S.D. Odintsov, EPL 89, 50003 (2010)
M. Sharif, M. Zubair, J. Cosmol. Astropart. Phys. 03, 028 (2012)
V. Sahni, A.A. Starobinsky, Int. J. Mod. Phys. D 9, 373 (2000)
T. Matos, L.A. Urena-Lopez, Phys. Rev. D 63, 063506 (2001)
T. Zhu, J.-R. Ren, Eur. Phys. J. C 62, 413 (2009)
R.-G. Cai et al., Class. Quant. Gravit. 26, 155018 (2009)
S.K. Modak, Phys. Lett. B 671, 167 (2009)
M. Jamil, M.U. Farooq, JCAP 03, 00 (2010)
S. Das, U. Debnath, A.A. Mamon. arXiv:1510.02573v1
H.M. Sadjadi, M. Jamil, Europhys. Lett. 92, 69001 (2010)
C. Rovelli, Phys. Rev. Lett. 77, 3288 (1996)
A. Ashtekar, J. Baez, A. Corichi, K. Krasnov, Phys. Rev. Lett. 80, 904 (1998)
V. Pettorino, C. Baccigalupi, G. Mangano, JCAP 0501, 014 (2005). doi:10.1088/1475-7516/2005/01/014. arXiv:astro-ph/0412334
Acknowledgements
S.B. is supported by the Comisión Nacional de Investigación Científica y Tecnológica (Becas Chile Grant No. 72150066). The authors would like to thank the anonymous referee for the interesting feedback and useful comments on the paper.
Author information
Authors and Affiliations
Corresponding author
New cosmological solutions
New cosmological solutions
1.1 Power-law solutions for \(f(\phi )=1+\kappa ^2\xi \phi ^2\) and \(g(\phi )=\kappa ^2\chi \phi ^2\)
In this section we are going to find analytical power-law solutions for the NMC-(B+T) case where the coupling functions are
where \(\xi \) and \(\chi \) are coupling constants. As we discussed before, for this specific choice we can recover NMC-B (\(\xi =0\)), TDE (\(\chi =0\)), NMC-R (\(\xi =-\chi \)) and quintessence theories (\(\chi =\xi =0\)). Let us now study power-law cosmology where the scale function and the scalar field take a power-law form
where \(a_{0}\), \(\phi _{0}\), m and n are constants. Under these ansatzes, from (6) we directly find that the energy potential becomes
Now, by replacing the above expression in (7) we find that the parameters need to satisfy
Since \(n\ne 0\), the exponents of the scalar field of the first and second terms on the r.h.s. must match otherwise the above equation will not hold. Therefore, the state parameter needs to be
Using this condition, Eq. (A6) becomes
This condition will be true for different choices of the parameters. For simplicity, we will assume the case that \(a_{0}=1\), which gives
Thus, the energy potential (A5) and the energy density are simplified to
For the first potential (\(\chi \ne 1/4\)), we can recover a self-interacting scalar field case \(V(\phi )\propto \phi ^4\) if \(m=-1\), which is the case where the coupling parameters satisfied \(\xi =\tfrac{-6 n \chi -6 \chi +1}{6n}\). It corresponds to the inverse potential if \(m=2/3\) with the additional constraint \(\xi =-\frac{2(1-\chi +9n\chi )}{3n}\) and the Ratra–Peebles potential is recovered by choosing \(0<m <1\).
1.2 Power-law solutions for Brans–Dicke: \(f(\phi )=\kappa ^2\xi \phi ^2\) and \(g(\phi )=\kappa ^2\chi \phi ^2\)
It is easy to see that if we choose
our action becomes a Brans–Dicke one in a canonical form with the Brans–Dicke parameter being \(w_{BD}=1\). The latter theory has been widely studied in the literature, so that it is an important coupling to consider.
To find solutions, we will follow the same approach as the previous section. Moreover, since the equations are so similar, we will not state all the steps. It is easy to see that if \(w=-1+\frac{2 (1-m)}{3 n}\ne -1\) we obtain the following solutions:
1.3 Exponential solutions for \(f(\phi )=1+\kappa ^2\alpha e^{m\phi }\) and \(g(\phi )=\kappa ^2\beta e^{k\phi }\)
In this section, we will assume that the coupling functions are exponential:
where \(\alpha \), \(\beta \), m and k are parameters. The cosmology for the specific case where \(\beta =-\alpha \) and \(k=m\) was studied in [73]. Additionally, we assume that the scale factor and the scalar field behave as
where \(n,m,\phi _{0}\) and \(a_{0}\) are constants. By using (6), we find that the energy potential becomes
Now, if we replace this equation in (7), we find that
needs to hold. For the specific case where \(\rho _{0}\ne 0\), we have three possibles cases for the state parameter,
Now, we will explore all the possible solutions under these state parameters. In general, all the solutions are very similar but they are not exactly the same.
1.3.1 Case 1: \(w=\frac{2 m-k \phi _0}{3 m n}-1\)
For this special case, from (A20) the other parameters must satisfy (\(k\ne 2m\))
Note that for the case \(k=2m\) we find that \(n=1/3\), which is not allowed. Hence, if \(k\ne 2m\) we find that the energy density and energy potential for the first state parameter, \(w_{1}\), are given by
The special case of non-minimal coupling with the Ricci scalar can be obtained by taking \(k=m\) and \(\beta =-\alpha \), which makes the potential become
1.3.2 Case 2: \(w=\frac{2-\phi _0}{3 n}-1\)
For this case, we need to have \(\phi _0\ne 2\) and also from (A20) the parameters must obey
and hence the energy density and the potential take the following form:
1.3.3 Case 3: \(w= -1\) (dark-energy fluid)
For a dark-energy fluid with \(w=-1\), from (A20) the parameters need to be
and therefore the energy density is a constant \(\rho _{0}\) and the potential becomes
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Zubair, M., Bahamonde, S. & Jamil, M. Generalized second law of thermodynamic in modified teleparallel theory. Eur. Phys. J. C 77, 472 (2017). https://doi.org/10.1140/epjc/s10052-017-5043-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-5043-y