Abstract
Using a novel analysis technique, the gluon polarisation in the nucleon is re-evaluated using the longitudinal double-spin asymmetry measured in the cross section of semi-inclusive single-hadron muoproduction with photon virtuality \(Q^2>1~(\mathrm{GeV}/c)^2\). The data were obtained by the COMPASS experiment at CERN using a 160 GeV/c polarised muon beam impinging on a polarised \(^6\)LiD target. By analysing the full range in hadron transverse momentum \(p_\mathrm{T}\), the different \(p_\mathrm{T}\)-dependences of the underlying processes are separated using a neural-network approach. In the absence of pQCD calculations at next-to-leading order in the selected kinematic domain, the gluon polarisation \(\Delta g/g\) is evaluated at leading order in pQCD at a hard scale of \(\mu ^2= \langle Q^2 \rangle = 3 (\mathrm{GeV}/c)^2\). It is determined in three intervals of the nucleon momentum fraction carried by gluons, \(x_\mathrm{g}\), covering the range \(0.04 \!<\! x_{ \mathrm g}\! <\! 0.28\) and does not exhibit a significant dependence on \(x_\mathrm{g}\). The average over the three intervals, \(\langle \Delta g/g \rangle = 0.113 \pm 0.038_\mathrm{(stat.)}\pm 0.036_\mathrm{(syst.)}\) at \(\langle x_\mathrm{g} \rangle \approx 0.10\), suggests that the gluon polarisation is positive in the measured \(x_\mathrm{g}\) range.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The experimental observation by EMC [1, 2] that quark spins contribute only a small fraction to the spin of the nucleon initiated a lot of new developments in spin physics (for a review see e.g. Ref. [3]). In order to investigate the origin of the nucleon spin, it is essential to also determine the contribution of gluons, \(\Delta g\). Information about this quantity can be obtained indirectly by studying scaling violations in the spin-dependent structure function \(g_1\) (see Refs. [4,5,6,7] and references therein) or directly by measurements of the gluon polarisation \(\Delta g/g\) in polarised lepton–nucleon or proton–proton interactions (see Refs. [8,9,10,11,12,13,14,15,16,17,18]). Indirect determinations of \(\Delta g\) suffer from poor accuracy due to the limited kinematic range, in which the structure function \(g_1\) is measured. Most recent direct determinations by fits performed in the context of perturbative Quantum Chromodynamics (pQCD) at next-to-leading order (NLO) in the strong coupling constant [19, 20], which include proton-proton data from RHIC, suggest that the gluon polarisation is positive in the measured range of the nucleon momentum fraction carried by gluons, \(0.05<x_\mathrm{g}<0.20\).
In deep inelastic scattering (DIS), the leading-order virtual-photon absorption process (LP) does not provide direct access to the gluon distribution since the virtual photon does not couple to the gluon. Therefore, higher-order processes have to be studied, i.e. QCD Compton scattering (QCDC) and Photon–Gluon Fusion (PGF), where only the latter is sensitive to the gluon helicity distribution. The diagrams for these two processes are shown in Fig. 1 together with that of the leading-order photon absorption process.
In the leading-order process, the (small) transverse momentum of the produced hadron originates from the intrinsic transverse momentum of the quark that was struck in the nucleon [21] and the transverse momentum generated by the fragmentation of this quark. Here, transverse is meant relative to the virtual-photon direction in a frame where the nucleon momentum is parallel to this direction. The hard QCDC and PGF processes, on the contrary, can provide hadrons with high transverse momentum. Therefore, including in the analysis events with hadrons of large transverse momentum \(p_\mathrm{T}\) enhances the contribution of higher-order processes. In earlier analyses, the contributions from LP and QCDC had to be subtracted in order to determine \(\Delta g/g\) [22]. A different approach is used in the present analysis, i.e. a simultaneous extraction of \(\Delta g/g\) and of the LP and QCDC asymmetries is performed using data that cover the full range in \(p_\mathrm{T}\). This “all-\(p_\mathrm{T}\) method” takes advantage of the different \(p_\mathrm{T}\)-dependences of the three processes in order to disentangle their contribution to the measured asymmetry. Furthermore, this approach reduces systematic uncertainties with respect to the one used previously [11]. In this paper, we re-analyse the semi-inclusive deep inelastic scattering (SIDIS) data from COMPASS [11], applying the new all-\(p_\mathrm{T}\) method.
2 Experimental set-up and data sample
The COMPASS experiment is a fixed-target setup at the M2 beam line of the CERN SPS. The data used in this analysis were collected during 4 years: 2002 to 2004 and 2006. For these measurements, longitudinally polarised positive muons were scattered off a large polarised solid-state \(^6\)LiD target. A detailed description of the experiment can be found elsewhere [23]. A major upgrade of the COMPASS spectrometer was performed in 2005. For this analysis, the most relevant improvement was a new target magnet that extended the angular acceptance from \(\pm 70\) mrad to \(\pm 180\) mrad.
The average muon momentum was 160 GeV/c and the average beam polarisation was \(\langle P_\mathrm{b} \rangle =-0.80\pm 0.04\). The target material consisted of \(^6\)LiD beads in a bath of \(^3\)He-\(^4\)He and was contained in two target cells in 2002–2004 and in three cells in 2006. The achieved target polarisation \(P_\mathrm{t}\) was about ±0.50 with a relative uncertainty of 5%. Neighbouring target cells were polarised in opposite directions. In order to cancel acceptance effects and to reduce systematic uncertainties, the direction of the polarisation was reversed three times per day in 2002–2004 and once per day in 2006. The fact that not all nucleons in the target material are polarisable is taken into account in the so-called effective dilution factor f. It is given by the ratio of the total cross section for muons on polarisable deuterons to the one on all nuclei taking into account their relative abundance in the target material. Its value includes a correction factor \(\rho = \sigma _\mathrm{d}^{1 \gamma } / \sigma _\mathrm{d}^\mathrm{tot}\) [24] accounting for radiative events on unpolarised deuterons and a correction factor for the relative polarisation of deuterons bound in \(^6\)Li compared to free deuterons. The dilution factor depends on the Bjorken scaling variable \(x_\mathrm{Bj}\) and on the energy fraction y carried by the exchanged virtual-photon; its average value for this analysis is about 0.37 with a relative uncertainty of 5%.
The data used for this analysis are selected by requiring an event to have an interaction vertex located within the target fiducial volume. An incoming and a scattered muon must be associated to this vertex. Moreover, the extrapolated trajectory of the incoming muon has to fully traverse all target cells to assure that they all are exposed to the same beam flux. In order to select DIS events, the photon virtuality is required to be \(Q^2>1~(\mathrm{GeV}/c)^2\). Events with \(y < 0.1\) or \(y > 0.9\) are rejected because the former are more sensitive to time instabilities of the spectrometer, while the latter are strongly affected by radiative effects. With these y limits, the squared invariant mass of the hadronic system, \(W^2\), is larger than \(5~(\mathrm{GeV}/c)^2\). For a semi-inclusive single-hadron measurement, at least one charged hadron has to be associated to the vertex together with incoming and scattered muons. For the hadron with the highest \(p_\mathrm{T}\), the requirement 0.05 GeV/c \(<p_\mathrm{T}<2.5\) GeV/c has to be fulfilled. Here, the lower limit excludes electrons from \(\gamma \) conversion and the upper limit is discussed in Sect. 4. In order to suppress diffractive processes (mainly \(\rho ^{0}\) production), events are not accepted if they have exactly two oppositely charged hadrons with \(z_1 + z_2 > 0.95\), where \(z_i\) is the energy fraction of hadron i with respect to the energy of the virtual photon.
Compared to the previous analysis [11], there are two major differences in the data selection process. First, at least one hadron instead of two hadrons is required in the final state. Second, the smallest \(p_\mathrm{T}\)-value allowed for the hadron leading in \(p_\mathrm{T}\) is lowered from 0.7 GeV/c to 0.05 GeV/c. After having applied all above described selection criteria, about 116 million events remain for the present analysis.
3 Determination of \(\Delta g/g\)
The predicted number of events \(N^\mathrm{pre}(x_\mathrm{Bj})\) can be calculated from the SIDIS cross sections of the three processes LP, QCDC, and PGF using the experimental acceptance a, the number n of scattering centres in the target, the integrated beam flux \(\Phi \), and the unpolarised cross section \(\sigma _0\) as
Here, the PGF part contains the gluon polarisation \(\Delta g/g\). The two symbols \(A_1^\mathrm{LP}\) and \(A_1^\mathrm{QCDC}\) denote the same asymmetry;Footnote 1 the distinction is only kept to emphasise the fact that in the new method there are two estimators of the same quantity. This fact will be used in some systematic studies presented in Sect. 5. In Eq. (1), the predicted number of events depends only on the Bjorken scaling variable \(x_\mathrm{Bj}\), as all other variables are integrated over the experimental kinematic domain. The label \(i\in \{ \mathrm{LP, QCDC, PGF} \}\) will be used to denote the three processes depicted in Fig. 1. Each process has a characteristic nucleon momentum fraction: \(x_\mathrm{LP} \equiv x_\mathrm{Bj}\), \(x_\mathrm{QCDC} \equiv x_\mathrm{C}\), \(x_\mathrm{PGF} \equiv x_\mathrm{g}\). For a given \(x_\mathrm{Bj}\), the corresponding nucleon momentum fractions carried by quarks in the QCDC process, \(x_\mathrm{C}\), and by gluons in the PGF process, \(x_\mathrm{g}\), are in general larger, and their values depend on the kinematics of the event. For each process i, the relative contribution is denoted by \(R_i\) and the analysing power \(a_\mathrm{LL}^i\) is given by the asymmetry of the partonic cross Sect. [25]. The analysing power is proportional to the depolarisation factor D that represents the fraction of the muon polarisation transferred to the virtual photon, where for LP holds \(a_\mathrm{LL}^\mathrm{LP}=D\).
Equation (1) is valid at leading order (LO) in pQCD assuming spin-independent fragmentation. A possible spin dependence of the fragmentation process [26] can be neglected in the COMPASS kinematic region. Equation (1) can be written in a more concise form as
Here, \(\alpha = a n \Phi \sigma _0\), \(\beta _i =fP_\mathrm{b} P_\mathrm{t}a_\mathrm{LL}^i R_i\) and \(\langle \beta _i A^i(x_i) \rangle \) denotes the average of \(\beta _i A^i(x_i)\) over the experimental kinematic domain. For simplicity of notation, a possible \(x_i\) dependence of \(\beta _i\) is omitted in Eq. (2).
The data were taken simultaneously for the upstream (u) and downstream (d) target cells, in which the material was polarised longitudinally in opposite directions. For the 2006 data taking, the label u refers to the two outer cells and d to the central cell. The directions of the polarisation were periodically reversed; the configuration before and after a reversal will be denoted by (u, d) and \((u',d')\), respectively. For a stable apparatus it is expected that \(\alpha _u/\alpha _{d}=\alpha _{u'}/\alpha _{d'}\). The data sample is divided into 40 periods, over which the apparatus is indeed found to be stable. Independent analyses are performed in each of these periods and the final result is obtained as weighted average of the 40 single ones.
The gluon polarisation \(\Delta g/g\) is evaluated using the set of four equations obtained from Eq. (1) for the four possible configurations of target cells and polarisation directions (\(k=u\), d, \(u'\), \(d'\)). The process fractions \(R_i\), the momentum fractions \(x_\mathrm{C}\), \(x_\mathrm{g}\), and the analysing powers \(a^\mathrm{QCDC}_\mathrm{LL}\), \(a^\mathrm{PGF}_\mathrm{LL}\) are determined using Monte Carlo (MC) simulations. In the previous analysis [11], the asymmetry \(A_1^\mathrm{LP}\) was evaluated from the inclusive lepton–nucleon asymmetry \(A_\mathrm{LL}^\mathrm{incl}\) . In this analysis, \(A_1^\mathrm{LP}\) is extracted simultaneously with \(\Delta g/g\) from the same data.
The method applied here was introduced in Ref. [27] and already used for a determination of the gluon polarisation using open-charm events [12]. Its main advantage is that it allows for an elegant and less CPU intensive way to obtain near optimal statistical uncertainty (in the sense of Cramer-Rao bound [28, 29]) in a multidimensional analysis.
In order to extract simultaneously the signal \(\Delta g/g\) and the background asymmetries \(A_1^\mathrm{LP}\) and \(A_1^\mathrm{QCDC}\), the event yields are considered separately for the three processes i. Moreover, since \(\Delta g/g\), \(A_1^\mathrm{LP}\), and \(A_1^\mathrm{QCDC}\) are known to be \(x_i\) dependent, the analysis is performed in bins of the corresponding variable \(x_i\), which are indexed by m.
For each configuration \(k=u\), d, \(u'\), \(d'\) we calculate weighted ‘predicted’ and ‘observed’ event yields, \(\mathcal {N}_{i_m,k}^\mathrm{pre}\) and \(\mathcal {N}_{i_m,k}^\mathrm{obs}\), respectively. Using the weight \(w=fP_\mathrm{b}a_\mathrm{LL}R\), the observed weighted yield of events for process i in the \(m{\mathrm{th}}\) bin of \(x_i\) is given by summing the corresponding weights \(w_{i,n}\):
The sum runs over \(N_k\), the number of events observed for configuration k, and \(\varepsilon _{m,i}\) is equal to 1 if for a given event its momentum fraction \(x_i\) falls into the \(m{\mathrm{th}}\) bin, and zero otherwise. The target polarisation is not included in the weight because its value changes with time. Since one knows only the probabilities \(R_i\) that the event originated from a particular partonic process, each event contributes to all three event yields \(\mathcal {N}_{\mathrm{PGF}_m,k}^\mathrm{obs}\), \(\mathcal {N}_{\mathrm{QCDC}_{m'},k}^\mathrm{obs}\), and \(\mathcal {N}_{ \mathrm{LP}_{m''},k}^\mathrm{obs}\). The correlation between these events yields is taken into account by the covariance matrix \(cov_{i_m j_{m'},k}=\sum _{n=1}^{N_k} \varepsilon _{m,i} \varepsilon _{m'\!,j} w_{i,n} w_{j,n}\).
The predicted weighted yield of events of each type, \(\mathcal {N}_{i_m,k}^\mathrm{pre}\), is approximated by
where \(\alpha _{k,w_{i_m}}\) is the weighted value of \(\alpha _k\) and
Here, the above confirmed assumption \(\alpha _{u,w_{i_m}}/ \alpha _{d,w_{i_m}}\) = \(\alpha _{{u'},w_{i_m}}/ \alpha _{{d'},w_{i_m}}\) is used as well as the additional assumption \(\langle \beta _j A^j(x_j) \rangle \simeq \langle \beta _j \rangle \langle A^{j}(x_j) \rangle \). Knowing the number of observed and predicted events as well as the covariance matrix, the standard definition of \(\chi ^2\) is used, \( \chi ^2= ( \pmb {\mathcal {N}}^\mathrm{\mathbf obs} - \pmb {\mathcal {N}}^\mathrm{\mathbf pre})^ T cov^{-1} ( \pmb {\mathcal {N}}^\mathrm{\mathbf obs} - \pmb {\mathcal {N}}^\mathrm{\mathbf pre})\), where \(\pmb {\mathcal {N}}^\mathrm{\mathbf obs}\) and \(\pmb {\mathcal {N}}^\mathrm{\mathbf pre}\) are vectors with the components \(\mathcal {N}_{i_m,k}^\mathrm{obs}\) and \(\mathcal {N}_{i_m,k}^\mathrm{pre}\), respectively. The values of \(\Delta g/g\), \(A_1^\mathrm{LP}\) and \(A_1^\mathrm{QCDC}\) are obtained by minimisation of \(\chi ^2\) using the programme MINUIT [30]. The HESSE method from the same package is used to calculate the uncertainties. In the present analysis we use 12 bins in \(x_\mathrm{Bj}\), 6 in \(x_\mathrm{C}\) and 1 or 3 bins in \(x_\mathrm{g}\). In the COMPASS kinematic region holds \(x_\mathrm{C} \gtrapprox 0.06\), so that the same binning can be used for \(x_\mathrm{C}\) as for the six highest bins in \(x_\mathrm{Bj}\). In order to further constrain \(\Delta g/g\), one can eliminate several parameters from the fit by using the relation \(A_1^\mathrm{LP}(x) = A_1^\mathrm{QCDC}(x)\). The presented equality does not hold for individual events, but only for classes of events, i.e. there are LP events with \(x_\mathrm{Bj}=0.10\) and there are QCDC events with \(x_\mathrm{C}=0.10\), for which \(x_\mathrm{Bj}\) is usually much smaller than 0.10 . Note that for a given event only the probability is known, to which class it belongs. Hence even if the above equality is used in the analysis, any event will be still characterised by different values of \(x_\mathrm{Bj}\) and \(x_\mathrm{C}\) in addition to \(x_\mathrm{g}\).
The data used for this analysis is almost entirely dominated by the LP process, as the required lower limit for \(p_T\) is as small as 0.05 GeV/c. It thus provides to the applied \(\chi ^2\) minimisation procedure enough lever-arm for a separation between the LP and PGF processes, which allows for a simultaneous extraction of their asymmetries. As a result, a significant reduction of both statistical and systematic uncertainties is achieved when comparing to Ref. [11]. The proposed method was fully tested using MC data, with given \(A_1^\mathrm{LP}\) and \(\Delta g/g\) as input parameters.
The presented method to extract \(\Delta g/g\) is model dependent. In order to facilitate possible future NLO analyses of \(\Delta g/g\), we also calculate the model-independent longitudinal double-spin asymmetries in the cross section of semi-inclusively measured single-hadron muoproduction, \(A^\mathrm{h}_\mathrm{LL}\). They are extracted in bins of \(x_\mathrm{Bj}\) and \(p_\mathrm{T}\) of the hadron leading in \(p_\mathrm{T}\) and are available in Appendix A. We note that these asymmetries are not used directly in the all-\(p_\mathrm{T}\) method presented in this paper.
4 Monte Carlo simulation and neural network training
The DIS dedicated LEPTO event generator [31] (version 6.5) is used to generate Monte Carlo (MC) events using the unpolarised cross sections of the three processes involved. A possible contribution from resolved photon processes, not described in LEPTO, is small in [11] and hence neglected.
The generated events are processed by the detector simulation programme COMGEANT (based on GEANT3) and reconstructed in the same way as real events by the reconstruction programme CORAL. The same data selection is then applied to real and MC events. In Ref. [32] it was found that simulations with the two hadron-shower models available in GEANT3, i.e. GHEISHA and FLUKA, give inconsistent results in the high-\(p_\mathrm{T}\) region. Hence events are included in the present analysis only, if the hadron leading in \(p_\mathrm{T}\) has \(p_\mathrm{T}\) \(<2.5\) GeV/c.
The best description of the data in terms of data-to-MC ratios for kinematic variables is obtained when using LEPTO with the parton shower mechanism switched on, the fragmentation-function tuning as described in Ref. [11], and the PDF set of MSTW08LO\(_\mathrm{3fl}\) from Ref. [33] together with the \(F_L\)-function option from LEPTO. A correction for radiative effects as described in Ref. [24] is applied. In Fig. 2, real and MC data are compared for the lepton variables \(x_\mathrm{Bj}\), \(Q^2\), y and for \(p_\mathrm{T}\), \(p_\mathrm{L}\) and z of the hadron leading in \(p_\mathrm{T}\). Here, \(p_L\) denotes the longitudinal component of the hadron momentum. The Monte Carlo simulation describes the data reasonably well over the full phase space. The largest discrepancy is observed for low values of \(p_\mathrm{T}\), where the LP process is dominant so that this region has only limited impact on the extracted \(\Delta g/g\) value. The best description of the data in terms of data-to-MC ratios is the reason to select the above described MC sample for the extraction of the final \(\Delta g/g\) value.
For a given set of input parameters, a neural network (NN) is trained to yield the corresponding expectation values for the process fractions \(R_i\), the momentum fractions \(x_i\) and the analysing powers \(a^i_\mathrm{LL}\). The input parameter space is defined by \(x_\mathrm{Bj}\), \(Q^2\) and by \(p_\mathrm{L}\), \(p_\mathrm{T}\) of the hadron leading in \(p_\mathrm{T}\). The NETMAKER tool kit from Ref. [34] is used in the analysis.Footnote 2 In the case that a clear distinction between the ‘true’ MC value and its NN parametrisation is needed, for the latter one the superscript ‘NN’ will be added to the symbol denoting this variable, e.g. \(x_\mathrm{g}^\mathrm{NN}\). An example of the quality of the NN parametrisation is given in the top panels of Fig. 3. It shows ‘true’ probabilities for LP, QCDC and PGF events as a function of \(p_\mathrm{T}\) and the NN probabilities obtained for the same MC data. While the LP probability falls with increasing \(p_\mathrm{T}\), QCDC and PGF probabilities rise with comparable strength. Another NN quality test is presented in the bottom panels of Fig. 3, where MC samples are selected in bins of the \(R_i\) values returned by the NN, which corresponds to the probability that the given event is of the process type i. Using the true MC information, it is possible to verify the generated fraction of each process i in the selected samples. A very good correlation is visible between NN output and the true MC composition.
5 Systematic studies
With respect to the analysis method used in Ref. [11], two contributions to the systematic uncertainty are eliminated, i.e. the one related to the \(x_\mathrm{C}\) approximationFootnote 3 and the one related to the parametrisation of \(A_{1,\mathrm{d}}^\mathrm{incl}\). The former approximation is simply not present in the current method of \(\Delta g/g\) extraction, and the latter input is not needed as \(A^\mathrm{LP}\) is extracted from the same data set simultaneously with \(\Delta g/g\). The other major contributions to the total systematic uncertainty are re-evaluated in the current analysis. These are the limit on experimental false asymmetries, \(\delta _\mathrm{false}\), the uncertainty related to the usage of MC in the analysis, \(\delta _\mathrm{MC}\), the impact of using a neural network to obtain the results, \(\delta _\mathrm{NN}\), and the uncertainty that is obtained by combining those of beam and target polarisations and of the dilution factor, which is denoted as \(\delta _{P_\mathrm{b}\!P_\mathrm{t}\!\mathrm{f}}\). All these contributions to the systematic uncertainty are given in Table 1 for the \(\Delta g/g\) results obtained in the full \(x_\mathrm{g}\) range and for those obtained in three bins of \(x^\mathrm{NN}_\mathrm{g}\). The systematic uncertainty of the \(\Delta g/g\) result, \(\delta _{syst.}\), is calculated as quadratic sum of the contributions \(\delta _\mathrm{false}\), \(\delta _\mathrm{MC}\), \(\delta _\mathrm{NN}\), and \(\delta _{P_\mathrm{b}\!P_\mathrm{t}\!f}\).
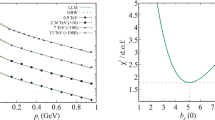
Left panel Extracted values of \(\Delta g/g\) and their statistical uncertainties for eight different MC simulations. A digit ‘1’ at a certain position in the 5-digit code shown on the ordinate means that the corresponding simulation parameter was used differently as compared to the code 00000 simulation that was used for the extraction of the final \(\Delta g/g\) results. The meaning of the digits is as follows (from left to right): 1st choice of the fragmentation functions tuning; 2nd usage of PS mechanism (here 0 means ON); 3rd choice of PDF; 4th usage of \(F_L\) function from LEPTO (here 0 means ON); 5th choice of a program to simulate secondary interactions. Right panel The results of the \(\chi ^2\) scan of \(\eta _\mathrm{QCDC}\), see text for details
The false asymmetries are related to the stability of the spectrometer. The contribution of \(\delta _\mathrm{false}=0.029\) is somewhat larger than that obtained in the previous analysis [11], where it was additionally assumed that false asymmetries are independent of \(p_T\).Footnote 4 The obtained uncertainty represents the difference between the final value of \(\Delta g/g\) and the one obtained in a separate determination, in which the phase space region at low \(x_\mathrm{Bj}\), low \(p_\mathrm{T}\) and high z, which contributes to less than 5% of the data sample, was removed from the analysis. The values of \(A^{h}_\mathrm{LL}\) obtained from this region are found to be different from those obtained in the main part of the phase space. From the detailed investigation of this discrepancy no clear conclusion could be drawn whether it is a sign of an interesting physics effect appearing in this specific region of phase space, or it might be attributed to possible instabilities of the spectrometer. It appears worth noting that the removal of this specific phase space region from the analysis results in a value of \(\Delta g/g\) that is larger by 0.029, albeit with very similar statistical uncertainties.
Although the present analysis depends on the MC model used, the uncertainty \(\delta _\mathrm{MC}\) is found to be small. It is evaluated by exploring the parameter space of the model using eight different MC simulations. These eight simulations differ by the tuning of the fragmentation functions (COMPASS High-\(p_\mathrm{T}\) [11] or LEPTO default), and by using or not using the parton shower (PS) mechanism, which also modifies the cut-off schemes used to prevent divergences in the LEPTO cross-section calculation [31]. Also, different PDF sets are used (MSTW08L or CTEQ5L [35]), the longitudinal structure function \(F_L\) from LEPTO is used or not used and alternatively FLUKA or GEISHA is used for the simulation of secondary interactions. Two observations are made when inspecting Fig. 4. The first one is that for the eight different MC simulations the resulting values of \(\Delta g/g\) are very similar; the root mean square (RMS) of the eight values, which is taken to represent \(\delta _{MC}\), amounts to only 0.017. The second observation is that the eight statistical uncertainties vary by up to a factor of two.
The explanation for the second observation is that, in a good approximation, the statistical uncertainty of \(\Delta g/g\) is proportional to \(1/R_\mathrm{PGF}\). As in the eight different MC simulations the values of \(R_\mathrm{PGF}\) can vary by up to a factor two, large fluctuations of statistical uncertainties of \(\Delta g/g\) are observed in Fig. 4. The observation of a small RMS value can be understood by the following consideration. We start by using an equivalent of Eq. (1) from Ref. [11], which is re-written for the one-hadron case. Taking into account the experimental fact that the \(A_\mathrm{LL}^{h}\) asymmetry weakly depends upon \(p_\mathrm{T}\), the left-hand side of the obtained equation is effectively cancelled by the second term on the right-hand side, which approximately corresponds to \(A_\mathrm{LL}\) obtained in the low \(p_\mathrm{T}\) region that is dominated by LP. Under these assumptions \(\Delta g/g\) is approximately given by
The value of \(A_1^\mathrm{LP}\) at \(\langle x_\mathrm{C} \rangle =0.14\) is \(\approx 0.087\), while the value of \((a_\mathrm{LL}^\mathrm{QCDC} R_\mathrm{QCDC})/(a_\mathrm{LL}^\mathrm{PGF} R_\mathrm{PGF} )\) is \(\approx 1.5\), resulting in \(\Delta g/g \approx 0.13\). This value is not very different from the result of the full analysis presented in Sect. 6, which justifies the usage of Eq. (6) for the explanation of the small RMS. The values of \(a_\mathrm{LL}^\mathrm{PGF}\) and \(a_\mathrm{LL}^\mathrm{QCDC}\) in Eq. (6) are quite stable with respect to the MC simulation used. As \(a_\mathrm{LL}^\mathrm{PGF}\) depends mostly on \(Q^2\) and y, which as inclusive variables are not affected by switching parton showers on or off nor by different fragmentation tunes, it is very similar in all eight MC simulations. A similar consideration is valid for \(a_\mathrm{LL}^\mathrm{QCDC}\), which depends mostly on y. The ratio \(R_\mathrm{QCDC}/R_\mathrm{PGF}\) is known more precisely than e.g. the ratio \(R_\mathrm{LP}/R_\mathrm{PGF}\) or \(R_\mathrm{PGF}\) itself.Footnote 5 One reason here is that both QCDC and PGF are treated in NLO, so that the strong coupling constant cancels in the cross-section ratio. In addition, the hadron \(p_\mathrm{T}\) in both processes is dominated by the partonic cross section calculable in LO pQCD and not by the fragmentation process, for which the parameters were tuned.
The usage of a neural-network method leads to a systematic uncertainty \(\delta _\mathrm{NN}=0.007\). This uncertainty is estimated based on the spread of \(\Delta g/g\) values obtained from several NN parametrisations. These parametrisations are obtained by varying internal parameters of the NN training algorithm.
The relative systematic uncertainties of the beam and target polarisation as well as of the dilution factor are estimated to be 5% each. Contrary to the method used in Ref. [11], in the all-\(p_\mathrm{T}\) method the systematic uncertainty \(\delta _{P_\mathrm{b}\!P_\mathrm{t}\!f}\) is proportional to the extracted value of \(\Delta g/g\). Therefore, it is evaluated to be 0.010 . The systematic uncertainties due to radiative corrections, due to the resolved-photon contribution, and due to remaining contributions from diffractive processes are estimated to be small and can hence be safely neglected.
In the present analysis method, \(A_1^\mathrm{LP}\) and \(A_1^\mathrm{QCDC}\) are two estimators of the same quantity. This fact allows us to perform additional consistency checks of the MC model used in the analysis, which were not possible in the analysis method used in Ref. [11]. The validity of the assumption \(A_1^\mathrm{LP}(x)=A_1^\mathrm{QCDC}(x)\) can be verified by performing a standard \(\chi ^2\) test. A possible failure of a \(\chi ^2\) test may indicate the use of incorrect \(R_i\) and/or \(a^i_\mathrm{LL}\) values in the analysis. This could happen if the MC tuning used in the analysis is wrong, or e.g. higher-order corrections are substantial. Such a consistency check was performed for all eight MC samples, yielding a \(\chi ^2\) value between 3.9 and 13.1 for 6 degrees of freedom. For the MC simulation used to obtain the quoted \(\Delta g/g\) value, \(\chi ^2= 8.1\) was found, which means that the values of \(A_1^\mathrm{QCDC}\) and \(A_1^\mathrm{LP}\) are compatible. Furthermore, one can also directly change the values of e.g. \(a_\mathrm{LL}^\mathrm{QCDC} R_\mathrm{QCDC}\) obtained from NN, and by checking the compatibility of the two \(A_1\) values verify the consistency of data and MC model. In the simplest test, we have added a multiplicative factor \(\eta _\mathrm{QCDC}\) to the MC value of \(a_\mathrm{LL}^\mathrm{QCDC} R_\mathrm{QCDC}\) and calculated the \(\chi ^2\) value of the compatibility test as a function of \(\eta _\mathrm{QCDC}\). As seen in the right panel of Fig. 4, the minimum value of \(\chi ^2\) is obtained for \(\eta _\mathrm{QCDC} \approx 1\), which supports the validity of the MC model.
The new results for \(\Delta g/g\) in three \(x_\mathrm{g}\) bins compared to results of Ref. [11] (left panel) and world data on \(\Delta g/g\) extracted in LO [8,9,10, 12] (right panel). The inner error bars represent the statistical uncertainties and the outer ones the statistical and systematic uncertainties combined in quadrature. The horizontal error bars represent the \(x_\mathrm{g}\) interval in which 68% of the MC events are found
The present analysis method assumes that \(A_1^\mathrm{LP}\) and \(\Delta g/g\) are independent of \(p_\mathrm{T}\). We have verified that if different minimum \(p_\mathrm{T}\) cuts between 0.05 GeV / c and 1 GeV/c are used in the data selection, the extracted values of \(A_1^\mathrm{LP}\) and \(\Delta g/g\) are compatible within statistical uncertainties with the final results when taking into account the correlations between data samples. It is worth noting that this \(p_\mathrm{T}\) scan in addition verifies that the removal of the region, in which the largest discrepancy between real and MC data is observed, does not bias the \(\Delta g/g\) result. Similarly, in another test it was verified that compatible \(\Delta g/g\) values are obtained with or without the cut \(p_\mathrm{T}<2.5\) GeV/c.
6 Results
The re-evaluation of the gluon polarisation in the nucleon, yields
which is obtained at an average hard scale \(\mu ^2 = \langle Q^2 \rangle = 3\) (GeV/c)\(^2\). In the analysis, a correction is applied to account for the probability that the deuteron is in a D-wave state [36]. The presented value of the gluon polarisation was obtained assuming the equality of \(A_1^\mathrm{LP}(x)\) and \(A_1^\mathrm{QCDC}(x)\). In the kinematic domain of the analysis, the average value of \(x_\mathrm{g}\), weighted by \(a_\mathrm{LL}^\mathrm{PGF} w_\mathrm{PGF}\), is \(\langle x_\mathrm{g} \rangle \approx 0.10\). In case \(\Delta g/g\) can be approximated by a linear function in the measured region of \(x_\mathrm{g}\), the obtained values of \(\langle \Delta g/g \rangle \) correspond to the value of \(\Delta g/g\) at this weighted average value of \(x_\mathrm{g}\). The obtained value of \(\Delta g/g\) is positive in the measured \(x_\mathrm{g}\) range and almost \(3 \sigma _\mathrm{stat}\) from zero. A similar conclusion is reached in the NLO pQCD fits [19, 20], which include recent RHIC data. The result of the present analysis agrees well with that of the previous one [11], which was obtained from the same data (\(\Delta g/g= 0.125 \pm 0.060 \pm 0.065\)). This comparison shows that the re-analysis using the new all-\(p_\mathrm{T}\) method leads to a reduction of the statistical and systematic uncertainty by a factor of 1.6 and 1.8, respectively.
The gluon polarisation is also determined in three bins of \(x_\mathrm{g}^\mathrm{NN}\), which correspond to three ranges in \(x_\mathrm{g}\). These ranges are partially overlapping due to an about 60% correlation between \(x_\mathrm{g}\) and \(x^\mathrm{NN}_\mathrm{g}\), which arises during the NN training. The result on \(\Delta g/g\) in three bins of \(x_\mathrm{g}^\mathrm{NN}\) are presented in Table 2. Within experimental uncertainties, the values do not show any significant dependence on \(x_\mathrm{g}\). Note that the events in the three bins of \(x_\mathrm{g}^\mathrm{NN}\) are statistically independent. In principle, for each \(x_\mathrm{g}^\mathrm{NN}\) bin one could extract simultaneously \(\Delta g/g\) and \(A_1^\mathrm{LP}\) in 12 \(x_\mathrm{Bj}\) bins, resulting in 36 \(A_1^\mathrm{LP}\) and three \(\Delta g/g\) values. However, in order to minimise the statistical uncertainties of the obtained \(\Delta g/g\) values, for a given \(x_\mathrm{Bj}\) bin only one value of \(A_1^\mathrm{LP}\) is extracted instead of three. As a result of such a procedure, a correlation between the three \(\Delta g/g\) results may arise from the fit. Indeed, a 30% correlation is found between \(\Delta g/g\) results obtained in the first and second \(x_\mathrm{g}^\mathrm{NN}\) bins. The correlations of the results between the first or second and the third \(x_\mathrm{g}^\mathrm{NN}\) bin are found to be consistent with zero.
Left panel Comparison of the LO results of the present analysis with the latest NLO QCD fit results from COMPASS [37]. Otherwise as in Fig. 5. Right panel Extracted values of \(A_{1,\mathrm{d}}^\mathrm{LP}(x_\mathrm{Bj})\) and \(A_{1,\mathrm{d}}^\mathrm{incl}\) from [6, 38]. Here, only statistical uncertainties are shown
A comparison of published [11] and present results is shown in the left panel of Fig. 5. In addition to a clear reduction of the statistical uncertainties, a small shift in the average value of \(x_\mathrm{g}\) is observed, which originates from using slightly different data selection criteria in the all-\(p_\mathrm{T}\) analysis and also from differences between the two methods. In the right panel of Fig. 5, the new results are compared with the world results on \(\Delta g/g\) extracted in LO analyses [8,9,10, 12], and good agreement is observed. The new COMPASS results have the smallest combined statistical and systematic uncertainty.
The left panel of Fig. 6 shows the present results, which are obtained at LO, in comparison to the most recent COMPASS NLO \(\Delta g/g\) parametrisation [37]. The present results support solutions that yield positive values of \(\Delta G\) in the NLO fit. Note that this comparison does not account for differences between LO and NLO analyses.
For completeness, in the right panel of Fig. 6 the extracted values of \(A_{1,\mathrm{d}}^\mathrm{LP}(x_\mathrm{Bj})\) are shown as full points. They are consistent with zero at low \(x_\mathrm{Bj}\) and rise at higher \(x_\mathrm{Bj}\). The LP process measured in this analysis is the dominating contribution to the inclusive asymmetry \(A_{1,\mathrm{d}}^\mathrm{incl}\), and the values of \(A_{1,\mathrm{d}}^\mathrm{LP}\) and \(A_{1,\mathrm{d}}^\mathrm{incl}\) show very similar trends, as expected. The values of \(A_{1,\mathrm{d}}^\mathrm{incl}\) for \(x_\mathrm{Bj}<0.3\) are from Ref. [38], while those for \(x_\mathrm{Bj}>0.3\) are from Ref. [6].
7 Conclusions
Using COMPASS data on semi-inclusively measured single-hadron muoproduction off deuterium for a re-evaluation of the gluon polarisation in the nucleon yields at LO in pQCD \(\langle \Delta g/g \rangle = 0.113 \pm 0.038_\mathrm{(stat.)} \pm 0.036_\mathrm{(syst.)}\) for a weighted average of \(\langle x_\mathrm{g} \rangle \approx 0.10\) and an average hard scale of 3 (GeV/c)\(^2\). This result is compatible with and supersedes our previous result [11] obtained from the same \(Q^2 > 1\) (GeV/c)\(^2\) data. It favours a positive gluon polarisation in the measured \(x_\mathrm{g}\) range. The novel ‘all-\(p_\mathrm{T}\) method’ employed in the present analysis leads to a considerable reduction of both statistical and systematic uncertainties, which is due to the cancellation of some uncertainties in the simultaneous determination of \(\Delta g/g\) and \(A_{1,\mathrm{d}}^\mathrm{LP}\).
Notes
They are also equal to \(A_1^\mathrm{LO}(x)\) in Eq. (1) of Ref. [11].
A feed-forward multi-layer perceptron neural network is selected with the cost function defined by the mean squared difference between expected output value and its neural network parametrisation.
i.e. \(x_\mathrm{C}=x_\mathrm{C'}\) in Eq. (3) of Ref. [11].
This assumption, when used in the current analysis, would lead to a much lower value of \(\delta _\mathrm{false}\) than previously. This is due to the simultaneous extraction of \(\Delta g/g\) and \(A_1^{LP}\), which are both affected by the same spectrometer instabilities, thereby eliminating relative contributions to \(\delta _\mathrm{false}\).
Note that the large instability of \(R_\mathrm{PGF}\) itself explains the large variation of the statistical uncertainty of \(\Delta g/g\).
References
EMC Collaboration, J. Ashman et al., Phys. Lett. B 206, 364 (1988)
EMC Collaboration, J. Ashman et al., Nucl. Phys. B 328, 1 (1989)
C.A. Aidala, S.D. Bass, D. Hasch, G.K. Mallot, Rev. Mod. Phys. 85, 655 (2013)
SMC Collaboration, B. Adeva et al., Phys. Rev. D 58, 112002 (1998)
E155 Collaboration, P.L. Anthony et al., Phys. Lett. B 493, 19 (2000)
COMPASS Collaboration, V.Yu. Alexakhin et al., Phys. Lett. B 647, 8 (2007)
HERMES Collaboration, A. Airapetian et al., Phys. Rev. D 75, 012007 (2007)
SMC Collaboration, B. Adeva et al., Phys. Rev. D 70, 012002 (2004)
COMPASS Collaboration, E.S. Ageev et al., Phys. Lett. B 633, 25 (2006)
HERMES Collaboration, A. Airapetian et al., J. High Energy Phys. 1008, 130 (2010)
COMPASS Collaboration, C. Adolph et al., Phys. Lett. B 718, 922 (2013)
COMPASS Collaboration, C. Adolph et al., Phys. Rev. D 87, 052018 (2013)
STAR Collaboration, L. Adamczyk et al., Phys. Rev. D 89, 012001 (2014)
PHENIX Collaboration, A. Adare et al., Phys. Rev. D 90, 012007 (2014)
PHENIX Collaboration, A. Adare et al., Phys. Rev. D 84, 012006 (2011)
STAR Collaboration, L. Adamczyk et al., Phys. Rev. Lett. 115, 092002 (2015)
PHENIX Collaboration, A. Adare et al., Phys. Rev. Lett. 106 (2011) 062001
STAR Collaboration, L. Adamczyk et al., Phys. Rev. Lett. 113, 072301 (2014)
D. de Florian, R. Sassot, M. Stratmann, W. Vogelsang, Phys. Rev. Lett. 113, 012001 (2014)
E.R. Nocera, R.D. Ball, S. Forte, G. Ridolfi, J. Rojo, Nucl. Phys. B 887, 276 (2014)
P. Renton, W.S.C. Williams, Ann. Rev. Nucl. Sci. 31, 193 (1981)
A. Bravar, D. von Harrach, A. Kotzinian, Phys. Lett. B 421, 349 (1998)
COMPASS Collaboration, P. Abbon et al., Nucl. Instrum. Methods A 577, 455 (2007)
A.A. Akhundov, DYu. Bardin, L. Kalinovskaya, T. Riemann, Fortschr. Phys. 44, 373 (1996)
A. Bravar, K. Kurek, R. Windmolders, Comput. Phys. Commun. 105, 42 (1997)
A. Kotzinian, Eur. Phys. J. C 44, 211 (2005)
J. Pretz, J.-M. Le Goff, Nucl. Instrum. Methods A 602, 594 (2009)
H. Cramer, Mathematical Methods of Statistics (Princeton University Press, Princeton, NJ, 1946)
C.R. Rao, Bull. Calcutta Math. Soc. 37, 81 (1945)
F. James, M. Roos, Comput. Phys. Commun. 10, 343 (1975)
G. Ingelman, A. Edin, J. Rathsman, Comput. Phys. Commun. 101, 108 (1997)
COMPASS Collaboration, C. Adolph et al., Phys. Rev. D 88, 091101 (2013)
A.D. Martin, W.J. Stirling, R.S. Thorne, G. Watt, Eur. Phys. J. C 64, 653 (2009)
R. Sulej, NetMaker. http://www.ire.pw.edu.pl/~rsulej/NetMaker/. Accessed 16 Mar 2017
CTEQ Collaboration, H.L. Lai et al., Eur. Phys. J. C 12, 375 (2000)
R. Machleidt et al., Phys. Rep. 149, 1 (1987)
COMPASS Collaboration, C. Adolph et al., Phys. Lett. B 753, 18 (2016)
COMPASS Collaboration, M. Alekseev et al., Phys. Lett. B 680, 217 (2009)
COMPASS Collaboration, E.S. Ageev et al., Phys. Lett. B 612, 154 (2005)
Acknowledgements
We gratefully acknowledge the support of the CERN management and staff and the skill and effort of the technicians of our collaborating institutes. This work was made possible thanks to the financial support of our funding agencies.
Author information
Authors and Affiliations
Consortia
Appendix A
Appendix A
Using the same data sample as used for the \(\Delta g/g\) analysis, which is described in this paper, also the longitudinal double-spin asymmetry \(A^\mathrm{h}_\mathrm{LL}\) is evaluated in a two-dimensional \(12 \times 5\) binning in \(x_\mathrm{Bj}\) and the transverse momentum of the hadron leading in \(p_\mathrm{T}\). The same 12 \(x_\mathrm{Bj}\) bins are chosen as used for the determination of \(A_{1}^\mathrm{LP}\) in the main analysis. As the contribution of higher-order processes increases with an increase of \(p_\mathrm{T}\), this variable is chosen as the second one. The longitudinal double-spin asymmetries are extracted with the 2nd-order weighted method described in Ref. [39] and shown in Table 3. In the selected 2-dimensional binning, the systematic checks performed have shown no presence of systematic effects within statistical uncertainties. As a result, the systematic uncertainties of the asymmetries presented in Table 3 are smaller than the respective statistical ones. Note that these asymmetries are not directly used for the extraction of \(\Delta g/g\) that is presented in this paper.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Adolph, C., Aghasyan, M., Akhunzyanov, R. et al. Leading-order determination of the gluon polarisation from semi-inclusive deep inelastic scattering data. Eur. Phys. J. C 77, 209 (2017). https://doi.org/10.1140/epjc/s10052-017-4716-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-017-4716-x