Abstract
We report on the measurement of the two-neutrino double-beta decay half-life of \(^{130}\)Te with the CUORE-0 detector. From an exposure of 33.4 kg year of TeO\(_2\), the half-life is determined to be \(T_{1/2}^{2\nu }\) = [8.2 ± 0.2 (stat.) ± 0.6 (syst.)] \(\times \) 10\(^{20}\) year. This result is obtained after a detailed reconstruction of the sources responsible for the CUORE-0 counting rate, with a specific study of those contributing to the \(^{130}\)Te neutrinoless double-beta decay region of interest.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Double-beta decay is a rare nuclear process in which two nucleons simultaneously decay and emit two electrons. The allowed Standard Model version of this process emits two (anti-)neutrinos and is called two-neutrino double-beta decay (\(2\nu \beta \beta \)). This decay is interesting in its own right as the slowest process ever directly observed [1, 2]. Moreover, it may represent an important source of background for the neutrinoless double-beta decay (\(0\nu \beta \beta \)), i.e. a related process with no neutrino emission [3]. \(0\nu \beta \beta \) manifestly violates lepton number and therefore its discovery would point to new physics beyond the Standard Model. Experiments searching for \(0\nu \beta \beta \) have made great leaps forward in sensitivity by using a variety of techniques and isotopes [1, 2, 4, 5].
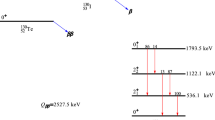
The Cryogenic Underground Observatory for Rare Events (CUORE) [6, 7] is the latest and most massive in a family of bolometric detectors designed to search for the \(0\nu \beta \beta \) decay of \(^{130}\)Te (Q-value \(=\) 2528 keV [8,9,10]). The detector combines the excellent energy resolution achievable with the bolometric technique (\(\sim \)5 keV at 2615 keV) with the exceptionally high natural abundance of \(^{130}\)Te (34%). The first phase of CUORE, named CUORE-0, was 1/19th the size of CUORE and operated at the Laboratori Nazionali del Gran Sasso (LNGS), in Italy, between 2013 and 2015. In addition to being a competitive \(0\nu \beta \beta \) experiment [5, 11, 12], CUORE-0 is a test of the assembly protocols for CUORE: the reconstruction of background sources responsible for the CUORE-0 counting rate enables us to verify that the necessary background requirements for CUORE are fulfilled.
In bolometers, the neutrinos emitted in \(2\nu \beta \beta \) are not detected, and the summed kinetic energy of the two electrons forms a continuous spectrum from 0 keV up to the Q-value of the decay. Conversely, \(0\nu \beta \beta \) produces no neutrinos and the experimental signature is a sharp peak at the Q-value of the decay, broadened by the energy resolution of the detector. This broadening smears \(2\nu \beta \beta \) events into the \(0\nu \beta \beta \) region of interest (ROI) around the Q-value and forms an irreducible background to the \(0\nu \beta \beta \) signal; thus a good energy resolution is key to mitigating this background.
The other background contributions in the ROI come from naturally occurring radioactivity in the detector components. These background sources can be disentangled and described quantitatively by carefully analyzing the shape of the measured spectrum and constructing a detailed background model, including both physics processes and instrumental effects.
This paper reports the CUORE-0 background model as well as a new precision measurement of the \(^{130}\)Te \(2\nu \beta \beta \) half-life. We use a detailed Geant4-based simulation and a Bayesian fitting algorithm with a priori constraints from materials assay to reconstruct the experimental data and form a posteriori estimates of the background source activities. A frequentist analysis, using the same model, is presented in [13].
We present the experimental details, including the data acquisition and analysis chain, in Sect. 2. Background constraints from external measurements are summarized in Sect. 3. The construction of the Monte Carlo simulation code is presented in Sect. 4. The validation of Monte Carlo simulations, by comparing external radioactive source calibration spectra with the data, is presented in Sect. 5. The set of identified background sources and their effects on the experimental data is discussed in Sect. 6. The Bayesian fitting tool is introduced in Sect. 7. We present the fit results and discuss their uncertainties in Sect. 8. Finally, the \(2\nu \beta \beta \) decay half-life evaluation is presented in Sect. 9 and the \(0\nu \beta \beta \) ROI reconstruction is discussed in Sect. 10.
2 Experiment
The CUORE-0 detector is one tower of 52 \(^{\mathrm {nat}}\)TeO\(_2\) crystals arranged in 13 floors, each with 4 crystals [14]. Each crystal is 750 g and is operated as an independent bolometer at \(\sim \)10 mK. At these temperatures, the interaction of a particle with the crystal generates a measurable temperature rise proportional to the energy deposited. The total detector mass is 39 kg of TeO\(_2\), or 10.8 kg of \(^{130}\)Te.
The tower is situated in a dilution refrigerator that provides the cooling power necessary to keep the TeO\(_2\) crystals at their working temperature. The copper and PTFE support structure holds the crystals and provides the thermal link to the refrigerator. The tower is surrounded by several layers of shielding, including low-background Roman lead and an anti-radon box. A schematic of the experiment is shown in Fig. 1 (left). The crystals temperatures are measured continuously using neutron transmutation doped (NTD) germanium thermistors, coupled to the crystals using epoxy. The thermistors convert temperature variations to a voltage output, which is digitized at a rate of 125 Samples/s. A software trigger is used to identify events and collect them in 5 s windows. Each window is divided into two periods: 1 s before the trigger and 4 s after it. The period before the trigger is used to establish the baseline temperature of the crystal and the remaining 4 s is used to determine the pulse amplitude. Together these are used to extract the energy deposited.
A silicon resistor is also coupled to each crystal with epoxy and is used to generate reference thermal pulses every 300 s. These are used to stabilize the gain of the bolometer against temperature fluctuations. Forced triggers are used for noise and threshold studies. The threshold (in the default high-energy triggered data used for this analysis) is bolometer dependent and is approximately between 30 and 120 keV. The energy response is calibrated by inserting thoriated tungsten wires inside the outer vessel of the cryostat, and using the \(\gamma \) lines from the \(^{232}\)Th decay chain to calibrate each bolometer independently.
The details of the CUORE-0 detector design, operation and performance are described in [14]. New protocols for material selection, cleaning, and handling were developed for the detector crystals and tower support structure. The dilution refrigerator, shielding, and other cryostat components are those from the Cuoricino experiment [15, 16].
2.1 Data production
This analysis uses data collected with CUORE-0 from March 2013 to March 2015. The data are grouped in datasets, which last approximately one month. Each dataset has approximately three days of calibration data at both the beginning and the end, collected while the detector was exposed to a radioactive calibration source. In total, 20 datasets were used in the \(0\nu \beta \beta \) analysis: however, in the present analysis we exclude the first dataset because of a substantial (\(\sim \)15 keV) miscalibration in the highest energy region (above 3 MeV). The physics data (i.e. excluding the calibration data of each dataset) use a total of 33.4 kg year of TeO\(_2\) exposure, or 9.3 kg year of \(^{130}\)Te exposure, after all data quality selections.
The data production converts the data from a series of triggered waveforms into a calibrated energy spectrum. The details of the data production can be found in [12], but we outline the general procedure here. The entire waveform is used to extract the amplitude of the pulse. Then each bolometer in each dataset is calibrated independently. A time-coincidence analysis is performed to search for events that deposit energy across multiple bolometers. Finally, the \(0\nu \beta \beta \) ROI (2470–2580 keV) is blinded for analysis.
Once the data are blinded, we implement a series of event selection cuts to maximize our sensitivity to physics events. We exclude periods of cryostat instability and malfunction. We enforce a pile-up cut of 7.1 s around each event: the 3.1 s before and 4 s after the event. We apply a series of pulse shape cuts to reject deformed or non-physical events mostly contaminating the low-energy region below \(\sim \)400 keV.
Double-beta decay events are usually confined within the crystal they originated from. However, many background sources deposit energy in multiple crystals within the response time of the detector. We use this information in the analysis by forming multiplets of events that occur within a coincidence window of ±5 ms in different crystals. Since the event rate is approximately 1 mHz, the probability of accidental (i.e. causally unrelated) coincidences is extremely small (\({\sim } 10^{-5}\)).
We then build energy spectra from these multiplets:
-
\({\mathcal {M}}\) spectrum is the energy spectrum of all events, with no coincidence criteria applied;
-
\({\mathcal {M}_1}\) spectrum is the energy spectrum of the events with the requirement that only one bolometer triggered (multiplicity 1 or \({\mathcal {M}_1}\) events);
-
\({\mathcal {M}_2}\) spectrum is the energy spectrum of the events with the requirement that two bolometers triggered (multiplicity 2 or \({\mathcal {M}_2}\) events);
-
\({\Sigma _2}\) spectrum is the energy spectrum associated to \(\mathcal {M}_2\) multiplets, each multiplet produces an entry with an energy E(\(\Sigma _2\) \()\) that is the sum of the energies of the two events composing the multiplet.
Higher-order multiplets are used only to evaluate the contribution of muons to the background.
The signal cut efficiency as a function of energy is defined as the fraction of true signal events that pass all the event cuts. In [12], we calculated the efficiency of these cuts by measuring their effect on \(\gamma \)-peaks in the energy spectrum. This takes advantage of the fact that the events in the \(\gamma \)-peaks are a nearly pure sample of true signal events. In the present analysis we use a new technique, which takes advantage of the coincidence analysis and allows a better reproduction of the energy dependence of the efficiency. Since accidental coincidences are negligible, \(\mathcal {M}_2\) events provide a pure sample of good events on the whole energy spectrum. The cut efficiency \(\varepsilon _C\) is modeled as an exponential function of the energy, \(\varepsilon _C(1-e^{-E/E_c})\), which is fitted to \(\mathcal {M}_2\) events on a bin-by-bin basis; it rapidly reaches a stable value of \(\varepsilon _C = 0.943\pm 0.002\) at energies above \( E_c\sim 100\,\mathrm {keV}\). This is consistent with the signal cut efficiency quoted in [12] of \(0.937\pm 0.007\). Above \(E\sim 7\,\mathrm {MeV}\) the \(\mathcal {M}_2\) spectra have insufficient statistics to give meaningful fit results. Therefore, in this analysis we do not include events with energy above 7 MeV.
3 Background sources
In rare event searches, some backgrounds are ubiquitous due to the natural decay of \(^{40}\)K and the daughters of the \(^{232}\)Th and \(^{238}\)U decay chains, including the surface implantation of \(^{210}\)Pb from environmental \(^{222}\)Rn. Based on the results of previous bolometric experiments [15,16,17], we expect these radioactive contaminants to be located in the whole experimental setup, including the detector itself. The cosmogenic activation, especially of copper and tellurium, resulting in \(^{60}\)Co is also of concern. A small contribution from cosmic muons [18], environmental gamma rays (\(\gamma \)) [19], and neutrons interacting directly in the detector is expected [19]. With this in mind, extreme care was taken into the selection of the materials used to build the CUORE-0 detector [14], and in the cleaning of all surfaces facing each TeO\(_2\) crystal [20, 21]. A lot of effort was also devoted to the detector design, to minimize both the total mass of the inactive parts of the detector tower and the surface area facing the array; the detector assembly procedure under controlled atmosphere [14]; and the optimization of the production protocol of every detector component to limit exposure to cosmic rays.
Tables 1 and 2 report the bulk and surface activities from the screening of the CUORE-0 components. A discussion of the different assay techniques that we used to derive the quoted contamination limits can be found in [17, 20]. The Cuoricino results (this experiment used the same cryostat and shield as CUORE-0) and screening results guide the construction of the background model and the definition of the priors on material contaminants.
4 Monte Carlo
The background sources are simulated using a Geant4-based Monte Carlo code called MCuoreZ. The code generates and propagates primary and any secondary particles through the CUORE-0 geometry until they are detected in the TeO\(_2\) crystals. The code outputs the energy and time of the energy depositions (time is used to properly take into account correlations in nuclear decay chains). A second program takes the output of MCuoreZ and applies a detector response function and incorporates other read-out features.
4.1 Monte Carlo simulation
MCuoreZ is implemented in Geant4 version 4.9.6.p03. \(\alpha \), \(\beta \), and \(\gamma \) particles, nuclear recoils, neutrons and muons are propagated down to keV energies, with an optimization done on the different volumes to balance simulation accuracy and speed. We have chosen the Livermore physics list, and particles can be generated and propagated in the bulk and on the surface of all components. The surface contamination is modeled, according to diffusion processes, with an exponential density profile and a variable depth parameter.
Single radioactive decays as well as the \(^{238}\)U and \(^{232}\)Th decay chains have been implemented using the G4RadioactiveDecay database. \(2\nu \beta \beta \) is parameterized according to [25]. The generation of external muons, neutrons and \(\gamma \) is described in [18, 19].
Due to the low counting statistics in CUORE-0 data some components are indistiguishable (i.e. exhibit degenerate spectral shapes)Footnote 1 and can be grouped, provided that the prior on their material contamination is properly evaluated. This simplification reduces the number of free parameters in the final fit of the simulation to the data. A similar case holds for components made of the same material (i.e., characterized by an identical contamination): their simulations can be grouped once scaled by mass or surface to properly equalize the contamination densities.
The detector as built and the geometry as implemented in MCuoreZ are shown in Fig. 1. The outermost volume included in CUORE-0 geometry is the external neutron shield. Although its contamination is negligible, its effect on the propagation of external neutrons and muons is important.
The next layer is the external lead shield made of modern lead (ExtPb). Only the inner 10 cm are simulated, since self-shielding is so high that the contribution from the outer volume is negligible.
The cryostat is then modeled as composed of two volumes: the Cryostat External Shields (CryoExt) and the Cryostat Internal Shields (CryoInt).
The CryoExt groups three components made of copper that has been underground for more than 25 years. These components exhibit degenerate spectra and the only prior considered for their contamination is that on \(^{60}\)Co derived from their identical history. Included in this volume are a small amount of superinsulation material (Mylar and Al) and the gap between the OVC (cryostat Outer Vacuum Chamber) and the ExtPb. The ExtPb is enclosed in acrylic glass and flushed with nitrogen (anti-radon box) to prevent radon from filling this gap and entering the experimental volume.
The CryoInt groups three shields made of the same newer copper, underground since 2002: the IVC (cryostat Inner Vacuum Chamber), the 600 and 50 mK shields. The roman lead [26] shield (IntPb) is inserted between the IVC and the 600 mK shield. The Holder is the structure that holds the crystals. It is made from NOSV copper, a special copper alloy from Aurubis company suitable for cryogenic use, cleaned according to the CUORE protocols [14]. It has two main parts: the frame that supports the crystals and the surrounding cylindrical box. Finally, the Crystals are designed as TeO\(_2\) cubes with identical contaminations.
In Table 3, the components listed as Small Parts are not included in the following analysis because of their small mass and negligible contamination (see Tables 1, 2). Only the PTFE spacers could provide a sizable contribution to the background, however, their spectra are degenerate with the Holder ones, therefore their contribution is included in the latter element.
4.2 Monte Carlo data production
In order to make the Monte Carlo reproduce experimental data – as already anticipated – a second code is used to recreate the detector time and energy response. We account for the timing resolution of each crystal by combining energy depositions that occur in the same crystal within a window of ±5 ms. The absolute time of events is assigned based on a random distribution with an event rate of 1 mHz (the experimental rate during physics runs) and any physical coincidences from MCuoreZ are preserved.
Once the simulated events are correlated correctly in time, the resulting energy depositions are smeared with a Gaussian energy response function. The width of the function varies linearly with energy and is based on the FWHM resolution measured on \(\gamma \)-peaks in the \(\mathcal {M}\) spectrum, between 511 and 2615 keV.
We reproduce also the energy dependence of the trigger efficiency. This is experimentally evaluated for each bolometer using heater-generated pulses with variable amplitudes. For each amplitude (then converted into a particle equivalent energy) the efficiency is defined as the number of triggered signals over the generated ones. The efficiency vs. energy curve is interpolated with an Erf function and used in simulation data production.
CUORE-0 source calibration measurement. Top panel Comparison of \(\mathcal {M}_1\) spectrum with its MCuoreZ simulation. Peaks are grouped in a single bin, while in the continuum the minimum bin size is 15 keV. Bottom panel bin-by-bin ratio between counts in the experimental spectrum and counts in the reconstructed one. We observe a less than 10% discrepancy in the rate at low energies (\({<}300\) keV) that is more likely due to small errors in the geometry reconstruction
As is done in the experiment, events with coincidences in multiple bolometers within a ±5 ms window are combined into multiplets. Pile-up events (i.e. events occurring in the same bolometer within the pile-up rejection window set by the analysis – see Sect. 2) are removed to account for dead time.
The simulation properly reproduce the \(\gamma \) particle energies, since we calibrate CUORE-0 spectra using \(^{232}\)Th \(\gamma \) lines. However, we observe in our data an energy quenching effect for \(\alpha \) particles compared to \(\gamma \), which makes the measured energies higher than the known energies [27, 28]. We account for this effect in the simulations by shifting \(\alpha \) energy depositions by 0.8%, which is the average shift observed for \(^{232}\)Th and \(^{238}\)U \(\alpha \) peaks visible in CUORE-0 background spectrum.
5 Reconstruction of the calibration source
We use calibration data to test the MCuoreZ simulation. The thoriated wire calibration source is deployed between the CryoExt and the ExtPb, therefore its simulation involves all volumes internal to the ExtPb. The calibration data rate is about 100 times higher than in physics runs, so pile-up effects become sizable. Figure 2 shows that with proper treatment of pile-up effects, we achieve a good data-simulation agreement. We observe small deviations in the low-energy region between 100 and 300 keV and on a few peaks. The deviation in the low-energy region (the origin is still unknown) is a potential source of systematic errors that will be considered in Sect. 8. For what concerns peaks, the largest deviation observed is a 7% difference on the \(^{228}\)Ac line at 1153 keV (branching ratio 0.1%). We traced this effect to the Geant4 versionFootnote 2; anyway it has no consequences on the background reconstruction since it involves only few very low intensity lines.
6 Construction of background model
The really critical part of the background model construction is the determination a priori of the most relevant sources to be included in the fit. Omitting a relevant source could lead to a poor fit or, even worse, a good fit to the wrong model. The degeneracy of many of the sources energy spectra introduces a further complication. The analysis reported in this section uses lines in the \(\mathcal {M}_1\) and \(\Sigma _2\) spectra to identify the radioactive isotopes contributing to the background counting rate, their possible location and any other characteristic feature that needs to be considered in the construction of the background model.
Sources such as the external muons, neutrons, and gammas are straight-forward to model since their fluxes are well known from independent laboratory measurements. The radioactive decays are more difficult to disentangle. The location and distribution of the contaminants must be specified, and in the case of decay chains a choice must be made between the secular equilibrium hypothesis and a break in the chain due to material handling. We use the external screening measurements presented in Sect. 3, estimates of cosmogenic exposure, and distinctive features in the data itself to select the most probable sources. These data also provide the priors for the fit.
Figure 3 shows the \(\mathcal {M}_1\) spectrum. The spectrum below the 2.615 MeV \(\gamma \) line of \(^{208}\)Tl includes many \(\gamma \) lines. Above 2.615 MeV it is dominated by \(\alpha \) events. These are the \(\gamma \) and \(\alpha \) regions respectively. The energies of the \(\gamma \) and \(\alpha \) lines, the time variation of their counting rates, and the observation of prompt or delayed coincidences can all be used to select the final list of sources to be included in the fit.
6.1 CUORE-0 \(\gamma \) region analysis
\(^{232}\)Th and \(^{238}\)U are natural long-lived radionuclides that generate radioactive decay chains. They can be found in almost all materials. The lines from the \(^{232}\)Th and \(^{238}\)U decay chains are clearly visible in Fig. 4; their intensities measured by fitting the \(\mathcal {M}\) spectrum are reported in Tables 4 and 5. The lines from \(^{40}\)K and other contaminants are also present; see Table 6.
The \(^{232}\)Th activity is basically unchanged relative to Cuoricino, especially at high energies. This suggests that most of the observed \(^{232}\)Th contamination is located in the cryostat and lead shields (i.e. the two structures present in both experiments). There is also a contribution from close sources, most likely the copper Holder, since we do not observe a large attenuation of the low-energy \(\gamma \) lines relative to the high-energy ones. Moreover, if the tower data are divided into floors of crystals, we do observe a floor by floor dependence that is not consistent with the one predicted by simulations. In Monte Carlo simulations this behavior can be reproduced by a point source close to the crystal that recorded the highest \(\gamma \) counting rate. However, the floor by floor dependence is not seen in the \(\alpha \) region, so the source cannot be directly facing the detectors, and is most likely located in the 50 mK copper shield. A similar anomaly was present in Cuoricino.
The two strongest \(\gamma \) emitters of the \(^{238}\)U chain are the \(^{222}\)Rn daughters: \(^{214}\)Pb and \(^{214}\)Bi. All of the observed \(^{238}\)U peaks are attributed to these two isotopes. Compared to Cuoricino, the average \(^{238}\)U activity is a factor two to three lower in CUORE-0, revealing a better cleaning of the detector components and/or a better \(^{222}\)Rn control. Indeed, the intensity of the observed lines, particular those from \(^{214}\)Bi, vary from dataset to dataset by as much as a factor of 3. Since \(^{222}\)Rn is a gas, it emanates from contaminated materials in the laboratory environment and its air concentration changes depending on ventilation conditions. As described in Sect. 4, the most likely place for \(^{222}\)Rn to enter the experimental setup is in the gap between the OVC and the ExtPb. Occasionally, the nitrogen flushing system inside the acrylic glass box malfunctions and the radon level increases in this volume. This additional varying component of the \(^{238}\)U contamination is well modeled by an increase in the contamination of the CryoExt.
In addition, we observe a line at 803 keV due to \(^{210}\)Po not in equilibrium with the \(^{238}\)U chain. This is fully explained by the \(^{210}\)Pb (\(\tau _{1/2}=22.3\) years) bulk contamination of the ExtPb. Before it was installed 25 years ago, this lead had a \(^{210}\)Pb activity of 16 Bq/kg, which is now reduced by a factor \(\sim \)2. This same line is also present in Cuoricino data. The activity reported in Table 6 for the 803 keV peak includes a contribution from a \(^{214}\)Bi line at 806 keV from the \(^{238}\)U chain, which cannot be disentangled.
\(^{40}\)K is a unique long-lived isotope that decays via both \(\beta ^{-}\) and electron capture, with a negligible \(\beta ^{+}\) branching. The signature of this contaminant is the single \(\gamma \) line at 1.46 MeV, which is produced in \(\sim \)10% of the decays. The single \(\gamma \) line is not sufficient to determine the activity in each volume, however, an asymmetry in the rate along the CUORE-0 tower suggests that in addition to bulk contaminants there is a \(^{40}\)K (extended) source at the bottom of the cryostat.
A number of isotopes produced by cosmogenic activation are also identified. The most critical of these contaminants is \(^{60}\)Co. The coincidence of its two \(\gamma \) lines in a single crystal produces a peak in the \(0\nu \beta \beta \) ROI (at 2505.7 keV). \(^{60}\)Co is primarily the result of fast neutron interactions on copper [29], but it can also be produced in tellurium [30, 31]. Exploiting a coincident \(\gamma \) analysis we can set an upper limit of \(3 \times 10^{-7}\) Bq/kg for the \(^{60}\)Co concentration in the crystals, i.e. well below the level needed to explain the observed rate. Therefore most of the \(^{60}\)Co contamination is located in the copper components.
The main copper components are the Holder, CryoInt, and CryoExt. Following [29], we derive upper limits on their \(^{60}\)Co activities based on the time they spent at sea-level and underground. The time spent underground before the start of data taking was a few months for the Holder, 14 years for the CryoInt, and 25 years for the CryoExt. Assuming the \(^{60}\)Co to be in saturation (i.e. the condition in which the production rate equals the decay rate) in both CryoInt and CryoExt just before the underground storage, its activity today would be about 180 \(\upmu \)Bq/kg for CryoInt and 42 \(\upmu \)Bq/kg for CryoExt. These are used as upper limits for the real contamination. We have only a very rough estimate for the cosmic ray exposure of the copper Holder (since this is made of many parts, each with its own history of exposure and underground storage), which results in an expected activity of \(\sim \)50 \(\upmu \)Bq/kg.
As expected, we also observe \(^{54}\)Mn and \(^{57}\)Co from the activation of copper [32]. Due to their short half-lives, they can only be located in the Holder. The nuclear fallout product \(^{137}\)Cs is also present as it was in Cuoricino, therefore it is located in the cryostat copper structures (since it cannot contaminate ancient Roman lead). Due to the low intensity of the peak CryoInt and CryoExt spectra are degenerate with each other, and we use the first to account for this contamination. The only expected contaminant due to the cosmogenic activation of the crystals themselves is \(^{125}\)Sb and its daughter \(^{125m}\)Te; in fact, \(^{125}\)Sb is the only long-lived isotope produced in tellurium with high cross-section [30].
CUORE-0 \(\mathcal {M}_1\) (blue) and \(\Sigma _2\) (red) in the \(\alpha \) region. The energy axis is calibrated on \(\gamma \). The peaks are labeled as follows: (1) \(^{190}\)Pt, (2) \(^{232}\)Th, (3) \(^{228}\)Th, (4) \(^{224}\)Ra, (5) \(^{220}\)Rn, (6) \(^{216}\)Po, (7) \(^{212}\)Bi, (8) \(^{238}\)U, (9) \(^{234}\)U and \(^{226}\)Ra, (10) \(^{230}\)Th, (11) \(^{222}\)Rn, (12) \(^{218}\)Po, (13) \(^{210}\)Po
There is evidence for cosmogenic activation of the Roman lead in the IntPb. We observe three \(\gamma \)s emitted by \(^{108m}\)Ag (see Table 6), a silver isotope produced by the neutron activation of silver impurities in the Roman lead with \(\tau _{1/2}=\) 438 years. We observe a peak at 439 keV that is ascribed to \(^{202}\)Tl, a daughter of the long-lived cosmogenic activation product \(^{202}\)Pb (\(\tau _{1/2}=\) 52.5 \(\times \) 10\(^3\) years). The presence of \(^{202}\)Tl contaminant is confirmed by a gamma spectroscopy measurement of a IntPb sample.
Finally, we observe the two high-energy \(\gamma \)-peaks at 1063.7 and 1770.2 keV from the decay of \(^{207}\)Bi without the more intense line at 569 keV, suggesting that this fallout product contaminates the ExtPb, as confirmed by MCuoreZ simulations.
6.2 CUORE-0 \(\alpha \) region analysis
The peaks observed in the \(\alpha \) region of CUORE-0 (Fig. 5) come from the \(^{238}\)U and \(^{232}\)Th decay chains and \(^{190}\)Pt. Due to the short range of \(\alpha \) particles and recoiling nuclei, the sources are contaminants close to or inside the bolometers: the Holder and the Crystals. The energy, multiplicity and intensity of the peaks can be used to efficiently constrain \(^{238}\)U and \(^{232}\)Th activities in these close components, simplifying the reconstruction of the more complicated \(\gamma \) region. Furthermore they allow us to differentiate bulk and surface as well as Holder and Crystals contaminations.
Contaminants in the bulk of the Crystals produce \(\mathcal {M}_1\) events with Gaussian peaks centered at the Q-value, since the \(\alpha \) and the nuclear recoil are detected in the same crystal.
\(\mathcal {M}_2\) events are a clear indication of the presence of contaminants on the surfaces of Crystals; they are produced when the \(\alpha \) or the recoiling nucleus escapes the source crystal to enter one of the neighboring ones. These events reconstruct in the \(\Sigma _2\) spectrum at the decay Q-value while in the \(\mathcal {M}_2\) spectra they produce two peaks each: one at the recoil energy (\(\sim \)70–100 keV) and one at the \(\alpha \) energy (\(\sim \)70–100 keV below Q-value); see Fig. 6. As the contaminants become deeper, the \(\alpha \) loses more energy in the material where it originates from and a low-energy tail on the \(\alpha \) peaks (or high-energy tail on the recoil peaks) becomes more pronounced.
Contaminants on surfaces of Crystals also contribute to the \(\mathcal {M}_1\) spectrum when both the \(\alpha \) and the recoiling nucleus are stopped within the source crystal or the escaping particles are not detected by another bolometer.
Contaminants in the Holder produce \(\mathcal {M}_1\) events with at most the energy of the \(\alpha \). Again, depending on the depth, the line shape can vary from a peak with a strong low-energy tail (shallow depth), to a flat continuum with no noticeable structures and extending far below the energy of the \(\alpha \) (deep surface or bulk contamination).
CUORE-0 \(\mathcal {M}_2\) spectrum (blue histogram, energy axis calibrated on \(\gamma \)). By selecting \(\mathcal {M}_2\) events with a \(\Sigma _2\) energy in the range 5.3–5.5 MeV, the peaks of \(\alpha \)s and nuclear recoils due to \(^{210}\)Pb on Crystals surfaces become visible (red histogram)
In general, the non-ideal behavior of the detector complicates the reconstruction of \(\alpha \) spectra. Some effects are well modeled in simulation: the energy threshold depletes \(\mathcal {M}_2\) in favor of \(\mathcal {M}_1\), and \(\alpha \)s are quenched with respect to \(\gamma \)s. Some effects are not fully understood, e.g. the broadening of all the peaks produced by surface contaminants, possibly explained by a different response of the bolometer to surface and bulk energy depositions. We choose a variable range binning to minimize these uncertainties as described in Sect. 7.
Table 7 lists the isotopes producing the most prominent \(\alpha \) peaks identified in CUORE-0 spectra.
Surface contaminants in the Crystals are identified on the basis of the \(\Sigma _2\) spectrum in Fig. 5. All the visible peaks belong to the \(^{232}\)Th or \(^{238}\)U chains. We observe breaks in secular equilibrium, particularly evident in the case of the 5.4 MeV peak. This line, due to \(^{210}\)Po (\(\tau _{1/2}=138\) days), is stable in time indicating an excess of \(^{210}\)Pb (\(\tau _{1/2}=22.3\) years).
The \(\mathcal {M}_1\) peaks are for the most part due to the same surface contaminations of Crystals with four exceptions, discussed below.
The activity of the 5.4 MeV line in the \(\mathcal {M}_1\) spectrum decreases with a time scale consistent with the \(^{210}\)Po half-life, indicating that there is a \(^{210}\)Po bulk contamination of the Crystals. From this fit the average activity during CUORE-0 exposure is 2.36 \(\upmu \)Bq/kg. This violation of the secular equilibrium of the \(^{238}\)U chain is quite common in TeO\(_2\) [22] due to the chemical similarities of tellurium and polonium.
\(^{232}\)Th and \(^{230}\)Th (a \(^{238}\)U chain product) produce sharp lines that can be explained by a bulk contamination of the Crystals . Most likely, these two long-lived isotopes are the only survivors of a \(^{232}\)Th and \(^{238}\)U contamination in the materials used for crystal production due to chemical affinity of thorium and oxygen.
Finally, we find evidence for a bulk \(^{190}\)Pt contamination of Crystals. The line in the CUORE-0 spectrum is shifted \(\simeq \)15 keV above the isotope Q-value of 3249 keV, a much higher shift than the one observed for all the other lines in the \(\alpha \) region. The crystals are grown in a platinum crucible. This contamination can be introduced during the crystal growth as a small grain of platinum locally modifying the detector response.
6.3 Source list
A list of the 57 sources used for the present analysis is shown in Table 8. The components in the first column are the 6 defined in the fifth column of Table 3. The priors in the fourth column derive mainly from Table 1. The priors for the \(^{60}\)Co activities are discussed in Sect. 6.1. There are two components included in the analysis but not included in Table 3. One is the 50 mK Spot, a point-like source located on the internal surface of the 50 mK thermal shield facing tower floor 10 (see Fig 1). The other is the Bottom Plate ExtPb, a disc-like source placed on the internal bottom plate of the external lead shield ExtPb. These two sources model the \(^{232}\)Th excess observed on the floor number 10 and the \(^{40}\)K excess observed on bottom floors, which are discussed in Sect. 6.1. In order to properly reproduce the shape of the \(\alpha \) peaks in \(\mathcal {M}_1\) and \(\mathcal {M}_2\) spectra, Crystals and Holder surface contamination with a few representative depths are included in the analysis (Fig. 7). The exact choice of contaminant depth is treated as a systematic uncertainty. This is discussed in Sect. 8.
Comparison between the experimental and the Monte Carlo \(\mathcal {M}_2\) with \(\Sigma _2\) energy equal to the Q-value of \(^{210}\)Po \(\alpha \) decay. The MC spectra refer to Crystals surface contamination with different depths parameters: 0.001, 1, and 10 \(\upmu \)m. The normalization here is chosen to approximately reproduce the profile of the experimental data
Violations of secular equilibrium in the \(^{238}\)U and \(^{232}\)Th decay chains are only considered when they produce a distinguishable signature in the spectrum. A background contribution due to muons is included in the analysis; contributions from neutrons and external \(\gamma \)s are negligible. Muons contribute mainly through \(\gamma \)s produced by interactions in the detector components. A prior is obtained from high multiplicity data, which is compatible with the muon flux measured by other experiments.
7 Bayesian fit construction
The activities of the sources used for the background model are determined by fitting the observed \(\mathcal {M}_1\), \(\mathcal {M}_2\), and \(\Sigma _2\) spectra with a linear combination of simulated source spectra. The expectation value of the counts in the ith bin of the experimental spectrum is given by
where \(\langle C_{ij, \alpha }^\mathrm{MC} \rangle \) is the expectation value for the ith bin of the simulated spectrum for the jth source and \(N_j\) is the unknown activity of the jth source. To ensure sufficient statistics, both the experimental and the simulated spectra are summed over all the active crystals.
Comparison between the experimental \(\mathcal {M}_1\) and JAGS reconstruction (top panel). In the bottom panel the bin-by-bin ratios between counts in the experimental spectrum over counts in the reconstructed one are shown; the corresponding uncertainties at 1, 2, 3 \(\sigma \) are shown as colored bands centered at 1. Fit residuals distribution is approximately Gaussian with \(\mu = (-0.03 \pm 0.09)\) and \(\sigma =(1.1 \pm 0.1)\)
Same as Fig. 8 for \(\mathcal {M}_2\). Fit residuals distribution is approximately Gaussian with \(\mu = (-0.13\pm 0.08)\) and \(\sigma =(1.00\pm 0.08)\)
The fit is performed with a Bayesian approach using Just Another Gibbs Sampler (JAGS) [33,34,35]. JAGS exploits Markov Chain Monte Carlo simulations to sample the joint posterior probability distribution function (pdf) of the model parameters. Following Bayes’ theorem the posterior pdf is evaluated combining the likelihood and the prior distributions. The available data to define the likelihoods are the observed counts in the bins of the experimental (\(C_{i, \alpha }^\mathrm{exp}\)) and simulated (\(C_{ij, \alpha }^\mathrm{MC}\)) spectra, both of which obey Poisson statistics. Therefore, the joint posterior pdf is
The priors for \(N_j\), which describe our prior knowledge about source activities, are specified in Table 8. In the case of a measured activity, we adopt a Gaussian prior centered at the measured value with the measurement uncertainty as the width of the Gaussian. For upper limits, we adopt a half Gaussian with a width such that our 90% upper limit is the 90% value of the prior. In all the other cases, we use a uniform non-informative prior with an activity that ranges from 0 to an upper limit higher than the maximum activity compatible with the CUORE-0 data. Similarly, we use uniform priors over wide ranges for \(\big \langle C_{ij, \alpha }^\mathrm{MC} \big \rangle \).
We chose a variable binning of the spectra to maximize the information content while minimizing the effects of statistical fluctuations and detector non-ideal behavior. Therefore, to avoid systematic uncertainties due to the lineshape, all the counts belonging to the same \(\gamma \) or \(\alpha \) peak are included in a single bin. The minimum bin size in the continuum is 15 keV, and bins with less than 30 counts are merged with their immediate neighbor. The fit extends from 118 keV to 7 MeV. The threshold at 118 keV is set to exclude the low-energy noise events (contaminating few datasets) and the nuclear recoil peak (which is mis-calibrated). In building the \(\Sigma _2\) spectrum, we require that the energy of each event is above threshold. An exception is set for events with \(E>2.7\) MeV in coincidence with events below the fit threshold, to correctly build-up the Q-value peaks in the \(\alpha \) region of \(\Sigma _2\) spectrum.
Same as Fig.8 for \(\Sigma _2\). Fit residuals distribution is approximately Gaussian with \(\mu = (-0.09 \pm 0.09)\) and \(\sigma =(1.0 \pm 0.1)\)
Correlation matrix among the \(N_j\) parameters. The list of sources is reported in Table 8. Note the anti-correlation between the \(2\nu \beta \beta \) and the \(^{40}\)K activity in Crystal bulk
8 Reference fit and systematics
The reference fit is the result of the fit to data from the total 33.4 kg year TeO\(_2\) exposure. The reconstructions of the experimental spectra are shown in Figs. 8, 9, and 10 for the \(\mathcal {M}_1\), \(\mathcal {M}_2\), and \(\Sigma _2\) spectra, respectively. The fit results for the 57 free parameters are summarized in Table 8. The marginalized posterior distributions are used to evaluate the central values and the statistical uncertainties of the activities, or to calculate 90% upper limits for undetermined contaminations.
The correlation matrix of the 57 sources is illustrated in Fig. 11. In general, most of the components used to fit the \(\alpha \) region are not correlated to those used to reconstruct the \(\gamma \) region. As expected, the same contaminants in neighboring components of the experimental setup are highly correlated due to the similar spectra.
For the \(\mathcal {M}_1\), \(\mathcal {M}_2\), and \(\Sigma _2\) spectra, the normalized fit residuals have a Gaussian-like distribution with mean 0 and standard deviation 1. The reduced chi-square with 57 parameters and 478 degrees of freedom is 1.36. We do not expect perfect statistical agreement between the data and reconstruction since the uncertainties associated with the simulated spectra account for only the statistical fluctuation in the bin counts. They do not include the systematic uncertainties in the MC simulations.
To check the stability of the background model, the dependence on priors, and the systematic uncertainties, especially those affecting the \(2\nu \beta \beta \) half-life, we run a number of different fits varying the binning, energy threshold, depth of surface contaminations, priors, list of background sources, and input data.
-
Binning: We repeat the fit with different minimum bin sizes set to 5, 10, 20, and 25 keV, and we test a uniform 15 keV binning. The latter is the only case where the reconstruction is worse, because the line shape of \(\gamma \)-peaks is not perfectly modeled. The \(2\nu \beta \beta \) activity changes by less than 1%. These tests also cover the systematics due to miscalibration [12].
-
Fit energy threshold: We run the fit with different energy thresholds ranging from 118 to 500 keV, covering the region where the reconstruction of the calibration source is slightly worse (Sect. 5). The quality of fit reconstruction is unchanged and the \(2\nu \beta \beta \) activity variations are below 2%.
-
Contamination depth uncertainty: We fit the \(\alpha \) region with different depths to model surface contaminations. Several models perform similarly to the reference fit, however, the results of the background reconstruction, particularly the \(2\nu \beta \beta \) rate, are unaffected.
-
Dependence on Prior distributions: To evaluate the systematic uncertainty related to the Prior choice, we perform two JAGS fits. In the first fit, the half-Gaussian priors used in the case of upper limits on source activities are changed to uniform priors with the minimum at 0 and the maximum at \(3\sigma \) above the upper limit. In the second fit, uniform non-informative priors are used for all components. In both cases, the global fit reconstruction is good and the \(2\nu \beta \beta \) result changes by \(\sim \)1%.
-
Selection of background sources: In the reference fit there are 14 undetermined sources whose activity is quoted as upper limit. To check the fit stability against the removal of these sources, we run a minimum model fit with only 43 sources. Once more, the global fit reconstruction and the \(2\nu \beta \beta \) result are not affected.
-
Subset of data: We compare fit results obtained with various subsets of data. We search for time-related systematics by dividing the data into alternating datasets or grouping Rn-low and Rn-high datasets. Each study is performed with at least 1/3 of the total exposure. The Rn-low and Rn-high data are obtained by grouping the datasets in which the \(^{214}\)Bi lines are more or less intense than the mean. This allows us to study if changes in the \(^{214}\)Bi background influence the fit quality. The reconstruction results are compatible with the reference fit. The \(^{238}\)U contamination in the CryoExt, which includes the air volume with the variable \(^{222}\)Rn source, converges on results compatible with the different \(^{222}\)Rn concentrations. Finally, we investigate the dependence of the reconstruction on geometry by grouping the data by different floors: odd and even floors, upper and lower floors, the floors from 3 to 8 (central), and the complementary ones (peripherals). In this way, we explore the systematics due to model approximations. In Monte Carlo simulations we assumed contaminants to be uniformly distributed in each component of the experimental setup (except for the point sources) and we modeled the average performance of bolometers. In all studies, the reconstruction is good, but we observe variations in the activities of the sources. In particular, the \(2\nu \beta \beta \) activity varies by about ±10%.
In the tests detailed above, the overall goodness of the fit remains stable, while we observe variations in the activities of the individual sources. These variations are used as an evaluation of the systematic uncertainty on the 57 source activities (Table 8, sixth column).
There are caveats using the reference fit results as an exact estimation of the material contamination. Indeed, degenerate source spectra allow us to use a single source to represent a group of possible sources. Examples are: the Holder that also accounts for the contribution of the Small Parts, surface contaminants in close components that are modeled with few representative depths, or bulk contamination in far components that also include surface ones.
9 \(^{130}\)Te \(2\nu \beta \beta \) decay
The background reconstruction allows us to measure the \(2\nu \beta \beta \) of \(^{130}\)Te with high accuracy. Figure 12 shows the fit result compared with the CUORE-0 \(\mathcal {M}_1\). \(2\nu \beta \beta \) produces \((3.27 \pm 0.08) \times 10^{4}\) counts, corresponding to \(\sim \)10% of the events in the \(\mathcal {M}_1\) \(\gamma \) region from 118 keV to 2.7 MeV. As shown in Fig. 13, removing the \(2\nu \beta \beta \) component results in a dramatically poorer fit in this region.
The \(2\nu \beta \beta \) activity is (3.43 ± 0.09) \(\times \) 10\(^{5}\) Bq/kg, with a statistical uncertainty that is amplified by the strong anti-correlation to the \(^{40}\)K contamination in crystal bulk (but not to other \(^{40}\)K sources). Indeed, this is the only case where the \(\beta \) spectrum of \(^{40}\)K (having a shape that resembles that of \(2\nu \beta \beta \)) contributes to the detector counting rate. For all the other \(^{40}\)K sources, only the EC decay (branching ratio 89%) contributes to the detector counting rate through the 1460 keV line and its Compton tail. The Posterior for the \(2\nu \beta \beta \) activity as obtained from the reference fit is shown in Fig 14. Also shown is the Posterior associated to the fit bias. This is derived from systematic studies discussed in Sect. 8 and is represented as a flat distribution. Figure 14 also shows the 68% Confidence Intervals associated to statistical and systematic errors.
The half-life value obtained for \(2\nu \beta \beta \) is
10 \(^{130}\)Te \(0\nu \beta \beta \) region of interest
The signature of \(^{130}\)Te \(0\nu \beta \beta \) is a Gaussian line centered at 2528 keV, the transition energy of the isotope, in \(\mathcal {M}_1\). Modeling the shape of the background in this region, especially possible subdominant peaks, and identifying the main sources of background is relevant not only for CUORE-0, but also for the future evolution of \(0\nu \beta \beta \) searches with bolometers.
It is useful to group the sources used for the fit into three major classes: the two elements that will be identical (though replicated 19 times) in CUORE, Holder and Crystals, and the element that will change, i.e. the cryogenic and radioactive shield systems (the sum of the CryoInt, CryoExt, IntPb, and ExtPb). The contribution from these elements to the \(0\nu \beta \beta \) region of interest (2470–2570 keV) in \(\mathcal {M}_1\) are shown in Fig. 15 and listed in Table 9. The largest contribution comes from the shields. This is mainly \(^{232}\)Th contamination. The Holder is the second largest contributor due to degraded \(\alpha \)s from \(^{238}\)U and \(^{232}\)Th deep surface contaminants. Bulk and shallow-depth contaminants account for less than 0.3% of the background. A very small fraction of the background comes from \(^{238}\)U, \(^{232}\)Th, and \(^{210}\)Pb Crystals surface contaminants, and from muon interactions. The systematic uncertainties are negligible.
Finally, Fig. 16 shows a wider region centered around the ROI. This plot is produced by tagging the energy depositions where at least 90% of the energy was deposited by \(\alpha \) particles. We found \({\sim }24\)% of the ROI background was produced by \(\alpha \) events. After reducing \(\gamma \) backgrounds from the shields, these \(\alpha \) events are expected to dominate the ROI rate in CUORE. This motivates the development of \(\alpha \) particle discrimination for future bolometer-based experiments; see [36] and references therein.
11 Conclusion
In this paper, we successfully reconstruct the CUORE-0 background using 57 sources modeled using a detailed Monte Carlo simulation. We find that 10% of the \(\mathcal {M}_1\) counting rate in the range [118–2700] keV is unequivocally due to \(^{130}\)Te \(2\nu \beta \beta \) decay. We measure its half-life to be
Compared to previous results obtained from MiDBD [6.1 ± 1.4 (stat.) \(^{+2.9}_{-3.5}\) (syst.)] \(\times \) 10\(^{20}\) years [37], from Cuoricino [38], and from NEMO [7.0 ± 0.9 (stat.) ± 1.1 (syst.)] \(\times \) 10\(^{20}\) years [39], this is the most precise measurement to date. We find that the background rate in the \(^{130}\)Te \(0\nu \beta \beta \) region of interest is dominated by the shields. This result gives us confidence that we are on track to achieve the requirements for CUORE.
Notes
Some degenerate sources could be disentangled by considering distribution of events across the detector. In order to keep the number of free parameters small and the number of simulated configurations tractable, we do not use position of the events in this analysis, and average the spectra over the entire tower.
We recently verified that this problem is gone in Geant4 version 4.10.
References
J. Albert et al. (EXO-200 Collaboration), Nature 510, 229 (2014)
A. Gando et al. (KamLAND-Zen Collaboration), Phys. Rev. Lett. 110, 062502 (2013)
W.H. Furry, Phys. Rev. 56, 1184 (1939)
M. Agostini et al. (GERDA Collaboration), Phys. Rev. Lett. 111, 122503 (2013)
K. Alfonso et al. (CUORE Collaboration), Phys. Rev. Lett. 115, 102502 (2015)
C. Arnaboldi et al. (CUORE Collaboration), Nucl. Instrum. Methods A 518, 775 (2004)
R. Ardito et al. (CUORE Collaboration), (2005). arXiv:hep-ex/0501010
M. Redshaw et al., Phys. Rev. Lett. 102, 212502 (2009)
N.D. Scielzo et al., Phys. Rev. C 80, 025501 (2009)
S. Rahaman et al., Phys. Lett. B 703(4), 412 (2011)
D.R. Artusa et al., Eur. Phys. J. C 74, 2956 (2014)
C. Alduino et al. (CUORE Collaboration), Phys. Rev. C 93, 045503 (2016)
B. Zhu, Ph. D. thesis (2016). https://cuore.lngs.infn.it/en/publications/theses
C. Alduino et al. (CUORE Collaboration), J. Inst. 11(07), P07009 (2016)
C. Arnaboldi et al. (Cuoricino Collaboration), Phys. Rev. C 78, 035502 (2008)
E. Andreotti et al. (Cuoricino Collaboration), Astropart. Phys. 34, 822 (2011)
C. Bucci et al., Eur. Phys. J. A 41, 155 (2009)
E. Andreotti et al. (Cuoricino Collaboration), Astropart. Phys. 34, 18 (2010)
F. Bellini et al., Astropart. Phys. 33, 169 (2010)
F. Alessandria et al. (CUORE Collaboration), Astropart. Phys. 45, 13 (2013)
C. Arnaboldi et al., J. Cryst. Growth 312, 2999 (2010)
F. Alessandria et al. (CUORE Collaboration), Astropart. Phys. 35, 839 (2012)
CUORE Collaboration, LNGS Annual Report. Tech. rep. (2005). https://www.lngs.infn.it/images/REIS/Annual_Report/annual_report_2005.pdf
CUORE Collaboration, LNGS Annual Report. Tech. rep. (2006). https://www.lngs.infn.it/images/REIS/Annual_Report/annual_report_2006.pdf
J. Kotila, F. Iachello, Phys. Rev. C 85, 034316 (2012)
A. Alessandrello et al., Nucl. Instrum. Methods B 142, 163 (1998)
A. Alessandrello et al., Phys. Lett. B 408, 465 (1997)
F. Bellini et al., J. Inst. 5, P12005 (2010)
S. Cebrián et al., Astropart. Phys. 33, 316 (2010)
B.S. Wang et al., Phys. Rev. C 92, 024620 (2015)
A.F. Barghouty et al., Nucl. Instrum. Methods B 295, 16 (2013)
M. Laubenstein, G. Heusser, Appl. Radiat. Isot. 67, 750 (2009)
A. Gelman, J.B. Carlin, H.S. Stern, D.B. Rubin, Bayesian Data Analysis, 2nd edn. (Chapman & Hall/CRC Press, Boca Raton, 2014)
M. Plummer, JAGS version 3.3.0 user manual (2012)
D. Chiesa, E. Previtali, M. Sisti, Ann. Nucl. Energy 70, 157 (2014)
G. Wang et al. (CUPID Interest Group), (2015). arXiv:1504.03599
C. Arnaboldi et al. (MiDBD Collaboration), Phys. Lett. B 557, 167 (2003)
L. K. Kogler, Ph. D. thesis (2011). https://cuore.lngs.infn.it/en/publications/theses
R. Arnold et al. (NEMO-3 Collaboration), Phys. Rev. Lett. 107, 062504 (2011)
Acknowledgements
The CUORE Collaboration thanks the directors and staff of the Laboratori Nazionali del Gran Sasso and the technical staff of our laboratories. This work was supported by the Istituto Nazionale di Fisica Nucleare (INFN); the National Science Foundation under Grant Nos. NSF-PHY-0605119, NSF-PHY-0500337, NSF-PHY-0855314, NSF-PHY-0902171, NSF-PHY-0969852, NSF-PHY-1307204, NSF-PHY-1314881, NSF-PHY-1401832, and NSF-PHY-1404205; the Alfred P. Sloan Foundation; the University of Wisconsin Foundation; and Yale University. This material is also based upon work supported by the US Department of Energy (DOE) Office of Science under Contract Nos. DE-AC02-05CH11231, DE-AC52-07NA27344, and DE-SC0012654; and by the DOE Office of Science, Office of Nuclear Physics under Contract Nos. DE-FG02-08ER41551 and DE-FG03-00ER41138. This research used resources of the National Energy Research Scientific Computing Center (NERSC).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Alduino, C., Alfonso, K., Artusa, D.R. et al. Measurement of the two-neutrino double-beta decay half-life of \(^{130}\)Te with the CUORE-0 experiment. Eur. Phys. J. C 77, 13 (2017). https://doi.org/10.1140/epjc/s10052-016-4498-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-016-4498-6