QCD sum rule study of hidden-charm pentaquarks

Abstract

We study the mass spectra of hidden-charm pentaquarks having spin $J = {1\over 2}/{3\over 2}/{5\over 2}$ and quark contents $uud c \bar{c}$. We systematically construct all the relevant local hidden-charm pentaquark currents, and we select some of them to perform QCD sum rule analyses. We find that the $P_c(4380)$ and $P_c(4450)$ can be identified as hidden-charm pentaquark states composed of an anti-charmed meson and a charmed baryon. Besides them, we also find (a) the lowest-lying hidden-charm pentaquark state of $J^P = 1/2^-$ has the mass $4.33^{+0.17}_{-0.13}$ GeV, while the one of $J^P = 1/2^+$ is significantly higher, that is, around 4.7–4.9 GeV; (b) the lowest-lying hidden-charm pentaquark state of $J^P = 3/2^-$ has the mass $4.37^{+0.18}_{-0.13}$ GeV, consistent with the $P_c(4380)$ of $J^P = 3/2^-$, while the one of $J^P = 3/2^+$ is also significantly higher, that is, above 4.6 GeV; (c) the hidden-charm pentaquark state of $J^P = 5/2^-$ has a mass around 4.5–4.6 GeV, slightly larger than the $P_c(4450)$ of $J^P = 5/2^+$.

1 Introduction

Since the discovery of the X(3872) [1], dozens of charmonium-like XYZ states have been reported [2]. They are good candidates of tetraquark states, which are made of two quarks and two antiquarks. In the past year, the LHCb Collaboration observed two hidden-charm pentaquark resonances, $P_c(4380)$ and $P_c(4450)$, in the $J/\psi p$ invariant mass spectrum [3]. They are good candidates of pentaquark states, which are made of four quarks and one antiquark. They all belong to the exotic states, which cannot be explained in the traditional quark model, and they are of particular importance to understand the low energy behaviors of quantum chromodynamics (QCD) [4].

Before the LHCb’s observation of the $P_c(4380)$ and $P_c(4450)$ [3], there had been extensive theoretical discussions on the existence of hidden-charm pentaquark states [5–13]. Yet, this experimental observation triggered more studies to explain their nature, such as meson–baryon molecules [14–20], diquark–diquark–antiquark pentaquarks [21–25], compact diquark–triquark pentaquarks [26, 27], the topological soliton model [28], genuine multiquark states other than molecules [29], kinematical effects related to the triangle singularity [30–32], etc. Their productions and decay properties are also interesting and have been studied in Refs. [33–43], etc. For more extensive discussions, see Refs. [4, 44, 45].

In this paper we use the method of QCD sum rule to study the mass spectrum of hidden-charm pentaquarks having spin $J = {1\over 2}/{3\over 2}/{5\over 2}$ and quark contents $uud c \bar{c}$. We shall investigate the possibility of interpreting the $P_c(4380)$ and $P_c(4450)$ as hidden-charm pentaquark states. We shall also investigate other possible hidden-charm pentaquark states. The present discussion is an extension of our recent work shortly reported in Ref. [46]. In the calculation we need the resonance parameters of the $P_c(4380)$ and $P_c(4450)$ measured in the LHCb experiment [3]:

$$\begin{aligned} M_{P_c(4380)}= & {} 4380\pm 8\pm 29\, \mathrm {MeV},\\ \Gamma _{P_c(4380)}= & {} 205\pm 18\pm 86\, \mathrm {MeV},\\ M_{P_c(4450)}= & {} 4449.8\pm 1.7\pm 2.5 \,\mathrm {MeV},\\ \Gamma _{P_c(4450)}= & {} 39\pm 5\pm 19\, \mathrm {MeV}, \end{aligned}$$

as well as the preferred spin–parity assignments $(3/2^-, 5/2^+)$ for the $P_c(4380)$ and $P_c(4450)$, respectively [3].

This paper organized as follows. After this Introduction, we systematically construct the local pentaquark interpolating currents having spin $J = 1/2$ and quark contents $uud c \bar{c}$ in Sect. 2. The currents having spin $J = 3/2$ and $J = 5/2$ are similarly constructed in Appendices A and B, respectively. These currents are used to perform QCD sum rule analyses in Sect. 3, and then are used to perform numerical analyses in Sect. 4. The results are discussed and summarized in Sect. 5. An example applying the Fierz transformation and the color rearrangement is given in Appendix C. This paper has a supplementary file “OPE.nb” containing all the spectral densities.

2 Local Pentaquark currents of spin 1/2

In this section we systematically construct local pentaquark interpolating currents having spin $J = 1/2$ and quark contents $uud c \bar{c}$. There are two possible color configurations, $[\bar{c}_d c_d][\epsilon ^{abc}q_a q_b q_c]$ and $[\bar{c}_d q_d][\epsilon ^{abc}c_a q_b q_c]$, where $a \cdots d$ are color indices, q represents the up, down or strange quark, and c represents the charm quark. These two configurations, if they are local, can be related by the Fierz transformation as well as the color rearrangement:

$$\begin{aligned} \delta ^{de} \epsilon ^{abc}= & {} \delta ^{da} \epsilon ^{ebc} + \delta ^{db} \epsilon ^{aec} + \delta ^{dc} \epsilon ^{abe}. \end{aligned}$$

(1)

With this relation, the color configurations $[\bar{c}^d c^d][\epsilon _{abc}q_1^a q_2^b q_3^c]$, $[\bar{c}^d q_1^d][\epsilon _{abc}c^a q_2^b q_3^c]$, $[\bar{c}^d q_2^d][\epsilon _{abc}c^a q_1^b q_3^c]$, and $[\bar{c}^d q_3^d][\epsilon _{abc}c^a q_1^b q_2^c]$ can actually be related, where $q_{1,2,3}$ represent three light quark fields. There are several formulas related to the Fierz transformation, some of which were given in Refs. [47, 48]. In this paper we also need to use the product of two Dirac matrices with two symmetric Lorentz indices:

$$\begin{aligned}&\left( \begin{array}{l} g_{\mu \nu } \mathbf {1} \otimes \mathbf {1}\\ g_{\mu \nu } \gamma _\rho \otimes \gamma ^\rho \\ g_{\mu \nu } \sigma _{\rho \sigma } \otimes \sigma ^{\rho \sigma }\\ g_{\mu \nu } \gamma _{\rho } \gamma _5 \otimes \gamma ^{\rho } \gamma _5\\ g_{\mu \nu } \gamma _5 \otimes \gamma _5\\ \gamma _\mu \otimes \gamma _\nu + (\mu \leftrightarrow \nu )\\ \gamma _\mu \gamma _5 \otimes \gamma _\nu \gamma _5 + (\mu \leftrightarrow \nu )\\ \sigma _{\mu \rho } \otimes \sigma _{\nu \rho } + (\mu \leftrightarrow \nu ) \end{array} \right) _{a b, c d}\nonumber \\&\quad = \left( \begin{array}{llllllll} {1\over 4} &{} {1\over 4} &{} {1\over 8} &{} -{1\over 4} &{} {1\over 4} &{} 0 &{} 0 &{}0\\ 1 &{} -{1\over 2} &{} 0 &{} -{1\over 2} &{} -1 &{} 0 &{} 0 &{} 0\\ 3 &{} 0 &{} -{1\over 2} &{} 0 &{} 3 &{} 0 &{} 0 &{} 0\\ -1 &{} -{1\over 2} &{} 0 &{} -{1\over 2} &{} 1 &{} 0 &{} 0 &{} 0\\ {1\over 4} &{} -{1\over 4} &{} {1\over 8} &{} {1\over 4} &{} {1\over 4} &{} 0 &{} 0 &{} 0\\ {1\over 2} &{} -{1\over 2} &{} {1\over 4} &{} -{1\over 2} &{} -{1\over 2} &{} {1\over 2} &{} {1\over 2} &{} -{1\over 2}\\ -{1\over 2} &{} -{1\over 2} &{} -{1\over 4} &{} -{1\over 2} &{} {1\over 2} &{} {1\over 2} &{} {1\over 2} &{} {1\over 2}\\ {3\over 2} &{} {1\over 2} &{} -{1\over 4} &{} -{1\over 2} &{} {3\over 2} &{} -1 &{} 1 &{} 0 \end{array} \right) \nonumber \\&\qquad \times \; \left( \begin{array}{l} g_{\mu \nu } \mathbf {1} \otimes \mathbf {1} g_{\mu \nu } \gamma _\rho \otimes \gamma ^\rho \\ g_{\mu \nu } \sigma _{\rho \sigma } \otimes \sigma ^{\rho \sigma }\\ g_{\mu \nu } \gamma _{\rho } \gamma _5 \otimes \gamma ^{\rho } \gamma _5\\ g_{\mu \nu } \gamma _5 \otimes \gamma _5\\ \gamma _\mu \otimes \gamma _\nu + (\mu \leftrightarrow \nu )\\ \gamma _\mu \gamma _5 \otimes \gamma _\nu \gamma _5 + (\mu \leftrightarrow \nu )\\ \sigma _{\mu \rho } \otimes \sigma _{\nu \rho } + (\mu \leftrightarrow \nu )\\ \end{array}\right) _{a d, b c}. \end{aligned}$$

(2)

However, the detailed relations between $[\bar{c}_d c_d][\epsilon ^{abc}q_a q_b q_c]$ and $[\bar{c}_d q_d][\epsilon ^{abc}c_a q_b q_c]$ cannot easily be obtained. We just show one example in Appendix C. We also systematically construct local pentaquark interpolating currents having spin $J = 3/2$ and $J = 5/2$, and list the results in Appendixes A and B, respectively.

2.1 Currents of $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$. We only investigate the currents of the following type:

$$\begin{aligned} \eta= & {} [\epsilon ^{abc} (u^T_a C \Gamma _i d_b) \Gamma _j u_c] [\bar{c}_d \Gamma _k c_d], \end{aligned}$$

(3)

where $\Gamma _{i,j,k}$ are various Dirac matrices. The currents of the other types $[\bar{c}_d \Gamma _k c_d][\epsilon ^{abc} (u_a^T C \Gamma _i u_b) \Gamma _j d_c]$ and $[\bar{c}_d \Gamma _k c_d][\epsilon ^{abc} (d_a^T C \Gamma _i u_b) \Gamma _j u_c]$ can be related to these currents by using the Fierz transformation. We can easily construct them based on the results of Ref. [48] that there are three independent local light baryon fields of flavor-octet and having the positive parity:

$$\begin{aligned}&N^N_1 = \epsilon _{abc} \epsilon ^{ABD} \lambda _{DC}^N (q_A^{aT} C q_B^b) \gamma _5 q_C^c,\nonumber \\&N^N_2 = \epsilon _{abc} \epsilon ^{ABD} \lambda _{DC}^N (q_A^{aT} C \gamma _5 q_B^b) q_C^c,\nonumber \\&N^N_{3\mu } = \epsilon _{abc} \epsilon ^{ABD} \lambda _{DC}^N (q_A^{aT} C \gamma _\mu \gamma _5 q_B^b) \gamma _5 q_C^c, \end{aligned}$$

(4)

where $A \cdots D$ are flavor indices, and $q_{A}=(u,d,s)$ is the light quark field of flavor-triplet. Together with light baryon fields having the negative parity, $\gamma _5 N^N_{1,2}$ and $\gamma _5 N^N_{3\mu }$, and the charmonium fields:

$$\begin{aligned}&\bar{c}_d c_d \, [0^+], \bar{c}_d \gamma _5 c_d \, [0^-], \nonumber \\&\bar{c}_d \gamma _\mu c_d \, [1^-], \bar{c}_d \gamma _\mu \gamma _5 c_d \, [1^+], \bar{c}_d \sigma _{\mu \nu } c_d \, [1^\pm ], \end{aligned}$$

(5)

we can construct the following currents having $J^P=1/2^+$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\eta _1 = [\epsilon ^{abc} (u^T_a C d_b) \gamma _5 u_c] [\bar{c}_d c_d], \nonumber \\&\eta _2 = [\epsilon ^{abc} (u^T_a C d_b) u_c] [\bar{c}_d \gamma _5 c_d], \nonumber \\&\eta _3 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) u_c] [\bar{c}_d c_d], \nonumber \\&\eta _4 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d], \nonumber \\&\eta _5 = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\mu c_d], \nonumber \\&\eta _6 = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\mu \gamma _5 c_d], \nonumber \\&\eta _7 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\mu c_d], \nonumber \\&\eta _8 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\mu \gamma _5 c_d], \nonumber \\&\eta _9 = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } \gamma _5 u_c] [\bar{c}_d \sigma _{\mu \nu } c_d], \nonumber \\&\eta _{10} = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } u_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 c_d], \nonumber \\&\eta _{11} = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } u_c] [\bar{c}_d \sigma _{\mu \nu } c_d], \nonumber \\&\eta _{12} = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 u_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 c_d].\nonumber \\&\eta _{13} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) u_c] [\bar{c}_d \gamma _\mu c_d], \nonumber \\&\eta _{14} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _\mu \gamma _5 c_d], \nonumber \\&\eta _{15} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu u_c] [\bar{c}_d \sigma _{\mu \nu } c_d], \nonumber \\&\eta _{16} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 u_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 c_d]. \end{aligned}$$

(6)

We can verify the following relations:

$$\begin{aligned}&\eta _{9} = \eta _{10},\nonumber \\&\eta _{11} = \eta _{12},\nonumber \\&\eta _{11} = \eta _{9} + 2i \eta _{15} - 2i \eta _{16}. \end{aligned}$$

(7)

Hence, only 13 currents are independent in Eq. (6). All of them have $J^P = 1/2^+$, while their partner currents, $\gamma _5 \eta _i$, have $J^P = 1/2^-$. We shall not use all of them to perform QCD sum rule analyses, but select those containing pseudoscalar ($\bar{c}_d \gamma _5 c_d$) and vector ($\bar{c}_d \gamma _\mu c_d$) components

$$\begin{aligned} \eta _2 - \eta _4= & {} [\epsilon ^{abc} (u^T_a C d_b) u_c] [\bar{c}_d \gamma _5 c_d]\nonumber \\&- [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d],\end{aligned}$$

(8)

$$\begin{aligned} \eta _5 - \eta _7= & {} [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\mu c_d]\nonumber \\&- [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\mu c_d],\end{aligned}$$

(9)

$$\begin{aligned} \eta _{13}= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) u_c] [\bar{c}_d \gamma _\mu c_d]. \end{aligned}$$

(10)

Their internal structures are quite simple, suggesting that they well couple to the $[p \eta _c]$, $[p J/\psi ]$, and $[N^{*} J/\psi ]$ channels, respectively. Especially, $\eta _2 - \eta _4$ and $\eta _5 - \eta _7$ both contain the “Ioffe’s baryon current”, which couples strongly to the lowest-lying nucleon state [49, 50].

2.2 Currents of $[\bar{c}_d u_d][\epsilon ^{abc} u_a d_b c_c]$

In this subsection, we construct the currents of the type $[\bar{c}_d \Gamma _k u_d][\epsilon ^{abc} (u_a^T C \Gamma _i d_b) \Gamma _j c_c]$. The currents of the other types $[\bar{c}_d \Gamma _k u_d][\epsilon ^{abc} (u_a^T C \Gamma _i c_b) \Gamma _j d_c]$ and $[\bar{c}_d \Gamma _k u_d][\epsilon ^{abc} (c_a^T C \Gamma _i d_b) \Gamma _j u_c]$, etc. can be related to these currents by using the Fierz transformation. We find the following currents having $J^P=1/2^+$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\xi _1 = [\epsilon ^{abc} (u^T_a C d_b) \gamma _5 c_c] [\bar{c}_d u_d],\nonumber \\&\xi _2 = [\epsilon ^{abc} (u^T_a C d_b) c_c] [\bar{c}_d \gamma _5 u_d],\nonumber \\&\xi _3 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) c_c] [\bar{c}_d u_d],\nonumber \\&\xi _4 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\nonumber \\&\xi _5 = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\nonumber \\&\xi _6 = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\nonumber \\&\xi _7 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\mu u_d],\nonumber \\&\xi _8 = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\nonumber \\&\xi _9 = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\nonumber \\&\xi _{10} = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\nonumber \\&\xi _{11} = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\nonumber \\&\xi _{12} = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\nonumber \\&\xi _{13} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d u_d],\nonumber \\&\xi _{14} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _5 u_d],\nonumber \\&\xi _{15} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d u_d],\nonumber \\&\xi _{16} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\nonumber \\&\xi _{17} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\nonumber \\&\xi _{18} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\nonumber \\&\xi _{19} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\mu u_d],\nonumber \\&\xi _{20} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\nonumber \\&\xi _{21} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\nonumber \\&\xi _{22} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\nonumber \\&\xi _{23} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\nu u_d],\nonumber \\&\xi _{24} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\nonumber \\&\xi _{25} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\nonumber \\&\xi _{26} = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\nonumber \\&\xi _{27} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\nonumber \\&\xi _{28} = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d], \end{aligned}$$

$$\begin{aligned}&\xi _{29} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d u_d],\nonumber \\&\xi _{30} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _5 u_d],\nonumber \\&\xi _{31} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d u_d],\nonumber \\&\xi _{32} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\nonumber \\&\xi _{33} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\nonumber \\&\xi _{34} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\nonumber \\&\xi _{35} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu u_d],\nonumber \\&\xi _{36} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\nonumber \\&\xi _{37} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\nonumber \\&\xi _{38} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\nonumber \\&\xi _{39} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\nonumber \\&\xi _{40} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\nonumber \\&\xi _{41} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d], \nonumber \\&\xi _{42} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d], \nonumber \\&\xi _{43} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } u_d], \nonumber \\&\xi _{44} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d]. \end{aligned}$$

(11)

We can verify the following relations:

$$\begin{aligned}&\xi _{9} = \xi _{10},\nonumber \\&\xi _{11} = \xi _{12},\nonumber \\&\xi _{29} = \xi _{31},\nonumber \\&\xi _{30} = \xi _{32},\nonumber \\&\xi _{37} = \xi _{40},\nonumber \\&\xi _{38} = \xi _{39}. \end{aligned}$$

(12)

Then there are only 38 independent currents left. To perform QCD sum rule analyses, we shall use

$$\begin{aligned} \xi _2 - \xi _4= & {} [\epsilon ^{abc} (u^T_a C d_b) c_c] [\bar{c}_d \gamma _5 u_d]\nonumber \\&- [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\end{aligned}$$

(13)

$$\begin{aligned} \xi _5 - \xi _7= & {} [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d]\nonumber \\&- [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\mu u_d],\end{aligned}$$

(14)

$$\begin{aligned} \xi _{14}= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _5 u_d],\end{aligned}$$

(15)

$$\begin{aligned} \xi _{16}= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\end{aligned}$$

(16)

$$\begin{aligned} \xi _{17}= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\end{aligned}$$

(17)

$$\begin{aligned} \xi _{19}= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\mu u_d], \end{aligned}$$

(18)

which well couple to the $[\Lambda _c {\bar{D}}]$, $[\Lambda _c {\bar{D}}^{*}]$, $[\Sigma _c {\bar{D}}]$, $[\Lambda ^{*}_c {\bar{D}}]$, $[\Sigma _c^{*} {\bar{D}}^{*}]$ and $[\Lambda ^{*}_c {\bar{D}}^{*}]$ channels, respectively.

2.3 Currents of $[\bar{c}_d d_d][\epsilon ^{abc} u_a u_b c_c]$

In this subsection, we construct the currents of the type $[\bar{c}_d \Gamma _k d_d][\epsilon ^{abc} (u_a^T C \Gamma _i u_b) \Gamma _j c_c]$. The currents of the other types $[\bar{c}_d \Gamma _k d_d][\epsilon ^{abc} (u_a^T C \Gamma _i c_b) \Gamma _j u_c]$ and $[\bar{c}_d \Gamma _k d_d][\epsilon ^{abc} (c_a^T C \Gamma _i u_b) \Gamma _j u_c]$ can be related to these currents by using the Fierz transformation. We find the following currents having $J^P=1/2^+$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\psi _1 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d d_d],\nonumber \\&\psi _2 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\mu c_c] [\bar{c}_d \gamma _5 d_d],\nonumber \\&\psi _3 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu d_d],\nonumber \\&\psi _4 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) c_c] [\bar{c}_d \gamma _\mu \gamma _5 d_d],\nonumber \\&\psi _5 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d],\nonumber \\&\psi _6 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\nonumber \\&\psi _7 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\nonumber \\&\psi _8 = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d],\nonumber \\&\psi _9 = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d d_d],\nonumber \\&\psi _{10} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _5 d_d],\nonumber \\&\psi _{11} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d d_d],\nonumber \\&\psi _{12} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _5 d_d],\nonumber \\&\psi _{13} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d],\nonumber \\&\psi _{14} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\nonumber \\&\psi _{15} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu d_d],\nonumber \\&\psi _{16} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\nonumber \\&\psi _{17} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\nonumber \\&\psi _{18} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d],\nonumber \\&\psi _{19} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\nonumber \\&\psi _{20} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d],\nonumber \\&\psi _{21} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\nonumber \\&\psi _{22} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\nonumber \\&\psi _{23} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\nonumber \\&\psi _{24} = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d]. \end{aligned}$$

(19)

We can verify the following relations:

$$\begin{aligned}&\psi _9 = \psi _{11},\nonumber \\&\psi _{10} = \psi _{12},\nonumber \\&\psi _{18} = \psi _{19},\nonumber \\&\psi _{17} = \psi _{20}. \end{aligned}$$

(20)

Then there are 20 independent currents left. To perform QCD sum rule analyses, we shall use

$$\begin{aligned} \psi _2= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\mu c_c] [\bar{c}_d \gamma _5 d_d], \end{aligned}$$

(21)

$$\begin{aligned} \psi _3= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu d_d], \end{aligned}$$

(22)

which well couple to the $[\Sigma ^{*}_c {\bar{D}}]$ and $[\Sigma _c^{*} {\bar{D}}^{*}]$ channels, respectively.

2.4 A short summary

In the previous subsections, we systematically construct all local pentaquark interpolating currents having $J^P=1/2^+$ and quark contents $uud c \bar{c}$. We find 13 independent currents of the color configuration $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$, 38 independent currents of the color configuration $[\bar{c}_d u_d][\epsilon ^{abc} u_a d_b c_c]$, and 20 independent currents of the color configuration $[\bar{c}_d d_d][\epsilon ^{abc} u_a u_b c_c]$. One may wonder that there are altogether 71 independent currents. Actually, some of these currents can be related by applying the color rearrangement in Eq. (1). Considering there are 71 currents in all, it will be too complicate to perform thorough transformation one by one. However, we can give an estimation that at least one third of these 71 currents are not independent and can be expressed by other currents.

We shall not discuss this any more, but start to perform QCD sum rule analyses using the currents selected in this section as well as those selected in Appendices A and B.

3 QCD sum rules analyses

In the following, we shall use the method of QCD sum rules [51–55] to investigate the currents selected in Sect. 2 and in Appendices A and B. The results obtained using the $J^P=1/2^+$ currents $\eta _2 - \eta _4$, $\eta _5 - \eta _7$, $\eta _{13}$, $\xi _2 - \xi _4$, $\xi _5 - \xi _7$, $\xi _{14}$, $\xi _{16}$, $\xi _{17}$, $\xi _{19}$, $\psi _2$, and $\psi _3$ are listed in Table 1, those obtained using the $J^P=3/2^-$ currents $\eta _{5\mu } - \eta _{7\mu }$, $\eta _{18\mu }$, $\eta _{19\mu }$, $\xi _{5\mu } - \xi _{7\mu }$, $\xi _{18\mu }$, $\xi _{20\mu }$, $\xi _{25\mu }$, $\xi _{27\mu }$, $\xi _{33\mu }$, $\xi _{35\mu }$, $\psi _{2\mu }$, $\psi _{5\mu }$, and $\psi _{9\mu }$ are listed in Table 2, and those obtained using the $J^P=5/2^+$ currents $\eta _{11\mu \nu }$, $\xi _{13\mu \nu }$, $\xi _{15\mu \nu }$, and $\psi _{3\mu \nu }$ are listed in Table 3.

Table 1 Numerical results for the spin $J=1/2$ hidden-charm pentaquark states

Table 2 Numerical results for the spin $J=3/2$ hidden-charm pentaquark states. $\psi _{9\mu }$ is denoted $J^{{\bar{D}}^{*} \Sigma _c}_\mu$ in Ref. [46]

Table 3 Numerical results for the spin $J=5/2$ hidden-charm pentaquark states. $\xi _{15\mu \nu }$, $\psi _{4\mu \nu }$ and $J^\mathrm{mix}_{\mu \nu }$ are denoted $J^{{\bar{D}}^{*} \Lambda _c}_{\{\mu \nu \}}$, $J^{{\bar{D}} \Sigma _c^{*}}_{\{\mu \nu \}}$ and $J^{{\bar{D}} \Sigma _c^{*} \& {\bar{D}}^{*} \Lambda _c}_{\{\mu \nu \}}$ in Ref. [46], respectively

We use J, $J_{\mu }$, and $J_{\mu \nu }$ to denote the currents having spin $J=1/2$, 3 / 2, and 5 / 2, respectively, and assume they couple to the physical states X through

$$\begin{aligned}&\langle 0 | J | X_{1/2} \rangle = f_X u (p),\nonumber \\&\langle 0 | J_{\mu } | X_{3/2} \rangle = f_X u_\mu (p),\nonumber \\&\langle 0 | J_{\mu \nu } | X_{5/2} \rangle = f_X u_{\mu \nu } (p). \end{aligned}$$

(23)

The two-point correlation functions obtained using these currents can be written as

$$\begin{aligned}&\Pi \left( q^2\right) = i \int d^4x e^{iq\cdot x} \langle 0 | T\left[ J(x) \bar{J}(0)\right] | 0 \rangle \nonumber \\&~~~~~~~~~~~~~= (q\!\!\slash ~ + M_X) \Pi ^{1/2}\left( q^2\right) ,\end{aligned}$$

(24)

$$\begin{aligned}&\Pi _{\mu \nu }\left( q^2\right) = i \int d^4x e^{iq\cdot x} \langle 0 | T\left[ J_{\mu }(x) \bar{J}_{\nu }(0)\right] | 0 \rangle \nonumber \\&~~~~~~~~~~~~~~~~= \left( \frac{q_\mu q_\nu }{q^2}-g_{\mu \nu }\right) (q\!\!\slash ~ + M_X) \Pi ^{3/2}\left( q^2\right) \nonumber \\&~~~~~~~~~~~~~~~~~~~~~~ + \cdots , \end{aligned}$$

(25)

$$\begin{aligned}&\Pi _{\mu \nu \rho \sigma }\left( q^2\right) = i \int d^4x e^{iq\cdot x} \langle 0 | T\left[ J_{\mu \nu }(x) \bar{J}_{\rho \sigma }(0)\right] | 0 \rangle \nonumber \\&~~~~~~~~~~~~~~~~~~~~= \left( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma } g_{\nu \rho } \right) (q\!\!\slash ~ + M_X) \Pi ^{5/2}\left( q^2\right) \nonumber \\&~~~~~~~~~~~~~~~~~~~~~~~~~~+ \cdots , \end{aligned}$$

(26)

where $\cdots$ in Eq. (25) contains the spin 1 / 2 components of $J_{\mu }$, and $\cdots$ in Eq. (26) contains the spin 1 / 2 and 3 / 2 components of $J_{\mu \nu }$.

We note that we have assumed that X has the same parity as J, and used the non-$\gamma _5$ coupling in Eq. (23). We can also use the $\gamma _5$ coupling

$$\begin{aligned} \langle 0 | J | X^\prime \rangle= & {} f_{X^\prime } \gamma _5 u (p), \end{aligned}$$

(27)

when $X^\prime$ has the opposite parity from J. Or we can use the partner of the current $\gamma _5 J$ having the opposite parity,

$$\begin{aligned} \langle 0 | \gamma _5 J | X \rangle= & {} f_X \gamma _5 u (p). \end{aligned}$$

(28)

See also discussions in Refs. [56–59]. These two assumptions both lead to the two-point correlation functions which are similar to Eqs. (24)–(26), but with $(q\!\!\!\slash ~ + M_{X^{(\prime )}})$ replaced by $(- q\!\!\!\slash ~ + M_{X^{(\prime )}})$. This difference would tell us the parity of the hadron $X^{(\prime )}$. Technically, in the following analyses we use the terms proportional to $\mathbf {1}$, $\mathbf {1} \times g_{\mu \nu }$ and $\mathbf {1} \times g_{\mu \rho } g_{\nu \sigma }$ to evaluate the mass of X, which are then compared with those proportional to $q\!\!\!\slash ~$, $q\!\!\!\slash ~ \times g_{\mu \nu }$ and $q\!\!\!\slash ~ \times g_{\mu \rho } g_{\nu \sigma }$ to determine its parity.

We can calculate the two-point correlation functions (24)–(26) in the QCD operator product expansion (OPE) up to certain order in the expansion, which is then matched with a hadronic parametrization to extract information as regards hadron properties. At the hadron level, it can be written as

$$\begin{aligned} \Pi (q^2)={\frac{1}{\pi }}\int ^\infty _{s_<}\frac{\mathrm{Im} \Pi (s)}{s-q^2-i\varepsilon }\mathrm{d}s, \end{aligned}$$

(29)

where we have used the form of the dispersion relation, and $s_<$ denotes the physical threshold. The imaginary part of the correlation function is defined as the spectral function, which is usually evaluated at the hadron level by inserting intermediate hadron states $\sum _n|n\rangle \langle n|$

$$\begin{aligned} \rho (s) \equiv \frac{1}{\pi }\mathrm{Im}\Pi (s)= & {} \sum _n\delta (s-M^2_n)\langle 0|\eta |n\rangle \langle n|{\eta ^\dagger }|0\rangle \nonumber \\= & {} f_X^2\delta (s-m_X^2)+ \text{ continuum }, \end{aligned}$$

(30)

where we have adopted the usual parametrization of one-pole dominance for the ground state X and a continuum contribution. The spectral density $\rho (s)$ can also be evaluated at the quark and gluon level via the QCD operator product expansion. After performing the Borel transform at both the hadron and the QCD levels, the two-point correlation function can be expressed as

$$\begin{aligned} \Pi ^{(all)}(M_B^2)\equiv \mathcal {B}_{M_B^2}\Pi (p^2) = \int ^\infty _{s_<} e^{-s/M_B^2} \rho (s) \mathrm{d}s. \end{aligned}$$

(31)

Finally, we assume that the contribution from the continuum states can be approximated well by the OPE spectral density above a threshold value $s_0$ (duality), and arrive at the sum rule relation which can be used to perform numerical analyses:

$$\begin{aligned} M^2_X(s_0, M_B)= & {} {\int ^{s_0}_{s_<} e^{-s/M_B^2} \rho (s) s \mathrm{d}s \over \int ^{s_0}_{s_<} e^{-s/M_B^2} \rho (s) \mathrm{d}s}, \end{aligned}$$

(32)

$$\begin{aligned} \rho ^{[N^{*} J/\psi ]}_{\mu \nu \rho \sigma }(s)= & {} \mathbf {1} \times \big ( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma }g_{\nu \rho } \big ) \times \left( \rho ^{\mathrm{pert}}_1(s)+\rho ^{\langle \bar{q}q\rangle }_1(s)+\rho ^{\langle GG\rangle }_1(s)+\rho ^{\langle \bar{q}q\rangle ^2}_1(s)+\rho ^{\langle \bar{q}Gq\rangle }_1(s)+\rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_1(s) \right) \nonumber \\&+\; q\!\!\!\slash ~\times \big ( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma }g_{\nu \rho } \big ) \times \left( \rho ^{\mathrm{pert}}_2(s)+\rho ^{\langle \bar{q}q\rangle }_2(s)+\rho ^{\langle GG\rangle }_2(s)+\rho ^{\langle \bar{q}q\rangle ^2}_2(s)+\rho ^{\langle \bar{q}Gq\rangle }_2(s)+\rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_2(s) \right) + \cdots . \nonumber \\ \rho ^{\mathrm{pert}}_1(s)= & {} 0, \nonumber \\ \rho ^{\langle \bar{q}q\rangle }_1(s)= & {} -\frac{\langle \bar{q}q\rangle }{49152\pi ^6} \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left\{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^4 \times \frac{(1-\alpha -\beta )(11 + 11\alpha + 11\beta + 8\alpha ^2 + 16\alpha \beta + 8\beta ^2)}{\alpha ^3\beta ^3} \right. \nonumber \\&\left. -\;m_c^2\left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \frac{4(1-\alpha -\beta )(11 - 7\alpha - 7\beta - 4\alpha ^2 - 8\alpha \beta - 4\beta ^2)}{\alpha ^3\beta ^3} \right\} ,\nonumber \\ \rho ^{\langle GG\rangle }_1(s)= & {} 0,\nonumber \\ \rho ^{\langle \bar{q}Gq\rangle }_1(s)= & {} \frac{\langle \bar{q}g_s\sigma \cdot Gq\rangle }{4096\pi ^6} \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left\{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \frac{\alpha + \beta + 2\alpha ^2 + 4\alpha \beta + 2\beta ^2}{\alpha ^2\beta ^2}\right. \nonumber \\&\left. -\; m_c^2\left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \frac{3(2 - \alpha - \beta - \alpha ^2 - 2\alpha \beta - \beta ^2)}{\alpha ^2\beta ^2} \right\} ,\nonumber \\ \rho ^{\langle \bar{q}q\rangle ^2}_1(s)= & {} 0,\nonumber \\ \rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_1(s)= & {} 0,\nonumber \\ \rho ^{\mathrm{pert}}_2(s)= & {} - \frac{1}{6553600\pi ^8}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left\{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^5 \times \frac{(1-\alpha -\beta )^3(57 + 31\alpha + 31\beta + 12\alpha ^2 + 24\alpha \beta + 12\beta ^2)}{\alpha ^4\beta ^4}\right. \nonumber \\&\left. -\; m_c^2 \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^4 \times \frac{5(1-\alpha -\beta )^3(19 - 13\alpha - 13\beta - 6\alpha ^2 - 12\alpha \beta - 6\beta ^2)}{\alpha ^4\beta ^4} \right\} ,\nonumber \\ \rho ^{\langle \bar{q}q\rangle }_2(s)= & {} 0,\nonumber \\ \rho ^{\langle GG\rangle }_2(s)= & {} \frac{\langle g_s^2GG\rangle }{23592960 \pi ^8}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left\{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \left( \frac{3(1-\alpha -\beta )(11 + 11\alpha + 11\beta - 4\alpha ^2 - 8\alpha \beta - 4\beta ^2)}{\alpha ^2\beta ^2} \right. \right. \nonumber \\&\left. +\; \frac{(1-\alpha -\beta )^3(83 + 29\alpha + 29\beta - 12\alpha ^2 - 24\alpha \beta - 12\beta ^2)}{\alpha ^3\beta ^3} \right) \nonumber \\&+\; m_c^2 \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \left( - \frac{3(1-\alpha -\beta )^3(57+31\alpha +31\beta +12\alpha ^2+24\alpha \beta +12\beta ^2)}{\alpha \beta ^4} \right. \nonumber \\&-\; \frac{9(1-\alpha -\beta )(11-13\alpha -13\beta +2\alpha ^2+4\alpha \beta +2\beta ^2)}{\alpha ^2\beta ^2} + \frac{9(1-\alpha -\beta )^4(19+6\alpha +6\beta )}{\alpha ^2\beta ^4} \nonumber \\&\left. -\; \frac{3(1-\alpha -\beta )^3(57+31\alpha +31\beta +12\alpha ^2+24\alpha \beta +12\beta ^2)}{\alpha ^4\beta } + \frac{9(1-\alpha -\beta )^4(19+6\alpha +6\beta )}{\alpha ^4\beta ^2}\right) \nonumber \\&+\; m_c^4 \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] \times \left( \frac{6(1-\alpha -\beta )^3(19-13\alpha -13\beta -6\alpha ^2-12\alpha \beta -6\beta ^2)}{\alpha \beta ^4} \right. \nonumber \\&\left. \left. +\; \frac{6(1-\alpha -\beta )^3(19-13\alpha -13\beta -6\alpha ^2-12\alpha \beta -6\beta ^2)}{\alpha ^4\beta }\right) \right\} ,\nonumber \\ \rho ^{\langle \bar{q}Gq\rangle }_2(s)= & {} 0,\nonumber \\ \rho ^{\langle \bar{q}q\rangle ^2}_2(s)= & {} -\frac{\langle \bar{q}q\rangle ^2}{512\pi ^4} \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \Bigg \{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \frac{5(\alpha + \beta )}{\alpha \beta } - m_c^2 \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] \times \frac{10(1 - \alpha - \beta )}{\alpha \beta } \Bigg \}, \nonumber \\ \rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_2(s)= & {} \frac{11\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma \cdot Gq\rangle }{1024\pi ^4} \times \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \Bigg \{ \left[ m_c^2-\alpha (1-\alpha ) s\right] - \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \Big (\left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] + m_c^2\Big ) \Bigg \}, \end{aligned}$$

(33)

$$\begin{aligned} \rho ^{[\Sigma _c {\bar{D}}^{*}]}_{\mu \nu }(s)= & {} \mathbf {1} \times g_{\mu \nu } \times \left( \rho ^{\mathrm{pert}}_3(s)+\rho ^{\langle \bar{q}q\rangle }_3(s)+\rho ^{\langle GG\rangle }_3(s)+\rho ^{\langle \bar{q}q\rangle ^2}_3(s)+\rho ^{\langle \bar{q}Gq\rangle }_3(s)+\rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_3(s) \right) \nonumber \\&+\; q\!\!\!\slash ~\times g_{\mu \nu } \times \left( \rho ^{\mathrm{pert}}_4(s)+\rho ^{\langle \bar{q}q\rangle }_4(s)+\rho ^{\langle GG\rangle }_4(s)+\rho ^{\langle \bar{q}q\rangle ^2}_4(s)+\rho ^{\langle \bar{q}Gq\rangle }_4(s)+\rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_4(s) \right) + \cdots .\nonumber \\ \rho ^{\mathrm{pert}}_3(s)= & {} \frac{m_c}{163840\pi ^8}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^5 \times \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{\alpha ^5\beta ^4}, \nonumber \\ \rho ^{\langle \bar{q}q\rangle }_3(s)= & {} -\frac{m_c^2\langle \bar{q}q\rangle }{512\pi ^6}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \frac{(1-\alpha -\beta )^2}{\alpha ^3\beta ^3},\nonumber \\ \rho ^{\langle GG\rangle }_3(s)= & {} \frac{m_c\langle g_s^2GG\rangle }{16384\pi ^8}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left\{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \left( -\frac{(1-\alpha -\beta )(1+\alpha +\beta )}{2\alpha ^3\beta ^2} \right. \right. \nonumber \\&\left. -\;\frac{(1-\alpha -\beta )^2(4-\alpha -\beta )}{9\alpha ^3\beta ^3} + \frac{(1-\alpha -\beta )^2(2+\alpha +\beta )}{3\alpha ^4\beta ^2} + \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{12\alpha ^5\beta ^2}\right) \nonumber \\&\left. +\;m_c^2 \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \left( \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{12\alpha ^2\beta ^4} + \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{12\alpha ^5\beta }\right) \right\} , \nonumber \\ \rho ^{\langle \bar{q}Gq\rangle }_3(s)= & {} \frac{m_c^2\langle \bar{q}g_s\sigma \cdot Gq\rangle }{1024\pi ^6}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \frac{3(1-\alpha -\beta )}{\alpha ^2\beta ^2}, \nonumber \\ \rho ^{\langle \bar{q}q\rangle ^2}_3(s)= & {} -\frac{m_c \langle \bar{q}q\rangle ^2}{32\pi ^4} \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \frac{(\alpha +\beta )}{\alpha ^2\beta }, \nonumber \\ \rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_3(s)= & {} \frac{m_c\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma \cdot Gq\rangle }{64\pi ^4} \times \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \Bigg \{ \left[ m_c^2-\alpha (1-\alpha ) s\right] \times \frac{2}{\alpha } - \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] \times \frac{(3\alpha +\beta )}{\alpha ^2} \Bigg \}, \nonumber \\ \rho ^{\mathrm{pert}}_4(s)= & {} \frac{1}{81920\pi ^8}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^5 \times \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{\alpha ^4\beta ^4}, \nonumber \\ \rho ^{\langle \bar{q}q\rangle }_4(s)= & {} -\frac{m_c\langle \bar{q}q\rangle }{256\pi ^6}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \frac{(1-\alpha -\beta )^2}{\alpha ^2\beta ^3}, \nonumber \\ \rho ^{\langle GG\rangle }_4(s)= & {} \frac{\langle g_s^2GG\rangle }{8192\pi ^8}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left\{ \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^3 \times \left( - \frac{(1-\alpha -\beta )^2(4-\alpha -\beta )}{9\alpha ^2\beta ^3} + \frac{(1-\alpha -\beta )^2(2+\alpha +\beta )}{6\alpha ^3\beta ^2}\right) \right. \nonumber \\&\left. +\;m_c^2 \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \left( \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{12\alpha \beta ^4} + \frac{(1-\alpha -\beta )^3(3+\alpha +\beta )}{12\alpha ^4\beta } \right) \right\} , \nonumber \\ \rho ^{\langle \bar{q}Gq\rangle }_4(s)= & {} \frac{m_c\langle \bar{q}g_s\sigma \cdot Gq\rangle }{512\pi ^6}\int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \frac{3(1-\alpha -\beta )}{\alpha \beta ^2}, \nonumber \\ \rho ^{\langle \bar{q}q\rangle ^2}_4(s)= & {} -\frac{\langle \bar{q}q\rangle ^2}{64\pi ^4} \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] ^2 \times \frac{(\alpha +\beta )}{\alpha \beta }, \nonumber \\ \rho ^{\langle \bar{q}q\rangle \langle \bar{q}Gq\rangle }_4(s)= & {} \frac{\langle \bar{q}q\rangle \langle \bar{q}g_s\sigma \cdot Gq\rangle }{128\pi ^4} \times \int ^{\alpha _{\mathrm{max}}}_{\alpha _{\mathrm{min}}}\mathrm{d}\alpha \left\{ 2 \left[ m_c^2-\alpha (1-\alpha ) s\right] - \int ^{\beta _{\mathrm{max}}}_{\beta _{\mathrm{min}}}\mathrm{d}\beta \left[ (\alpha +\beta )m_c^2-\alpha \beta s\right] \times \frac{(3\alpha +\beta )}{\alpha } \right\} . \end{aligned}$$

(34)

In this paper we evaluate the QCD spectral density $\rho (s)$ at the leading order on $\alpha _s$ and up to dimension eight, including the perturbative term, the quark condensate $\langle \bar{q} q \rangle$, the gluon condensate $\langle g_s^2 GG \rangle$, the quark–gluon mixed condensate $\langle g_s \bar{q} \sigma G q \rangle$, and their combinations $\langle \bar{q} q \rangle ^2$ and $\langle \bar{q} q \rangle \langle g_s \bar{q} \sigma G q \rangle$. The results of these spectral densities are too lengthy, so we list them in the supplementary file “OPE.nb”. In the calculations we ignore the chirally suppressed terms with the light quark mass and adopt the factorization assumption of vacuum saturation for higher dimensional condensates ($D=6$ and $D=8$). We shall find that the $D=3$ quark condensate $\langle \bar{q}q\rangle$ and the $D=5$ mixed condensate $\langle \bar{q}g_s\sigma \cdot Gq\rangle$ are both multiplied by the charm quark mass $m_c$, which are thus important power corrections to the correlation functions.

Fig. 1

In the left panel we show CVG, defined in Eq. (36), as a function of the Borel mass $M_B$. In the right panel we show the relative contribution of each term on the OPE expansion, as a function of the Borel mass $M_B$. The current $\psi _{9\mu }$ of $J^P = 3/2^-$ ($J^{{\bar{D}}^{*} \Sigma _c}_\mu$ in Ref. [46]) is used here

To illustrate our numerical analysis, we use the current $\eta _{11\mu \nu }$ defined in Eq. (55) as an example. It has the quantum number $J^P = 5/2^+$ and couples to the $[N^{*} J/\psi ]$ channel (or the P-wave $[p J/\psi ]$ channel). Its spectral density $\rho ^{[N^{*} J/\psi ]}_{\mu \nu \rho \sigma }(s)$ are listed in Eq. (33), where $m_c$ is the heavy quark mass, and the integration limits are $\alpha _{\mathrm{min}}=\frac{1-\sqrt{1-4m_c^2/s}}{2}$, $\alpha _{\mathrm{max}}=\frac{1+\sqrt{1-4m_c^2/s}}{2}$, $\beta _{\mathrm{min}}=\frac{\alpha m_c^2}{\alpha s-m_c^2}$, $\beta _{\mathrm{max}}=1-\alpha$. We only list the terms proportional to $\mathbf {1} \times \big ( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma }g_{\nu \rho } \big )$ and $q\!\!\!\slash ~ \times \big ( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma }g_{\nu \rho } \big )$, and $\cdots$ denotes other Lorentz structures, such as $\mathbf {1} \times g_{\mu \rho } \sigma _{\nu \sigma }$, etc. We find that the results are not useful, because many terms vanish in this spectral density: its $q\!\!\!\slash ~ \times \big ( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma }g_{\nu \rho } \big )$ part only contains the perturbative term, $\langle g_s^2 GG \rangle$, $\langle \bar{q} q \rangle ^2$ and $\langle \bar{q} q \rangle \langle g_s \bar{q} \sigma G q \rangle$, but its $\mathbf {1} \times \big ( g_{\mu \rho }g_{\nu \sigma } + g_{\mu \sigma }g_{\nu \rho } \big )$ part only contains $\langle \bar{q} q \rangle$ and $\langle g_s \bar{q} \sigma G q \rangle$. This makes a bad OPE convergence and leads to unreliable results. Moreover, the parity cannot be determined because these two parts are quite different. We shall not use these currents to perform QCD sum rule analyses from which the parity cannot be determined.

We use the current $\psi _{9\mu }$ defined in Eq. (54) as another example. It has the quantum number $J^P = 3/2^-$ and couples to the $[\Sigma _c {\bar{D}}^{*}]$ channel. Its spectral density $\rho ^{[\Sigma _c {\bar{D}}^{*}]}_{\mu \nu }(s)$ is listed in Eq. (34). We find that the terms proportional to $\mathbf {1} \times g_{\mu \nu }$ are almost the same as those proportional to $q\!\!\!\slash ~\times g_{\mu \nu }$. Hence, the parity of X can be well determined to be negative, the same as $\psi _{9\mu }$. In the next section we shall use the terms proportional to $\mathbf {1} \times g_{\mu \nu }$ to evaluate the mass of X.

4 Numerical analysis

In this section we still use the current $\psi _{9\mu }$ as an example to perform the numerical analysis. We use the following QCD parameters of quark masses and various condensates in our analysis [2, 60–67]:

(35)

where the running mass in the $\overline{MS}$ scheme is used for the charm quark.

There are two free parameters in Eq. (32): the Borel mass $M_B$ and the threshold value $s_0$. We use two criteria to constrain the Borel mass $M_B$. In order to ensure the convergence of the OPE series, the first criterion is to require that the dimension eight term be less than 10 % to determine its lower limit $M_B^{\mathrm{min}}$:

$$\begin{aligned} \text{ Convergence } \text{(CVG) } \equiv \left| \frac{ \Pi _{\langle \bar{q} q \rangle \langle g_s \bar{q} \sigma G q \rangle }(\infty , M_B) }{ \Pi (\infty , M_B) }\right| \le 10\,\%. \end{aligned}$$

(36)

We show this function obtained using $\psi _{9\mu }$ in the left panel of Fig. 1. We find that the OPE convergence improves with the increase of $M_B$. This criterion has a limitation on the Borel mass that $M_B^2 \ge 3.94$ GeV$^2$. Actually, the convergence can be even better if there is a clear trend of convergence with the higher order terms giving a progressively smaller contribution. Accordingly, we also show the relative contribution of each term on the OPE expansion in the right panel of Fig. 1. We find that a good convergence can be achieved in the same region $M_B^2 \ge 3.94$ GeV$^2$. We shall still use the previous criterion to determine the lower limit of the Borel mass, which can be applied more easily.

To ensure that the one-pole parametrization in Eq. (30) is valid, the second criterion is to require that the pole contribution (PC) be larger than 10 % to determine the upper limit on $M_B^2$:

$$\begin{aligned} \text{ PC } \equiv \frac{ \Pi (s_0, M_B) }{ \Pi (\infty , M_B) } \ge 10\,\%. \end{aligned}$$

(37)

We show the variation of the pole contribution obtained using $\psi _{9\mu }$ in Fig. 2, with respect to the Borel mass $M_B$ and when $s_0$ is chosen to be 21 GeV$^2$. We find that the PC decreases with the increase of $M_B$. This criterion has a limitation on the Borel mass that $M_B^2 \le 4.27$ GeV$^2$. Together we obtain the working region of Borel mass 3.94 GeV$^2< M_B^2 < 4.27$ GeV$^2$ for the current $\psi _{9\mu }$ with the continuum threshold $s_0 = 21$ GeV$^2$. The most important drawback of this current, as well as other pentaquark currents used in this paper, is that their pole contributions are small. One reason is that the two $P_c$’s poles are both mixed with the $J/\psi p$ continuum, so the continuum contribution may not be well suppressed by the Borel transformation. Another reason is due to the large powers of s in the spectral function; see other sum rule analyses for the six-quark state $d^{*}(2380)$ [68] and the F-wave heavy mesons [69].

Fig. 2

The variation of PC, defined in Eq. (37), as a function of the Borel mass $M_B$. The current $\psi _{9\mu }$ of $J^P = 3/2^-$ ($J^{{\bar{D}}^{*} \Sigma _c}_\mu$ in Ref. [46]) is used here and the threshold value is chosen to be $s_0 =21$ GeV$^2$

Fig. 3

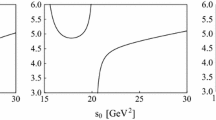
The variation of $M_{[\Sigma _c {\bar{D}}^{*}],3/2^-}$ with respect to the threshold value $s_0$ (left) and the Borel mass $M_B$ (right), calculated using the current ($J^{{\bar{D}}^{*} \Sigma _c}_\mu$ in Ref. [46]) $\psi _{9\mu }$ of $J^P = 3/2^-$. In the left figure, the long-dashed, solid and short-dashed curves are obtained by fixing $M_B^2 = 3.9$, 4.1 and 4.3 GeV$^2$, respectively. In the right figure, the long-dashed, solid and short-dashed curves are obtained for $s_0 = 19$, 21 and 23 GeV$^2$, respectively

Anyway, the Borel mass $M_B$ is just one of the two free parameters. We should also pay attention to the other one, that is, the threshold value $s_0$, and try to find a balance between them. Actually, we can increase $s_0$ to achieve a large enough pole contribution (then the obtained mass would also be increased and not so reasonable), but there is another criterion more important, that is, the $s_0$ stability. We note that in Ref. [70] the author used the requirements on $M_B$ (called the $\tau$ stability) to extract the upper bound on the $0^{++}$ glueball mass, and used the requirement on $s_0$ (called the $t_c$ stability) to evaluate its optimal mass. In this paper we shall use a similar requirement on $s_0$, as discussed in the following.

To determine $s_0$, we require that both the $s_0$ dependence and the $M_B$ dependence of the mass prediction be the weakest in order to obtain reliable mass prediction. We show the variation of $M_X$ with respect to the threshold value $s_0$ in the left panel of Fig. 3, in a large region 15 GeV$^2< s_0 < 25$ GeV$^2$. We find that the mass curves have a minimum against $s_0$ when $s_0$ is around 18 GeV$^2$. Hence, the $s_0$ dependence of the mass prediction is the weakest at this point. However, this value of $s_0$ is too small to give a reasonable working region of $M_B$. A working region can be obtained as long as $s_0>19$ GeV$^2$. Consequently, we choose the region 19 GeV$^2\le s_0\le 23$ GeV$^2$ as our working region, where the $s_0$ dependence is still weak and the mass curves are flat enough.

Fig. 4

The variation of $M_{[\Lambda _c^{*} {\bar{D}}^{*}],5/2^+}$ with respect to the threshold value $s_0$ (left) and the Borel mass $M_B$ (right), calculated using the current $\xi _{15\mu \nu }$ ($J^{{\bar{D}}^{*} \Lambda _c}_{\{\mu \nu \}}$ in Ref. [46]) of $J^P = 5/2^+$. In the left figure, the long-dashed, solid and short-dashed curves are obtained by fixing $M_B^2 = 4.0$, 4.3 and 4.6 GeV$^2$, respectively. In the right figure, the long-dashed, solid and short-dashed curves are obtained for $s_0 = 24$, 26 and 28 GeV$^2$, respectively

Fig. 5

The variations of $M_{[\Sigma _c^{*} {\bar{D}}],5/2^+}$ with respect to the threshold value $s_0$ (left) and the Borel mass $M_B$ (right), calculated using the current $\psi _{4\mu \nu }$ ($J^{{\bar{D}} \Sigma _c^{*}}_{\{\mu \nu \}}$ in Ref. [46]) of $J^P = 5/2^+$. In the left figure, the long-dashed, solid and short-dashed curves are obtained by fixing $M_B^2 = 4.3$, 4.5 and 4.7 GeV$^2$, respectively. In the right figure, the long-dashed, solid and short-dashed curves are obtained for $s_0 = 25$, 27 and 29 GeV$^2$, respectively

Hence, our working regions for the current $\psi _{9\mu }$ are 19 GeV$^2\le s_0\le 23$ GeV$^2$ and 3.94 GeV$^2\le M_B^2 \le 4.27$ GeV$^2$, where the following numerical results can be obtained [46]:

$$\begin{aligned} M_{[\Sigma _c {\bar{D}}^{*}]} = 4.37^{+0.18}_{-0.13}\,\text{ GeV }. \end{aligned}$$

(38)

Here the central value corresponds to $M_B=4.10$ GeV$^2$ and $s_0 = 21$ GeV$^2$, and the uncertainty comes from the Borel mass $M_B$, the threshold value $s_0$, the charm quark mass and the various condensates [55]. We also show the variation of $M_X$ with respect to the Borel mass $M_B$ in the right panel of Fig. 3, in a broader region 2.5 GeV$^2\le M_B^2 \le 5.0$ GeV$^2$. We find that these curves are more stable inside the Borel window 3.94 GeV$^2\le M_B^2 \le 4.27$ GeV$^2$. We note that the threshold value used here, $\sqrt{s_0} \approx 4.58$ GeV, is not far from the obtained mass of 4.37 GeV (but still acceptable), indicating it is not easy to separate the pole and the continuum.

As we have found in Sect. 3 for the current $\psi _{9\mu }$ that the terms proportional to $q\!\!\!\slash ~\times g_{\mu \nu }$ are quite similar to those proportional to $\mathbf {1} \times g_{\mu \nu }$, suggesting that X has the same parity as $\psi _{9\mu }$, which is negative [46]:

$$\begin{aligned} M_{[\Sigma _c {\bar{D}}^{*}],3/2^-} = 4.37^{+0.18}_{-0.13}\,\text{ GeV }. \end{aligned}$$

(39)

This value is consistent with the experimental mass of the $P_c(4380)$ [3], and supports it as a $[\Sigma _c {\bar{D}}^{*}]$ hidden-charm pentaquark with the quantum number $J^P=3/2^-$.

5 Results and discussions

We use the currents selected in Sect. 2 and in Appendixes A and B to perform QCD sum rule analyses. Some of them lead to the OPE series from which the parity can be well determined. We further use these currents to perform numerical analyses. The masses obtained using the $J^P=1/2^+$ currents $\xi _{14}$, $\xi _{16}$, $\xi _{17}$, $\xi _{19}$, $\psi _2$, and $\psi _3$ are listed in Table 1, those obtained using the $J^P=3/2^-$ currents $\xi _{18\mu }$, $\xi _{20\mu }$, $\xi _{25\mu }$, $\xi _{27\mu }$, $\xi _{33\mu }$, $\xi _{35\mu }$, $\psi _{2\mu }$, $\psi _{5\mu }$, and $\psi _{9\mu }$ are listed in Table 2, and those obtained using the $J^P=5/2^+$ currents $\xi _{13\mu \nu }$, $\xi _{15\mu \nu }$, and $\psi _{3\mu \nu }$ are listed in Table 3.

Especially, in the previous sections we have used the current $\psi _{9\mu }$ and obtained the mass $M_{[\Sigma _c {\bar{D}}^{*}],3/2^-} = 4.37^{+0.18}_{-0.13}$ GeV [46]. This value is consistent with the experimental mass of the $P_c(4380)$ [3], and supports it as a $[\Sigma _c {\bar{D}}^{*}]$ hidden-charm pentaquark with the quantum number $J^P=3/2^-$.

Fig. 6

The variations of $M_{\mathrm{mix},5/2^+}$ with respect to the threshold value $s_0$ (left) and the Borel mass $M_B$ (right), calculated using the mixed current $J^\mathrm{mix}_{\mu \nu }$ ($J^{{\bar{D}}\Sigma _c^{*} \& {\bar{D}}^{*}\Lambda _c}_{\{\mu \nu \}}$ in Ref. [46]) of $J^P = 5/2^+$. In the left figure, the long-dashed, solid and short-dashed curves are obtained by fixing $M_B^2 = 3.2$, 3.35 and 3.5 GeV$^2$, respectively. In the right figure, the long-dashed, solid and short-dashed curves are obtained for $s_0 = 20$, 22 and 24 GeV$^2$, respectively

We also use the current $\xi _{15\mu \nu }$ and obtain the mass $M_{[\Lambda _c^{*} {\bar{D}}^{*}],5/2^+} = 4.76^{+0.15}_{-0.19}$ GeV. This value is significantly larger than the experimental mass of the $P_c(4450)$ [3]. Moreover, we show the mass as a function of the threshold value $s_0$ in the left panel of Fig. 4, and find that the mass curves do not have a minimum against $s_0$, which is quite different from the current $\psi _{9\mu }$. We also show the mass as a function of the Borel mass $M_B$ in the right panel of Fig. 4.

To find a good solution consistent with the experiment, we found the mixed current consisting of $\xi _{15\mu \nu }$ and $\psi _{4\mu \nu }$ [46]:

$$\begin{aligned} J^\mathrm{mix}_{\mu \nu } = \cos \theta \times \xi _{15\mu \nu } + \sin \theta \times \psi _{4\mu \nu }. \end{aligned}$$

(40)

We note that $\psi _{4\mu \nu }$ is defined in Eq. (59) and well couples to the P-wave $[\Sigma _c^{*} {\bar{D}}]$ channel. However, it contains the axial-vector ($\bar{c}_d \gamma _\mu \gamma _5 c_d$) component, so not our first choice in this paper. We show the mass obtained using this current $\psi _{4\mu \nu }$ as a function of the threshold value $s_0$ and the Borel mass $M_B$ in Fig. 5. We find that the mass curves have a minimum against $s_0$ when $s_0$ is around 20 GeV$^2$. Moreover, this mass minimum is just around 4.45 GeV, similar to the mass of the $P_c(4450)$ [3]. However, a working region can be obtained as long as $s_0>25$ GeV$^2$, in which region the mass prediction is $4.82^{+0.15}_{-0.14}$ GeV, significantly larger than the mass of the $P_c(4450)$ [3].

To solve this problem, we further use the mixed current $J^\mathrm{mix}_{\mu \nu }$ to perform QCD sum rule analysis. We find that it gives a reliable mass sum rule, when the mixing angle $\theta$ is fine-tuned to be $-51\pm 5^\circ$, and the hadron mass is extracted as [46]

$$\begin{aligned} M_{\mathrm{mix},{5/2^+}} = 4.47^{+0.18}_{-0.13}\,\text{ GeV }, \end{aligned}$$

(41)

with 20 GeV$^2$ $\le s_0 \le 24$ GeV$^2$ and 3.22 GeV$^2$ $\le M_B^2 \le 3.50$ GeV$^2$. This value is consistent with the experimental mass of the $P_c(4450)$ [3], and supports it as an admixture of P-wave $[\Lambda _c{\bar{D}}^{*}]$ and $[\Sigma _c^{*} {\bar{D}}]$ with the quantum number $J^P=5/2^+$. We show the mass as a function of the threshold value $s_0$ and the Borel mass $M_B$ in Fig. 6.

In summary, in this paper we adopt the QCD sum rule approach to study the mass spectrum of hidden-charm pentaquarks. We systematically construct the local pentaquark interpolating currents having spin $J = {1\over 2}/{3\over 2}/{5\over 2}$ and quark contents $uud c \bar{c}$, and select those currents containing pseudoscalar ($\bar{c}_d \gamma _5 c_d$) and vector ($\bar{c}_d \gamma _\mu c_d$) components to perform QCD sum rule analyses. We find some of them lead to the OPE series from which the parity can be well determined, and further use these currents to perform numerical analyses. The results are listed in Tables 1, 2, and 3.

We find that the $P_c(4380)$ and $P_c(4450)$ can be identified as hidden-charm pentaquark states composed of an anti-charmed meson and a charmed baryon. We use $\psi _{9\mu }$ to perform QCD sum rule analysis and the result supports the $P_c(4380)$ as a S-wave $[\Sigma _c{\bar{D}}^{*}]$ hidden-charm pentaquark with the quantum number $J^P=3/2^-$. We use the mixed current $J^\mathrm{mix}_{\mu \nu }$ to perform QCD sum rule analysis, and the result supports the $P_c(4450)$ as an admixture of P-wave $[\Lambda _c {\bar{D}}^{*}]$ and $[\Sigma _c^{*} {\bar{D}}]$ with the quantum number $J^P=5/2^+$. Besides them, our results suggest that

• 1. The lowest-lying hidden-charm pentaquark state of $J^P = 1/2^-$ has the mass $4.33^{+0.17}_{-0.13}$ GeV. This result is obtained by using the current $\psi _2$, which is defined in Eq. (21), and it well couples to the S-wave $[\Sigma _c^{*} {\bar{D}}]$ channel. The one of $J^P = 1/2^+$ is significantly higher, that is, around 4.7–4.9 GeV;

• 2. The lowest-lying hidden-charm pentaquark state of $J^P = 3/2^-$ has the mass $4.37^{+0.18}_{-0.13}$ GeV, consistent with the experimental mass of the $P_c(4380)$ of $J^P = 3/2^-$ [3]. This result is obtained by using the current $\psi _{9\mu }$, which is defined in Eq. (54), and it well couples to the S-wave $[\Sigma _c {\bar{D}}^{*}]$ channel. The one of $J^P = 3/2^+$ is also significantly higher, that is, above 4.6 GeV;

• 3. However, the hidden-charm pentaquark state of $J^P = 5/2^-$ has a mass around 4.5–4.6 GeV, that is, just slightly larger than the experimental mass of the $P_c(4450)$ of $J^P = 5/2^+$ [3].

The discovery of the $P_c(4380)$ and $P_c(4450)$ opens a new page on the exotic hadron states. In the near future, further theoretical and experimental efforts are required to study these hidden-charm pentaquark states.

Appendices

Appendix A: Local Pentaquark currents of spin 3/2

1.1 Currents of $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$. We find the following currents having $J^P=3/2^-$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\eta _{1\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d c_d],\\&\eta _{2\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _5 c_d],\\&\eta _{3\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d c_d],\\&\eta _{4\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d],\\&\eta _{5\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _5 u_c] [\bar{c}_d \gamma _\mu c_d],\\&\eta _{6\mu } = [\epsilon ^{abc} (u^T_a C d_b) u_c] [\bar{c}_d \gamma _\mu \gamma _5 c_d],\\&\eta _{7\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) u_c] [\bar{c}_d \gamma _\mu c_d],\\&\eta _{8\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _\mu \gamma _5 c_d],\\&\eta _{9\mu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } \gamma _5 u_c] [\bar{c}_d \gamma _\nu c_d],\\&\eta _{10\mu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d],\\&\eta _{11\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } u_c] [\bar{c}_d \gamma _\nu c_d],\\&\eta _{12\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d],\\&\eta _{13\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\nu \gamma _5 u_c] [\bar{c}_d \sigma _{\mu \nu } c_d],\\&\eta _{14\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\nu u_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 c_d],\\&\eta _{15\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\nu u_c] [\bar{c}_d \sigma _{\mu \nu } c_d],\\&\eta _{16\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\nu \gamma _5 u_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 c_d],\\&\eta _{17\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) u_c] [\bar{c}_d c_d],\\&\eta _{18\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d],\\&\eta _{19\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu u_c] [\bar{c}_d \gamma _\nu c_d],\\&\eta _{20\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d],\\&\eta _{21\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\nu c_d],\\&\eta _{22\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d],\\&\eta _{23\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) u_c] [\bar{c}_d \sigma _{\mu \nu } c_d],\\&\eta _{24\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 c_d],\\&\eta _{25\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } u_c] [\bar{c}_d \sigma _{\nu \rho } c_d],\\&\eta _{26\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 u_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 c_d],\\&\eta _{27\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \nu } u_c] [\bar{c}_d \sigma _{\nu \rho } c_d],\\&\eta _{28\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 u_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 c_d]. \end{aligned}$$

We can verify the following relation:

$$\begin{aligned} \eta _{25\mu }= & {} \eta _{26\mu }. \end{aligned}$$

To perform QCD sum rule analyses, we shall use

$$\begin{aligned}&\eta _{5\mu } - \eta _{7\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _5 u_c] [\bar{c}_d \gamma _\mu c_d]\nonumber \\&~~~~~~~~~~~~~~~~~~~~ -\;[\epsilon ^{abc} (u^T_a C \gamma _5 d_b) u_c] [\bar{c}_d \gamma _\mu c_d],\end{aligned}$$

(42)

$$\begin{aligned}&\eta _{18\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d],\end{aligned}$$

(43)

$$\begin{aligned}&\eta _{19\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu u_c] [\bar{c}_d \gamma _\nu c_d], \end{aligned}$$

(44)

which well couple to the $[p J/\psi ]$, $[N^{*} \eta _c]$, and $[N^{*} J/\psi ]$ channels, respectively.

We note that the following currents actually have spin $J=1/2$:

$$\begin{aligned}&\eta _{2\mu } - \eta _{4\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _5 c_d] \\&~~~~~~~~~~~~~~~~~~~~-\;[\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d], \\&\eta _{9\mu } - \eta _{11\mu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } \gamma _5 u_c] [\bar{c}_d \gamma _\nu c_d] \\&~~~~~~~~~~~~~~~~~~~~~-\;[\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } u_c] [\bar{c}_d \gamma _\nu c_d], \\&\eta _{21\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\nu c_d]. \end{aligned}$$

1.2 Currents of $[\bar{c}_d u_d][\epsilon ^{abc} u_a d_b c_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d u_d][\epsilon ^{abc} u_a d_b c_c]$. We find the following currents having $J^P=3/2^-$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\xi _{1\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d u_d], \\&\xi _{2\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _5 u_d], \\&\xi _{3\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d u_d],\\&\xi _{4\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{5\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\\&\xi _{6\mu } = [\epsilon ^{abc} (u^T_a C d_b) c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\\&\xi _{7\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\mu u_d],\\&\xi _{8\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\\&\xi _{9\mu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{10\mu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{11\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{12\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{13\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{14\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\nu c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\&\xi _{15\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{16\mu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\&\xi _{17\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _5 c_c] [\bar{c}_d u_d],\\&\xi _{18\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{19\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) c_c] [\bar{c}_d u_d],\\&\xi _{20\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{21\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d u_d],\\&\xi _{22\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{23\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d u_d],\\&\xi _{24\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{25\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{26\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{27\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{28\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{29\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{30\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{31\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{32\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{33\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\\&\xi _{34\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\\&\xi _{35\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\mu u_d],\\&\xi _{36\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\\&\xi _{37\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{38\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\&\xi _{39\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{40\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\ \end{aligned}$$

$$\begin{aligned}&\xi _{41\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{42\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{43\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{44\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{45\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{46\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{47\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{48\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{49\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{50\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\&\xi _{51\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{52\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\&\xi _{53\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d u_d],\\&\xi _{54\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{55\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d u_d],\\&\xi _{56\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{57\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{58\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{59\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{60\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d],\\&\xi _{61\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho u_d],\\&\xi _{62\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d],\\&\xi _{63\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho u_d],\\&\xi _{64\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d],\\&\xi _{65\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\rho u_d],\\&\xi _{66\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d],\\&\xi _{67\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\rho u_d],\\&\xi _{68\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d],\\&\xi _{69\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\\&\xi _{70\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\\&\xi _{71\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\mu u_d],\\&\xi _{72\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\mu \gamma _5 u_d],\\&\xi _{73\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{74\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } d_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{75\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{76\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{77\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{78\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{79\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } u_d],\\&\xi _{80\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d],\\&\xi _{81\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{82\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } d_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d],\\&\xi _{83\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\mu \nu } u_d],\\&\xi _{84\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 u_d]. \end{aligned}$$

We can verify the following relations:

$$\begin{aligned} \xi _{41\mu }= & {} \xi _{42\mu },\\ \xi _{43\mu }= & {} \xi _{44\mu },\\ \xi _{69\mu }= & {} \xi _{71\mu },\\ \xi _{70\mu }= & {} \xi _{72\mu },\\ \xi _{77\mu }= & {} \xi _{80\mu },\\ \xi _{78\mu }= & {} \xi _{79\mu }. \end{aligned}$$

To perform QCD sum rule analyses, we shall use

$$\begin{aligned}&\xi _{5\mu } - \xi _{7\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d] \nonumber \\&~~~~~~~~~~~~~~~~~~~ -\; [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\mu u_d],\end{aligned}$$

(45)

$$\begin{aligned}&\xi _{18\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) c_c] [\bar{c}_d \gamma _5 u_d],\end{aligned}$$

(46)

$$\begin{aligned}&\xi _{20\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\end{aligned}$$

(47)

$$\begin{aligned}&\xi _{25\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\end{aligned}$$

(48)

$$\begin{aligned}&\xi _{27\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\nu u_d],\end{aligned}$$

(49)

$$\begin{aligned}&\xi _{33\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\mu u_d],\end{aligned}$$

(50)

$$\begin{aligned}&\xi _{35\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\mu u_d], \end{aligned}$$

(51)

which well couple to the $[\Lambda _c {\bar{D}}^{*}]$, $[\Sigma _c^{*} {\bar{D}}]$, $[\Lambda _c^{*} {\bar{D}}]$, $[\Sigma _c^{*} {\bar{D}}^{*}]$, $[\Lambda _c^{*} {\bar{D}}^{*}]$, $[\Sigma _c {\bar{D}}^{*}]$ and $[\Lambda _c {\bar{D}}^{*}]$ channels, respectively.

We note that the following currents actually have spin $J=1/2$:

$$\begin{aligned}&\xi _{2\mu } - \xi _{4\mu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _5 u_d]\\&~~~~~~~~~~~~~~~~~~ -\; [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{9\mu } - \xi _{11\mu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d]\\&~~~~~~~~~~~~~~~~~~~ -\; [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{22\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{24\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d],\\&\xi _{29\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d],\\&\xi _{31\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu u_d]. \end{aligned}$$

1.3 Currents of $[\bar{c}_d d_d][\epsilon ^{abc} u_a u_b c_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d d_d][\epsilon ^{abc} u_a u_b c_c]$. We find the following currents having $J^P=3/2^-$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\psi _{1\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _5 c_c] [\bar{c}_d d_d],\\&\psi _{2\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) c_c] [\bar{c}_d \gamma _5 d_d],\\&\psi _{3\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d d_d],\\&\psi _{4\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _5 d_d],\\&\psi _{5\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d],\\&\psi _{6\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\\&\psi _{7\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d],\\&\psi _{8\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\\&\psi _{9\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\mu d_d],\\&\psi _{10\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\mu \gamma _5 d_d],\\&\psi _{11\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\\&\psi _{12\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d],\\&\psi _{13\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\\&\psi _{14\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\\&\psi _{15\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\\&\psi _{16\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\\&\psi _{17\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\\&\psi _{18\mu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d],\\&\psi _{19\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d d_d],\\&\psi _{20\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _5 d_d],\\&\psi _{21\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _\nu c_c] [\bar{c}_d d_d],\\&\psi _{22\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _5 d_d],\\&\psi _{23\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d],\\&\psi _{24\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\\&\psi _{25\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) c_c] [\bar{c}_d \gamma _\nu d_d],\\ \end{aligned}$$

$$\begin{aligned}&\psi _{26\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d],\\&\psi _{27\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho d_d],\\&\psi _{28\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d],\\&\psi _{29\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho d_d],\\&\psi _{30\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d],\\&\psi _{31\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\rho d_d],\\&\psi _{32\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d],\\&\psi _{33\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _\rho d_d],\\&\psi _{34\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \sigma _{\mu \nu } \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d],\\&\psi _{35\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\mu d_d],\\&\psi _{36\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\mu \gamma _5 d_d],\\&\psi _{37\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\mu d_d],\\&\psi _{38\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\mu \gamma _5 d_d],\\&\psi _{39\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\\&\psi _{40\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } u_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\\&\psi _{41\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\\&\psi _{42\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \nu } \gamma _5 u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\\&\psi _{43\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\\&\psi _{44\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\\&\psi _{45\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } d_d],\\&\psi _{46\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d],\\&\psi _{47\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\\&\psi _{48\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } u_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d],\\&\psi _{49\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\mu \nu } d_d],\\&\psi _{50\mu } = [\epsilon ^{abc} (u^T_a C \sigma _{\nu \rho } \gamma _5 u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\mu \nu } \gamma _5 d_d]. \end{aligned}$$

We can verify the following relations:

$$\begin{aligned} \psi _{13\mu }= & {} \psi _{14\mu },\\ \psi _{35\mu }= & {} \psi _{37\mu },\\ \psi _{36\mu }= & {} \psi _{38\mu },\\ \psi _{43\mu }= & {} \psi _{46\mu },\\ \psi _{44\mu }= & {} \psi _{45\mu }. \end{aligned}$$

To perform QCD sum rule analyses, we shall use

$$\begin{aligned} \psi _{2\mu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) c_c] [\bar{c}_d \gamma _5 d_d], \end{aligned}$$

(52)

$$\begin{aligned} \psi _{5\mu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d],\end{aligned}$$

(53)

$$\begin{aligned} \psi _{9\mu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\mu d_d], \end{aligned}$$

(54)

which well couple to the $[\Sigma ^{*}_c {\bar{D}}]$, $[\Sigma _c^{*} {\bar{D}}^{*}]$ and $[\Sigma _c {\bar{D}}^{*}]$ channels, respectively.

We note that the following currents actually have spin $J=1/2$:

$$\begin{aligned} \psi _{4\mu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \sigma _{\mu \nu } c_c] [\bar{c}_d \gamma _5 d_d],\\ \psi _{7\mu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\nu u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d]. \end{aligned}$$

Appendix B: Local Pentaquark currents of spin 5/2

1.1 Currents of $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d c_d][\epsilon ^{abc}u_a d_b u_c]$. We find the following currents having $J^P=5/2^+$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\eta _{1\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\nu c_d] + \{ \mu \leftrightarrow \nu \} \,,\\&\eta _{2\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{3\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\nu c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{4\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{5\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \rho } \gamma _5 u_c] [\bar{c}_d \sigma _{\nu \rho } c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{6\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \rho } u_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{7\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \rho } u_c] [\bar{c}_d \sigma _{\nu \rho } c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{8\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \rho } \gamma _5 u_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{9\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu u_c] [\bar{c}_d c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{10\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{11\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) u_c] [\bar{c}_d \gamma _\nu c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{12\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 u_c] [\bar{c}_d \gamma _\nu \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{13\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } u_c] [\bar{c}_d \gamma _\rho c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{14\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 u_c] [\bar{c}_d \gamma _\rho \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{15\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\rho u_c] [\bar{c}_d \sigma _{\nu \rho } c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{16\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\rho \gamma _5 u_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \}.\\&\eta _{17\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \sigma _{\nu \rho } c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{18\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \} \,. \end{aligned}$$

To perform QCD sum rule analyses, we shall use

$$\begin{aligned} \eta _{11\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) u_c] [\bar{c}_d \gamma _\nu c_d] + \{ \mu \leftrightarrow \nu \}, \end{aligned}$$

(55)

which well couples to the $[N^{*} J/\psi ]$ channel.

We note that the following currents actually have spin $J=3/2$:

$$\begin{aligned}&\eta _{1\mu \nu } - \eta _{3\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 u_c] [\bar{c}_d \gamma _\nu c_d]\\&~~~~~~~~~~~~~~~~~~~~~~~~ -\;[\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu u_c] [\bar{c}_d \gamma _\nu c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{10\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 u_c] [\bar{c}_d \gamma _5 c_d] + \{ \mu \leftrightarrow \nu \},\\&\eta _{13\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } u_c] [\bar{c}_d \gamma _\rho c_d] + \{ \mu \leftrightarrow \nu \}. \end{aligned}$$

1.2 Currents of $[\bar{c}_d u_d][\epsilon ^{abc} u_a d_b c_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d u_d][\epsilon ^{abc} u_a d_b c_c]$. We find the following currents having $J^P=5/2^+$ and quark contents $uud c \bar{c}$:

$$\begin{aligned}&\xi _{1\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{2\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{3\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{4\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{5\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{6\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{7\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{8\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{9\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{10\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{11\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{12\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{13\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{14\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{15\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{16\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{17\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{18\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{19\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{20\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{21\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{22\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{23\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{24\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{25\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{26\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{27\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{28\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{29\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{30\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\ \end{aligned}$$

$$\begin{aligned}&\xi _{31\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{32\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{33\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{34\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{35\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{36\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{37\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\rho u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{38\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{39\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\rho u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{40\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{41\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{42\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \gamma _\rho c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{43\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \gamma _\rho c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{44\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{45\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{46\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{47\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) c_c] [\bar{c}_d \sigma _{\nu \rho } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{48\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{49\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\nu \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\rho \sigma } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{50\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\nu \sigma } c_c] [\bar{c}_d \sigma _{\rho \sigma } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{51\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\nu \sigma } c_c] [\bar{c}_d \sigma _{\rho \sigma } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{52\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\nu \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\rho \sigma } \gamma _5 u_d]\\&~~~~~~~~~~~ +\;\{ \mu \leftrightarrow \nu \},\\&\xi _{53\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\rho \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{54\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } d_b) \sigma _{\rho \sigma } c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{55\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\rho \sigma } c_c] [\bar{c}_d \sigma _{\nu \sigma } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{56\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 d_b) \sigma _{\rho \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 u_d]\\&~~~~~~~~~~~~~~ +\;\{ \mu \leftrightarrow \nu \},\\&\xi _{57\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{58\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{59\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } \gamma _5 d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \sigma _{\nu \sigma } u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{60\mu \nu } = [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } \gamma _5 d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 u_d]\\&~~~~~~~~~~~~ +\;\{ \mu \leftrightarrow \nu \}. \end{aligned}$$

To perform QCD sum rule analyses, we shall use

$$\begin{aligned} \xi _{13\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\end{aligned}$$

(56)

$$\begin{aligned} \xi _{15\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \}, \end{aligned}$$

(57)

which well couple to the $[\Sigma _c^{*} {\bar{D}}^{*}]$ and $[\Lambda _c^{*} {\bar{D}}^{*}]$ channels, respectively.

We note that the following currents actually have spin $J=3/2$:

$$\begin{aligned}&\xi _{1\mu \nu } - \xi _{3\mu \nu } = [\epsilon ^{abc} (u^T_a C d_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d]\\&~~~~~~~~~~~~~~~~~~~~~~ -\; [\epsilon ^{abc} (u^T_a C \gamma _5 d_b) \gamma _\mu c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{10\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \gamma _\nu c_c] [\bar{c}_d \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{12\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _5 u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{17\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu d_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{19\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{21\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho d_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \},\\&\xi _{23\mu \nu } = [\epsilon ^{abc} (u^T_a C \gamma _\rho \gamma _5 d_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \gamma _\nu u_d] + \{ \mu \leftrightarrow \nu \}. \end{aligned}$$

1.3 Currents of $[\bar{c}_d d_d][\epsilon ^{abc} u_a u_b c_c]$

In this subsection, we construct the currents of the color configuration $[\bar{c}_d d_d][\epsilon ^{abc} u_a u_b c_c]$. We find the following currents having $J^P=5/2^+$ and quark contents $uud c \bar{c}$:

$$\begin{aligned} \psi _{1\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{2\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{3\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{4\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{5\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{6\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{7\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{8\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{9\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{10\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\rho c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{11\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \gamma _\mu \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{12\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \gamma _\mu c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{13\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{14\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{15\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\nu \rho } c_c] [\bar{c}_d d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{16\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{17\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\rho d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{18\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{19\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _\rho d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{20\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \gamma _\nu \gamma _5 c_c] [\bar{c}_d \gamma _\rho \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \end{aligned}$$

$$\begin{aligned} \psi _{21\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{22\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \gamma _\rho c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{23\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \gamma _\rho c_c] [\bar{c}_d \gamma _\nu d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{24\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \gamma _\rho \gamma _5 c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{25\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{26\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{27\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) c_c] [\bar{c}_d \sigma _{\nu \rho } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{28\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \rho } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{29\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\nu \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\rho \sigma } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{30\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\nu \sigma } c_c] [\bar{c}_d \sigma _{\rho \sigma } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{31\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\nu \sigma } c_c] [\bar{c}_d \sigma _{\rho \sigma } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{32\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\nu \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\rho \sigma } \gamma _5 d_d]\\&+\;\{\mu \leftrightarrow \nu \},\\ \psi _{33\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\rho \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{34\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } u_b) \sigma _{\rho \sigma } c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{35\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\rho \sigma } c_c] [\bar{c}_d \sigma _{\nu \sigma } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{36\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\mu \rho } \gamma _5 u_b) \sigma _{\rho \sigma } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 d_d]\\&+\;\{\mu \leftrightarrow \nu \},\\ \psi _{37\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } u_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{38\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } u_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{39\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } \gamma _5 u_b) \sigma _{\mu \rho } c_c] [\bar{c}_d \sigma _{\nu \sigma } d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{40\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \sigma _{\rho \sigma } \gamma _5 u_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \sigma _{\nu \sigma } \gamma _5 d_d]\\&+\;\{\mu \leftrightarrow \nu \}. \end{aligned}$$

To perform QCD sum rule analyses, we shall use

$$\begin{aligned} \psi _{3\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d] + \{ \mu \leftrightarrow \nu \}, \end{aligned}$$

(58)

which well couples to the $[\Sigma _c^{*} {\bar{D}}^{*}]$ channel. We also need to use

$$\begin{aligned} \psi _{4\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) c_c] [\bar{c}_d \gamma _\nu \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \}. \end{aligned}$$

(59)

which well couples to the P-wave $[\Sigma _c^{*} {\bar{D}}]$ channel.

We note that the following currents actually have spin $J=3/2$:

$$\begin{aligned} \psi _{2\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \gamma _\nu c_c] [\bar{c}_d \gamma _5 d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{5\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\mu u_b) \sigma _{\nu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\rho d_d] + \{ \mu \leftrightarrow \nu \},\\ \psi _{7\mu \nu }= & {} [\epsilon ^{abc} (u^T_a C \gamma _\rho u_b) \sigma _{\mu \rho } \gamma _5 c_c] [\bar{c}_d \gamma _\nu d_d] + \{ \mu \leftrightarrow \nu \}. \end{aligned}$$

Appendix C: One example

In this appendix, we show one example and express the current $\eta _1$ as a combination of $\xi _i$ and $\psi _i$:

$$\begin{aligned} \eta _1= & {} [\epsilon _{abc} (u^T_a C d_b) \gamma _5 u_c] [\bar{c}_d c_d],\\= & {} [\epsilon _{abc} (u^T_a C d_b) \gamma _5 u_d] [\bar{c}_d c_c] + [\epsilon _{abc} (u^T_a C d_d) \gamma _5 u_c] [\bar{c}_d c_b]\\&+\;[\epsilon _{abc} (u^T_d C d_b) \gamma _5 u_c] [\bar{c}_d c_a]\\= & {} + { 5\over 4 } \times [\epsilon _{abc} (u^T_a C d_b) \gamma _5 u_d] [\bar{c}_d c_c]\\&+\;{ 1\over 4 } \times [\epsilon _{abc} (u^T_a C \gamma _\mu d_b) \gamma _\mu \gamma _5 u_d] [\bar{c}_d c_c]\\&-\;{ 1\over 8 } \times [\epsilon _{abc} (u^T_a C \sigma _{\mu \nu } d_b) \sigma _{\mu \nu } \gamma _5 u_d] [\bar{c}_d c_c]\\&+\;{ 1\over 4 } \times [\epsilon _{abc} (u^T_a C \gamma _\mu \gamma _5 d_b) \gamma _\mu u_d] [\bar{c}_d c_c]\\&+\;{ 1\over 4 } \times [\epsilon _{abc} (u^T_a C \gamma _5 d_b) u_d] [\bar{c}_d c_c]\\&-\;{ 1\over 4 } \times [\epsilon _{abc} (u^T_a C \gamma _\mu u_b) \gamma _\mu \gamma _5 d_d] [\bar{c}_d c_c]\\&+\;{ 1\over 8 } \times [\epsilon _{abc} (u^T_a C \sigma _{\mu \nu } u_b) \sigma _{\mu \nu } \gamma _5 d_d] [\bar{c}_d c_c]\\= & {} -\;{5\over 16} \xi _1 - {5\over 16} \xi _2 - {1\over 16} \xi _3- {1\over 16} \xi _4- {5\over 16} \xi _5\\&+\;{5\over 16} \xi _6+ {1\over 16} \xi _7- {1\over 16} \xi _8- {5\over 32} \xi _{10}\\&-\;{1\over 32} \xi _{11}- {1\over 16} \xi _{13}- {1\over 16} \xi _{14}- {1\over 16} \xi _{15}\\&-\;{1\over 16} \xi _{16}- {1\over 16} \xi _{17}+ {1\over 16} \xi _{18}- {1\over 16} \xi _{19}+ {1\over 16} \xi _{20}\\&+\;{i\over 16} \xi _{21}- {i\over 16} \xi _{22}+ {i\over 16} \xi _{23}- {i\over 16} \xi _{24}- {i\over 16} \xi _{25}\\&-\;{i\over 16} \xi _{26}- {i\over 16} \xi _{27}- {i\over 16} \xi _{28}+ {1\over 32} \xi _{29}+ {1\over 32} \xi _{30}\\&-\;{i\over 16} \xi _{33}+ {i\over 16} \xi _{34}+ {i\over 16} \xi _{35}- {i\over 16} \xi _{36}+ {1\over 32} \xi _{37}\\&+\;{1\over 32} \xi _{38}- {i\over 16} \xi _{43}\\&+\;{1\over 16} \psi _1+ {1\over 16} \psi _2+ {1\over 16} \psi _3- {1\over 16} \psi _4- {i\over 16} \psi _5\\&+\;{i\over 16} \psi _6+ {i\over 16} \psi _7+ {i\over 16} \psi _8- {1\over 32} \psi _9- {1\over 32} \psi _{10}\\&+\;{i\over 16} \psi _{13}- {i\over 16} \psi _{14}- {i\over 16} \psi _{15}\\&+\;{i\over 16} \psi _{16}- {1\over 32} \psi _{18}- {1\over 32} \psi _{19}+ {i\over 16} \psi _{23}. \end{aligned}$$