Production of $\Lambda$-hyperons in inelastic p+p interactions at 158 ${\mathrm{GeV}}\!/\!c$

Abstract

Inclusive production of $\Lambda$-hyperons was measured with the large acceptance NA61/SHINE spectrometer at the CERN SPS in inelastic p+p interactions at beam momentum of 158 ${\mathrm{GeV}}\!/\!c$. Spectra of transverse momentum and transverse mass as well as distributions of rapidity and x$_{_F}$ are presented. The mean multiplicity was estimated to be $0.120\,{\pm }\,0.006\;(stat.)\;{\pm }0.010\;(sys.)$. The results are compared with previous measurements and predictions of the Epos, Urqmd and Fritiof models.

1 Introduction

Hyperon production in proton–proton (p+p) interactions has been studied in a long series of fixed target and collider experiments. However, the resulting experimental data suffers from low statistics, incomplete beam momentum coverage, and large differences between the measurements reported by different experiments. Also popular models of proton–proton interactions mostly fail to reproduce the measurements. The data on $\Lambda$ production and the model predictions are reviewed at the end of this paper.

At the same time rather impressive progress was made in measurements of hyperon production in nucleus–nucleus (A+A) collisions [1]. This has two reasons. Firstly, mean multiplicities of all hadrons in central heavy ion collisions are typically two to three orders of magnitude higher than the corresponding multiplicities in inelastic p+p interactions. Secondly, the hyperon yields per nucleon are enhanced by substantial factors in A+A collisions with respect to p+p interactions. This enhancement, which increases with the strangeness content of the hyperon in question, has raised considerable interest over the past decades. It has in particular been brought into connection with production of the Quark–Gluon Plasma, a ’deconfined’ state of matter at that time hypothetical [2, 3]. Nowadays, for the energies well below the LHC energy range, nucleus–nucleus collisions are investigated mainly to find the critical point of strongly interacting matter as well as to study the properties of the onset of deconfinement [4, 5]. In particular, precise measurements of inclusive hadron production properties as a function of beam momentum (13A–158A ${\mathrm{GeV}}\!/\!c$) and size of colliding nuclei (p+p, p+Pb, Be+Be, Ar+Sc, Xe+La) are performed by NA61/SHINE  [6]. Results on inelastic p+p interactions are an important part of this scan.

NA61/SHINE already published results on $\pi ^{\pm }$, K$^{\pm }$, proton, $\Lambda$ and $K^0_S$ production in p+C interactions at beam momentum of 31 ${\mathrm{GeV}}\!/\!c$  [7–10], as well as $\pi ^-$ production in p+p collisions at 20–158 ${\mathrm{GeV}}\!/\!c$  [11].

This paper presents the first NA61/SHINE results on strange particle production in p+p interactions. Since all $\Sigma ^0$ hyperons decay electromagnetically via $\Sigma ^0\rightarrow \Lambda \gamma$, which is indistinguishable from direct $\Lambda$ production, $\Lambda$ in the following denotes the sum of both $\Lambda$ directly produced in strong p+p interactions and $\Lambda$ from decays of $\Sigma ^0$ hyperons produced in these interactions.

The particle rapidity is calculated in the collision centre of mass system (cms): $y = {{\mathrm{atanh}}}(\beta _\mathrm {L})$, where $\beta _\mathrm {L} = p_\mathrm {L}/E$ is the longitudinal component of the velocity, $p_\mathrm {L}$ and E are longitudinal momentum and energy in the cms and $x_\mathrm {F} = p_\mathrm {L}/p_{beam}$ is Feynman’s scaling variable with $p_{beam}$ the incident proton momentum in the cms. The transverse component of the momentum is denoted as $p_\mathrm {T}$ and the transverse mass $m_\mathrm {T}$ is defined as $m_\mathrm {T} = \sqrt{m^2 + p_\mathrm {T} ^2}$, where m is the particle mass. The collision energy per nucleon pair in the centre of mass system is denoted as $\sqrt{s_\mathrm {NN}}$.

Fig. 1

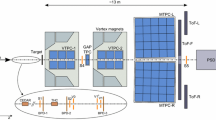
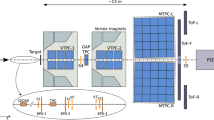
Schematic layout of the NA61/SHINE experiment at the CERN SPS (horizontal cut in the beam plane, not to scale). The beam and trigger counter configuration used for data taking on p+p interactions in 2009 is presented. The chosen right-handed coordinate system is shown on the plot. The incoming beam direction is along the z axis. The magnetic field bends charged particle trajectories in the x-z (horizontal) plane. The drift direction in the TPCs is along the y (vertical) axis [6]. See details in Sect. 2

2 The experimental setup

The NA61/SHINE experiment [6] uses a large acceptance hadron spectrometer located in the H2 beam-line at the CERN SPS accelerator complex. The layout of the experiment is schematically shown in Fig. 1. Hereby we describe only the components relevant for the analysis. The main detector system is a set of large volume time projection chambers (TPCs). Two of them (VTPC-1 and VTPC-2) are placed inside super-conducting magnets (VTX-1 and VTX-2) with a combined bending power of 9 Tm. The standard current setting for data taking at 158 ${\mathrm{GeV}}\!/\!c$ corresponds to full field, 1.5 T, in the first and reduced field, 1.1 T, in the second magnet. Two large TPCs (MTPC-L and MTPC-R) are positioned downstream of the magnets, symmetrically to the undeflected beam. A fifth small TPC (GAP-TPC) is placed between VTPC-1 and VTPC-2 directly on the beam line and covers the gap between the sensitive volumes of the other TPCs. The NA61/SHINE TPC system allows a precise measurement of the particle momenta p with a resolution of $\sigma (p)/p^2\approx (0.3 - 7)\!\times \!10^{-4}\;\mathrm {(GeV/c)}^{-1}$ at the full magnetic field used for data taking at 158 ${\mathrm{GeV}}\!/\!c$ and provides particle identification via the measurement of the specific energy loss, $\mathrm{d}E\!/\!\mathrm{d}x$, with relative resolution of about 4.5 %.

A set of scintillation and Cherenkov counters, as well as beam position detectors (BPDs) upstream of the main detection system provide a timing reference, as well as identification and position measurements of the incoming beam particles. The 158 ${\mathrm{GeV}}\!/\!c$ secondary hadron beam was produced by 400 ${\mathrm{GeV}}\!/\!c$ primary protons impinging on a 10 cm long beryllium target. Hadrons produced at the target are transported downstream to the NA61/SHINE experiment by the H2 beamline, in which collimation and momentum selection occur. Protons from the secondary hadron beam are identified by a differential Cherenkov counter (CEDAR) [12]. Two scintillation counters, S1 and S2, together with the three veto counters V0, V1 and V1$^p$ were used to select beam particles. Thus, beam particles were required to satisfy the coincidence $S1\cdot S2\cdot \overline{V0}\cdot \overline{V1}\cdot \overline{V1^p}\cdot$CEDAR in order to become accepted as a valid proton. Trajectories of individual beam particles were measured in a telescope of beam position detectors placed along the beam line (BPD-1/2/3 in Fig. 1). These are multiwire proportional chambers with two orthogonal sense wire planes and cathode strip readout, allowing to determine the transverse coordinates of the individual beam particle at the target position with a resolution of about 100 $\mu$m. For data taking on p+p interactions a liquid hydrogen target (LHT) of 20.29 cm length (2.8 % interaction length) and 3 cm diameter was placed 88.4 cm upstream of VTPC-1.

Data taking with inserted and removed liquid hydrogen (LH) in the LHT was alternated in order to calculate a data-based correction for interactions with the material surrounding the liquid hydrogen. Interactions in the target are selected by requiring an anti-coincidence of the selected beam protons with the signal from a small scintillation counter of 2 cm diameter (S4) placed on the beam trajectory between the two spectrometer magnets. Further details on the experimental setup, beam and the data acquisition can be found in Ref. [6].

3 Analysis technique

In the following section the analysis technique is described, starting with the event reconstruction followed by the event and V$^0$ selections. Next the $\Lambda$ signal extraction and the calculation of $\Lambda$-yields are presented. Then the correction procedure and the estimation of statistical and systematic uncertainties are discussed. Finally quality tests are performed on the final results. More details can be found in Ref. [13].

3.1 Track and main vertex reconstruction

The main steps of the track and vertex reconstruction procedure are:

• (i) cluster finding in the TPC raw data, calculation of the cluster centre-of-gravity and total charge,

• (ii) reconstruction of local track segments in each TPC separately,

• (iii) matching of track segments into global tracks,

• (iv) track fitting through the magnetic field and determination of track parameters at the first measured TPC cluster,

• (v) determination of the interaction vertex using the beam trajectory (x and y coordinates) fitted in the BPDs and the trajectories of tracks reconstructed in the TPCs (z coordinate),

• (vi) matching of ToF hits with the TPC tracks.

3.2 Event selection

A total of $3.5\times 10^{6}$ events recorded with the LH inserted (denoted I) and $0.43\times 10^6$ with the LH removed from the target (denoted R) were used for the analysis. The two configurations were realised by filling the target vessel with LH and emptying it.

Interaction events were selected by the following requirements:

• (i) no off-time beam particle was detected 1 $\mu$s before and after the trigger particle,

• (ii) the trajectory of the beam particle was measured in at least one of BPD-1 or BPD-2 and in the BPD-3 detector and was well reconstructed (BPD-3 is positioned close to and upstream of the LHT),

• (iii) the fit of the z-coordinate of the primary interaction vertex converged and the fitted z position is found within $\pm 40$ cm of the centre of the LHT.

The number of events after these selections ($N^I=1.66\times 10^6$ for the LH inserted configuration of the target, $N^R=43\times 10^3$ for the LH removed) is treated as the raw number of recorded inelastic events.

Fig. 2

Definition of distance of the closest approach (dca), and $b_x$. The variable $b_y$ is defined on the yz-plane in analogy with $b_x$. The target plane is defined as the plane parallel to the xy-plane containing the main vertex marked with a cross (taken from Ref. [14])

3.3 V$^0$ reconstruction and selection

$\Lambda$ hyperons are identified by reconstructing their decay topology $\Lambda \rightarrow p + \pi ^{-}$ (branching ratio 63.9 %). In the first step pairs were formed from all measured positively and negatively charged particles. V$^0$ candidates were required to have a distance of closest approach (dca, Fig. 2) between the two trajectories of less than 1 cm anywhere between the position of the first measured points on the tracks and the primary vertex. In the second step, the position of the secondary vertex and the momenta of the decay tracks were fitted by performing a 9-parameter $\chi ^{2}$ fit employing the Levenberg–Marquardt fitting procedure [15, 16]. In the fit the fitted secondary vertex was added as the first point to the tracks at which the momenta were recalculated. Finally, for each candidate the invariant mass was calculated assuming proton (pion) mass for positively (negatively) charged particles. To ensure a good momentum determination and reduce the combinatorial background from random pairs, a set of quality cuts was imposed:

Fig. 3

Definition of $\Delta z$ variable used for the $V^{0}$ selection (see text)

• (i) For each track, the minimum number of clusters in at least one of VTPC-1 and VTPC-2 was required to be 15.

• (ii) Proton and pion candidates were selected by requiring their specific energy loss measured by the TPCs to be within 3 $\sigma$ around the nominal Bethe–Bloch value. This cut was applied only to experimental data.

• (iii) For the simulated data (see below) the background was totally discarded by matching, i.e. by using only those reconstructed tracks which were identified as originating from the corresponding $\Lambda$ decay. The identification was performed by matching the clusters found in the TPCs with the clusters generated in the simulation. In case more than one reconstructed track was matched to a $\Lambda$ decay daughter the one with the largest number of matched clusters was selected.

• (iv) The combinatorial background concentrated in the vicinity of the primary vertex is reduced by imposing a distance cut on the difference between the z coordinate of the primary and $\Lambda$ vertex ($\Delta z = z_\Lambda - z_{primary}$, see Fig. 3). To maximise the fraction of rejected background while minimising the number of lost $\Lambda$ candidates, a rapidity dependent cut was applied: $\Delta z>10$ cm for $y<0.25$, $\Delta z>15$ cm for $y\in [0.25,0.75]$, $\Delta z>40$ cm for $y\in [0.75,1.25]$, and $\Delta z>60$ cm for higher rapidities.

• (v) A further significant part of the background (e.g. pairs from photon conversions) was rejected by imposing a cut on $\cos {\phi }$, where $\phi$ is defined as the angle between the vectors $y'$, and n, where $y'$ is the vector perpendicular to the momentum of the V$^0$-particle which lies in the plane spanned by the y-axis and the V$^0$-momentum vector, and n is a vector normal to the decay plane (see Fig. 4). A rapidity dependent cut was used: $|\cos {\phi }|<0.95$ for $y<-0.25$, $|\cos {\phi }|<0.9$ for $y\in [-0.25,0.75]$, $|\cos {\phi }|<0.8$ for higher rapidities.

• (vi) The trajectories of the $\Lambda$ candidates were calculated using the decay vertex and the momentum vectors of the decay particles. Extrapolation back to the primary vertex plane resulted in impact parameters $b_{x}$ (in the magnetic bending plane) and $b_{y}$ (see Fig. 2). As the resolution of impact parameters is approximately twice better in y than in x direction, an elliptic cut $\sqrt{(b_{x}/2)^2+b_{y}^{2}}< 1$ cm was imposed in order to reduce the background from $\Lambda$ candidates which do not originate from the primary vertex.

The selection cuts lead to a high degree of purification of the $\Lambda$ signal. This is demonstrated by the Armenteros–Podolanski plots [17] of Fig. 5 in which the $\Lambda$ decays populate the ellipses on the lower right.

Fig. 4

Definition of $\phi$-variable used for the $V^{0}$ selection (see text)

Fig. 5

Armenteros–Podolanski plot for reconstructed $V^0$ decays before the $\Lambda$ candidate selection cuts (a), and after the cuts are applied (b). The shading indicates the number of entries per bin. The axis variables are: $p_T^{Arm}$, the transverse momentum of the decay particles with respect to the direction of motion of the $V^0$ and $\alpha ^{Arm} = (p_L^+ - p_L^-)/(p_L^+ + p_L^-)$ where $p_L^+$ and $p_L^-$ are the longitudinal momenta of the positive and negative decay particle respectively

3.4 Signal extraction

The raw yield of $\Lambda$ hyperons was obtained by performing a fit of the invariant mass spectra with the sum of a background and a signal function. The shape of the $\Lambda$ signal was described by the Lorentzian function:

$$\begin{aligned} L(m)=A\frac{\frac{1}{2}\Gamma }{\left( m-m_0\right) ^2+\left( \frac{1}{2}\Gamma \right) ^2}, \end{aligned}$$

(1)

where m is the invariant mass of the candidate ($p\pi ^-)$ pair, A is a normalisation factor, $m_0$ is the mass parameter and $\Gamma$ is the FWHM (full width at half maximum) of the $\Lambda$ peak. As the natural width of $\Lambda$ decay is negligible, the observed width of the $\Lambda$ peak is caused almost solely by the detector response. In the standard approach, the background was represented by a Chebyshev polynomial of 2nd order. The uncertainty introduced by choosing this particular functional form was estimated by trying other background functions (see Sec. 3.6).

The sum of the Lorentzian and the background function was fitted in the mass range from 1.080 (1.076 for $y=0.5$, 1.073 for $y=1.0$) to 1.250 ${\mathrm{GeV}}\!/\!c^2$. In order to ensure the stability of the fit results, even in the case of low statistics, a three step procedure was developed. In the first step, a pre-fit was performed in order to estimate the initial parameters of the background function. For that purpose, the invariant mass region containing the $\Lambda$ peak (1.100–1.135 ${\mathrm{GeV}}\!/\!c^2$) was excluded from the fit. In the second step, the invariant mass spectrum was fitted to the sum of the signal and the background. The initial values for the parameters of the background function were taken from the first step, while the mass parameter $m_0$ was fixed to the PDG value $m_\Lambda =1.115683$ ${\mathrm{GeV}}\!/\!c^2$ [18] and the width was set to 3 MeV. The obtained values were used as the initial parameters for the third step, where no parameter was fixed. The invariant mass distribution of the $\Lambda$ candidates for the intervals $y\in [-0.75,-0.25]$ and $p_{_T}\in [0.2,0.4]$ ${\mathrm{GeV}}\!/\!c$, together with the result of the final fit is shown in Fig. 6. For the data set with LH inserted, the fits were performed in (k, l) bins, where k stands for the bin in rapidity y or Feynman $x_{_F}$, and l for the bin in transverse momentum $p_{_T}$ or transverse mass $m_{_T}-m_{_\Lambda }$. The raw number of $\Lambda$-hyperons ($n^I(k,l)$) was then obtained by subtracting the fitted background and integrating the remaining signal distributions in the mass window $m_0\pm 3\Gamma$ (see Fig. 7), where $m_0$ is the fitted $\Lambda$ mass. The low statistics of the LH removed data set, forced to restrict the fits to y ($x_{_F}$) bins summed over the transverse variable, resulting in $n^R(k)$. In order to obtain the raw number of $\Lambda$-hyperons in (k, l) bins, it was assumed that the shape of the $p_{_T}$ distributions and the efficiencies for a given y ($x_{F}$) bin were the same for the two data sets, and $n^R(k,l)$ was calculated as $n^R(k,l)=n^R(k)\frac{n^I(k,l)}{\sum \nolimits _{l}{n^I(k,l)}}$.

Fig. 6

The invariant mass distribution of $\Lambda$ candidates for $y\in [-0.75,-0.25]$ and $p_{_T}\in [0.2,0.4]$ ${\mathrm{GeV}}\!/\!c$ is shown in the upper plot (LH inserted). The solid line shows a fit to signal plus background, while the dashed line represents the background contribution. The lower part of the plot shows the difference between the data points and the fit, normalised to the statistical error of the data points

Fig. 7

The invariant mass distribution of $\Lambda$ candidates for $y\in [-0.25,0.25]$ and $p_{_T}\in [0.2,0.4]$ ${\mathrm{GeV}}\!/\!c$ with the LH inserted after subtraction of the fitted background (a), and for the simulation (b)

3.5 Correction factors

In order to determine the number of $\Lambda$ hyperons produced in inelastic p+p interactions, three corrections were applied to the extracted raw number of $\Lambda$ hyperons:

• 1. The contribution from interactions in the material outside of the liquid hydrogen volume of the target was subtracted:

  $$\begin{aligned} \frac{n^I(k,l)-Bn^R(k,l)}{N^I-BN^R}. \end{aligned}$$

  (2)

  The normalisation factor B was derived by comparing the distribution of the fitted z coordinate of the interaction vertex far away from the target [9] for filled and empty target vessel:

  $$\begin{aligned} B=\frac{N^I_{far\;z}}{N^R_{far\;z}}~=3.93, \end{aligned}$$

  (3)

  where $N^I_{far\;z}$ ($N^R_{far\;z}$) is the number of events in the region $100 < z < 280$ cm downstream of the target centre for the data sample with inserted (removed) hydrogen in the target vessel.

• 2. The loss of the $\Lambda$ hyperons due to the $\mathrm{d}E\!/\!\mathrm{d}x$ requirement, was corrected by a constant factor

  $$\begin{aligned} c_{\mathrm{d}E\!/\!\mathrm{d}x} =\frac{1}{\epsilon ^{2}} = 1.005, \end{aligned}$$

  (4)

  where $\epsilon = 0.9973$ is the probability for the proton (pion) to lie within 3$\sigma$ around the nominal Bethe–Bloch value.

• 3. A detailed Monte Carlo simulation was performed to correct for geometrical acceptance, reconstruction efficiency, losses due to the trigger bias, the branching ratio of the $\Lambda$ decay, the feed-down from hyperon decays as well as the quality cuts applied in the analysis. The correction factors are based on $20\times 10^6$ inelastic p+p events produced by the Epos1.99 event generator [19]. The particles in the generated events were tracked through the NA61/SHINE apparatus using the Geant3 package [20]. The TPC response was simulated by dedicated NA61/SHINE software packages which take into account all known detector effects. The simulated events were reconstructed with the same software as used for real events and the same selection cuts were applied (except the identification cut). As seen from Fig. 7 the shape and position of the $\Lambda$ peak is well reproduced by the simulation while the width is about 10 % narrower. More details on MC validation can be found in Ref. [11].

  For each (k, l) bin, the correction factor $c_{_{MC}}(k,l)$ was calculated as

  $$\begin{aligned} c_{_{MC}}(k,l)=\frac{n_{MC}^{gen}(k,l)}{N_{MC}^{gen}}\Bigg /\frac{n_{MC}^{acc}(k,l)}{N_{MC}^{acc}}, \end{aligned}$$

  (5)

  where

  • $n_{MC}^{gen}(k,l)$ is the number of $\Lambda$ hyperons produced in a given (k, l) bin in the primary interactions, including $\Lambda$ hyperons from the $\Sigma ^0$ decays,

  • $n_{MC}^{acc}(k,l)$ is the number of reconstructed $\Lambda$ hyperons in a given (k, l) bin, determined by matching the reconstructed $\Lambda$ candidates to the simulated $\Lambda$ hyperons based on the cluster positions,

  • $N_{MC}^{gen}$ is the number of generated inelastic p+p interactions ($19\,961\times 10^3$),

  • $N_{MC}^{acc}$ is the number of accepted p+p events ($15\,607\times 10^3$),

  • $k=y$ or $x_{_F}$, and $l=p_{_T}$ or $m_{_T}-m_{_\Lambda }$.

  These factors also include the correction for feed-down from weak decays (mostly of $\Xi ^{-}$ and $\Xi ^{0}$, see Fig. 8). The $\Xi ^{-}$ yields as function of rapidity generated by the Epos1.99 simulation agree within 10 % with the measurements reported in Ref. [21]. The values of the correction factors are presented in Fig. 9. Statistical errors of the correction factors were calculated using the following approach: The correction factor ($c_{_{MC}}$) consists of two parts:

  $$\begin{aligned} c_{_{MC}}\left( k,l\right)&=\frac{n_{MC}^{gen}(k,l)}{N_{MC}^{gen}}\Bigg /\frac{n_{MC}^{acc}(k,l)}{N_{MC}^{acc}}\nonumber \\&=\frac{N^{acc}_{MC}}{N^{gen}_{MC}}\Bigg /\frac{n^{acc}_{MC}(k,l)}{n^{gen}_{MC}(k,l)}=\frac{\alpha }{\beta (k,l)}, \end{aligned}$$

  (6)

  where $\alpha$ describes the loss of inelastic events due to the event selection, and $\beta$ takes into account the loss of $\Lambda$ hyperons due to the $V^0$-cuts, efficiency, and the other aforementioned effects. The error of $\alpha$ was calculated assuming a binomial distribution, while the part $\beta$ involving the fitting procedure takes into account the error of the fit:

  $$\begin{aligned} \Delta \alpha =\sqrt{\frac{\alpha (1-\alpha )}{N_{MC}^{gen}}}, \end{aligned}$$

  (7)
  $$\begin{aligned} \Delta \beta (k,l)=\sqrt{\left( \frac{\Delta n^{acc}_{MC}(k,l)}{n^{gen}_{MC}(k,l)}\right) ^2+ \left( \frac{n^{acc}_{MC}(k,l)\Delta n^{gen}_{MC}(k,l)}{(n^{gen}_{MC}(k,l))^2}\right) ^2}, \end{aligned}$$

  (8)

  where $\Delta n^{acc}_{MC}(k,l)$ is the uncertainty of the fit, and $\Delta n^{gen}_{MC}(k,l)=\sqrt{n^{gen}_{MC}(k,l)}$. The total statistical error of $c_{_{MC}}$ was calculated as follows:

  $$\begin{aligned} \Delta c_{_{MC}}=\sqrt{\left( \frac{\Delta \beta }{\alpha }\right) ^2+\left( -\frac{\beta \Delta \alpha }{\alpha ^2}\right) ^2}. \end{aligned}$$

  (9)

Fig. 8

Feed-down correction: the contribution from $\Xi ^-$ and $\Xi ^0$ to total $\Lambda$ decays calculated using Epos1.99 model

Fig. 9

Correction factors $c_{_{MC}}$ for binning in ($y,p_T$) at top, ($y,m_T-m_{\Lambda }$) at centre and ($x_F,p_T$) at bottom. The error $\Delta c_{_{MC}}$ ranges from 0.02 to 1.48 for binning in ($y,p_T$) and ($y,m_T$), and from 0.02 to 8.70 for ($x_F,p_T$)

Finally, the double-differential yield of $\Lambda$ hyperons per inelastic event in a bin (k, l) amounts to:

$$\begin{aligned} \frac{d^2n}{dkdl}=\frac{c_{dE/dx}c_{_{MC}}(k,l)}{\Delta k \Delta l} \frac{n^I(k,l)-Bn^R(k,l)}{N^I-BN^R}, \end{aligned}$$

(10)

with

• $n^{I/R}$ the uncorrected number of $\Lambda$ hyperons for the hydrogen inserted/removed target configurations,

• $N^{I/R}$ the number of events for the hydrogen inserted/removed data after event cuts,

• $c_{dE/dx}$, $c_{_{MC}}$ the correction factors described in Sec. 3.5,

• B the normalisation factor (defined in Sec. 3.5),

• $k=y$ or $x_{_F}$, and $l=p_{_T}$ or $m_{_T}-m_{_\Lambda }$,

• $\Delta k$ and $\Delta l$ the bin widths.

3.6 Statistical and systematic uncertainties

The statistical errors of the corrected double differential yields (see Eq. 10) take into account the statistical errors of $c_{_{MC}}$ (see Eq. (9)) and the statistical errors on the fitted $\Lambda$ yields in the LH inserted and removed configurations. The statistical errors on B and $c_{dE/dx}$ were neglected.

The systematic uncertainties were estimated taking into account four sources. For each source modifications to the standard analysis procedure were applied and the deviation of the results from the standard procedure were calculated. As the effects of the modifications are partially correlated, the maximal positive and negative deviation from the standard procedure was determined for each bin and source separately. Then, the positive (negative) systematic uncertainties were calculated separately by adding in quadrature the positive (negative) contribution from each source.

The considered sources of the systematic uncertainty and the corresponding modifications of the standard method were the following:

• (i) The uncertainty due to the signal extraction procedure:

  • The standard function used for background fit, a Chebyshev polynomial of 2nd order, was changed for a Chebyshev polynomial of 3rd order and for a standard polynomial of 2nd order.

  • The range within which the raw number of $\Lambda$ particles is summed up was changed from 3$\Gamma$ to 2.5$\Gamma$ and $3.5\Gamma$.

  • The lower limit of the fitting range was changed from 1.08 ${\mathrm{GeV}}\!/\!c^2$ (1.076 for $y=0.5$, 1.073 for $y=1.0$) to 1.083 ${\mathrm{GeV}}\!/\!c^2$ (1.079 for $y=0.5$, 1.076 for $y=1.0$).

  • The initial value of the $\Gamma$ parameter of the signal function was changed by $\pm$8 %.

  • the initial value for the mass parameter of the Lorentz function was changed by $\pm$0.3 MeV.

• (ii) The effect of the event and quality cuts were checked by performing the analysis with the following cuts changed compared to the values presented in Secs. 3.2 and 3.3.

  • The cut on the z-position of the interaction vertex was changed from $\pm$40 to $\pm$30 cm and $\pm$50 cm with respect to the centre of the target.

  • The window in which off-time beam particles are not allowed was increased from 1 to 1.5 $\mu$s.

  • The elliptic cut on the impact parameters was reduced by a factor of 2: $\sqrt{b_{x}^2+(2b_{y})^{2}}< 1$ cm.

  • The $\mathrm{d}E\!/\!\mathrm{d}x$ cut was modified to $\pm$2.8$\sigma$ or 3.2$\sigma$ to estimate possible systematic effects of $\mathrm{d}E\!/\!\mathrm{d}x$ calibration.

  • The matching procedure used to reject background in the simulation was turned off.

  • The required minimal number of charge clusters in at least one of the VTPCs for both $V^0$-decay products was decreased to 12 or increased to 18.

  • The cut on $\Delta z$, the distance between the decay and the primary interaction vertex, was changed from the standard values to the values shown in columns A and B in the following table:

    Minimal $\Delta z$ (cm) allowed
    $y_{min}$	$y_{max}$	Standard	A	B
    $-$1.75	0.25	10	7.5	12.5
    0.25	0.75	15	11.25	18.75
    0.75	1.25	40	30	50

  • The limits for the cut on $\cos {\phi }$ were changed from the standard values to the values shown in columns A and B in the following table:

    Maximal $|\cos {\phi }|$ allowed
    $y_{min}$	$y_{max}$	Standard	A	B
    $-$1.75	$-$0.25	0.95	0.975	0.925
    $-$0.25	0.75	0.9	0.95	0.85
    0.75	1.25	0.8	0.85	0.75

• (iii) In order to find the systematic uncertainty of the normalisation factor B in Eq. (3) for the LH removed configuration, the limits of the region for which this parameter was calculated was varied in steps of 0.1 m. For each combination of the lower limit (ranging from 0.8 to 1.8 m from the target) and upper limit in z (from 2.8 to 3.8 m from the target) the B-factor was calculated. The smallest and the highest value of B obtained in this way is taken as the systematic uncertainty range of B.

• (iv) For estimation of the uncertainty due to the feed-down correction a conservative systematic uncertainty of 30 % on the $\Xi ^{-}$ and $\Xi ^{0}$ yields predicted by Epos1.99 was assumed.

The systematic uncertainties are shown in the figures as light blue shaded bars. They are asymmetric (larger downward) mainly due to the differences between the results with or without track matching and the change of the background function to a Chebyshev polynomial of $3^{rd}$ order. For both changes the shift of the results increases with rapidity.

The distribution of the proper life-time of $\Lambda$ hyperons was obtained using an analysis procedure analogous to the one presented in Sec. 4. The data for the lifetime analysis were binned in rapidity $k=y$ (from $-$1.5 to +1.0, in steps of 0.5) and life-time normalised to the mean lifetime $t/\tau _{PDG}$ [18] (from 0.00 to 4.75, in steps of 0.25) with $c\tau _{PDG}=7.89$ cm. The life-time was calculated using the distance r between the V$^0$-decay vertex and the interaction vertex of the V$^0$-candidates ($t=r/(\gamma \beta )$, where $\gamma$, $\beta$ are the Lorentz variables). Then $d^2n/(dydt)$ was calculated and an exponential function was fitted to the life-time distribution for each rapidity bin separately (see the example in Fig. 10a for $y=-1.0$). The ratio of the fitted mean life-time $\tau$ to the corresponding PDG value $\tau _{PDF}$ is shown in Fig. 10b as a function of rapidity. The fitted mean life-times are seen to agree with the PDG value for all rapidities indicating good accuracy of the correction procedure.

The expected forward-backward symmetry of the data was also checked. The final double- and single-differential distributions used for this test were found to agree for the corresponding backward and forward rapidities within the statistical errors.

In addition, the stability of results in different periods during the data taking was investigated. For that purpose, the data set was divided into two subsets, containing runs from the first and the second half of the data taking period. These subsets were analysed separately and the results are found to be consistent.

Fig. 10

Top an example of the corrected proper life-time distribution for $\Lambda$ hyperons produced in inelastic p+p interactions at 158 ${\mathrm{GeV}}\!/\!c$ in the rapidity interval $y=-1.0\pm 0.25$. Bottom the ratio of the fitted mean life-time to its PDG [18] value as a function of rapidity

Fig. 11

Spectra $\frac{d^2n}{dydp_{_T}}$ for six bins in rapidity y. The fitted function is given by Eq. (12). The numerical data are listed in the Table 1 and the fitted inverse slope parameter for each of the bins in Table 5

Fig. 12

Spectra $\frac{d^2n}{dydm_{_T}}$ for six bins in rapidity y. The fitted function is given by Eq. (12). The numerical data are listed in Table 2 and the mean transverse mass $\langle m_{_T}\rangle -m_{_\Lambda }$ for each of the bins in Table 5

Fig. 13

Spectra $\frac{d^2n}{dx_{_F}dp_{_T}}$ for eight bins in $x_{_F}$. The fitted function is given by Eq. (12). The numerical data are listed in Table 3 for $x_{_F} > 0$ and in Table 4 for $x_{_F} > 0$

Fig. 14

Spectra $f_n$ for eight bins in $x_{_F}$. The fitted function was obtained from Eq. (12) by multiplying the right-hand side by $p_{_T}$. The numerical data are listed in Table 3 for $x_{_F} > 0$ and in Table 4 for $x_{_F} < 0$

4 Results

4.1 Formalism

The double-differential yields of $\Lambda$ hyperons in inelastic p+p interactions at 158 GeV/c were calculated in kinematic (k, l) bins (with $k=y$ or $x_{_F}$, and $l=p_{_T}$ or $m_{_T}-m_{_\Lambda }$) using Eq. (10). The following spectra are presented: $\frac{d^2n}{dydp_{_T}}$, $\frac{d^2n}{dydm_{_T}}$, $\frac{d^{2}n}{dx_{F}dp_{T}}$ and $f_n(x_{_F},p_{_T})$, where

$$\begin{aligned} f_n(x_{_F},p_{_T})&= \frac{2E^*}{\pi \sqrt{s}}\frac{d^2n}{dx_{_F}dp^2_{_T}}= \frac{1}{\pi \sqrt{s}}\frac{E^*}{p_{_T}}\frac{d^2n}{dx_{_F}dp_{_T}}. \end{aligned}$$

(11)

$E^{*}$ is the energy of the $\Lambda$ hyperon in the centre of mass system. The weighting factor, $E^*/p_{_T}$, was calculated at the centre of each $(x_{_F},p_{_T})$ bin and is consistent with the average value $\left\langle E^*/p_{_T}\right\rangle$ obtained using the EPOS generator.

Table 1 Double-differential yield $\frac{d^2n}{dydp_{T}}$

Table 2 Double-differential yield $\frac{d^2n}{dydm_{_T}}$

Single-differential $\frac{dn}{dk}$ distributions are obtained by summing the double-differential yields for a given k over l. In order to estimate the yield in the unmeasured high $p_{T}$ range, the function

$$\begin{aligned} u = \frac{1}{p_{_T}}\frac{d^2n}{dkdp_{_T}}=\frac{1}{m_{_T}}\frac{d^2n}{dkdm_{_T}}=Ae^{-\frac{m_{_T}}{T}} \end{aligned}$$

(12)

was fitted to the data and integrated beyond the measured $p_{T}$, where A denotes the normalisation factor and T the inverse slope parameter. Single-differential invariant yields $F_n(x_{_F})$ were obtained by performing an integration of Eq. (11) with respect to $p_{_T}^2$:

$$\begin{aligned} F_n(x_{_F})=\int \limits _0^{+\infty }f_n(x_{_F},p_{_T})dp_{_T}^2= \frac{2}{\pi \sqrt{s}}\int \limits _0^{+\infty }{E^* \frac{d^2n}{dx_{_F}dp_{_T}}dp_{_T}}. \end{aligned}$$

(13)

For the calculation of $F_n(x_{_F})$, the weighting factor $E^*$ was calculated at the centre of each $(x_{_F},p_{_T})$ bin. For the extrapolation into the unmeasured high $p_{T}$ region Eq. (12) was used.

Invariant cross-section is obtained from $F_n(x_{_F})$ by multiplying it by the inelastic cross-section $\sigma _{inel}$:

$$\begin{aligned} F(x_{_F})=\sigma _{inel}F_n(x_{_F}). \end{aligned}$$

(14)

The mean transverse mass $\langle m_{_T}\rangle$ was calculated from the function Eq. (12) fitted to the $m_{_T}$ distribution as follows:

$$\begin{aligned} \langle m_{_T}\rangle =\frac{\int _0^{+\infty }{m_{_T}u(m_{_T})dm_{_T}}}{\int _0^{+\infty }{u(m_{_T})dm_{_T}}}. \end{aligned}$$

(15)

4.2 Spectra

Double-differential $\frac{d^2n}{dydp_{_T}}$, $\frac{d^2n}{dydm_{_T}}$, $\frac{d^{2}n}{dx_{F}dp_{T}}$ and $f_n(x_{_F},p_{_T})$ spectra are shown in Figs. 11, 12, 13, 14. The numerical values for $\frac{d^2n}{dydp_{_T}}$ and $\frac{d^2n}{dydm_{_T}}$ are presented in Tables 1 and 2, while invariant and non-invariant $x_{F}$ yields are shown in Table 3 for $x_{_F}<0$ and Table 4 for $x_{_F}>0$.

Table 3 Double-differential yields, $\frac{d^{2}n}{x_{_F}p_{_T}}$ and $f_n(x_{_F},p_{T})$, for $x_{_F}<0$

Table 4 Double-differential yields, $\frac{d^{2}n}{x_{_F}p_{_T}}$ and $f_n(x_{_F},p_{T})$, for $x_{_F}>0$

The values of the $p_{T}$ integrated $\frac{dn}{dy}$ rapidity distribution are presented in Table 5. The table also contains the values of the inverse slope parameter T and the mean transverse mass $\langle m_{_T}\rangle -m_{_\Lambda }$ as function of rapidity. The single-differential $x_{F}$ distributions are summarised in Table 6. In Sec. 5 below, the obtained single-differential distributions are compared to model predictions and previously published experimental results.

Table 5 $p_{_T}$ integrated yield $\frac{dn}{dy}$, the inverse slope parameter T and the mean transverse mass $\langle m_{_T}\rangle - m_{\Lambda }$

Table 6 $p_{_T}$ integrated yield $\frac{dn}{x_{_F}}$ and the invariant cross section $F(x_{_F})$

The mean multiplicity of $\Lambda$ hyperons ($\langle \Lambda \rangle$) was determined from the $x_{_F}$ distribution. As the models applicable in the SPS energies range show large discrepancies in the region not measured by NA61/SHINE (see Fig. 20), the $\Lambda$ yield in the unmeasured $x_{F}$ region ($|x_{F}| >$0.4) was approximated by the straight line shown in Fig. 20. The line is defined assuming symmetry of the distribution. It crosses the points $A_\pm =\left( \pm 0.35,\frac{1}{2}\left( \frac{dn}{dx_{_F}}(-0.35)+\frac{dn}{dx_{_F}}(0.35)\right) \right)$ and $B_\pm =(\pm 1,0)$. For the estimation of statistical part of the extrapolation error, the value of the point A was increased/decreased by $\frac{1}{2}\left( \Delta \frac{dn}{dx_{_F}}(-0.35)+\Delta \frac{dn}{dx_{_F}}(0.35)\right)$. The extrapolation amounts to 34.3 % of the total $\Lambda$ yield and results in $\langle \Lambda \rangle =0.120\pm 0.006\;(stat.)$ of the mean $\Lambda$ multiplicity.

For the Epos model, not used for this extrapolation, the yield outside of NA61/SHINE acceptance to the total yield amounts to 38.0 %.

The systematic uncertainty of the mean multiplicity was calculated following the procedure described in Sec 3.6. An additional source of systematic uncertainty arises from the extrapolation of the $\Lambda$ multiplicity to full phase-space. This was estimated by an alternative procedure based on a parametrisation of published rapidity distributions. In an iterative procedure a symmetric polynomial of 4$^{th}$ order [22] was fitted to the $(1/\langle n\rangle )(dn/dz)$ distributions obtained by five bubble-chamber experiments [23–27] and the NA61/SHINE data, where z stands for $y/y_{beam}$. First, the fit included only the five bubble-chamber datasets. Next, the NA61/SHINE spectrum was normalised to the fit result obtained in the first step and added as the 6$^{th}$ set for the fit. Finally, the procedure was iterated using those six datasets until the normalisation factor converged. The ratio of the integral of the fitted function $\frac{1}{\langle \Lambda \rangle }\frac{dn}{dz}\left( z\right) =0.394+1.99z^2-2.66z^4$ (see Fig. 15) for the full range of rapidity to the integral in the range outside of the NA61/SHINE acceptance was used as the extrapolation factor for the NA61/SHINE results. This ratio amounted to $1.92\pm 0.12$, i.e. 48 % of the total production is outside of the acceptance for this procedure resulting in a mean multiplicity of $\langle \Lambda \rangle =0.129\pm 0.008$. The difference between this result and the linear extrapolation of the $x_F$ distribution is added in quadrature to the (positive) systematic error.

The final result for the $\Lambda$ multiplicity in inelastic p+p interactions at 158 GeV/c then reads as follows:

$$\begin{aligned} \langle \Lambda \rangle =0.120\pm 0.006\;(stat.)\;\pm 0.010\;(sys.) \end{aligned}$$

5 Comparison with world data and model predictions

The single-differential spectra from NA61/SHINE are compared in Fig. 15 to results from five bubble-chamber experiments which measured p+p interactions at beam momenta close to 158 ${\mathrm{GeV}}\!/\!c$. The experiments published data for the backward hemisphere, however, with rather small statistics [23–27] and correspondingly large uncertainties. In order to account for the difference in beam momentum the spectra are shown in terms of the scaled rapidity $z=y/y_{beam}$ and were normalised to unity in order to compare the shapes. Note, that the same data sets were also used to compute the alternative correction factor used to estimate the systematic uncertainty of $\langle \Lambda \rangle$ (see Sec. 4) obtained by NA61/SHINE.

Fig. 15

The scaled $\Lambda$ yield as function of scaled rapidity $z=y/y_{beam}$ in inelastic p+p interactions measured by NA61/SHINE and selected bubble-chamber experiments [23–27]. The symmetric polynomial of 4$^{th}$ order used for estimation of the systematic uncertainty of $\Lambda$ mean multiplicity (see Sec. 4.2) is plotted to guide the eye

Fig. 16

Collision energy dependence of mean multiplicity of $\Lambda$ hyperons produced in inelastic p+p interactions. Full symbols indicate bubble chamber results [23–27], the solid red dot shows the NA61/SHINE result. Open symbols depict the remaining world data [28]. The Epos1.99  [19] prediction is shown by the curve. The systematic uncertainty of the NA61/SHINE result is indicated by the shaded bar

Fig. 17

Comparison of the invariant $x_{F}$ spectra (see Eq. (14), $\sigma _{inel.}=31.8$ mb [18]) from the NA61/SHINE with the data from bubble-chamber experiments at beam momenta close to 158 ${\mathrm{GeV}}\!/\!c$  [23, 25, 26, 29–31]. The NA61/SHINE data points are indicated by filled circles. The systematic uncertainty is shown as a band around the points

Fig. 18

Rapidity spectra of $\Lambda$ hyperons divided by the mean number of wounded nucleons in inelastic p+p interactions (NA61/SHINE) and central C+C, Si+Si [32], and Pb+Pb [33] collisions at 158 $A\,{\mathrm{GeV}}\!/\!c$

Fig. 19

Spectra of m$_{_T}$ at mid-rapidity ($|y|\le 0.4$ for A+A, $|y|\le 0.25$ for p+p) from NA61/SHINE inelastic p+p interactions and central C+C, Si+Si [32], and Pb+Pb [33] collisions for beam momentum of 158 $A\,{\mathrm{GeV}}\!/\!c$. The lines are fitted using Eq. (12)

Fig. 20

Comparison of $\frac{dn}{dy}$ (a), and $\frac{dn}{dx_{_F}}$ (b) distributions with calculations of the Epos  [19], Urqmd  [34, 35] and Fritiof  [36] models. The chain line was used to extrapolate the NA61/SHINE measurements to full phase space. For details see text

Though the statistical error and the systematic uncertainty of the NA61/SHINE measurement is much smaller than for the other experiments, and the results are consistent with all the datasets used for the comparison, the general tendency obtained by fitting a symmetric polynomial of 4$^{th}$ order does not describe well the NA61/SHINE data. On the other hand, the result of Brick et al. for which the beam momentum (147 ${\mathrm{GeV}}\!/\!c$) differs the least from the NA61/SHINE momentum, shows the best agreement.

The mean multiplicity of $\Lambda$ for 158 ${\mathrm{GeV}}\!/\!c$ inelastic p+p interactions is compared in Fig. 16 with the world data [28] as well as with predictions of the Epos1.99 model in its validity range. A steep rise in the threshold region is followed by a more gentle increase at higher energies that is well reproduced by the Epos1.99 model.

The dependence of the invariant spectrum on $x_{_F}$ for NA61/SHINE and published results from bubble chamber experiments [23, 25, 26, 29–31] at nearby beam momenta is shown in Fig. 17. The NA61/SHINE results are consistent with the experiments performed at proton beams of lower energy, although the dip-like structure visible at central $x_{_F}$ in the data from the experiments operating at higher energies is not observed.

Figure 18 shows a comparison of rapidity spectra divided by the mean number of wounded nucleons $1/\langle N_W\rangle$ in inelastic p+p interactions (this paper) and central C+C, Si+Si and Pb+Pb collisions (NA49 [32, 33]) at 158 $A\,{\mathrm{GeV}}\!/\!c$. The yield of $\Lambda$ hyperons per wounded nucleon increases with increasing $\langle N_W\rangle$ as a consequence of strangeness enhancement in nucleus–nucleus collisions.

Figure 19 displays $m_T$ spectra at mid-rapidity for inelastic p+p interactions (this paper) and central nucleus–nucleus collisions (NA49 [32, 33]) at 158 $A\,{\mathrm{GeV}}\!/\!c$. The inverse slope parameter of the spectrum increases with increasing nuclear size due to increasing transverse flow.

A comparison with calculations from the models Epos1.99 [19], Urqmd3.4  [34, 35], and Fritiof7.02  [36] embedded in Hsd2.0  [37] is presented in Fig. 20.

The best agreement is found for the Epos1.99 model.

6 Summary

Inclusive production of $\Lambda$-hyperons was measured with the large acceptance NA61/SHINE spectrometer at the CERN SPS in inelastic p+p interactions at beam momentum of 158 ${\mathrm{GeV}}\!/\!c$. Spectra of transverse momentum (up to 2 ${\mathrm{GeV}}\!/\!c$) and transverse mass as well as distributions of rapidity (from $-$1.75 to 1.25) and x$_{_F}$ (from $-$0.4 to 0.4) are presented. The mean multiplicity was found to be $0.120\pm 0.006\;(stat.)\;\pm 0.010\;(sys.)$. The new results are in reasonable agreement with measurements from bubble-chamber experiments at nearby beam momenta, but have much smaller uncertainties.

Predictions of the Epos, Urqmd and Fritiof models were compared to the new NA61/SHINE measurements reported in this paper. While Epos describes the data quite well, significant discrepancies are observed with the latter two models.

The results expand our knowledge of elementary proton-proton interactions, allowing for a more precise description of strangeness production. They are expected to be used not only as an important input in the research of strongly interacting matter, but also as an input for tuning MC-generators, including those used for cosmic-ray shower and neutrino beams simulations.