1 Introduction

Neutrinoless double-beta decay (\(0\nu \mathrm {DBD}\)) is a hypothetical lepton number violating process in which two neutrons in an atomic nucleus simultaneously decay to two protons, two electrons, and no electron-antineutrinos: \({(A,Z)\rightarrow }{(A,Z+2) + 2e^-}\). Observation of \(0\nu \mathrm {DBD}\) would establish the Majorana nature of the neutrino, i.e., that the neutrino is its own antiparticle, and may provide insights on the neutrino mass scale and mass hierarchy, depending on \(0\nu \mathrm {DBD}\) rate or rate limit (cf. [1]). The experimental signature for \(0\nu \mathrm {DBD}\) is a peak at the \(0\nu \mathrm {DBD}\) Q-value in the two-electron energy sum spectrum. Several recent experiments have reported new limits on the \(0\nu \mathrm {DBD}\) half-life of \(\mathrm {^{136}Xe}\) [2, 3] and \(\mathrm {^{76}Ge}\) [4]. For comparison between experiments, half-life limits of different isotopes are usually converted to limits on the effective Majorana mass. This conversion, however, takes into account the phase space factors and nuclear matrix elements, the latter of which introduce large uncertainties from different model calculations [5–11]. The current \(0\nu \mathrm {DBD}\) half-life limit for \(\mathrm {^{130}Te}\) was set by Cuoricino at \(2.8\times 10^{24}\,\mathrm {y}\) (90 % C.L.) [12].

CUORE-0 is a cryogenic detector that uses an array of \(\mathrm {TeO_2}\) bolometers to search for \(0\nu \mathrm {DBD}\) in the \(\mathrm {^{130}Te}\) of the bolometers themselves. \(\mathrm {^{130}Te}\) is an attractive isotope for a \(0\nu \mathrm {DBD}\) search because of its relatively high Q-value at \(2528 \,\mathrm {keV}\) [13–15] and its very high natural isotopic abundance at 34.2 % [16]. Cryogenic bolometers measure energy through a rise in the temperature of the detector and have energy resolutions comparable to high purity Ge detectors: for CUORE-0 style bolometers, the energy resolution (full width at half maximum, FWHM) is typically 0.2 % at the \(0\nu \mathrm {DBD}\) Q-value. \(0\nu \mathrm {DBD}\) data taking with CUORE-0 began in March 2013.

CUORE-0 also serves as a technical prototype for CUORE (Cryogenic Underground Observatory of Rare Events) [17], which will consist of 19 towers identical to the single CUORE-0 tower. CUORE-0 is the first tower produced on the CUORE assembly line, and its successful commissioning represents a major milestone towards CUORE. CUORE is in the advanced stages of detector construction at the time of this writing and is scheduled to begin data taking in 2015.

2 CUORE-0 detector

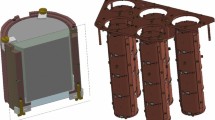
CUORE-0 is a single tower of 52 \(\mathrm {TeO_2}\) crystal bolometers operating at a typical base temperature of 13–15 mK in Hall A of the Laboratori Nazionali del Gran Sasso (LNGS) underground facility in Italy. As shown in Fig. 1a, the tower consists of 13 planes of four \(5\times 5\times 5\,\mathrm {cm^3}\) crystals, held securely inside a copper frame by specially designed polytetrafluoroethylene (PTFE) brackets. The copper frame serves as a thermal bath to cool the crystals through the weak thermal coupling provided by PTFE. Each crystal weighs \(750\,\mathrm {g}\), which results in a total detector mass of \(39\,\mathrm {kg}\) and a total \(^{130}\mathrm {Te}\) mass of \(11\,\mathrm {kg}\). Each crystal is instrumented with a single neutron transmutation doped (NTD) germanium thermistor for the signal readout (see Fig. 1b). The typical signal amplitude \(\Delta T/\Delta E\) is \(10 - 20\,\mathrm {\mu K}\)/MeV. Figure 1c shows an example of a bolometer signal. Additionally, one silicon Joule heater [18] is also glued to the crystal for the offline correction of thermal gain drift caused by temperature variation of the individual bolometer.

Fig. 1
figure 1

a CUORE-0 tower array rendering. The tower consists of 13 planes of 4 crystals, mounted in the frame made of copper. b Schematic of a single CUORE-0 bolometer showing the thermistor (T), the heater (H), and the weak thermal link (L) between \(\mathrm {TeO_2}\) crystal and copper thermal bath (not to scale). c An example of a bolometer signal with the energy of approximately \(2615\,\mathrm {keV}\). The rise and fall times of this signal are \(0.04\,\mathrm {s}\) (defined as the time for the pulse amplitude to evolve from 10 to 90 % of its maximum) and \(0.26\,\mathrm {s}\) (90–30 % of maximum), respectively

Full size image

We put significant effort into the selection and handling of the detector materials with the objective of minimizing the background contamination for CUORE-0. In collaboration with the \(\mathrm {TeO_2}\) crystal grower at the Shanghai Institute of Ceramics, Chinese Academy of Sciences, we developed a radiopurity control protocol [19] to limit bulk and surface contaminations introduced in crystal production. Only materials certified for radiopurity were used to grow the crystals. After production, the crystals were transported to LNGS at sea level to minimize cosmogenic activation. Upon arrival at LNGS, a few crystals from each batch were instrumented as bolometers for characterization tests. For \(\mathrm {^{238}U}\) (\(\mathrm {^{232}Th}\)) decay chain, the measured bulk and surface contaminations are less than \(6.7\times 10^{-7}\,\mathrm {Bq/kg}\) (\(8.4\times 10^{-7}\,\mathrm {Bq/kg}\)) and \(8.9\times 10^{-9}\,\mathrm {Bq/cm^2}\) (\(2.0\times 10^{-9}\,\mathrm {Bq/cm^2}\)) at \(90\,\mathrm {\,}{\%}\) C.L., respectively [20]. Material screening of small parts, including NTD thermistors and silicon heaters, indicates that their radioactive content contributes to less than 10 % of the total background in the \(0\nu \mathrm {DBD}\) region of interest (ROI).

Based on the experience of Cuoricino, we expect the most significant background contributions to come from the tower frame and the surrounding cylindrical thermal shield, both of which are made from radiopure electrolytic tough pitch copper [21]. Relative to Cuoricino, the total mass and surface area of the tower frame of CUORE-0 was reduced by a factor of 2.3 and 1.8, respectively. Monte Carlo studies predict a factor of 1.3 decrease in \(\alpha \) background from the thermal shield arriving at the crystals due to the change in the geometry [22]. To further mitigate the surface contamination of the copper structure, we tested three surface treatment techniques [23] and chose a series of tumbling, electropolishing, chemical etching, and magnetron plasma etching for the surface treatment. The upper limit of the surface contamination of the cleaned copper was measured in R&D bolometers to be \(1.3\times 10^{-7}\,\mathrm {Bq/cm^2}\) (90 % C.L.) for both \(\mathrm {^{238}U}\) and \(\mathrm {^{232}Th}\) [23].

The CUORE-0 detector assembly procedure was designed to minimize the recontamination of clean components. Tower assembly takes place in a dedicated class 1000 clean room in Hall A of the LNGS underground facility. To minimize exposure to radon (and radon progeny) in air, all steps of the assembly were performed under nitrogen atmosphere inside glove boxes [24]. All tools used inside the glove boxes, and especially those that would physically touch the detector components, were cleaned and certified for radiopurity. The assembled tower was enclosed in a copper thermal shield and mounted in the Cuoricino cryostat. To minimize exposure to the environment during mounting to the cryostat, mounting was performed in the Cuoricino clean room, and the tower was kept under nitrogen flux for as long as possible.

CUORE-0 uses for the first time flexible printed circuit board (PCB) cables and in situ wire bonding for electrical wiring of the tower. This is one of the major upgrades that significantly improved the robustness of bolometer readout wiring compared to the Cuoricino design. A set of flexible PCB cables with copper traces [25, 26] was attached to the copper frame from the bottom plane to the top. The lower ends of the PCB copper traces were bonded to the metal contact pads of the thermistors and heaters using \(25\,\mathrm {\mu m}\) diameter gold wires. The upper ends of the PCB cables were connected through another custom-made flexible PCB at the \(10\,\mathrm {mK}\) plate to a set of Manganin twisted pair flat ribbon cables running un-interrupted to the feedthroughs on the top plate of the cryostat. Overall, only 3 bolometers (6 %) are not fully functional from the loss of 1 thermistor and 2 heaters. The two heater-less bolometers can be used in non-standard analysis without thermal gain correction in the future.

CUORE-0 is operated in the same cryostat, uses the same external lead and borated-polyethylene neutron shielding, and is enclosed in the same Faraday cage that was used for Cuoricino [12, 27]. The front-end electronics [28–30] and data acquisition hardware are also identical to those used in Cuoricino. We implemented a new automated bias voltage scanning algorithm to locate the optimal working point that maximizes the signal-to-noise ratio (SNR). The bolometer signals are amplified and then filtered with six-pole Bessel low-pass filters. Subsequently, signals are digitized by two 32-channel National Instruments PXI analog-to-digital converters with a \(125\,\mathrm {S/s}\) sampling rate, 18-bit resolution, and \(21\,\mathrm {V}\) full scale. All samples are stored continuously on disk. Afterwards, in almost real-time, a constant fraction analysis trigger identifies triggered pulses with 626 sampling points (\(5.008\,\mathrm {s}\)), including a pre-trigger segment of 125 samples. Each bolometer has an independent trigger threshold, ranging from \(50\) to \(100 \,\mathrm {keV}\). In addition to the signal triggers, each bolometer is pulsed periodically at \(300\,\mathrm {s}\) intervals with a fixed and known energy through the heater. These “pulser” events are used to monitor and correct the gain of the bolometers [31]. Finally, a baseline trigger identifies a baseline pulse every \(200\,\mathrm {s}\) to provide snapshots of the detector working temperatures and noise spectra.

CUORE-0 data are grouped into “data sets”. Each data set consists of a set of initial calibration runs, a series of physics runs, and a set of final calibration runs. Calibration data refers to the sum of all calibration runs, while background data refers to the sum of all physics runs to search for \(0\nu \mathrm {DBD}\). During calibrations, the detector is irradiated using two thoriated tungsten wires, each with a \(\mathrm {^{232}Th}\) activity of \(50 \,\mathrm {Bq}\). The wires are inserted into two vertical tubes on opposite sides of the tower that run between the outer vacuum chamber and the external lead shielding. We calibrate each channel using \(\gamma \) rays from daughter nuclei of \(\mathrm {^{232}Th}\) in the energy range from \(511\) to \(2615\,\mathrm {keV}\). The signal rates on each bolometer for the calibration and background data are 60–70 and 0.5–1.0\(\,\mathrm {mHz}\), respectively.

3 CUORE-0 performance and background

The CUORE-0 data reported in this article was collected between March and September 2013, with interruptions for dilution refrigerator maintenance. To account for temporary degraded performances on each individual bolometer due to large baseline excursions or elevated noise levels, we reject low-quality data intervals on a channel-by-channel basis. Consequently, the total exposure is obtained by summing the individual exposures of each bolometer. The accumulated \(\mathrm {TeO_2}\) exposure on 49 fully active channels is \(7.1 \,\mathrm {kg \cdot y}\) for a \(^{130}\mathrm {Te}\) isotopic exposure of \(2.0 \,\mathrm {kg\cdot y}\), excluding all low-quality data intervals.

CUORE-0 data analysis follows the same procedure as was used for Cuoricino [12]. This includes amplitude evaluation, gain correction, energy calibration, and time coincidence analysis among the bolometers. Pulse amplitude is evaluated by first maximizing the SNR with an optimum filter. Fourier components of each pulse are weighted at each frequency by the expected SNR, which is calculated for each channel with an average pulse of \(2615 \,\mathrm {keV}\) \(\gamma \) rays and the average power spectra of the noise events. For the gain correction of each bolometer, the amplitudes of pulser events are fit against their baseline voltages to determine the gain dependence on temperature, and this temperature dependence is backed out for each signal pulse. For the energy calibration, we use a third order polynomial fit in the energy range from 0 to \(3.9\,\mathrm {MeV}\) since the relationship between energy and stabilized amplitude is found to be slightly nonlinear. The deviation from a linear fit is less than \(10 \,\mathrm {keV}\) at the \(2615\,\mathrm {keV}\) peak. If any two or more crystals register signal pulses within \(100\,\mathrm {ms}\) of each other, the events are tagged as coincidence events. These are mostly attributed to backgrounds such as Compton-scattered \(\gamma \) rays or \(\alpha \) decays on the surface of two adjacent crystals.

The event selection criteria can be categorized as follows: basic data quality, pile-up, pulse shape, and anti-coincidence. The basic data quality cut rejects events within low-quality data intervals, as mentioned in the beginning of the section. The pile-up cut requires that only one pulse exists in a \(7.1\,\mathrm {s}\) window around the measured trigger time (see Fig. 1c). Due to the relatively long rise and decay times of a pulse and negligible pulse shape dependence on energy at energies above \(1\,\mathrm {MeV}\), the pulse shape of the possible \({}^{130}\mathrm Te \) \(0\nu \mathrm DBD \) signal is expected to be similar to that obtained from the \(2615\,\mathrm {keV}\) \(\gamma \)-ray peaks. Therefore, the pulse shape cut requires that the signal shape is comparable to that obtained from the average pulse recorded with \(2615 \,\mathrm {keV}\) \(\gamma \)-ray events, and that the pre-trigger baseline slope is smaller than \(0.1\,\mathrm {mV/Sample}\). The anti-coincidence cut requires that no other pulse in coincidence is recorded in the entire tower.

We evaluate the selection efficiency mainly using the \(2615\,\mathrm {keV}\) \(\gamma \)-ray peak since it offers sufficient statistics at the energy closest to the ROI. However, since the \(2615\,\mathrm {keV}\) \(\gamma \)-ray events occasionally occur in coincidence with other physical events, the efficiency of anti-coincidence cut was evaluated using the \(1461\,\mathrm {keV}\) \(\gamma \) rays from \({}^{40}\mathrm {K}\) decay, which are truly individual events. The selection efficiency was averaged over all active channels. The efficiency was obtained by first evaluating the slowly varying background rate under the peak by counting the number of events in the energy regions between 3 and \(15\sigma \) above and below the peak. The background rate was then subtracted from the peak rate which was measured by counting the number of events within \(\pm 3\sigma \) of the peak. The result was cross-checked by fitting the combined peak and background region (\(\pm 15\sigma \)) with a Gaussian plus linear function. The difference between the two methods was integrated as the systematic uncertainty of the selection efficiency. The obtained efficiency is \({92.9 \pm 1.8\,\%}\), which is the efficiency of all cuts other than the anti-coincidence cut, obtained from the \(2615\,\mathrm {keV}\) \(\gamma \)-ray peak, multiplied by the efficiency of the anti-coincidence cut, obtained from the \(1461\,\mathrm {keV}\) peak after applying all other cuts, as described above. Since we are considering only single crystal events, we must include the confinement efficiency, i.e. the probability that both \(0\nu \mathrm {DBD}\) electrons are contained inside the single crystal. This probability has been estimated by simulation to be \({87.4 \pm 1.1\,\%}\) [12]. Taking into account the \({99.00 \pm 0.01\,\%}\) signal trigger efficiency, which is evaluated on pulser events, the total \(0\nu \mathrm {DBD}\) detection efficiency of CUORE-0 is \({80.4\pm 1.9\,\%}\). This result is compatible with the value obtained from Cuoricino, which was found to be \({82.8\pm 1.1\,\%}\) [12].

The top panel in Fig. 2 shows the energy spectrum obtained using the \(^{232}\mathrm {Th}\) calibration source. The spectrum is the sum of all 49 fully functional channels. The histogram in the bottom panel shows the background spectrum of CUORE-0 for the analysis presented. The presence of the pronounced \(\gamma \)-ray peaks from \(^{214}\mathrm {Bi}\) decay, a daughter nucleus of \(^{222}\mathrm {Rn}\), is attributed to the inclusion of data taken without the nitrogen gas purge in the Faraday cage around the dilution refrigerator. The nitrogen purge effectively suppresses \(^{214}\mathrm {Bi}\) \(\gamma \)-ray intensities by more than a factor of 5. The energy resolution in the ROI is defined as the FWHM of \(2615 \,\mathrm {keV}\) \(\gamma \)-ray peak, determined by a fit to the summed background spectrum of all fully functional channels. The median resolution of the individual channels in the calibration data is \(6.0 \,\mathrm {keV}\), with a mean of \(6.8\,\mathrm {keV}\) and a root mean square deviation of \(2.1\,\mathrm {keV}\). The relatively larger mean and root mean square deviation are attributed to a few underperforming channels. The energy resolution of calibration data slightly deteriorates due to accidental coincidence events and a higher overall noise level compared to background data.

Fig. 2
figure 2

CUORE-0 calibration (top panel) and background spectrum (bottom panel) over the data taking period presented in this work. \(\gamma \)-ray peaks from known radioactive sources in the background spectrum are labeled as follows: (1) \(e^+e^-\) annihilation; (2) \(\mathrm {^{214}Bi}\); (3) \(\mathrm {^{40}K}\); (4) \(\mathrm {^{208}Tl}\); (5) \({}^{60}\mathrm {Co}\); and (6) \(\mathrm {^{228}Ac}\)

Full size image

When compared to Cuoricino, one new noise contribution is correlated microphonic noise on multiple channels introduced by the new flexible PCB wiring. The vibration of one PCB cable might introduce common-mode noise in all the channels on that cable, which is apparent in the low-frequency part of the signal band and degrades the energy resolution. However, even with the correlated noise in play, the energy resolution of \(5.7 \,\mathrm {keV}\) (FWHM) is better, on average, than that of Cuoricino. Furthermore, we have on-going studies seeking to improve the energy resolution by regressing the correlated noise out of the bolometer signals [32].

As of this writing, we have kept the \(0\nu \mathrm {DBD}\) region blinded. Our blinding procedure is a form of data salting, where we randomly exchange a blinded fraction of events within \(\pm 10\,\mathrm {keV}\) of the \(2615\,\mathrm {keV}\) \(\gamma \)-ray peak with events within \(\pm 10\,\mathrm {keV}\) of the \(0\nu \mathrm {DBD}\) Q-value. The exchange probability varies between 1 and 3 % and is randomized run by run. Since the number of \(2615 \,\mathrm {keV}\) \(\gamma \)-ray events is much larger than that of possible \(0\nu \mathrm {DBD}\) events, the blinding algorithm produces an artificial peak around the \(0\nu \mathrm {DBD}\) Q-value and blinds the real \(0\nu \mathrm {DBD}\) rate of \({}^{130}\mathrm {Te}\). This method of blinding the data preserves the integrity of the possible \(0\nu \mathrm {DBD}\) events while maintaining the spectral characteristics with measured energy resolution and introducing no discontinuities in the spectrum.

The background rate in the ROI is evaluated using the blinded spectrum in the energy range 2470–2570\(\,\mathrm {keV}\). This region includes the \(\mathrm {^{60}Co}\) sum-peak at 2506\(\,\mathrm {keV}\) and the salted peak at the \(0\nu \mathrm {DBD}\) Q-value, as shown in Fig. 3. We use an unbinned maximum-likelihood fit to estimate the background rate in the ROI. The likelihood function consists of the sum of a \(\mathrm {^{60}Co}\) Gaussian peak, a salted \(0\nu \mathrm {DBD}\) Gaussian peak, and a flat background. In the fit, the mean of the \(\mathrm {^{60}Co}\) peak is initialized to \(2506 \,\mathrm {keV}\) and the mean of the salted \(0\nu \mathrm {DBD}\) peak at \(2528 \,\mathrm {keV}\). The FWHM of both peaks is fixed to the detector resolution at \(5.7 \,\mathrm {keV}\). As shown in Fig. 3, the fit reveals that the overall background rate in the ROI is \({0.071 \pm 0.011 ~\mathrm {(stat)} ~\,\mathrm {counts/(keV\cdot kg\cdot y)}}\). For comparison, the background rate of the Cuoricino crystals with the same dimension is \({0.153 \pm 0.006 \,\mathrm {counts/(keV\cdot kg\cdot y)}}\). Systematic uncertainties arising from background shape are studied by comparing a constant and a linear background models, and are found to be less than 3 %. The systematic contribution from the uncertainty in energy calibration is less than 1 %.

Fig. 3
figure 3

Blinded energy spectrum and \(0\nu \mathrm {DBD}\) global fit in the region of interest. The unbinned maximum-likelihood fit is shown in solid red line. The dotted blue line illustrates the peak from \({}^{60}\mathrm {Co}\) and the linear background only to highlight the difference between salted \(0\nu \mathrm {DBD}\) peak and background. The flat background from the fit is \({0.071 \pm 0.011 \,\mathrm {counts/(keV\cdot kg\cdot y)}}\). \(\mathrm {^{60}Co}\) peak position, salted peak position, and rate are \({2506.8 \pm 1.1\,\mathrm {keV}}\), \({2528.4 \pm 1.0\,\mathrm {keV}}\), and \({1.3\pm 0.5 \,\mathrm {counts/(keV\cdot kg\cdot y)}}\), respectively

Full size image

The two major sources of background in the ROI are degraded \(\alpha \) particles from surface contamination on the detector components and \(\gamma \) rays that originate from the cryostat. Degraded \(\alpha \) particles with a decay energy of 4 to \(8 \,\mathrm {MeV}\) may deposit part of their energy in the \(0\nu \mathrm {DBD}\) ROI. These \(\alpha \) events form a continuous energy spectrum extending from their decay energy to well below \(0\nu \mathrm {DBD}\) region. The \(\alpha \) background rate in the ROI is estimated by counting events in the “\(\alpha \) flat continuum region”, which is defined to be from \(2.7\) to \(3.9\,\mathrm {MeV}\) (excluding the \(\mathrm {^{190}Pt}\) peak region from 3.1 to \(3.4\,\mathrm {MeV}\)). This energy range is above almost all naturally occurring \(\gamma \) rays, in particular the \(2615 \,\mathrm {keV}\) \(\gamma \) rays from \({}^{208}\mathrm {Tl}\) decay. Figure 4 shows the background energy spectrum of CUORE-0 (shaded red) and Cuoricino (black). The measured rate for CUORE-0 is \(0.019\pm 0.002 \,\mathrm {counts/(keV\cdot kg\cdot y)}\), which improves on the Cuoricino result (\(0.110\pm 0.001 \,\mathrm {counts/(keV\cdot kg\cdot y)}\)) by a factor of 6.

Fig. 4
figure 4

Background spectrum of CUORE-0 (red with shades) and Cuoricino (black) in the region dominated by degraded \(\alpha \) particles. The figure shows reduction of the flat background caused by degraded \(\alpha \) particles in the energy region of [2.7–3.1] and \([3.4-3.9] \,\mathrm {MeV}\)

Full size image

The \(\gamma \)-ray background in the ROI is predominantly Compton-scattered \(2615 \,\mathrm {keV}\) \(\gamma \) rays originating from \({}^{208}\mathrm {Tl}\) in the cryostat. Since CUORE-0 is hosted in the same cryostat as was used for Cuoricino, the \(\gamma \)-ray background is expected to be similar. The \(\gamma \)-ray background is estimated as the difference between overall background in the ROI and the degraded \(\alpha \) background in the continuum. The measured \(\gamma \)-ray backgrounds of CUORE-0 and Cuoricino are indeed compatible [12], consistent with the hypothesis that the background in the ROI is composed of \(\gamma \) rays from the cryostat and degraded \(\alpha \) particles.

4 Projected sensitivity of CUORE-0

Using the measured background rate and energy resolution of the \(2615\,\mathrm {keV}\) \(\gamma \)-ray peak, we obtain the CUORE-0 sensititvity with the approach outlined in [33]. With the excellent energy resolution, we construct a single-bin counting experiment with a \(5.7 \,\mathrm {keV}\) bin centered at the \(0\nu \mathrm {DBD}\) Q-value. The sensitivity is obtained by comparing the expected number of signal events with Poissonian fluctuations from the expected background rate in this bin. Figure 5 shows the 90 % C.L. sensitivity of CUORE-0. With one year of live time, or \(11\,\mathrm {kg\cdot y}\) isotope exposure, CUORE-0 is expected to surpass the \(^{130}\mathrm {Te}\) \(0\nu \mathrm {DBD}\) half-life sensitivity achieved by Cuoricino, \(2.8 \times 10^{24} \,\mathrm {y}\).

Fig. 5
figure 5

Sensitivity of CUORE-0 with the measured background rate in the ROI of \({0.071 \,\mathrm {counts/(keV\cdot kg\cdot y)}}\) and energy resolution of \(5.7 \,\mathrm {keV}\) FWHM. The CUORE-0 sensitivity is expected to surpass that of Cuoricino with 1 year of live time

Full size image

5 Summary and outlook

We present the energy resolution and background measurements of CUORE-0 detector from the \(7.1 \,\mathrm {kg\cdot y}\) exposure accumulated up to September 2013. The measured \(5.7\,\mathrm {keV}\) FWHM in the \(0\nu \mathrm {DBD}\) ROI represents a slight improvement over Cuoricino and validates the CUORE-0 wiring scheme and assembly procedure. The background rates have been measured to be \({0.071 \pm 0.011 \,\mathrm {counts/(keV\cdot kg\cdot y)}}\) in the ROI and \({0.019 \pm 0.002 \,\mathrm {counts/(keV\cdot kg\cdot y)}}\) in the \(\alpha \) continuum region. These results are a factor of 2 and 6 improvement compared to Cuoricino, due to more rigorous copper surface treatment, improved crystal production and treatment protocols, and more stringent assembly procedures in the clean environment. The CUORE-0 sensitivity is expected to surpass that of Cuoricino with one year of live time.

As a technical prototype for CUORE, CUORE-0 demonstrates the feasibility of instrumenting an ultra-pure ton-scale bolometer array with 988 channels. By enhancing the procedure of the on-going CUORE assembly, we have improved assembly success rate to close to 100 %, which is a crucial achievement for large arrays such as CUORE. We have started implementing the noise decorrelation algorithms into the CUORE-0/CUORE data analysis package, with the aim of further improving energy resolution. CUORE-0 reconfirms the effectiveness of the copper cleaning technique and clean assembly procedure developed for CUORE. Compared to CUORE-0, the larger array of CUORE affords more powerful time coincidence analysis and more effective self-shielding from external backgrounds, particularly those originating from the copper thermal shields or cryostat. With this stronger background rejection and the already demonstrated reduction of surface contamination, the CUORE background goal of \(0.01 \,\mathrm {counts/(keV\cdot kg\cdot y)}\) is expected to be within reach. The projected half-life sensitivity to \(\mathrm {^{130}Te}\) \(0\nu \mathrm {DBD}\) is \(9.5\times 10^{25} \,\mathrm {y}\) (90 % C.L.) with 5 years of live time [33], reaching an effective Majorana neutrino mass sensitivity of 0.05 to \(0.13\,\mathrm {eV}\) [5–11, 34].