Abstract
We have developed a new method to measure krypton traces in xenon at unprecedented low concentrations. This is a mandatory task for many near-future low-background particle physics detectors. Our system separates krypton from xenon using cryogenic gas chromatography. The amount of krypton is then quantified using a mass spectrometer. We demonstrate that the system has achieved a detection limit of 8 ppq (parts per quadrillion) and present results of distilled xenon with krypton concentrations below 1 ppt.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Low-background particle physics experiments rely on liquid xenon (LXe) detectors in the fields of direct dark matter detection, neutrinoless double beta decay and solar neutrino research [1–3]. LXe is used as a target material due to its high mass, good self-shielding and scintillation properties. Xenon is commercially produced by extraction from the atmosphere. The relative abundances of krypton and xenon in ambient air are 1.14 parts per million by volume (ppmv) and 0.09 ppmv, respectively [4]. The separation from atmospheric constituents in this extraction process has limited efficiency resulting in traces of krypton at the level of parts per million (ppm) and, for high purity xenon, parts per billion (ppb).
The inert gas krypton with its unstable isotope \({}^{85}{\mathrm{Kr }}\) is one of the most serious internal background sources for LXe detectors used in low-background experiments. It is homogeneously distributed in the xenon and cannot be discriminated by shielding or fiducial volume cuts. \({}^{85}{\mathrm{Kr }}\) has a half life of 10.8 years and is an almost pure \(\beta ^{-}\) emitter (99.56 % branching ratio) with end-point energy of 687 keV [5]. The activity of the man-made isotope \({}^{85}{\mathrm{Kr }}\) in the atmosphere, produced in sizable quantities by nuclear fission and released by nuclear-fuel reprocessing plants and nuclear weapon tests, has been steadily increasing over time. The present-day activity concentration is approximately 1.4 Bq/m\(^{3}\) [6, 7], corresponding to a relative isotopic abundance of \({}^{85}{\mathrm{Kr }}\)/\({}^\mathrm{nat }{\mathrm{Kr }}\) of 2 \(\times 10^{-11}\) mol/mol [8].
Purification techniques are established to remove krypton from xenon to the parts per trillion (ppt) level [2, 9]. Techniques for the quantification of such ultra-low levels of contamination so far only exist until the few hundreds ppq level [9–11]. However, krypton/xenon concentrations below 100 parts per quadrillion (ppq) are needed for near future experiments [12].
In this work we present a measurement technique with an extrapolated detection limit of 8 ppq, almost two orders of magnitude lower than what has been previously achieved. Section 2 describes the measuring system based on gas chromatographic separation of the bulk xenon from the krypton traces and quantification by means of a sector field mass spectrometer. In Sect. 3, the data analysis is described, the system acceptance for krypton is characterized, a detailed study of the experimental uncertainties is presented and the system’s detection limit is given. Finally, in Sect. 4 the results of seven different samples that prove the claimed performance are shown and the assay of xenon with a krypton concentration below the ppt level is presented.
2 Experimental setup
The mass spectroscopic technique is used to quantify the abundance of natural krypton in given xenon gas batches down to the ppq regime. The setup can be separated into four parts: sample preparation, ion source, mass analyzer and detector. The ion source, mass analyzer and detector belong to a customized sector field mass spectrometer (Vacuum Generators model VG 3600) that is described in Sect. 2.1. The sample preparation, based upon cryogenic gas chromatography, is the essential new development and will be discussed in Sect. 2.2.
2.1 The mass spectrometer
The mass spectrometer is a customized version of a VG 3600 (Fig. 1) capable of quantifying an amount of natural krypton of less than 10\(^{-13}\) cm\(^{3}\) STPFootnote 1 [14]. It is located at the Max-Planck-Institut für Kernphysik in Heidelberg, Germany.
The sample is collected by cryogenic pumping on a cold finger which contains a small amount of activated carbon, which is installed between the sample preparation part and ion source. When warming up the cold finger, the gaseous sample distributes in the entire volume of ion source, mass analyzer and detectors. Ionization, acceleration and focusing take place in the ion source of the mass spectrometer. Electrons are emitted from a hot filament and ionize the sample gas. The ions are accelerated and focused in electric fields. Their mass separation is achieved by a variable magnetic dipole-field. The ions are detected by a continuous dynode amplifier (SEM = secondary electron multiplier) counting events above a predefined threshold optimized for its signal/background ratio. In order to achieve the high sensitivity goals batch sizes on the order of 1 cm\(^{3}\) xenon gas are needed. However, this amount of xenon gas would result in a pressure much above the critical pressure of 10\(^{-6}\) mbar [15] in the spectrometer. Thus, the krypton must be separated from the bulk xenon before it is fed into the spectrometer. This separation is achieved by the gas chromatography system.
2.2 The gas chromatography system
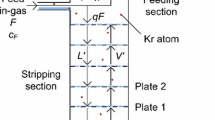
The krypton/xenon separation is performed via gas chromatography in the setup sketched in Fig. 2. The amount of helium carrier gas used in this process exceeds the size of the xenon batch by more than a factor of 50. Therefore, the purity specifications in terms of krypton inside the helium gas are strict. To reach sub-ppt sensitivity, the krypton concentration in the helium has to be at or below the ppq level. In this work grade 6.0 helium is purified using an adsorbent filled packed column T1 (10 mm inner diameter, 8.18 g Carbosieve S-III by Supelco Analytical) immersed in a liquid nitrogen bath. Pushed forward by the helium carrier, the gas mixture passes another adsorbent filled column T2 (6 mm inner diameter, 0.64 g Chromosorb 102 by Johns Manville) immersed in a coolant liquid (ethanol). Due to differences in the interaction strength of each constituent with the adsorbent, krypton and xenon can be separated if the flow of the carrier gas, the pressure gradients and the temperature are properly adjusted (see Fig. 3). The temperature of the ethanol coolant and the helium gas flow for the separation in this work were fixed to \(-\)80 \(^{\circ }\)C and 7 standard cubic centimetre per minute.
The separated krypton is trapped in a third adsorbent filled packed column T3, identical to T2. By heating up T3 after the chromatographic process the krypton is released and can be transferred to the mass spectrometer by cryogenic pumping to the cold finger mounted next to the ion source of the mass spectrometer.
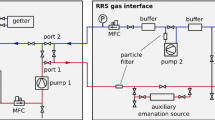
Apart from the three adsorbent filled traps, the ultra-high vacuum system is constructed completely from stainless steel, and all flanges are sealed with copper gaskets. The adsorbent filled traps are made from borosilicate glass with special glass-to-metal seals well suited for the high purity demands. To avoid dust from the adsorbent entering the mass spectrometer, a PTFE nano particle filter is installed. The stainless steel and glass part of the system is bakeable to above 300 \(^{\circ }\)C, however the adsorbent materials and the PTFE can only withstand temperatures up to 150 \(^{\circ }\)C and 120 \(^{\circ }\)C, respectively, setting the upper limit on the temperature during bakeout. The system provides a turbomolecular pump backed up by a dry and oil free piston vacuum pump. The latter one is important to avoid hydrocarbons entering the system and altering the performance of the adsorbents. All of the valves used in the system are full-metal, bellow sealed, 3/4 in. valves with a leak rate specification of \(<\)5 \(\times \) 10\(^{-11}\) mbar l/s. A precise capacitance manometer from Edwards (Barocel 600 series, 0.15 % accuracy, labelled P2 in Fig. 2) is installed to determine the initial batch size of xenon gas. The system is further characterized by an analog, fully metal sealed pressure gauge (P1) and a combined Pirani/cold cathode vacuum gauge (V1) that can be separated from the sample by a valve.
2.3 Drawing samples
In terms of sampling, two different tasks have to be accomplished: First, the assay of xenon that must be extracted in situ from immobile experiments and, second, the assay of xenon in movable storage containers, e.g. xenon gas cylinders. While the latter type of samples can be shipped to the laboratory and mounted directly at the device, the sampling of the former requires the use of an intermediate transport vessel.
Sampling from gas cylinders: The gas chromatographic setup facilitates two ports (see Fig. 2) where gas cylinders can be connected to either directly or via a pressure regulator. The former has the advantage of having less volumes potentially contaminated, but is difficult since the gas cylinders may be filled with pressures up to 65 bar.
Sampling with the xenon sampling device Initially developed for a similar purpose in the framework of the Borexino experiment [16], four 1/2 in., fully metal sealed valves were welded together in series enclosing three volumes of \(\sim \) 10 cm\(^{3}\) to be filled with pressures up to 70 bar. The central volume is shielded by the two adjacent volumes from ambient air that might penetrate the sample through tiny leaks.
The initial preparation of the xenon sampling device consists of baking (\(\sim \) 100 \(^{\circ }\)C) and evacuating the three volumes that will hold the samples to a pressure \(<\)10\(^{-7}\) mbar for several days. Then the sample volumes are sealed, left under vacuum for several days and finally checked for remaining krypton background using the mass spectrometer. Once the krypton background is sufficiently low, the device can be used for taking samples.
The preparation at the site of the xenon extraction consists of mounting the xenon sampling device to a port of the setup that contains the xenon and setting up a vacuum system. Next, the parts that have been in contact with air, that is between the setup’s port and the first valve of the xenon sampling device, are baked and evacuated to a pressure below 10\(^{-7}\) mbar. To remove possible impurities from the surfaces and to avoid effects of different impurity compositions in the xenon gas that might be present close to the port, a small amount of xenon is flushed from the setup to the vacuum system. Then the valve to the vacuum system is closed and the samples are drawn by expanding the xenon into the prepared volumes of the xenon sampling device.
3 Calibration and data analysis
A gas standard is available to calibrate the mass spectrometer and to determine the acceptance of the full gas chromatographic process. The gas standard consists of a metal-sealed container with a volume of a few liters that is filled with the noble gases argon, krypton, and xenon. Connected to this container is a second, much smaller volume (\(\sim \) 0.2 cm\(^{3}\)) that is separated from the latter by a fully metal sealed valve. This volume is used to extract a constant fraction of the gas standard (standard pipette). The amount of krypton in one standard pipette was calibrated using a sample of commercially available helium containing a well-known admixture of krypton. This calibration defines the amount of krypton in our standard pipette to be 3.9 \(\times 10^{-11}\) cm\(^{3}\) (\(\pm 16.5\,\%\)).
3.1 SEM response
The response of the mass spectrometer to the amount of one standard pipette is determined at least once before the measurement of a xenon batch. In the analysis we are interested in the amount of gas initially transferred to the cold finger, that is at time zero (\(\mathrm t _0\)), before other processes (like implanting accelerated ions into the walls of the mass spectrometer’s vacuum tube) start to change its amount. The time-dependence of the count rate of the background and signal are fitted and extrapolated to \(\mathrm t _0\) where the size of the pedestal, as seen in Fig. 4, is a measure of the amount of gas from the respective isotope in the batch.
In standard data taking mode a loop over the isotopes \({}^{36}\mathrm{Ar }\), \({}^{40}\mathrm{Ar }\), \({}^{84}{\mathrm{Kr }}\), \({}^{86}{\mathrm{Kr }}\) and \({}^{132}\mathrm{Xe }\) is recorded. The ratios of \({}^{40}\mathrm{Ar }\)/\({}^{36}\mathrm{Ar }\) and \({}^{84}{\mathrm{Kr }}\)/\({}^{86}{\mathrm{Kr }}\) provide an intrinsic cross-check since they should match the natural abundances (mole fractions). The amount of gas at time zero is determined for \({}^{84}{\mathrm{Kr }}\) and \({}^{86}{\mathrm{Kr }}\) independently (see Sect. 3.3). From both isotopes the amount of natural krypton is computed using the respective relative abundance. Both numbers are combined in the final result. The gas amount of the initial xenon batch is determined in a calibrated volume (\(\mathrm V _{\mathrm{cal}}\)) equipped with a precise capacitive pressure gauge (P2, see Fig. 2).
3.2 Krypton acceptance
The standard pipette is used to determine the acceptance of the gas chromatographic process for krypton. The calibrated mixture of krypton and xenon is transferred by cryogenic pumping to the adsorbent trap T2 (immersed in liquid nitrogen) used for the krypton/xenon separation. Then the full chromatographic procedure is performed—identical to the standard procedure for a normal xenon batch—and the spectrometer’s response to the krypton isotopes is compared to its response without the chromatographic separation process. This calibration procedure yields a krypton acceptance of \(\varepsilon _a = (0.97 \pm 0.02)\).
The procedure described above employs microscopic krypton and xenon gas samples on the order of a few 10\(^{-12}\) cm\(^{3}\), while the standard procedure foresees xenon batches of up to several cm\(^{3}\) containing only traces of krypton. When combining 3.9 \(\times \) 10\(^{-11}\) cm\(^{3}\) of \({}^{nat}{\mathrm{Kr }}\) from the standard pipette with approximately 1.2 cm\(^{3}\) of xenon from sample XE100-3 (1.8 ppt intrinsic krypton, see Sect. 4), we measure (3.2 \(\pm \) 0.7) \(\times \) 10\(^{-11}\) cm\(^{3}\) \({}^{nat}{\mathrm{Kr }}\). Reevaluating the acceptance for krypton \(\varepsilon _a\), we find \(\varepsilon _a = (0.79 \pm 0.18)\) in agreement with above result. The larger uncertainty in this value is dominated by the uncertainty in the intrinsic krypton level of the bulk xenon and the sample standard deviation of a single measurement (see Sect. 3.4). The weighted average of both, \(\varepsilon _a = (0.97 \pm 0.02)\), will be used throughout this work.
3.3 Computation of the krypton level
The krypton level of a given batch is the ratio of the amount of krypton gas measured by the mass spectrometer and the initial batch size determined by its pressure in the calibrated volume. We can write:
where \(i\) represents the individual isotope, \(f_m(i)\) is the mole fraction of the respective isotope, \(\langle \dots \rangle _i\) denotes the average over the isotopes \(i\) and \(\varepsilon _a\) is the acceptance of the full chromatographic process for krypton. \({}^{i}{\mathrm{Kr }}\) is the amount of gas of the krypton isotope \(i\) as measured with the spectrometer. It is computed from the abundance of the krypton isotope \(i\) in the standard pipette (\(\textit{std}_{i}\)) and from the ratio of the pedestals of the batch (\(s_i^\text {batch}\)) and the standard pipette (\(s^\text {std}_{i}\)):
Finally, \(B_i\) is the procedure blank of the full process for the isotope \(i\), as will be explained in Sect. 3.5, and can be written similar to (2) substituting \(s_i^\text {batch}\) by \(s_i^{B}\). \(^{nat}\)Xe can be computed, if the pressure \(p\) and the temperature \(T\) in the calibrated volume \(\text {V}_\text {cal}\) are known.
3.4 Uncertainty budget estimation
Systematic effects common to all measurements are the uncertainty of the standard pipette, the uncertainty in determining the initial xenon batch size and the uncertainty of the chromatographic acceptance for krypton (\(\Delta \varepsilon _a\)). Summing them quadratically, we end up with a relative uncertainty of 17.0 % dominated by the uncertainty of the standard pipette.
Statistical fluctuations of the number of ions detected by the SEM, variations in performing the chromatographic separation and variations in the electrical fields of the ion optics due to high voltage drifts individually affect single measurements. The sum of these effects is estimated (for each sample individually) from the fluctuations of the measurement of several batches around their mean. The resulting uncertainty estimator is added quadratically to the aforementioned systematic uncertainties. In those cases where only a single batch was measured, we estimate its uncertainty by averaging the sample standard deviations of all measurements so far done with this setup. We find 13.5 % to be a single measurement’s standard deviation. Combining both uncertainties by summing them quadratically we find the total relative uncertainty of a single batch to be 21.7 %. If more than one single batch is measured, the relative uncertainty decreases being limited to the systematic uncertainty of 17 %.
3.5 Sensitivity—procedure blank and detection limit
The sensitivity is limited by the traces of krypton which are collected during the full process and increase the signal in the mass spectrometer. Sources for this type of krypton are potential microscopic leaks allowing external krypton to enter the system, outgassing of the surfaces involved in the measurement and krypton introduced by the helium carrier gas. The amount of these krypton traces is accessed by performing the full procedure, identical to a normal measurement, but without a xenon batch introduced (procedure blank). A value of (1.00 \(\pm \) 0.04) \(\times \) 10\(^{-12}\) cm\(^{3}\) is found averaging several measurements done between the presented xenon samples of Sect. 4. After a recent system upgrade (refurbished high voltage control of ion optics and identification and removal of tiny air leak in the sample preparation part) the current procedure blank was measured to be (0.081 \(\pm \) 0.004) \(\times \) 10\(^{-12}\) cm\(^{3}\). This is a reduction by more than a factor ten with respect to the value mentioned above. The first xenon sample measured at this significantly reduced background level is in excellent agreement with earlier results at the higher background level (see Sect. 4). The systematic uncertainty of the absolute calibration is neglected in the estimate of the uncertainty of the procedure blank. This is justified as measurements are corrected for the procedure blank before being converted from a count rate to an amount of gas using the absolute calibration factor.
The decision threshold (DT) and detection limit (DL) are computed following [17] and result in 0.007 \(\times \) 10\(^{-12}\) cm\(^{3}\) and 0.015 \(\times \) 10\(^{-12}\) cm\(^{3}\) (\({}^{nat}{\mathrm{Kr }}\)), respectively, assuming a 21.7 % uncertainty of the outcome of a single measurement. The maximal size of the xenon batch that can be processed by the gas chromatographic separation determines the performance of the system. Up to now the largest xenon batch was 1.9 cm\(^{3}\) and we find at 95 % confidence level:
Note that likely larger xenon batches can be processed by the chromatographic process. The upper threshold for acceptable batch sizes was not determined yet. Consequently, the detection limit of currently 8 ppq may still be lowered in the future.
4 Results
Table 1 lists the results of the individual measurements together with the amount of processed xenon gas. In total, measurements of seven different samples are presented. Two of them (CYL-1 and CYL-2) are xenon gas cylinders with krypton concentrations at the low ppb and high ppt level, i.e. sufficiently abundant to be measured with more common devices for cross checks. The remaining five samples were drawn in the context of the XENON100 experiment [1].
CYL-1 Sample drawn from a carbon steel gas cylinder containing high-purity xenon depleted in the isotope \({}^{136}\mathrm{Xe }\) from the supplier Iceblick. Combining the four measurements and adding the systematic uncertainty as described in Sect. 3.4, we find a krypton level of (7.3 \(\pm \) 1.3) ppb. With this level in the low ppb regime a completely independent measurement using a customized gas chromatograph (Trace GC Ultra from Thermo Scientific) employing a pulsed helium discharge photo-ionization detector (He-PDPI) was possible. This measurement (performed also at MPIK) yielded a krypton concentration of (6.3 \(\pm \) 1.3) ppb in agreement with the mass spectroscopic result.
CYL-2 Sample drawn from an aluminum gas cylinder containing high-purity xenon from the supplier Air Liquide. The xenon was purchased by our colleagues from the University of Münster and measured also by their device combining a cold-trap with a quadrupole mass-spectrometer. The three measurements done with our system combine to a final value of (0.29 \(\pm \) 0.05) ppb. This is again in good agreement with the completely independent analysis from our colleagues that found a krypton concentration of (0.33 \(\pm \) 0.20) ppb in this very same gas sample [18].
XE100-1 Sample drawn from the XENON100 detector [1] during dark matter data taking of the first XENON100 science run [19]. In total there are four measurements with a combined result of (340 \(\pm \) 60) ppt. In [19] a krypton/xenon level of (700 \(\pm \) 100) ppt is given based on a spectral fit to \({}^{85}{\mathrm{Kr }}\). This result was obtained assuming a \({}^{85}{\mathrm{Kr }}/{}^{\text {nat}}{\mathrm{Kr }}\) ratio of \(1\times 10^{-11}\). Using the better motivated number of \(2\times 10^{-11}\) [8, 20], the modified value of (350 \(\pm \) 50) ppt agrees with the result obtained in this work.
XE100-2 During the data taking of the second XENON100 science run [20], a sample was drawn again from the XENON100 detector. In total four measurements were performed resulting in (14 \(\pm \) 2) ppt. Note the different value of (19 \(\pm \) 4) ppt reported in [20], that was evaluated in advance of the precise calibration of our system reported in this work. The correct number of (14 \(\pm \) 2) ppt is in agreement with the value of (18 \(\pm \) 8) ppt obtained from counting the number of delayed \(\beta - \gamma \) coincidences associated with the \({}^{85}{\mathrm{Kr }}\) beta decay [20]. Here the \({}^{85}{\mathrm{Kr }}/{}^{\text {nat}}{\mathrm{Kr }}\) ratio of \(2\times 10^{-11}\) is used.
XE100-3 Sample drawn from the XENON100 gas system during a maintenance period after the second science run. Taking into account the systematic uncertainty, we measure a value of (1.8 \(\pm \) 0.4) ppt for the one measurement done of this sample.
XE100-4 Sample drawn from the output of the XENON100 cryogenic distillation column (similar to the one described in [9]) optimized to remove krypton from xenon gas. Combining the results of the two measurements yields a value of (0.97 \(\pm \) 0.19) ppt for this sample. While the first xenon batch had a size of about 0.7 cm\(^{3}\) giving a signal well above the detection limit, the second xenon batch was smaller by a factor of four. Still the central value is in very good agreement with the first measurement proving the linearity of the spectrometer for such small signals. Comparing the size of this second xenon batch with the second one from XE100-5 (Table 1) we see that the amount of xenon can be increased by a factor of ten giving sensitivity to krypton concentrations below 100 ppq as suggested by the detection limit (Eq. 3).
XE100-5 The last two samples reported here were again drawn from the XENON100 detector. A single measurement of the first sample resulted in (0.71 \(\pm \) 0.24) ppt. At the significantly improved background conditions of our system the second sample was measured to contain (0.96 \(\pm \) 0.22) ppt. Combining both results we find a krypton concentration in the XENON100 detector of (0.95 \(\pm \) 0.16) ppt. To our knowledge, this is the purest xenon target ever employed in a LXe particle detector.
5 Summary
We have presented our new approach of assaying krypton concentrations in xenon at the ppq level using a gas chromatographic krypton/xenon separation followed by a mass spectroscopic krypton measurement. We explained the data analysis and absolute calibration of our device and discussed in detail its uncertainties. By comparing our assay results of two xenon gas samples at the low ppb and high ppt level with results obtained by two independent devices, we confirmed the thorough understanding of the absolute calibration and linearity of the instrument. We showed that with the current setup the system’s detection limit is 8 ppq which may be further improved by enlarging the xenon sample size.
Notes
In this work gas quantities will be always given at standard temperature and pressure using the International Union of Pure and Applied Chemistry (IUPAC) recommendation of 0 \(^{\circ }\)C and 100 kPa [13].
References
E. Aprile et al. (XENON100), Astropart. Phys. 35, 573 (2012). arXiv:1107.2155 [astroph.IM]
M. Auger et al., JINST 7, 5010 (2012). arXiv:1202.2192 [physics.ins-det]
K. Abe et al., NIM A 716, 78 (2013). arXiv:1301.2815 [physics.ins-det]
German Institute for Standardization DIN 1871 (1999)
Laboratoire National Henri Becquerel. http://www.nucleide.org/DDEP_WG/DDEPdata.htm
H.H. Loosli, B.E. Lehmann, W.M.J. Smethie, in Environmental Tracers in subsurface Hydrology, ed. by P. Cook, A.L. Herczeg (Kluwer Academic Publishers, Dordrecht, 2000) pp. 379–397
J. Bieringer, C. Schlosser, H. Sartorius, S. Schmid, Appl. Radiat. Isot. 67, 672 (2009)
X. Du et al., Geophys. Res. Lett. 30, 2068 (2003). arXiv:physics/0311118
K. Abe et al., Astropart. Phys. 31, 290 (2009). arXiv:0809.4413 [physics.ins-det]
A. Dobi et al., NIM A 665, 1 (2011). arXiv:1103.2714 [physics.ins-det]
E. Aprile, T. Yoon, A. Loose, L.W. Goetzke, T. Zelevinsky, Rev. Sci. Instr. 84(9), 093105 (2013). doi:10.1063/1.4821879. arXiv:1305.6510 [physics.atom-ph]
E. Aprile (XENON1T Collaboration). (2012). arXiv:1206.6288 [astro-ph.IM]
J.G. Clavert, Pure Appl. Chem. 62, 2167 (1990)
J. Hopp, M. Trieloff, R. Altherr, Earth Planet. Sci. Lett. 261, 635 (2007)
E. de Hoffmann, V. Stroobant, Mass Spectrometry: Principles and Applications (Wiley-Interscience, New York, 2007)
G. Zuzel, H. Simgen, G. Heusser, Appl. Radiat. Isot. 61, 197 (2004)
International Standards ISO 11929 (2010)
E. Brown, S. Rosendahl, C. Huhmann, C. Weinheimer, H. Kettling, JINST 8, 2011P (2013). arXiv:1212.5136 [physics.ins-det]
E. Aprile et al. (XENON100 Collaboration), Phys. Rev. Lett. 107, 131302 (2011). arXiv:1104.2549 [astro-ph.CO]
E. Aprile et al. (XENON100 Collaboration), Phys. Rev. Lett. 109, 181301 (2012). arXiv:1207.5988 [astro-ph.CO]
Acknowledgments
We are grateful to the XENON collaboration for their support in drawing xenon samples and providing the purest xenon gas. We greatly acknowledge the help of Jens Hopp, Hans Richter, Dominik Stolzenburg and Grzegorz Zuzel for their support with the sector field mass spectrometer and thank Teresa Marrodán Undagoitia for her support during the final stage of this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
About this article
Cite this article
Lindemann, S., Simgen, H. Krypton assay in xenon at the ppq level using a gas chromatographic system and mass spectrometer. Eur. Phys. J. C 74, 2746 (2014). https://doi.org/10.1140/epjc/s10052-014-2746-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-014-2746-1