Abstract
We present the hybrid model connecting the parton–hadron–string dynamic model (PHSD) and a hydrodynamic model taking into account shear viscosity within the Israel–Stewart approach. The numerical scheme, initialization, and particlization procedure are discussed in detail. The performance of the code is tested on the pion and proton rapidity and transverse mass distributions calculated for Au + Au and Pb+Pb collisions at AGS–SPS energies. The influence of the switch time from transport to hydro models, the viscous parameter, and freeze-out time are discussed. Since the applicability of the Israel–Stewart hydrodynamics assumes the perturbative character of the viscous stress tensor, \(\pi ^{\mu \nu }\), which should not exceed the ideal energy–momentum tensor, \(T_{\mathrm{id}}^{\mu \nu }\), hydrodynamical codes usually rescale the shear stress tensor if the inequality \(\Vert \pi ^{\mu \nu }\Vert \ll \Vert T_{\mathrm{id}}^{\mu \nu }\Vert \) is not fulfilled in some sense. There are several conditions used in the literature and we analyze in detail the influence of different conditions and values of the cut-off parameter on observables. We show that the form of the corresponding condition plays an important role in the sensitivity of hydrodynamic calculations to the viscous parameter – a ratio of the shear viscosity to the entropy density, \(\eta /s\). It is shown that the constraints used in the vHLLE and MUSIC models give the same results for the observables. With these constraints, the rapidity distributions and transverse momentum spectra are most sensitive to a change of the \(\eta /s\) ratio. We demonstrate that these constraints do not guarantee that each element of the \(\pi ^{\mu \nu }\) tensor is smaller than the corresponding element \(T_{\mathrm{id}}^{\mu \nu }\). As an alternative, a strict condition is used. When applied it reduces the sensitivity of the proton and pion momentum distributions to the viscosity parameter. We performed global fits of the rapidity and transverse mass distributions of pion and protons. It was also found that \(\eta /s\) as a function of the collision energy monotonically increases from \(E_{\mathrm{lab}}=6\,A\text {GeV}\) up to \(E_{\mathrm{lab}}=40\,A\text {GeV}\) and saturates for higher SPS energies. We observe that it is difficult to reproduce simultaneously pion and proton rapidity distribution within our model with the present choice of the equation of state without a phase transition.


















Similar content being viewed by others
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a theoretical study, there are not external data associated with the manuscript.]
Notes
Recall that in the standard implementation of SHASTA, e.g., for solving ideal hydrodynamics in UrQMD, the mid-point rule is used to achieve the second-order accuracy in time.
Equation (11) is applied before the antidiffusion step.
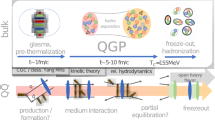
It was noted [36, 37] that the system created in high energy nuclear collisions reaches or at least comes close to equilibrium. In particular, it was realized that because of the expansion of the matter into the vacuum, the system would cool and thus freeze into a hadronic gas quickly. Thus, it became apparent that a fluid dynamic approximation to the system dynamics had to start early, on a time-scale of \(\tau \sim 1\) fm/c or less.
Generally, one can use different mask coefficients, \(A_{\mathrm{ad}}^{x,y,z}\), see Eq. (A9), for every direction, x, y, and z, but for simplicity we take one value for all axes.
Particularly we use version 1.0 of the Parton–Hadron String Dynamics model with the switched off partonic option.
As one can see from the function QuestRevert of MUSIC code or [82], the developers use an energy-dependent cut-off parameter \(C=C(\varepsilon )\) in Eq. (13). We take just a constant value for simplicity. Our results do not changes if one takes \(C(\varepsilon )\propto \tanh \frac{\varepsilon }{\varepsilon _0}\) with small \(\varepsilon _0\).
References
E. Molnár, H. Niemi, D.H. Rischke, Numerical tests of causal relativistic dissipative fluid dynamics. Eur. Phys. J. C 65, 615 (2010)
L.D. Landau, On the multiparticle production in high-energy collisions. Izv. Akad. Nauk Ser. Fiz. 17, 5164 (1953)
L.D. Landau, Collected Papers of L.D.Landau, Ed. D. Ter-Haar (Pergamon Press, Oxford, 1965), p. 74
P.F. Kolb, U.W. Heinz, Hydrodynamic Description of Ultrarelativistic Heavy Ion Collisions, Quark-Gluon Plasma 3, Ed. by R. Hwa and X.-N. Wang (World Scientific, Singapore, 2004), p. 634
U.W. Heinz, R. Snellings, Collective flow and viscosity in relativistic heavy-ion collisions. Annu. Rev. Nucl. Part. Sci. 63, 123 (2013)
C. Gale, S. Jeon, B. Schenke, Hydrodynamic modeling of heavy-ion collisions. Int. J. Mod. Phys. A 28, 1340011 (2013)
S. Jeon, U. Heinz, Introduction to hydrodynamics. Int. J. Mod. Phys. E 24, 1530010 (2015)
S. Jeon, U. Heinz, Quark-Gluon plasma 5, Ed. by X.-N.Wang (World Scientific, Singapore, 2016) [arXiv: 1503.03931]
R. Derradi de Souza, T. Koide, T. Kodama, Hydrodynamic approaches in relativistic heavy ion reactions. Prog. Part. Nucl. Phys. 86, 35 (2016)
W. Florkowski, M.P. Heller, M. Spalinski, New theories of relativistic hydrodynamics in the LHC era. Rept. Prog. Phys. 81, 046001 (2018)
A.S. Khvorostukhin, V.D. Toneev, Rapidity distributions of hadrons in the HydHSD hybrid model. Phys. Atom. Nucl. 80, 285 (2017)
A.S. Khvorostukhin, V.D. Toneev, Hadron rapidity spectra within a hybrid model, Phys. Part. Nucl. Lett. 14, 9 (2017) [arXiv: 1606.00987]
H. Song, U. Heinz, Suppression of elliptic flow in a minimally viscous quark-gluon plasma. Phys. Lett. B 658, 279 (2008)
H. Song, U. Heinz, Causal viscous hydrodynamics in 2 + 1 dimensions for relativistic heavy-ion collisions. Phys. Rev. C 77, 064901 (2008)
L.D. Landau, E.M. Lifshitz, Fluid Mechanics (Pergamon Press, Oxford, 1987)
G.S. Denicol, E. Molnár, H. Niemi, D.H., Rischke Derivation of fluid dynamics from kinetic theory with the 14-moment approximation. Eur. Phys. J. A 48, 170 (2012)
W. Israel, J.M. Stewart, Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 118, 341 (1979)
Iu. Karpenko, P. Huovinen, M. Bleicher, 3+1 dimensional viscous hydrodynamic code for relativistic heavy ion collisions. Comput. Phys. Commun. 185, 3016 (2014)
B. Schenke, S. Jeon, C. Gale, Elliptic and Triangular Flow in Event-by-Event D\(=3+1\) Viscous Hydrodynamics, Phys. Rev. Lett. 106, 042301 (2011) (www.physics.mcgill.ca/music/)
F.S. Bemfica, M.M. Disconzi, V. Hoang, J. Noronha, M. Radosz, Nonlinear Constraints on Relativistic Fluids Far From Equilibrium. Phys. Rev. Lett. 126, 222301 (2021)
Ch. Plumberg, D. Almaalol, T. Dore, J. Noronha, J. Noronha-Hostler, Causality violations in realistic simulations of heavy-ion collisions, arXiv:2103.15889
E. Molnár, H. Holopainen, P. Huovinen, H. Niemi, Influence of temperature-dependent shear viscosity on elliptic flow at backward and forward rapidities in ultrarelativistic heavy-ion collisions. Phys. Rev. C 90, 044904 (2014)
A. Muronga, Relativistic dynamics of nonideal fluids: Viscous and heat-conducting fluids. I. General aspects and 3+1 formulation for nuclear collisions. Phys. Rev. C 76, 014909 (2007)
J.P. Boris, D.L. Book, Flux-corrected transport. I. SHASTA, a fluid transport algorithm that works. J. Comp Phys. A 11, 38 (1973)
D.L. Book, J.P. Boris, K. Hain, Flux-corrected transport II: Generalizations of the method. J. Comp. Phys. A 18, 248 (1975)
D.H. Rischke, S. Bernard, J.A. Maruhn, Relativistic hydrodynamics for heavy-ion collisions. I. General aspects and expansion into vacuum. Nucl. Phys. A 595, 346 (1995)
D.H. Rischke, Fluid dynamics for relativistic nuclear collisions. In: Cleymans J., Geyer H.B., Scholtz F.G. (eds) Hadrons in Dense Matter and Hadrosynthesis. Lecture Notes in Physics, vol 516. Springer, Berlin, Heidelberg (1999). https://doi.org/10.1007/BFb0107310, (arXiv:nucl-th/9809044)
E. Molnár, Comparing the first- and second-order theories of relativistic dissipative fluid dynamics using the \(1+1\) dimensional relativistic flux corrected transport algorithm. Eur. Phys. J. C 60, 413 (2009)
Iu.A. Karpenko, P. Huovinen, H. Petersen, M. Bleicher, Estimation of the shear viscosity at finite net-baryon density from A+A collision data at \(\sqrt{s_{NN}}\) = 7.7-200ĠeV, Phys. Rev. C 91, 064901 (2015)
C. Shen, Z. Qiu, H. Song, J. Bernhard, S. Bass, U. Heinz, The iEBE-VISHNU code package for relativistic heavy-ion collisions. Comp. Phys. Commun 199, 61 (2016)
E. Shuryak, Why does the quark gluon plasma at RHIC behave as a nearly ideal fluid? Prog. Part. Nucl. Phys. 53, 273 (2004)
E.V. Shuryak, What RHIC experiments and theory tell us about properties of quark-gluon plasma? Nucl. Phys. A 750, 64 (2005)
U. W. Heinz, Thermalization at RHIC, AIP Conf. Proc. 739, 163 (2005) [arXiv: nucl-th/0407067]
J.M. Maldacena, The large \(N\)-limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 2, 231 (1998)
E. Witten, Anti De Sitter Space And Holography. Adv. Theor. Math. Phys. 2, 253 (1998)
P. Romatschke, Do nuclear collisions create a locally equilibrated quark-gluon plasma? Eur. Phys. J. C 77, 21 (2017)
M. Attems, Y. Bea, J. Casalderrey-Solana, D. Mateos, M. Trianaa, M. Zilhão, Phase transitions, inhomogeneous horizons and second-order hydrodynamics. JHEP 2017, 129 (2017)
M.P. Heller, R.A. Janik, P. Witaszczyk, Characteristics of thermalization of boost-invariant plasma from holography. Phys. Rev. Lett. 108, 201602 (2012)
B. Wu, P. Romatschke, Shock wave collisions in AdS\(_5\): approximate numerical solutions. Int. J. Mod. Phys. C 22, 1317 (2011)
L. Keegan, A. Kurkela, P. Romatschke, W. van der Scheee, Y. Zhuf, Weak and strong coupling equilibration in nonabelian gauge theories. JHEP 2016, 31 (2016)
V.V. Skokov, V.D. Toneev, Hydrodynamics of an Expanding Fireball. Phys. Atom. Nucl. 70, 109 (2007)
L. Del Zanna, V. Chandra, G. Inghirami, V. Rolando, A. Beraudo, A. De Pace, G. Pagliara, A. Drago, F. Becattini, Relativistic viscous hydrodynamics for heavy-ion collisions with ECHO-QGP. Eur. Phys. J. C 73, 2524 (2013)
H. Niemi, G.S. Donicol, P. Huovinen, E. Molnar, D.H. Rischke, Influence of a temperature-dependent share viscosity on the azimuthal asymmertries of transverse momentum spectra in ultrarelativistic heavy-ion collisions. Phys. Rev. C 86, 014909 (2012)
L. Ahle et al., (E802 Collaboration) Particle production at high baryon density in central Au+Au reactions at 11.6 \(A\) GeV/\(c\). Phys. Rev. C 57, R466 (1988)
J. Barrette et al., (E877 Collaboration), Proton and pion production in Au+Au collisions at 10.8 \(A\)GeV/\(c\). Phys. Rev. C 62, 024901 (2000)
B.B. Back et al., (E917 Collaboration), Baryon rapidity loss in relativistic Au\(+\)Au collisions. Phys. Rev. Lett. 86, 1970 (2001)
W. Ehehalt, W. Cassing, Relativistic transport approach for nucleus-nucleus collisions from SIS to SPS energies. Nucl. Phys. A 602, 449 (1996)
J. Geiss, W. Cassing, C. Greiner, Strangeness production in the HSD transport approach from SIS to SPS energies. Nucl. Phys. A 644, 107 (1998)
W. Cassing, E.L. Bratkovskaya, Hadronic and electromagnetic probes of hot and dense nuclear matter. Phys. Rept. 308, 65 (1999)
D. Oliinychenko, H. Petersen, Deviations of the energy-momentum tensor from equilibrium in the initial State for hydrodynamics from transport approaches. Phys. Rev. C 93, 034905 (2016)
F.G. Gardim, F. Grassi, Y. Hama, M. Luzum, J.-Y. Ollitrault, Directed flow at midrapidity in event-by-event hydrodynamics. Phys. Rev. C 83, 064901 (2011)
P. Huovinen, H. Petersen, Particlization in hybrid models. Eur. Phys. J. A 48, 171 (2006)
P. Arnold, G.D. Moore, L.G. Yaffe, Transport coeffcients in high temperature gauge theories, 1. Leading-log results. J. High. Energy Phys. 11, 001 (2000)
D. Teaney, Effect of shear viscosity on spectra, elliptic flow, and Hanbury Brown-Twiss radii. Phys. Rev. C 68, 034913 (2003)
M. McNelis, D. Everett, U. Heinz, Particlization in fluid dynamical simulations of heavy-ion collisions. The iS3D module, arXiv:1912.08271
H. Petersen, J. Steinheimer, G. Burau, M. Bleicher, H., Stöcker Fully integrated transport approach to heavy ion reactions with an intermediate hydrodynamic stage. Phys. Rev. C 78, 044901 (2008)
N.S. Amelin, R. Lednicky, T.A. Pocheptsov, I.P. Lokhtin, L.V. Malinina, A.M. Snigirev, Iu.A. Karpenko, M. Yu, Sinyukov, Fast hadron freeze-out generator. Phys. Rev. C 74, 064901 (2006)
L.M. Satarov, M.N. Dmitriev, I.N. Mishustin, Equation of state of hadron resonance gas and the phase diagram of strongly interacting matter. Phys. Atom. Nucl. 72, 1390 (2009)
J.D. Ramshaw, Partial chemical equilibrium in fluid dynamics. Phys. Fluids 23, 675 (1980)
A. Monnai, T. Hirano, Relativistic dissipative hydrodynamic equations at the second order for multi-component systems with multiple conserved currents. Nucl. Phys. A 847, 283 (2010)
K. Peach, M. Reiter, A. Dumitru, H. Stöcker, W. Greiner, On the observation of phase transitions in collisions of elementary matter. Nucl. Phys. A 681, 41 (2001)
T. Anticic et al., (NA49 Collaboration), Centrality dependence of proton and antiproton spectra in Pb+Pb collisions at 40 \(A\)GeV and 158 \(A\)GeV measured at the CERN Super Proton Synchrotron. Phys. Rev. C 83, 014901 (2011)
T. Anticic et al., (NA49 Collaboration), Energy and centrality dependence of deuteron and proton production in Pb+Pb collisions at relativistic energies. Phys. Rev. C 69, 024902 (2004)
S.V. Afanasiev et al., (The NA49 Collaboration), Energy dependence of pion and kaon production in central Pb+Pb collisions. Phys. Rev. C 66, 054902 (2002)
L. Du, U. Heinz, \((3+1)\)-dimensional dissipative relativistic fluid dynamics at non-zero net baryon density. Comput. Phys. Commun. 251, 107090 (2020)
J.L. Klay et al., (E895 Collaboration), Longitudinal flow of protons from 2\(A\)-8\(A\) GeV central Au+Au collisions. Phys. Rev. Lett 88, 102301 (2002)
J.L. Klay et al., (E895 Collaboration), Charged pion production in 2\(A\) to 8\(A\) GeV central Au+Au ollisions. Phys. Rev. C 68, 054905 (2003)
L. Ahle et al., (E802 Collaboration), Simultaneous multiplicity and forward energy characterization of particle spectra in Au+Au collisions at 11.6 \(A\)GeV/\(c\). Phys. Rev. C 59, 2173 (1999)
Y. Akiba et al., (E802 Collaboration), Particle Production in Au+Au collisions from BNL E866. Nucl. Phys. A 610, 139c (1996)
C. Alt et al., (NA49 Collaboration), Energy and centrality dependence of \({\bar{p}}\) and \(p\) production and the \({\bar{\Lambda }}/{\bar{p}}\) ratio in Pb+Pb collisions between 20A GeV and 158A GeV. Phys. Rev. C 73, 044910 (2006)
C. Blume, Recent results from the NA49 experiment. J. Phys. G 35, 044004 (2008)
S.V. Afanasiev et al., Recent results on spectra and yields from NA49. Nucl. Phys. A 715, 161c (2003)
A. Andronic, P. Braun-Munzinger, J. Stachel, Hadron production in central nucleus nucleus collisions at chemical freeze-out. Nucl. Phys. A 772, 167 (2006)
G. Denicol, A. Monnai, B. Schenke, Moving forward to constrain the shear viscosity of QCD matter. Phys. Rev. Lett 116, 212301 (2016)
Yu.B. Ivanov, V.N. Russkikh, V.D. Toneev, Relativistic heavy-ion collisions within three-fluid hydrodynamics: Hadronic scenario. Phys. Rev. C 73, 044904 (2006)
Yu.B. Ivanov, Baryon stopping signal for mixed phase formation in HIC. J. Phys. Conf. Ser. 668, 012061 (2016)
Yu.B. Ivanov, Alternative Scenarios of Relativistic Heavy-Ion Collisions: III. Transverse Momentum Spectra. Phys. Rev. C 89, 024903 (2014)
W. Florkowski, W. Broniowski, Hydro-inspired parametrization of freeze-out in relativistic heavy-ions. Acta Phys. Pol. B 35, 2895 (2004)
W. Florkowski, Particle spectra and hydro-inspired model. Nucl. Phys. A 774, 179 (2006)
E. Schnedermann, J. Sollfrank, U. Heinz, Thermal phenomenology of hadrons from 200-A/GeV S+S collisions. Phys. Rev. C 48, 2462 (1993)
S.P. Rode, P.P. Bhaduri, A. Jaiswal, A. Roy, Kinetic freeze out conditions in nuclear collisions with 2–150 A GeV beam energy within a non boost-invariant blast wave model. Phys. Rev. C 98, 024907 (2018)
G.S. Denicol, Ch. Gale, S. Jeon, A. Monnai, B. Schenke, Ch. Shen, Net baryon diffusion in fluid dynamic simulations of relativistic heavy-ion collisions, Phys. Rev. C 98, 034916 (2018) [arXiv: 1804.10557]
S.R. de Groot, W.A. van Leeuwen, Ch.G. van Weert, Relativistic Kinetic Theory-Principles and Applications (North-Holland, Amsterdam, 1980)
K. Heun, Neue Methoden zur approximativen Integration der Differentialgleichungen einer unabhängigen Veränderlichen. Z. Math. Phys. 45, 23 (1900)
Acknowledgements
We thank E. Bratkovskaya and W. Cassing for providing the HSD code and consultations. We appreciate very much extensive discussions with Iu. Karpenko and Yu.B. Ivanov and constructive remarks by G. Sandukovskaya. The work is supported by Slovak Grant VEGA-1/0348/18 and by THOR the COST Action CA15213. A.S.K and E.E.K. acknowledge the support by the Plenipotentiary of the Slovak Government at JINR, Dubna. The work of A. Khvorostukhin was supported by the RFBR Grant no. 18-02-40137 and the NARD project, no. 20.80009.5007.07.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Giorgio Torrieri.
Appendices
Appendix A: Numerical realization
In this Appendix we discuss the numerical scheme used to integrate the hydrodynamic equations (1b), (9), and (6). The 10-dimensional vector \(\mathbf {S}\) in the right-hand side of Eq. (10) can be written as a combinations of two 5-dimensional vectors
corresponding to the conservation equations (1b) and (9),
and to Israel–Stewart relaxation equations (6) for viscous fields
In Ref. [43] it was noted that the algorithm could become more stable if the relaxation equations are solved by a simple centered second-order differences scheme for spatial gradients on the left-hand side of Eqs. (6). We have tested such a separation for the full \(3+1\)D calculations and find out that it leads to uncontrolled solutions. The same phenomenon was observed also for calculation done in the Milne coordinates in Ref. [22], where the authors used also the full SHASTA method for both conservation and relaxation equations. We think that such behaviour is caused by weak steadiness of the Euler method which leads to uncontrolled inaccuracy of a numerical solution of relaxation equations.
Thus we apply the SHASTA method to all ten equations included in Eq. (10). To reach the quadratic precision in time we use Heun’s method [84] which allows storing fewer intermediate points than the mid-point rule.
1.1 1. 3\(+\)1D implementation of the SHASTA algorithm
For completeness, we provide the complete set of formulas for the 3+1 implementation of the SHASTA algorithm extending expressions provided in Ref [1].
For lattice realization of quantities U(x, y, z, t) we will use notations \(U^{[n]}_{ijk}\), where index n stands for temporal steps and i, j, k for spatial lattice cells in x, y, and z directions respectively.
At the first stage of the SHASTA algorithm for the subsequent \((n +1)\)th time step, one calculates the so-called transport-diffused solution
where \(U_{ijk}^{[n]}\) is the full solution at the previous time step and auxiliary quantities \({\tilde{U}}_{ijk}^{x,y,z}\) are defined as
with
The velocity components are taken here at the nth time step. Here, parameter \(\lambda =\Delta t/\Delta x=\Delta t/\Delta y=\Delta t/\Delta z\) is the Courant number which is the same for all special directions. In the SHASTA it is restricted to values \(\lambda \le 1/2\).
Further, using the transport-diffused solution one calculates an antidiffusion flux that takes into account an anomalous diffusion
where \(A_{\mathrm{ad}}^{x,y,z}\) are the antidiffusive mask coefficients. For simplicity, one takes them to be equal for all special directions and set \(A_{\mathrm{ad}}=1\) as the default value. Next, we calculate the limited antidiffusion fluxes
The total incoming and outgoing antidiffusive fluxes in the cell are calculated as
The maximal and minimal values of the transport-diffused solution \(U^{[n+1]}_{ijk}\) after the antidiffusion stage are between
This information is then used to determine the fractions of the incoming and outgoing fluxes,
The final anti-diffusion fluxes are calculated as
Finally, the full solution for \(n+1\) time step is given by
In Fig. 19 we compare the numerical results of the 3\(+\)1D SHASTA code with the one-pass method in the time evolution, as given by Eq. (A4) and of the SHASTA code improved by Heun’s method with the exact results of the Bjorken model [42] with the viscosity \(\eta =10\) MeV/fm\(^2\). The exact solutions for energy density, \(\epsilon \), longitudinal velocity, \(v_z\) and one component of the viscous tensor, \(\pi ^{yy}\) are shown in Fig. 19 by dotted lines for two times elapsed after initialization, \(\Delta t=4\,\mathrm{fm}/c\) and \(8\,\mathrm{fm}/c\). The solid lines show the results for the one-step 3D SHASTA. We see typical increasing oscillation expanding from the boundaries (with the square-root divergent boundary conditions) inwards the small z regions. This is typical behaviour for algorithms using a single-time step approach. Applying Heun’s method, we obtain much smoother behaviour of the solution shown by dashed lines. Although such scheme works well for model tasks, we observe that for actual 3\(+\)1D calculations in the cartesian coordinates the algorithm becomes sometimes unstable (in contrast with the 2\(+\)1D calculation reported in [43]). Also the described entirely-3D approach can lead to problems with anti-diffusion as was noted in [22, 43]. To avoid the instability of the code and other possible troubles, we applied the 3D splitting method for solving the 3D problem.
Comparison of the exact results for energy density, \(\epsilon \), longitudinal velocity, \(v_z\) and one component of the viscous tensor, \(\pi ^{yy}\) of the Bjorken model [42] with the numerical results of the 3\(+\)1D SHASTA code with the one-pass method in the time evolution, Eq. (A4), and of the SHASTA code improved by Heun’s method. Calculations are done for the viscosity \(\eta =10\) MeV/fm\(^2\). The exact solutions are shown two times elapsed after initialization, \(\Delta t=4\,\mathrm{fm}/c\) and \(8\,\mathrm{fm}/c\)
1.2 Implementation of 3D splitting SHASTA for viscous hydrodynamics
We split the 3D task (10) into three sequential 1D propagations
Here, we replace the 3D propagation with three 1D propagations and the source term (A1) is split into three terms corresponding to the propagation along the separate axes. The source terms (A2) and (A3) contain time derivatives and since we replace the 3D propagation by three 1D propagations, we have to include factors 1/3 before the corresponding terms in \(\mathbf {S}^{\mathrm{1D}}_{x,y,z}\). As the result, the final expression for the source term responsible for the propagation along axis \(k=x,y,z\) is
where
and
As we see, after summation over index k
we recover \(\theta \) and \(W^{\mu \nu }\) defined in Eq. (6), and \({\mathcal {D}}u^i= u_\mu \partial ^\mu u^i\).
Every 1D equation in Eq. (A20) is solved using the standard one-dimensional SHASTA method [24,25,26].
If in some fluid cells the relaxation time becomes smaller than the time step, \(\gamma \tau _\pi <\Delta t\), then we must obtain the formal solution (11),
after completion of the propagation along all three axes. To obtain the correct result in the 3D splitting approach, we start with the full solution at the nth time step, \(\pi ^{ij}(t_{n})\), and perform the following sequence of steps in the spatial directions staring,e.g., with the x directions
so that after the third step we recover the expected expression.
When one uses 3D splitting method, it is necessary to change the order of 1D propagations to decrease numerical errors. A similar kind of inaccuracy would appear if one uses the same relations among \(\pi ^{ij}\) matrix elements, e.g., \(\pi ^{xx}=\pi ^{xx}(\pi ^{yy},\pi ^{zz})\) permanently. Therefore, we change the independent spatial diagonal components, \(\pi ^{ii}\) and \(\pi ^{jj}\), at every time step, see Eq. (B10).
The results of the application of the 3D splitting scheme for the viscous 2nd-order Bjorken expansion are shown in Fig. 19 by dash-dotted lines. The calculations are performed for the same spatial step, \(\Delta x=0.2\) fm, as used for the 3D SHASTA and Heun’s-improved 3D SHASTA calculations. We see that the numerical results are very close to the theoretical predictions and fluctuations are weaker than for the Heun’s-method improved algorithm. These fluctuations decrease even further if one takes a shorter step. The results of calculations with \(\Delta x=0.1\) fm are shown by dot-dot-dashed lines in Fig. 19. For the most shown quantities, the 3D splitting results are smooth and almost coincide with the exact solutions, only the energy density \(\epsilon \) for the later time, \(\Delta t=8\,\mathrm{fm}/c\), deviates from the exact solution. This deviation vanishes if we go to a smaller step, e.g., \(\Delta x=0.05\) fm, as shown by short dashes. In the actual calculations we have verified on several examples that our results do not change when we reduce the spatial steps from 0.2 fm to 0.1 fm.
Appendix B: Reconstruction of local quantities and exact initialization
The hydrodynamics code evolves the components of the energy-stress tensor and baryon current. The equation of state is formulated in the local system where the energy density and the particle number should be defined. To make a Lorentz transformation from the laboratory frame in the local rest frame one also needs to define a 4-velocity of the fluid element. If we know the components of the ideal stress tensor, \(T_{\mathrm{id}}^{\mu \nu }=T^{\mu \nu }-\pi ^{\mu \nu }\) and the baryon current \(J^\mu =n\, u^\mu \), other quantities can be recovered as follows:
The modulus of the fluid velocity can be found as a root of the equation
and, therefore, depends on the chosen equation of state \(P=P(\epsilon ,n)\). The direction of the fluid velocity is determined as
Relations (B1), (B2), and (B3) can be used for the ’ideal’ initialization of the hydrodynamic phase when \(\pi ^{\mu \nu }=0\) and \(T^{0\nu }=T^{0\nu }_{\mathrm{id}}\). For the ’exact’ initialization we have to solve the eigenvalue problem \(u_\mu T^{\mu \nu }=\varepsilon u^\nu \), which leads to the quartic algebraic equation
where coefficients \(a_{1,2,3,4}\) are functions of the energy–momentum tensor invariants,
The corresponding velocity is calculated as
Given the four velocity, \(u^\mu =\gamma (1,\mathbf {v})\), we calculate baryon density as
Then knowing the equation of state \(P=P(\varepsilon ,n)\), we can define the ideal part of the energy–momentum tensor \(T_{\mathrm{id}}^{\mu \nu }\) in Eq. (3). The viscous parts of the full \(T^{\mu \nu }\) tensor (2) follow as
and the baryon diffusion current as
In the code we use quantities \(\pi ^{xy}\), \(\pi ^{xz}\), \(\pi ^{yz}\), \(\pi ^{ii}\), and \(\pi ^{jj}\) as independent variables. Other components can be recovered with the help of the following expressions
We emphasize that these expressions do not develop anomalously large values for the case of small fluid velocities.
Rights and permissions
About this article
Cite this article
Khvorostukhin, A.S., Kolomeitsev, E.E. & Toneev, V.D. Hybrid model with viscous relativistic hydrodynamics: a role of constraints on the shear-stress tensor. Eur. Phys. J. A 57, 294 (2021). https://doi.org/10.1140/epja/s10050-021-00599-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-021-00599-1