Abstract
Neutron-induced fission reactions play a crucial role in a variety of fields of fundamental and applied nuclear science. In basic nuclear physics they provide important information on properties of nuclear matter, while in nuclear technology they are at the basis of present and future reactor designs. Finally, there is a renewed interest in fission reactions in nuclear astrophysics due to the multi-messenger observation of neutron star mergers and the important role played by fission recycling in r-process nucleosynthesis. Although studied for several decades, many fundamental questions still remain on fission reactions, while modern applications and the development of more reliable nuclear models require high-accuracy and consistent experimental data on fission cross sections and other fission observables. To address these needs, an extensive fission research programme has been carried out at the n_TOF neutron time-of-flight facility at CERN during the last 18 years, taking advantage of the high energy resolution, high luminosity and wide energy range of the neutron beam, as well as of the detection and data acquisition systems designed for this purpose. While long-lived isotopes are studied on the 185 m long flight-path, the recent construction of a second experimental area at a distance of about 19 m has opened the way to challenging measurements of short-lived actinides. This article provides an overview of the n_TOF experimental programme on neutron-induced fission reactions along with the main characteristics of the facility, the various detection systems and data analysis techniques used. The most important results on several major and minor actinides obtained so far and the future perspectives of fission measurements at n_TOF are presented and discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since its discovery in 1938, neutron-induced fission has been one of the most extensively studied nuclear reactions, being of great importance for a variety of fields in basic and applied nuclear science. In fundamental nuclear physics, fission studies provide important information on a variety of properties of nuclear matter. In nuclear astrophysics, fission recycling has been postulated as one of the important processes responsible for the production of heavy elements in explosive scenarios in combination with neutron capture, while the recent observation of r-process nucleosynthesis in a neutron star merger (NSM) event has triggered a renewed interest in the modelling of fission processes. Finally, neutron-induced fission is the reaction at the basis of nuclear energy production in current and future nuclear reactors.
Neutron-induced fission has been extensively studied since the early times at neutron facilities around the world. In view of its importance, in particular for energy production, an enormous amount of data has been collected over many decades on major and minor actinides, as well as on some lighter elements characterised by a high fission threshold. However, the need of additional data on neutron-induced fission was still present about 20 years ago, when a new neutron facility came in operation at CERN. The main requests were related to the development of innovative systems for energy production and nuclear waste transmutation, in particular for accelerator-driven systems and Generation IV reactors, as well as for reactors based on the Th/U fuel cycle [1]. High-accuracy, high-resolution cross section data were needed, in a wide energy range, for a variety of major and minor actinides, from Th to Cm, as well as on coolant and spallation material, namely Pb and Bi. The possibility to burn long-lived actinides that constitute the main component of the long-term radiotoxicity of the spent fuel of current nuclear reactors is linked to the availability of sufficiently reliable data needed for the development and safe operation of these innovative nuclear systems [2].
The n_TOF facility at CERN was built, among other motivations, with the aim of addressing those needs of new, accurate fission data. Since the start of its operation in 2001, a vast experimental programme has been carried out, which has led to a wealth of high quality results. For the measurements, a variety of detectors have been specifically built over the years, with constantly improving performances. Furthermore, since 2014, a new, high-flux experimental area has greatly enhanced the capability of the n_TOF facility for fission-related studies, allowing one to measure challenging reactions with unprecedented accuracy, resolution and energy range.
Together with other neutron facilities currently operating worldwide [3], such as LANSCE [4], GELINA [5], J-PARC [6], as well as with new powerful facilities recently completed or near completion, such as NFS [7] and CSNS [8], n_TOF will continue to play a key role in addressing the need of new, high-accuracy data on fission reactions. As we all learn from past experience, it may be beneficial for future studies, when new challenges will have to be faced, to discuss the experimental programme carried out in the last two decades at n_TOF. In this spirit, we have written this review paper, making it as comprehensive as possible of the many tasks involved in a successful fission measurement, from detector R&D to sample preparation, from signal reconstruction to data processing, from dead-time and pile-up corrections to Monte Carlo simulations. The most important results obtained so far at n_TOF are discussed in this paper, and their impact in the field analysed, together with the perspectives of a future experimental programme.
The paper is organised as follows: Sect. 2 introduces the scientific motivations that have driven the experimental programme on fission at n_TOF, in terms of basic nuclear physics, energy applications and astrophysics-related needs. The n_TOF facility, the two experimental areas and the features of the neutron beam that make it well-suited for fission studies are described in Sect. 3. Section 4 presents a review of the various detectors specifically developed for fission studies at n_TOF and of the techniques for sample preparation, which is one of the most important ingredients for a successful fission programme. Data acquisition, pulse reconstruction and the main issues in data analysis are discussed in Sect. 5, together with the Monte Carlo simulations of the facility and the detector response. Finally, the main results of the n_TOF experimental programme obtained so far are presented in Sect. 6 and perspectives of a continuing programme are discussed at the end.
2 Scientific motivations
2.1 Cross section data and other fission observables for improving fission modelling
Hahn and Strassman separated barium from the products of neutron-irradiated uranium [9] and Meitner and Frisch offered a fundamental picture of fission on the basis of the liquid-drop model [10] in 1939, forming an interdependence between experiment and theory. By overcoming a potential barrier, the parent nucleus is divided into two smaller droplets releasing a large amount of energy. The fact that a neutron can split a large nucleus into two parts of comparable sizes was not predicted by nuclear scientists, even though for nuclei with masses \(A > 120\) the fission into two nearly equal fragments is exothermic.
A complex picture of the fission mechanism that is a source of all present descriptions was offered by Bohr and Wheeler [11]. The main features of that picture can be summarized as follows: (1) the nucleus overcomes a fission barrier obtained at the critical deformation of the unstable equilibrium and undergoes fission; (2) statistically the neutron-induced fission cross section is proportional to the number of transition states available at a given excitation energy in the saddle point; (3) the fission process is in competition with neutron emission and \(\gamma \)-de-excitation, and (4) the fission cross section is relatively constant up to several MeV. Furthermore, for larger excitation energies some neutrons can escape and the residual nucleus can undergo fission. In its essential features, this description has remained unchanged to the present time.
In 1953, Hill and Wheeler [12] provided the key ingredients used to understand the fission process from a theoretical point of view. The nucleus being an extremely saturated many-body system, the potential felt by a nucleon is nearly independent of the positions of the surrounding nucleons. This implies that the nucleus can be characterised by a nuclear shape. As a result, the single particle potential is essentially collective and it is controlled mainly by its surface boundaries, that is, by the state of the system as a whole. Accordingly, it is convenient to characterise the collective state of a nucleus with the help of some constraints or some generalised coordinates pertaining to several macroscopic degrees of freedom. The nucleons move independently in a mean field managed by these degrees of freedom. The mean field can be constructed by using phenomenological prescriptions [13] or within self-consistent models [14]. The constraints associated to the degrees of freedom are allowed to vary in time leading to the split of the initial parent nucleus into two fragments.
The more detailed understanding of the nuclear fission mechanism properties was primarily empirical in the early stages of the development of the field. Data concerning the mass distributions of the fission fragments or experimental discoveries such as fission isomers [15, 16] have contributed to the development of new concepts in theoretical physics, as will be seen below. Even now there is no complete theory describing the richness and complexity of empirical behaviour inferred from fission processes. Nevertheless, increasingly precise experimental results are of great importance and help to continuously improve the knowledge in this field.
It is now established that the fission barrier in the actinide region exhibits a double- or triple-humped shape. This shape of the barrier can explain a large number of experimental results. A triple barrier is schematically displayed in Fig. 1. At sub-threshold excitation energies, or at energies close to the barrier peak, the fission cross section is characterised by a large number of intermediate resonances. These phenomena are controlled by many discrete excited states built in the region of the second well, named class-II states, and in the region of the third well, named class-III states, in the case of a triple-humped fission barrier. When the fission cross section is represented against the excitation energy, these states manifest themselves as resonances. Information about the shape of the potential barrier can also be obtained by measuring the isomer excitation. Shape isomers can be obtained by a large variety of nuclear reactions if the energy brought into the system is large enough to overcome the first barrier. Thus, patterns due to inelastic neutron scattering leading to isomer states and involving a pre-scission neutron evaporation should be identifiable in the fission cross section [17]. Rotational bands built on the class-II states give indications about the highly deformed nuclear states. Sub-threshold fission displays pronounced clusters of resonances, the fission strength being modulated by the states built in the second well. Information about the coupling matrix elements between the class-II states and the class-I states or about the fission of class-II states can be obtained from the detailed structure of each cluster. Moreover, the average values of the coupling matrix elements give indications about the penetrabilities of the first and second barrier at a given excitation energy. At some energies, some resonance doublets can be identified in the experimental data [18]. They are explained as a degeneracy of unperturbed class-I and class-II states. Experimental investigations made with a polarised neutron beam allowed for an unambiguous spin assignment for known resonances at low energy [19]. Theoretical predictions of such resonant peaks cannot be made realistically on the basis of present-day models.
a Triple fission barrier obtained by means of smoothed joined parabolae as a function of a dimensionless elongation variable \(\epsilon \). The parameters of the barrier are taken from the work of Ref. [20] for the nucleus \(^{233}\)Th. b Dependence between the logarithm of the penetrability P and the excitation energy \(E^*\) of the compound nucleus. The Schrödinger equation was solved within the exact method by extending the formalism of Ref. [21]. The \(\beta \)-resonances in the penetrabilities are connected to the eigenstates constructed in the second and the third potential wells displayed in a. The compound resonant states created in the first well are “filtered” by the resonances of the second and third wells
Many experimentally detected features of nuclear fission appeared as a surprise for the community. Input from these findings has made theoretical treatments increasingly predictive. It was possible to predict an island of stability for super-heavy nuclei and the spontaneous heavy ion emission. Even recently, a new type of asymmetric fission was experimentally observed in the neutron-rich \(^{180}\)Hg nucleus [22]. Theoretically, a symmetric distribution of fission fragments was expected with a maximum yield for two semi-magic \(^{90}\)Zr products. The explanation followed in the framework of the macroscopic–microscopic approach by revealing a so-called local minimum in the potential energy surface. Experimental advances concerning recent developments of this subject are reviewed in Ref. [23]. Bimodal fission phenomena were also discovered [24], characterised by two components in the kinetic energy spectrum of fission fragments. An inversion of the odd-even effect of the low-energy fission fragment distributions was also observed. The odd-odd yields dominate for excitation energies of the fragments lower than 4–5 MeV [25]. Finally, the fine structure in the fission cross section known as the Th anomaly is attributed to the occurrence of the triple barrier[26]. A shallow ternary minimum of about 1 MeV was theoretically predicted at large asymmetric shape distortions [27]. The third minimum should be deep enough to produce a fine structure in the fission cross section. Alternatively, the Th anomaly can be explained within dynamical single particle effects [28].
Despite the advances in the theoretical description of the fission process, the behaviour of the fission cross section can only be reproduced by using phenomenological approaches. For instance, the heights of the double-humped fission barrier peaks are determined empirically in accordance with a given parametrisation of the nuclear level density and the cross section is proportional to the number of states calculated in the transient point or saddle point configuration following the Bohr–Wheeler hypothesis. The evaluated fission cross sections always depend on some input parameters that rely on experimental observables. For example, in the evaluation procedure described in Ref. [29] the double-peaked barrier is reproduced by three smoothly joined parabolae [21]. Accordingly, at least six parameters are needed to describe correctly the shape of the potential barrier, with three values needed to fix the heights of the maxima of the inner and outer barriers together with the minimum of the intermediate well, plus the values of the corresponding stiffness parameters. By using a similar fission cross section evaluation treatment, in Ref. [20] the triple barrier can be parametrised with ten parameters and each bandhead transition state requires five additional energy values at the maximum and the minimum points of the barrier. As considered in Ref. [30], the fission barrier heights can be extracted with an uncertainty of 0.5–1.0 MeV in the framework of the current evaluations. Evaluations of nuclear data demand accurate experimental inputs and a sustained effort is needed for their better determination. At the present stage, the phenomenological approach used in fission cross section analysis is still limited by some ambiguities. Some of them are the following:
- 1.
The deviation of the realistic barrier shape from the harmonic one used to represent double or triple fission barriers [21] can alter the penetrability values. Reliable values of the penetrabilities can therefore only be obtained for energies close to the barrier peak.
- 2.
The cross section is simulated by using a set of values for the barrier heights and for the nuclear level density, but two different sets of such values can give the same cross section value. Statistically, the total excitation energy of the thermalised compound nucleus is shared between collective and intrinsic degrees of freedom equiprobably, in accordance with the ergodic theory. In these circumstances, the parameters of the fission barrier should be modified when the intrinsic excitation energy increases, due to the disappearance of the shell effects. Therefore, we are left with a distribution of fission barriers [31]. Current evaluations cannot include such a distribution in the calculations.
- 3.
Nuclear level densities depend on the nuclear deformation [32]. In the region of the outer barrier, the level density increases. The variation of the level densities during fission is subject to many phenomenological corrections. Collective vibrational and rotational enhancements of nuclear level densities close to the top of fission barriers and other corrections, such as the Porter–Thomas distributions, are also considered in a phenomenological way.
- 4.
Some parameters, such as the heights of the fission barriers, are obtained from experimental data and the empirical systematics is used afterwards to predict the cross section of unmeasured nuclei. This is based on the assumptions that the nuclear structure, which may change dramatically from one nucleus to another, plays a minor role. But a difference of only one neutron can change the overall fragment mass distribution from asymmetric to symmetric, as observed for example in the case of \(^{257,258}\)Fm [33].
To predict the number of neutrons emitted in the fission process [34] or to reproduce the characteristics of the odd-even effects in the fragment distributions [35], the models used in evaluations require knowledge of the fragment excitation energies. This information is usually extracted from experimental data. The fission cross section data carry information not only about the nuclear structure, but also about effects due to the dynamics of the fragmentation. From the theoretical point of view, information about the dissipation can be obtained only from a dynamical treatment of the fission process.
The anisotropy in the angular distribution of fission fragments is strongly related to the spin projection K of the transition states on the fission axis, as a direct consequence of the angular momentum conservation [36]. For lighter nuclei, the angular distributions exhibit abrupt variations with respect to the excitation energy (or equivalently to the incident neutron energy, as will be shown later on in Fig. 56), at energies close to the barrier peak, suggesting a manifestation of the role played by each fission channel. Instead, an attenuated variation of the structure in the angular distribution is experimentally observed for heavier nuclei at threshold energies. It was argued [37] that this behaviour is a sign of the existence of an intermediate equilibrium state due to the presence of the isomer minimum. In this case, the transition states do not drastically affect the angular distributions of the heavier nuclei, their outer barrier heights being lowered. From statistical considerations, an effective moment of inertia is defined as a combination between the parallel and the perpendicular rigid body moments of inertia. The mean square value of the projections of the fragment angular momenta on the fission axis \(K_0\) gives information about the effective moment of inertia in the saddle configuration, and hence about hyperdeformations. In the case of transuranic elements, investigations based on experimental data indicated that the effective moment of inertia is compatible with the outer barrier deformation at low excitation energies. For larger values of the excitation energies, the effective moment of inertia corresponds to smaller deformations consistent with saddle configurations calculated within the liquid-drop model. These results indicate that the shell effects dissolve with excitation energies larger than 50 MeV. For lighter elements, the deformations obtained from the anisotropy data are in agreement with the liquid-drop model expectations. The modifications of the angular distributions for different mass regions were in accordance with theoretical results. For example, in comparison with the results obtained within the liquid-drop model, a shift of the saddle point towards smaller deformations was predicted with the microscopic-macroscopic theory, by using the reflection-symmetric two centre shell model. It was also noted in Ref. [38] that this effect becomes smaller from the mass region \(A=200\) to \(A>230\), since for heavier nuclei the saddle is obtained at smaller deformations in the framework of the liquid-drop model alone, exhibiting more compact shapes. In this model, the properties of the fragments manifest in the region of the outer barrier. For mass \(A\approx 230\), the fragment shell effects are important, as an influence of the strong shell effects of the doubly magic nucleus \(^{132}\)Sn. It was also suggested that the variation of \(K_0\) at low excitation energy is due to the persistence of superfluid effects. An accurate measurement of the angular distributions can offer valuable information about the nuclear structure at hyperdeformation to test the validity of current models.
The distributions of the total angular momenta in the primary fragments contain information on the fission mechanism. The initial angular momentum of the compound nucleus is distributed between intrinsic fragment spins and the angular momentum of the relative motion. The average spin of the primary fragments in low-energy fission is about 7 \(\hbar \). Surprisingly, this is also the case of the spontaneous fission of \(^{252}\)Cf, as reported in Ref. [39], where a mechanism to generate fragment spins by postulating an equilibrium at scission was investigated. The fragment spins vary as a function of the fragment mass and the mass asymmetry of the reaction. There is currently no consistent theory to predict the spin distributions. A better experimental description will definitely contribute to developments in the theory. As already mentioned, the present understanding of the angular distributions of fission fragments is based on statistical arguments by taking into account an effective moment of inertia and including ingredients to simulate the dynamics of the process [40]. Accurate data to be obtained at n_TOF concerning the fine structure of the fission cross section of \(^{230}\)Th and the angular distribution of the fragments should be able to elucidate some unclear aspects concerning the fission mechanisms.
In summary, the present theoretical evaluations of fission cross sections depend on some input parameters extracted from experimental data, as also shown in Ref. [41]. Therefore, the predictions concerning the unmeasured nuclei are questionable due to the lack of consistency. The predictive power of the theoretical approaches can be improved by investigating microscopically the fission process and by providing new information concerning its mechanism. The microscopic approaches should be able to reproduce a large set of experimental data, like fission barriers, fission mass distributions, total kinetic energies of fission fragments and spontaneous fission lifetimes. This is clearly a challenging and often daunting task. Experimental data carry information about all these interdependent mechanisms that follow from the structure and the dynamics of fission. As a consequence, there still exists a pressing need for new data on neutron-induced fission, to be used as benchmarks for the theoretical investigations.
2.2 Intermediate energy fission
The upper limit to the incident neutron energy in evaluated nuclear data libraries is traditionally set to 20 MeV, although the most recent libraries have extended it to 30 MeV, and some fission cross sections used as reference have recently been extended up to 1 GeV [42]. Hereafter, we refer to the interval from 20 MeV to 1 GeV, the maximum neutron energy that can be presently reached at n_TOF, as the intermediate energy range for fission measurements. Moreover, it is useful to distinguish two sub-intervals, from 20 to 200 MeV and from 200 MeV to 1 GeV, both from an experimental and a theoretical point of view. In fact, 200 MeV is at present the upper limit of the incident energy region where an absolute determination of (n,f) cross sections exists [43, 44], thanks to the simultaneous measurement of fission events and (n,p) scattering events by means of proton recoil telescopes, from which the neutron flux can be derived. From a theoretical point of view, the 20–200 MeV region can be investigated with fully quantum-mechanical reaction models, like those contained in well-known publicly available nuclear reaction codes, such as EMPIRE [29] and TALYS [45].
In the energy range up to 200 MeV, the target nucleus may emit nucleons and/or light clusters, such as deuterons, tritons and alphas, through a pre-equilibrium process before forming an equilibrated remnant, which then decays by nucleon evaporation or fission. The pre-equilibrium phase is commonly described by a semi-classical exciton model or by a quantum-mechanical multi-step compound plus direct model, while the compound nucleus decay of the remnant is treated within the framework of the statistical Hauser–Feshbach formalism.
Using the TALYS code, which includes such models, it was possible to reproduce the n_TOF data on the \(^{234}\)U(n,f) cross section [46] in the energy range from 0.6 to 200 MeV, with some adjustment of crucial model parameters, such as level density parameters in the neutron channels and heights and curvatures of fission barriers of remnants encountered in the multi-chance fission process. On the contrary, the simplified formalism of a double-humped fission barrier with complete damping of the vibrational resonances in the intermediate well for the fissioning compound nucleus \(^{235}\)U was unable to reproduce the fine structure of the cross section below threshold, at \(E_\mathrm {n}<0.8\) MeV. There, better agreement with data could be achieved in Ref. [47] with the EMPIRE code (version 3.2) in the framework of the optical model for fission [48], where use was made of a three-humped fission barrier with partial damping of the vibrational states in the intermediate wells. It is worth pointing out that the authors of Ref. [47] carried out extensive calculations of neutron-induced reactions in the energy range from 10 keV to 30 MeV for the whole isotopic chain \(^{232{-}237}\)U by taking into account, among others, all relevant fission data of U isotopes taken at n_TOF until then. The agreement between theory and experiment was in general very good. The important fission standard \(^{238}\)U, not included in the previous analysis, had already been studied, with other U and Pu isotopes, in the energy range from 1 keV to 30 MeV by means of the TALYS code in the framework of the Bruyères–le-Châtel evaluation of actinides in Ref. [49]: here again, use of a three-humped fission barrier was crucial in reproducing the fine structure in the sub-threshold cross section. A more complex fission process, based on the superposition of symmetric and asymmetric fission modes, was investigated in the framework of the statistical model in Ref. [50] for the neutron-induced fission of \(^{238}\)U, resulting in a good reproduction of the experimental cross section up to 200 MeV.
In the same energy range, the angular distribution of fission fragments (FFAD) can be analysed in the framework of the statistical saddle point model, combining pre-equilibrium and Hauser–Feshbach calculations of partial fission cross sections. The model described in detail in Ref. [51] was successfully applied by the same authors to the analysis of angular distributions of fragments emitted in the neutron-induced fission of \(^{232}\)Th and \(^{238}\)U in the incident energy range from 20 to 100 MeV and could be usefully applied to analogous measurements carried out at n_TOF once final results are available. Unfortunately, neither TALYS nor EMPIRE, or, at least, their publicly available versions, have implemented statistical models for the angular distributions of fission fragments.
A quantity commonly used for characterising angular distributions is the anisotropy coefficient A, defined as
where the numerator represents the FF yield along the beam axis and the denominator the FF yield at 90\(^{\circ }\) with respect the beam axis. Plotted as a function of incident neutron energy, A displays oscillations at the thresholds of multi-chance fission, which are strongly damped beyond the onset of the (n,4nf) reaction, at around 30 MeV. Above this energy the model predicts a smooth decrease of A with increasing incident energy, in agreement with experimental data. The anisotropy coefficient turns out to be sensitive to the ratio \(a_\mathrm {f}/a_\mathrm {n}\) of the level density parameters in the fission channel and in the neutron channel, which is also crucial in reproducing fission cross sections as a function of incident energy, but is also sensitive to the square of the standard deviation \(K_0^2\) of the distribution of projections of the fissioning nuclei spin on the nuclear symmetry axis at the later chances of the fission process.
At incident energies above 200 MeV the projectile “sees” the target as a collection of individual nucleons. When the de Broglie wavelength of relative motion of projectile and target nucleons, \(\lambda = \frac{\hbar }{p}\), satisfies the inequalities
where r is the range of the nuclear forces and d the average distance between neighbouring nucleons, it is reasonable to describe the propagation of the particle as a succession of binary collisions with the target nucleons, which can be ejected from the nucleus or can eject other nucleons in turn, thus giving rise to a fast intra-nuclear cascade, which can conveniently be computed by Monte Carlo methods. As long as the participating nucleons are fast enough, their motion lends itself to a classical description, characteristic of the cascade stage, but the concept of classical trajectories loses its validity with decreasing nucleon energy. A natural choice, suggested by the reaction models valid below 200 MeV, is to switch the time evolution to a pre-equilibrium stage using a semi-classical exciton model, easier to combine with the classical cascade model, resulting in a thermally equilibrated residual nucleus, which can decay by particle evaporation or fission in the final compound nucleus stage. The three-stage description of nucleon-induced spallation reactions is adopted, among others, by the Cascade-Exciton Model (CEM), originally formulated at Dubna [52] and finally evolved into a version currently used in some widely used radiation transport codes, like MCNPX [53] and MCNP6 [54].
An alternative description of a spallation reaction as a two-stage process, i.e. intra-nuclear cascade plus evaporation and fission, is adopted in other codes, such as the Liège Intra-nuclear Cascade Model (INCL) [55] (and the references therein), used until now in the study of the intermediate energy fission reactions measured at n_TOF. In the INCL model the pre-equilibrium stage is replaced by a self-consistent calculation of the stopping time of the fast cascade, chosen as the time at which the evolution of basic physical quantities like the excitation energy of the target nucleus and the average kinetic energy of the ejectiles turns from fast to slow. Such a simplified description has proven to be valid above 200 MeV, but it might be questionable at lower incident energies, where quantum-mechanical reaction models can be applied and where a smooth overlap with intra-nuclear cascade results would be desirable.
The decay of the equilibrated remnant at the end of the cascade stage can be described by coupling to INCL a code based on a fission-evaporation model: the decay models most frequently used in combination with INCL are GEMINI [56] (and the references therein) and ABLA07 [57].
GEMINI is a statistical model that deals with particle evaporation in the framework of the Hauser–Feshbach formalism, where angular momentum is strictly conserved. Symmetric fission, dominant at high excitation energies, is treated in the Bohr–Wheeler approach and asymmetric fission in a formalism worked out by Moretto [58] based on the concept of a conditional fission barrier, i.e. a saddle point configuration with a fixed mass-charge asymmetry of pre-fragments. Fission barriers are evaluated by means of the finite-range droplet model by Sierk [59], with shell and pairing corrections from Ref. [60]. Level densities in neutron and fission channels are represented by Bethe formulae with energy-dependent level density parameters, \(a_\mathrm {n}\) and \(a_\mathrm {f}\), respectively. The ratio \(a_\mathrm {f}/a_\mathrm {n}\) has a default value of 1.036 [61] which can be adjusted in order to fit experimental fission data. The energy dependence of \(a_\mathrm {n}\) is fully phenomenological, from a low-energy limit of A/7.3 MeV\(^{-1}\), derived from the average spacing of neutron s-wave resonances, for a nucleus of mass number A, to a high-energy limit of A/12 MeV\(^{-1}\), derived from energy spectra of evaporated particles. Ground-to-saddle transient effects resulting in a time-dependent fission width are not explicitly taken into account. Dissipative effects related to the light particle evaporation from the fissioning nucleus during the slow motion from the saddle point to the scission point are treated in a simplified way by assuming that evaporation takes place only from the scission point configuration.
ABLA07 is a dynamical model, which takes the time evolution of the fission degree of freedom explicitly into account, treating it as a diffusion process through the interaction of collective degrees of freedom with the heat bath formed by the individual nucleons. The process is described by a one-dimensional Fokker–Planck equation leading to a time-dependent fission width. An approximate analytical solution, which makes the problem computationally tractable, depends also on the nuclear temperature T and on a reduced dissipation coefficient \(\beta \) first introduced in fission theory by Kramers [62]. In turn, \(\beta \) might depend on temperature and deformation. The nuclear evolution beyond the saddle point is based on the work of Hofmann and Nix [63]. The formalism is described in detail in Refs. [64, 65]. Liquid-drop barriers and shell and pairing corrections are computed like in GEMINI. Two important differences with respect to GEMINI are the use of the Weisskopf–Ewing theory in particle evaporation, instead of the more rigorous (and more time consuming) Hauser–Feshbach theory, with an approximate conservation of angular momentum based on phase space arguments and the use of a composite formula for level densities, namely a constant temperature formula at low excitation energy and a Bethe formula at high energy, with a level density parameter corrected as suggested by Ignatyuk [66, 67] for shell and pairing effects, including also an energy-dependent collective enhancement factor.
The INCL/ABLA07 chain has largely been used by the Darmstadt–Santiago Collaboration in the analysis of (p,f) experiments in inverse kinematics below 1 GeV/A incident energy; a recent review of experimental results and of their theoretical interpretation is given in Ref. [68]. In particular, the authors point out the importance of transient and dissipative effects in the analysis of a number of fission observables in addition to cross sections, such as charge distributions of fission fragments and coincident light particles, that could be the subject of future experimental activity at n_TOF or at other neutron facilities.
Up to the time of the present review, the (n,f) cross section measurements performed at n_TOF in the incident energy region up to 1 GeV are determined relative to the reference fission cross section of \(^{235}\)U and/or \(^{238}\)U. Absolute cross sections could only be derived by model calculations of the last two cross sections in the intermediate energy range. The original choice of the collaboration, made in the first two articles dedicated to intermediate energies, namely Ref. [69] on \(^{234}\)U and \(^{237}\)Np and Ref. [70] on natural lead and \(^{209}\)Bi, was the normalisation to the U fission cross sections of the JENDL/HE-2007 library [71], evaluated up to 3 GeV. However, a later systematic study [72] of (n,f) and (p,f) reactions up to 1 GeV, using version 5.1.14 of INCL/GEMINI and INCL/ABLA07 codes, showed that the JENDL cross sections were strongly underestimated beyond 500 MeV. As a consequence, for all later fission measurements at high energy it was decided to report only the ratio relative to the fission cross section of \(^{235}\)U, rather than the model-dependent absolute cross section. This was done, for example, in an article dedicated to \(^{238}\)U [73] and published soon after Ref. [72]. The measurement of the quasi-absolute fission cross section of \(^{235}\)U at intermediate energies (described in Sect. 4.6), recently performed at n_TOF and presently being analysed, will hopefully allow for a proper experimental normalisation in the near future.
An example of this computational procedure is provided in Fig. 2, where the calculated \(^{238}\)U(p,f) and (n,f) cross sections up to 3 GeV are compared with experimental data. The basic references are the measurement performed by the Gatchina group in the energy range from 200 MeV to 1 GeV for the (p,f) reaction [74], and, for the (n,f) reaction, the absolute measurements below 200 MeV [43, 44], as well as the n_TOF data up to 1 GeV [73], relative to the \(^{235}\)U(n,f) reaction, whose cross section has been evaluated in Ref. [75] with the computer codes mentioned above.
The fission cross section of \(^{238}\)U from 100 MeV to 3 GeV. Left panel: \(^{238}\)U(p,f); right panel: \(^{238}\)U(n,f). Solid lines: INCL/GEMINI calculations, dashed lines: INCL/ABLA07 calculations, with model parameters from Ref. [75]. The experimental data are extracted from the EXFOR database
The Monte Carlo simulation of FFADs measured at n_TOF in the intermediate energy region remains an open question, because the only experimental anisotropy coefficients versus neutron energy published until now are those of the \(^{232}\)Th(n,f) reaction up to 100 MeV[76], an energy region outside the range of validity of the computational models presently available, and of \(^{235,238}\)U(n,f) up to 200 MeV [77], at the lower limit of applicability of intra-nuclear cascade models.
2.3 Needs related to applications (reactor technology)
Neutron-induced fission cross sections on actinides are a key ingredient for the safety and criticality assessment of nuclear systems for energy production, transmutation of nuclear waste and nuclear fuel cycle investigations, as well as for the design of the new generation of reactors which aim at safer and cleaner nuclear energy production. The rapid expansion of global energy demands leads to serious environmental concerns, since existing energy sources are mainly based on fossil fuel consumption, which is responsible for the release of CO\(_2\) in the atmosphere and is considered as the main cause of global warming and climate change [78]. On the other hand, “carbon free” energy sources, such as hydropower and renewable energy technologies, do not represent an extensive replacement, capable of substituting fossil fuels in the medium term [79]. Nuclear energy is therefore one of the possible options to mitigate the above-mentioned issues in the coming decades, mainly because it is already available on the market, as there are about 450 nuclear reactors in operation worldwide [80]; it is essentially free from CO\(_2\) emission and it can be developed on a large scale. There are, however, three major concerns regarding the use of nuclear energy, with significant implications to both the general public and the authorities: (1) the safety of the operation of nuclear power plants, (2) the efficient management of nuclear waste accumulated over the past 60 years of power plant operation and (3) the proliferation of nuclear material and its potential use in military or terrorist activities. However, these three issues could be effectively addressed with the development of nuclear systems with low-risk operation, tighter operational margins and nuclear fuel recycling capabilities.
In order to study the feasibility and development of such reactors, the Generation-IV Forum (GIF) was founded in 2000 [81] to evaluate all possible solutions and select the one(s) deemed more suitable to address the aforementioned needs. The new Generation IV reactors, which will be hybrids of thermal and fast neutron reactors, are expected to have more efficient burn-up capabilities and, most importantly, use nuclear waste from currently operating reactors as fuel [82]. The nuclear waste that is planned to be used consists mainly of minor actinides, such as plutonium, neptunium, americium and curium isotopes, whose neutron-induced fission cross sections exhibit an effective threshold above 1 MeV incident neutron energies. The incineration of these isotopes, which constitute a considerable fraction of the high radiotoxicity component of nuclear waste, requires a fast neutron spectrum to match the fission cross sections and transmute them into nuclides with much shorter half-lives or into stable nuclei. Thus, Generation IV systems are envisaged to make sustainable use of fuel resources and to minimise nuclear waste and long-term waste management needs. Finally, they would be inherently unattractive as sources of nuclear material for military applications and provide increased physical security against attacks.
An alternative option for nuclear systems that meet the criteria described above is in sub-critical accelerator-driven systems (ADSs) [83, 84]. Their operation is based on the production of high-energy neutrons via spallation caused when charged particles, usually electrons or protons, are accelerated at high energies (\(\sim \)1 GeV) by LINACs or cyclotrons and impinge on high atomic mass targets, such as tungsten, depleted uranium, lead etc. A prominent advantage of these systems is the ability to efficiently control the chain reaction that powers the reactor, as well as the possibility to operate in sub-critical conditions, since the neutron spectrum that is injected in the reactor after the spallation can be instantly cut off by simply stopping the accelerator. In addition, the fast neutron spectrum of ADS makes neutrons the most suitable solution at present to incinerate and transmute long-lived nuclear waste, such as plutonium and neptunium isotopes, by using the nuclear waste of conventional reactors as fuel.
Apart from different reactor designs, the amount and availability of natural uranium resources, which comprise only \(\sim \)0.7% of the fissile \(^\mathrm {235}\)U isotope, could become a limiting factor for the long-term use of nuclear energy, thereby increasing the interest for breeders which make full use of the natural resources, like the well-known U/Pu cycle with a fast neutron spectrum. In this respect, another fuel cycle is considered, the Th/U cycle. Natural thorium does not contain any fissile material and consists of 99.98% of the fertile \(^{232}\)Th which, through one neutron capture and two consecutive \(\beta \)-decays, leads to the production of the fissile isotope \(^{233}\)U. The main asset of this cycle is that it leads to a far lower production of long-lived actinides which are the main problem in a waste repository because they have to remain confined over a geological time scale. This is due to the low capture cross section of \(^{233}\)U and to the fact that the heavier isotopes are burned through fission when they reach \(^{235}\)U by neutron capture. Therefore, if the chemical partitioning of the spent fuel is efficient enough, the wastes are radiotoxic over a much shorter time scale. Concerning proliferation, the isotopes involved in this cycle are not used for conventional nuclear weapons and, most importantly, the \(^{233}\)U is unavoidably contaminated by \(^{232}\)U which has a hard photon of 2.6 MeV in its decay chain, making the fissile material difficult to transport and easy to detect.
The above-mentioned solutions, which are in the R&D phase, can make nuclear waste management more efficient. Feasibility and sensitivity studies of these next-generation nuclear reactor designs require the accurate and consistent knowledge of cross sections of all involved reactions, mainly of the neutron-induced reactions on minor actinides at energies that range from thermal up to tens of MeV. However, severe discrepancies exist in the evaluations and the cross section data in literature; thus, new accurate data are required in order to reduce the uncertainties in the design of the proposed systems. The importance of accurate nuclear data for advanced reactor design and other applications is described in the High Priority Request List (HPRL) of the Nuclear Energy Agency (NEA) [85], while the needs and their target accuracies are summarised by the Organisation for Economic Co-operation and Development (OECD/NEA) [86].
The n_TOF neutron time-of-flight facility has provided a considerable amount of experimental data relevant to the pressing needs for advanced nuclear technologies since the beginning of its operation in 2001 [87]. A detailed list of the fission cross section measurements that were performed during the three working periods of n_TOF (Phase-I in 2001–2004, Phase-II in 2009–2012 and Phase-III in 2014–2018), will be presented in Sect. 6.
2.4 Needs related to nuclear astrophysics
Neutron-induced, \(\beta \)-delayed and spontaneous fission reactions play a key role in the nucleosynthesis of heavy elements that takes place in the universe following explosive events like supernovae or neutron star mergers (NSM) [88,89,90]. The recent multi-messenger observation, by means of gravitational waves, \(\gamma \)-ray burst and other electromagnetic radiation, of the neutron star merger event GW170817 [91] has triggered a renewed interest in the so-called r-process nucleosynthesis, i.e. the production of heavy elements by means of rapid neutron capture reactions and subsequent \(\beta \)-decay of the short-lived neutron-rich isotopes produced in the process. The wealth of data collected in the GW170817 event, in particular on the associated kilonova [92], have provided precious information on the nucleosynthesis processes that occur in the aftermath of NSM events, and more information of this kind is expected in the future. The astonishing progress in multi-messenger astronomy is now calling for advances in the model description of r-process nucleosynthesis of heavy elements.
The r-process abundances in the solar system (solid symbols) are compared to SKYNET [93] calculations performed assuming an electron fraction \(Y_\mathrm {e}=0.1\), with and without fission recycling. Fission processes are fundamental to reproduce the observed abundance distribution, in particular in the peak at \(A\sim 130\) and in the lanthanides region (shaded area)
In the explosive scenarios described above, the extremely high neutron densities available lead to the formation of nuclei heavier than iron, all the way up to unstable actinides. Spontaneous, \(\beta \)-delayed and, to a lesser extent, neutron-induced fission of these actinides produce fission fragments that in turn act as seeds for a new cycle of rapid neutron capture reactions. This process, referred to as “fission recycling”, is predicted to play an important role in shaping the r-process abundance distribution of heavy elements. The effect of fission recycling is illustrated in Fig. 3, that shows the final abundances expected from an expanding material that experiences r-process nucleosynthesis. The calculations have been performed with the SKYNET code [93] with a reasonable value of the electron fraction \(Y_\mathrm {e}\) of 0.1 (such value is representative of neutron-rich matter, as the one dynamically ejected from a NSM event). Compared with the observed solar system r-process abundances [94], the calculation clearly demonstrate the fundamental role of fission recycling, generally believed to be responsible for an important component of the observed r-process heavy element abundances.
The r-process nucleosynthesis is computed by means of theoretical models that couple the physical evolution of the environment to a very large nuclear network (see for example Refs. [95,96,97,98]). The calculations of the various nucleosynthesis processes at play during those powerful events require detailed and reliable nuclear inputs. In particular, fission recycling relies on the fission rates and the mass distribution of fission fragments for a number of heavy and highly unstable actinides. Current efforts aim at refining those nuclear models so that they can provide a comprehensive and self-consistent description of the fission process, and can be used by stellar modellers to predict the behaviour of super-heavy actinides. Research activity is concentrating on the optimisation of various nuclear physics parameters, such as fission barriers, nuclear level densities etc., that are at the basis of most fission models. In this respect, new fission data on a variety of actinides are needed, as the predictive power of current nuclear models can only be improved by comparison with a large set of experimental results. We recall here that, apart from neutron-induced fission cross sections, \(\beta \)-delayed fission and spontaneous fission probabilities, models are needed to predict the fission yield, i.e. the mass and charge distribution of fission fragments that strongly affect the abundance distribution, in particular in the mass region between the second and third r-process peak (\(130<A<180\)). New experimental data on fission are therefore essential for optimising these nuclear models and increasing the predictive power of nucleosynthesis models that use their output.
Current knowledge of r-process nucleosynthesis does not allow one yet to unambiguously identify the dominating fission channel(s) in r-process nucleosynthesis following a NSM (see for example Ref. [99]). However, while \(\beta \)-delayed and spontaneous fission cannot be extensively studied in laboratories [3], neutron-induced fission reactions are experimentally accessible at neutron facilities around the world. In particular, thanks to the high luminosity of the neutron beam, a wealth of fission data on actinides spanning from \(^{230}\)Th to \(^{245}\)Cm have been collected at the CERN n_TOF facility CERN in its 18 years of operation. The higher flux expected in the second experimental area (EAR-2) after the installation of the new spallation target in the near future will give a further boost to fission studies at n_TOF, allowing the collaboration to study actinides with half-lives as short as a few years.
Stronger constraints on fission models may come in particular from measurements of neutron-induced fission cross sections and fission yields of an entire isotopic chain. In fact, a combination of data for various isotopes of the same element allows one to simultaneously study multiple-chance fission, thus better defining relevant model parameters. One of these chains regards curium. While \(^{245}\)Cm has already successfully been measured at n_TOF in the past, new measurements can be performed in the future on all other isotopes of the chain, from \(^{244}\)Cm to \(^{248}\)Cm. Such data would represent a unique opportunity to refine fission models to be used for calculations of fission recycling in r-process nucleosynthesis. Another chain that has already been partially investigated at n_TOF regards plutonium, with \(^{240}\)Pu and \(^{242}\)Pu already measured in recent years. These two isotopes could be complemented with the short-lived \(^{238}\)Pu and \(^{241}\)Pu after the installation of the new spallation target, providing data on a rather long isotopic chain. It should be noted that available data are scarce and affected by large uncertainties on all mentioned isotopes. In particular, very few data are available on the fission yield. The use of a sophisticated 2E2v device (the STEFF apparatus, described in Sect. 4.4), in combination with the unique features of the n_TOF neutron beam, allows the collaboration to measure fission fragment distributions with high resolution on the atomic mass and charge, thus providing crucial data for model optimisation.
3 The n_TOF facility
The n_TOF neutron time-of-flight facility became operational at CERN in 2001 with the aim of providing new and accurate cross section data for neutron-induced reactions relevant to fundamental and applied nuclear science. Neutrons are produced by spallation reactions induced by 20 GeV/c pulses of \(7{-}8\times 10^{12}\) protons with a 7 ns (rms) width and a maximum repetition rate of 0.8 Hz, delivered by the CERN Proton Synchrotron (PS), impinging on a massive lead target. The layout of the n_TOF facility is shown in Fig. 4.
The facility is based on an idea proposed by Rubbia [100] and includes one experimental area (EAR-1) at the end of an horizontal neutron flight-path approximately 185 m long, commissioned in 2001 and a second one (EAR-2), constructed vertically above the neutron source at a distance of approximately 19 m, commissioned in 2014. After the first 4 years of operation (Phase-I), the \(80\times 80\times 60\) cm\(^3\) spallation target, made of lead blocks, had to be replaced due to corrosion problems caused by insufficient cooling. The new spallation target was installed and commissioned in 2008–2009, when a new experimental campaign started (Phase-II).
The present spallation target, a cross section of which is shown in Fig. 5, is a monolithic 1.3 ton lead cylinder, 40 cm in length and 60 cm in diameter, surrounded by a circulating 1 cm water layer for cooling. Contrary to the original target (2001–2004), in which a 5.7 cm water layer acted both as coolant and neutron moderator, in the new target the moderator system was decoupled from the cooling circuit to allow the use of different materials to moderate the fast spallation neutrons and produce a white spectrum ranging down to thermal neutron energy. Along the horizontal neutron beam-line, the layer of cooling water is followed by a second 4 cm thick layer of either de-mineralised water or borated water, obtained with the addition of boric acid enriched with \(^{10}\)B (\(1.28\%\) H\(_3\)BO\(_3\)), for additional moderation of the neutron spectrum. The choice of borated water strongly affects both the low-energy neutron spectrum, considerably suppressing thermal neutrons, and the in-beam photon background, by reducing the number of 2.223 MeV \(\gamma \)-rays from neutron capture by hydrogen, as shown in Sect. 5.3. More details on the spallation target that has been in use for the last 10 years (2008–2018), as well as on the effects of borated water, studied by means of extensive MCNP and FLUKA simulations and verified during the dedicated commissioning campaign, can be found in Refs. [101, 102].
The neutron energy \(E_\mathrm {n}\) is determined by means of the time-of-flight (TOF) technique, by measuring the time elapsed between the production of the neutron inside the spallation target, i.e. the time-of-arrival of the primary proton beam on the target, and the time of detection of a neutron-induced reaction. Because of the stochastic nature of the moderation process, neutrons entering the beam-line with a given energy are recorded with different times-of-flight, due to a spread in the time spent by the neutron inside the target-moderator assembly, the so-called moderation time. The effect of the moderation can also be viewed as a spread in the “effective” flight-paths, i.e. the sum of a fixed geometrical distance and the moderation length, defined as the moderation time multiplied by the neutron velocity of the neutron when entering the beam-line. The spread in the moderation length is responsible for the energy resolution \(\varDelta E_\mathrm {n}\) of the neutron beam. The distribution of the moderation length as a function of the neutron energy represents the so-called resolution function of the facility. At n_TOF it has been studied for both the horizontal and vertical beam-line by means of extensive Monte Carlo simulations, using the GEANT4, FLUKA and MCNP codes [101, 103,104,105,106]. The distributions are typically non-Gaussian and highly asymmetric, with a shape that strongly depends on the neutron energy, as shown in Sect. 5.3. Together with the Doppler broadening, mostly dominant for low neutron energy, and the time resolution of the proton beam and of the detector system, that dominates in the high-energy region (from a few MeV up), the resolution function of the neutron beam affects the overall energy resolution of the data collected at n_TOF, determining in particular the broadening of measured resonances in the cross section. The reliability of the predicted resolution function has been confirmed through a comparison with experimental data by analysing the reaction yield of well-known resonances, such as the neutron resonances of the \(^{25}\)Mg, \(^{56}\)Fe, \(^{197}\)Au capture reactions [105, 106].
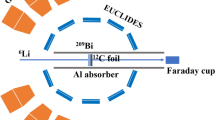
As a consequence of the long flight-path towards the first experimental area (\(\sim \)185 m), an excellent energy resolution, \(10^{-4}< \varDelta E/E < 10^{-2}\) (0.06 for 1 GeV neutrons), is achieved, while the shorter flight-path of the vertical beam-line (\(\sim \)19 m) leads to the worse, although still remarkable, resolution of \(10^{-3}< \varDelta E/E < 10^{-2}\), despite the fact that the target assembly was not optimised for the vertical beam-line, in terms of moderator thickness, at the time of its design and installation in 2008. A comparison of the neutron beam characteristics in the two experimental areas is reported in Table 1.
Together with the high instantaneous neutron flux and the wide energy range, the high energy resolution represents the main advantage of the n_TOF neutron beams for measurements of neutron-induced fission cross sections. In particular, the high resolution of EAR-1 allows one to accurately study the resolved resonance region (RRR), while the high flux of EAR-2 is fundamental for measurements with high-activity and/or low mass samples, as it minimises the relative contribution of the background related to the radioactivity of the sample and allows one to collect high-quality data in particular in the unresolved resonance region and for fast neutrons. In this sense, the two experimental areas can be considered complementary to each other and a combination of data collected in both areas can provide, in some cases for the first time, high-accuracy and high-resolution data in a wide energy range.
Accurate measurements of neutron-induced reaction cross sections require very good knowledge of the various features of the neutron beam in the experimental area, in particular its resolution function, previously discussed, its energy spectrum, i.e. the total number of neutrons entering the area as a function of energy (determined from the time-of-flight), the spatial profile and the neutron and \(\gamma \)-ray background in and outside the beam. All these features may slightly change depending on the spallation target. For this reason, a measurement campaign specifically devoted to the neutron beam characterisation has been performed for each spallation target installed so far at n_TOF. In particular, a large effort is dedicated to the measurement of the neutron flux and its energy dependence. As explained more in detail later on, the cross section of neutron-induced fission reactions are mostly determined by means of the so-called ratio method, relative to a standard or reference reaction (most commonly \(^{235}\)U(n,f)) in order to minimise systematic errors related to the knowledge of the neutron flux. However, due to the non-smooth behaviour of the reference cross section, the ratio method cannot be used in some energy regions, such as in the resolved resonance region, and it is more convenient to rely on the neutron flux, that has a generally smooth behaviour in that region.
The n_TOF neutron flux and energy distribution have been determined by means of reference reactions, in particular \(^6\)Li(n,\(\alpha \)), \(^{10}\)B(n,\(\alpha \)) and \(^{235}\)U(n,f), using different detection systems for different energy ranges, such as silicon detectors, Micromegas detectors, a calibrated fission chamber from Physikalisch Technische Bundesanstalt (PTB) and Parallel Plate Avalanche Counters (PPAC). More details on the measurements and on the neutron flux characterisation for the second spallation target (2008–2018) can be found in Ref. [102]. Monte Carlo simulations have also been used to complement the flux measurements, by means of major radiation transport codes, i.e. FLUKA [107, 108], GEANT4 [109,110,111] and MCNP/MCNPX [53, 54] and typically a fair agreement is observed between experimental and simulated neutron energy distribution, over the whole energy range [104,105,106].
A final consideration regards the low repetition rate of the pulsed proton beam that eliminates the so-called “wrap-around” background even for very low neutron energies (or equivalently, long times-of-flight). In fact, the minimum time separation of 1.2 s between consecutive neutron pulses avoids the overlap of neutron bunches, where slow neutrons from a bunch would be identified as high-energy neutrons belonging to the following one. Furthermore, the high neutron flux within a small time interval (high instantaneous neutron flux) limits the acquisition time and maximises the signal-to-background ratio.
More details on the features of the two experimental areas are provided in the following sections. A new spallation target, now under construction with the aim of replacing the old one for the next experimental campaign (scheduled to start in 2021), will further improve the features of the neutron beams, in particular with higher flux and better resolution of the EAR-2 neutron beam.
3.1 The first experimental area (EAR-1)
The first neutron beam is transported through a horizontal vacuum tube over a distance of approximately 185 m and has been used since the start of the facility in 2001. As shown in Fig. 6, the vacuum tube consists of several sections of stainless steel pipes with progressively reduced diameter and two collimators inside a 200 m long time-of-flight tunnel. The experimental area (EAR-1) is located inside the tunnel centred at around 186 m from the spallation target. The beam-line is extended for another 12 m after the experimental area to the beam dump made of polyethylene and cadmium, in order to minimise the effect of back-scattered neutrons.
Together with neutrons, an intense “flash” of \(\gamma \)-rays and ultra-relativistic particles are produced in the spallation process, giving rise to the so-called \(\gamma \)-flash. For charged particles, a sweeping magnet is placed on the beam-line, while other backgrounds are minimised by appropriate shielding, in particular after the two collimators used to shape the neutron beam. The signal produced in the detectors by the \(\gamma \)-flash can be used as the start time reference for the time-of-flight measurement. The shielding walls along the tunnel are made of concrete and iron and the two collimators are placed at approximately 137 and 178 m from the lead target. The first collimator is 2 m long with an inner diameter of 11 cm and an outer diameter of 50 cm. The second collimator has an inner diameter of 8 cm for fission measurements and a smaller diameter of 1.8 cm for capture measurements (although fission measurements have also been performed with the smaller collimator). The collimators are made of steel and borated polyethylene, so as to moderate fast neutrons and capture the slow ones.
The first experimental area (EAR-1), a picture of which can be seen in Fig. 7, is obtained by delimiting the final section of the time-of-flight tunnel with two shielding walls placed immediately after the last collimator, and before the beam dump. At the start of the second campaign (Phase-II) in 2009, the area was equipped with several safety features, so as to meet the requirements of a Type A Work Sector [112], where unsealed radioactive sources can be handled. This modification represented a big step forward in particular for fission studies, as it made possible to use fission chambers with thin entrance and exit windows, thus minimising the background induced by heavy structural material in the beam. A more detailed description of the characteristics and performance of EAR-1 can be found in Refs. [113, 114] for the experimental campaign of Phase-I and in Refs. [101, 102] for Phase-II.
Photo of the first experimental area (EAR-1). At the entrance of the neutron beam, on the left side, the carbon-fiber chamber of the SiMon (Silicon Monitor) apparatus, used to monitor the neutron flux, is mounted directly on the beam-line. The beam-line layout is configured according to the needs of each experiment. The total absorption calorimeter (TAC) used for capture measurements permanently installed in EAR-1 is also visible
3.2 The second experimental area (EAR-2 )
A big boost to the n_TOF fission programme came from the construction of a second short beam-line and corresponding experimental area at ground level above the spallation target. The new installation, completed in 2014, was built with the aim of allowing challenging measurements on short-lived radioisotopes, considerably expanding the already rich programme on neutron-induced reactions performed at the n_TOF facility. For such isotopes, the count-rate in the first experimental area (EAR-1) is dominated by the background due to the radioactivity of the sample. A suppression of this background component required a higher instantaneous neutron flux, a goal that can be achieved by measuring closer to the neutron source. To this purpose, a new experimental area was designed and built, together with the corresponding beam-line, at approximately 19 m distance from the spallation target, i.e. a factor of 10 shorter than EAR-1.
Since the spallation target is located underground, and given the prohibitive cost and complexity of excavating a new tunnel, the new area was conveniently built on the surface, just on top of the spallation target (see Fig. 4), at the end of a vertical beam-line [104]. Along the line, two collimators and a permanent magnet are used to shape the neutron beam and sweep away charged particles, while a multi-layer beam dump is placed on the top of the experimental area in order to minimise the background in the experimental area and the dose to personnel outside the installation (Fig. 8).
The second collimator, placed just below the floor of the experimental area, was designed with a conical shape in order to minimise the beam divergence and induced background. It consists of various layers of boron carbide, borated polyethylene, steel and lead, and it produces a beam of \(\sim \)3 cm diameter at the focal plane, located approximately 1.5 m above the floor, where the experimental setups are typically mounted. Similarly to EAR-1, the new area is classified as a Type A work sector, being equipped with several safety and radio-protection systems, as well as controlled ventilation, thus allowing for the handling of unsealed radioactive sources. This is a fundamental prerequisite for fission cross section measurements, given that in general highly radioactive actinide samples are mounted inside vacuum chambers and detectors, equipped with thin windows and with gas circulation, that therefore do not meet the requirements of a “sealed source”. A picture of the interior of EAR-2 is shown in Fig. 9.
After completion of the new measuring station, a comprehensive experimental campaign was undertaken for the commissioning of the neutron beam. In particular, the neutron flux was measured in the whole energy range with different detectors and using various reference reactions, i.e. the \(^{6}\)Li(n,t), the \(^{10}\)B(n,\(\alpha \)) and the \(^{235}\)U(n,f) reactions. The results have been reported in Ref. [115]. Figure 10 shows the total number of neutrons per proton bunch in EAR-2 compared with the one in EAR-1, for the more commonly used small-aperture collimators (see Table 1). A large gain is evident in the figure, although this is partially due to a slightly larger aperture of the collimator in EAR-2, relative to the one in EAR-1. The gain depends on the neutron energy, going from a factor of 100 around thermal energy, to a factor of 35 in the eV and keV region, and a factor of 20 from 1 to approximately 100 MeV, the maximum neutron energy reached in EAR-2 (since high-energy neutrons are preferentially emitted in the direction of the proton beam, their contribution in the vertical direction is suppressed).
The large gain in the flux that characterises the neutron beam in EAR-2 allows one to perform measurements with samples of correspondingly smaller mass or in a shorter time. Another advantage, relative to EAR-1, is related to the shorter flight-path of the vertical beam, that results in a smaller time-of-flight for a given neutron energy by approximately a factor of 10. The combination of the higher flux and shorter time-of-flight results in an increase of the signal-to-background ratio of more than two orders of magnitude for the background related to the radioactive decay of the sample. Such a very large increase represents a breakthrough in fission studies, as it makes it finally possible to measure actinides with half-lives as short as a few tens of years with a still reasonable energy resolution compared, for example, to lead-slowing-down spectrometers or to measuring stations of other TOF facilities, at much shorter distance from the neutron source. The commissioning campaign also aimed at characterising the neutron beam spatial profile, its energy resolution and the background induced by the neutron beam in the experimental area. The results will be reported in a forthcoming paper.
The big improvement of the second experimental area for measurements of fission reactions relative to EAR-1 can be appreciated in Fig. 11, which shows the amplitude spectra of signals recorded in Micromegas detectors in a measurement of the \(^{240}\)Pu(n,f) reaction performed in EAR-1 (black line) and in EAR-2 (red line). Even though a sample of only a few mg was used to limit the background related to the \(\alpha \)-particle decay, in EAR-1 the count-rate of \(\alpha \)-particles and the correspondingly high pile-up probability (of two or more signals), was much larger than the count-rate of fission events, making it impossible to clearly identify the fission fragment region. Conversely, in EAR-2 the fission events dominate over the background, leading to much cleaner results, and ultimately to a high-accuracy, high-resolution measurement of the cross section for this reaction [116]. These results demonstrate the enormous potential of the second experimental area in performing challenging measurements of neutron-induced fission reactions on short-lived actinides.
4 Detection systems and samples for fission measurements
Over the course of almost 20 years of operation, a rich experimental programme on neutron-induced fission reactions has been carried out at the n_TOF facility. Together with the very convenient features of the neutron beam, the measurements have benefited from high-performance detection and acquisition systems specifically developed at n_TOF, as well as from new analysis techniques and the extensive use of the most advanced Monte Carlo simulation tools. Finally, a key role in the successful completion of the fission measurements has been played by the sample preparation and characterisation, which in many cases is in itself a challenging and delicate task.
A large fraction of the fission programme at n_TOF has so far regarded measurements of neutron-induced fission cross sections, although a programme on the study of fission fragment angular distributions has also been carried out recently, and a dedicated setup for studying the FF-\(\gamma \)-ray correlation has been installed in EAR-2 since a few years. Since the first fission chamber used in Phase-I, the performance of the experimental setups has constantly improved to fully exploit the innovative features of the n_TOF neutron beam and to cope with the very large flux of the second experimental area, with the severe dead-time and pile-up problems, consequence of the high count-rate, and with the harsh radiation environment related to the neutron beam and the high \(\alpha \)-particle activity of the samples. The main characteristics required are a high efficiency for fission fragments, low mass for background minimisation, in particular along the neutron beam direction, fast timing and low sensitivity to the \(\gamma \)-flash in order to reach high neutron energies and, finally, high radiation resistance.
Neutron-induced fission cross sections are typically measured at n_TOF by means of the so-called ratio method, i.e. relative to a standard reaction. The reference reaction most commonly used at n_TOF is \(^{235}\)U(n,f), considered standard at thermal neutron energy and between 150 keV and 200 MeV [42, 117]. In this method, the fission cross section of a nuclide \(^\mathrm {A}\)X is determined as a function of neutron energy \(E_\mathrm {n}\) according to the following equation:
where \(\sigma _\mathrm {f}\)(\(^{235}\)U,\(E_\mathrm {n}\)) is the energy-dependent cross section of the neutron-induced fission of \(^{235}\)U and \(ratio(E_\mathrm {n})\) is the ratio between the number of events recorded for the nuclide being investigated and for the reference reaction, respectively, corrected for the areal density of the samples, the detection efficiency and other experimental effects (dead-time corrections, neutron beam attenuation etc.), as summarised in the following expression:
Here (\(C-B\)) is the background-corrected count-rate, N is the areal density of the samples, \(\epsilon \) is the detection efficiency, and CF stands for all other correction factors (including the one for the angular anisotropy of fission fragments emission). The main advantage of the ratio method is that it minimises systematic uncertainties, since the energy-dependent neutron flux cancels out, and other experimental effects, in particular efficiency and dead-time corrections, mostly compensate each other, provided that both the sample being investigated and the reference one are measured simultaneously and in similar experimental conditions. In particular, the samples have to be mounted inside the same detector, and should have the same transverse dimensions and similar thickness, so as to minimise efficiency and beam-related corrections. With this method, overall systematic uncertainties of a few percent can easily be obtained on the fission cross section.
A final remark regards the measurement technique. At n_TOF, two methods have been (and are currently being) used for fission cross section determination. The most common one, used in conjunction with various fission chambers, relies on the detection of one fragment per fission event. Samples are mounted inside the gas volume, so as to reach a detection efficiency close to 100%. The second technique relies on the coincident detection of both fragments emitted in a fission event, and is therefore referred to as the “coincidence method”. At n_TOF, this technique has been used with a particular type of detectors, characterised by very thin windows and low gas pressure, with the sample mounted on very thin backings between a pair of such detectors. While a lower efficiency is typically achieved in this case, the coincidence method results in an extremely high rejection of the \(\alpha \)-background from the actinide samples, as well as from other competing reactions with single particle emission, and is therefore ideal for the measurement of short-lived actinides.
In this section, the experimental setups used for the fission programme at n_TOF are described and discussed, from the various detectors developed and employed over the years, to the sample preparation techniques, and finally to the data acquisition system specifically designed to match the particular features of the neutron beam and of the detection systems.
4.1 The fast ionisation chamber (FIC)
The fast ionisation chamber (FIC) [118, 119] is an ionisation chamber with fast timing properties specially built at CERN for measuring neutron-induced fission on minor actinides at the n_TOF facility. This detector was developed within a collaboration between the Joint Institute of Nuclear Research (JINR), Dubna, the Institute of Physics and Power Engineering (IPPE), Obninsk (Russian Federation) and the EET group of CERN. At the time of construction this detector presented advantages such as: (a) easy mounting in vacuum and simple installation of radioactive samples, (b) a low amount of material in the neutron beam (i.e. thin windows and electrodes) and (c) a fast collection time for reliable operation at the very high counting rates expected at n_TOF.
Two fission chambers of similar design were built to comply with the safety regulations at CERN for the handling of radioactive sources. The first type of detector was designed for the measurement of isotopes with very high \(\alpha \)-activity (\(^{237}\)Np, \(^{234}\)U etc.), following the requirements of the ISO2919 standard as ISO/04/43323 (“sealed source for a general neutron source application”). Another chamber was also built with a simplified design, and used only as a neutron flux monitor, operated with \(^{235}\)U and \(^{238}\)U samples.
As shown in the drawing of Fig. 12, the FIC detector consists of a stack of cells mounted one after the other along the beam direction. Each cell consists of three electrodes with a diameter of 12 cm. The central 100 \(\upmu \)m thick Al electrode is actually the backing of the actinide targets, plated, usually on both sides, with a disk of the chosen actinide isotope, typically of 5 or 8 cm diameter. The external Al electrodes, 15 \(\upmu \)m thick, are used to apply the electric field in the active gas-filled volume of the detector cell, which was typically 600 V/cm. In this way, two separate active detection volumes are created, but the corresponding signals are taken through the same DAQ channel, so in the end there is one signal coming out from each cell. The stack of cells was placed in a sealed Al chamber, filled with a fast Ar:CF\(_4\) mixture (90 : 10) at 720 mbar.
The principle of operation of the FIC for fission cross section measurements is the recording of the energy deposited in the detector gas by the fission fragments produced in very thin targets. The detector gas is in physical contact with the target in order to reduce the energy lost by the fission fragments before entering the detection volume and to obtain a solid angle coverage very close to 2\(\pi \) (one fragment is detected from each fission reaction). The FIC operates in the ionisation mode, i.e. the ion pairs created by the incoming particle are detected without further multiplication. The typical FIC signal has a FWHM of \(\sim \)200 ns. The neutron flux attenuation through the chamber electrodes was calculated with Monte Carlo simulations to be a few per thousand for one plate and less than 1% for the whole chamber hosting 16 actinide targets.
The FIC detector has been used for fission cross section measurements at n_TOF since the beginning of its operation, providing interesting results for several isotopes, such as \(^{233}\)U [120, 121], \(^{234}\)U [46], \(^{236}\)U [122], \(^{238}\)U [73, 123], \(^{237}\)Np [124], \(^{241}\)Am [125], \(^{243}\)Am [126] and \(^{245}\)Cm [127]. More details on these measurements and results are presented in Sect. 6.
4.2 Parallel plate avalanche counters (PPAC)
An important setup used at n_TOF for studies of fission reactions is based on parallel plate avalanche counters (PPAC) for the detection of fission fragments. A PPAC is made of three electrodes, a central anode surrounded by two cathodes, defining two detecting gaps of 3.2 mm thickness. The detecting medium is low-pressure octofluoropropane (C\(_3\)F\(_8\)) maintained at 4 mbar (absolute value). The electrodes are made of 1.7 \(\upmu \)m thick mylar foils, coated with aluminium or gold. For the anode the coating is uniform and double sided, whereas for cathodes it is divided into 2 mm wide strips to allow for a localisation of the avalanche by using a delay line. In order to be detected, a fission fragment coming from outside the counter has to cross a cathode. If it crosses also the anode it is seen in both gaps and, as the strips of the two cathodes are perpendicular to each other, the detector can record the X and Y coordinates of the fission fragment crossing point.
The peculiarity of the measurements with PPACs is that both fission fragments are detected in coincidence. This feature, combined with a very fast timing response of the device (of a few ns), makes the PPAC setup practically insensitive to the background related to \(\alpha \)-particle decay of the isotope being measured, so that an extremely high signal-to-background ratio is obtained even for highly radioactive samples. For this reason, PPACs can be suitably employed for measuring the fission cross section and fission fragment angular distribution of several actinides, including those with short half-lives.
In order to apply the coincidence technique, a detection cell is made of a sample surrounded by two PPACs, as shown in Fig. 13. As a consequence, the backing supporting the deposited layer of the isotope being measured has to be thin enough to allow the backward-emitted fragment to be detected. In the case of actinides the backing is made of an aluminium foil, 2 \(\upmu \)m or 0.7 \(\upmu \)m thick, on which the actinide is deposited by electroplating.
In measurements performed at n_TOF during Phase-I, the detector assembly was made of a stack of ten PPACs interleaved with 9 samples, mounted perpendicularly to the neutron beam, as illustrated in Fig. 14. As a result, each PPAC detector views two different samples. The size of the actinide deposit is a disk of 8 cm in diameter, covering the beam spot size, and the active area of PPACs is 20\(\,\times \,\)20 cm.
Since the second experimental campaign (Phase-II) a tilted geometry was used, in which the detectors and samples are mounted at an angle of 45\(^{\circ }\) relative to the neutron beam direction. In this case as well, the full setup consisted of ten PPACs and nine samples, as shown in Fig. 15, where a photo of the setup is also shown. The targets and PPACs are identical to those used in Phase-I. The motivations and advantages of this tilted geometry are explained later.
As previously described, fission cross sections of a given actinide are obtained relative to a reference cross section. In measurements with the PPAC setup, \(^{235}\)U is used as reference, so that a well-characterised \(^{235}\)U sample is always included among the nine samples mounted in each measurement. In the analysis, the reference cross section of \(^{235}\)U based on ENDF/B-VII.0 is used below 30 MeV, complemented by JENDL-HE at higher energy, while above 200 MeV the in-house evaluation outlined in Sect. 2.2 is also available.
In the first n_TOF experimental campaign, the neutron-induced fission cross section of several isotopes was measured with the PPAC setup, namely \(^{232}\)Th, \(^{233}\)U, \(^{234}\)U, \(^{238}\)U, \(^{237}\)Np, \(^{209}\)Bi and \(^\mathrm {nat}\)Pb. More details on these measurements and results are presented in Sect. 6. In all these measurements, the localisation on the cathodes was not yet working so that the fission events where recognised only as a coincidence between the anode signals from detectors placed on either side of the sample. In such situation the event was detected as soon as both fragments reached the entrance of the detecting gap.
The main advantages of the PPAC setup are its fast time response (anode signal of 9 ns FWHM) and the very low thickness of material present in the neutron beam. This last feature, combined with the low gas pressure, makes the detector essentially insensitive to the large flux of prompt \(\gamma \)-rays and relativistic particles generated in the spallation target, the so-called \(\gamma \)-flash, that reach the experimental area, as well as to recoils from neutron scattering inside the detector volume. The combination of the fast timing and low sensitivity to the \(\gamma \)-flash results in the detection of fission signals even at very short times-of-flight, or equivalently at very high energies. In fact, PPACs allow the n_TOF Collaboration to study fission reactions up to 1 GeV, providing data in the high neutron energy region, which cannot be obtained at any other neutron facility in the world. Several interesting results have indeed been obtained so far with this unique beam–detector combination in an energy range covering almost 11 orders of magnitude, from thermal neutron energy to 1 GeV. Figure 16 shows the \(^{237}\)Np cross section measured at n_TOF in the range of 0.7 eV–1 GeV. A rather unique feature of the setup is that in the same measurement the resonance region and the high-energy region can be covered.
\(^{237}\)Np cross section measured in EAR-1 with the PPAC system, using the \(^{235}\)U evaluated cross section as reference [69]
An important factor in the measurement with the PPAC system is the detection efficiency. Since the coincidence between the two fission fragments is required to identify a fission reaction and because the backward-emitted fragment has to cross the sample backing, the efficiency is typically lower than in the case of an ionisation chamber. In particular, the efficiency is defined by the limiting angle at which the fragment is stopped in the dead layers of the backing or the entrance PPAC window (acting as the cathode). It should be noted that the geometric active area of the detectors is larger than this limit and does not affect the efficiency. Based on the fact that all electrodes and backings have the same nominal thickness, it was assumed that the limiting angle was almost the same for all samples, so that the ratio of efficiencies departs from unity by a small amount estimated from known differences, like the thickness of the actinide layer and its oxygen and hydrogen content. From simulations the efficiency for isotropic emission can be estimated to be about 0.65. However, the angle cut (or limiting angle) implies a good efficiency at 0\(^{\circ }\) and a complete insensitivity at 90\(^{\circ }\). This behaviour makes the global detection efficiency dependent on the anisotropy of the fission fragment angular distribution, which in turn depends on the neutron energy. To avoid such a drawback, the tilted configuration was introduced in Phase-II for measurements of the neutron-induced fission cross sections and of fission fragment angular distributions (FFAD). In this configuration, the PPACs are mounted at 45\(^{\circ }\) relative to the neutron beam direction. Another improvement introduced in the setup in Phase-II was the identification of the crossing point of each fragment through the detector, thanks to the position-sensitivity of the cathode. This feature allows one to reconstruct the fission trajectory, i.e. the line defined by the two crossing points. In this respect, it should be considered that in principle the fission trajectory is a straight line in the centre of mass system, while in the laboratory system the fragment velocities are not aligned with this trajectory, due to the boost imparted by the incoming neutron. However, simulations show that the line joining the FF crossing points in the detectors is a good approximation of the fission trajectory in the center-of-mass even up to 1 GeV [128], due to the limitation of the linear momentum transfer at high energy [129].
The motivation of the tilted geometry is two-fold. As previously mentioned, in the perpendicular geometry, an angle cut prevents to probe the fission fragment distribution at large angles with respect to the neutron beam. As a consequence the efficiency is very sensitive to the FFAD, as well as on the sample thickness, both of which have to be known with good accuracy in order to calculate efficiency corrections. On the contrary, in the 45\(^{\circ }\) setup the efficiency is almost independent of the angular distribution because its dependence on the FF emission angle is almost flat and, most importantly, it is not affected by a limiting angle. Figure 17 shows a comparison of the simulated efficiency, as a function of the emission angle, for the perpendicular and tilted configuration [128]. The advantage of this last setup is evident in the figure.
Another advantage of the tilted configuration is that it allows one to experimentally determine the efficiency for each sample, without the need of simulations. This last feature can be explained as follows: the fission trajectory can be defined by the polar and azimuthal angles \(\theta \) and \(\varphi \) with respect to the beam axis, as well as by the angles \(\theta '\) and \(\varphi '\) relative to the axis normal to the detectors and samples. The geometrical efficiency depends only on \(\theta '\) whereas the FFAD is a function of \(\theta \). However, a correspondence exists between these two angles. In particular, a given value of the emission angle \(\theta \) corresponds to a range of \(\theta '\), with varying \(\varphi \) and \(\varphi '\). The variation of the fission rate in this interval goes exactly as the efficiency. By taking different \(\theta \) values the efficiency can be re-constructed by pieces knowing that it should be equal to 1 at \(\theta '=0\) (trajectory perpendicular to detectors and samples). Conversely at a given \(\theta '\) the efficiency is constant and the \(\theta \) dependence of the fission rate is proportional to the angular distribution [130].
In summary the tilted setup allows one to probe all angles, and to disentangle the angular distribution from the detection efficiency. From this procedure the efficiency \(\epsilon (\cos \theta ')\) and the angular distribution \(W(\cos \theta )\) can be obtained, thus providing an additional important information on the fission process. More details on the procedure can be found in Ref. [130]
Detection efficiency as a function of the FF emission angle \(\theta \) for the two geometrical configurations of the PPACs used at n_TOF [73]
Examples of FFADs determined with the PPAC in the tilted configuration are shown in Fig. 18 for the cases of \(^{235}\)U and \(^{232}\)Th. In the former case an isotropic emission is expected below 100 keV due to the low l partial waves involved (\(l=0\) is dominant) and due to de-orientation of the spin of the target. The measurement indeed shows a flat angular distribution, as can be observed in the figure, from the behaviour of the angular anisotropy, defined as the ratio W(0\(^{\circ }\))/W(90\(^{\circ }\)). On the contrary, in the case of \(^{232}\)Th the initial spin is 0 and the FFAD becomes very sensitive to the angular momentum l involved and to the projection K of the spin along the fission axis. At the vibrational resonance around 1.6 MeV, the anisotropy is known to be lower than 1, as shown in Fig. 18.
Angular distributions obtained for \(^{235}\)U for low neutron energies and for \(^{232}\)Th at the level of the 1.6 MeV vibrational resonance. The error bars account for statistical uncertainties. The lines are fits with symmetric Legendre polynomials of degree 4. More details can be found in Ref. [130]
An illustration of the basic principle of operation of a Micromegas detector (not to scale). An ionising particle (e.g. a fission fragment) ionises the gas in the drift region. The ionisation electrons drift towards the micromesh and are multiplied inside the amplification region, inducing a signal. Indicative values are given for the electrical field strengths and dimensions
4.3 Micromegas detectors
The Micromegas (MICRO-MEsh GAsesous Structure) detector [131, 132] is a micro-pattern gas detector (MPGD). It differs from a conventional parallel plate avalanche chamber, which features a single gas volume between the anode and cathode, in that the gas volume is separated into two regions: a conversion (or drift) region, whose width can vary from several hundreds of \(\upmu \)m to a few cm, and an amplification region, typically up to 100 \(\upmu \)m wide. These two regions are separated by a porous “micromesh”, a thin (\(\sim \)5 \(\upmu \)m) conductive layer with holes with a typical diameter of a few tens of \(\upmu \)m in a triangular lattice pattern with a typical pitch between several tens and a few hundreds of \(\upmu \)m, such as the one shown in Fig. 19.
The basic principle of operation of the Micromegas is illustrated in Fig. 20. The detection of ionising particles is based on the electron-ion pairs that are produced by the particles in the drift volume. The weak field that is applied in this region (\(\sim \)1 kV/cm) is high enough to prevent recombination of the electrons, but it is still below the gas multiplication threshold and drives the electrons towards the micromesh. The electron multiplication takes place in the narrow amplification region where the electrical field is of the order of 50 kV/cm. This fast amplification process results in an improved signal-to-noise ratio and in practically 100% detection efficiency for particles depositing even a small amount of energy in the gas.
The electrical field in both the drift and amplification gaps is homogeneous, but the large ratio between the electrical field values in the two regions causes the field lines at the centre of the micromesh holes to be highly compressed and to exhibit a funnel-like shape [133, 134]. Thus, with a high enough ratio, the micromesh becomes 100% transparent to the drifting electrons, while it is ensured that the positive ions produced in the amplification region are all captured in the micromesh and do not enter the drift region to create further electron-ion pairs. Under these conditions, since each electron avalanche is of roughly the same size, the detector operates as a proportional counter, with the generated signal being proportional to the number of electron-ion pairs produced by the detected particle. The dependence of the mesh transparency on the ratio of the two electrical field strengths is plotted in Fig. 21, showing that for sufficiently high field ratios the electron collection efficiency reaches a plateau. Values near the beginning of the plateau are chosen in order to maximise the transparency while minimising the probability of sparking in the detector.
The electron transparency (in arbitrary units, normalised to its maximum value) measured as a function of the ratio of the electrical field strengths in the amplification and drift regions \(E_\mathrm {amp}\)/\(E_\mathrm {drift}\), while applying a constant voltage to the micromesh of a Micromegas detector with a 50 \(\upmu \)m amplification gap filled with an Ar:CF\(_4\):isoC\(_4\)H\(_{10}\) gas mixture. A plateau is reached for values above roughly 60
In the “microbulk” [135, 136] variant used at n_TOF, the kapton layer between the micromesh and the anode is etched only at the location of the holes, leaving the rest intact to act as a support for the micromesh. This guarantees the flatness of the micromesh and therefore a constant width of the amplification region, as opposed to the use of pillars employed in the past. At the same time, the low thickness of the detector, consisting of a few tens of \(\upmu \)m of kapton and copper, constitutes one of the major advantages of Micromegas detectors for use in neutron measurements. The minimal mass of the detector ensures a negligible perturbation of the neutron beam along the detector-sample assembly, suppressing sources of systematic uncertainty. Furthermore, neutron and neutron-induced backgrounds produced by the interaction of the neutron beam with the detector material are also minimised.
In measurements at n_TOF, the sample backing acts as the detector cathode, with the sample deposit facing the conversion region, as shown in Fig. 20. Typically, drift gaps of about 5 mm have been adopted for fission measurements, with an electrical field strength of about 0.5 kV/cm in the drift region, leading to an estimated electron drift velocity of the order of 10 cm/\(\upmu \)s and a maximum drift time of 50 ns. With a gap of 5 mm, neither \(\alpha \)-particles nor fission fragments are expected to deposit their entire energy, unless they are emitted at large angles. Nevertheless, due to the different energy loss profiles along the paths of the two types of particles, the highest ratio between the deposited energies of fission fragments and \(\alpha \)-particles—and therefore a better separation between the two—is obtained with a gap of a few mm, which is significantly shorter than the range of the particles in the gas.
The Micromegas detectors used at n_TOF have an amplification gap of 50 \(\upmu \)m and a field of about 50 kV/cm is applied in this region. The dependence of the detector gain on the electrical field strength in the amplification region (for a given voltage applied to the cathode) is shown in Fig. 22. Knowledge of the detector gain curve allows one to estimate the change of the micromesh voltage needed to obtain a desired variation of the gain. Although not needed for the optimisation of the experimental setup, the absolute value of the gain can be determined with a dedicated study. Typical gain values for microbulks with a 50 \(\upmu \)m amplification gap are between 10\(^3\)–10\(^5\) [135], however, lower gain values between 10\(^2\)–10\(^3\) are sufficient for the detection of fission fragments. In general, the high voltages are set to values suitably chosen so as to suppress the \(\alpha \)-background while still recording clear fission signals and taking full advantage of the digitiser range. It should be noted that, under these low-gain conditions, the detectors also display a negligible sensitivity to \(\gamma \)-rays which are present in the neutron beam and are further generated by neutron interactions in beam-line elements, such as collimators and vacuum windows, and in the detectors themselves.
A typical gain curve obtained with a Micromegas detector with a 50 \(\upmu \)m amplification gap filled with an Ar:CF\(_4\):isoC\(_4\)H\(_{10}\) gas mixture, with the voltage applied to the cathode kept constant at 600 V. The gain (here arbitrarily set equal to 1 for an electrical field in the amplification region \(E_\mathrm {amp}\)=40kV/cm) changes exponentially with the electrical field strength \(E_\mathrm {amp}\) (an exponential fit of the data points is shown, dashed line). Typical values of the absolute gain are between 10\(^3\) and 10\(^5\) [135]
The good time resolution of a detector is a crucial aspect for time-of-flight measurements in order to achieve the best possible determination of the time-stamp of each recorded signal. A fast time response is also important when high counting rates have to be tolerated, as it minimises pile-up effects that require special treatment during the analysis, as described in Sect. 5.2. In the Micromegas detector, signals with a FWHM of 50–200 ns can be obtained depending on the configuration (gas, drift gap, drift field) and the signal shaping and amplification method which is generally the dominant factor in determining the time characteristics of the signal. Using the proper sampling rate for signal digitisation and pulse-shape analysis techniques, as described in Sect. 5.1, a time resolution of the order of a few ns can be achieved.
The Micromegas detectors are housed in aluminium alloy chambers that can hold up to ten sample-detector modules, which are fixed on an internal support frame in such a way as to be perpendicular to the beam axis (Fig. 23). The entrance and exit windows of the chamber are made of 25 \(\upmu \)m-thick kapton and have a diameter of 15 cm, much larger than the neutron beam size for any collimator configuration at n_TOF. The detectors are operated with a circulating Ar:CF\(_4\):isoC\(_4\)H\(_{10}\) gas mixture (88 : 10 : 2) at a pressure of \(\sim \)1 bar and the outflow is filtered to prevent and detect any escape of radioactive isotopes. A number of reference samples are also placed in the chamber along with the studied samples in order to deduce the fission reaction cross section from the ratio method previously described. The commonly adopted reference reactions, covering various energy ranges, are \(^{235}\)U(n,f), \(^{238}\)U(n,f) and \(^{10}\)B(n,\(\alpha \)).
While the relatively simple construction of the detector contributes to its robustness and long-term stability, it has been observed [137] that prolonged exposure (about 1 year) to high \(\alpha \)-activity samples (\(\sim \)8.5 kBq/mm\(^2\)) can lead to significant physical damage to the micromesh, contributing to a gradual deterioration of the electrical field near the holes and of the overall detector performance. This issue has been addressed in recent measurements by taking advantage of the increased neutron fluence in EAR-2 to shorten the measurement time to about 4–6 weeks and by operating the detectors at lower gain. No deterioration was observed under these conditions with samples of similar activity.
Until today, Micromegas detectors have been used at n_TOF for fission measurements on \(^{240}\)Pu [116], \(^{242}\)Pu [138, 139] and more recently on \(^{230}\)Th [140], \(^{237}\)Np [141] and \(^{241}\)Am [142], taking advantage of the increased neutron fluence in EAR-2. Furthermore, different setups based on Micromegas detectors have been used for neutron beam characterisation and monitoring [115], for fission tagging in capture measurements of fissile isotopes (see Sect. 4.5), for (n,\(\alpha \)) reaction studies [143] and for the characterisation of the spatial profile of the neutron beam using a recently developed variant with both mesh and anode electrodes segmented into strips [144].
4.4 The SpecTrometer for Exotic Fission Fragments (STEFF)
Since the 1960s there have been many measurements of fission yield and fragment kinetic energy distributions for spontaneous and neutron-induced fission of actinide nuclei[145]. These measurements have been performed by a variety of methods, including both radiochemical analyses and event-by-event fragment-detection experiments. The event-by-event measurements may be broadly separated into different categories according to the technique used to obtain the fragment mass A : 2E measurements, in which both fission fragment energies are measured; 2v measurements, in which time-of-flight measurements are made for both fragments; Ev measurements, in which the energy and the time-of-flight are measured for one fragment and the other fragment is typically undetected; mass-separator measurements (such as those performed using the Lohengrin [146, 147] setup), in which mass, energy and charge-state distributions are obtained for one fragment.
These approaches have their own strengths and limitations. Since the parent fissioning nucleus has effectively zero momentum in the lab frame, either the measurement of two energies or two velocities gives the experimentalist the mass ratio of the fragments. In the 2E and 2v approaches, the energies and velocities are measured post neutron-emission, placing limitations on the accuracy due to the assumptions that must be made about the prompt neutrons. The 2E method suffers the most; with velocity measurements it can be assumed that the neutron emission is isotropic in the centre-of-mass frame such that on average the velocities are unchanged [148]. However, the 2E approach has an advantage in that it can be performed in very close geometry with a windowless double-gridded ion chamber, yielding good energy resolution, high efficiency and angular distributions [149], but nevertheless it does not give atomic number sensitivity, due to uncertainty over the fragment velocities. Mass spectrometers and Ev devices do not make assumptions about neutron evaporation. However, since these measurements are made on one fragment only there is no direct handle on the number of neutrons evaporated in a given event. Also, while Lohengrin gives unsurpassed mass resolution, the relatively small solid angle requires the use of very high fission rates in the target. This, and the prohibitively long (few microseconds) flight-time, prevents the use of \(\gamma \)-ray detectors close to the target in experiments that measure the correlation between prompt \(\gamma \) radiation and the mass and kinetic energy of the fission product; isomeric\(\gamma \)-rays may of course be studied at the spectrometer focal plane. None of the above event-by-event methodologies make a direct measurement of the atomic number Z of either of the fission fragments, to which, by contrast, radiochemical measurements are sensitive.
The STEFF spectrometer, shown in Fig. 24, is a 2E2v device with Z sensitivity, i.e. it measures the energy and time-of-flight of both fission fragments to obtain A (to ±4 u), in addition to the specific energy loss of the fragments in isobutane (for Z determination to an accuracy of around 1%). The measurement of the kinetic energy for both fragments allows for the determination of the fragment excitation energy \(E^{\star }\) distribution and the segmentation of the anodes allows for measurement of the direction \((\theta ,\phi )\) of the fission axis (to an accuracy of \(\pm 2^{\circ }\)). The \(\gamma \)-ray detection is performed in an array of 12 NaI scintillators around the target that may be augmented (or replaced) by faster detectors, such as LaBr\(_3\) scintillators. In the n_TOF programme the array of scintillators is used to make measurements of the \(\gamma \)-ray total energy spectrum and \(\gamma \)-ray multiplicities in conjunction with the measurement of \(A,Z,E,\theta ,\phi \mathrm{\,and\,}E^{\star }\) of the fission fragments. This allows one to perform a complete analysis of the fission process to within the above-mentioned resolution of STEFF.
The STEFF device in the new configuration for EAR-2 shown as a section in a vertical plane through the centre-line of the spectrometer. The neutron beam travels from bottom to top in the figure. The TOF arms contain the START detector and two STOP detectors. The short arms have STOP detectors (MCP1 and MCP2) but no STARTs
The motivation for studying a large set of parameters of the fission process in one experiment lies in the ability to address correlations of relevance to the fission mechanism and to better determine nuclear data of relevance to the nuclear industry. The array of scintillators, labelled in Figs. 24 and 25, together with the capability to measure the contributions of prompt neutrons and prompt \(\gamma \)-rays by time-of-flight, allow one to determine \(\gamma \)-ray multiplicity and energy distributions as a function of the fragment mass. The prompt \(\gamma \)-ray distributions are of significant importance to the development of fast reactors. About \(10\%\) of the total energy released in the reactor core is in the form of \(\gamma \)-radiation. Of this contribution, \(40\%\) is emitted before \(\beta \)-decay and \(30\%\) comes from the later decay of the fission products. Since the other sources of \(\gamma \)-radiation (radiative capture and inelastic scattering reactions) are smaller in their contribution and considered to be better known, the details of the prompt flash is the major uncertainty in calculating the \(\gamma \)-heating in a reactor. In a fast reactor, the \(\gamma \)-heating of the fuel-free assemblies is significant, due to the relatively easy propagation of the \(\gamma \)-radiation and is a major contribution to the total energy release in uranium oxide or mixed-oxide cores. Much of the data that contribute to current nuclear data libraries regarding the total \(\gamma \)-ray energy, multiplicity and spectrum shape dates from the early 1970s (e.g. Refs. [150,151,152]) and shows significant variations (on the level of \(15\%\) in the measured total energy). The NEA high-priority request list has prompted recent experiments to address these uncertainties, e.g. Refs. [153, 154].
Figures 24 and 25 show STEFF installed at the EAR-2 station with the large collimator which offers the maximum neutron flux at n_TOF currently. In a measurement, the target is angled with respect to the beam axis, so that the beam spot fully covers the fissionable material and the effective thickness to the various fragment detectors is minimised in order to reduce straggling within the target; for a typical target of 5–8 cm diameter this results in an optimum angle of 20\(^{\circ }\)–50\(^{\circ }\) to the vertical. STEFF has thus far been used to measure neutron-induced fission on \(^{235}\)U[155] and \(^{239}\)Pu with an 8 cm diameter 100 \(\upmu \)g/cm\(^{2}\) and 5 cm diameter 30 \(\upmu \)g/cm\(^{2}\) target, respectively. The \(^{235}\)U measurement can be considered typical and representative of the various detector capabilities. For this setup, a binary fission rate is measured in Braggs 1 and 2 of \(\sim \)0.5 events per neutron pulse with 2E and 2v information with a further five fission events per neutron pulse detected without velocity information. This is as expected from the total fragment acceptance detection solid angle of 0.134 sr combined with the intrinsic start-stop efficiency of 50%. A typical STEFF experiment at n_TOF receives 0.5\(\,\times \,10^{6}\) pulses and thus a total of over 10\(^6\) fission events are recorded with around 10% of events with full 2E2v information. Fission events are recorded for the full range of neutron energies available at n_TOF EAR-2, however, some of the detectors are unable to measure the most energetic neutrons due to being blinded by the \(\gamma \)-flash and interaction of the most energetic neutrons with the counting gas and internals of the detectors. The gas ionisation chambers are situated far from the beam centre, therefore are almost completely unaffected by the \(\gamma \)-flash and thus can detect fission fragments at all available neutron energies at EAR-2. The timing detectors are only able to detect fragments after the \(\gamma \)-flash signal and for these, the start detector is the limiting factor which is able to detect fission up to neutron energies of \(\sim \)30 MeV, covering a range still very suitable for technological applications. Digital traces are shown in Fig. 26 where correlated timing and energy signals from a single fission event are apparent. In this example event, an MCP start signal and MWPC stop signal are recorded \(\sim \)80 ns apart, corresponding to the fragment time-of-flight and the fragment energy is recorded in the amplitude of the ionisation chamber anode and Frisch-grid signals.
Digital traces for the Start, Stop and Bragg detectors on the main axis of STEFF for a single fission event. The fragment velocity and energy can be extracted allowing determination of the fragment mass. The rising edge of the anode signal can be used to determine the range of the fragment in the gas, and the differential energy loss \(\frac{\mathrm {d}E}{\mathrm {d}x}\), both of which depend on the atomic number of the fragment
The prompt \(\gamma \)-ray information from fission is measured by the array of scintillators which suffer from the large neutron and \(\gamma \) background present in EAR-2; here they are saturated well beyond the \(\gamma \)-flash and are limited to below \(\sim \)100 keV neutron energies. Here, the signal to background rate is still extremely low (0.001), however, the time of each fission event is determined with \(\sim \)600 ps resolution, therefore coincidence timing gates allow prompt fission \(\gamma \)-rays to be clearly identified. The typical raw experimental observables from a STEFF measurement are shown in Fig. 27 collected over a period of 12 h. Analytical techniques and procedures are then applied to extract the nuclear data associated with these observables.
Various experimental observables from STEFF, here taken from the \(^{235}\)U measurement: a fission fragment time-of-flight vs energy; b fission rate compared with calculation based on the known EAR-2 neutron flux; c\(\varDelta T_{\gamma F}\) distribution of time-of-flight of \(\gamma \)-rays (and fast fission-neutrons) from the target to the NaI scintillators.; d background-subtracted deposited energy in the LaBr\(_{3}\) within the fission timing peak
4.5 The fission-tagging setup
A new fission detector was recently developed at n_TOF for measurements of the neutron capture cross sections of actinides in conjunction with the total absorption calorimeter (TAC) [156]. When measuring fissile isotopes with a large fission-to-capture ratio, fission \(\gamma \)-rays produce a large background underneath the capture \(\gamma \)-ray spectrum that may be extremely difficult to disentangle. One possibility in this case is to mount the samples inside a highly efficient fission detector, so as to identify fission events and reject the corresponding fission \(\gamma \)-rays on an event-by-event basis. This technique, called “fission tagging”, can also be used to measure the capture-to-fission ratio of major actinides, an important quantity for reactor technology.
For an efficient tagging of the fission \(\gamma \)-rays, a compact, multi-stack fission detector has been developed, that fits inside the n_TOF total absorption calorimeter, the 4\(\pi \) BaF\(_2\) detector system permanently installed in EAR-1 (Fig. 7). A first measurement had been performed in the past with a detector based on microbulk micromegas technology [135, 136]. The technique proved to be reliable and capable of producing high quality data on the capture-to-fission cross section ratios [157, 158]. However, the copper present in the electrodes produced a large background that prevented us from measuring capture cross sections with sufficient accuracy above a few hundreds of eV neutron energy [159, 160].
The development of a new fission chamber focussed on different points: compact design, fast and heavy ionising gas and optimised electronics to ensure unambiguous \(\alpha \)-particle/fission fragment discrimination; very low mass of structural material to avoid neutron scattering background as well as parasitic reactions; and finally, a reasonable amount of sample material, so as to obtain sufficient statistics in a reasonable time. This development was based on an existing setup [161] adapted to fulfil all requirements mentioned above.
The resulting detector [162] is a compact multi-plate fission chamber containing two stacks of axial ionisation cells. Figure 28 shows a CAD drawing (left) and a picture (right) of the chamber. The housing is made of a tube of 1.5 mm thick aluminium with an outer diameter of 66 mm and a length of 78 mm. Two stacks of 4 anodes and 7 cathodes each are mounted inside the housing.
The stacks are directly attached to their respective motherboards hosting, outside the aluminium housing, the preamplifiers and shapers, developed at CEA Bruyères-le-Châtel [162]. In order to reduce the amount of in-beam material, thus limiting the neutron scattering, the anodes and cathodes were made out of aluminium with thicknesses of 20 and 10 \(\upmu \)m, respectively. Those thicknesses ensure that \(\alpha \)-crossing between the different ionising cells is avoided. A potential difference of 420 V is applied between the electrodes, with a 3 mm wide inter-electrode gap. Special aluminium flanges are mounted on the chamber to hold the gas feed-throughs, while another pair of flanges support 25 \(\upmu \)m thick aluminised Kapton windows along the neutron beam direction that isolate the chamber from the vacuum beam pipe and create a Faraday cage.
The internal diameter of all parts of the chamber is at least 50 mm, in order not to interfere with the neutron beam whose dimension (for the so-called “capture” collimator) is \(\sim \)30 mm at the TAC location. Tetrafluoromethane (CF\(_4\)) was chosen as ionising gas, since it has been proven that it fulfils the specifications of the n_TOF measurements [161].
Typical signals resulting from such a setup are shown in Fig. 29. A rise-time from 10 to 90% of the peak of 16 ns and a signal duration (FWHM) of about 30 ns have been measured for fission events. This excellent timing performance significantly reduces \(\alpha \)-pile-up in case of highly radioactive samples (up to about 1 MBq per sample) allowing one to unambiguously discriminate \(\alpha \)-particle from fission fragment events by achieving a very high fission detection efficiency (up to about 87%). More details can be found in Ref. [163].
Typical signals associated with the fission-tagging chamber, taken from the n_TOF event display. Top: raw anode signals in a 20 \(\upmu \)s time window containing the \(\gamma \)-flash. Middle: Derivative of the raw signal. Bottom: zoom of the raw signals on a \(\sim \)2 \(\upmu \)s time window. Insert: zoom on a fission signal after baseline removal and signal inversion
The first fissile isotope studied with the new detection system is \(^{233}\)U [163]. The nearly finalised analysis of the data from this experiment proved that it was successful and it is planned to extend its use to similar studies.
4.6 Recoil-proton telescopes for quasi-absolute fission measurements
The normalisation of neutron-induced fission cross section experimental data usually relies on a reference or standard reaction. The reaction most commonly used for this purpose is \(^{235}\)U(n,f), whose cross section is a standard at thermal neutron energy (0.025 eV) and between 0.15 and 200 MeV [42, 117]. However, despite its widespread use in the high-energy range, between 20 and 200 MeV the recommended \(^{235}\)U(n,f) cross section is based on two measurements only [44, 164]. Above this energy, the situation is even worse, as no data exist, and evaluations rely on theoretical estimates. Hence, there is a clear and long-standing demand from the International Atomic Energy Agency (IAEA) to improve this situation between 20 MeV and 1 GeV[165].
The \(^{235}\)U(n,f) cross section is mostly determined, below 1 MeV, relative to non-fission reference cross sections, such as \(^{6}\)Li(n,t) and \(^{10}\)B(n,\(\alpha \)). Above this energy, the primary and most important reference cross section is the neutron–proton (n–p) elastic scattering. Below the pion production threshold, the non-elastic cross section for interaction of neutrons with protons is very small. Hence, the differential n–p scattering cross section can be determined from a measurement of a relative angular distribution and the total cross section, which is typically considered a “primary” standard (up to 350 MeV) [165]. For this reason, measurements of fission cross sections relative to the differential n-p scattering cross section are termed “quasi-absolute”.
In such measurements, setups based on recoil-proton telescopes (RPTs) [166] are used to measure the fluence (or intensity) of a neutron beam impinging on a hydrogenous sample, also called “proton radiator”. The energy of the recoil-proton emitted at a given angle is directly related to the energy \(E_\mathrm {n}\) of the incident neutron, so that for monoenergetic neutrons the recoil-proton energy distribution displays an isolated prominent peak that allows one to easily discriminate n-p scattering events from the background, provided that recoil protons are fully stopped in the RPT. At the same time, fission events are counted by detecting fission fragments emitted from a fissile deposit, mounted inside a detector (for example an ionisation chamber) placed in the neutron beam together with the proton radiator. In this case, the fission cross section can be simply obtained from the ratio of the number of detected fission and recoil-proton events, and from the differential n-p cross section, according to the following expression:
Here \(C_\mathrm {f}\) and \(C_\mathrm {p}\) are the number of detected fission and recoil-proton events, respectively, \(\varOmega _\mathrm {p}\) denotes the solid angle covered by the recoil-proton telescope and \(\epsilon _\mathrm {p}\) and \(\epsilon _\mathrm {f}\) are the detection efficiencies for recoil protons and fission fragments, respectively, both usually very close to unity. Finally, \(n_\mathrm {H}\) and \(n_\mathrm {F}\) represent the number of hydrogen and fissile atoms per unit area, respectively, and d\(\sigma \)/d\(\varOmega _\mathrm {p}\) is the differential cross section for the emission of a recoil proton at the laboratory angle \(\theta _\mathrm {p}\). It is important to remark that the number of hydrogen atoms per unit area can be determined to better than 1% by dimensional measurements, weighing and combustion analysis [167].
The energy distribution of the neutron beam in EAR-1 extends to several hundreds of MeV, a feature that finally allows the determination of the quasi-absolute cross section of the \(^{235}\)U(n,f) cross section at high energy. The measurement, however, presents several challenging aspects that need to be addressed. The main one is related to the presence of relativistic particles and \(\gamma \)-rays from spallation reactions in the beam. These particles produce a strong prompt signal in all detectors, the so-called \(\gamma \)-flash. The second challenge is the very large range of charged particles produced by neutron interactions. As a consequence, in contrast to RPTs designed for neutron energies below 20 MeV, the detectors of a recoil-proton telescope at n_TOF must be positioned outside the neutron beam, and consist of several detectors to allow a clear identification of recoil protons emitted from the radiator and their discrimination from other spurious neutron-induced events, in particular on carbon contained in hydrogenous sample materials, such as polyethylene (CH\(_2\)). Charged-particle discrimination based on the \(\varDelta E-E\) technique is used to identify and suppress deuteron and \(\alpha \)-particles produced in the sample by \(^{12}\)C(n,dx) and \(^{12}\)C(n,\(\alpha \)x) reactions. On the contrary, the background related to the \(^{12}\)C(n,px) reactions cannot completely be discriminated from recoil protons, and must therefore be measured and subtracted using pure carbon samples. The influence of this background can nevertheless be reduced by selecting a small proton emission angle, where the energy of recoil protons is higher than that of protons from the n+\(^{12}\)C reaction. In this case the background can be discriminated based on the total recorded energy, provided that the recoil protons are fully stopped in the telescope. Another important source of background is related to neutrons scattered from the sample and inducing (n,p) reactions in the detector material or support structures.
The most critical aspect for the uncertainty level to be reached with the n_TOF RPTs is the definition of the solid angle \(\varOmega _\mathrm {p}\). Up to neutron energies of about 50 MeV, this could be achieved by selecting the recoil-proton angle with a collimator made from a high-Z metal such as tantalum. At higher energies, however, this is no longer practical because of the increasing importance of grey-edge effects, i.e. the leaking of charged particles through the edge of the aperture. For this reason, the solid angle of the RPTs designed for n_TOF is defined actively by the size of one of the detectors in the telescope arrangement, or by the full telescope made of detectors of trapezoidal shape (as shown later). Another important feature of a recoil-proton telescope regards its energy resolution, i.e. the width of the recoil-proton peak for a given neutron energy. At n_TOF, the resolution is determined by the kinematical broadening of the recoil-proton energy distribution due to the finite range of proton emission angles accepted by the RPT, as well as by the energy loss of the recoil protons in a sample of finite thickness. To optimise the resolution, several neutron energy ranges were defined and for each of them the thickness of the sample was selected so that the two broadening mechanisms were of equal importance.
As already mentioned, one of the key issues in the quasi-absolute measurement of the \(^{235}\)U(n,f) cross section at n_TOF is the presence of an intense \(\gamma \)-flash, a prompt signal with a tail extending to long times that can prevent from measuring at high neutron energies. Therefore, the measurement requires an RPT design based on detectors with low photon sensitivity and excellent timing properties. The latter property is also required for a good time resolution and to minimise the probability of signal pile-up. In particular, the detector signal must exhibit very fast rise and decay times. To this end, the RPTs to be used at n_TOF were constructed from low-Z detector materials, i.e. fast plastic scintillators and thin silicon diodes. The drawback in the use of low density materials is that it limits the neutron energy up to which recoil protons can be stopped within a reasonable detector thickness and an isolated recoil peak can be clearly identified.
Drawing of the setup used at n_TOF for the quasi-absolute measurement of the \(^{235}\)U(n,f) cross section. Fission reactions are measured with a fission chamber and a set of Parallel Plate Avalanche Counters (described in Sect. 4.2). Recoil protons are detected and identified in three different telescopes (two of which of identical design), placed at a small angle outside the neutron beam. Polyethylene and pure carbon samples of various thickness are used in the measurement
To address the various issues described above, two RPTs were built at n_TOF following slightly different design guidelines. The RPTs can be used simultaneously with radiators of different thickness, leading to a more efficient use of the neutron beam. The diversity of the designs also helps to reduce systematic uncertainties in the measurements.
One of the two devices, indicated in Fig. 30 as RPT-INFN (since it was designed and built by the INFN group) has a compact design [168]. It is made of four scintillators and two silicon detectors operated in coincidence and grouped together to form a trapezoidal shape 16 cm long and with an increasing transverse size, from 3\(\,\times \,\)3 cm\(^{2}\) to 7.2\(\,\times \,\)7.2 cm\(^{2}\), in order to cover a fixed solid angle relative to the target centre. Two silicon pad detectors 300 \(\upmu \)m thick are used as the first \(\varDelta E\) element for protons of a few tens of MeV. They are encapsulated inside a box with thin aluminium foils as entrance and exit windows. Following the silicon detectors, the other four elements are made of BC408 fast plastic scintillators with a light decay time of 2.1 ns and with increasing thickness (except for the last two) of 0.5, 3, 6 and 6 cm. Each scintillator is coupled to a 1” Hamamatsu R1924A Photomultiplier by means of optical glue, except for the first scintillator, where two PMTs are coupled on opposite sides of the detector by means of suitable light-guides. The mechanical support of the telescope is a light Al structure, so as to keep the background produced by scattered neutrons as low as possible. Thanks to the specially designed voltage divider, the width of the output pulses is kept below 30 ns. Considering the very fast response of the scintillators, the telescope is able to identify events generated by neutrons arriving as close as 80 ns after the \(\gamma \)-flash, corresponding to an energy of \(\sim \)1 GeV.
Depending on the energy of the particles entering the telescope, different elements of the telescope are involved. Low-energy protons up to about 10 MeV are stopped and identified by means of the silicon detectors and, as the energy increases, by the first scintillator. The range from 10 MeV to 1 GeV neutron energy is covered by two to four scintillators in coincidence, acting either as a \(\varDelta E\) or stopping detector, for particle identification and suppression of the background from \(\gamma \)-rays and \(^{12}\)C(n,charged particle) reactions. The maximum energy lost by protons in the whole telescope is approximately 150 MeV, so that above that energy the telescope operates in transmission. Two identical telescopes with the design described above were built for n_TOF in order to measure the n-p scattering at different angles and increase the statistics, as well as to minimise systematic uncertainties related to the angular position.
The second RPT concept, specifically designed and built for n_TOF by the group from PTB (thus indicated in Fig. 30 as RPT-PTB), consists of three discrete detectors. As shown in the figure, the two \(\varDelta E\) detectors are separated by about 150 mm. They consist of a square EJ204 plastic scintillator, 45\(\,\times \,\)45 mm (\(\varDelta E_1\)) and 38\(\,\times \,\)38 mm (\(\varDelta E_2\)) in size, respectively. The first detector is positioned at a distance of 200 mm from the sample. The thickness of the detectors is adapted to the neutron energy range to be covered and varies between 0.5 and 5 mm. The third E detector, acting as stopping element is a cylindrical EJ204 scintillator with a diameter of 80 mm and lengths of 50 mm, 100 mm or 150 mm, positioned 50 mm behind the \(\varDelta E_2\) detector. The use of the thickest E detector allows one to stop recoil protons up to 150 MeV energy. The \(\varDelta E\) detectors are enclosed in housings with 0.1 mm aluminium walls covered with a diffuse white reflector on the inside and coupled via an air gap and a small Lucite light-guide to XP2020Q photomultipliers (PMTs). Due to the diffuse reflector the inhomogeneity of the light collection is less than 10%. The envelope and the front side of the cylindrical E detectors are also covered with a white diffuse reflector and coupled to XP2020 PMTs via conical light-guides. In the RPT data analysis, a triple coincidence is required, with the effective solid angle determined by the middle (\(\varDelta E_2\)) detector, which has the smallest transverse dimensions of all three detectors. The \(\varDelta E_1\) and the E detector are larger to ensure that all charged particles originating from the sample and passing through the middle detector also produce signals in the first and last detectors. The diameter of the E detectors is also sufficiently large to limit incomplete energy deposition to a tolerable level, thus avoiding “tails” in the shape of the recoil peak. The elongated design of this RPT results in a directional sensitivity of the telescope to events originating from the sample, suppressing background events originating elsewhere.
The three recoil-proton telescopes were mounted in EAR-1 together with a fission ionisation chamber and a set of Parallel Plate Avalanche Counters, both equipped with \(^{235}\)U samples, for the measurements of the fission reactions, and the setup was tested in the n_TOF neutron beam to verify its predicted performances. Figure 31 shows a picture of the whole assembly, mounted along the neutron beam in EAR-1. The test proved that both RPT concepts were adequate for the measurement of recoil protons up to several hundreds of MeV, thus opening the way to a first-of-a-kind measurement of the quasi-absolute \(^{235}\)U(n,f) cross section up to 1 GeV neutron energy. A complete measurement was performed at the end of the 2018 measurement campaign and the data are now being analysed. One of the main issues that has to be addressed is that the effective solid angle and efficiency of the RPTs is influenced by the geometry of the instrument as well as by the transport of the recoil protons in the sample and in the various elements of the device. For high-accuracy results, it is important that all these effects be estimated and suitably considered in the analysis, together with the residual background contributions, in particular the one produced by neutrons scattered from the sample and inducing n-p reactions in the telescope itself. To this purpose, one has to rely on detailed Monte Carlo simulations of the setup. Considering the complexity of the setup and the variety of neutron interactions with the sample, detectors and support structures, reliable simulations are of fundamental importance in this measurement for obtaining accurate results. A software replica of the setup was implemented in two of the major radiation transport codes, MCNPX and GEANT4, and simulations were performed starting with the neutron beam impinging on the samples. More details on the setup and on the related Monte Carlo simulations will be reported in an upcoming paper.
4.7 Sample preparation
A major challenge for successful fission experiments is to have samples with the right amount of material of interest on appropriate substrates and with a minimum energy loss of the reaction products when passing through the deposit and the substrate. These kinds of targets are typically produced by evaporative deposition or molecular plating on mechanically stable substrates which are as thin as reasonably possible and which do not undergo any nuclear reaction leading to products that interfere with the measurement.
The principle of evaporative deposition is to heat the source material in vacuum in order to increase the vapour pressure by allowing atoms or molecules to go into the vapour phase and subsequently condense as a thin film on a substrate. The heating of the source material is realised by resistance heating of a crucible or by means of an electron beam for materials requiring higher temperatures. A mask is positioned directly in front of the substrate and determines the spot area. The distance between the source material and the substrate determines the yield of the process and the homogeneity of the thin film. During the deposition process the film thickness can be monitored with a quartz crystal microbalance [169,170,171]. Prior to the vapour deposition, the substrate can be cleaned in situ with plasma generated e.g. by a glow discharge module. The substrate can also be heated during and after the deposition process by quartz lamps [172]. Vapour deposition on heat-sensitive substrates like thin plastic foils is preferably done by resistance heating to avoid too high temperatures during the process and damage of the foils. In that case, the original oxide material, like for example U\(_3\)O\(_8\), first needs to be converted into UF\(_4\), which has a lower sublimation temperature [173]. Figure 32 shows a boron layer prepared by electron beam physical vapour deposition. The areal density is 22 \(\upmu \)g/cm\(^2\) and the deposit has a diameter of 80 mm. The substrate is a 0.03 mm thick aluminised mylar foil glued onto an aluminium ring. The target has been produced for monitoring the neutron fluence during cross section measurements at n_TOF.
Thin films prepared by evaporative deposition are homogeneous smooth deposits [171]. Because of a possible difference in travelling distance of the evaporated atoms or molecules, a variation of the areal density between the centre and the edge of the deposit is likely and more pronounced for large areas deposited in close proximity to the evaporation source. Homogeneity measurements of 70 mm diameter deposits prepared by evaporative deposition showed a decrease of the areal density of \(\sim \)5% between the centre and the edge of the deposits. Target substrates with a diameter of 84 mm were placed on rotating holders that can simultaneously accommodate three substrates at a distance of 195 mm from the source material [174]. The drawback of evaporative deposition is the very low deposition yield and the expensive equipment.
A boron layer with an areal density of 22 \(\upmu \)g/cm\(^2\) and a diameter of 80 mm prepared by electron beam physical vapour deposition on a 0.03 mm thick aluminised mylar foil (the latter produced at CEA Saclay) glued on an aluminium ring with the mask, which determines the requested spot area, still positioned in front of the substrate
The molecular plating technique consists in the cathodic deposition of the source material onto an electrically conductive substrate in an organic solution like isopropanol [169, 175, 176] or isobutanol [177]. This technique is performed in a molecular plating cell designed according to the required dimensions of the substrate and the deposit. A mask is positioned in front of the substrate and determines the spot area. Figure 33 shows a cross section and a picture of the molecular plating cell designed and produced at JRC-Geel. The use of an organic solution minimises the current density during the plating process and minimises the production of H\(_2\) on the surface of the substrate (acting as cathode), which can disturb the deposition process [171, 175, 176]. Therefore, the actinide dissolved in low-molarity nitric acid is also added by small aliquots. Figure 34 shows a \(^{233}\)U layer prepared by molecular plating. The areal density is 220 \(\upmu \)g/cm\(^2\) and the deposit has a diameter of 40 mm. The substrate is a 0.01 mm thick aluminium foil glued onto an aluminium ring. A set of 14 similar targets has been produced and mounted in a compact multi-plate fission chamber for the simultaneous measurement of \(^{233}\)U capture and fission cross sections at CERN n_TOF [162], as described in Sect. 4.5.
Layers prepared by molecular plating are uniform deposits, but are not as smooth as the ones prepared by evaporative deposition. They can have a maze like pattern [171] or can display cracks [178]. The distribution of the deposited material depends on several parameters of the molecular plating process, the material to be deposited and the spot area. An increase of the amount of material of about 7–10% on the border of the deposit with respect to the centre was observed for targets with a diameter of 30 mm [179]. Up to now the chemical plating process itself and the composition of the deposit are not well known. The plated layer also contains organic solvent electrolysis products, besides the material under investigation [171]. The big advantage of this method is the high deposition yield, in the range of 75% up to 95% and the capability to produce layers with an areal density of up to 1000 \(\upmu \)g/cm\(^2\). The technique is widely applied, especially for target preparation of precious material.
If the actinide material contains a daughter nuclide that would interfere with the characterisation of the target or with the nuclide under investigation, the material is purified prior to the deposition on a substrate. The purification of the mother solution is performed by ion exchange [175, 177]. It is advisable to apply the deposition techniques in different setups dedicated to each material to avoid cross-contamination. According to radiation safety rules and regulations, the radiochemistry and deposition processes of actinides are performed in a glove box in a nuclear controlled area.
The choice of the substrate is made as a function of the experiment, the target preparation technique and the available substrate materials. In general the substrate needs to be as thin as possible, mechanically stable during and after the deposition process, during the transport, during the experiment and may not contain material that takes part in a nuclear reaction resulting in products that disturb the experiment. Typical substrates are made of aluminium [169], occasionally with a 50 nm titanium layer [177], with a thickness in the \(\upmu \)m range glued onto a frame. While molecular plating requires a conductive substrate, evaporative deposition can be performed on plastic foils like mylar and polyimide foils [170]. The latter are produced by in situ polymerisation at JRC-Geel with a typical areal density of 35 \(\upmu \)g/cm\(^2\) [180].
Another challenge for a successful fission experiment is to have well-characterised targets. In general, the areal density of the nuclide under investigation is determined along with the presence of contaminants and impurities which can influence the measurement and the homogeneity of the target, as far as possible. For stable deposits the areal density is calculated from the mass of the deposit which is determined by accurate difference weighing applying the substitution method and corrected for the isotopic abundance and impurities as provided by the supplier, and from the area of the deposit given by the inner diameter of the mask used during the deposition [169]. The hydrogen content of tristearin targets, for example, can be measured by combustion analysis [167].
For actinide layers the areal density of a specific radionuclide is calculated from the mass derived from the total activity measured by \(\alpha \)-particle counting in a low-efficiency counting geometry and corrected for isotopic abundance determined by mass spectrometry and from the area derived from the inner diameter of the mask in front of the substrate during the deposition process [169]. The homogeneity is measured by scanning the target with a diaphragm with an \(\alpha \)-particle counter [174] or by autoradiographic imaging [181]. The thickness of the metal foils is taken from the supplier. The areal density of the polyimide foils is measured by visible light spectrophotometry in light transmission mode [180]. In some cases, in particular for \(^{235}\)U, \(^{238}\)U, \(^{237}\)Np, \(^{209}\)Bi and \(^\mathrm {nat}\)Pb, the characterisation of the samples has also been performed by means of Rutherford back-scattering (RBS), that allows one to assess the content of light elements, as well as of the element of interest when it is stable (as in the case of Pb and Bi).
4.8 Data acquisition system
The data acquisition system used for the Phase-I and Phase-II campaigns was based on Acquiris (later Agilent) 8-bit flash-ADCs with a sampling rate of up to 1 GHz and an 8 Mb memory limit of the internal buffer. Fast electronics are of major importance at n_TOF in order to resolve short times-of-flight and high counting rates in the various detector setups. The trigger signal for the start of the data acquisition is given by a beam current transformer (BCT) from the PS and corresponds to the arrival of a proton pulse that hits the spallation target. The full output signal from the start time is recorded during a time window limited by the on-board internal memory within the range of 100 \(\upmu \)s to 200 ms which, for the 185 m flight-path, corresponds to neutron energies down to 20 keV and 4 meV, respectively. The first signal to be recorded is the so-called \(\gamma \)-flash generated by the impact of the proton pulse on the spallation target. This signal serves for the accurate determination of the neutron time-of-flight. Complementary information on each recorded signal is also stored, such as the detector number, the bunch number, the type of proton bunch, i.e. “dedicated” (nominal intensity) or “parasitic” (low intensity, about half of the nominal), and the proton bunch intensity, provided by the PS accelerator beam information system. An event display program allows the raw data files to be read and the digitised signals from all detectors to be visualised.
In order to reduce the amount of data to store and process, a zero-suppression algorithm is applied to select only fragments of data with useful signals. After the digitisation of the analogue detector output, the raw data are temporarily saved on a local disk and later transferred to the CERN Central Advanced STORage System (CASTOR) [182] for subsequent off-line analysis (see Sect. 5.1). More details on the n_TOF DAQ system can be found in Ref. [183].
For the Phase-III campaign an upgraded data acquisition system was developed, based on SP Devices digitisers which offer high sampling rates in the 14–1800 MHz range, a resolution between 8 and 14 bits and a total acquisition time up to 100 ms. In conjunction with the larger buffer memory, this has considerably increased the time-of-flight range that can be recorded at high sampling rates, which now extends down to thermal neutron energies.
5 Data analysis
While the rather unique features of the n_TOF neutron beam and the high-performance detection and DAQ systems allow to collect high quality data, a large effort is required to extract high-accuracy results on neutron-induced fission from the raw signals. This procedure involves several steps, from signal identification and reconstruction, needed to extract related information such as signal amplitude, time-of-flight etc., to the study of the detector response and interaction with the neutron beam that often relies on detailed Monte Carlo simulations of the neutron beam and of the experimental setup, and finally to a series of important corrections, such as the dead-time correction (related to the problem of signal pile-up), particularly severe in EAR-2.
In this section, the various steps of the data reduction and analysis are presented and discussed, with particular emphasis on the new techniques specifically developed at n_TOF to address certain important issues that could hinder the attainment of high-accuracy fission results.
5.1 Pulse-shape analysis
A general-purpose pulse-shape analysis (PSA) framework was developed and adopted at n_TOF. Its most notable feature is the implementation of the most generic and versatile PSA routines, relying on the least amount of assumptions about the specific nature of the input signals, thus aiming at being applicable to a wide range of detectors [184]. The functionality of this framework is adapted to a specific detector by adjusting a set of user-provided external input parameters. The basic procedures include the pulse identification, \(\gamma \)-flash recognition (since this signal is used as a physical start for the time-of-flight technique at n_TOF), baseline calculation, noise suppression and the extraction of the physical parameters of the identified pulses (amplitude, area, polarity, width, time-of-arrival etc.). The PSA code includes several advanced routines that users may activate for specific detectors, making the entire signal analysis procedure highly sophisticated, versatile and adjustable. Although the adopted PSA framework relies on a wide variety of well-established procedures, it also features many innovative solutions, such as the particularly robust pulse recognition technique. The computational efficiency of the adopted procedures is among the most important characteristics of the PSA framework—certainly being the most important consideration during their implementation. As the digitised data streams from the n_TOF Data Acquisition System may reach the size of \(\sim \)10\(^8\) samples per detector per proton pulse, the computational efficiency was the mandatory requirement to be met in order for the data to be analysed within a reasonable time. Already the \(\mathcal {O}(N^2)\) computational complexity – N being the number of samples in the stream – was entirely unacceptable to this end. Thus, all the adopted procedures were optimised so as to reduce their complexity to the \(\mathcal {O}(N)\) or, at worst, to the \(\mathcal {O}(N\log N)\) level. The most prominent technical details on the PSA framework may be found in Ref. [184].
The PSA code was written as a general-purpose framework that could meet widely varying needs from many different detector types. In this respect, such a development has greatly benefited from, and has been of advantage for, the fission programme at n_TOF, considering the variety of specific challenges posed by the fission detectors, in particular the Micromegas chambers, such as slightly bipolar pulses, a high frequency noise resembling true signals, an intense response to the initial \(\gamma \)-flash heavily distorting the baseline at larger time-of-flights etc.
Figures 35 and 36 show several aspects of signals from two different configurations of the Micromegas detectors in terms of internal amplification gain. In particular, Fig. 35 shows the response of a detector operated at high gain, while Fig. 36 refers to a Micromegas detector with low gain, as typically used in fission measurements. The figures illustrate some of the most prominent PSA features, including the adaptive baseline calculation, \(\gamma \)-flash handling and the powerful pulse-shape fitting capabilities. The top panel in Fig. 35 presents the baseline recovered by the adaptive baseline procedure in the vicinity of an intense, detector-blinding pulse caused by the initial \(\gamma \)-flash preceding the arrival of the neutron beam and of the corresponding pulses. The bottom panel shows the powerful pulse-shape fitting capabilities in rejecting the noise. The displayed ringing signal is a noise picked-up during that particular measurement, with individual oscillations resembling real signals in width and shape. However, real pulses feature a lower rebound, which may be used for their discrimination from noise fluctuations. In this panel each oscillation was first recognised as a potential signal and a fitting to the externally delivered numerical pulse shape (shown by a single surviving fit) was attempted. Based on a quantity similar to a reduced \(\chi ^2\) (see Ref. [184] for details) the fits to the “false” pulses were rejected and only a single one was retained for further analysis.
Example of signals recorded with a Micromegas detector operated at high gain (used for neutron beam monitoring at n_TOF). The top panel shows the adaptive baseline procedure applied to the signal heavily distorted by an intense (and saturated) \(\gamma \)-flash. The bottom panel shows the powerful noise rejection capabilities based on the pulse-shape fitting, i.e. on the agreement between the actual and the fitted pulses
In the waveform shown in Fig. 35 (detector at high gain), it is practically impossible for the PSA routine to reproduce the \(\gamma \)-flash signal, often saturated and characterised by large oscillations. On the contrary, Micromegas detectors operated at low gain, such as those commonly used for fission measurements, exhibit a remarkably consistent response to the initial \(\gamma \)-flash signal, as shown in Fig. 36. In this case one can identify a separate pulse shape corresponding to an average baseline distortion caused by the \(\gamma \)-flash and use a special instance of the pulse-shape fitting (applied only to the initial part of the stream where the \(\gamma \)-flash is recorded) to identify and remove this distortion from the overall signal. The top panel of Fig. 36 shows this average distortion adjusted to the signal induced by the \(\gamma \)-flash, clearly revealing the true pulses rising above the baseline, thus allowing for access to short times-of-flight, i.e. to the high neutron energy region. The bottom panel shows a signal remaining after the subtraction of the \(\gamma \)-flash distortion, to which a regular pulse-shape fitting procedure is applied, successfully recovering the individual pulses and their parameters even in a case of triple pile-up. This is made possible by subtracting each fitted pulse shape from the subsequent signal before proceeding to the next pulse in line.
Example of signals recorded with a micromegas detector operated at low gain, typically used for fission measurements, exhibiting a consistent response to the initial \(\gamma \)-flash. The top panel shows the average \(\gamma \)-flash-induced distortion adjusted to the actual signal. The bottom panel shows the signal corrected for this distortion and being subjected to the separate pulse-shape fitting
5.2 Dead-time correction
The high cross section of fission reactions above the fission threshold combined with a high instantaneous flux, such as the one in EAR-2, can lead to instantaneous event rates that can reach up to MHz frequencies. These rates in turn can lead to severe pile-up effects and thus to counting losses that can reach up to \(60\%\).
To address such issues that could not be accommodated by analytical expressions found in literature, a new correction methodology was recently developed which is based on exponential decay fits of waiting time distributions, reconstructed in time-of-flight regions where the reaction rate is considered constant, and on the use of detector emulation devices [185].
More specifically, according to poissonian statistics, for a given constant counting rate R the time difference distribution between consecutive pulses, commonly referred to as the waiting time distribution, can be described by an exponential decay. Concurrently, each detection system is characterised by a finite resolving time \(\tau \), below which incoming pulses are most probably not recognised. Experimental waiting time distributions, reconstructed in time-of-flight regions where the counting rate does not vary appreciably, can be therefore fitted with an exponential decay function and extrapolated below the resolving time \(\tau \) in order to estimate the counting losses that occurred in this specific region. As can be seen in Fig. 37, the experimental waiting time distribution recorded during the \(^{240}\)Pu(n,f) measurement using Micromegas detectors in EAR-2 [116], begins to deviate from the expected exponential behaviour below \(\tau \approx 150\) ns. The integral that lies between the extrapolated red dashed curve and the experimental points can be considered as the counting losses in the corresponding incident neutron energy region.
An alternative approach, described in Ref. [185], is to use sophisticated signal generators to emulate the detector signals during the experiment and feed them to the acquisition system for a wide bandwidth of frequencies (true counting rate, \(R_\mathrm {true}\)) in order to cover the measured counting rates in the experiment (experimental counting rate, \(R_\mathrm {exp}\)). The ratio between the true and experimental counting rates \(f_\mathrm {DT}\) for each given frequency provides a correction function calculated by fitting the experimental points with a parabolic function, as can be seen in Fig. 38, which can later be applied to the experimental counting rate spectra.
The two proposed methodologies were benchmarked in the test case of the \(^{238}\)U(n,f) cross section relative to \(^{235}\)U(n,f) from data collected in EAR-2. The cross section values derived using correction factors estimated with the two methodologies are in quite satisfactory agreement, as can be seen in Fig. 39, and they are furthermore in agreement with the ENDF/B-VII.1 evaluation in the incident neutron energy range between 1.8 and 4.0 MeV where the \(^{238}\)U(n,f) cross section is considered a neutron standard.
5.3 Monte Carlo simulations
Beyond the techniques described in the previous sections, which concern the acquisition and software treatment of the raw data recorded during the experiments, Monte Carlo simulations are used to study particular features and sources of uncertainty of the various experimental setups and of the facility itself, including information that may not be experimentally accessible. This section provides an overview and a few examples from the simulation activities at n_TOF.
5.3.1 Monte Carlo study of the facility
The production of accurate nuclear data requires the optimisation of the neutron beam characteristics, such as its energy dependence and spatial profile, as well as the minimisation and characterisation of unwanted backgrounds. The sensitivity of these characteristics to specific elements needs to be well understood and in certain cases specific solutions need to be designed to optimise the performance or mitigate unwanted effects.
Such studies are carried out at n_TOF by means of Monte Carlo simulations with the FLUKA [107, 108] and MCNPX [53] radiation transport codes and, more recently, also with GEANT4 [109,110,111]. One of the main goals was to produce an evaluated neutron flux of the facility, but the studies extended to the collimation system, shielding optimisation, backgrounds generated from interactions in beam-line elements, such as collimators, vacuum windows and dumps, the in-beam photon background and the neutron moderation process, a study of which is critical in achieving a reliable TOF-to-energy calibration. The validation of the simulations, achieved mainly with experimental data on the neutron flux and spatial profile, allows one to extract further information that is not experimentally accessible, as is the case, e.g., of the neutron moderation in the target-moderator assembly.
The facility has been studied through a very detailed model that has tracked the changes made over the years, such as the replacement of the original spallation target and, of course, the construction of EAR-2. A section of this model showing the target and its immediate surroundings can be seen in Fig. 40. The geometry is built based on the technical drawings of relevant components (spallation target, proton, neutron and vacuum windows, cooling and moderator layers, vacuum tubes etc.) and civil engineering layouts of the facility (tunnels, target area, shielding etc.), with particular attention paid to the precise definition of material compositions, especially of the aluminium alloys which constitute the various windows and beam-line components and strongly influence the neutron flux. The primary proton source is defined to match the characteristics of the beam provided by the PS accelerator.
A significant computational challenge is posed by the large distance between the spallation target and the experimental areas. As an example, the solid angle subtended by the second collimator of the EAR-1 beam-line is less than \(10^{-8}\) sr (see Fig. 6). This makes a direct evaluation of the neutron flux in the experimental areas prohibitive in terms of CPU time. In order to address this difficulty, for most studies particles are tracked only up to scoring planes located within a few tens of centimetres of the spallation target, at the beginning of the vacuum tubes that lead to the two experimental areas. This information is then processed with a specially developed program that performs the propagation of the particles (neutrons and photons) towards the experimental area, accounting for collimating elements, and implements a variance reduction algorithm. Further details on this technique can be found in Refs. [101, 186].
The neutron flux is the main experimental quantity that can be used to benchmark the simulations. The good agreement and reproduction of salient features increases the confidence in the predictive power of the calculations on quantities that are not experimentally measurable. The accurate reproduction of the neutron flux depends not only on the description of the target and moderator and the primary proton beam, but also on small misalignments of the collimators. Figure 41 shows a comparison of the simulated and experimental neutron flux in EAR-1.
The spatial profile of the neutron beam is also a very important feature, especially when dealing with samples of small dimensions, and can provide further validation of the simulations. The neutron beam is shaped by two collimators, and both the neutron flux and beam profile are sensitive to their alignment. For example, simulations indicated that a 7% increase in neutron flux over a wide energy range could be achieved with a re-alignment of the first EAR-1 collimator, that was embedded in concrete and suffered from a known misalignment. This was confirmed after the operation was carried out during the long CERN accelerator complex shut-down (LS1) in 2013–2014. A comparison of the simulated beam profile, obtained using survey information on collimator misalignments, with the profile obtained with a stripped Micromegas detector with a \(^{10}\)B converter [187] offered further validation of the simulations.
For a particular sample, an important related quantity is the beam interception factor (BIF), which is the fraction of beam neutrons intercepted by the sample. Since the neutron spatial profile is different for neutrons of different energies (e.g. thermal neutrons are emitted almost isotropically, whereas fast neutrons are forward-peaked), the BIF is given as a function of neutron energy, as shown in Fig. 42 for samples of different diameters in EAR-1. The beam interception factor can vary significantly if the sample is not well-aligned with respect to the neutron beam, as shown for a 1 mm misalignment of a 2 cm diameter sample.
Estimated beam interception factor for perfectly aligned circular samples of 1, 2, 3 and 4 cm diameter in EAR-1. For the 2 cm sample, the grey band shows the effect of a 1 mm horizontal or vertical misalignment of the sample. Differences of up to 8% with respect to a perfectly aligned sample are predicted
The accurate reconstruction of the neutron energy from the measured time-of-flight is obviously one of the most important aspects of data analysis. The relation between energy and time-of-flight, however, is not unambiguous. This is because neutrons of the same energy do not arrive at the exact same time, but with a certain time distribution due to the different paths they follow in the material of the target-moderator assembly. While the moderation length and the corresponding moderation time cannot be experimentally measured, it is possible from simulations to obtain the relationship between the neutron energy and moderation time of each neutron defined as the time elapsed between the primary proton impact on the spallation target and the neutron entering the vacuum tube.
With this information, the flight-path travelled by a neutron detected at a given time can be expressed as the sum of a fixed geometrical length L and a smaller length \(\lambda (E_\mathrm {n})\) that is a function of neutron energy and accounts for the distribution of neutron energies for a given time-of-flight. This quantity is called the effective moderation length and can be obtained as the product of the neutron speed and moderation time \(t_\mathrm {mod}\) obtained from the simulations:
It should be noted that this is not the real path travelled by the neutron in the target-moderator assembly, hence the term “effective”. In addition to the neutron moderation, the time-spread of the proton bunch (7 ns rms) also introduces an uncertainty in the timing of detected events which becomes dominant at short times-of-flight (i.e. at high neutron energies). Although it can be treated separately, it can be conveniently included in the moderation time used to calculate the effective moderation length. As shown in Fig. 43, the shape of the \(\lambda \) distribution varies significantly with neutron energy. This information represents the resolution function of the neutron beam and, while sharing certain broad features, is different for the two experimental areas, reflecting the different layers of materials that neutrons encounter moving towards the two areas, especially in the vicinity of the spallation target. As discussed in the introduction of Sect. 3, these results are validated by the correct reconstruction of neutron capture resonances.
The effective neutron moderation length distribution of the EAR-1 neutron beam, including the effect of the proton beam width of 7 ns rms which becomes the dominant effect above several MeV The behaviour in the figure is a consequence of different physical processes neutrons undergo in the target/moderator assembly, depending on the neutron energy, as explained in Ref. [101]
Another aspect that was studied is the in-beam photon flux. These photons are mainly produced in the spallation target and travel through the neutron beam-line to reach the experimental areas, where they can be a source of unwanted background. The simulations permit us to estimate their time-of-arrival in the experimental areas and confront it to the neutron time-of-flight spectrum, as shown for EAR-1 in Fig. 44, where a prompt and a delayed \(\gamma \)-ray components are clearly visible before and after a time-of-flight of \(\sim \)10\(^{-6}\) s. The very different energy spectra of these two components shown in Fig. 45 reflect the different physical processes behind the production of each. The effect on this background of the use of borated water as moderator is also shown in these two figures.
Time-of-arrival of in-beam photons in EAR-1 obtained with Monte Carlo simulations. A prompt (earlier than \(\sim \)10\(^{-6}\) s) and delayed (later than \(\sim \)10\(^{-6}\) s) component can be clearly observed. The presence of \(^{10}\)B in the moderator leads to a significant suppression of the photon background, especially at neutron energies of astrophysical interest. The time-of-flight spectrum of the neutrons is also shown for comparison
Energy spectra of the prompt (upper panel) and delayed (lower panel) in-beam photon components shown in Fig. 44. While the presence of \(^{10}\)B in the moderator has very little influence on the prompt component, it leads to a significant reduction of the higher energy part of the delayed component
Extensive use of Monte Carlo simulations was also made during the design phase of EAR-2 [104]. In particular, detailed studies were performed to optimise the design of the second collimator and of the beam dump with the goal of minimising unwanted backgrounds from secondary particle production in the collimator and neutron back-scattering from the beam dump. Both these factors were expected to be more important due to the greater proximity of the collimator and the dump to EAR-2 compared to the corresponding elements of EAR-1.
5.3.2 Detector simulations
Apart from a good understanding of the particular features of the neutron beam and various backgrounds present in the experimental areas, the data analysis also requires and benefits from simulations of the experimental setups. For fission measurements in particular, there are many useful quantities that can be estimated by means of Monte Carlo simulations. These include the fraction of fission fragments that are stopped inside the sample, the sensitivity of the detection efficiency to different geometric or operational parameters, the estimation of corrections arising from event rejection algorithms and others.
A simple but useful Monte Carlo model of a generic ionisation detector, consisting of a fission sample and the active volume of the detector, that is meant to represent detectors such as the FIC (Sect. 4.1) and the Micromegas (Sect. 4.3), has been constructed and used to study the response of these detectors to fission fragments. In recent years, the GEF (GEneral Fission) code [188, 189], based on a semi-empirical model of the fission process, has been used as a fission event generator. The simulation accounts for the energy loss of the fragments inside the sample and estimates their energy deposition in the gas along their path on an event-by-event basis. A post-processing program combines this information with the electron drift velocity for a given electrical field strength to obtain the charge collection as a function of time. The electron drift velocity as a function of the electrical field strength is experimentally known for certain gases and gas mixtures and can be estimated for an arbitrary gas mixture with the GARFIELD code [190]. This raw signal is further assumed to pass through a shaping circuit, finally producing signals resembling those recorded experimentally. This method is described in greater detail in Ref. [186].
The simulated signals can be appropriately combined to construct artificial data containing known particle distributions that can be used to evaluate the performance and to optimise the pulse recognition algorithms used for the experimental data. In this manner, the model can be used to reproduce experimental observables such as the pulse-height spectrum. The sensitivity of the spectrum to various parameters, such as the sample thickness, the gas composition and pressure, the electrical field strength, the drift gap, signal pile-up due to high count-rates and others can be studied. Once the simulated and experimental spectra are in good agreement, the comparison of the two can also be used to estimate the fraction of fission fragments lost due to the pulse-height threshold applied for \(\alpha \)-particle signal rejection. An example of this is shown in Fig. 46.
Simulated fission fragment pulse-height spectrum compared with an experimental pulse-height spectrum obtained from a \(^{242}\)Pu sample. The signals from the \(\alpha \)-activity of the sample are also visible in the experimental spectrum, while the peak at 255 channels consists of signals with an amplitude exceeding the 8-bit digitiser range. The fraction of fission fragment signals rejected for a given pule-height threshold (shaded area) can be estimated
The event-by-event signal reconstruction also makes it possible to study and understand observables such as the signal shape and its dependence on other parameters. This is particularly interesting since the experimental data are analysed via pulse-shape recognition algorithms, as described in Sect. 5.1. As an example, Fig. 47 shows the simulated signal rise-time distributions for fission fragments emitted at 0\(^{\circ }\) and 80\(^{\circ }\) with respect to the beam axis in a generic ionisation chamber. It can be observed that fragments emitted at larger angles tend to generate signals with shorter rise-times, reflecting the different charge collection times. This can have implications in the exact assignment of a TOF value to detected event. Furthermore, changes in the detection efficiency with emission angle can be studied, although they are small for sufficiently thin samples.
6 Results
In the course of almost 20 years of activity, a rich experimental programme on fission has been carried out at the n_TOF facility. The measurements have focussed on two major objectives: (1) improving the accuracy and energy range of the fission cross section standards, in particular for \(^{235}\)U, \(^{238}\)U and other isotopes used as reference; and (2) collecting accurate, high-resolution data on minor actinides, so as to meet the high-priority requests related in particular to the development of new systems for energy production, such as Generation IV fast reactors, and reactors based on the Th/U fuel cycle. Table 2 reports a list of all fission measurements performed so far at n_TOF, together with the setup used, the experimental area where the data were collected, the energy range covered, and the relative publication (for the most recent measurements, for which data analysis is in progress, a reference to the proposal is included). In the following, we review the most important results obtained within the experimental fission programme at n_TOF. In accordance with CERN open data policy, and in line with the recommended nuclear data dissemination and long-term preservation procedure, all final n_TOF data are uploaded in the international EXFOR library [191]. In fact, since the beginning the n_TOF Collaboration has made a large effort aiming at preserving its unique data, facilitating access to them in standardised format, and ultimately allowing their use by a wide community in the fields of nuclear physics, nuclear astrophysics and various nuclear technologies. More details on the dissemination activity carried out at n_TOF can be found in Refs. [192, 193].
6.1 Cross section standards
The cross section of the \(^{235}\)U(n,f) reaction is one of the most important standards, widely used in a variety of fields. Apart from being a reference for cross section measurements of other actinides, this reaction is commonly used for the neutron flux determination. Its cross section is considered standard at thermal neutron energy and between 150 keV and 200 MeV [42, 117]. In these regions, the uncertainty of the evaluated cross section is well below 1%. However, a high accuracy of around 1% is also claimed for this reaction in other energy regions, in particular in the eV region and above a few keV. For this reason, this reaction is considered a reference at all energies, and to this purpose an official file is compiled and maintained by the IAEA [200].
The very convenient features of the n_TOF neutron beam, in particular the high resolution, high flux and wide energy range that characterise the neutron beam in the first experimental area (EAR-1), have been exploited to extract new, accurate and high-resolution data on the \(^{235}\)U(n,f) cross section, with the aim in particular of improving the accuracy on this cross section in the regions where it is not considered standard. To this end, the collaboration has exploited the large amount of data collected over the years on this reaction, used as reference for all fission cross section measurements performed at n_TOF and, especially, for the determination of the neutron flux. Data have been collected with a variety of detectors, from the Fast Ionisation Chamber described in Sect. 4.1, to the Micromegas detectors of Sect. 4.3 and finally with the Parallel Plate Avalanche Counters of Sect. 4.2. In all these cases, the \(^{235}\)U(n,f) cross section has been determined relative to the \(^{6}\)Li(n,t)\(^{4}\)He and \(^{10}\)B(n,\(\alpha \))\(^{7}\)Li reactions, either directly (i.e. measured with the same detectors at the same time), or indirectly, i.e. relative to the neutron flux previously determined by means of these reactions. In order to determine the absolute value of the cross section, n_TOF data have been normalised to the standard cross section at thermal neutron energy, or in some cases to the cross section integral in the 7–11 eV neutron energy range [201, 202]. High-accuracy data (with uncertainties below 2%) have been extracted up to 10 keV. Above this energy, the intrinsic uncertainty in the flux used as reference, of the order of 5% (see Ref. [102]), was too high to obtain useful data on the \(^{235}\)U(n,f) reaction. Nevertheless, as shown in Ref. [102], the n_TOF data hinted at some problems in the evaluated cross section in the 10–30 keV energy range.
Recently, the collaboration has undertaken a dedicated experimental programme aiming at collecting high-accuracy data in the resolved and unresolved resonance region (up to 150 keV), and above 200 MeV. In particular, a measurement was recently performed to directly determine the \(^{235}\)U(n,f) cross section relative to the \(^{6}\)Li(n,t)\(^{4}\)He and \(^{10}\)B(n,\(\alpha \))\(^{7}\)Li standards. A new apparatus, made of a stack of silicon detectors, was specifically built for the measurement, so as to detect and identify the fission fragments and the reaction products of the reference reactions in a wide angular range, thus minimising the uncertainty related to anisotropy in the angular distribution of the tritons and \(\alpha \)-particles emitted in the n+\(^{6}\)Li and n+\(^{10}\)B reactions, respectively. The new setup allowed the collaboration to collect data with 1.5% accuracy all the way from thermal neutron energy to around 200 keV [199]. The results pointed to a slight overestimation of the evaluated \(^{235}\)U(n,f) cross section at neutron energies around and slightly above 10 keV. Furthermore, the analysis of the data in the Resolved Resonance Region, characterised by a high resolution and low background, is expected to lead to improved resonance parameters that could be used to refine the evaluation in this energy region as well.
A large effort has also been made by the n_TOF Collaboration to measure the \(^{235}\)U(n,f) cross section at high energy, i.e. above a few MeV. Although this cross section is considered standard up to 200 MeV, the evaluations above 20 MeV are based on a few datasets, while above 200 MeV they are based purely on theoretical predictions and on experimental results on the proton-induced fission reaction. The wide energy range of the n_TOF beam, extending up to \(\sim \)1 GeV neutron energy, has offered the unique opportunity to provide much-needed additional data on the \(^{235}\)U(n,f) cross section up to 200 MeV and cover for the first time the region between 200 MeV and 1 GeV. For this high-energy measurement, the n-p elastic scattering which is a primary cross section standard up to 20 MeV, and known with good accuracy above this energy, is used as reference. For this reason, the two recoil-proton telescopes described in Sect. 4.6 were specifically built, one optimised for the energy region below 200 MeV, and the other one for neutron energies from a few tens of MeV up to 1 GeV. The data are currently being analysed, but preliminary results indicate that the goal of the measurement was fully reached and a new dataset covering the high-energy side of the cross section standard with high accuracy is expected to be available in the near future.
Ratio of the \(^{238}\)U(n,f) to \(^{235}\)U(n,f) cross sections [73]. The n_TOF results shown in the figure have confirmed one of the only two previous datasets up to 200 MeV, finally helping to clarify the long-standing discrepancy and providing the first data above this energy, up to 1 GeV
The n_TOF Collaboration has provided important data at high neutron energies for another cross section standard: the \(^{238}\)U(n,f) reaction. Prior to the n_TOF measurement, only two datasets were available above the fission threshold of this reaction, but they were discrepant by as much as 8% at 200 MeV neutron energy, the upper limit of those measurements. With the aim of solving the existing discrepancy and extending the energy range to higher energy, data were collected both with the Fast Ionisation Chamber (FIC) and with Parallel Plate Avalanche Counters (PPAC), previously described. Several \(^{238}\)U and \(^{235}\)U samples were used in the measurements and the datasets were combined with each other in order to minimise statistical and systematic uncertainties. The \(^{238}\)U/\(^{235}\)U fission cross section ratio was determined all the way from the \(^{238}\)U fission threshold (\(\sim \)800 keV) to 1 GeV [73]. As shown in Fig. 48, the results confirmed evaluated data from major libraries below 200 MeV and provided for the first time new data above this energy.
The neutron-induced fission cross section of \(^{209}\)Bi (top panel) and \(^{\text {nat}}\)Pb (bottom panel) measured at the n_TOF facility from threshold to 1 GeV. The blue curve represents the new IAEA evaluation reported in Ref. [203], while the dashed curve shows the previous evaluation, performed before the n_TOF results became available. For comparison, the proton-induced fission cross section is also shown in the figure as a dotted curve
Finally, neutron-induced fission cross sections were determined at n_TOF for \(^{\text {nat}}\)Pb and \(^{209}\)Bi, all the way from \(\sim \)50 MeV to 1 GeV [70]. Cross section data on bismuth and lead are of crucial importance for the development and operation of accelerator-driven systems, since lead-bismuth eutectic has been proposed as coolant in ADS, as well as being a target in spallation sources. Furthermore, the \(^{\text {nat}}\)Pb(n,f) and \(^{209}\)Bi(n,f) reactions can conveniently be used as reference for the measurement of other cross sections or for neutron flux determination at high energy. The main advantages in the use of such reactions are the relatively high fission threshold (\(\sim \)20 MeV), that minimises the background related to low-energy neutrons, and the availability of the material that allows an easy and inexpensive procurement and handling. For this reason, the IAEA has recommended a new evaluation of these two reaction cross sections, from threshold to 1 GeV, by including the most recent measurements [203]. In this respect, the n_TOF results played an important role in the development of the new high-energy reference by the IAEA, thanks to the high quality of the n_TOF results and the unprecedented energy range covered, being to date the only available data between 400 MeV and 1 GeV.
Figure 49 shows the cross section for the \(^{\text {nat}}\)Pb(n,f) and \(^{209}\)Bi(n,f) reactions measured at n_TOF relative to the \(^{235}\)U(n,f) standard. It should be noted that the results shown here are different at high energy than those reported in Ref. [70], since in that publication the \(^{235}\)U(n,f) evaluated cross section from the JENDL/HE-2007 file, later discovered to be affected by an error above 200 MeV, was used as reference. The results shown here have been obtained by a re-analysis of the n_TOF data relative to the IAEA reference file [203]. In the figure, the proton-induced fission cross section is also shown for comparison, indicating agreement at the highest energies, where (p,f) and (n,f) cross sections are indeed expected to converge. The blue curve shows the latest IAEA evaluation, which as already mentioned is mainly based on the n_TOF results above 400 MeV. It is interesting to notice that for \(^{209}\)Bi the previous IAEA evaluation, performed in 2005 before the n_TOF data were available, grossly underestimated the fission cross section above a few hundreds of MeV.
6.2 Fission cross sections of minor actinides
Since the first experimental campaign at n_TOF, a large effort has been made to measure the fission cross sections of the most important minor actinides, of interest mainly for waste transmutation and a new generation reactors for energy production and for the optimisation of fission models used in nuclear astrophysics, in particular for fission recycling in r-process nucleosynthesis.
One of the first results obtained at n_TOF regarded the neutron-induced fission cross section of \(^{233}\)U, the key reaction of the Th/U fuel cycle. Data on this reaction were collected with the Fast Ionisation Chamber up to 20 MeV [120, 121], complemented with the PPAC setup all the way up to 1 GeV [195, 196]. High-accuracy results, characterised by systematic uncertainties slightly above 3%, were obtained for the first time on this reaction in a wide energy range. While the n_TOF results confirmed the evaluations for neutron energies below 100 eV and above 10 keV, they pointed to the need of an important revision of the evaluations in the intermediate energy region, of interest for fast reactors, as shown in Fig. 50.
Ratio between the \(^{233}\)U(n,f) cross section measured at n_TOF [121] and the evaluated one from two major libraries, integrated over a decade in neutron energy. For comparison, a previous measurement covering a more limited energy range is also shown in the figure by the red curve
Another uranium isotope whose neutron-induced fission cross section has been measured at n_TOF is \(^{234}\)U. Data on this isotope are needed for the development of Th/U fuel cycle, where it plays the same role as \(^{240}\)Pu in the Pu/U cycle used in present-day reactors. During the Phase-I campaign, the \(^{234}\)U(n,f) reaction was studied with the PPAC system (in the perpendicular configuration). The measurement provided the first set of data in literature covering a wide energy range from 1 eV to 1 GeV with an uncertainty of 4% [69], shown in Fig. 51. An additional measurement was performed with the FIC detector assembly and the resulting data covered the energy range from 20 keV up to 200 MeV with high energy resolution, high statistics and systematic uncertainties below 3% [46]. Due to the high energy resolution of these data, previously observed fine structures around the fission threshold were confirmed in the energy ranges 300–600 keV and 0.8–1 MeV. The first of these structures could be attributed to \(\beta \)-vibrational levels in the second minimum of the fission barrier of \(^{235}\)U (class-II states), while the second one around 1 MeV could only be explained by considering a triple-humped barrier (class-III states).
The \(^{234}\)U(n,f) cross section measured with the PPAC setup (perpendicular configuration), above the fission threshold [69]. High-accuracy data have been obtained for the first time up to 1 GeV neutron energy
An interesting case was the measurement of the fission cross section of \(^{236}\)U [122]. For this reaction, the n_TOF data unambiguously demonstrated that two major evaluations, namely JEFF-3.2 and ENDF/B-VII.0 were overestimating the cross section at low energy by more than two orders of magnitude and that several resonances present in the evaluations were not related to the neutron-induced fission of \(^{236}\)U, but rather to an unrecognised \(^{235}\)U contamination in the sample used in the previous measurements included in the evaluations. Also in this case, the n_TOF results called for a re-evaluation of the \(^{236}\)U(n,f) cross section (a re-evaluation still missing in the latest JEFF-3.3 and ENDF/B-VIII.0 evaluations).
In some cases, the measurements of several important minor actinides were repeated with improved detector systems, purer and better characterised samples, and taking advantage of the much higher flux in the second experimental area (EAR-2). One such case is the measurement of the \(^{237}\)Np(n,f) reaction cross section. A first measurement was performed with the PPAC system in the first experimental area covering the neutron energy range from 1 eV to 1 GeV (see Sect. 4.2). An additional measurement was also performed in EAR-1 by employing the FIC detection setup, covering incident neutron energies between 150 keV and 10 MeV. The cross section measured with the PPAC setup [69] was found to be systematically higher, by 4–6% in the plateau of first-chance fission, than the FIC measurement [124] and evaluations of the major nuclear data libraries, a somewhat unexpected result shown in Fig. 52. The discrepancy in the PPAC results was later understood as related to the sample preparation. The measurement was repeated with the improved “tilted” setup (described in Sect. 4.2), characterised by an almost complete coverage of the angular distribution [128], contrary to the original setup that covered emission angles only up to 60\(^{\circ }\). The new geometry was conceived so as to minimise the effects of the angular anisotropy in fragment emission at high energy that could potentially affect the cross section determination. More recently, an additional measurement was performed with Micromegas detectors in EAR-2. The results, which are expected to be submitted for publication in the near future, showed agreement with the FIC data and the major evaluations, thus finally solving the long-standing discrepancy.
Another minor actinide whose neutron-induced fission cross section has been measured twice at n_TOF is \(^{241}\)Am. A first measurement was performed in EAR-1 with the fission ionisation chamber [125, 204]. While the n_TOF results showed good agreement with major evaluations from thermal neutron energy to 10 eV, in the resolved and unresolved resonance region they indicated that current evaluated nuclear data libraries systematically underestimate the cross section by \(\sim \)20%. However, the cross section in the high-energy region was given as an average in wide energy bins due to low statistics. In order to verify and improve these results, the measurement of the \(^{241}\)Am(n,f) cross section has recently been repeated with Micromegas detectors in the second experimental area, taking advantage of the higher neutron flux and of the much more favourable signal-to-background ratio in the new measuring station for the background related to the \(\alpha \)-decay of this relatively short-lived actinide. The analysis of this measurement is currently in progress.
The \(^{237}\)Np(n,f) cross section measurement was performed during the first phase of operation in EAR-1 using the PPAC [69] and the FIC [124] detection setups. The measurements had a 4–6% discrepancy in the 1–6 MeV region (inset) therefore the measurement was repeated in EAR-1 and EAR-2 with the “tilted PPAC” and Micromegas detectors, respectively
Together with \(^{241}\)Am, the neutron-induced fission cross section of \(^{243}\)Am was also measured in EAR-1 with the Fast Ionisation Chamber. While the \(\alpha \)-particle background for this long-lived actinide (\(T_{1/2}=7.37\times 10^{3}\) y) was not a problem, the analysis at low energy was complicated by the presence of contaminants, in particular \(^{242m}\)Am and \(^{239}\)Pu. The latter contamination builds up in the sample as a result of \(\alpha \)-decay, and constitutes a problem, even for trace amounts, due to its large fission cross section at low neutron energies. On the contrary, contaminants do not pose a problem above the fission threshold, where high-accuracy data were obtained [126], confirming current evaluations and definitively ruling out a previous, 15% higher result.
An interesting result obtained at n_TOF regards the \(^{245}\)Cm(n,f) cross section, one of the most challenging measurements performed so far at this facility. The main difficulty in this case was related to a contamination of the sample with the short-lived \(^{244}\)Cm isotope (\(T_{1/2}\)=18.1 y). This 6.6% contamination was the main responsible for the high \(\alpha \)-activity, of the order of 100 MBq, which constituted a very large source of background together with spontaneous fission. However, thanks to the high instantaneous neutron flux of n_TOF, both problems did not hinder the measurement, and at the end data affected by a relatively small uncertainty of 5% were obtained. For this reaction, very few measurements had previously been performed: below 30 eV only two datasets were reported in literature, highly discrepant from each other, while above 30 eV a unique high-resolution measurement, performed with the neutron field from a nuclear detonation, was available. The resonance kernels obtained at n_TOF are compared with the ones determined from two major evaluations in Fig. 53, which are based on the three datasets mentioned above. Below 30 eV, large discrepancies can be seen between n_TOF results and evaluated data (and among evaluations themselves), indicating the need of significant corrections in the evaluations. On the contrary, an almost perfect agreement is observed above 30 eV, demonstrating that the resolution and accuracy that can be obtained with the n_TOF neutron beam are comparable to those reached in the past only with the use of the very intense neutron source of a nuclear explosion. This result is particularly important as it demonstrated the possibility of performing challenging measurements at n_TOF.
On the basis of these results, two more difficult measurements were attempted in the first experimental area: the \(^{240}\)Pu and \(^{242}\)Pu fission cross sections. Both measurements were performed with Micromegas detectors. However, while the latter measurement was successfully completed [138, 139], the very high activity of the \(^{240}\)Pu samples, of the order of 6 MBq per sample, made it practically impossible to obtain reliable results on this isotope. Apart from the large \(\alpha \)-particle background, the natural radioactivity of the sample led to severe damage on the Micromegas foils during the measurement, that had to last nearly 1 year in order to collect suitable statistics, with a consequent degradation of the detector’s response, as discussed in Sect. 4.3.
Ratio of the resonance kernels of the \(^{245}\)Cm(n,f) cross section measured at n_TOF and those extracted from evaluated data of two major libraries (see Ref. [127]). Below 30 eV evaluations are based on two highly discrepant measurements, while above this energy they are based on a unique dataset, obtained with a neutron beam produced in a nuclear explosion. The very good agreement of the n_TOF data with evaluations above 30 eV demonstrates the unique features, in terms of flux and resolution, of the n_TOF neutron beam
The radiation damage resulting from the use of a highly radioactive sample can be avoided by minimising the duration of the measurement and reducing the detector gain. To this end, the newly completed second experimental area at n_TOF represented the ideal place for performing the challenging measurement on the \(^{240}\)Pu(n,f) cross section. The much higher neutron flux, in this case, made it possible to collect the needed statistics in just a few weeks, without any appreciable damage to the detectors. Furthermore, the combination of the higher flux and shorter time-of-flight than EAR-1 resulted in a suppression of the background of more than two orders of magnitude, as clearly shown in Fig. 11. The measurement of the \(^{240}\)Pu(n,f) reaction was successfully performed in EAR-2; it was, in fact, the first one carried out after the commissioning of the new experimental area and demonstrated the potential of EAR-2 for challenging measurements on highly radioactive samples. Relative to the scarce and discrepant previous measurements, the n_TOF results are characterised by a higher resolution, wider energy range from 9 meV up to 6 MeV, as shown in Figs. 54 and 55, and higher accuracy.
The study of the neutron-induced fission of \(^{240}\)Pu, which was the first measurement performed in EAR-2, yielded a cross section with high resolution in a broad energy range between 9 meV and 6 MeV [205]
The \(^{240}\)Pu fission cross section measurement performed in EAR-2 offers better energy resolution compared to the latest time-of-flight measurement by Tovesson et al. [206] and major evaluation libraries. The energy region between 10 and 30 keV is shown
Very recently, a measurement of the neutron-induced fission cross section of \(^{230}\)Th was performed, both in EAR-1, for high resolution, and in EAR-2, to probe the sub-threshold region where the cross section is very low and practically no data exist. Micromegas detectors were used in this case as well. \(^{230}\)Th is important for the Th/U fuel cycle and there is a lack of experimental data in the low-energy region, while the existing data of the \(^{230}\)Th(n,f) reaction cross section above the fission threshold only cover the energy range up to 25 MeV with many discrepancies and low accuracy. Furthermore, the peak in the excitation function of the cross section observed in the vicinity of 720 keV has been interpreted in terms of a vibrational mode resonance state in the secondary minimum of a double-humped fission barrier, with K = 1/2. Better experimental data in the energy region close to the fission barrier may enable one to reveal finer structures of the fission mode and extract all possible spectroscopic information on the states associated with the second well of the fission potential. The main challenge in this case was related to the sample availability, due to the fact that \(^{230}\)Th is a very rare isotope and can be produced in very small quantities, a problem that at present represents a bottleneck for measurements of short-lived radioisotopes. The \(^{230}\)Th samples were prepared at JRC-Geel, where there was a sufficient quantity of 91.54% purity \(^{230}\)Th with 8.46% \(^{232}\)Th content, in the form of thorium oxide (ThO\(_2\)). The contribution of \(^{232}\)Th can be accurately subtracted since the \(^{232}\)Th(n,f) cross section is very well known. The material was electro-deposited on an aluminium backing with a surface density of 100 \(\upmu \)g/cm\(^2\) corresponding to 5 mg per sample with an activity of 3.8 MBq. The measurements have been successfully performed in both experimental areas in 2018 and the data are currently under analysis.
6.3 Measurements of FF angular anisotropy
Apart from cross sections, other features of fission reactions have been investigated at n_TOF. In particular, the use of position-sensitive parallel plate avalanche counters, described in Sect. 4.2, allows one to study the fission fragment angular distribution (FFAD). This is an important observable that provides information on the fission mechanism, in particular on the spin of the levels of the fissioning nucleus at energies close to the threshold of the various multiple-chance fission channels [207], and it makes it possible to characterise vibrational structures around the fission threshold for the light Th, Pa and U isotopes [208]. Finally, together with fission cross sections, FFADs are important for determining the optimal set of model parameters, in particular on the fission barriers. At high energy, above a few tens of MeV, theoretical models predict an isotropic behaviour, in any case similar to the one predicted for proton-induced fission, although non-isotropic behaviour has been observed up to 100 MeV neutron energy. Finally, FFAD also affects the cross section determination for experimental setups characterised by an incomplete coverage of the solid angle. This is the case, in particular, for the PPAC mounted in a geometrical configuration perpendicular to the neutron beam and used in the coincidence mode, that is characterised by a limited angular acceptance, as discussed in Sect. 4.2. In this case, the fission fragment angular distribution must be taken into account in order to calculate the detection efficiency.
Data on FFAD are scarce and often discrepant, in particular at high energy, due to the lack of neutron beams with adequate spectral features, as well as of suitable detection systems. The n_TOF facility offered the unique possibility of studying FFAD all the way to 1 GeV with high resolution, provided that a proper detection system was developed. To this end, the geometrical configuration of the position-sensitive parallel plate avalanche counters was suitably modified, by mounting the detectors at an angle of 45\(^{\circ }\) relative to the neutron beam direction, as described in Sect. 4.2 and in Ref. [128].
The fission fragment angular distribution is very sensitive to the neutron energy. A concise way to represent this variation is to consider the energy dependence of the anisotropy, defined as the ratio between the double differential cross section at 0\(^{\circ }\) and 90\(^{\circ }\). Figure 56 shows the angular anisotropy measured at n_TOF for \(^{232}\)Th from the fission threshold to 10 MeV [209]. Data have been collected all the way to 1 GeV and will be the subject of a forthcoming publication. In the plotted energy range the PPAC measurement is very well consistent with existing data. The sideward peaking is well exhibited by the drop of anisotropy around 1.6 MeV, where the quantum number K, i.e. the projection of the spin along the fission axis, is close to l, the total angular momentum involved. The peaking of the anisotropy around 7 MeV is a common feature coinciding with the opening of second-chance fission. After emission of the neutron the excitation energy drops, shrinking the distribution of K to low values, producing the steep rise in anisotropy. Apart from \(^{232}\)Th, the angular anisotropy has been measured at n_TOF for other actinides, such as \(^{234}\)U and \(^{237}\)Np [130]. The analysis of these data is near completion and the results will soon become available.
Energy dependence of the FFAD of \(^{232}\)Th, measured with the PPAC system (tilted configuration), compared to previous measurements (see Ref. [209])
7 Perspectives
After the end of the measurement campaign in 2018, n_TOF operations were stopped, along with all other experiments at CERN, due to the second long accelerator shut-down period (LS2). Operations are scheduled to resume in 2021. Taking advantage of the shut-down period, a major upgrade is being performed for both beam-related components and detection systems. In particular, the lead spallation target is being replaced, as the old one has reached its foreseen life-time of 10 years. Modifications are being implemented in order to improve the neutron flux, the resolution function and the background conditions in both experimental areas, with emphasis on EAR-2. In particular, with the installation of the new spallation target, the neutron flux in EAR-2 will be increased by a factor of 2, without significantly affecting the flux, excellent resolution and low background in EAR-1. The extremely high instantaneous flux in EAR-2 already proved to be a key factor for the feasibility of fission reaction studies with highly radioactive samples. Examples (discussed in Sect. 6) were the challenging cross section measurements for the \(^{240}\)Pu(n,f) and \(^{241}\)Am(n,f) reactions, successfully completed with samples of up to \(\sim \)20 MBq of \(\alpha \)-activity.
The further enhanced flux in EAR-2 after the target replacement will expand the potential of the facility for measurements of isotopes of high specific activity or, equivalently, short half-life. Specifically, fission reaction cross section measurements on isotopes like \(^{241}\)Pu (\(T_{1/2} = 14\) y), \(^{242m}\)Am (\(T_{1/2} = 141\) y) and \(^{244}\)Cm (\(T_{1/2} = 18\) y) will be within reach in the near future at n_TOF, with the possibility of obtaining high-accuracy and high-resolution data in a wide energy range for the first time ever for these actinides. Additionally, there are numerous physics cases, (e.g. \(^{243}\)Am(n,f) and \(^{232}\)Th(n,f)) of fission reaction studies performed in the past at n_TOF in EAR-1, or in other neutron beam facilities, where the uncertainties, in particular the systematic ones, can be significantly improved. The expected high instantaneous flux of EAR-2, along with the improved signal-to-background conditions is indeed expected to result in higher-quality data compared to the past.
Another advantage of the n_TOF facility is that the fission reaction rate for a given isotope can be measured in both experimental areas. In this way a measurement can profit both from the high instantaneous flux of EAR-2 and the excellent time resolution of EAR-1. This combination can be extremely useful in studies of threshold fission reactions. In these cases, the resonance and the sub-threshold energy region, where the reaction cross section is low, can be better accessed in EAR-2, while for higher neutron energies (above threshold) the measurement in EAR-1 would provide data with higher resolution and extending all the way to 1 GeV. The measurement of one reaction with the same experimental setup in both experimental areas has already successfully been performed for the \(^{230}\)Th(n,f) reaction, just before the end of the last campaign (see Sect. 6.2). This opportunity can be exploited in the future for several isotopes, drastically improving the quality of available data.
Together with the expected improvements of the neutron beam characteristics, the fission experimental programme at n_TOF will greatly benefit from advances in the detection systems and the development of new techniques, which are expected to extend current capabilities. As shown in Table 2, the majority of the measurements performed so far have focussed on fission cross sections. However, a more complete understanding of the fission process requires experimental information on additional observables and correlations between them, in particular for isotopes for which one or more experimental information is missing. In particular, studies of mass and charge distribution of the fission products along with the angular distribution, are significant pieces of information for the understanding on the fission mechanism. A complete, “inclusive” study of the fission process is now possible at n_TOF, thanks to improvements both in the neutron beam and detection systems, and will be an aim of the future experimental programme on fission at n_TOF.
In view of the importance of the fission process in the interpretation of the observed r-process abundances (Fig. 3), knowledge of the excitation function should be also accompanied by information of the fission yield, i.e. the mass and charge distribution of the fission products. Accurate knowledge of the yield of the fission products is also important for the design and safe operation of Generation IV fast reactor and ADS systems, as the decay of fission products affects the total energy release, while the production yield of the radioactive isotopes is an important parameter for the energy balance and the neutron economy modelling.
For these reasons, the development and upgrade of the detection systems in order to collect additional information on fission events is of primary importance. By extending the observables related to the fission process, the corresponding theoretical models can be benchmarked, tested and finally improved. In the end, more reliable theoretical calculations are of the utmost importance for predictions of physics cases that are not experimentally accessible. While measurements of fission fragment yields have already been performed on major actinides at n_TOF with the STEFF setup (described in Sect. 4.4), it is foreseen to extend this programme to minor actinides, in particular the heaviest ones, to provide better constraints to theoretical calculations, related in particular to the modelling of fission recycling in r-process nucleosynthesis. In this respect, the experimental programme might benefit from the development of high-acceptance detectors with good FF identification capabilities and with fast time response to be able to sustain the high reaction count-rate that can be achieved at n_TOF.
Another important observable to be studied in the future fission programme at n_TOF is the angular distribution of fission fragments. The feasibility of FFAD measurements all the way to 1 GeV neutron energy has recently been demonstrated with two isotopes, \(^{232}\)Th and \(^{237}\)Np, studied with position-sensitive PPAC detectors (described in Sect. 4.2). Apart from PPAC data, segmented position-sensitive Micromegas detectors, recently tested at n_TOF, could replace the existing single-plate configurations so as to allow measurements of fission fragment angular distributions.
A successful experimental programme on fission necessarily relies on the availability of samples of suitable mass, purity and homogeneity, and on their accurate characterisation. As only a few laboratories in Europe and world-wide are licensed, skilled and equipped to prepare and characterise actinide samples, this task is expected to pose increasing challenges, in particular for short-lived isotopes. The limited amount of suitable sample material and of producers, the difficulty in procuring the material with the required isotopic and chemical purity, the decreasing capabilities in terms of deposition of highly radioactive material, due to loss of facilities and expertise, and the long and cumbersome procedure for transporting, handling and disposal of such material, are making the preparation and use of tailor-made samples a challenge by itself. A possible solution to these problems is to transfer knowledge and share resources in a network of sample producers, and efforts are on-going in this respect. Finally, interaction of the sample producers with the users, such as in the case of the n_TOF Collaboration, is very important to ensure the efficient delivery of high-quality samples, according to the required specifications.
Among other issues, the preparation of thin layers on substrate foils with a maximum thickness of 1 \(\upmu \)m is still a challenge. The foils are difficult to stretch and glue onto a frame and be positioned in a molecular plating cell or vacuum evaporation system without breaking. Furthermore, foils of such thickness are fragile, while they have to be resistant to the electrolyte solution or to the heat during the molecular plating process or vacuum evaporation process, respectively. Investigation in this sense is on-going at JRC-Geel. A novel method based on the so-called “Drop-on-Demand” technique (DoD), as used in inkjet printers, has been developed at the Johannes Gutenberg-Universität of Mainz [210]. The big advantage is that any kind of manageable substrate can be used and that the chance of thin foil-break is much lower compared to the molecular plating and vacuum evaporation processes. Furthermore, the areal density can be kept constant for deposits with a larger diameter, which is not the case with molecular plating and vacuum evaporation.
In summary, a rich experimental programme has been carried out on fission at n_TOF in the last two decades. Long-needed high-quality results have been obtained on several major and minor actinides, as well as on Pb and Bi. The main reason for the successful completion of the programme relies on the features of the n_TOF neutron beams, very convenient and in some cases unique for fission studies, in particular the high instantaneous flux, the wide energy range, covering more than 12 orders of magnitude, and the high energy resolution. The development of suitable detection and acquisition systems, the competences of the collaborating target laboratories, such as the one at JRC-Geel, and finally the large effort of the whole collaboration in data reduction and analysis, as well as in the theoretical interpretation of the results, have been fundamental ingredients towards the completion of the successful experimental programme. After the installation of the new spallation target and subsequent commissioning, a new campaign on fission will start, with dedicated studies aiming at improving the knowledge in this field and to provide valuable and long-needed experimental data of interest for different fields, such as nuclear energy applications, nuclear astrophysics and modelling of nuclear reactions. Another decade of exciting measurements lies in front of us, on a subject now more intriguing and interesting than ever before.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: As explained in the text (Sect. 6), in accordance with CERN open data policy, and in line with the recommended nuclear data dissemination and long-term preservation procedure, all data related to \(\mathrm{n}\_\mathrm{TOF}\) measurements discussed in this paper are uploaded in the publicly available international EXFOR library [191].]
References
M. Salvatores, J. Nucl. Sci. Tech. Suppl. 2, 4–12 (2002). https://doi.org/10.1080/00223131.2002.10875028
G. Aliberti et al., Ann. Nucl. Energy 22, 700–733 (2006). https://doi.org/10.1016/j.anucene.2006.02.003
N. Colonna, F. Gunsing, F. Kaeppeler, Prog. Part. Nucl. Phys. 101, 177–203 (2018). https://doi.org/10.1016/j.ppnp.2018.02.002
P.W. Lisowski et al., Nucl. Sci. Eng. 106, 208–218 (1990). https://doi.org/10.13182/NSE90-A27471
W. Mondelaers, P. Schillebeeckx, Notiziario Neutroni e Luce di Sincrotrone 11, 19–25 (2006). statistics.roma2.infn.it/notiziario/2006/11_2_06/pag19.pdf
M. Igashira, Y. Kiyanagi, M. Oshima, Nucl. Instrum. Methods A 600, 332–334 (2009). https://doi.org/10.1016/j.nima.2008.11.085
X. Ledoux et al., Radiat. Prot. Dosim. 180(1–4), 115–119 (2017). https://doi.org/10.1093/rpd/ncx257
J. Wei et al., Nucl. Instrum. Methods A 600, 10–13 (2009). https://doi.org/10.1016/j.nima.2008.11.017
O. Hahn, F. Strassmann, Naturwissenschaften 27(1), 11–15 (1939). https://doi.org/10.1007/BF01488241
L. Meitner, O. Frisch, Nature 143, 239–240 (1939). https://doi.org/10.1038/143239a0
N. Bohr, J.A. Wheeler, Phys. Rev. 56, 426–450 (1939). https://doi.org/10.1103/PhysRev.56.426
D.L. Hill, J.A. Wheeler, Phys. Rev. 89, 1102–1145 (1953). https://doi.org/10.1103/PhysRev.89.1102
R.D. Woods, D.S. Saxon, Phys. Rev. 95, 577–578 (1954). https://doi.org/10.1103/PhysRev.95.577
N. Schunck, L.M. Robledo, Rep. Prog. Phys. 79(11), 116301 (2016). https://doi.org/10.1088/0034-4885/79/11/116301
S.M. Polikanov et al., Sov. Phys. JETP 15, 1016 (1962)
P. Thirolf, D. Habs, Progr. Part Nucl. Phys. 49(2), 325–402 (2002). https://doi.org/10.1016/S0146-6410(02)00158-8
S.M. Polikanov, Sov. Phys. Uspekhi 15(4), 486–496 (1973). https://doi.org/10.1070/pu1973v015n04abeh004997
G.F. Auchampaugh, L.W. Weston, Phys. Rev. C 12, 1850–1857 (1975). https://doi.org/10.1103/PhysRevC.12.1850
M.S. Moore et al., Phys. Rev. C 18, 1328–1348 (1978). https://doi.org/10.1103/PhysRevC.18.1328
M. Sin et al., Phys. Rev. C 74, 014608 (2006). https://doi.org/10.1103/PhysRevC.74.014608
J.D. Cramer, J.R. Nix, Phys. Rev. C 2, 1048–1057 (1970). https://doi.org/10.1103/PhysRevC.2.1048
A.N. Andreyev et al., Phys. Rev. Lett. 105, 252502 (2010). https://doi.org/10.1103/PhysRevLett.105.252502
A.N. Andreyev, K. Nishio, K.-H. Schmidt, Rep. Prog. Phys. 81(1), 016301 (2017). https://doi.org/10.1088/1361-6633/aa82eb
E.K. Hulet et al., Phys. Rev. Lett. 56, 313–316 (1986). https://doi.org/10.1103/PhysRevLett.56.313
W. Schwab et al., Nucl. Phys. A 577(3), 674–690 (1994). https://doi.org/10.1016/0375-9474(94)90939-3
J. Blons et al., Phys. Rev. Lett. 41, 1282–1285 (1978). https://doi.org/10.1103/PhysRevLett.41.1282
P. Möller, Nucl. Phys. A 192(3), 529–580 (1972). https://doi.org/10.1016/0375-9474(72)90090-5
M. Mirea et al., Europhys. Lett. 73(5), 705–711 (2006). https://doi.org/10.1209/epl/i2005-10454-x
M. Herman et al., Nucl. Data Sheets 108(12), 2655–2715 (2007). https://doi.org/10.1016/j.nds.2007.11.003
G.F. Bertsch et al., J. Phys. G Nucl. Part. 42(7), 077001 (2015). https://doi.org/10.1088/0954-3899/42/7/077001
V.Y. Denisov, I.Y. Sedykh, Eur. Phys. J. A 54(12), 231 (2018). https://doi.org/10.1140/epja/i2018-12660-9
A. Junghans et al., Nucl. Phys. A 629(3), 635–655 (1998). https://doi.org/10.1016/S0375-9474(98)00658-7
D.C. Hoffmann, M.R. Lane, Radiochim. Acta 70(71), 135–146 (1995). https://doi.org/10.1524/ract.1995.7071.special-issue.135
R. Capote et al., Nucl. Data Sheets 131, 1–106 (2016). https://doi.org/10.1016/j.nds.2015.12.002
B. Jurado, K.-H. Schmidt, J. Phys. G Nucl. Part. Phys. 42, 055101 (2015). https://doi.org/10.1088/0954-3899/42/5/055101
A. Bohr, in Proceedings of the International Conference on the Peaceful of the Atomic Energy, 8–20 August 1955 (United Nations, Geneva, 1956), p. 155
S. Bjørnholm, V. Strutinsky, Nucl. Phys. A 136(1), 1–24 (1969). https://doi.org/10.1016/0375-9474(69)90035-9
U. Mosel, H.W. Schmitt, Phys. Rev. C 4, 2185–2201 (1971). https://doi.org/10.1103/PhysRevC.4.2185
J.B. Wilhelmy et al., Phys. Rev. C 5, 2041–2060 (1972). https://doi.org/10.1103/PhysRevC.5.2041
K. Mazurek et al., Eur. Phys. J. A 53(4), 79 (2017). https://doi.org/10.1140/epja/i2017-12262-1
K.-H. Schmidt, B. Jurado, Rep. Prog. Phys. 81(10), 106301 (2018). https://doi.org/10.1088/1361-6633/aacfa7
A. Carlson et al., Nucl. Data Sheets 148, 143 (2018). https://doi.org/10.1016/j.nds.2018.02.002
P.W. Lisowski, NEANDC-305/U (IAEA, Vienna, 1991). inis.iaea.org/search/search.aspx?orig_q=RN:23033167
R. Nolte et al., Nucl. Sci. Eng. 156(2), 197–210 (2007). https://doi.org/10.13182/NSE06-14
A. Koning, D. Rochman, Nucl. Data Sheets 113(12), 2841–2934 (2012). https://doi.org/10.1016/j.nds.2012.11.002
D. Karadimos et al., Phys. Rev. C 89, 044606 (2014). https://doi.org/10.1103/PhysRevC.89.044606
M. Sin et al., Nucl. Data Sheets 139, 138–170 (2017). https://doi.org/10.1016/j.nds.2017.01.003
M. Sin et al., Phys. Rev. C 93, 034605 (2016). https://doi.org/10.1103/PhysRevC.93.034605
P. Romain, B. Morillon, H. Duarte, Nucl. Data Sheets 131, 222–258 (2016). https://doi.org/10.1016/j.nds.2015.12.003
V. Maslov, Nucl. Phys. A 717(1), 3–20 (2003). https://doi.org/10.1016/S0375-9474(03)00593-1
I. Ryzhov et al., Nucl. Phys. A 760(1), 19–39 (2005). https://doi.org/10.1016/j.nuclphysa.2005.06.003
K. Gudima, S. Mashnik, V. Toneev, Nucl. Phys. A 401(2), 329–361 (1983). https://doi.org/10.1016/0375-9474(83)90532-8
D.B. Pelowitz (ed.), LA-CP-07-1473 (LANL, Los Alamos, 2011). mcnpx.lanl.gov/docs/MCNPX_2.6.0_Manual.pdf
C.J. Werner (ed.), LA-UR-17-29981 (LANL, Los Alamos, 2017). laws.lanl.gov/vhosts/mcnp.lanl.gov/pdf_files/la-ur-17-29981.pdf
A. Boudard et al., Phys. Rev. C 87, 014606 (2013). https://doi.org/10.1103/PhysRevC.87.014606
R.J. Charity, Phys. Rev. C 82, 014610 (2010). https://doi.org/10.1103/PhysRevC.82.014610
A. Kelić, K.-H. Schmidt, M.V. Ricciardi, in Proc. Joint ICTP-IAEA Advanced Workshop on Model Codes for Spallation Reactions, vol. INDC(NDS)-530 (IAEA, Vienna, 2008), p. 181. www.nds.iaea.org/publications/indc/indc-nds-0530/
L.G. Moretto, G.J. Wozniak, Prog. Part. Nucl. Phys. 21, 401–457 (1988). https://doi.org/10.1016/0146-6410(88)90036-1
A.J. Sierk, Phys. Rev. C 33, 2039–2053 (1986). https://doi.org/10.1103/PhysRevC.33.2039
P. Möller et al., Atom. Data Nucl. Data 59(2), 185–381 (1995). https://doi.org/10.1006/adnd.1995.1002
D. Mancusi, R.J. Charity, J. Cugnon, Phys. Rev. C 82, 044610 (2010). https://doi.org/10.1103/PhysRevC.82.044610
H. Kramers, Physica 7(4), 284–304 (1940). https://doi.org/10.1016/S0031-8914(40)90098-2
H. Hofmann, J.R. Nix, Phys. Lett. B 122(2), 117–120 (1983). https://doi.org/10.1016/0370-2693(83)90776-1
B. Jurado et al., Nucl. Phys. A 747(1), 14–43 (2005). https://doi.org/10.1016/j.nuclphysa.2004.09.123
B. Jurado et al., Nucl. Phys. A 757(3), 329–348 (2005). https://doi.org/10.1016/j.nuclphysa.2005.04.020
A.V. Ignatyuk, G.N. Smirenkin, A.S. Tishin, Yad. Fiz. 21, 255–257 (1975)
A. Ignatyuk, G. Smirenkin, A. Tishin, Sov. J. Nucl. Phys. 21(3), 485–490 (1975)
J. Benlliure, J.L. Rodríguez-Sánchez, Eur. Phys. J. Plus 132(3), 120 (2017). https://doi.org/10.1140/epjp/i2017-11377-0
C. Paradela et al., Phys. Rev. C 82, 034601 (2010). https://doi.org/10.1103/PhysRevC.82.034601
D. Tarrío et al., Phys. Rev. C 83, 044620 (2011). https://doi.org/10.1103/PhysRevC.83.044620
Y. Watanabe et al., J. Korean Phys. Soc. 59, 1040–1045 (2011). https://doi.org/10.3938/jkps.59.1040
S. Lo Meo et al., Nucl. Phys. A 933, 43–67 (2015). https://doi.org/10.1016/j.nuclphysa.2014.09.040
C. Paradela et al., Phys. Rev. C 91, 024602 (2015). https://doi.org/10.1103/PhysRevC.91.024602
A.A. Kotov et al., Phys. Rev. C 74, 034605 (2006). https://doi.org/10.1103/PhysRevC.74.034605
I. Duran et al., EPJ Web Conf. 146, 02032 (2017). https://doi.org/10.1051/epjconf/201714602032
D. Tarrío et al., Nucl. Data Sheets 119, 35–37 (2014). https://doi.org/10.1016/j.nds.2014.08.011
E. Leal-Cidoncha et al., EPJ Web Conf. 111, 10002 (2016). https://doi.org/10.1051/epjconf/201611110002
R. Pachauri, L. Meyer, In Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) (2014). www.ipcc.ch/report/ar5/syr/
International Energy Agency (IEA), Renewables in Global Energy Supply (2018). http://webstore.iea.org/key-world-energy-statistics-2018
International Atomic Energy Agency, Power Reactor Information System (2018). www.iaea.org/PRIS/
Generation-IV International Forum (2011). www.gen-4.org
F. Goldner, R. Versluis, Transmutation capabilities of Generation 4 Reactors (2007). inis.iaea.org/search/search.aspx?orig_q=RN:39088792
OECD, NEA, Accelerator-driven Systems (ADS) and Fast Reactors (FR) in Advanced Nuclear Fuel Cycles (2002). www.oecd-nea.org/ndd/reports/2002/nea3109.html
A. Stanculescu, Ann. Nucl. Energy 62, 607–612 (2013). https://doi.org/10.1016/j.anucene.2013.02.006
The High Priority Request List (HPRL). www.oecd-nea.org/dbdata/hprl/
WPEC Subgroup 26, M. Salvatores (Coordinator), 6410 (NEA, Paris, 2008). www.nea.fr/html/science/wpec/volume26/volume26.pdf
N. Colonna et al., Energy Environ. Sci. 3, 1910–1917 (2010). https://doi.org/10.1039/C0EE00108B
F.-K. Thielemann et al., Annu. Rev. Nucl. Part. S. 67(1), 253–274 (2017). https://doi.org/10.1146/annurev-nucl-101916-123246
C. Winteler et al., Astrophys. J. 750, L22 (2012). https://doi.org/10.1088/2041-8205/750/1/l22
S. Goriely, Eur. Phys. J. A 51, 22 (2015). https://doi.org/10.1140/epja/i2015-15022-3
B.P. Abbott et al., Astrophys. J. 848(2), L12 (2017). https://doi.org/10.3847/2041-8213/aa91c9
E. Pian et al., Nature 551, 67 (2017). https://doi.org/10.1038/nature24298
J. Lippuner, L.F. Roberts, Astrophys. J. Suppl. S. 233, 18 (2017). https://doi.org/10.3847/1538-4365/aa94cb
S. Goriely, Astron. Astrophys. 342, 881 (1999). http://aa.springer.de/bibs/9342003/2300881/small.htm
S. Shibagaki et al., Astrophys. J. 816, 79 (2016). https://doi.org/10.1140/epja/i2013-13027-6
S. Goriely, G.M. Pinedo, Nucl. Phys. A 944, 158–176 (2015). https://doi.org/10.1016/j.nuclphysa.2015.07.020
M.-R. Mumpower et al., Astrophys. J. 869, 14 (2018). https://doi.org/10.3847/1538-4357/aaeaca
M. Eichler et al., Astrophys. J. 808(1), 30 (2015). https://doi.org/10.1088/0004-637x/808/1/30
Y. Zhu et al., Astrophys. J. Lett. 863, L23 (2018). https://doi.org/10.3847/2041-8213/aad5de
C. Rubbia et al., CERN-LHC-98-002-EET (CERN, Geneva, 1998). http://cds.cern.ch/record/357112
C. Guerrero et al., Eur. Phys. J. A 49(2), 27 (2013). https://doi.org/10.1140/epja/i2013-13027-6
M. Barbagallo et al., Eur. Phys. J. A 49(12), 156 (2013). https://doi.org/10.1140/epja/i2013-13156-x
C. Borcea et al., Nucl. Instrum. Methods A 513(3), 524–537 (2003). https://doi.org/10.1016/S0168-9002(03)02072-2
C. Weiss et al., Nucl. Instrum. Methods A 799, 90–98 (2015). https://doi.org/10.1016/j.nima.2015.07.027
S.L. Meo et al., Eur. Phys. J. A 51, 160–166 (2015). https://doi.org/10.1140/epja/i2015-15160-6
J. Lerendegui-Marco et al., Eur. Phys. J. A 52(4), 100 (2016). https://doi.org/10.1140/epja/i2016-16100-8
A. Ferrari et al., FLUKA: A multi-particle transport code (program version 2005), CERN. Geneva (2005). https://doi.org/10.5170/CERN-2005-010
G. Battistoni et al., Ann. Nucl. Energy 82, 10–18 (2015). https://doi.org/10.1016/j.anucene.2014.11.007
S. Agostinelli et al., Nucl. Instrum. Methods A 506(3), 250–303 (2003). https://doi.org/10.1016/S0168-9002(03)01368-8
J. Allison et al., IEEE Trans. Nucl. Sci. 53(1), 270–278 (2006). https://doi.org/10.1109/TNS.2006.869826
J. Allison et al., Nucl. Instrum. Methods A 835, 186–225 (2016). https://doi.org/10.1016/j.nima.2016.06.125
V. Vlachoudis et al., CERN EDMS No. 934369 (2012). edms.cern.ch/document/934369/0.13
U. Abbondanno et al., CERN-SL-2002-053-ECT (CERN, Geneva, 2003). cds.cern.ch/record/601511
F. Gunsing et al., Nucl. Instrum. Methods B 261(1), 925–929 (2007). https://doi.org/10.1016/j.nimb.2007.03.096
M. Sabaté-Gilarte et al., Eur. Phys. J. A 53(10), 210 (2017). https://doi.org/10.1140/epja/i2017-12392-4
A. Stamatopoulos et al., EPJ Web Conf. 146, 04030 (2017). https://doi.org/10.1051/epjconf/201714604030
A. Carlson et al., Nucl. Data Sheets 110, 3215 (2009). https://doi.org/10.1016/j.nds.2009.11.001
M. Calviani et al., Nucl. Instrum. Methods A 594(2), 220–227 (2008). https://doi.org/10.1016/j.nima.2008.06.006
D. Karadimos et al., Nucl. Instrum. Methods B 268(16), 2556–2562 (2010). https://doi.org/10.1016/j.nimb.2010.05.006
F. Belloni et al., Eur. Phys. J. A 47(1), 2 (2011). https://doi.org/10.1140/epja/i2011-11002-y
M. Calviani et al., Phys. Rev. C 80, 044604 (2009). https://doi.org/10.1103/PhysRevC.80.044604
R. Sarmento et al., Phys. Rev. C 84, 044618 (2011). https://doi.org/10.1103/PhysRevC.84.044618
M. Diakaki et al., EPJ Web Conf. 111, 02002 (2016). https://doi.org/10.1051/epjconf/201611102002
M. Diakaki et al., Phys. Rev. C 93, 034614 (2016). https://doi.org/10.1103/PhysRevC.93.034614
F. Belloni et al., Eur. Phys. J. A 49(1), 2 (2013). https://doi.org/10.1140/epja/i2013-13002-3
F. Belloni et al., Eur. Phys. J. A 47(12), 160 (2011). https://doi.org/10.1140/epja/i2011-11160-x
M. Calviani et al., Phys. Rev. C 85, 034616 (2012). https://doi.org/10.1103/PhysRevC.85.034616
D. Tarrío et al., Nucl. Instrum. Methods A 743, 79 (2014). https://doi.org/10.1016/j.nima.2013.12.056
M. Fatyga et al., Phys. Rev. C 32, 1496–1505 (1985). https://doi.org/10.1103/PhysRevC.32.1496
L.S. Leong, Ph.D. thesis, Université Paris Sud (2013). cds.cern.ch/record/1644168
Y. Giomataris et al., Nucl. Instrum. Methods A 376(1), 29–35 (1996). https://doi.org/10.1016/0168-9002(96)00175-1
Y. Giomataris, Nucl. Instrum. Methods A 419(2–3), 239–250 (1998). https://doi.org/10.1016/S0168-9002(98)00865-1
I. Giomataris, ICFA Instrum. Bul. 19 (1999). www.slac.stanford.edu/pubs/icfa/fall99/paper1/paper1a.html
J. Pancin, Ph.D. thesis, Saclay, SPhT (2004). cds.cern.ch/record/1474098
S. Andriamonje et al., J. Instrum. 5(02), P02001 (2010). https://doi.org/10.1088/1748-0221/5/02/P02001
S. Andriamonje et al., J. Korean Phys. Soc. 59(23), 1597 (2011). https://doi.org/10.3938/jkps.59.1597
A. Tsinganis et al., In Fission cross section measurements for \(^{240}\)Pu, \(^{242}\)Pu: Deliverable 1.5 of the ANDES project, Ch. 3 (European Commission, Joint Research Centre, Belgium, 2013). https://doi.org/10.2787/81004
A. Tsinganis et al., Nucl. Data Sheets 119, 58–60 (2014). https://doi.org/10.1016/j.nds.2014.08.018
A. Tsinganis et al., EPJ Web Conf. 66, 03088 (2014). https://doi.org/10.1051/epjconf/20146603088
R. Vlastou et al., CERN-INTC-2017-009. INTC-P-493 (CERN, Geneva, 2017). http://cds.cern.ch/record/2241241
L. Audouin et al., CERN-INTC-2015-007. INTC-P-431 (CERN, Geneva, 2015). http://cds.cern.ch/record/1981292
A. Tsinganis et al., CERN-INTC-2017-008. INTC-P-492 (CERN, Geneva, 2017). http://cds.cern.ch/record/2241236
J. Praena et al., Phys. Rev. C 97, 064603 (2018). https://doi.org/10.1103/PhysRevC.97.064603
M. Diakaki et al., Nucl. Instrum. Methods A 903, 46–55 (2018). https://doi.org/10.1016/j.nima.2018.06.019
F. Gönnenwein, In Mass, Charge and Kinetic Energy of Fission Fragments (CRC, Boca Raton, 1991). inis.iaea.org/search/search.aspx?orig_q=RN:24065353
P. Armbruster et al., Nucl. Instrum. Methods 139, 213–222 (1976). https://doi.org/10.1016/0029-554X(76)90677-7
G. Fioni et al., Nucl. Instrum. Methods A 332(1), 175–180 (1993). https://doi.org/10.1016/0168-9002(93)90756-8
J. Terrell, Phys. Rev. 127(3), 880–904 (1962). https://doi.org/10.1103/PhysRev.127.880
S. Bennett et al., Nucl. Inst. Methods A, 162846 (2019). https://doi.org/10.1016/j.nima.2019.162846
R.W. Peelle, F.C. Maienschein, Phys. Rev. C 3(1), 373–390 (1971). https://doi.org/10.1103/PhysRevC.3.373
F. Pleasonton, R.L. Ferguson, H.W. Schmitt, Phys. Rev. C 6(3), 1023–1039 (1972). https://doi.org/10.1103/PhysRevC.6.1023
V.V. Verbinski, H. Weber, R.E. Sund, Phys. Rev. C 7(3), 1173–1185 (1973). https://doi.org/10.1103/PhysRevC.7.1173
A. Oberstedt et al., Phys. Rev. C 87, 051602 (2013). https://doi.org/10.1103/PhysRevC.87.051602
I. Stetcu et al., Phys. Rev. C 88, 044603 (2013). https://doi.org/10.1103/PhysRevC.88.044603
E. Murray et al., Nucl. Data Sheet 119, 217–220 (2014). https://doi.org/10.1016/j.nds.2014.08.060
C. Guerrero et al., Nucl. Instrum. Methods A 608(3), 424–433 (2009). https://doi.org/10.1016/j.nima.2009.07.025
C. Guerrero et al., Eur. Phys. J. A 48(3), 29 (2012). https://doi.org/10.1140/epja/i2012-12029-2
J. Balibrea, Ph.D. thesis, Universida Complutense de Madrid, Facultat de Ciencias Física, Departamento de Física Teórica II (2018). http://eprints.ucm.es/47661/1/T39925.pdf
J. Balibrea et al., Nucl. Data Sheets 119, 10–13 (2014). https://doi.org/10.1016/j.nds.2014.08.005
J. Balibrea-Correa et al., EPJ Web Conf. 146, 11021 (2017). https://doi.org/10.1051/epjconf/201714611021
J. Taieb et al., Nucl. Instrum. Methods A 833, 1–7 (2016). https://doi.org/10.1016/j.nima.2016.06.137
M. Bacak et al., EPJ Web Conf. 146, 03027 (2017). https://doi.org/10.1051/epjconf/201714603027
M. Bacak et al., EPJ Web Conf. 211, 03007 (2019). https://doi.org/10.1051/epjconf/201921103007
A. Carlson et al., NEANDC–305-U (IAEA, 1991). inis.iaea.org/search/search.aspx?orig_q=RN:23033175
A. Carlson et al., INDC(NDS)-368 (IAEA, 1997). www.nds.iaea.org/publications/indc/indc-nds-0368/
V. Dangendorf et al., Nucl. Instrum. Methods A 469(2), 205–215 (2001). https://doi.org/10.1016/S0168-9002(01)00767-7
D. Vanleeuw, G. Sibbens, A. Plompen, J. Radioanal. Nucl. Chem. 305(3), 957–962 (2015). https://doi.org/10.1007/s10967-015-4156-8
A. Manna et. al, In Proceedings of the European Nuclear Physics Conference (Bologna, 2018) (in press)
G. Sibbens et al., Target preparation for neutron-induced reaction measurements. Eur. Phys. J. A
G. Sibbens et al., Appl. Radiat. Isotopes 87, 229–232 (2014). https://doi.org/10.1016/j.apradiso.2013.11.061
G. Sibbens et al., AIP Conf. Proc. 1962(1), 030007 (2018). https://doi.org/10.1063/1.5035524
D. Vanleeuw et al., Preparation and characterization of \(^{10}\)B targets at JRC-Geel. Eur. Phys. J. A
G. Vanleeuw, D. Sibbens, A. Plompen, J. Radioanal. Nucl. Chem. 305, 957 (2015). https://doi.org/10.1007/s10967-015-4156-8
J. Heyse et al., J. Radioanal. Nucl. Chem. 299(2), 1055–1059 (2014). https://doi.org/10.1007/s10967-013-2716-3
G. Sibbens et al., J. Radioanal. Nucl. Chem. 299(2), 1093–1098 (2014). https://doi.org/10.1007/s10967-013-2668-7
G. Sibbens et al., EPJ Web Conf. 146, 03022 (2017). https://doi.org/10.1051/epjconf/201714603022
K. Eberhardt et al., AIP Conf. Proc. 1962(1), 030009 (2018). https://doi.org/10.1063/1.5035526
A. Vascon et al., J. Radioanal. Nucl. Chem. 299(2), 1085–1091 (2014). https://doi.org/10.1007/s10967-013-2631-7
P. Marini et al., Phys. Rev. C 96, 054604 (2017). https://doi.org/10.1103/PhysRevC.96.054604
G. Sibbens et al., Nucl. Instrum. Methods A 655(1), 47–52 (2011). https://doi.org/10.1016/j.nima.2011.06.018
D. Liebe et al., Nucl. Instrum. Methods A 590(1), 145–150 (2008). https://doi.org/10.1016/j.nima.2008.02.075
CASTOR website. http://castor.web.cern.ch
U. Abbondanno et al., Nucl. Instrum. Methods A 538(1–3), 692–702 (2005). https://doi.org/10.1016/j.nima.2004.09.002
P. Žugec et al., Nucl. Instrum. Methods A 812, 134–144 (2016). https://doi.org/10.1016/j.nima.2015.12.054
A. Stamatopoulos et al., Nucl. Instrum. Methods A 913, 40–47 (2019). https://doi.org/10.1016/j.nima.2018.10.032
A. Tsinganis, Ph.D. thesis, Dept. of Physics, National Technical University of Athens (2014). http://cds.cern.ch/record/2248465
F. Belloni et al., Nucl. Data Sheets 119, 365–367 (2014). https://doi.org/10.1016/j.nds.2014.08.100
GEF code website. www.cenbg.in2p3.fr/-GEF-
K.-H. Schmidt, B. Jurado, General model description of fission observables, www.cenbg.in2p3.fr/IMG/pdf_final_efnudat_report2.pdf
R. Veenhof, GARFIELD: Simulation of Gas Detectors. http://garfield.web.cern.ch
N. Otuka et al., Nucl. Data Sheets 120, 272–276 (2014). https://doi.org/10.1016/j.nds.2014.07.065
E. Dupont et al., EPJ Web Conf. 146, 07002 (2017). https://doi.org/10.1051/epjconf/201714607002
n_TOF Data Dissemination web page. twiki.cern.ch/NTOFPublic/DataDissemination
C. Carrapiço et al., Nucl. Instrum. Methods A 704, 60–67 (2013). https://doi.org/10.1016/j.nima.2012.11.082
L. Audouin et al., In Proceedings of the International Conference on Nuclear Data for Science and Technology (EDP Sciences, Nice, 2007), pp. 421–424. https://doi.org/10.1051/ndata:07675
D. Tarrío et al., Measurement of the neutron-induced fission cross section of \(^{232}\)Th and \(^{233}\)U using PPACs at the CERN n_TOF facility (2020) (in preparation)
E. Leal-Cidoncha et al., Nucl. Data Sheets 119, 42–44 (2014). https://doi.org/10.1016/j.nds.2014.08.013
M. Barbagallo, CERN-INTC-2014-048. INTC-P-416 (CERN, Geneva, 2014). http://cds.cern.ch/record/1706674
S. Amaducci et al., Eur. Phys. J. A 55(7), 120 (2019). https://doi.org/10.1140/epja/i2019-12802-7
IAEA standards website. www.nds.iaea.org/standards/
C. Paradela et al., EPJ Web Conf. 111, 02003 (2016). https://doi.org/10.1051/epjconf/201611102003
E. Leal-Cidoncha et al., EPJ Web Conf. 146, 04057 (2017). https://doi.org/10.1051/epjconf/201714604057
B. Marcinkevicius, S. Simakov, V. Pronyaev, INDC(NDS)-0681 (IAEA, Vienna, 2015). www.nds.iaea.org/publications/indc/indc-nds-0681.pdf
M. Mastromarco, Ph.D. thesis, Universitá di Bari (2014). www.infn.it/thesis/thesis_dettaglio.php?tid=9196
A. Stamatopoulos, Ph.D. thesis, Dept. of Physics, National Technical University of Athens (2019). www.didaktorika.gr/eadd/handle/10442/45573?locale=en
F. Tovesson et al., Phys. Rev. C 79, 014613 (2009). https://doi.org/10.1103/PhysRevC.79.014613
R. Vandenbosch, Phys. Rev. C 7, 2092–2097 (1973). https://doi.org/10.1103/PhysRevC.7.2092
A. Goverdovski, In Proceedings of the Workshop on Nuclear Reaction Data and Nuclear Reactors: Physics, Design and Safety, Trieste, Italy (ICTP, Trieste, 2002) p. 034601. http://cds.cern.ch/record/515280
L. Tassan-Got et al., EPJ Web Conf. 211, 03006 (2019). https://doi.org/10.1051/epjconf/201921103006
R. Haas et al., Nucl. Instrum. Methods A 874, 43–49 (2017). https://doi.org/10.1016/j.nima.2017.08.027
Author information
Authors and Affiliations
Consortia
Corresponding author
Additional information
Communicated by N. Alamanos
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Colonna, N., Tsinganis, A., Vlastou, R. et al. The fission experimental programme at the CERN n_TOF facility: status and perspectives. Eur. Phys. J. A 56, 48 (2020). https://doi.org/10.1140/epja/s10050-020-00037-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-020-00037-8