Abstract
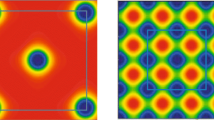
When skyrmions representing nucleons are put on crystal lattice and compressed to simulate high density, there is a transition above the normal nuclear matter density (n0) from a matter consisting of skyrmions with integer baryon charge to a state of half-skyrmions with half-integer baryon charge. We exploit this observation in an effective field theory framework to access dense baryonic system. We find that the topology change involved in the transition implies changeover from a Fermi liquid structure to a non-Fermi liquid with the chiral condensate in the “melted-off” nucleon. The ∼ 80% of the nucleon mass that remains “unmelted”, invariant under chiral transformation, points to the possible origin of the (bulk of) proton mass that is not encoded in the standard mechanism of spontaneously broken chiral symmetry. The topology change engenders a drastic modification of the nuclear tensor forces, thereby non-trivially affecting the EoS, in particular, the symmetry energy, for compact star matter. It brings in stiffening of the EoS needed to accommodate a neutron star of ∼ 2 solar mass. The strong effect on the EoS in general and in the tensor force structure in particular will also have impact on processes that could be measured at RIB-type accelerators.
Similar content being viewed by others
References
S. Lee (Editor), From Nuclei to Stars: Festschrift in Honor of Gerald E. Brown (World Scientific, Singapore, 2011).
G.E. Brown, M. Rho, Phys. Lett. B 237, 3 (1990).
T. Skyrme, Nucl. Phys. 9, 615 (1959).
B.D. Serot, J.D. Walecka, Int. J. Mod. Phys. E 6, 515 (1997).
T. Matsui, Nucl. Phys. A 370, 365 (1981).
G. Gelmini, B. Ritzi, Phys. Lett. B 357, 431 (1995).
T.-S. Park, D.-P. Min, M. Rho, Nucl. Phys. A 596, 515 (1996).
R. Shankar, Rev. Mod. Phys. 66, 129 (1994).
J. Polchinski, in Boulder 1992, Proceedings, Recent directions in particle theory, pp. 235-274, and Calif. Univ. Santa Barbara - NSF-ITP-92-132 (92, rec. Nov.) p. 39 (220633) Texas Univ. Austin - UTTG-92-20 (92, rec. Nov.) p. 39.
C. Song, G.E. Brown, D.-P. Min, M. Rho, Phys. Rev. C 56, 2244 (1997).
C. Song, Phys. Rep. 347, 289 (2001).
T. Niksic, D. Vretenar, P. Ring, Prog. Part. Nucl. Phys. 66, 519 (2011).
H.K. Lee, M. Rho, arXiv:1301.0067 [nucl-th].
G.E. Brown, M. Rho (Editors), The Multifaceted Skyrmion (World Scientific, Singapore, 2011).
A.D. Shapere, F. Wilczek, Z. Xiong, arXiv:1210.3545 [hep-th].
M. Harada, K. Yamawaki, Phys. Rep. 381, 1 (2003).
T. Sakai, S. Sugimoto, Prog. Theor. Phys. 113, 843 (2005).
T. Sakai, S. Sugimoto, Prog. Theor. Phys. 114, 1083 (2005).
D.K. Hong, M. Rho, H.-U. Yee, P. Yi, Phys. Rev. D 76, 061901 (2007).
D.K. Hong, M. Rho, H.-U. Yee, P. Yi, JHEP 09, 063 (2007).
K. Hashimoto, T. Sakai, S. Sugimoto, Prog. Theor. Phys. 120, 1093 (2008).
Y.-L. Ma, Y. Oh, G.-S. Yang, M. Harada, H.K. Lee, B.-Y. Park, M. Rho, Phys. Rev. D 82, 074025 (2012).
Y.-L. Ma, G.-S. Yang, Y. Oh, M. Harada, Phys. Rev. D 87, 034023 (2013).
D.T. Son, M.A. Stephanov, Phys. Rev. D 69, 065020 (2004).
A.S. Goldhaber, N.S. Manton, Phys. Lett. B 198, 231 (1987).
N. Manton, P. Sutcliffe, Topological Solitons (Cambridge University Press, 2004).
B.-Y. Park, V. Vento, in The Multifaceted Skyrmion, edited by G.E. Brown, M. Rho (World Scientific, Singapore, 2011).
H. Dong, T.T.S. Kuo, H.K. Lee, R. Machleidt, M. Rho, Phys. Rev. C 87, 054332 (2013).
R.A. Battye, N.S. Manton, P.M. Sutcliffe, in The Multifaceted Skyrmion, edited by G.E. Brown, M. Rho (World Scientific, Singapore, 2011).
Y.-L. Ma, M. Harada, H.K. Lee, Y. Oh, B.-Y. Park, M. Rho, Phys.Rev. D 88, 014016 (2013).
W.-G. Paeng, H.K. Lee, M. Rho, C. Sasaki, arXiv:1303.2898 [nucl-th].
G.E. Brown, M. Rho, Phys. Rev. Lett. 66, 2720 (1991).
H.K. Lee, M. Rho, Int. J. Mod. Phys. E 22, 1330005 (2013).
G.E. Brown, R. Machleidt, Phys. Rev. C 50, 1731 (1994).
C. Xu, B.-A. Li, arXiv:1104.2075 [nucl-th].
I. Vidana, A. Polls, C. Providencia, Phys. Rev. C 84, 062801 (2011).
H.K. Lee, B.-Y. Park, M. Rho, Phys. Rev. C 83, 025206 (2011) C 84.
R. Ritz et al., Nature 497, 231 (2013).
C.E. DeTar, T. Kunihiro, Phys. Rev. D 39, 2805 (1989).
W.-G. Paeng, H.K. Lee, M. Rho, C. Sasaki, Phys. Rev. D 85, 054022 (2012).
S. Weinberg, Phys. Rev. Lett. 105, 261601 (2010).
G.E. Brown, M. Rho, Phys. Lett. B 82, 177 (1979).
G.E. Brown, M. Rho, V. Vento, Phys. Lett. B 84, 383 (1979).
M. Rho, A.S. Goldhaber, G.E. Brown, Phys. Rev. Lett. 51, 747 (1983).
D.B. Kaplan, arXiv:1306.5818 [nucl-th].
N. Tsunoda, T. Otsuka, K. Tsukiyama, M. Hjorth-Jensen, Phys. Rev. C 84, 044322 (2011).
T. Otsuka, T. Suzuki, R. Fujimoto, H. Grawe, Y. Akaishi, Phys. Rev. Lett. 95, 232502 (2005).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Ramos
We dedicate this paper, prepared for a contribution to the EPJA Topical Issue “Nuclear Symmetry Energy”, to Gerry Brown.
Contribution to the Topical Issue “Nuclear Symmetry Energy” edited by Bao-An Li, Ángels Ramos, Giuseppe Verde, Isaac Vidaña.
Rights and permissions
About this article
Cite this article
Lee, H.K., Rho, M. Topology change and tensor forces for the EoS of dense baryonic matter. Eur. Phys. J. A 50, 14 (2014). https://doi.org/10.1140/epja/i2014-14014-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/i2014-14014-1