Skip to main content
SpringerLink
Log in

Aspects of Computer Simulation of Transport and Cleaning Processes from Cuttings in Horizontal Well Sections

  • Published:
Mathematical Models and Computer Simulations Aims and scope

Abstract

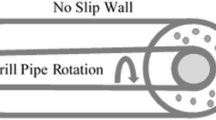
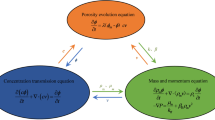
The relevance of this study is related to the need to form clear ideas about the factors involved in successful drilling operations and make a number of generalizations to existing methods for predicting the transport and cleaning of wells with a horizontal section, taking into account the features and patterns of the flow of drilling fluids in real drilling modes. The aim of this paper is to study the features of the spatial flow of a mixture of drilling fluid with solid particles in the coaxial and eccentric areas of the well; establish the patterns of the developing steady flow of the mixture through the well; and issue recommendations for applied calculations to improve the process of cleaning wells by using hydraulic methods. A well with a 12-meter horizontal eccentric section is chosen as the object of study, in which the flow is carried out in conditions that are as close as possible to actual drilling parameters. The methods of the mechanics of inhomogeneous continuums for viscous homogeneous and heterogeneous mixtures and computational fluid dynamics (CFD) combined with the ideas of a complex physical, mathematical, and numerical study of the internal flows of rheologically complex viscous media are the universal key to understanding the features and identifying the patterns of the processes considered in this study. It is established that particles can significantly affect the structure of the averaged and pulsating flow of a liquid droplet and their settling leads to the formation of an inhomogeneous anisotropic flow structure, the calculation of which requires modern two parameter turbulence models for Reynolds stresses. It is shown that in the bottom region of the annular space there is a zone with equivalent phase velocities, where the effects of a decrease in the intensity of molar transfer are manifested with an increase in the size of the sediment layer. The real drilling conditions are characterized by processes that accompany laminarization and stabilization of the mixture flow along the entire length of the well, and near the boundary of the fixed layer of settled particles, a narrow layer of their suspended state is formed. Moreover, the flow of particles of cuttings from the reservoir surface and their transition to a suspended state are mainly determined by convection-diffusion mechanisms, the intensity of the pulsating small-scale movement of vortices with an anisotropic structure, and the presence of local areas with moderately high flow velocities in contact with a curvilinear surface unstable to small disturbances of the section. The conditions for the formation of a stagnant zone in which sedimentation and growth in the size of deposits are intense are noted. In practice, a technology and algorithm for modeling the process of the interaction of two-phase flows with the walls of an eccentric pipe, based on demonstrations of CFD capabilities, is recommended. In addition, conclusions are made on improving the criterion relationships for determining the minimum flow rates of the drilling fluid, taking into account the correction of parameters characterizing the rheological features of the mixture, the intensity of turbulence, and the geometry of the annular space and connecting nodes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.

Similar content being viewed by others

REFERENCES

  1. S. N. Kharlamov and D. S. Fatyanov, “Investigation of natural raw materials turbulent flow structure in pipelines at confuser-diffuser section,” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 331 (8), 53–67 (2020). https://doi.org/10.18799/24131830/2020/8/2768

  2. S. N. Kharlamov and D. S. Fatyanov, “Simulation of viscous media spatial flows in the system of channels with sections of complex form junctions,” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 332 (5), 70–88 (2021). https://doi.org/10.18799/24131830/2021/5/3187

  3. S. N. Kharlamov, M. Janghorbani, and K. A. Filippov, “Mathematical modeling and research methods of horizontal wells hydrodynamic cleaning,” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 332 (8), 53–73 (2021). https://doi.org/10.18799/24131830/2021/8/3305

  4. S. N. Kharlamov and M. Janghorbani, “Numerical modeling of the currents of viscous mixtures of drilling sludge and the flow of crude oil on horizontal sections of wells with eccentric drilling pipes,” in New Challenges of Basic and Applied Geology of Oil and Gas — XXI Century: Proc. All-Russian Scientific Conference with the participation of foreign scientists, dedicated to the 150th Anniversary of Academician I. M. Gubkin and the 110th Anniversary of Academician A. A. Trofimuk (Novosib. Gos. Univ., Novosibirsk, 2021), pp. 221–224 [in Russian]. https://doi.org/10.25205/978-5-4437-1248-2-221-224

  5. S. N. Kharlamov and M. Janghorbani, “Numerical simulation of viscous-inertial laminar swirling flow in a circular tube with an eccentric round core,” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 332 (11), 7–21 (2021). https://doi.org/10.18799/24131830/2021/11/3423

  6. H. I. Bilgesu, M. W. Ali, K. Aminian, and S. Ameri, “Computational Fluid Dynamics (CFD) as a tool to study cutting transport in wellbores,” in SPE Eastern Regional Meeting (Lexington, KY, USA, October 2002), Paper SPE-78716-MS (Soc. Pet. Eng., 2002). https://doi.org/10.2118/78716-MS

  7. S.-M. Han, Y.-K. Hwang., N.-S. Woo, and Y.-J. Kim, “Solid–liquid hydrodynamics in a slim hole drilling annulus,” J. Pet. Sci. Eng. 70 (3–4), 308–319 (2010). https://doi.org/10.1016/j.petrol.2009.12.002

    Article  Google Scholar 

  8. U. Mme and P. Skalle, “CFD calculations of cuttings transport through drilling annuli at various angles,” Int. J. Pet. Sci. Technol. 6 (2), 129–141 (2012).

    Google Scholar 

  9. X.-H. Z., C. Sun, and H. Tong, “Distribution features, transport mechanism and destruction of cuttings bed in horizontal well,” J. Hydrodyn. 25 (4), 628–638 (2013). https://doi.org/10.1016/S1001-6058(11)60405-9

    Article  Google Scholar 

  10. X. Sun, K. Wang, T. Yan, S. Shao, and J. Jiao, “Effect of drillpipe rotation on cuttings transport using computational fluid dynamics (CFD) in complex structure wells,” J. Pet. Explor. Prod. Technol. 4 (3), 255–261 (2014). https://doi.org/10.1007/s13202-014-0118-x

    Article  Google Scholar 

  11. Ya. Demiralp, “Effects of drill-pipe whirling motion on cuttings transport performance for horizontal drilling,” MSc Thesis (Louisiana State University, 2014).

  12. T. N. Ofei, S. Irawan, and W. Pao, “CFD method for predicting annular pressure losses and cuttings concentration in eccentric horizontal wells,” J. Pet. Eng. 2014, 486423 (2014). https://doi.org/10.1155/2014/486423

    Article  Google Scholar 

  13. T. N. Ofei and S. A. Alhemyari, “Computational fluid dynamics simulation of the effect of drill pipe rotation on cuttings transport in horizontal wellbores using a Newtonian fluid,” in 2015 International Field Exploration and Development Conference (IFEDC 2015) (Xi’an, China, 2015), pp. 1–8. https://doi.org/10.1049/cp.2015.0582

  14. T. N. Ofei, “Effect of yield power law fluid rheological properties on cuttings transport in eccentric horizontal narrow annulus,” J. Fluids 2016, 4931426 (2016). https://doi.org/10.1155/2016/4931426

    Article  Google Scholar 

  15. M. Kamyab and V. Rasouli, “Experimental and numerical simulation of cuttings transportation in coiled tubing drilling,” J. Nat. Gas Sci. Eng. 29, 284–302 (2016). https://doi.org/10.1016/j.jngse.2015.11.022

    Article  Google Scholar 

  16. S. Sayindla, B. Lund, J. D. Ytrehus, and A. Saasen, “Hole-cleaning performance comparison of oil-based and water-based drilling fluids,” J. Pet. Sci. Eng. 159, 49–57 (2017). https://doi.org/10.1016/j.petrol.2017.08.069

    Article  Google Scholar 

  17. O. Heydari, E. Sahraei, and P. Skalle, “Investigating the impact of drillpipe’s rotation and eccentricity on cuttings transport phenomenon in various horizontal annuluses using computational fluid dynamics (CFD),” J. Pet. Sci. Eng. 156, 801–813 (2017). https://doi.org/10.1016/j.petrol.2017.06.059

    Article  Google Scholar 

  18. S. N. Kharlamov, V. Yu. Kim, and S. I. Silvestrov, “Numerical modeling of a vortical investigation of heat transfer in fields of centrifugal mass forces in elements of the power equipment with a curvilinear wall,” in Proc. 5th International Forum on Strategic Technology (IFOST 2011) (Ulsan, South Korea, October 2010), pp. 105–109. https://doi.org/10.1109/IFOST.2010.5667992

  19. F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications,” AIAA J. 32 (8), 1598–1605 (1994). https://doi.org/10.2514/3.12149

    Article  Google Scholar 

  20. E. I. Epelle and D. I. Gerogiorgis, “Transient and steady state analysis of drill cuttings transport phenomena under turbulent conditions,” Chem. Eng. Res. Design 131, 520–544 (2018). https://doi.org/10.1016/j.cherd.2017.11.023

    Article  Google Scholar 

  21. E. I. Epelle and D. I. Gerogiorgis, “CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle sphericity,” J. Pet. Sci. Eng. 170, 992–1004 (2018). https://doi.org/10.1016/j.petrol.2018.06.041

    Article  Google Scholar 

  22. M. Syamlal and T. J. O’Brien, “The derivation of a drag coefficient formula from velocity-voidage correlations,” Technical Note (US Department of Energy, Office of Fossil Energy, NETL, Morgantown, WV, 1987).

  23. D. Gidaspow, Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions (Academic Press, San Diego, 1994).

    MATH  Google Scholar 

  24. S. Akhshik and M. Rajabi, “CFD-DEM modeling of cuttings transport in underbalanced drilling considering aerated mud effects and downhole conditions,” J. Pet. Sci. Eng. 160, 229–246 (2018). https://doi.org/10.1016/j.petrol.2017.05.012

    Article  Google Scholar 

  25. Y. Ignatenko, O. Bocharov, A. Gavrilov, and R. May, “Steady-state cuttings transport simulation in horizontal borehole annulus,” in ASME 2018 37th International Conference on Ocean, Offshore Mechanics and Arctic Engineering (Madrid, Spain, June 2018), vol. 8, p. OMAE2018-77266. https://doi.org/10.1115/OMAE2018-77266.

  26. B. Pang, S. Wang, G. Liu, X. Jiang, H. Lu, and Z. Li, “Numerical prediction of flow behavior of cuttings carried by Herschel–Bulkley fluids in horizontal well using kinetic theory of granular flow,” Powder Technol. 329, 386–398 (2018). https://doi.org/10.1016/j.powtec.2018.01.065

    Article  Google Scholar 

  27. B. Pang, S. Wang, X. Jiang, and H. Lu, “Effect of orbital motion of drill pipe on the transport of non-Newtonian fluid-cuttings mixture in horizontal drilling annulus,” J. Pet. Sci. Eng. 174, 201–215 (2019). https://doi.org/10.1016/j.petrol.2018.11.009

    Article  Google Scholar 

  28. R. I. Nigmatulin, Dynamics of Multiphase Media, Vol. 1 (Nauka, Moscow, 1987; Hemisphere / Taylor & Francis, New York, 1991).

  29. G. H. Yeoh and J. Tu, Computational Techniques for Multiphase Flows (Butterworth-Heinemann / Elsevier, New York, 2010).

    Google Scholar 

  30. C. T. Crowe, “Review–numerical models for dulite gas-particle flows,” ASME J. Fluids Eng. 104 (3), 297–303 (1982). https://doi.org/10.1115/1.3241835

    Article  Google Scholar 

  31. S. N. Kharlamov, N. S. Kudelin, and P. O. Dedeyev, “Hydrodynamic, heat and acoustic processes modelling in transport of rheologically complex viscous media technology in pipelines,” IOP Conf. Ser.: Earth Environ. Sci. 21, 012040 (2014). https://doi.org/10.1088/1755-1315/21/1/012040

  32. S. N. Kharlamov, V. Yu. Kim, S. I. Silvestrov, R. A. Alginov, and S. A. Pavlov, “Prospects of RANS models with effects multiparameter at modeling of complex non-isothermal flows of viscous media in devices with any configuration of surface,” in Proc. 6th International Forum on Strategic Technology (IFOST 2011) (Harbin, China, 2011), vol. 2, pp. 787–791. https://doi.org/10.1109/IFOST.2011.6021139.

  33. B. E Launder., “On the computation of convective heat transfer in complex turbulent flows,” J. Heat Transfer 110, 1112–1128 (1988). https://doi.org/10.1115/1.3250614

    Article  Google Scholar 

  34. W. L. Chen, F. S. Lien, and M. A. Leschziner, “Computational modelling of turbulent flow in turbomachine passage with low-Re two-equation models,” in Computational Fluid Dynamics’94: Proc. 2nd European Computational Fluid Dynamics Conference (ECCOMAS CFD) (Stuttgart, Germany, 1994), Ed. by S. Wagner et al. (Wiley, Chichester, 1994), pp. 517–524.

  35. A. M. Bubenchikov and S. N. Kharlamov, Mathematical Models of Inhomogeneous Anisotropic Turbulence in Internal Flows (Tomsk. Gos. Univ., Tomsk, 2001) [in Russian].

    Google Scholar 

  36. H. Miloshevich, “Modelling of two-phased turbulent flows in jets with burning particles and phase transition in them,” Computational Fluid Dynamics’98: Proc. 4th European Computational Fluid Dynamics Conference (ECC-OMAS CFD) (Athens, Greece, 1998), Ed. by K. D. Papailiou et al., (Wiley, Chichester, 1998), vol. 1, part 1, pp. 175–179.

  37. M. Di Giacinto, F. Sabetta, and R. Piva, “Two-way coupling effects in dilute gas-particle flows,” Trans. ASME, Ser. D: J. Fluids Eng. 104 (3), 304–311 (1982). https://doi.org/10.1115/1.3241836

    Article  Google Scholar 

  38. S. A. Morsi and A. J. Alexander, “An investigation of particle trajectories in two-phase flow systems,” J. Fluid Mech. 55 (2), 193–208 (1972). https://doi.org/10.1017/S0022112072001806

    Article  MATH  Google Scholar 

  39. S. V. Patankar and D. B. Spalding, “A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows,” Int. J. Heat Mass Transfer 15 (10), 1787–1806 (1972). https://doi.org/10.1016/0017-9310(72)90054-3

    Article  MATH  Google Scholar 

  40. J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics: With Special Applications to Particular Media (Prentice-Hall, Englewood Cliffs, NJ, 1965).

    MATH  Google Scholar 

  41. N. A. V. Piercy, M. S. Hooper, and H. F. Winney, “Viscous flow through pipes with cores,” London, Edinburgh, Dublin Philos. Mag. J. Sci. 15 (99), 647–676 (1933). https://doi.org/10.1080/14786443309462212

    Article  MATH  Google Scholar 

  42. R. I. Shishenko, B. I. Es’man, and P. I. Kondratenko, Hydraulics of Drilling Fluids (Nedra, Moscow, 1976) [in Russian].

    Google Scholar 

  43. B. Guo and G. Liu, Applied Drilling Circulation Systems: Hydraulics, Calculations and Models (Gulf Professional Publishing / Elsevier, Burlington, MA, 2011). https://doi.org/10.1016/C2009-0-30657-1

  44. Pressure drop in piping elements (Software-Factory H. Schmitz, Schifferstadt, Germany). http://www.druckverlust.de/Online-Rechner

  45. V. Dokhani, Y. Ma, Z. Li, T. Geng, and M. Yu, “Effects of drill string eccentricity on frictional pressure losses in annuli,” J. Pet. Sci. Eng. 187, 106853, 1–12 (2020). https://doi.org/10.1016/j.petrol.2019.106853

    Article  Google Scholar 

  46. E. V. Podryabinkin and V. Ya. Rudyak, “Modeling of turbulent annular flows of Hershel–Bulkley fluids with eccentricity and inner cylinder rotation,” J. Eng. Thermophys. 23 (2), 137–147 (2014). https://doi.org/10.1134/S1810232814020064

    Article  Google Scholar 

  47. Y. Hashemian, M. Yu, S. Miska, S. Shirazi, and R. Ahmed, “Accurate predictions of velocity profiles and frictional pressure losses in annular YPL-fluid flow,” J. Can. Pet. Technol. 53 (6), 355–363 (2014). https://doi.org/10.2118/173181-PA

    Article  Google Scholar 

  48. A. A. Schrayber, L. B. Gavin, and V. A. Naumov, Turbulent Gas Suspension Flows (Naukova Dumka, Kiev, 1987) [in Russian].

    Google Scholar 

  49. S. Santos Costa, S. Stuckenbruck, S. A. B da Fontoura, and A. L. Martins, “Simulation of transient cuttings transportation and ECD in wellbore drilling,” in Europec/EAGE Conference and Exhibition (Soc. Pet. Eng., 2008), p. SPE-113893-MS. https://doi.org/10.2118/113893-MS

  50. H. Grutzner, Beitrage zur Theoretischen und Experuncntellen Untersuchung der Turbulenz (Akademic, Berlin, 1976).

    Google Scholar 

  51. A. R. Barbin and J. B. Jones, “Turbulent flow in the inlet region of a smooth pipe,” ASME J. Basic Eng. 85 (1), 29–33 (1963). https://doi.org/10.1115/1.3656521

    Article  Google Scholar 

  52. A. Busch, “On particle transport and turbulence in wellbore flows of non-Newtonian fluids-Findings from acuttings transport process analysis by means of computational fluid dynamics, rheometry and dimensional analysis,” PhD Thesis (Norwegian Univ. of Science and Technology, Trondheim, 2020).

  53. S. N. Kharlamov and M. Janghorbani, “Procedures and instruments for monitoring processes and mechanisms of cutting transport in hydraulic cleaning of horizontal wells,” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 331 (12), 22–40 (2020). https://doi.org/10.18799/24131830/2020/12/2936

  54. S. N. Kharlamov and M. Janghorbani, “Cuttings transport in hole cleaning considering well orientation, pipe eccentricity and pipe rotation: problems, results, prospects (survey),” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 331 (7), 131–149 (2020). https://doi.org/10.18799/24131830/2020/7/2725

  55. S. N. Kharlamov and R. A. Alginov, “Engineering approaches' progress in calculation of inhomogeneous turbulence in pipelines,” in Society of Petroleum Engineers – SPE Russian Oil and Gas Technical Conference and Exhibition (Moscow, Russia, October 2010), vol. 2, pp. 798–805. https://doi.org/10.2118/136292-MS

  56. A. A. Gavignet and I. J. Sobey, “Model aids cuttings transport prediction,” J. Pet. Technol. 41 (9), 916–921 (1989). https://doi.org/10.2118/15417-PA

    Article  Google Scholar 

  57. D. Nguyen and S. S. Rahman, “A three-layer hydraulic program for effective cuttings transport and hole cleaning in highly deviated and horizontal wells,” in SPE/IADC Asia Pacific Drilling Technology (Kuala Lumpur, Malaysia, September 1996) (Soc. Pet. Eng., 1996), pp. 1–15. https://doi.org/10.2118/36383-MS

  58. T. Esch and F. R. Menter, “Heat transfer predictions based on two-equation turbulence models with advanced wall treatment,” in Turbulence, Heat and Mass Transfer 4: Proc. 4th Int. Symposium (Antalya, Turkey, October 2003) (Begell House, New York, 2003), pp. 633–640.

  59. D. Mehta, A. K. T. Radhakrishnan, J. B. van Lier, and F. H. L. R. Clemens, “Assessment of numerical methods for estimating the wall shear stress in turbulent Herschel–Bulkley slurries in circular pipes,” J. Hydraul. Res. 59 (2), 196–213 (2021). https://doi.org/10.1080/00221686.2020.1744751

    Article  Google Scholar 

  60. S. N. Kharlamov and M. Janhorbani, “Optimization of rheological properties of drilling mud intensifying transportation and cleaning of horizontal wells from cuttings,” Izv. Tomsk. Politekh. Univ. Inzh. Georesur. 333 (8), 91–108 (2022). https://doi.org/10.18799/24131830/2022/8/3751

  61. O. Erge and E. van Oort, “Modeling the effects of drillstring eccentricity, pipe rotation and annular blockage on cuttings transport in deviated wells,” J. Nat. Gas Sci. Eng. 79, 103221 (2020). https://doi.org/10.1016/j.jngse.2020.103221

    Article  Google Scholar 

  62. H. Ferroudji, A. Hadjadj, A. Haddad, and T. N. Ofei, “Numerical study of parameters affecting pressure drop of power-law fluid in horizontal annulus for laminar and turbulent flows,” J. Pet. Explor. Prod. Technol. 9 (4), 3091–3101 (2019). https://doi.org/10.1007/s13202-019-0706-x

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National Research Tomsk Polytechnic University, Tomsk, Russia

    S. N. Kharlamov, M. Janghorbani & M. R. Bryskin

  2. Tomsk Branch, Gazprom Invest, Tomsk, Russia

    S. N. Kharlamov, M. Janghorbani & M. R. Bryskin

Authors
  1. S. N. Kharlamov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Janghorbani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. R. Bryskin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to S. N. Kharlamov, M. Janghorbani or M. R. Bryskin.

Ethics declarations

The authors declare that they have no conflicts of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kharlamov, S.N., Janghorbani, M. & Bryskin, M.R. Aspects of Computer Simulation of Transport and Cleaning Processes from Cuttings in Horizontal Well Sections. Math Models Comput Simul 15, 502–519 (2023). https://doi.org/10.1134/S2070048223030080

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S2070048223030080

Keywords:

Search

Navigation