Skip to main content
SpringerLink
Log in

Solving a second-order nonlinear singular perturbation ordinary differential equation by a Samarskii scheme

  • Published:
Numerical Analysis and Applications Aims and scope Submit manuscript

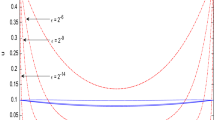
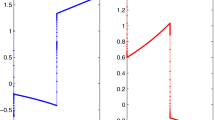
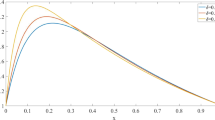
Abstract

A boundary value problem for a second-order nonlinear singular perturbation ordinary differential equation is considered. A method based on Newton and Picard linearizations using a modified Samarskii scheme on a Shishkin grid for a linear problem is proposed. It is proved that the difference schemes are of second-order and uniformly convergent. To decrease the number of arithmetic operations, a two-grid method is proposed. The results of some numerical experiments are discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ilyin, A.M., A Difference Scheme for a Differential Equation with a Small Parameter at the Highest Derivative, Mat. Zametki, 1969, vol. 6, no. 2, pp. 237–248.

    MathSciNet  Google Scholar 

  2. Bakhvalov, N.S., On Optimization of Methods to Solve Boundary Value Problems in the Presence of a Boundary Layer, Zh. Vych. Mat. Mat. Fiz., 1969, vol. 9, no. 4, pp. 841–859.

    MATH  Google Scholar 

  3. Shishkin, G.I., Setochnye approksimatsii singulyarno vozmushchyonnykh ellipticheskikh i parabolicheskikh uravnenii (Grid Approximations of Singular Perturbation Elliptic and Parabolic Equations), Yekaterinburg: UB RAS, 1992.

    Google Scholar 

  4. Farrell, P.A., Hegarty, A.F., Miller, J.J., O’Riordan, E., and Shishkin, G.I., Robust Computational Techniques for Boundary Layers, Boca Raton, FL: Chapman and Hall, CRC Press, 2000.

    MATH  Google Scholar 

  5. Bagayev, B.M., Karepova, E.D., and Shaidurov, V.V., Setochnye metody resheniya zadach s pogranichnym sloem, ch. 2 (Grid Methods to Solve Problems with a Boundary Layer. Part. 2), Novosibirsk: Nauka, 2001.

    Google Scholar 

  6. Shishkin, G.I., A High-Accuracy Method for a Quasi-Linear Singularly Perturbed Elliptic Convection-Diffusion Equation, Zh. Vych. Mat., 2006, vol. 9, no. 1, pp. 81–108.

    MATH  Google Scholar 

  7. Roos, H.-G., Stynes, M., and Tobiska, L., Numerical Methods for Singularly Perturbed Differential Equations. Convection-Diffusion and Flow Problems, Springer Ser. Comp. Math., vol. 24, Berlin: Springer-Verlag, 1996.

    Google Scholar 

  8. Andreev, V.B. and Savin, I.A., On the Convergence, Uniform with Respect to a Small Parameter, of A.A. Samarskii’s Monotone Scheme and Its Modifications, Zh. Vych. Mat. Mat. Fiz., 1995, vol. 35, no. 5, pp. 739–752.

    MathSciNet  Google Scholar 

  9. Vulanovic, R., A Uniform Numerical Method for Quasilinear Singular Perturbation Problems without Turning Points, Computing, 1989, vol. 41, pp. 97–106.

    Article  MathSciNet  MATH  Google Scholar 

  10. Vulkov, L.G. and Zadorin, A.I., Two-Grid Algorithms for an Ordinary Second Order Equation with Exponential Boundary Layer in the Solution, Int. J. Num. Anal. Model., 2010, vol. 7, no. 3, pp. 580–592.

    MathSciNet  MATH  Google Scholar 

  11. Zadorin, A.I., An Interpolation Method on a Condensing Grid for a Function with a Boundary Layer Component, Zh. Vych. Mat. Mat. Fiz., 2008, vol. 48, no. 9, pp. 1673–1684.

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Omsk Branch of Sobolev Institute of Mathematics, Siberian Branch, Russian Academy of Sciences, ul. Pevtsova 13, Omsk, 644099, Russia

    A. I. Zadorin & S. V. Tikhovskaya

Authors
  1. A. I. Zadorin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. V. Tikhovskaya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. I. Zadorin.

Additional information

Original Russian Text © A.I. Zadorin, S.V. Tikhovskaya, 2013, published in Sibirskii Zhurnal Vychislitel’noi Matematiki, 2013, Vol. 16, No. 1, pp. 11–25.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zadorin, A.I., Tikhovskaya, S.V. Solving a second-order nonlinear singular perturbation ordinary differential equation by a Samarskii scheme. Numer. Analys. Appl. 6, 9–23 (2013). https://doi.org/10.1134/S1995423913010023

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1995423913010023

Keywords

Search

Navigation