Abstract
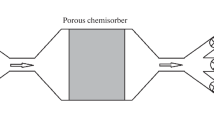
The work is devoted to the development of a multiscale approach for modeling multiphase liquid and gas flows in a porous medium. The problem of reprocessing organic fuels, including natural gas, has been chosen as an application. One of the important stages of such reprocessing is the purification of hydrocarbon raw materials from accompanying impurities (metal particles, solid organic compounds, etc.) in chemisorbers. To model treatment processes in such technical systems, a multiscale mathematical model is proposed that combines macroscopic and microscopic descriptions of multiphase fluid flows in a treatment system. The first part of the model refers to macroscopic scales and includes equations of gas and/or hydrodynamics for describing the multiphase multicomponent fluid flows, supplemented by convection-diffusion-reaction (CDR) equations for impurity concentrations. The second part of the model refers to microscopic scales and describes the processes in the boundary layers of the treatment system and in the pores. It is based on the equations of molecular dynamics and analytical chemistry. Both parts are conjugated within the method of splitting by physical processes. The work considers the problem of natural gas purification from hydrogen sulfide by passing contaminated fluid through a porous material. In it, the first part of the model is represented by quasistationary Navier–Stokes equations averaged over the volume. For their numerical implementation, an implicit grid algorithm implemented by Newton’s method is proposed. The CDR equations are solved according to an implicit time scheme. The second part of the model is represented by the dependencies of the permeability tensor components on porosity and impurity concentrations. The separate parts of the model have been calibrated in numerical experiments. In particular, model calculations of flows in a scrubber with a porous plug have been carried out. The calculations are performed using the FEniCS computing platform.






Similar content being viewed by others
REFERENCES
W. Strauss, Industrial Gas Cleaning (Pergamon, Oxford, 1966).
S. A. Akhmetov, Physical and Chemical Technology of Deep Processing of Oil and Gas (UGNTU, Ufa, 1997) [in Russian].
A. K. Manovyan, Technology of Primary Oil and Natural Gas Processing (Khimiya, Moscow, 2001) [in Russian].
N. V. Busygina and I. G. Busygin, Natural Gas and Gas Condensate Processing Technology (Gazprompechat, Orenburg, 2002) [in Russian].
J. G. Speight, Encyclopedia of Hydrocarbon Fuel Science and Technology (Wiley, New York, 2012), Vol. 1.
J. G. Speight, Encyclopedia of Hydrocarbon Fuel Science and Technology (Wiley, New York, 2012), Vol. 2.
A. Nag, Distillation and Hydrocarbon Processing Practices (PennWell Corp, Tulsa, Oklahoma, 2015).
J. G. Speight, Handbook of Petrochemical Processes (CRC, Boca Raton, FL, 2019).
M. L. Danzig, E. V. Turcheninova, G. A. Danzig, V. S. Sobolevsky, V. N. Menshov, V. V. Zhavoronkov, T. A. Kondrashchenko, and Z. E. Yermina, ‘‘Development of an industrial technology for the production of active zinc oxide for the production of desulfurization masses,’’ Khim. Prom-st’ 8, 30–32 (1980).
V. G. Ikonnikov, L. I. Titelman, G. A. Danzig, A. V. Obysov, and M. L. Danzig, ‘‘Experience in the preparation and industrial operation of molded zinc oxide absorbers for sulfur compounds,’’ Khim. Prom-st’ 9, 25–28 (1983).
M. Yumura and E. Furimsky, ‘‘Comparison of CaO, ZnO and Fe\({}_{2}\)O\({}_{3}\) as H\({}_{2}\)S adsorbent at high temperatures,’’ Ind. Eng. Chem. Process Des. Dev. 24, 1165–1168 (1985).
L. A. Fenouil, G. P. Towler, and S. Linn, ‘‘Removal of H\({}_{2}\)S from coal gas using limestone: Kinetic considerations,’’ Ind. Eng. Chem. Res. 33, 265–272 (1994).
V. I. Lazarev, ‘‘Methods for purifying natural gas from hydrogen sulfide with solid sorbents,’’ Nauch. Tekh. Asp. Zashch. Okruzh. Sredy 4, 84–113 (1999).
V. L. Hartmann, ‘‘Effect of sulphur removal catalyst granules properties on the commercial-scale bed macrokinetics,’’ Chem. Eng. J. 107, 39–43 (2005).
V. L. Hartmann, ‘‘Gas–solid reaction modeling as applied to the fine desulfurization of gaseous feedstocks,’’ Chem. Eng. J. 134, 190–194 (2007).
M. A. Berlin, V. G. Gorechenkov, and V. P. Kapralov, Qualified Primary Processing of Petroleum and Natural Hydrocarbon Gases (Sov. Kuban, Krasnodar, 2012) [in Russian].
S. V. Afanasyev, A. A. Sadovnikov, V. L. Hartmann, A. V. Obysov, and A. V. Dulnev, Industrial Catalysis in Gas Chemistry (RAS SamSC, Samara, 2018) [in Russian].
V. O. Podryga, S. V. Polyakov, and N. I. Tarasov, ‘‘Developing of multiscale approach to HPC-simulation of multiphase fluid flows,’’ Lobachevskii J. Math. 42, 2623–2633 (2021).
B. N. Chetverushkin, Kinetic Schemes and Quasi-Gas Dynamic System of Equations (CIMNE, Barcelona, 2008).
T. G. Elizarova, Quasi-Gas Dynamic Equations (Springer, Berlin, 2009).
S. Whitaker, The Method of Volume Averaging (Springer Science, Dordrecht, Netherlands, 1999).
D. A. Nield and A. Bejan, Convection in Porous Media (Springer Int., Cham, Switzerland, 2017).
FEniCS Project. https://fenicsproject.org/. Accessed 2022.
H. P. G. Darcy, Les Fontaines Publiques de la Ville de Dijon (Victor Dalmont Editeur, Paris, France, 1856).
H. C. Brinkman, ‘‘A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles,’’ Appl. Sci. Res. A 1, 2–34 (1947).
P. Forchheimer, ‘‘Wasserbewegung durch Boden,’’ Zeitschr. Verein. Deutsch. Ingen. 45, 1782–1788 (1901).
C. T. Hsu and P. Cheng, ‘‘Thermal dispersion in a porous medium,’’ Int. J. Heat Mass Transfer 33, 1587–1597 (1990).
P. Nithiarasu, K. N. Seetharamu, and T. Sundararajan, ‘‘Natural convective heat transfer in a fluid saturated variable porosity medium,’’ Int. J. Heat Mass Transfer 40, 3955–3967 (1997).
A. Tamayol and M. Bahrami, ‘‘In-plane gas permeability of proton exchange membrane fuel cell gas diffusion layers,’’ J. Power Sources 196, 3559–3564 (2011).
R. Eymard, T. R. Gallouet, and R. Herbin, ‘‘The finite volume method,’’ in Handbook of Numerical Analysis, Ed. by P. G. Ciarlet and J. L. Lions (North-Holland, Amsterdam, 2000), Vol. 7, pp. 713–1020.
Gmsh. https://gmsh.info/. Accessed 2022.
ParaView. https://www.paraview.org/. Accessed 2022.
TecPlot. https://www.tecplot.com/. Accessed 2022.
V. John, Finite Element Methods for Incompressible Flow Problems (Springer Int., Cham, Switzerland, 2016).
C. T. Kelley, Solving Nonlinear Equations with Newton’s Method (SIAM, Philadelphia, PA, 2003).
Funding
The work was supported by the Russian Foundation for Basic Research and National Science Foundation of Bulgaria (project no. 20-51-18004-Bolg_a). The work was supported by the Russian Foundation for Basic Research (project no. 19-31-90140_aspiranty).
Author information
Authors and Affiliations
Corresponding authors
Additional information
(Submitted by A. B. Muravnik)
Rights and permissions
About this article
Cite this article
Podryga, V.O., Churbanov, A.G., Tarasov, N.I. et al. Multiscale Approach for Modeling Multiphase Fluid Flows in Installations for Reprocessing of Natural Gas. Lobachevskii J Math 43, 1560–1571 (2022). https://doi.org/10.1134/S1995080222090219
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1995080222090219