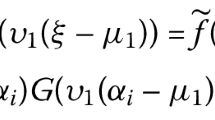Skip to main content
SpringerLink
Log in

Stable regimes of dynamic systems with impulsive influences

  • Published:
Lobachevskii Journal of Mathematics Aims and scope Submit manuscript

Abstract

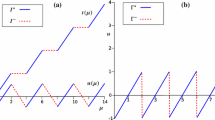
Let us consider a mathematical model of dynamic system, which is presented as a chain of three connected, singularly perturbed nonlinear differential equations. In the further text there were researched the questions of existence and stability of periodic solutions of this system due to a bifurcational analysis of special two-dimensional map. Also the special attention is paid to the number of coexisting stable regimes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. S. D. Glyzin, A. Yu. Kolesov, and N. Kh. Rozov, “Relaxation self-oscillations in neuron systems. II,” Differ. Equations 47, 1697–1713 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  2. S. D. Glyzin, A. Yu. Kolesov, and N. Kh. Rozov, “Relaxation self-oscillations in neuron systems. III,” Differ. Equations 48, 159–175 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  3. S. D. Glyzin, A. Yu. Kolesov, and N. Kh. Rozov, “Self-excited relaxation oscillations in networks of impulse neurons,” Russ. Math. Surv. 70, 383–452 (2015).

    Article  MATH  Google Scholar 

  4. S. D. Glyzin, A. Yu. Kolesov, and N. Kh. Rozov, “Self-excited wave processes in chains of unidirectionally coupled impulse neurons,” Model. Anal. Inform. Sist. 22, 404–419 (2015).

    Article  Google Scholar 

  5. S. D. Glyzin, A. Yu. Kolesov, and N. Kh. Rozov, “Self-sustained relaxation oscillations in time-delay neural systems,” J. Phys.: Conf. Ser. 727, 012004 (2016).

    MathSciNet  MATH  Google Scholar 

  6. L. I. Ivanovsky and S. O. Samsonov, “Dynamics of two-dimensional mapping and stable regimes of singularly perturbed neuron system,” in Computer Technologies in Natural Sciences. Methods of Simulations on Supercomputers, Collection of Articles, Ed. by R. R. Nazirov and L. N. Shchur (IKI RAN, Moscow, 2015), Vol. 2, pp. 121–132 [in Russian].

    Google Scholar 

  7. L. I. Ivanovsky, “Dynamic properties of one class of impulse systems,” in Computer Technologies in Natural Sciences. Methods of Simulations on Supercomputers, Collection of Articles, Ed. by R. R. Nazirov and L. N. Shchur (IKI RAN, Moscow, 2015), Vol. 3, pp. 126–131 [in Russian].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Yaroslavl State University, Yaroslavl, 150000, Russia

    L. I. Ivanovsky

  2. Scientific Center in Chernogolovka of Russian Academy of Sciences, Chernogolovka, Moscow oblast, 142432, Russia

    L. I. Ivanovsky

Authors
  1. L. I. Ivanovsky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. I. Ivanovsky.

Additional information

Submitted by A. M. Elizarov

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ivanovsky, L.I. Stable regimes of dynamic systems with impulsive influences. Lobachevskii J Math 38, 921–925 (2017). https://doi.org/10.1134/S199508021705016X

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S199508021705016X

Keywords and phrases

Search

Navigation