Pricing maturity guarantee under a refracted Brownian motion

Abstract

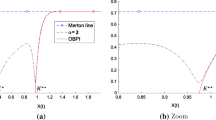
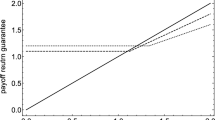
The cost of maturity minimum guarantee of an investment fund is typically deducted upfront or at the beginning of each period, together with other costs such as sales commissions and management fees. This practice gives a significant negative impact on the short term returns of the investment. In this paper, we propose a way to compensate the cost of investment guarantee by continuous withdrawals whenever the fund value stays below or at a predetermined threshold. The corresponding dynamics of fund price follows a (geometric) refracted Brownian motion, where the two drifts are state dependent. We derive integral formulas for the prices of fund and maturity minimum guarantee. Given the cost deduction threshold and the maturity guarantee level, the fair deduction rate can be determined numerically.